Introduction

Topological phase transitions in many materials can be described by a massive Dirac equation at a time reversal invariant momenta. When the energy gap closes and reopens, the mass term in the corresponding Dirac equation changes sign, which can be reflected by the evolution of Berry phase along the Fermi surface if the system is slightly doped1,2,3,4,5,6. Both the evolution of the band gap and the Berry phase can be probed in quantizing magnetic fields, where Shubnikov de Haas (SdH) oscillations from Landau level quantization provides a tool to probe “Fermiology”7,8,9,10,11. In addition to Landau level quantization, the Zeeman effect splits the spin-degenerate Landau levels. The difference in the Berry phases between the spin-split Landau levels plays a crucial rule in the SdH oscillations. Interestingly, while the Zeeman effect has been extensively studied over the past decades12,13, its connection to band topology and non-trivial Berry phase has emerged only recently. A Dirac band with a finite mass gap hosts spin-dependent Berry phase which can modify the SdH oscillations through the Zeeman effect, as recently demonstrated in the spin-zero effect14,15. Such a spin-dependent Berry phase is expected to be fundamentally generic for Dirac-like bands, and is band parameter dependent. It is therefore desirable to conduct a comprehensive study of such effect in a system with tunable band parameters.

Despite the significant developments in topological materials study in recent years, it remains a challenge to tune between different topological phases, and correspondingly the Berry phase, in the same material. Strain is a widely proposed mechanism for driving a topological phase transition16,17,18,19,20,21,22,23,24,25,26. And transition metal pentatelluride ZrTe5 is a promising material for such study. ZrTe5 is a van der Waals layered material with orthorhombic lattice structure, with layer planes extending along the a- and c- lattice directions and stacking along the b direction. Its electronic properties of is largely dominated by the Fermi surface centered around the Γ point with a Dirac dispersion, but can also have contribution from the parabolic side bands with Fermi surfaces centered between the R and E points in the Brillouin zone (see Supplementary Note 2). ZrTe5 hosts intriguing properties such as a resistance peak (Lifshitz transition)27,28,29, chiral magnetic effect30, and 3D quantum Hall effect31. In its 3D bulk form, ZrTe5 has a Dirac-like low energy band structure, with sample-dependent mass gap rendering the material from Dirac semimetal to topological insulator30,32,33,34,35,36, suggesting extreme sensitivity to lattice deformations. Recently a strain-induced weak topological insulator (WTI) to strong topolgical insulator (STI) transition has been proposed37,38, followed by experimental evidence in angle-resolved photoemission spectroscopy (ARPES) study39, and indirect charge transport evidences via the chiral anomaly effect40. A charge transport study of the quantum oscillations which directly map the topological phase transition is still lacking. Such bulk transport measurements would be complementary to the surface-sensitive ARPES study, and also reveal the spin-dependent Berry phase over tunable band parameters.

In this work, we study charge transport and SdH oscillations in ZrTe5 under tunable uniaxial strain. In a magnetic field perpendicular to the a–c plane and the applied current, SdH oscillations and their evolution over strain allow direct mapping of the WTI-STI transition through the closing and reopening of the Dirac band mass gap. The dependence of the SdH oscillation amplitude on the Fermi energy and Dirac mass gap, tunable through the strain, is analyzed and compared with the quantum oscillation theory. Our results reveal that the spin-dependent Berry phase intrinsic to the Dirac bands, which has been largely neglected in previous studies, is critical in modeling the SdH oscillations in such topological materials.

Results and discussion

Magnetotransport under tunable strain

The samples studied in this work are ZrTe5 microcrystals mechanically exfoliated onto flexible Polyimide substrates (Fig. 1a–c), which allow application of external tensile and compressive strains along the a-axis through substrate bending, over a wide temperature range from room temperature down to below 4K (see Methods: Sample fabrication and characterization, and Supplementary Note 3). Our ZrTe5 exhibits a strain-tunable resistance peak at Tp ≈ 140K(Fig. 1e). At T = 20K a non-monotonic resistance versus strain dependence is observed (Fig. 1f), consistent with the report in macroscopic ZrTe5 crystals40. A large strain gauge factor ranging 102−103 generally presents throughout the temperature range up to room temperature. The gauge factor observed here is very large compared to that of the metal thin films (~2), and is comparable to typical single crystal semiconductors such as Si and Ge (~100). The large gauge factor manifests a strain-sensitive band structure and a small Fermi surface.

Fig. 1: ZrTe5 under strain.
figure 1

a Crystal structure of ZrTe5. b Optical microscope image of ZrTe5 microcrystal on Polyimide substrate with predefined current and voltage electrodes. c Atomic force microscope image of the sample. d The cross section of the ZrTe5 crystal, with a thickness of ~190 nm. e Resistance versus temperature dependence under various external strains. f Non-monotonic strain dependence of resistance at the fixed temperature of 20K, showing a resistance minimum at compressive strain ≈ −0.2%. Inset: application of uniaxial strain through substrate bending.

Full size image

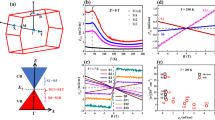
Next, we characterize the electrical resistance in magnetic field perpendicular to the a–c crystal plane. At the base temperature of ≈4K, SdH oscillations are clearly visible on the magnetoresistance background and evolve with changing strain (Fig. 2a). Plotting the oscillatory part ΔR versus inverse magnetic field 1/B, equally spaced resistance oscillations can be resolved (Fig. 2b). In the limits of large compressive and tensile strains applied here, the oscillation amplitude monotonically decreases with increasing 1/B. Under mild compressive strains, however, the SdH oscillation amplitude appears non-monotonic, suggesting contributions from more than a single Fermi surface.

Fig. 2: Magnetotransport measurements on ZrTe5 under strain.
figure 2

a Resistance versus magnetic field in various external strains. The curves are shifted in proportion to the strain for clarity, from the bottom to the top: −0.44, −0.34, −0.3, −0.24, −0.21, −0.19, −0.17, −0.15, −0.13, −0.11, −0.09, −0.07, −0.05, −0.03, 0, 0.1, 0.2, 0.3%. b SdH oscillations versus inverse magnetic field in various external strains. The curves ares shifted in proportion to the strain for clarity, from the bottom to the top: −0.44, −0.34, −0.3, −0.24, −0.17, −0.11, −0.05, 0, 0.1, 0.2, 0.3%. Symbols are experimental data and solid lines are simulations using the two-component LK formula. c Landau index, obtained from SdH oscillations, versus inverse magnetic field in large compressive and tensile strains (red square: −0.34%, green sqaure: −0.24%, brown circle: 0.2%, blue circle 0.3%). Here resistance peaks and valleys are assigned integer and half integer indices, respectively. The inset show the pockets of Fermi surface, with the Dirac band at the Γ point and a parabolic side band between the R and E points dominating the SdH oscillations under strong compressive and tensile strains, respectively. d, e SdH amplitude versus inverse magnetic field and temperature in strong compressive (−0.3%) and tensile (0.3%) strains. The symbols are experimental data and the solid lines are fittings using the LK formula. From the fittings, the effective cyclotron mass and Dingle temperature can be obtained. The vertical error bars denote the uncertainty in identifying the SdH oscillation amplitude. f Under medium strains the SdH oscillations (open symbols) are directly simulated (solid lines) with the two-component LK formula at various temperatures: black: 3K; red: 8K; and blue: 12K.

Full size image

Analysis of SdH oscillations

Our analysis of the SdH oscillations focuses on mapping out the strain-dependent mass gap, Fermi level, and the spin-dependent Berry phase. We model ZrTe5 by an anisotropic Dirac Hamiltonian (see Methods: Computing the g-factor). Starting from a full Hamiltonian including all the Bloch bands, we divide the Hilbert space into a low energy subspace consisting of the Dirac bands, and a high energy subspace containing all the other bands. When a magnetic field is applied, the vector potential couples the two subspaces and must be downfolded into the low energy bands at the Fermi level, which gives rise to the nonzero g-factor terms in the two-band Dirac model for the low energy subspace, gp and gs. We note that such a down folding process includes the contribution to the orbital magnetic moments (the importance of which in the analysis of quantum oscillations has been recently pointed out11) from the high energy bands and the contribution from the low energy bands can be captured by the Landau quantization with the Berry curvature being considered15,41.

In quantizing magnetic fields, the extremal cross-sectional area of the Fermi surface is SF = π(μ2 − Δ2)/(ℏ2v2). The corresponding cyclotron mass is \({m}_{c}=\frac{{\hslash }^{2}\partial {S}_{k}}{2\pi \partial \mu }=\frac{\mu }{{v}^{2}}\). Here μ is the Fermi energy, Δ is the mass gap, and v ≈ 5 × 105 m s−1 is the Dirac band velocity in the a–c plane32. The SdH oscillations can be modeled with the Lifshitz–Kosevich (LK) formula: up to the second order in the B field, each single band contributes to the SdH oscillations:

$$\Delta R/{R}_{0}\propto {R}_{D}{R}_{T}\cos \left(\frac{\hslash {S}_{F}}{eB}+{\phi }_{B}+\pi +\delta \right)$$
(1)

We note that the conventional (parabolic band) LK formula and its Dirac version42 have the same mathematical form with their corresponding band parameters (see Supplementary Note 5). In Eq. (1) R0 is the zero magnetic field resistance. Defined for Dirac band, \({R}_{D}=\exp (-2{\pi }^{2}{k}_{B}{T}_{d}| \mu | /\hslash eB{v}^{2})\) is the amplitude reduction factor from disorder scattering, where Td is the Dingle temperature characterizing the level of disorder,and kB is the Boltzmann constant. \({R}_{T}=\xi /\sinh (\xi )\) is the amplitude reduction factor from temperature, where ξ = 2π2kBTμ/ℏeBv2. ϕB is the Berry phase, and δ = ± π/4 in 3D materials.

Zeeman effect and spin-dependent Berry phase

Now we consider the Zeeman effect, which splits a spin-degenerate band into two, each with a different Fermi surface extremal cross-sectional area: SF↑/↓ = SF ± αB, and Berry phase: ϕB↑/↓ = ϕB ± ϕs15. Here α describes the splitting of extremal cross-sectional area of the Fermi surface and ϕs is the spin-dependent part of the Berry phase. Due to the strong spin-orbit coupling in ZrTe5 spin is not a good quantum number at general momenta: here spin up and spin down refer to “pseudo spins” defined as the two eigenstates of the mirror reflection operator through the kz = 0 plane, which contains the extremum projection of the Fermi surface. The overall quantum oscillation is a summation of the two oscillation terms from the two spin bands: \(\cos \left(\frac{\hslash {S}_{F\uparrow }}{eB}+{\phi }_{B\uparrow }+\pi +\delta \right)+\cos \left(\frac{\hslash {S}_{F\downarrow }}{eB}+{\phi }_{B\downarrow }+\pi +\delta \right)=2\cos \left(\frac{\hslash {S}_{F}}{eB}+{\phi }_{B}+\pi +\delta \right)\cos \left(\frac{\hslash \alpha }{e}+{\phi }_{s}\right)\) Interestingly SF and ϕB, which are the common (spin-independent) part of the two spin bands before the Zeeman splitting, determines the period and phase offset of the quantum oscillations; while the difference between the two spin bands determines the amplitude.

For systems with non-trivial Berry curvature, the Berry phase splitting ϕs along the Fermi surface will be nonzero. In particular, for a Dirac electron system, we find (see Methods: Quantum oscillations)

$${\phi }_{s}=\pi \frac{\Delta }{\mu }$$
(2)
$$\begin{array}{l}{\phi }_{B\uparrow }=\pi +{\phi }_{s}=\pi \left(1+\frac{\Delta }{\mu }\right)\\ {\phi }_{B\downarrow }=\pi -{\phi }_{s}=\pi \left(1-\frac{\Delta }{\mu }\right)\end{array}$$
(3)

Defining the Zeeman effect-induced SdH amplitude reduction factor: \({R}_{s}=\cos \left(\frac{\hslash \alpha }{e}+{\phi }_{s}\right)\), we derive for the Dirac band:

$$\Delta R/{R}_{0}=A{R}_{D}{R}_{T}{R}_{s}\cos \left(\frac{\pi ({\mu }^{2}-{\Delta }^{2})}{eB\hslash {v}^{2}}+\delta \right),$$
(4)

Further, the coefficient α is computed from the g-factor tensor obtained from first-principle calculations at given values of Δ and μF.

Under large compressive and large tensile strains, we observed approximately single SdH oscillation frequencies and a monotonic decay of SdH oscillation amplitude over increasing 1/B, suggesting that SdH oscillations are dominated by single bands there. The linear dependence of the Landau level indices on 1/B (Fig. 2c) extrapolates to the index values of close to 0 and 1/2 at 1/B = 0, corresponding to a SdH oscillation phase change from approximately zero to π. Fitting the 1/B and T dependence of the SdH oscillation amplitude to the LK formula (examples shown in Fig. 2d–f) provides estimations to the cyclotron mass and the Dingle temperature at these particular strains.

More generally, the SdH oscillations show a complex 1/B dependence which can be modeled considering contributions from two bands: ΔR = ΔR1 + ΔR2. Here band 1 is a Dirac band (with corresponding Fermi surface centered around the Γ point) with a common Berry phase of π for its two spins bands and hence a overall SdH phase which is much smaller than π (Fig. 2c). Band 2, a “trivial” parabolic band (with corresponding Fermi surface between the R and E points) possess a overall SdH phase which is close to π. We note that evidence of charge transport contribution from a secondary band has been reported previously28. The change of SdH phase shown in Fig. 2c is due to the strain-evolution of the relative contribution from the two bands, instead of band topology transition within the same band.

Figure 2b compares the measured SdH oscillations with the two-component LK formula simulations at base temperatures. Here the Dirac band SdH oscillations are modeled with Eq. (4), while the SdH oscillations from the trivial band are modeled with the conventional LK formula, with parameters including Td, Fermi energy and cyclotron mass mc. The band parameters used in the simulations are chosen so that they evolve smoothly with changing strain, and yield SdH oscillations which agrees with the experimental observations (with small deviations which may be attributed to the choices of background curves when extracting the oscillatory part of the data). The more general comparisons including temperature dependence are shown in the Supplementary Note 4. Figure 3 plots the key simulation parameters. Here we also include the estimated uncertainties of the parameters beyond which the simulated SdH oscillations deviate noticeably from the measurements. Focusing on the the Dirac band, a closing and re-opening of mass gap with tuning external strain happens at a compressive strain of ≈ − 0.2%. This, remarkably, is a direct transport evidence of the theoretically predicted WTI to STI transition. Associated with such transition, the Fermi energy (measured from the center of the mass gap) shows a non-monotonic strain dependence, reaching a minimum close to the transition strain where mass gap vanishes. From the mass gap and the Fermi energy, we calculate the electron doping: μ − Δ, which characterizes the energy of the Fermi level in relation to the bottom of the conduction band. The result indicates a maximum electron doping at the WTI-STI transition, which decreases when strain-tuned away from the transition. Generally the analysis of the band parameters suggests a band evolution with strain which is depicted in Fig. 4a.

Fig. 3: Strain tuning of band structure and spin-dependent Berry phase.
figure 3

a Strain dependence of SdH oscillation period in inverse magnetic field, for the Dirac band (band 1) and the trivial band (band 2).The results are obtained by simulating the SdH oscillations. The semitransparent data points correspond to when the band has relatively small contribution to the SdH oscillations. The vertical error bars present the interval beyond which the simulated SdH oscillations become noticeably different from the data. For low strains, the error bars are too short to be displayed. The mean values and uncertainties for the other simulation parameters are listed in Supplementary Note 4. b, c Strain tuning of mass gap size and Fermi energy. The mass gap and the Fermi energy are obtained by simulating the magnetic field and temperature dependence of the SdH oscillation curves with the two-component LK formula. Tuning the external strain from compressive to tensile, the mass gap closes and reopens at around −0.2%, consistent with the STI-WTI topological phase transition. The vertical error bars are determined through standard error propagation. d Strain dependence of doping energy, the energy of the Fermi surface counted from the bottom of the conduction band. The vertical error bars are determined through standard error propagation. e Theoretical intensity plot of SdH oscillation amplitude reduction factor from Zeeman effect, RS, as functions of Fermi energy and mass gap. The dotted line shows the boundary between the STI phase (positive mass gap) and the WTI phase (negative mass gap). The symbols in the mass gap-Fermi energy parameter space correspond to the experimental data points at various external strains, evolving following the arrow from compressive to tensile. By convention we assign a negative sign to the mass gap on the WTI side with external strain larger than ≈ − 0.2%. f Theory(solid lines)/experiment(open symbols) comparison of RS as functions of mass gap and Fermi energy at various strains. The experimental values of RS are scaled by a common constant factor of 0.6 for comparison with the theory. The theoretical model qualitatively reproduces the experiment results by considering the spin-dependent Berry phase. By contrast, the inset shows the theoretical curve without considering the spin-dependent phase, which fails to explain the experimental data (see Supplementary Note 6). The vertical error bars are determined through standard error propagation.

Full size image
Fig. 4: Evolution of band structure and Zeeman effect over strain.
figure 4

a Evolution of Dirac band and Fermi level through the STI to WTI phase transition with increasingly tensile strain. b Schematic energy dispersion with kz = 0 and magnetic field in the z(b) direction. Green circles indicate the boundary of extremal cross-sections for the spin bands. The spin-dependent Berry phases are ϕ and − ϕ over the two circles. c spin-dependent Berry phase ϕs as a function of strain, calculated with mass gap and Fermi energy obtained from the SdH oscillations. d Strain tuning of effective g-factor. In both (c and d), the vertical error bars are determined through standard error propagation.

Full size image

Compared to the previous (ARPES and chiral magnetic effect) reports on WTI-STI transition, a similar order of magnitude of strain was applied in our studied here ( ≈ few − 0.1%). The absolute value of the strain at the transition point, however, is randomly shifted by a random built-in stress (typically tensile), resulting from the hot-transfer fabrication process. We note that the observed STI-WTI transition coincides with the minimum resistance point (Fig. 1e), consistent with the previous experimental study on chiral magnetic effect in ZrTe5 under strain40. The strain-tunable bandgap observed through our magnetotransport, within the range of strain of a ≈ few − 0.1%, varies by a few 10 meV. This is in good agreement with the previous report on ARPES study of ZrTe5 under strain39.

Next we focus on the impact of Zeeman effect on SdH oscillation amplitude (Rs). Experimentally we obtain Rs at every strain by quantitative simulation of the SdH oscillations. We then compare the results with the theoretical expectation: \({R}_{s}=\cos \left(\frac{\hslash \alpha }{e}+{\phi }_{s}\right)\). Here \(\frac{\hslash \alpha }{e}\), which is associated with the splitting of extremal cross-sectional area of the Fermi surface, follows (see Methods: Quantum oscillations):

$$\frac{\hslash \alpha }{e}=-\pi \frac{\Delta }{\mu }-\pi \frac{\mu }{{m}_{e}{v}^{2}}\left(\frac{{g}_{z}^{p}}{2}\left(1+\frac{\Delta }{\mu }\right)-\frac{{g}_{z}^{s}}{2}\left(1-\frac{\Delta }{\mu }\right)\right)$$
(5)

We adopt the g-factors for the s and p orbitals \({g}_{z}^{p}=9.66,{g}_{z}^{s}=-6.45\), as computed from first-principle calculations (DFT-mBJ)41. We note that Eq (5) represents a generalization of the calculation in Ref. 11 by including the effect of higher energy non-Dirac bands, which cause gp and gs to deviate from one. ϕs, which is associated with the Berry phase splitting along the Fermi surface (Fig. 4b), is calculated from the mass gap and Fermi energy obtained from simulating the SdH oscillations: \({\phi }_{s}=\pi \frac{\Delta }{\mu }\). The theory shows good qualitative agreement with the data on the strain dependence of Rs, as illustrated in Fig. 3f with the band parameters tuned along the trajectory in the (Δ, μ) parameter space shown in Fig. 3e. By contrast, the conventional modeling of Zeeman effect on SdH oscillations which only considers the Fermi surface splitting (Eq. (5)) completely fails to match with the experimental observations. This comparison definitively highlights the importance of spin-dependent Berry phase in the Zeeman effect. We also note that in our theoretical model, the value of RS is dependent on both the amplitude and the sign of the energy gap Δ. The quantitative comparison between the theoretical model and our data on RS, as shown in Fig. 3e and f, therefore reveals a sign-change in band gap near where its amplitude vanishes. This is consistent with the occurrence of a topological phase transition.

The significant strain-tunability of the spin-dependent Berry phase ϕs is shown in Fig. 4c. Accompanied by the topological phase transition where the mass gap vanishes, ϕs passes through zero when the system is in the Dirac semimetal phase. We also compute the effective g-factor by comparing Rs with the conventional Zeeman effect-induced SdH amplitude reduction factor \(\cos (\pi g{m}_{c}/(2{m}_{e}))\)7,32. This leads to g = 2me(ℏα/e + ϕs)/(πmc), whose strong strain tunability is shown Fig. 4d.

Conclusion

In conclusion, we have carried out a magnetotransport study on the evolution of band topology and non-trvial Berry phase over strain-tunable band parameters in ZrTe5. The strain-dependent SdH oscillations allow direct mapping of the closing and reopening of the Dirac band mass gap, which is consistent with a WTI-STI transition in ZrTe5. Moreover we observed the non-trivial Berry phase and its dependence on band parameters over the transition. Such a spin-dependent Berry phase is generic and intrinsic to Dirac band structure, and is a critical factor in modeling Zeeman effect in SdH oscillations in topological materials.

Methods

Sample fabrication and characterization

The samples studied in this work are ZrTe5 microcrystals mechanically exfoliated onto flexible Polyimide substrates (Fig. 1a, b), which allow application of tensile and compressive strains over a wide temperature range from room temperature down to 4K. ZrTe5 single crystals were synthesized by chemical vapor transport method, with iodine as transport agency. Stoichiometry amounts of Zr(4N) and Te(5N) powder, together with 5mg/mL I2, were loaded into a quartz tube under argon atmosphere. The quartz tube was flame sealed and then placed in a two-zone furnace, a temperature gradient from 480 °C to 400 °C was applied. After 4 weeks reaction, golden, ribbon-shaped single crystals were obtained, of typical size about 0.6 × 0.6 × 5 mm. The X-ray diffraction characterization of the crystals is shown in the Supplementary Note 1.

To avoid degradation of the material from ambient exposure, the crystals are exfoliated and press-contacted on predefined gold electrodes on 120 μm-thick Polyimide substrates in Ar environment, and are encapsulated with poly(methyl methacrylate) (PMMA) which both protects the crystals from degradation and facilitates the application of strain. A detailed description on the sample fabrication and on the contact/crystal interface can be found in reference43. Uniaxial strain is applied through substrate bending. The strain homogeneity is facilitated by the total emersion of the crystal in PMMA, and more importantly the extremely small ratio of crystal thickness (~190 nm) to the total crystal length (~100 μm, we note that the length of the crystal outside the electrodes also helps creating an uniform strain throughout the thickness of the crystal). All measurements were done with electric current applied along the a-axis. Typical contact resistance over a 10 μm2 contact area is between few hundred ohms to a few kilo-ohms, and does not change significantly over the application of strain through substrate bending. Uniaxial strain is applied to the samples using a four-point bending setup, with motorized precision control to the substrate curvature44,45. Because the substrate is much thicker than the microcrystals, significant uniaxial strain can be achieved at relatively mild substrate curvatures under which the strain on the microcrystals is predominantly tensile/compressive due to the elongation/compression of the top substrate surface where the microcrystals are PMMA-pinned. Besides external strain applied through substrate bending, both the crystals, the substrates, and the encapsulating PMMA layer go through thermal expansion/contraction upon temperature change. Because of such complication it is difficult to precisely characterize the absolute strain on the crystals. Here we focus on the dependence of the transport characteristics on the change of strain induced by substrate bending, which is described in the discussion below as “external strain”. In magnetotransport measurements, we limit the temperature range between 3 and 20K, where the change of thermal expansion is small in comparison to the range of the external strain. All charge transport measurements were performed in a Oxford Variable Temperature Insert with a superconducting magnet, using standard lock-in technique.

Computing the g-factor

To compute the effect of Zeeman coupling on quantum oscillations, we study the k ⋅ p Hamiltonian near Γ, which is an anisotropic gapped Dirac Hamiltonian41:

$$H({{{{{{{\bf{k}}}}}}}})=\left(\begin{array}{cc}\Delta {\sigma }_{0}&\hslash {\sum }_{i}{v}_{i}{k}_{i}{\sigma }_{i}\\ \hslash {\sum }_{i}{v}_{i}{k}_{i}{\sigma }_{i}&-\Delta {\sigma }_{0}\end{array}\right),$$
(6)

in the basis \(\left\vert p,\frac{1}{2}\right\rangle\), \(\left\vert p,-\frac{1}{2}\right\rangle\), \(\left\vert s,\frac{1}{2}\right\rangle\), \(\left\vert s,-\frac{1}{2}\right\rangle\), where \(\pm \frac{1}{2}\) refers to the z-component of spin. In Eq. (6), Δ is half the mass gap; vx,y,z are the anisotropic Dirac cone velocities; σx,y,z are the Pauli matrices; and σ0 is the 2 × 2 identity matrix. The eigenvalues of H(k) are

$${E}_{\pm }=\pm \sqrt{{\Delta }^{2}+{\hslash }^{2}\mathop{\sum}\limits_{i}{v}_{i}^{2}{k}_{i}^{2}},$$
(7)

where all bands are doubly-degenerate due to the combination of time-reversal and inversion symmetry. The eigenvectors are given by

$$\left\vert {\psi }_{m,{{{{{{{\bf{k}}}}}}}}}^{\pm }\right\rangle =\sqrt{\frac{{E}_{\pm }+\Delta }{2{E}_{\pm }}}\left(\begin{array}{c}{u}_{m}\\ \frac{\hslash v}{{E}_{\pm }+\Delta }{{{{{{{\boldsymbol{p}}}}}}}}\cdot {{{{{{{\boldsymbol{\sigma }}}}}}}}{u}_{m}\end{array}\right),$$
(8)

where u1 = (1, 0)T, u2 = (0, 1)T and we have defined the rescaled coordinates pi = viki/v.

The Zeeman coupling for the four-band model is:

$${H}_{0}^{Z}={\mu }_{B}\left(\begin{array}{cc}{\sum }_{i}{g}_{i}^{p}{B}_{i}&0\\ 0&{\sum }_{i}{g}_{i}^{s}{B}_{i}\end{array}\right),$$
(9)

where \({g}_{x,y,z}^{s,p}\) are the matrix-valued g-factors for the s and p orbitals, which are anisotropic due to the crystal symmetry and which differ from their bare value due to coupling with all the other bands not in the four-band model.

To compute the quantum oscillations, we must downfold this four-band model into the two bands at the Fermi level. We seek an effectiveg-factor for the two degenerate bands that make up the Fermi surface, such that when projected onto those bands, the Zeeman Hamiltonian takes the form:

$${H}_{m{m}^{{\prime} }}^{Z}={\mu }_{B}{{{{{{{{\bf{g}}}}}}}}}_{m{m}^{{\prime} }}\cdot {{{{{{{\bf{B}}}}}}}},$$
(10)

where \({\mu }_{B}=\frac{e\hslash }{2{m}_{e}}\) is the Bohr magneton and \(m,{m}^{{\prime} }\) index the two bands at the Fermi surface.

The effective g-factor has two contributions:

$${{{{{{{\boldsymbol{g}}}}}}}}={{{{{{{{\boldsymbol{g}}}}}}}}}_{0}+{{{{{{{{\boldsymbol{g}}}}}}}}}_{D},$$
(11)

where g0 is the projection of gs and gp (defined by \({H}_{0}^{Z}\)) onto the two conduction bands at the Fermi level and gD is an extra orbital contribution that we will describe below. For a magnetic field in the z direction, using the expressions for the conduction band eigenstates from Eq. (8),

$${{{{{{{{\boldsymbol{g}}}}}}}}}_{0,z}=\left(\frac{{E}_{+}+\Delta }{2{E}_{+}}\right)\left({g}_{z}^{p}+{g}_{z}^{s}\frac{{\hslash }^{2}{v}^{2}({p}_{z}^{2}-{p}_{x}^{2}-{p}_{y}^{2})}{{({E}_{+}+\Delta )}^{2}}\right){\sigma }_{z},$$
(12)

where the Pauli matrix σz acts in the basis of the two bands at the Fermi level. Ultimately, we will only need the g-factor at the extremum of the Fermi surface, where pz = 0 and \({\hslash }^{2}{v}^{2}({p}_{x}^{2}+{p}_{y}^{2})={\mu }^{2}-{\Delta }^{2}\). In this case,

$${{{{{{{{\boldsymbol{g}}}}}}}}}_{0,z}^{{{{{{{{\rm{ext}}}}}}}}}=\frac{1}{2}\left({g}_{z}^{p}\left(1+\frac{1}{\gamma }\right)-{g}_{z}^{s}\left(1-\frac{1}{\gamma }\right)\right){\sigma }_{z}$$
(13)

where \(\gamma =\frac{\mu }{\Delta }\) is a dimensionless constant.

Returning to the second term in Eq. (11), gD is the orbital contribution to the g-factor from the Dirac cone46:

$${{{{{{{{\bf{g}}}}}}}}}_{D,m{m}^{{\prime} }}({{{{{{{\bf{k}}}}}}}})=\frac{i{m}_{e}}{{\hslash }^{2}}\mathop{\sum}\limits_{ijk}{\varepsilon }_{ijk}{\hat{{{{{{{{\bf{e}}}}}}}}}}_{k}\left\langle {\partial }_{i}{\psi }_{m,{{{{{{{\boldsymbol{k}}}}}}}}}\right\vert \left(H({{{{{{{\boldsymbol{k}}}}}}}})-{E}_{m,{{{{{{{\boldsymbol{k}}}}}}}}}\right)\left\vert {\partial }_{j}{\psi }_{{m}^{{\prime} },{{{{{{{\boldsymbol{k}}}}}}}}}\right\rangle ,$$
(14)

where ψm,k are the eigenvectors of Eq. (6).

The first step to evaluate gD is to find the derivatives of the eigenstates:

$$\frac{\partial \left\vert {\psi }_{m,{{{{{{{\boldsymbol{k}}}}}}}}}\right\rangle }{\partial {p}_{i}}=\sqrt{\frac{E+\Delta }{2E}}\left(\begin{array}{c}-\frac{\Delta {\hslash }^{2}{v}^{2}{p}_{i}}{2{E}^{2}(E+\Delta )}{u}_{m}\\ -\frac{(\Delta +2E){\hslash }^{3}{v}^{3}{p}_{i}}{{(E+\Delta )}^{2}2{E}^{2}}{{{{{{{\boldsymbol{p}}}}}}}}\cdot {{{{{{{\boldsymbol{\sigma }}}}}}}}{u}_{m}+\frac{\hslash v}{E+\Delta }{\sigma }_{i}{u}_{m}\end{array}\right),$$
(15)

where we have dropped the subscript/superscript ± on E and ψ to reduce clutter. After some algebra, it follows that:

$$\left(H-{E}_{m,{{{{{{{\boldsymbol{k}}}}}}}}}\right)\frac{\partial \left\vert {\psi }_{m,{{{{{{{\boldsymbol{k}}}}}}}}}\right\rangle }{\partial {p}_{i}}=\sqrt{\frac{E+\Delta }{2E}}\frac{1}{E(E+\Delta )}\left(\begin{array}{c}\Delta {\hslash }^{2}{v}^{2}{p}_{i}{u}_{m}+iE{\hslash }^{2}{v}^{2}{\sum }_{jk}{\varepsilon }_{jik}{p}_{j}{\sigma }_{k}{u}_{m}\\ {\hslash }^{3}{v}^{3}{p}_{i}{{{{{{{\boldsymbol{p}}}}}}}}\cdot {{{{{{{\boldsymbol{\sigma }}}}}}}}{u}_{m}-E(E+\Delta )\hslash v{\sigma }_{i}{u}_{m}\end{array}\right),$$
(16)

which yields the matrix element

$$\left\langle \frac{\partial {\psi }_{m,{{{{{{{\boldsymbol{k}}}}}}}}}}{\partial {p}_{i}}\right\vert H({{{{{{{\boldsymbol{k}}}}}}}})-{E}_{m,{{{{{{{\boldsymbol{k}}}}}}}}}\left\vert \frac{\partial {\psi }_{{m}^{{\prime} },{{{{{{{\boldsymbol{k}}}}}}}}}}{\partial {p}_{j}}\right\rangle = \frac{{\hslash }^{2}{v}^{2}}{2{E}^{2}}{u}_{m}^{{{{\dagger}}} }\left[\frac{-i{\hslash }^{2}{v}^{2}{\varepsilon }_{jkl}{p}_{i}{p}_{k}{\sigma }_{l}+i{\hslash }^{2}{v}^{2}{\varepsilon }_{ikl}{p}_{j}{p}_{k}{\sigma }_{l}}{E+\Delta } - iE{\varepsilon }_{ijk}{\sigma }_{k}+\frac{{\hslash }^{2}{v}^{2}{p}_{i}{p}_{j}}{E}-E{\delta }_{ij}\right]{u}_{{m}^{{\prime} }}$$
(17)

The terms symmetric under the exchange of the i and j indices (i.e., the last two terms) will cancel in the sum in Eq. (14). Thus, applying Eq. (14), the extra orbital contribution to the g-factor is given by:

$${{{{{{{{\boldsymbol{g}}}}}}}}}_{D}=\frac{{g}^{L}}{2{\tilde{\gamma }}^{2}}\mathop{\sum}\limits_{ijk}\left[\tilde{\gamma }{\varepsilon }_{ijk}{\varepsilon }_{ijk}{\sigma }_{k}-\frac{2{\hslash }^{2}{v}^{2}/{\Delta }^{2}}{1+\tilde{\gamma }}\mathop{\sum}\limits_{qr}{\varepsilon }_{iqr}{\varepsilon }_{ijk}{p}_{q}{p}_{j}{\sigma }_{r}\right]\frac{{v}_{i}{v}_{j}}{{v}^{2}}{\hat{{{{{{{{\boldsymbol{e}}}}}}}}}}_{k}$$
(18)

where \({g}^{L}\equiv \frac{{m}_{e}{v}^{2}}{\Delta }\) and \(\tilde{\gamma }\equiv \frac{E}{\Delta }\) are dimensionless constants.

We now simplify this result by taking B in the z-direction and restricting to the boundary of the extremal cross-section, where pz = 0 and \({\hslash }^{2}{v}^{2}({p}_{x}^{2}+{p}_{y}^{2})={\mu }^{2}-{\Delta }^{2}\). Plugging this into Eq. (18), we obtain the z-component of g:

$${{{{{{{{\boldsymbol{g}}}}}}}}}_{D,z}^{{{{{{{{\rm{ext}}}}}}}}}=\frac{{g}^{L}}{{\tilde{\gamma }}^{2}}\frac{{v}_{x}{v}_{y}}{{v}^{2}}{\sigma }_{z}$$
(19)

The total effective g-factor at the extremal cross-section of the Fermi surface is found by combining Eqs. (13) and (19):

$${{{{{{{{\boldsymbol{g}}}}}}}}}_{z}^{{{{{{{{\rm{ext}}}}}}}}}=\left[\frac{{m}_{e}\Delta {v}_{x}{v}_{y}}{{\mu }^{2}}+\frac{{g}_{z}^{p}}{2}\left(1+\frac{\Delta }{\mu }\right)-\frac{{g}_{z}^{s}}{2}\left(1-\frac{\Delta }{\mu }\right)\right]{\sigma }_{z}$$
(20)

This expression shows that the g-factor in the \(\hat{z}\)-direction is independent of momentum on the boundary of the extremal cross-section and is diagonal, i.e., \(\vert {\psi }_{m,{{{{{{{\boldsymbol{k}}}}}}}}}\rangle\) are eigenstates of the Zeeman coupling.

Quantum oscillations

We now discuss the quantum oscillations of the anisotropic Dirac semi-metal. As discussed in the main text, the quantum oscillations for a doubly degenerate electronlike Fermi surface are proportional to

$$\Delta R/{R}_{0}\propto \cos \left(\frac{\hslash {S}_{F}}{eB}+{\phi }_{B}+\pi +\delta \right)\cos \left(\frac{\hslash \alpha }{e}+{\phi }_{s}\right)$$
(21)

where ϕB,↑/↓ = ϕB ± ϕs are the Berry phases around the extremal Fermi surface for each of the two spins and SF,↑/↓ = SF ± αB are the extremal areas of the Fermi surface for each spin.

The Berry connection is defined by46: \({{{{{{{{\boldsymbol{A}}}}}}}}}_{m{m}^{{\prime} }}({{{{{{{\boldsymbol{k}}}}}}}})={\sum }_{k}i\langle {\psi }_{m,{{{{{{{\boldsymbol{k}}}}}}}}}| \frac{\partial }{\partial {k}_{k}}| {\psi }_{{m}^{{\prime} },{{{{{{{\boldsymbol{k}}}}}}}}}\rangle {{{{{{{{\boldsymbol{e}}}}}}}}}_{k}\). By plugging in the expressions for the eigenstates and derivatives of eigenstates in Eqs. (8) and (15), we find the explicit expression:

$${{{{{{{\boldsymbol{A}}}}}}}}({{{{{{{\boldsymbol{k}}}}}}}}) = \; \frac{{\hslash }^{2}v}{{\Delta }^{2}}\frac{1}{2\tilde{\gamma }(\tilde{\gamma }+1)}\left[({p}_{y}{\sigma }_{z}-{p}_{z}{\sigma }_{y}){v}_{x}{{{{{{{{\boldsymbol{e}}}}}}}}}_{x}+\right.\\ \left.({p}_{z}{\sigma }_{x}-{p}_{x}{\sigma }_{z}){v}_{y}{{{{{{{{\boldsymbol{e}}}}}}}}}_{y}+({p}_{x}{\sigma }_{y}-{p}_{y}{\sigma }_{x}){v}_{z}{{{{{{{{\boldsymbol{e}}}}}}}}}_{z}\right]$$
(22)

To find the Berry phase, we ultimately need A(k) ⋅ dk on the extremal cross-section, where pz = 0 and dk is in the x–y plane, which yields:

$${{{{{{{\boldsymbol{A}}}}}}}}({{{{{{{\boldsymbol{k}}}}}}}})\cdot{{{{{{{\boldsymbol{\cdot }}}}}}}}{{{{{{{\rm{d}}}}}}}}{{{{{{{\boldsymbol{k}}}}}}}}=\frac{{\hslash }^{2}{v}_{x}{v}_{y}}{{\Delta }^{2}}\frac{{\sigma }_{z}}{2\tilde{\gamma }(\tilde{\gamma }+1)}\left({k}_{y}{{{{{{{{\boldsymbol{e}}}}}}}}}_{x}-{k}_{x}{{{{{{{{\boldsymbol{e}}}}}}}}}_{y}\right)\cdot{{{{{{{\boldsymbol{\cdot }}}}}}}}{{{{{{{\rm{d}}}}}}}}{{{{{{{\boldsymbol{k}}}}}}}},$$
(23)

where σz is acting in the space of the two conduction bands at the Fermi level. We find the Berry phase around each extremal ring of the Fermi surface by integrating over the the boundary of the extremal cross-section:

$$\oint {{{{{{{\boldsymbol{A}}}}}}}}({{{{{{{\boldsymbol{k}}}}}}}})\cdot{{{{{{{\boldsymbol{\cdot }}}}}}}}{{{{{{{\rm{d}}}}}}}}{{{{{{{\boldsymbol{k}}}}}}}}=\frac{{\hslash }^{2}{v}_{x}{v}_{y}}{2{\Delta }^{2}\tilde{\gamma }(\tilde{\gamma }+1)}\oint \left({k}_{y}{{{{{{{{\boldsymbol{e}}}}}}}}}_{x}-{k}_{x}{{{{{{{{\boldsymbol{e}}}}}}}}}_{y}\right)\cdot{{{{{{{\boldsymbol{\cdot }}}}}}}}{{{{{{{\rm{d}}}}}}}}{{{{{{{\boldsymbol{k}}}}}}}}$$
(24)

The loop integral can be turned into an area integral using Stokes theorem:

$$\iint {\nabla }_{{{{{{{{\boldsymbol{k}}}}}}}}}\times \left({k}_{y}{{{{{{{{\boldsymbol{e}}}}}}}}}_{x}-{k}_{x}{{{{{{{{\boldsymbol{e}}}}}}}}}_{y}\right)\cdot {{{{{{{\rm{d}}}}}}}}{{{{{{{{\boldsymbol{S}}}}}}}}}_{{{{{{{{\boldsymbol{k}}}}}}}}}=-2\iint d{S}_{{{{{{{{\bf{k}}}}}}}}}$$
(25)
$$=-2\pi \frac{{\mu }^{2}-{\Delta }^{2}}{{v}_{y}{v}_{x}},$$
(26)

which yields:

$${\phi }_{B,\uparrow /\downarrow }=\pi \left(1\pm \frac{\Delta }{\mu }\right),$$
(27)

where we have added 2π in order to ensure the Berry phase in the range of 0 to 2π.

The last term that we need to evaluate the Lifschitz-Kosevich formula is the area of the extremal Fermi surfaces. Since the effective g-factor at the extremal Fermi surfaces (Eq. (20)) is diagonal in the basis of the two conduction bands, the two extremal Fermi surfaces satisfy the equation:

$$\mu =\sqrt{{\Delta }^{2}+{\hslash }^{2}{v}_{x}^{2}{k}_{x}^{2}+{\hslash }^{2}{v}_{y}^{2}{k}_{y}^{2}}\pm {\mu }_{B}{{{{{{{{\boldsymbol{g}}}}}}}}}_{z}^{{{{{{{{\rm{ext}}}}}}}}}B,$$
(28)

accounting for the fact that the magnetic field is in the z direction and the extremal Fermi surfaces have pz = 0. Thus, each extremal cross-section forms an ellipse whose area is given by:

$$S=\frac{\pi }{{\hslash }^{2}{v}_{x}{v}_{y}}\left[{\left(\mu \mp {\mu }_{B}{{{{{{{{\boldsymbol{g}}}}}}}}}_{z}^{{{{{{{{\rm{ext}}}}}}}}}B\right)}^{2}-{\Delta }^{2}\right]$$
(29)

Thus, the area-splitting term α in Eq. (21) is given by:

$$\alpha =-\frac{\pi e\mu {{{{{{{{\boldsymbol{g}}}}}}}}}_{z}^{{{{{{{{\rm{ext}}}}}}}}}}{\hslash {m}_{e}{v}_{x}{v}_{y}},$$
(30)

where we have used μB = eℏ/2me. Plugging in the result for \({{{{{{{{\boldsymbol{g}}}}}}}}}_{z}^{{{{{{{{\rm{ext}}}}}}}}}\) from Eq. (20),

$$\frac{\hslash \alpha }{e}=-\frac{\pi \Delta }{\mu }-\frac{\pi \mu }{{m}_{e}{v}_{x}{v}_{y}}\left[\frac{{g}_{z}^{p}}{2}\left(1+\frac{\Delta }{\mu }\right)-\frac{{g}_{z}^{s}}{2}\left(1-\frac{\Delta }{\mu }\right)\right]$$
(31)

Plugging in the calculation of the Berry phase (Eq. (27)) and the area difference (Eq. (31)) to the Lifschitz-Kosevich formula (Eq. (21)), we derive the expression for quantum oscillations:

$$\Delta \rho \propto \cos \left(\frac{\pi \mu }{{m}_{e}{v}_{x}{v}_{y}}\left[\frac{{g}_{z}^{p}}{2}\left(1+\frac{\Delta }{\mu }\right)-\frac{{g}_{z}^{s}}{2}\left(1-\frac{\Delta }{\mu }\right)\right]\right)\cos \left(\frac{\hslash {S}_{F}}{eB}\pm \frac{\pi }{4}\right)$$
(32)