Introduction

Berry curvature from a nontrivial band topology1 is well established to play a central role in both the anomalous Hall coefficient2,3 and negative longitudinal magnetoresistance (LMR) in a Weyl metallic state4,5,6,7,8,9. For instance, an LMR, originating from the nontrivial topological structure of the chiral anomaly10,11,12,13,14, i.e., non-conservation of chiral charges, in a Weyl band induced by an external magnetic field was measured in Dirac and Weyl metals. However, various disorder scattering channels are also well known to cause similar effects on these linear transport coefficients15,16,17, which hinders the understanding of the nontrivial band topology based on the linear transport coefficients. In this respect, considering nonlinear transverse and longitudinal transport coefficients as measures for the appearance of the Berry curvature associated with a topological phase transition (TPT) of an electronic band structure is natural. The present experiments suggest that such nonlinear transport coefficients are more sensitive in verifying a TPT than linear coefficients, reflecting the nature of the electronic wavefunctions.

Recently, various kinds of nonlinear transport coefficients have been proposed, which are classified by intraband scattering18,19 and interband transition20,21 mechanisms in the presence of Berry curvature. Specifically, the Berry curvature dipole22,23,24, Berry-connection polarizability (BCP) tensor25,26, and quantum geometric tensor27,28 are responsible for nonlinear transport coefficients. Some of them were measured26,27. The nonlinear electrical transport resulting from these quantities has been contrasted with the electrical nonlinearity caused by the opening of a ballistic channel. Despite these recent developments, the present study shows that all these proposed mechanisms for nonlinear transport coefficients cannot explain our experimental results that confirm the existence of a TPT in ZrTe5.

Here, we investigate the nonlinear electrical transport phenomena of ZrTe5, which has an orthorhombic layered structure with space group Cmcm (\({D}_{2h}^{17}\))2,29,30. For our purpose, ZrTe5, a topological metal with a TPT, is an appropriate system. Because the present ZrTe5 is not sufficiently clean, it will not show ballistic conduction and the resultant nonlinearity31,32. Along with a nonlinear longitudinal conductivity ΔσL for E // B, which violates Ohm’s law, we uncover a nonlinear Hall conductivity Δσxy quadratic in the applied current for E ⊥ B. This result is consistent with the presence of inversion symmetry. Both ΔσL and Δσxy arise at the same temperature T* ~ 30 K, and their emergence is intimately related to the TPT known to occur in the vicinity of the resistivity peak temperature. Remarkably, T* is the ‘transition temperature’ of the TPT, which is revealed by ΔσL and Δσxy but hidden in linear transport coefficients. In addition, the (linear) longitudinal conductivity σxx, the (linear) Hall conductivity σxy, Δσxy for E ⊥ B, and ΔσL for E // B are found to show scaling relations. In particular, σAHE ~ σxx suggests skew scattering as a dominant mechanism of the anomalous Hall effect (AHE) in ZrTe5. A scaling relation of ΔσL ~ (σAHE)3 and a crossover from Δσxy ~ ΔσL to Δσxy ~ (ΔσL)2 are also observed, which manifest the underlying mechanism of the nonlinear Hall effect in ZrTe5. These extended scaling relations provide a framework to understand the interplay between a nontrivial band topology and disorder scattering as the conventional conductivity scaling laws do. The AHE, usually observed in ferromagnetic metals, is more ‘anomalous’ in nonmagnetic ZrTe5, and it cannot be understood within existing Weyl metal frameworks. This AHE resembles the three dimensional (3D) quantum Hall effect reported in ZrTe533. However, a later study ruled out this possibility by confirming that the charge density wave, which is requisite for the 3D quantum Hall effect, is absent in ZrTe534. This AHE with unknown origin implies an elusive ground state of ZrTe5. The nature of the AHE also changes at T*, as discussed below.

The topological nature of ZrTe5 remains controversial because of its sensitivity to the details of the lattice parameters and the purity of the crystals. Some angle-resolved photoemission spectroscopy (ARPES)11 and transport11,35 studies have suggested a 3D Dirac metallic state with no finite gap. This picture was also supported by an infrared (IR) spectroscopy36, magneto-optical37, and other transport38 measurements. In contrast, two scanning tunnelling microscopy (STM)39,40 and laser-based ARPES41 studies concluded that ZrTe5 is a weak topological insulator (TI). In addition, other ARPES and STM studies detected a metallic surface state, which indicates that ZrTe5 is a strong TI42,43. This contradictory situation changed when a TPT between a strong TI and a weak TI with an intermediate Dirac metallic region was observed44,45. A pronounced peak in the temperature dependence of the resistivity indirectly signifies the intermediate Dirac metallic state. An IR spectroscopy study found that the energy gap closes around the peak temperature, where the optical response exhibits the characteristic signatures of a Dirac metallic state44. A nuclear magnetic resonance (NMR) study also demonstrated temperature-dependent topological characteristics with an intermediate TPT, whose transition temperature was found to be lower than the peak temperature45. However, unlike the IR spectroscopy study, this NMR study suggested a weak TI at low temperatures. Despite the ambiguity about the topological nature below and above the peak region, the peak region was identified as corresponding to a Dirac metallic state. This identification offers a chance to observe phenomena related to a Dirac metal with an intermediate TPT. This peak appears at a relatively high temperature ( ~ 130 K) and at a lower temperature in the crystals grown by the chemical vapour transport (CVT) and flux methods, respectively. Thus, the Dirac metallic state may be a ground state in flux-grown crystals. This study investigates flux-grown crystals, whose resistivity peak is at T = 40 K but whose high resistivity extends down to T = 0 K. Negative LMR originating in the chiral anomaly29 and the AHE from the Berry curvature were observed in flux-grown ZrTe52,46,47,48, supporting the Dirac and Weyl metallicity. The band structure of ZrTe5 in the Dirac metallic state is simple, as revealed by ARPES36,40,49. A single Dirac band exists at Г in reciprocal space [Fig. 1a], and the Fermi energy crosses near the nodal point. In this study, we optimized the growth conditions of ZrTe5 single crystals to produce crystals that exhibit pronounced topological properties, such as the AHE and negative LMR.

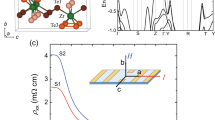
Fig. 1: Electronic structure and basic characterization of topological semimetal ZrTe5 grown under different conditions.
figure 1

a Schematic band structures and Brillouin zones of ZrTe5. The Dirac band appears at the Г point38,46,47,48,50,63. The positions of the Fermi energy for the S1-S13 samples are shown along with a schematic diagram of the Dirac band. b Temperature dependence of the resistivity for four ZrTe5 single crystals (S11, S12, S13, and S1) grown under different conditions. In particular, the three ‘insulating’ samples (S11, S12, S13) show a characteristic peak at approximately 40 K. This peak is a precursor of the topological phase transition at T* ~ 30 K. c Field dependence of the Hall resistivity ρxy(B) for several ZrTe5 single crystals grown under different conditions. All measurements were performed at T = 1.7 K. The origin of the step-like ρxy(B) is still elusive2,11,47 d Hall resistivity ρxy(B) for S11, S6, and S1 samples at T  =  200 K. The anomalous Hall effect is absent above 80 K. The dashed lines fit the experimental data to a linear function. e Absolute value of carrier density n estimated at T = 200 K as a function of residual resistivity ρ0 at T = 1.7 K. The samples that show the AHE and negative LMR have small |n| and large ρ0.

Full size image

Results

Basic characterization of topological semimetal ZrTe5 grown

Using the Te-flux method, we grew 13 single crystals (S1–S13) with different heating profiles and characterized them [see Supplementary Fig. 1 and Supplementary Table 1]11,50,51. Among these single crystals, only three samples (S11, S12, and S13) with low carrier density and large residual resistivity exhibit very pronounced AHE and negative LMR. These results indicate that the Fermi energy position of these particular samples is close enough to the nodal point to reveal topological properties, as shown in Fig. 1a. Hall effect, magnetoresistance (MR), and current (I)-voltage (V) measurements were conducted in the six-probe configuration, where the longitudinal (ρxx) and transverse (ρxy) resistivities can be simultaneously measured. We tested three different magnetic field B and current I (or E) configurations for the I-V measurements: transverse (B ⊥ E, B is out of plane), longitudinal (B // E), and in-plane Hall (B ⊥ E, B is in the plane) configurations.

Figure 1b presents the temperature dependence of the resistivity for the S1, S11, S12, and S13 samples. Compared to the S1-S10 samples, S11, S12, and S13 have a more pronounced insulating behaviour with a relatively large residual resistivity ρ0 [Supplementary Fig. 2a, b]. Even though the values of ρ0 are large, they are still on the order of a few mΩcm for S11, S12, and S13. The relatively large ρ0 is correlated with a pronounced AHE at T = 1.7 K, as shown in Fig. 1c and Supplementary Fig. 2c. While the Hall resistivity is linear in B for S1–S10, a pronounced step occurs at low B for S11, S12, and S13. This step is a signature of the AHE, as reported in previous studies2,47. How such shape and magnitude of anomalous Hall signals emerge in the nonmagnetic metal ZrTe5 needs to be understood. As previously noted2, ferromagnetism plays no role here because of its absence. The Hall resistivity in the Dirac metal should be linear in B because the separation between two nodal points, which determines the Hall resistivity, is proportional to B. However, this is not the case here, which suggests the essential roles of exotic mechanisms for the AHE in ZrTe5. Relatively large ρ0 and the occurrence of the AHE are connected with a low carrier density. We analysed the Hall resistivity at T = 200 K to estimate the carrier density, as illustrated in Fig. 1d [Supplementary Fig. 2d]. We selected T = 200 K because the S11, S12, and S13 samples show the AHE at low temperatures. The S11, S12, and S13 samples have the smallest carrier density n at T = 200 K among the S1–S13 samples. Consequently, these three samples are located at the lower-right corner of the |n | -ρ0 plane, as shown in Fig. 1e. In a previous study, the researchers argued that charge puddles significantly affect their low-carrier-density ZrTe5 samples29. Our system also displays low carrier density, but at ~1019 cm−3, it is notably higher than the ~1016 cm−3 density reported in the previous report. This likely leads to a less substantial influence of charge puddles on our sample, as the higher carrier density suppresses the formation of charge inhomogeneities.

In S11, S12, and S13, we observe a negative LMR. Supplementary Fig. 3a displays the LMR at T = 1.7 K. A dip exists near B = 0 T, which was attributed to a weak antilocalization effect in a previous study12,52. Outside the dip region, the MR decreases with increasing B. Interestingly, the magnitude of the negative LMR at B = + 9 T scales well with ρ0 and the magnitude of the anomalous Hall conductivity σAHE at B = + 9 T [Supplementary Fig. 3b]. To determine the temperature at which the negative LMR and anomalous Hall conductivity vanish, we measured the LMR and anomalous Hall conductivity at different temperatures. At low temperatures, the MR is negative. With increasing temperature, the MR undergoes a sign change. A crossover from a negative MR to a positive MR occurs at approximately 80 K. Similarly, a very pronounced σAHE is observed at low temperatures, reaching 3 kΩ−1 cm−1 at T = 1.7 K for the S11 sample. With increasing temperature, σAHE decreases and eventually vanishes above approximately 80 K. To quantify the magnitude of the negative LMR, we analysed the negative LMR based on the weak-field conductivity formula for a Weyl metal12. In this formula, the B dependence of the conductivity \({{\sigma }}_{{{{{{\rm{L}}}}}}}(B)\) is given by \({{\sigma }}_{{{{{{\rm{L}}}}}}}(B)=(1+{C}_{{{{{{\rm{W}}}}}}}{B}^{2})\cdot {{\sigma }}_{{{{{{\rm{WAL}}}}}}}\). Here, \({C}_{{{{{{\rm{W}}}}}}}\) is a correction factor for a negative LMR due to the chiral anomaly, and \({{\sigma }}_{{{{{{\rm{WAL}}}}}}}\) is the conductivity with weak antilocalization correction. The conductivity from other electron or hole carriers \({{\sigma }}_{{{{{{\rm{n}}}}}}}\) is absent due to their nonexistence in ZrTe5, which is supported by the band structure47,48,50. As expected, \({C}_{{{{{{\rm{W}}}}}}}\) decreases with increasing temperature, reaching a zero value at approximately 80 K [Supplementary Fig. 3c–e]. The value of σAHE at B = − 9 T also becomes zero near the same temperature [Supplementary Fig. 3f–h], suggesting a strong correlation between the negative LMR and the AHE [see Supplementary Note 1 for more details].

Current–voltage measurements in different experimental configurations

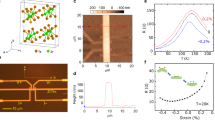
Figure 2 presents the I–V characteristic curves obtained in four different configurations for the S1, S11, S12, and S13 samples. The most remarkable curves are those obtained in the longitudinal configuration with B = + 9 T (E // B), in which the I–V curves become nonlinear for the S11, S12, and S13 samples. The deviation from linearity implies a violation of Ohm’s law10,53, which is impossible in a conventional metallic system. The nonlinearity can be more clearly seen in the difference curve between the data and the linear fitting (the regular residual of the voltage ΔVRR as shown in Fig. 2). Remarkably, a systemic structure, which would not exist if it were due to random errors, is present in this difference curve for the S11, S12, and S13 samples. In contrast, no such structure is detected for the S1 sample. These results suggest that the nonlinearity is genuine, and the AHE, negative LMR, and nonlinear I–V curves share a common origin, i.e., the existence of Weyl nodes. The presence of nonlinear I-V curves is intimately related to the condition of E // B for the S11, S12, and S13 samples. In all the conditions other than E // B that we investigated (B = 0, E ⊥ B, and in-plane Hall configurations), the I–V curves are strictly linear, and the difference curve has no apparent structure. We effectively eliminated the heating effect, as demonstrated in Supplementary Fig. 4 and Supplementary Fig. 5, and established low-resistance contacts with the samples, evidenced by Supplementary Fig. 6. These measures were crucial in further confirming the authenticity of the observed nonlinearity. It is crucial to note that our samples fall within the so-called “dirty” limit, as the lack of Shubnikov-de Haas oscillations indicates. This is consistent with our observed negative LMR, and violation of Ohm’s law found in these samples. These phenomena can be understood within the scope of the quasi-classical Boltzmann transport theory, as described in references10,54. This theory implies that the system operates in a quasi-classical regime, where Landau quantization is smeared out due to disorder. The ‘dirtiness’ of our samples should not be interpreted as poor quality but rather an indication of a specific charge transport regime induced by a high level of disorder.

Fig. 2: Current–voltage measurements in different experimental configurations.
figure 2

a–d Voltage V as a function of current I at T = 1.7 K in the longitudinal configuration (B//I) at B = 9 T, at B = 0 T, in the transverse configuration (B⊥I) at B = 9 T, and in the in-plane Hall configuration at B = 9 T, respectively, and corresponding regular residual data obtained by subtraction of a linear slope for four different samples S11, S12, S13, and S1. The current–voltage curve is nonlinear only in the longitudinal configuration. The corresponding insets show a schematic diagram of the experimental setup.

Full size image

Field-temperature dependence of the nonlinear conductivity

Next, we examined the field and temperature dependence of the nonlinear I–V curves. The deviation ΔI from the linear curve with a slope at V = 0 was defined to quantify the magnitude of the nonlinearity for the S11 sample, as shown in Fig. 3c, d. In the longitudinal configuration (E // B) [Fig. 3a], ΔI becomes larger overall with increasing B and decreasing T. Notably, the nonzero ΔI persists up to T* ~ 30 K, which is a slightly higher temperature than that in the case of Bi1-xSbx (x = 3-4%)10,53. Remarkably, T* is quite close to the peak temperature in the temperature dependence of the resistivity44,45. As the TPT with an intermediate Dirac metallic state was reported to reside near this peak temperature, T* is identified as the ‘transition temperature’ of the TPT. Nevertheless, the precise nature of the phase transition in ZrTe5 is still a matter of ongoing debate. Some evidence points towards a transition from a weak TI to a Dirac metal state44,45, while other studies propose the transition stem from a trivial insulator or strong TI state42,43. Unfortunately, our experimental setup does not allow a definitive determination of the initial state, which would likely require more advanced spectroscopic techniques. From the nonlinear I–V curves, we calculated the nonlinear longitudinal conductivity ΔσL as a function of the voltage V. ΔσL(V) is found to be quadratic in V, as Boltzmann transport theory predicts10,54. As with ΔI, ΔσL increases overall with increasing B [Fig. 3e] and decreasing T [Fig. 3f]. The B dependence of ΔσL is well described by the formula \({\Delta }{{\sigma }}_{{{{{{\rm{L}}}}}}}={b}_{2}(B)\cdot {E}^{2}\), with \({b}_{2}(B)={C}^{(2)}{B}^{2}+{C}^{(1)}{B}^{4}\). This experimental result is in perfect agreement with the previous results [10], ensuring the validity of Fig. 3g. The temperature dependence of ΔσL was also investigated, as shown in Fig. 3h, and \({b}_{2}(T)\) vanishes at T* ~ 30 K. \({b}_{2}(T)\) is well described by the formula \({b}_{2}(T)={b}_{2}(0)\cdot [1-{(T/{T}^{\ast })}^{t}]\), where b2(0) is a coefficient and t is the characteristic exponent [t = 1.2]. The T* extracted is consistent with the temperature at which b2 vanishes. Our ZrTe5 samples, which undergo a transition around 30 K, display low carrier densities [see Supplementary Note 2, Supplementary Figs. 7–10 for more details]. However, our observations of linear I–V curves in the E and B configurations other than E // B imply a persisting metallic state. Moreover, there are ARPES results confirming the presence of Fermi surfaces for the samples whose properties are similar to ours42.

Fig. 3: Negative longitudinal magnetoresistance and field/temperature dependence of the nonlinear conductivity.
figure 3

a Schematic diagram of the longitudinal experiment (B//I). b Longitudinal magnetoresistance (LMR) measurement for sample S11 at different temperatures. Here, the MR is defined as [ρ(B)- ρ(0)]/ρ(0) × 100. The negative MR turns into a positive MR at approximately 80 K. c, d ΔI curves obtained by subtraction of a linear slope in different magnetic fields B at T = 1.7 K and at different temperatures at B = 9 T, respectively. ΔI is a measure of the nonlinearity. e, f Nonlinear longitudinal conductivity ΔσL as a function of voltage at different magnetic fields B and temperatures T, respectively. The quadratic dependence of ΔσL on the voltage is consistent with theoretical calculations based on the Boltzmann transport equation10,54. g B dependence of b2 extracted from the conductivity curves in e. b2 follows the relation \({b}_{2}(B)={C}^{(2)}{B}^{2}+{C}^{(1)}{B}^{4}\), which is also in agreement with the Boltzmann transport approach10,54. h Temperature dependence of b2 extracted from the conductivity curves in f. b2 vanishes at T* ~ 30 K.

Full size image

Field-temperature dependence of the nonlinear Hall effect

Now, we discuss the nonlinear Hall voltages Vxy probed for E ⊥ B [Fig. 4a]. At a low electric field, we first measured the B dependence of Vxx and Vxy and converted it into that of σxx and σAHE [Fig. 4b]. Unexpectedly, we observe that the Vxy signals are nonlinear in the electric current. Here, we present ΔVxy, in which the part linear in the current has been subtracted. As shown in Fig. 4c, ΔVxy is substantial at high currents. We rule out the heating effect as the origin of the nonlinearity in ΔVxy because the nonlinearity is absent at B = 0. ΔVxy systematically varies with B, but unusually, the values at B = +9 T and −9 T are different. This is because ΔVxy contains signals both symmetric and antisymmetric with respect to B. If ΔVxy is a ‘Hall’ signal, then it should be antisymmetric. Thus, we consider the possibility that ΔVxy is contaminated by the symmetric signals resulting from ΔσL due to the slight misalignment of the contacts and the B direction. We antisymmetrize ΔVxy to remove the symmetric component and obtain the antisymmetric component \({\Delta }{V}_{xy}^{{{{{{\rm{A}}}}}}}\). We find \({\Delta }{V}_{xy}^{{{{{{\rm{A}}}}}}}=\alpha \cdot {I}^{3}\). α is almost linear in B, as shown in Fig. 4e, and vanishes around T* ~ 30 K, where ΔσL also vanishes even though α is small above 20 K [Fig. 4f]. Using the nonlinear Hall voltage \({\Delta }{V}_{xy}^{{{{{{\rm{A}}}}}}}\) and the resistivity-to-conductivity conversion method, we calculate Δσxy and find that it follows \({\Delta }{{\sigma }}_{xy}=\beta \cdot {I}^{2}\)[see Supplementary Note 3]. A second-order nonlinear Hall effect was reported18,22,55,56,57, which follows the relation \({J}_{\alpha }={\chi }_{\alpha \beta \gamma }{E}_{\beta }{E}_{\gamma }\), where \({J}_{\alpha }\), \({E}_{\beta }\), and \({\chi }_{\alpha \beta \gamma }\) are the current in the α direction, electric field in the β direction, and nonlinear conductivity tensor, respectively. This second-order nonlinear Hall effect, originating from the Berry curvature dipole and observed in a system with broken inversion symmetry at B = 0, gives rise to a nonlinear Hall voltage quadratic in E. The \({\Delta }{V}_{xy}^{{{{{{\rm{A}}}}}}}\) that we observe is therefore not the signal from this second-order nonlinear Hall effect as shown in Supplementary Fig. 11 due to the third-order nature of \({\Delta }{V}_{xy}^{{{{{{\rm{A}}}}}}}\), i.e., \({\Delta }{V}_{xy}^{{{{{{\rm{A}}}}}}}=\alpha \cdot {I}^{3}\). This third-order nonlinear Hall effect is also observed in AC transport experiments [Supplementary Fig. 12 and Supplementary Note 4]. These observations are consistent with the presence of inversion symmetry within our system. The third-order nature of the effect aligns with our understanding that the ZrTe5 studied here is a centrosymmetric system. This consistency corroborates our experimental findings and the theoretical expectations for such a system.

Fig. 4: Anomalous Hall conductivity and field/temperature dependence of the nonlinear Hall effect.
figure 4

a Schematic diagram of the transverse configuration (B⊥I). b Anomalous Hall conductivity for the S11 sample at different temperatures. The nature of the curves changes at T* ~ 30 K. c, d Antisymmetrized nonlinear Hall voltage \({\Delta }{V}_{xy}^{{{{{{\rm{A}}}}}}}\). These curves are obtained by subtracting the linear component and then performing antisymmetrization. The dotted curve is a fit based on \({\Delta }{V}_{xy}^{{{{{{\rm{A}}}}}}}=\alpha {I}^{3}\). e, f Coefficient α obtained from the fit of c, d as a function of magnetic field B and temperature T, respectively. g, h Nonlinear Hall conductance Δσxy as a function of the applied current at different magnetic fields B and temperatures T, respectively. Both α and Δσxy vanish at T* ~ 30 K.

Full size image

Scaling relations among linear and nonlinear conductivities

For ferromagnetic metals that exhibit the AHE, three different scaling regimes exist between σxy and σxx depending on their mechanisms: σxy ~ (σxx)1.6, σxy ~ const., and σxy ~ σxx58,59,60. The first relationship holds when the side jump is dominant. In contrast, the last regime occurs when skew scattering is the main factor in the super clean limit. A constant σxy implies that the Berry curvature governs the AHE. To understand the underlying mechanism for the AHE of ZrTe5, we derived the scaling relation between σAHE and σxx. The scaling relationship in a log–log plot is displayed in Fig. 5a, where interesting structures exist, with a linear scaling curve in the upper part and three parallel lines with an exponent of ~ 3 in the lower part. The former curve is composed of the low-temperature data (T = 1.7 K, 10 K, and 30 K), where the σAHE(B) curve shows an abrupt step near B = 0 T. In contrast, the three parallel lines present below this scaling curve consist of the high-temperature data (T = 40 K, 50 K, and 70 K). At these high temperatures, σAHE(B) is more rounded compared to low temperature σAHE(B) [Fig. 4b]. The different exponents in the scaling relations indicate different mechanisms for the AHE in ZrTe5 at different temperatures. The scaling exponent of ~ 1 suggests that ZrTe5 belongs to the skew-scattering-dominant region [Fig. 5b]. In contrast, the scaling exponent of ~ 3 has not yet been reported. However, regardless of the exponent value, the entire scaling curves for the S11-S13 samples are located in the intrinsic region of the phase diagram because of low σxx values. This discrepancy may be due to the inapplicability of the frameworks developed for ferromagnetic metals to nonmagnetic topological metals such as ZrTe5.

Fig. 5: Scaling relations among linear and nonlinear conductivities.
figure 5

a σAHE versus σxx for the S11, S12 and S13 samples in log-log plot. The upper curve shows an exponent of ~ 1, and the three lower curves exhibit an exponent of ~ 3. The exponent of ~ 1, which occurs below T* ~ 30 K, implies that the samples are in the skew-scattering region, whereas the exponent of ~ 3, which covers the temperature region between 40 K and 70 K, has not yet been reported in the conductivity scaling of ferromagnetic metals. b σAHE versus σxx for a variety of materials58,60,64,65,66 spanning the various anomalous Hall effect regimes from the side-jump regime to the intrinsic and skew-scattering regimes. Regardless of the exponent value, all the scaling curves for the S11, S12, and S13 samples reside in the intrinsic region of the phase diagram because of low σxx values. The discrepancy between the exponent value and the region of the scaling law is not well understood, and the origin of σAHE has not been clarified. c Scaling relation between b2 and anomalous Hall conductivity σAHE. b2 follows b2 ~ (σAHE)3. While the scaling for the linear conductivities (σAHE and σxx) holds below ~ 80 K, this nonlinear scaling curve holds below T* ~ 30 K. This nonlinear scaling may be a property of the skew-scattering region below T* ~ 30 K. d A scaling relation exists between ΔσL and Δσxy at a given voltage and below T* ~ 30 K. This scaling curve undergoes a crossover from the region of an exponent of one at low conductivities (high temperatures) [Δσxy ~ ΔσL] to the region of an exponent of two at high conductivities (low temperatures) [Δσxy ~ (ΔσL)2]. While simple dimensional analysis applies to the low conductivity region [Δσxy ~ ΔσL], it cannot explain the scaling relation at high conductivities [Δσxy ~ (ΔσL)2].

Full size image

In the skew-scattering region [σAHE ~ σxx], other scaling relations are uncovered. The first is the scaling relation between the nonlinear transport coefficient b2(B) (or ΔσL) and σAHE. Figure 5c shows a linear scaling curve with a slope of ~3 in the log-log plot between b2(B) and σAHE. This linearity, which implies a power-law behaviour with an exponent of ~3, holds in a given sample and among different samples. Additionally, all the curves at different B are scaled into a single universal curve when b2 is divided by B2.8 [Fig. 5c]. Thus, all these scaling analyses suggest b2(B) ~(σAHE)3·B2.8. This scaling relation between b2(B) and σAHE has not been previously observed. While σAHE is a property of both the Fermi sphere and Fermi surface caused by nonzero Berry curvature61, ΔσL is solely a contribution of the Fermi surface originating from the chiral anomaly according to the previous results10. Moreover, while σAHE is given by the second-order current-current correlation function ~ \(\langle {j}^{2}\rangle\), where j is the current density, b2(B) is given by the fourth-order current-current-current-current correlation function ~ \(\langle {j}^{4}\rangle\). Thus, the scaling relation of b2(B) ~ (σAHE)3 indicates that naive dimensional analysis does not work.

We also found another interesting scaling relation between Δσxy and ΔσL at a given voltage, as presented in Fig. 5d [Supplementary Fig. 13]. It also occurs in the skew-scattering region [σAHE ~ σxx]. The slope of this log-log plot changes from ~ 1 at low ΔσL to ~ 2 at high ΔσL, suggesting that different scaling regions may exist. The lower slope at low ΔσL indicates that the naive dimensional analysis holds, distinct from the scaling relation of b2 ~(σAHE)3. In contrast, the higher slope suggests that this simple picture breaks down. At different voltages, the observed curve shapes are similar [Supplementary Fig. 3]. Along with b2(B) ~ (σAHE)3, this scaling relation with a crossover extends the scaling law of the AHE from the linear to nonlinear regime. The linear scaling law between σAHE and σxx has been a guideline to interpret the linear AHE. Likewise, the extended scaling relations provide a framework to understand the mechanisms of nonlinear transport coefficients and the influence of Berry curvature. The implication of the nonlinear scaling relation with a crossover is the existence of another scaling region that divides the skew-scattering region. At high temperatures in the skew-scattering region, where Δσxy and ΔσL are small, simple dimensional analysis applies for both nonlinear scaling relations. Therefore, the region of importance is the new low temperature region where Δσxy ~ (ΔσL)2 is satisfied [see Supplementary Note 5 for more details]. To clarify the nature of this region, further theoretical studies are needed.

Discussion

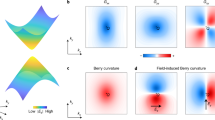
The observation of nonlinear electrical responses, such as the violation of Ohm’s law and the third-order nonlinear Hall effect, in ZrTe5 is quite surprising because such responses are believed to be impossible in metals in the diffusive limit. Without a nontrivial band topology, this would not occur in ZrTe5. For the E // B configuration, a finite difference in the Fermi energy of 2μ5 is developed owing to the chiral anomaly. The carriers corresponding to the 2μ5 range respond to the external perturbations E and B. This situation drastically differs from the metals with a trivial band topology, where only a tiny fraction of carriers at the Fermi energy reacts to the perturbations. This is why the violation of Ohm’s law is present in the Weyl metallic state realized for E // B. The Boltzmann transport theory that considers the above mechanism successfully described the experimental results54. Thus, the present result implies that Ohm’s law can be violated in other Weyl and topological metals with similar band topologies. However, the Weyl metal picture cannot explain all the experimental results in the present study. First, the presence of the \({\Delta }{V}_{xy}^{{{{{{\rm{A}}}}}}}\) signals in the transverse configuration (B ⊥ E) cannot be elucidated by the chiral anomaly effect because of the perpendicular field configuration. One possible origin is the recently reported third-order nonlinear Hall effect26. This Hall effect results from the BCP tensor19,25,26. BCP is an intrinsic band geometric quantity that characterizes the positional shift of Bloch electrons under applied E and B fields. It should be strongly enhanced in small gap regions, especially band degeneracies. Phenomenologically, \({\Delta }{V}_{xy}^{{{{{{\rm{A}}}}}}}\) proportional to I3 (or E3) is consistent with the third-order nature expected by the BCP scenario. However, the possibility that BCP alone can fully explain the finite \({\Delta }{V}_{xy}^{{{{{{\rm{A}}}}}}}\) at B ≠ 0 is unlikely. It cannot explain ΔσL below T* ~ 30 K. Irrespective of the BCP scenario as a relevant one for the third-order nonlinear Hall effect in ZrTe5, one notable point is the possible change in the band topology at T*, which is not detected in the linear transport coefficients. This may be because nonlinear conductivities are more sensitive to changes in the band topology, such as the Berry curvature dipole, BCP, and chiral anomaly, reflecting the nature of the wavefunctions. Another possible origin of nonlinear conductivities is ballistic conduction29,62. However, this scenario is not relevant to the present case, as previously discussed. While the scaling laws among different linear and nonlinear conductivities suggest essential influences of the nontrivial band topology on these conductivities, the origin of the nonlinear Hall conductivity still needs to be completely understood. Thus, this calls for further theoretical and experimental studies that can reveal a solid connection between the band topology and nonlinear responses in topological materials.

Conclusion

In conclusion, by uncovering a violation of Ohm’s law and the third-order Hall effect, we could identify the temperature at which a TPT occurs in ZrTe5. While a subtle change in the band topology is hidden in linear transport coefficients, it is detected by nonlinear conductivities due to the sensitivity of nonlinear transport to the band topology. In addition, we propose scaling relations for both linear and nonlinear transport coefficients, extending the existing scaling theory between linear transport coefficients. The microscopic mechanism for this generalized scaling theory is elusive at present, and thus, determining this mechanism is an interesting future problem to consider by taking into account the interplay between Berry curvature and disorder scattering. The role of disorder scattering in nonlinear transport coefficients has not been appropriately addressed, in which various geometrical objects27 associated with the Berry curvature would affect the scaling relation. Even for a typical ferromagnetic metal, verifying the interplay between disorder scattering and Berry curvature in nonlinear transport coefficients remains an interesting future study.

Methods

Sample synthesis and characterization

The ZrTe5 single crystals used in this study were grown by the Te-flux method. High-purity Zr and Te with an elemental ratio of Zr0.0025Te0.9975 were sealed under vacuum in a double-walled quartz ampoule. As the melting (Tm) and remelting (Trm) temperatures are the main growth parameters during the flux method process, we explored their effects on the growth of the ZrTe5 single crystal. They control the amount of Te deficiency, which determines the position of the Fermi energy as a dopant. We heated the sealed ampoules to Tm in a box furnace and left them at that temperature for 12 h to achieve homogeneity. The furnace was cooled to Trm and further cooled to 420 °C in 60 h. The ZrTe5 crystals were isolated from the Te flux by centrifugation at 420 °C. The flux-grown ZrTe5 crystals had a needle shape with a typical size of approximately 1.20–5 mm in length and 0.01–0.23 mm in the other two dimensions. We systematically varied the melting temperature Tm between 900 °C and 1000 °C and the remelting temperature Trm between 650 °C and 500 °C and grew thirteen high-quality ZrTe5 single crystals. We thoroughly investigated the potential interference of trapped flux inclusions in our measurements by performing comprehensive Energy-Dispersive X-ray spectroscopy (EDX) mapping on our samples as shown in Supplementary Fig. 1. This process helped us assess the uniformity of the sample composition, thereby validating the optimal quality of ZrTe5. Our EDX results reveal that the atomic ratio of S11, S12, and S13 among thirteen single crystals are close to stoichiometry [Supplementary Table 1]. Hence, it is improbable that our findings would be influenced by potential anomalies, such as trapped flux inclusions.

Transport measurements

Electrical and MR transport measurements of the ZrTe5 single crystals were performed in a cryogen-free magnet system (Cryogenic, Inc.) from 1.7 to 300 K and from B = − 9 T to B = + 9 T using the six-probe method. In the longitudinal configuration, B and I were applied parallel in the ac-plane (B // I // a), while in the transverse configuration (E ⊥ B), B was applied along the b-axis (B // b) and I in the ac-plane (I // a). Those single crystals close to stoichiometry showed a pronounced negative LMR and a large anomalous effect. We conducted current-voltage measurements using a current source (Keithley 220) and a nanovoltmeter (Agilent 34420 A) to examine the signature of nonlinear electrical transport phenomena. Third harmonic signals in the Hall (transverse) channel were measured using lock-in amplifiers (NF Corporation LI 5640 and Stanford Research Systems SR830) with excitation frequencies between 77 Hz and 2177 Hz. A voltage-to-current converter (Stanford Research Systems CS580) supplied a sinusoidal current with a constant amplitude to the samples. We carefully monitored the temperature stability in all the experiments and successfully ruled out the heating effect as the origin of the nonlinear transport phenomena. We limited the applied current to below the value of a sudden slope change in the I–V curves when sample heating was induced. Additionally, we conducted additional measurements with a thermometer attached directly to the sample, providing real-time thermal data [Supplementary Fig. 4]. Furthermore, measurements were performed on the same sample with different distances between contacts [Supplementary Fig. 5], which provided further evidence to confirm the stability of the sample under the experimental conditions. This comprehensive approach has allowed us to convincingly rule out heating effects as a contributing factor to the nonlinear transport phenomena observed.

Next, we tackle the issue of establishing low-resistance contacts with these samples, a challenge that we met by adopting the methods outlined in the provided references, thus ensuring the quality of our contacts. We have gathered comprehensive evidence to validate the quality of our contacts, including measurements of contact resistance at 2 K, 2-point IV curves, as well as 4-point IV curves using voltage probes at varying contact distances measured on the same sample [Supplementary Fig. 6]. This evidence affirms our ability to maintain low-resistance contacts, a critical factor in our investigations.