Main

Creating materials with tailored properties has gained popularity across disciplines since additive manufacturing enabled the manipulation of multi-material and cellular architectures across scales. Instead of choosing from the limited catalogue of natural materials, engineers and designers now have access to the drastically expanded design and property spaces of so-called metamaterials, which have been designed, among others, to achieve mechanical properties previously not attainable. Realizations of metamaterials have various forms, most commonly involving the periodic arrangements of small-scale structural building blocks1,2,3.

The physical mechanisms governing the mechanical behaviour of such architected materials are mostly well understood, and various numerical frameworks such as the finite element (FE) method provide accurate structure-to-property relations, predicting the effective material properties based on an underlying small-scale architecture. By contrast, the inverse problem of identifying possible small-scale designs yielding a desired property has remained a challenge. Methods to address the latter include topology optimization4,5,6 and, more recently, data-driven algorithms. Most of these approaches have, however, been restricted to linear material properties such as the effective elastic stiffness in three dimensions7,8 or Poisson’s ratio9. Extensions to nonlinearity (for example, via multi-material configurations) have been presented recently10 but involve computationally expensive simulations. To the best of our knowledge, there is no topology optimization technique that is suitable for the complex mechanical set-up studied here, including large deformation, nonlinear material behaviour including plasticity, structural buckling and frictional contact, although these are relevant effects in structures undergoing large deformation.

While tuning a material’s stiffness is sufficient for applications involving small deformation (such as patient-specific bone implants matching the native bone properties, or vibration insulation by attenuating linear waves), controlling the nonlinear response of soft metamaterials over a finite deformation path can unlock advanced functionality for emerging fields such as soft robotics11, tissue engineering12 and impact energy absorption13. Metamaterials with tailored stress–strain responses can, for example, mimic the nonlinear response of human fingers14, enable actuation of soft robots via ‘snap-through instabilities’15 or serve as biomimetic scaffolds assisting in artery restoration16.

Unfortunately, the nonlinear setting markedly adds to the complexity of the (inverse) map from property to structure. Extensions of topology optimization to nonlinear properties exist17,18 but remain challenging due to strong dependence on the initial guess and discretization19, lack of physical effects such as contact20 and degrading solver stability when considering non-trivial mechanisms such as post-buckling21. Most importantly, a single optimization study may require hours of runtime, which is a prime reason why recent studies focused on rather simple design spaces and optimization objectives22,23.

Over the past decade, the rise of deep learning models with their unparalleled ability to identify highly nonlinear maps has presented a potential alternative. When applied to nonlinear material property prediction, deep learning has served as an efficient forward approximation (replacing costly FE simulations) in combination with genetic algorithms to iteratively identify structures with tailored buckling strength24 and as-designed deformed configurations25, with extensions to the full nonlinear response via shell-like metamaterials and quadrilateral structures26,27. However, the considered design spaces have remained limited, and predictions may lack physical intuition and rely on costly FE simulations to validate up to a hundred generated designs and to select the one closest to the desired stress–strain response27. In addition, generative models such as variational autoencoders and generative adversarial networks have been explored recently, although these have mainly been restricted to linear properties28,29 with extensions to the compressive strength30, but far from nonlinear material behaviour including plasticity, buckling and frictional contact.

These challenges resemble those addressed recently in the image-generation community by (video) diffusion models. Diffusion models31 have gained attention due to their ability to generate seemingly photo-realistic images based on text descriptors, a famous representative being DALL-E 2 (ref. 32), and have recently been extended to generate short video sequences with remarkable results33. Compared with variational autoencoders34 or generative adversarial networks35, diffusion models offer improved sample quality36 and more stable training protocols. This has also been confirmed in the context of mechanical optimization37. Such data-driven models operate by iteratively removing noise from a sample drawn from a prior distribution (typically unit Gaussian), which comes with an increased computational cost due to the multiple forward passes required.

The shift from linear to nonlinear material properties can, at a high level, be compared with going from image to video generation. In both cases, a new data dimension must be learned, which requires some notion of consistency—whether in a temporal (consecutive images in a video must maintain temporal consistency) or mechanical (stresses in consecutive deformation steps must ensure mechanical consistency) sense. Analogous to a text descriptor prompting an image sequence, the nonlinear target response here serves as input to predict a sequence of mechanically deformed microstructural configurations along the deformation path, ultimately resulting in the effective stress–strain response. This requires the definition of an efficient design/property space to be considered as training data for our generative model, the key concepts and the considered model architecture of which are summarized in the following.

Results

Generation of metamaterials with diverse properties

As our diffusion framework operates in a data-driven setting, we require a large collection of paired mechanical designs and their corresponding nonlinear stress–strain responses. The options for potential design spaces are virtually unlimited, ranging from truss descriptors7 over shells2 to composite structures38. We here consider a pixel-based design space parameterization with minimal constraints (aside from a periodic structure) to fully harness the generative power of diffusion models. While two-material composites could be generated with randomly drawn binary pixels and span a tremendous design space38, the subset of structures with a non-trivial stress–strain response is comparably small. We therefore consider cellular structures (each pixel representing solid or void) as our design space to enable interesting mechanical behaviour such as buckling—an instability that quickly transitions between distinct equilibrium configurations—and contact, arising under compressive loads and producing a sudden stiffness increase, overall resulting in a rich and possibly non-monotonic stress–strain curve. Although modelling these effects using the FE method is challenging, inversely designing such structures is even more difficult due to the sensitivity of, for example, the buckling response to small changes in the design. At the same time, incorporating such effects guarantees a highly diverse range of achievable stress–strain responses. To keep the problem tractable yet without loss of generality, we restrict our study to two dimensions and a periodic structure based on a square unit cell (UC).

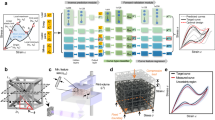
The generation of the dataset used for model training is performed as follows (Fig. 1). To generate a random design with a certain level of structural features, we sample from a two-dimensional (2D) Gaussian random field on a square domain and apply a binary threshold. Values above a specific threshold are considered material; those below are void. We ensure that opposite boundaries of the domain are connected with each other (and repeat the sampling until this condition is met) and mirror the pattern sequentially along both edges (Fig. 1) to obtain mechanically intricate, periodic structures. Despite its simplicity, this stochastic approach produces a diverse dataset of designs with a broad range of stress–strain responses. We further induce different levels of relative density (or fill fraction) by randomly shifting the threshold within a specified range. Higher values promote low-density structures prone to buckling, which is important for the aforementioned reasons.

Fig. 1: Metamaterial generation process.
figure 1

a, A 2D cellular UC is generated by sampling from a 2D Gaussian random field, applying a varying threshold to extract a binary field and mirroring the resulting pattern when connectivity to the boundaries is ensured. b, To obtain the stress–strain response, we place the UC between two rigid plates with periodic boundary conditions in the horizontal direction and apply a compressive strain of up to 20%. The corresponding stress and displacement fields within the UC are computed by FE simulations, and the overall effective stress–strain response σeff (indicated in black) is extracted from the nodal reaction forces, although they can be equally obtained from the full-field data. A representative selection of responses of the generated designs is plotted in grey.

Full size image

The stress–strain response of each design is obtained from FE simulations. As a technologically relevant load case, we place all samples between two rigid plates and apply a quasi-static compressive strain of up to ε = 20% in the vertical direction. Uniaxial compression is a frequent load characteristic of, for example, impact applications26, the compression of shoe soles39 or so-called passive compliance in soft robotics (for example, allowing a soft gripper to adapt its shape to the object being grabbed40). By applying periodic boundary conditions along the horizontal directions, we simulate an infinite periodic layer of the chosen design, as found in sandwich-type configurations. Within the cellular UC, we account for frictional contact and use an experimentally calibrated elastoplastic material model 41 (representative of a thermoplastic resin) to ensure realistic responses. Simulation details are provided in Methods.

Using this set-up, we generate 53,007 pairs of unique designs and the corresponding stress–strain responses. We also collect the full-field stress distribution in the vertical direction, σ22, as well as displacement components u1 and u2 (all in the Lagrangian frame), as these data contain valuable information about the underlying physics, as also observed in ref. 42. The overall effective stress response can be extracted either from the nodal reaction forces or directly from the full-field data, as in the considered quasi-static setting, internal forces must be in equilibrium for any free cut of the UC (for example, for any pixel row; Supplementary Section 5.1). We evaluate all fields on a 96 × 96 pixel grid together with the overall (average) vertical stress at 11 equidistant strain increments between 0 and 20% (see Methods for further details). This strikes a reasonable balance between accuracy and computational feasibility and provides the training data for the generative model.

Video denoising diffusion model

Diffusion models are trained to reverse a stochastic forward process that gradually converts a data point x0 (for example, an image) drawn from the underlying data distribution x0 ∼ q(x) to a prior distribution in T steps, typically a standard Gaussian31,43 \(\mathcal{N}(\bf{0},I)\), where I is the identity matrix. This can formally be understood as a fixed Markov chain with Gaussian transitions parameterized by a given variance schedule \({\left\{{\beta }_{t}\in (0,1)\right\}}_{t = 1}^{T}\) as

$$\begin{array}{rcl}q({{{{\bf{x}}}}}_{1:T}| {{{{\bf{x}}}}}_{0})&=& \mathop{\prod }\limits_{t=1}^{T}q({{{{\bf{x}}}}}_{t}| {{{{\bf{x}}}}}_{t-1}), \\ q({{{{\bf{x}}}}}_{t}| {{{{\bf{x}}}}}_{t-1})&=&{{{\mathcal{N}}}}({{{{\bf{x}}}}}_{t};\sqrt{1-{\beta }_{t}}{{{{\bf{x}}}}}_{t-1},{\beta }_{t}{{{I}}}).\end{array}$$
(1)

This allows to sample xt at any time step t via \({\bf{x}}_{t}=\sqrt{{\bar{\alpha }}_{t}}{{{{\bf{x}}}}}_{0}+\sqrt{1-{\bar{\alpha }}_{t}}{{{\bf{\upepsilon }}}}\) with \({{{\bf{\upepsilon }}}} \sim {{{\mathcal{N}}}}({{{\bf{0}}}},{{{I}}})\) and where \({\bar{\alpha }}_{t}=\mathop{\prod }\nolimits_{i = 1}^{t}{\alpha }_{i},\,{\alpha }_{t}=1-{\beta }_{t}\).

We approximate the reverse process q(xt−1∣xt) by a neural network pθ(xt−1∣ xt) parameterized by θ. To generate new samples x* ∼ q(x), we run the reverse Markov chain to arrive at

$$\begin{array}{rcl}{p}_{\theta }({{{{\bf{x}}}}}_{0:T})&=& p({{{{\bf{x}}}}}_{T})\mathop{\prod }\limits_{t=1}^{T}{p}_{\theta }({{{{\bf{x}}}}}_{t-1}| {{{{\bf{x}}}}}_{t}),\\ {p}_{\theta }({{{{\bf{x}}}}}_{t-1}| {{{{\bf{x}}}}}_{t}) &=& {{{\mathcal{N}}}}({{{{\bf{x}}}}}_{t-1};{{{{\bf{\upmu }}}}}_{\theta }({{{{\bf{x}}}}}_{t},t),{{{\Sigma}}}({{{{\bf{x}}}}}_{t},t)),\end{array}$$
(2)

where μθ is the predicted mean and we set the covariance to be purely time dependent: \(\Sigma({\mathbf{x}}_t,t)=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t} \beta_t I\) 43. Such models are typically trained to maximize the variational lower bound of the log-likelihood, which can be computed in closed form when conditioned on x0. As observed in ref. 43, μθ can be decoupled into two terms relating to xt and ϵθ, allowing to simplify and re-parameterize the loss in terms of the Gaussian noise as

$${{{\mathcal{L}}}}(\theta )={{\mathbb{E}}}_{t,{{{{\bf{x}}}}}_{0},\epsilon }\left[\left\vert {{{\bf{\epsilon }}}}-{{{{\bf{\epsilon }}}}}_{\theta }\left({{{{\bf{x}}}}}_{t},t\right)\right\vert \right].$$
(3)

To condition the model on some additional input c, we consider classifier-free guidance44, not requiring an additional classifier pθ(c∣xt). We steer the reverse diffusion process by replacing ϵθ by a linear combination of the conditional and unconditional noise estimates, that is

$${\tilde{{{{\bf{\epsilon }}}}}}_{\theta }\left({{{{\bf{x}}}}}_{t},{{{\bf{c}}}}\right)={{{{\bf{\upepsilon }}}}}_{\theta }\left({{{{\bf{x}}}}}_{t},{{{\bf{c}}}}={{\emptyset}}\right)+w\left[{{{{\bf{\upepsilon }}}}}_{\theta }\left({{{{\bf{x}}}}}_{t},{{{\bf{c}}}}\right)-{{{{\bf{\upepsilon }}}}}_{\theta }\left({{{{\bf{x}}}}}_{t},{{{\bf{c}}}}={{\emptyset}}\right)\right],$$
(4)

where w ≥ 1 is the guidance weight, allowing to trade-off sample quality with conditioning augmentation, and \({{\emptyset}}\) denotes a fixed random embedding to represent the lack of conditioning. Details are provided in Supplementary Section 2.

Diffusion models map noisy input data to less distorted data, making symmetric U-Net architectures45 a common choice for ϵθ. As our primary interest is in mapping from a target stress–strain curve to a design, training the model on simple images of UCs conditioned on the corresponding stress–strain curve is a straightforward approach and has been explored in recent work46. In our investigations, we observed similar success of such approaches for generating structures with a relatively simple stress–strain response (like the ones shown in ref. 46). However, the same set-up proved ineffective in modelling more challenging responses such as those induced by contact and buckling. We attribute this limitation to the highly indirect mapping the model must learn—from geometry to response (or vice versa) with no direct knowledge of the full deformation history and the corresponding internal stress distributions (which in turn dictate the sought effective response). To facilitate the training, to improve the sample efficiency and to obtain a full-field prediction of the expected deformation path and internal stresses for physical validation, we train the model not on the UC design but on the full-field data of the vertical stresses σ22 for each strain step, as described in ‘Generation of metamaterials with diverse properties’. We observed the best results when using a Lagrangian frame instead of a Eulerian one (that is, evaluating all evolving fields on the undeformed initial configuration), which we additionally supply with the horizontal and vertical displacements u1 and u2. This allows us to optionally convert data to the Eulerian frame and provide information about the deformation path to the model.

Instead of simply concatenating these data along the image channels of the U-Net, we distinguish between the two fundamentally different causal relations of the data—space and applied strain—similar to recently proposed video generative models33. Here variants of the 2D (space only) U-Net architecture are extended by a temporal dimension, which effectively is treated as a batch axis and thus leaves the base architecture unaffected. The extension is a temporal attention47 block (taking the pixels as batch axis and computing self-attention over the applied strain steps) after the spatial convolution and attention (taking the strain steps as batch axis and computing convolutions and self-attention over the pixels) to learn physical consistency across different strain steps.

This architecture (schematically shown in Fig. 2) allows for mechanically motivated conditioning of the model on a given nonlinear stress–strain response. The conditioned effective stress at the 11 strain steps is directly associated with the corresponding full-field response as mechanical equilibrium requires that the effective, overall stress at any strain level matches the averages of all pixel stress values across any row of pixels in the UC. Unlike in video generation, in which words, as conditioning, do not directly correspond to specific image frames, we can leverage this link in our model architecture by converting each stress value to a high-dimensional token embedding by a (learnable) linear layer and fusing it with the pixel representation via cross-attention47 in the spatial attention module of the corresponding strain step. In the subsequent temporal attention layer across all strain steps, we add a relative position encoding48 to both the strain steps and token embeddings, so that the model receives information on the strain step order, and we apply ‘pseudo-temporal’ cross-attention over the strain steps. Lastly, we augment the conditioning by adding a latent representation of the tokens to the diffusion time embedding (required as input to the model to indicate the diffusion time step). For further details see Methods, Supplementary Sections 3 and 4, and ‘Code availability’.

Fig. 2: Denoising diffusion model architecture.
figure 2

The denoising diffusion model is based on the three-dimensional U-Net video architecture33, which iteratively adds information to a Gaussian prior. To include a temporal dimension, each spatial convolution and attention layer is followed by temporal attention computed over the 11 strain steps. We condition the model by transforming the stress–strain response to a token embedding, which is added via cross-attention into both spatial and temporal attention layers.

Full size image

Full-field predictions for generated metamaterials

A key advantage of our set-up over other deep learning frameworks is its capability to provide physical insight into the deformation mechanisms of the generated metamaterial and the associated stress response. By reversing the diffusion process conditioned on the desired stress–strain curve, we obtain not only a potential design but also a predicted full-field σ22 distribution subjected to the applied strain throughout the deformation path. This enables us to evaluate the proposed deformation mechanism for physical validity and extract the predicted stress–strain response by row-wise pixel averaging of the internal stress σ22. In contrast to alternative approaches46, our framework unifies inverse design and forward prediction in a single model without the need for an ad hoc secondary model to evaluate the performance of the predicted designs. This also allows for the adoption of further design criteria (for example, enforcing a maximum local stress to prevent failure).

We demonstrate the ability of the model to predict designs matching a given target stress–strain response by considering 100 responses of randomly generated designs (unseen during training). For this and subsequent studies, we set the guidance weight to w = 5, as this was observed to enhance the match between generated design and target response without sacrificing the accuracy of the generated full-field predictions. We plot four predictions and their effective responses in Extended Data Figs. 1 and 2, respectively, and compute the average normalized root mean square error (NRMSE; Methods) of the FE-reconstructed response versus the target response as ϵ = 6.98%. This is close to the mismatch of ϵ = 2.74% between the predicted and target responses, which underlines the model’s ability to propose designs and concurrently estimate their mechanical behaviour. The agreement between the predicted and true (that is, high-fidelity FE) responses suggests an accurate estimate of the stress distribution, confirmed both qualitatively in Extended Data Fig. 1 and quantitatively with a relative L2 error of \({\epsilon }_{{{{L}}}_{2}}=14.39 \%\), averaged over all samples and strain steps. (Extended Data Figs. 3 and 4 and Supplementary Section 6.1 summarize a similar study on unconditionally sampled designs.)

Inverse design of unseen stress–strain responses

The above results provide only a limited measure of the model’s generalization performance: although the conditioned stress–strain responses are based on designs not seen during training, they are, on average, well represented by samples in the training data. To assess the model’s generalization capability, we next examine its performance on such responses not closely represented in the training data. We create four benchmark examples of diverse stress–strain responses that cover a wide range of material responses of engineering interest and include the non-trivial mechanisms of contact and buckling. For each case, we leverage the probabilistic nature of the model and generate ten samples conditioned on the target response and plot the best match.

First, we generate a design with high stiffness, strong (nonlinear) hardening and large deformability, as used, for example, in impact applications. We condition the model with an effective stress response 20% above the stiffest sample of the training set. As illustrated in Fig. 3a, the model generates a structure with a large fill fraction, closely matching the ground truth in both the FE-reconstructed response (with ϵ = 1.5%; compared with ϵ = 20% of the best match in the training data) and the underlying stress distribution (ranging from \({\epsilon }_{{{{{\rm{L}}}}}_{2}}=18.2 \%\) to \({\epsilon }_{{{{{\rm{L}}}}}_{2}}=5.8 \%\)). Analogously, compliant low-density designs can be generated by choosing a target stress–strain response well below the most compliant design in the training data (Supplementary Section 6.5), which is matched with ϵ = 4.3%.

Fig. 3: Metamaterial synthesis for four stress–strain responses not represented in the training dataset.
figure 3

a–d, The model is conditioned on four technically relevant, challenging target responses, considering high stiffness in a, non-smooth stress increase in b, high compliance and drastic stiffness increase in c, and softening in d. Validation of the predicted effective stress response σeff (‘Fwd eval.’; NRMSE with respect to the target response in brackets) of the generated designs is achieved by FE simulations (‘FE eval.’), agreeing with the predicted response and substantially outperforming the best match in the training dataset (‘Best match’). We additionally compare the predicted full-field σ22 distribution (indicated in MPa in the Eulerian frame) with the FE ground truth and provide the corresponding relative L2 errors. To highlight the range of responses in the training dataset, we plot a representative selection in grey in a. aThe relative L2 error is numerically inflated due to the small magnitude of the stress field and is hence not truly indicative (but included for completeness).

Full size image

Second, we consider a more complex target response exhibiting an abrupt stiffness increase midway through the loading path (at 10% applied strain; Fig. 3b), which necessitates a change in deformation mode. Such stiffness changes can be leveraged, for example, in soft robotic grippers49. The design proposed by the model indeed closely matches the target response (ϵ = 1.4%) and decidedly outperforms the closest match in the training data (ϵ = 10.1%). Moreover, we observe that the generated design contains a fillet in its interior, which establishes contact at 10% strain in both forward prediction and FE simulation, leading to the desired stiffness increase.

Third, we consider the more exotic target of a highly compliant response until 15% strain, followed by a marked stiffness increase. (Such behaviour can be caused by contact within the UC but is also characteristic of, for example, structural transformations in metals50.) While, as expected, the generated design is not as close as the previous targets (ϵ = 14.1%), it considerably outperforms the best match in the training set (ϵ = 39.6%). The initial compliance and sudden stiffness increase are realized through a delicate interplay of an almost purely rotational, auxetic response of an inner segment of the UC and the subsequent emergence of contact at the critical strain level where hardening sets in (Fig. 3c). Although this does not readily translate into general design guidelines, it highlights that the model allows us to accurately discern the physical rationale behind the proposed design in terms of the full-field deformation and stress response, unlike previous work that mainly focused on the direct property–structure map without such insight. Moreover, the model can introduce unseen contact mechanisms to match unseen responses, while contact has so far been a challenge for, for example, computational topology optimization51. Of course, contact is represented in our dataset. Nevertheless, we emphasize that the trained model creates designs that go substantially beyond simple ‘interpolation’ of the seen structures, such as simple alterations in relative density (which we have verified in Supplementary Section 6.8).

Fourth, we consider a response with notable softening, which is utilized, for example, in snapping and release mechanisms. As illustrated in Fig. 3d, the model’s design again outperforms the best match (ϵ = 2.4% versus ϵ = 8.3%). The response is accommodated by a buckling mechanism. Interestingly, the relative L2 error of the predicted stress fields greatly increases in the post-buckling regime. This, however, stems from the symmetric buckling mode of the design and the fact that the FE simulation buckles to the right while the model predicts buckling to the left. (Buckling is highly sensitive to the design (unlike contact): when a vertical column is compressed in two dimensions, it can buckle to the left or to the right and is sensitive to the smallest imperfections.) In this case, we cannot reasonably expect the model to match this response. Instead, this demonstrates its temporal consistency and logically completes the deformation trajectory—once buckled to the right, the post-buckling follows this trend. (An example of a generated design with a predicted deformation mode matching the FE simulation is shown in Supplementary Section 6.6.) We provide the full image sequence predictions of the considered four target responses in Extended Data Fig. 5 and in video form in Supplementary Videos 1–4. In Extended Data Figs. 6 and 7 and Supplementary Section 6.7, we present additionally generated designs for selected responses and compare them with the underlying ground truth, overall observing notable differences and hence showcasing the generative capabilities of the model.

Discussion

Soft robots and biomimetic structures, among others, require materials with precise nonlinear mechanical functionality—a challenge for conventional optimization techniques due to the complex inherent deformation mechanics including buckling and contact. Gradient-based optimizers may become numerically unstable due to the nonlinear and non-convex objective function. This issue worsens when considering contact, which leads to abrupt, non-smooth kinks in the stress response. Our model, inspired by generative video modelling, is particularly suited to this nonlinear setting and overcomes many of these challenges, although being, from a mechanical perspective, comparably simple to implement. It accurately captures the non-trivial mechanics at play and unifies an efficient surrogate forward model with the ability to generate unseen metamaterial designs exhibiting complex nonlinear responses, which must leverage buckling and contact. This is accomplished by training the model on the complete deformation trajectory rather than solely on the underlying designs (akin to extending image to video generative models), which may suffice for linear conditioning but is inadequate for complex nonlinear situations (see the ablation study in Supplementary Section 7).

The complex target responses may be associated with multiple designs, posing a challenge for direct optimization. Addressing this one-to-many mapping is a recurring issue in inverse problems across disciplines, for which the probabilistic nature inherent in the diffusion architecture is ideally suited. By repeatedly generating samples for identical target responses, our model proposes a variety of designs (which may be checked for secondary objectives such as manufacturability). Our work further demonstrates the efficacy of video diffusion models when data of different modalities, such as the effective stress–strain response and the full-field internal stress distribution, must be synthesized and optimized—a task where conventional optimization techniques may fail. Alternatively, our framework can also complement such classical methods by identifying a favourable initial guess that is then further refined (as topology optimization schemes depend strongly on the initial guess).

We note that the presented framework in its current set-up is confined to generating responses for the specific boundary conditions and constitutive law used during training (based on the application scenario, it may be interesting for metamaterials, for example, to consider periodic boundary conditions in all directions). In principle, it is straightforward to extend the current framework by conditioning the model not only on the target properties but also on diverse load scenarios and the (base) material response. This requires additional training data and probably extends the training time. Operating in a latent space52 and at step-wise increasing resolutions53 could balance the increased computational complexity, presenting an interesting direction for future work. Moreover, alternative design spaces such as trusses7 provide a more compact design parameterization for three-dimensional structures and low fill fractions. As trusses can naturally be represented by graphs, graph diffusion models, mainly used in molecule design, can serve as a viable model architecture. Lastly, the presented framework admits extension to related fields such as fluid dynamics, serving both as a surrogate simulator and nonlinear optimizer.

Methods

We here provide details of the data-generation procedure, the methods employed for creating the metamaterials under consideration and the FE set-up to evaluate the nonlinear mechanical response of UCs. We further present the model architecture as well as the training and sampling protocol. Additional explanations can be found in Supplementary Information.

Design generation

We generate a random mechanical metamaterial by sampling a 2D Gaussian random field on a square domain based on the algorithm proposed in ref. 54. To do so, we sample complex Gaussian noise for a centred (even) N × N grid of Fourier coordinates

$${{{\mathcal{K}}}}=\left\{({k}_{1},{k}_{2})\in {{\mathbb{Z}}}^{2}\,:\,-N/2\le {k}_{1} < N/2,-N/2\le {k}_{2} < N/2\right\}$$

and introduce spatial correlation by a power law of the type \(P({k}_{1},{k}_{2})\propto {({k}_{1}^{2}+{k}_{2}^{2})}^{-\alpha /2}\), where we set α = 3 to ensure sufficient smoothness for manufacturable structures. This representation is converted to the corresponding real N × N pixel set \({{{\mathcal{X}}}}\) by considering the standardized real part of the inverse discrete Fourier transform. Next, we convert it to binary values (1 representing material and 0 representing void) by considering a threshold t sampled as \(t \sim {{{\mathcal{U}}}}(0,{t}_{\max })\) with tmax = 3/5, which was chosen to increase the variance (in terms of sparsity) of the sampled structures. Lastly, we check for the connectedness of the four boundaries of the square grid, which is defined as given if there exists a single material domain that covers at least 10% of the pixels (rounded down) of each side. This avoids structures with extremely sparse connectivity (and hence questionable manufacturability). We repeat the process until a valid structure has been found. The metamaterial is created by mirroring the found structure sequentially along the vertical and horizontal boundaries to ensure periodicity. Although we focus on only periodicity in the horizontal direction in the examples presented in this work, the generated structures can also be tessellated along the vertical direction to produce 2D tessellations. Note that the Gaussian random fields are by construction periodic, so they can also be tessellated without mirroring. However, we found that mirroring generates in general more diverse stress–strain responses and further simplifies the mesh generation for periodic boundary conditions, which is why we chose this procedure. The pseudocode of this process is given in Algorithm 1 in Supplementary Section 1.

FE simulations

To evaluate the stress–strain responses of the generated structures, we use Abaqus CAE 2020. All of the following steps are implemented via user subroutines. Note that we apply a smoothening of the boundary of the generated pixel structures to bypass issues with the meshing, presented in Supplementary Section 1.2. We generate a mesh compatible with periodic boundary conditions (that is, featuring matching nodes on opposite boundaries) and select three-node linear (CPE3) and four-node bilinear elements with reduced integration and hourglass control (CPE4R) using default settings. The mesh was refined until sufficient convergence in the stress distributions and overall stress–strain responses was observed. We consider plane-strain conditions to represent the realistic scenario of an extruded structure in the out-of-plane dimension (thus avoiding challenges with out-of-plane buckling under compression).

The metamaterial is virtually positioned between two rigid horizontal platens, to which we attach the nodes on the top and bottom boundary. We assume lubricated surfaces, so that nodes may slip horizontally relative to the horizontal platens. Within the UC, we consider frictional self-contact with a friction coefficient kfric = 0.4. Owing to the presence of large deformations including buckling and contact, an implicit dynamic solver is chosen for numerical stability. We ensure a quasi-static simulation by setting the mass density to ρ = 10−8, applying displacements with a smooth amplitude from time t = 0 to t = 1 and confirming that the kinetic energy (ALLKE) does not exceed 1% of the internal energy (ALLIE) for all strain steps. We furthermore verify that artificial energy measures (ALLAE and ALLSD), introduced for stability reasons, do not individually exceed 1% of the internal energy across all strain steps. In general, we use unitless values for all lengths in simulations (due to size invariance) and stresses are presented in units of megapascals.

We record the horizontal and vertical displacement components (u1 and u2, respectively), as well as the vertical stress component σ22 on a 96 × 96 pixel grid at 11 equidistant strain increments from the undeformed configuration to the total applied vertical strain in the Lagrangian (undeformed reference) frame. Note that instead of taking the initial step at 0% strain, we consider all fields at 0.2% strain, as this provides information on the small-strain response of the structure instead of trivial all-zero values. To compute the effective, overall stress response (which is the net vertical force per initial (undeformed) area on the top or bottom surfaces) at any strain level, we record the vertical reaction forces (RF2) of those nodes in contact with the upper rigid surface. Details on the considered base material can be found in Supplementary Section 1.3. All simulations were carried out on the Euler high-performance cluster of ETH Zurich.

Spatial 2D U-Net architecture

We refer to ‘Code availability’ for full technical details and below provide a high-level summary of the denoising diffusion model architecture. The PyTorch framework55 was used throughout our implementation. Diffusion models iteratively remove noise from data, typically images. Consequently, their input and output dimensions must be equal, making U-Net architectures a prevalent choice. Our model builds on the work of ref. 33 and its implementation provided by ref. 56, which, in turn, are based on derivations of the original 2D U-Net architecture45. This encoder–decoder architecture incrementally reduces spatial information while increasing latent feature information before reversing this operation by reducing the latent representation back to the spatial domain. In our work, each down- and upsampling pass comprises two ResNet57 blocks consisting of a series of convolutional layers and sigmoid-weighted linear unit activation functions58, spatial linear self-attention59 (to reduce computational complexity) across the (latent) pixel representation, and a down- or upsampling convolutional layer. The middle block between the encoder and decoder equally consists of two ResNet blocks with a (full) spatial self-attention layer in-between. We use 4 feature map resolutions (96 × 96 → 12 × 12) with expanding latent dimensions (64 → 512). Each attention block consists of 8 attention heads, each with a dimension of 32. We summarize the most relevant hyperparameters in Supplementary Table 2 in Supplementary Section 3.

Extension to temporal three-dimensional U-Net architecture

We extend the 2D U-Net by incorporating a temporal dimension33, where we understand the ‘temporal’ dimension as the applied strain steps. In all building blocks described above, the temporal dimension is treated as a batch dimension and therefore does not affect the set-up. The key difference is that we insert a temporal self-attention layer at the beginning before the encoder–decoder architecture and additionally, after every spatial attention layer, which treats the spatial dimension as batch axes and performs attention over the 11 strain steps. We consider relative positional encoding48 to pass information on the strain step order to the model.

Conditioning on nonlinear stress–strain responses

To condition the model on the stress–strain response, we convert all 11 scalar stress values at the corresponding strain steps to an embedding via a (learnable) linear layer. Note that we omit the corresponding strain value as we keep these fixed in this work, thus providing no further information, although a future extension can explore adaptive stepping techniques, such as sampling more densely at strain steps with substantial deformation changes. These token embeddings are concatenated to the spatial attention tokens at the corresponding strain step for cross-attention, while we concatenate all 11 token embeddings with a relative positional encoding to the temporal attention tokens in the temporal attention layer. Note that for cross-attention, we derive the queries from the pixel embedding but the keys and values from the conditioning embedding. To further enhance the conditioning, we average all 11 token embeddings over the strain steps and convert this to a latent representation by a two-layer multilayer perceptron and sigmoid-weighted linear unit activation function58, which transforms this representation to the same dimension as the latent embedding of the diffusion time step t. The latter is necessary for the model to determine the current step of the denoising process. We add both embeddings and incorporate them into the ResNet blocks.

Training protocol

We first pre-process the data as follows. We apply a min–max normalization to transform all input data x (that is, stress and displacement distributions) and conditioning (that is, stress–strain responses) to the range [−1, 1], that is

$${x}_{i}\leftarrow \frac{2\left[{x}_{i}-\min ({{{\bf{x}}}})\right]}{\max ({{{\bf{x}}}})-\min ({{{\bf{x}}}})}-1,$$
(5)

where the min and max operators are applied across all corresponding data points. For the stress and displacement fields, we consider all corresponding pixel values for all strain steps in the entire training dataset. For the stress–strain responses, we consider the minimum and maximum recorded stress response for all strain steps in the entire training dataset. Note that we store the image/video data generated with Abaqus in the gif format to reduce storage requirements.

We provide the training hyperparameters in Supplementary Table 4 and the loss plots in Supplementary Section 4. The model was trained on the Euler high-performance cluster of ETH Zurich, utilizing parallel and mixed precision processing. We use the Accelerate library from Hugging Face to facilitate the training set-up, which was conducted on eight Nvidia Quadro RTX 6000 graphics processing units, each equipped with 24 GB GDDR6 memory. The training process took approximately 70 h.

Sampling protocol

As the model does not directly predict binary pixels but stress and displacement distributions (which may be close to zero at the initial deformation stages), we require a robust method of extracting the underlying (undeformed) structure. We achieve this by considering the vertical displacement u2 of the upper left quarter (corresponding to the grey area in Fig. 1a) of the predicted field, which is sufficient to extract the full topology due to symmetry. For each pixel, we check whether its value is within a 2% tolerance around zero displacement (relative to the maximum displacement range) across all strain steps. If so, we consider it void (and otherwise material). We found this method to be highly robust, as the upper boundary of the structure is compressed and thus all ‘material pixels’ will probably undergo some level of displacement (exceeding the set tolerance). We remove any disconnected subdomains of the obtained design (although these were rarely observed). Further details on the effective stress response prediction and the mitigation of accuracy losses are provided in Supplementary Section 5.

Error measures

To obtain an objective and scale-invariant error norm of the stress–strain curves, we consider the NRMSE computed as

$$\epsilon \left({{{{\mathbf{\upsigma }}}}}_{{{{\rm{eff}}}}}^{{{{\rm{pred}}}}},{{{{\mathbf{\upsigma }}}}}_{{{{\rm{eff}}}}}^{{{{\rm{true}}}}}\right)=\sqrt{\frac{\left\Vert{{{{\mathbf{\upsigma }}}}}_{{{{\rm{eff}}}}}^{{{{\rm{pred}}}}}-{{{{\mathbf{\upsigma }}}}}_{{{{\rm{eff}}}}}^{{{{\rm{true}}}}}\right\Vert^{2}}{\left\Vert{{{{\mathbf{\upsigma }}}}}_{{{{\rm{eff}}}}}^{{{{\rm{true}}}}}\right\Vert^{2}}},$$
(6)

where \({{{{\bf{\upsigma }}}}}_{{{{\rm{eff}}}}}\in {{\mathbb{R}}}^{11}\) is the vector collecting the effective stress values σeff at the 11 strain steps, and ∥⋅∥ is the Euclidean norm.

For the full-field responses, we compute the analogous relative L2 error per strain step as

$${\epsilon }_{{L}_{2}}\left({{{\sigma}}}_{22}^{\rm{pred}},{{{\sigma }}}_{22}^{{{{\rm{true}}}}}\right)=\sqrt{\frac{\left\Vert{{{\sigma }}}_{22}^{{{{\rm{pred}}}}}-{{{\sigma }}}_{22}^{{{{\rm{true}}}}}\right\Vert^{2}}{\left\Vert {{{\sigma }}}_{22}^{{{{\rm{true}}}}}\right\Vert^{2}}},$$
(7)

where \({{{{\sigma}}}}_{22}\in {{\mathbb{R}}}^{N\times N}\) denotes the σ22 stress values of the discretized pixel grid in the Lagrangian frame for the corresponding strain step, and ∥⋅∥ is the Frobenius norm.