Introduction

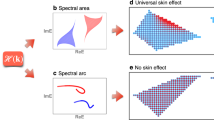
Recent theoretical and experimental studies on non-Hermitian systems have revealed many interesting phenomena without Hermitian counterparts, and thus greatly expanded our cognition of physics laws1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18. A quintessential feature of non-Hermitian systems is skin modes19,20,21,22,23,24,25,26, which are the accumulation of the majority of eigenstates at system boundaries. The non-Hermitian skin effect causes nullities of conventional bulk-boundary correspondence19. Specifically, the eigenvalues under different boundary conditions have a crucial distinction. Non-Bloch band theory was subsequently proposed, from which generalized Brillouin zone and continuum bands can be obtained to redefine the topological invariant and reproduce the open boundary band structures19,20. The exotic accumulation phenomenon of the eigenstates has important applications for topological sensors27,28, the integrated optical chip29, and topological lasing30,31. Presently, it is widely believed that the non-Hermitian skin effect is tantamount to the topologically nontrivial point gap21,32,33,34,35,36,37 and vice versa, which can be explained as follows. The Hamiltonian under open boundary conditions is always topologically trivial for the point gap. Thus, if the Hamiltonian under periodic boundary conditions is nontrivial, the non-Hermitian skin effect is present inevitably [Fig. 1].

Fig. 1: Relationship between point gap and the non-Hermitian skin effect.
figure 1

It is taken for granted that the topologically nontrivial (trivial) point gap is equivalent to the presence (absence) of skin modes. However, we question whether this is a universal conclusion. In our work, we exhibit a consequence of the anomalous non-Hermitian skin effect: the open boundary eigenstates being localized for the topologically trivial point gap while extended for the nontrivial point gap.

Full size image

However, we reveal that open boundary eigenstates can exhibit anomalous non-Hermitian skin effect, where skin modes can be ever absent even though the point gap is nontrivial, whereas skin modes are present for trivial point gap. This phenomenon occurs only when unidirectional hopping leading to decoupling-like behaviors is considered, where some subsystems contribute only to energy levels under periodic boundaries, and have no eigenstate distribution under open boundary conditions. That is to say, the curve in momentum space formed by the Bloch Hamiltonian will have a loop around a reference point and all sub-chains of the system affect the point gap. Yet under open boundary conditions, there is no wave function distribution on some sub-chains. With the emergence of the inequivalence of skin modes and point gap, there is a sudden change in open boundary eigenvalues. Specifically, there are multifold exceptional points, whose degree of degeneracy is proportional to the system size, among the open boundary eigenvalues that are appreciably different from the continuum bands. The physical properties of the eigenvalues may have relevance in the field of sensors. Finally, an experimental setup with electric circuits is proposed to realize our system.

Results

We consider a non-Hermitian three-band system (Fig. 2a), whose Hamiltonian reads as

$$H = \mathop{\sum }\limits_{n=1}^{N}\left[{t}_{a}{{C}^{{{{\dagger}}} }}_{A,n+1}{C}_{A,n}+{t}_{c}{{C}^{{{{\dagger}}} }}_{C,n}{C}_{C,n+1}\right.\\ + {t}_{b}({{C}^{{{{\dagger}}} }}_{B,n}{C}_{B,n+1}+{{C}^{{{{\dagger}}} }}_{B,n+1}{C}_{B,n})+{\gamma }_{1}{{C}^{{{{\dagger}}} }}_{A,n}{C}_{B,n}\\ +{\gamma }_{2}{{C}^{{{{\dagger}}} }}_{B,n}{C}_{A,n}+{\gamma }_{3}{{C}^{{{{\dagger}}} }}_{B,n}{C}_{C,n}+{\gamma }_{4}{{C}^{{{{\dagger}}} }}_{C,n}{C}_{B,n} \\ + \left.{V}_{a}{{C}^{{{{\dagger}}} }}_{A,n}{C}_{A,n}+{V}_{b}{{C}^{{{{\dagger}}} }}_{B,n}{C}_{B,n}+{V}_{c}{{C}^{{{{\dagger}}} }}_{C,n}{C}_{C,n}\right],$$
(1)

where \({{C}^{{{{\dagger}}} }}_{A,n}\) (CA,n), \({{C}^{{{{\dagger}}} }}_{B,n}\) (CB,n) and \({{C}^{{{{\dagger}}} }}_{C,n}\) (CC,n) represent the creation (annihilation) operators for sublattice A, B and C in the n-th unit cell. For sub-chain A, only right hopping ta is considered. Conversely, only left tunneling tc is considered for sub-chain C. Meanwhile, sub-chain B is Hermitian with the hopping amplitude being tb. γ1 and γ2 stand for non-Hermitian hopping between A and B sub-chain, while γ3 and γ4 are non-Hermitian hopping between B and C sub-chain. Va, Vb and Vc stand for the on-site potentials for sub-chains A, B and C, respectively. Without loss of generality, we take all parameters as real numbers.

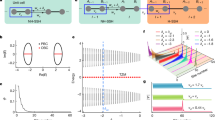
Fig. 2: Brief of the non-Bloch band theory.
figure 2

a Non-Hermitian three-band system with the number of unit cells N. ta (Va), tb (Vb) and tc (Vc) are the hopping amplitudes (on-site potentials) for sub-chain A, B and C, respectively. γi (i = 1, 2, 3, 4) stands for couplings between sub-chains. b Normal case that the topologically nontrivial point gap stands for the occurrence of skin modes. The green curve encircling the reference point \({E}_{b}=\frac{1}{2}i\) in left sub-figure is eigenvalues under periodic boundary conditions, and therefore non-Hermitian skin effect is displayed in the right sub-figure. The parameters are N = 200, ta = 1, \({t}_{b}=\frac{4}{5}\), tc = 2, γ1 = γ2 = 1, \({\gamma }_{3}=\frac{1}{10}\), \({\gamma }_{4}=\frac{1}{2}\), Va = 2 and Vb = Vc = 1.

Full size image

We start with normal case for comparison. The non-Hermitian skin effect can be generally confirmed by nontrivial point gap, or equivalently, by non-zero spectral winding \(W=\frac{1}{2\pi i}\int\nolimits_{0}^{2\pi }dk{\partial }_{k}\ln \det [H(k)-{E}_{b}]\)21,33,34,35,36, where Eb is an arbitrary reference point. As an example, we can choose \({E}_{b}=\frac{1}{2}i\) and W = 1 will be received [see Supplementary Note II for more details]. The system thus holds non-Hermitian skin modes, as shown in Fig. 2b. Specifically, all sub-chains have distributions of open boundary eigenstates.

Anomalous absence of skin modes for nontrivial point gap

We now explore the localization properties of open boundary eigenstates under unidirectional hopping amplitudes (γ1 = γ4 = 0). In this case, three eigenvalue branches in momentum space are Ek1 = Va + tae−ik, Ek2 = Vc + tceik and \({E}_{k3}={V}_{b}+2{t}_{b}\cos (k)\). The complex energy spectra Ek1 (Ek2) will rotate clockwise (counterclockwise) on the complex plane, and Ek3 simply forms a line as k varies from 0 to 2π. Therefore, as long as Va ≠ Vc or ta ≠ tc, there must exist a reference point Eb (Here we can choose \({E}_{b}=\frac{1}{2}i\)) surrounded only once and the area of the curve must be nonzero36, as shown in Fig. 3a. Hence, it seems that our system exhibits the non-Hermitian skin effect.

Fig. 3: Anomalous non-Hermitian skin effect.
figure 3

a Nontrivial point gap obtained from (Re[det[H(k)]], Im[det[H(k)]]) as k varies from 0 to 2π for the reference point \({E}_{b}=\frac{1}{2}i\). Namely, the effects of all energy bands are taken into account in calculation of spectral winding. b Open boundary eigenvalues colored by their inverse participation ratio for the s-th eigenstate \(\left\vert {\Psi }^{s}\right\rangle\) (IPRs), remaining constant approaching zero. c Distribution of the open boundary eigenstate corresponding to the blue asterisk EOBC = 0.0001 in b, where occupation is non-zero only on sub-chain B, while both sub-chain A and sub-chain C have no occupation. d Normalized eigenstates with the change of eigenvalues. All eigenstates are extended, rather than localized, on the open chain. e Non-Hermitian three-band system will be simplified as a Hermitian one-band model when γ1 = γ4 = 0. f Momentum space spectra, where Ek1 and Ek2 will display two circles with the same radius but opposite rotation directions when k changes from 0 to 2π. Thus, the point gap is topologically trivial for any reference point. In other words, all energy levels in momentum space contribute to the point gap. g Open boundary eigenvalues. Different colors are different values of IPRs, which is finite for the corresponding eigenstate. h Distribution of the open boundary eigenstate, which is localized, rather than extended. i Eigenstates as a function of all open boundary eigenvalues E. All eigenstates have been normalized and are localized at the boundaries of the system. The A sub-chain only contributes the energy level while without wavefunction distribution. j Open boundary non-Hermitian three-band system will become the non-Hermitian two-band system from both eigenstates and eigenvalues perspectives when γ1 = γ3 = 0. The parameters for a–e are γ1 = γ4 = 0, ta = 1, \({t}_{b}=\frac{1}{2}\), tc = 2, γ2 = 2, γ3 = 1, Va = 2 and Vb = Vc = 1. f–j γ1 = γ3 = 0, ta = tc = 8, \({t}_{b}=\frac{1}{2}\), γ2 = 2, γ4 = 1, \({V}_{a}={V}_{c}=\frac{3}{5}\) and Vb = 1.

Full size image

However, in addition to adopting an indirect perspective of the point gap in momentum space, i.e., from the Bloch Hamiltonian to analyze the skin modes, we can directly examine the distributions of eigenstates under open boundary conditions and find that the conclusion mentioned above is not suitable. To characterize the localization properties of all wave functions quantitatively, the inverse participation ratio (IPR) is introduced as IPR\({\,\!}^{s}= (\mathop{\sum}\limits_{i=1}| {\Psi }_{i}^{s}{| }^{4})/{(\mathop{\sum}\limits_{i = 1}| {\Psi }_{i}^{s}{| }^{2})}^{2}\) for the s-th eigenstate \(\left\vert {\Psi }^{s}\right\rangle\)38,39. For large system size, IPRs is finite for the localized eigenstate, whereas it approaches zero for extended eigenstate. As shown in Fig. 3b, IPRs ≡ 0.0075, which indicates that all eigenstates should be extended, not localized on open chain. One eigenvalue in Fig. 3b can be selected to exhibit the distribution of the eigenstates. As shown in Fig. 3c, the open boundary eigenstates are indeed extended only on the B sub-chain, which conforms to the non-Hermitian skin effect disappearance numerically. We further plot the distribution of all open boundary eigenstates corresponding to eigenvalues in Fig. 3d. There is no large number of eigenstates localized at system boundary, i.e., the non-Hermitian skin effect is absent whereas the point gap is nontrivial. Physically, sub-chain A (C) has only unidirectional hopping to sub-chain B, but the reverse does not happen when γ1 = 0 (γ4 = 0), and B sub-chain is Hermitian, which can be solved analytically (Supplementary Note II). Hence, there is no probability distribution on sub-chain A (C), and Bloch waves survive in B sub-chain (Fig. 3e).

Anomalous presence of skin mode for trivial point gap

The non-Hermitian skin effect is present at unidirectional hopping amplitudes for γ1 = γ3 = 0. To confirm that the spectral winding number is zero, corresponding to trivial point gap, conditions of the Hamiltonian (1) are further restricted as Va = Vc and ta = tc, i.e., generalized Brillouin zone of non-Hermitian three-band Hamiltonian (1) is a unit circle (Supplementary Note I). In addition to quantitative calculations of spectral windings, topological properties of the point gap can be gained intuitively. Namely, if the area of the curve surrounded by (Re[det[H(k)]], Im[det[H(k)]]) is zero, non-Hermitian skin modes will vanish and vice versa21,33,34,35,36. For our system, three eigenvalue branches in momentum space satisfy ∣Ek1∣ = ∣Va + tae−ik∣ = ∣Ek2∣ = ∣Vc + tceik∣ and \({E}_{k3}={V}_{b}+2{t}_{b}\cos (k)\), i.e., Ek1 and Ek2 will trace two circles with same radius but in opposite direction of rotation when k changes from 0 to 2π [Fig. 3f]. Therefore, for any reference point Eb, the spectral winding is equal to zero exactly, and it seems that there is no non-Hermitian skin effect.

However, we can also examine the localization properties of open boundary eigenstates from IPRs. As shown in Fig. 3g, \(\min\)(IPRs) = 0.9406 as the energy changes under numerical simulation, which means that all eigenstates are localized, rather than extended, even if spectral winding number is constantly zero. Here, the information on the exceptional points [discussed next] and the corresponding eigenstates has been excluded. We can arbitrarily present the distribution of an open boundary eigenstate in Fig. 3h. It is obviously localized at the left C sub-chain of the system. Furthermore, Fig. 3i presents the distribution of all open boundary eigenstates associated with eigenvalues, where eigenstates have been normalized. Globally, all open boundary eigenstates are pinned at the left system boundaries, i.e., the non-Hermitian skin effect is present. Physically, one can analytically find that there only exists unidirectional hopping from sub-chain A to a subsystem comprising sub-chains B and C when γ1 = 0 [Supplementary Note II], and this subsystem is still non-Hermitian essentially. Hence, there is no probability distribution on sub-chain A, while the non-Hermitian skin effect also can be exhibited in the subsystem (Fig. 3j).

Changes of open boundary eigenvalues

We now analyze the properties of energy spectrum when anomalous non-Hermitian skin effect occurs. According to Hamiltonian (1), the characteristic polynomial of our system is

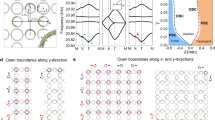
$$f(\beta ,E)={a}_{2}{\beta }^{2}+{a}_{1}{\beta }^{1}+{a}_{0}{\beta }^{0}+{a}_{-1}{\beta }^{-1}+{a}_{-2}{\beta }^{-2}=0.$$
(2)

The coefficients from a2 to a−2 can be seen in Supplementary Note I. The characteristic polynomial f(β, E) is a quartic equation. The solutions can be numbered as \(\left\vert {\beta }_{1}\right\vert \le \left\vert {\beta }_{2}\right\vert \le \left\vert {\beta }_{3}\right\vert \le \left\vert {\beta }_{4}\right\vert\) for a given E and \(\left\vert {\beta }_{2}\right\vert =\left\vert {\beta }_{3}\right\vert\) is required to determine generalized Brillouin zone and derivative continuum bands. As shown in Fig. 4a, generalized Brillouin zone is displayed, and correspondingly, the open boundary energy spectrum is well recovered by continuum bands with \({\gamma }_{1}=\frac{1}{500}\) and \({\gamma }_{4}=\frac{1}{400}\) (Fig. 4b).

Fig. 4: Changes in open boundary eigenvalues.
figure 4

a Generalized Brillouin zone (red curve) and Brillouin zone (green curve). b Energy spectra under open boundary conditions (blue curve) and continuum bands (red curve). c Generalized Brillouin zone (red curve) and Brillouin zone (green curve). d Energy spectra under open boundary conditions (blue curve) and continuum bands (red curve). After bringing two open boundary eigenvalues into f(β, E), one energy value obtains ∣β2∣ = ∣β3∣ (EOBC = 4) while the other corresponds to ∣β1∣ = ∣β2∣ (\({E}_{OBC}=\frac{6}{5}\)). e Auxiliary generalized Brillouin zone (red curve) containing all information of ∣βm∣ = ∣βn∣ ({m, n} = {1, 2, 3, 4}) with f(β, E) = 0, and generalized Brillouin zone obtained from the open boundary eigenvalues (blue curve). f Number of certain open boundary eigenvalues versus the system size. a and b \({\gamma }_{1}=\frac{1}{500}\) and \({\gamma }_{4}=\frac{1}{400}\). c-f γ1 = γ4 = 0. Other parameters: ta = 2, tb = 1, \({t}_{c}=\frac{1}{2}\), γ2 = 1, \({\gamma }_{3}=\frac{1}{10}\), Va = 1Vb = 3 and Vc = 2.

Full size image

However, the situation is remarkably different when γ1 = γ4 = 0, corresponding to presence anomalous non-Hermitian skin effect. Generalized Brillouin zone shown in Fig. 4c is slightly different from the one in Fig. 4a, and there is very little change for continuum bands [comparing red curve in Fig. 4b with the one in Fig. 4d], while open boundary eigenvalues differ and lie on the real axis. Hence, open boundary energies and continuum bands will not be compatible with each other.

Further, it is taken for granted that if every open boundary eigenvalue is brought into the characteristic polynomial f(β, E), and the second and third largest ∣β∣ are selected, the data should belong to generalized Brillouin zone obtained from non-Bloch band theory19,20,21,26,40. However, unlike the case in the established scenarios, this rule is nullified in singular phenomenon. Detailedly, we can choose an open eigenvalue in Fig. 4d, such as EOBC = 4, and bring it into the characteristic polynomial f(β, E). After calculation, one can receive \({\left\{| {\beta }_{1}| ,| {\beta }_{2}| ,| {\beta }_{3}| ,| {\beta }_{4}| \right\}}_{E = 4}=\left\{0.6667,1.000,1.000,4.000\right\}\), i.e., ∣β2∣ = ∣β3∣. This equality is exactly the condition of obtaining generalized Brillouin zone and corresponding continuum bands. Therefore, EOBC = 4 can be reproduced by continuum bands based on non-Bloch band theory40. Yet, another open boundary eigenvalue \({E}_{OBC}=\frac{6}{5}\) can be considered as well. Similarly, \({\left\{| {\beta }_{1}| ,| {\beta }_{2}| ,| {\beta }_{3}| ,| {\beta }_{4}| \right\}}_{E = \frac{6}{5}}=\left\{1.000,1.000,1.600,10.00\right\},\) i.e., ∣β2∣ ≠ ∣β3∣ but ∣β1∣ = ∣β2∣. Evidently, this equality contradicts the condition of obtaining generalized Brillouin zone, i.e., this open boundary eigenvalue must not belong to continuum bands determined by ∣β2∣ = ∣β3∣. Figure 4d visually confirms these results.

The singular energy spectrum can also be examined from a more general perspective. In Ref. 26, authors proposed a concept of the auxiliary generalized Brillouin zone, which is obtained by solving the characteristic equation f(β, E) = 0 when E takes every value of the complex number field with ∣βm∣ = ∣βn∣ ({m, n} = {1, 2, 3, 4}). However, as shown in Fig. 4e, even though the auxiliary generalized Brillouin zone possesses all equality information of f(β, E) = 0, it remains impossible to recover generalized Brillouin zone obtained from open boundary eigenvalues. This further confirms the emergence of singular energy spectrum.

Meanwhile, we analytically exhibit that the determinant of open boundary Hamiltonian has the form \(\det \left[{H}_{OBC}-{E}_{OBC};N\times N\right]={2}^{-N}{({V}_{a}-{E}_{OBC})}^{N}{({V}_{c}-{E}_{OBC})}^{N}y({V}_{b},{t}_{b},{E}_{OBC})\) with unidirectional hopping being satisfied (Supplementary Note II), with N being total number of the system size. Hence, EOBC = Va and EOBC = Vc must be solutions of \(\det \left[{H}_{OBC}-{E}_{OBC};N\times N\right]=0\), and be N-fold exceptional points41,42. In Fig. 4f, we exhibit the number of the open boundary eigenvalues of EOBC = Va and EOBC = Vc with different system sizes. Explicitly, the number of degeneracy points is proportional to the system size.

Additionally, sensors have penetrated aspects of daily life. The core part of a sensor is transformation circuit, which amplifies weak signals43,44,45. Interestingly, it has been displayed that minute perturbations of parameters will affect the eigenvalues. Moreover, Refs. 46,47,48,49,50,51 also show that higher-order exceptional points have advantages for sensor applications, and it is significant to seek higher-order exceptional points in various systems. Coincidentally, we also have shown that the emergence of the singular phenomenon is accompanied by the multifold exceptional point. Hence, our non-Hermitian systems may have potential applications in the sensor field.

Proposed experimental implementation

There exist several physical incarnations that can be used to explore non-Hermitian systems52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68, including cold atoms52,53,54,55, electrical circuits56,57,58,59,60,61,62,63, photonic and acoustic systems64,65,66,67,68. Among them, electric circuits have been widely used because the circuit structure can be flexibly designed to facilitate integration and mass production. Here, we propose an experimental scheme to realize our system through electric circuits (Supplementary Note III). The essential part of the electric system is the negative converter with current inversion (INIC), the impedance of which is changed from negative to positive with the orientation of the current being reversed, or vice versa, as shown in Fig. 5. Our system can be achieved by choosing appropriate impedances for these electric devices. Explicitly, the parameters of the devices are YA1 = Va, YAj = Va + ta(1 < j ≤ N), \({Y}_{Aj}^{{\prime} }=-{\gamma }_{1}\), \({Y}_{AB}=-\frac{{\gamma }_{1}+{\gamma }_{2}}{2}\), \({Y}_{AB}^{{\prime} }=\frac{{\gamma }_{1}-{\gamma }_{2}}{2}\), \({Y}_{AA}={Y}_{AA}^{{\prime} }=-\frac{{t}_{a}}{2}\), YB1 = YBN = Vb, YBj = Vb + tb(1 < j < N), \({Y}_{BC}=-\frac{{\gamma }_{3}+{\gamma }_{4}}{2}\), \({Y}_{BC}^{{\prime} }=\frac{{\gamma }_{3}-{\gamma }_{4}}{2}\), YBB = − tb, YCj = Vc(1 ≤ j < N), YCN = Vc − tc, \({Y}_{Cj}^{{\prime} }=-({\gamma }_{4}+{t}_{c})\), \({Y}_{CC}=-\frac{{t}_{c}}{2}\) and \({Y}_{CC}^{{\prime} }=\frac{{t}_{c}}{2}\).

Fig. 5: Proposed electric circuit configurations for realizing the Hamiltonian.
figure 5

The Hamiltonian is given in Eq. (1). The electric elements contain the negative converter with current inversion (INIC), capacitor and wires. YAA, YBB and YCC are capacitance of the capacitor. \({Y}_{AA}^{{\prime} }\) and \({Y}_{CC}^{{\prime} }\) are capacitance of the INIC for a capacitor. A sub-chain, B sub-chain and C sub-chain are respectively connected by those electric devices. YAB and \({Y}_{AB}^{{\prime} }\) being respectively the capacitance of the capacitor and INIC for a capacitor connect A sub-chain and B sub-chain, while YBC and \({Y}_{BC}^{{\prime} }\) connect B sub-chain and C sub-chain. On-site potential is obtained by grounding each node with suitable circuit devices.

Full size image

Conclusion

We unravel that open boundary eigenstates exhibit an anomalous non-Hermitian skin effect in which they are extended for the topologically nontrivial point gap but localized for trivial point gap, provided that there are one-directional coupling amplitudes among the sub-chains. Additionally, with the presence of anomalous non-Hermitian skin effect, open boundary eigenvalues will have wide distinction compared with continuum bands. Notably, there exist multifold exceptional points in an open chain, and the degree of degeneracy grows as the system size increases. The physical properties of the eigenvalues may have applications in sensors field. Our results presented here demonstrate the unique irrelevance of the non-Hermitian skin effect and point gap, which could advance non-Bloch theory and our understanding of critical phenomenon in non-Hermitian field. Meanwhile, the conclusions can be generalized to various non-Hermitian systems (such as the four-band system in Supplementary Note IV).

Methods

The spectral winding number defined as \(W=\frac{1}{2\pi i}\int\nolimits_{0}^{2\pi }dk{\partial }_{k}\ln \det [H(k)-{E}_{b}]\)21,33,34,35,36 can be calculated quantitatively from the residue theorem via eik → z and \(dk\to \frac{1}{iz}dz\).

Such as, one can see that five first-order poles are distributed on the complex plane for a given \({E}_{b1}=\frac{1}{6}i\) in Fig. 6a, where four of them are contributed to spectral winding and W = 1 can be obtained, i.e., the point gap is topologically nontrivial. However, three poles are surrounded by the unit circle in Fig. 6b for different parameters and the point gap is trivial. Precisely, the spectral winding W ≡ 0 for any reference point as long as ta = tc, Va = Vc and γ1γ2 = γ3γ4 (Supplementary Note II).

Fig. 6: Distribution of poles under anomalous non-Hermitian skin effect.
figure 6

a z1, z2, z3 and z4 being encircled by the unit circle, which induces the nonzero spectral winding, or the nontrivial point gap. Parameters are \({E}_{b1}=\frac{1}{6}i\), γ1 = γ4 = 0, ta = 1, \({t}_{b}=\frac{1}{2}\), tc = 2, γ2 = 2, γ3 = 1, Va = 2 and Vb = Vc = 1. b z1, z3 and z5 being encircled by the unit circle, while z2 and z4 being excluded for reference point \({E}_{b2}=\frac{1}{6}i\). Thus, the system corresponds to the trivial point gap. Parameters are γ1 = γ3 = 0, ta = tc = 8, \({t}_{b}=\frac{1}{2}\), γ2 = 2, γ4 = 1, \({V}_{a}={V}_{c}=\frac{3}{5}\) and Vb = 1.

Full size image