Introduction

Transition metal (TM) compounds provide a versatile platform for exploring a wide variety of strongly correlated phenomena, such as high-TC superconductivity, multiferroicity, or unusual magnetism1,2,3. These phenomena are accompanied by various types of charge, spin and orbital orders, arising from competition between interactions such as the local crystal field, inter-site exchange interactions, spin-orbit coupling and on-site Coulomb repulsion3. Several phase transitions can occur in a single compound at different temperatures, as observed in multi-orbital systems with partially filled d-shells, including cuprates4, manganites5,6, and ruthenates7.

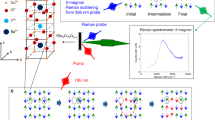
Chromates are an intriguing member of this class of materials, due to their active degrees of freedom (DOFs), multiple electronic symmetry breaking pathways, and competing order parameters. The case of α-Sr2CrO4 is particularly interesting, as it has been shown to exhibit multiple spin and orbital ordering transitions in the Mott insulating ground state (Fig. 1(a))8,9,10,11,12. α-Sr2CrO4 presents a unique electronic configuration, with two electrons in t2g orbitals and total spin of S = 1. Recent resonant X-ray scattering (RXS)8 and neutron powder diffraction studies9 demonstrated antiferromagnetic (AFM) order by tracking a magnetic Bragg peak below the Néel temperature (TN = 112 K), consistent with the temperature (T)-dependent magnetic susceptibility10. The RXS study also revealed another in-plane order below TS = 50 K8, which was attributed to stripe-type spin-orbital order in the dyz/dzx orbital sub-manifold (Fig. 1(a)). α-Sr2CrO4 also manifests a signature of a broad transition around TO = 140 K in the specific heat, which is likely unrelated to spin order, as the magnetic susceptibility follows a typical Curie-Weiss law across TO10. The exact origin of this feature has not been unveiled yet, though it was suggested to arise from a distinct antiferro(AF)-type orbital order in the dyz and dzx orbitals (Fig. 1(a)), as in Sr2VO410,13. Therefore, more experimental insight is needed to unravel the origin of this phase transition at TO above the Néel temperature.

Fig. 1: Spin and orbital order in α-Sr2CrO4.
figure 1

a Schematic diagrams of the spin- and orbital-ordered ground state in α-Sr2CrO4, showing different types of antiferro-type spin ordering and dyz/dzx orbital ordering. We note that the four-lobed shapes of the d-orbitals are projected into the ab-plane. Arrows indicate possible 1 eV transitions from occupied (filled shapes) to unoccupied (dotted shapes) orbital states in a given ordered phase; transitions from Cr(1) to Cr(2) ions are shown for simplicity, but the reverse can also occur. b Energy (E) levels and orbital structures on neighboring sites with Cr(1) and Cr(2) ions at a temperature (T) below the Néel temperature (TN): T≤TN. The d-d transitions between dzx orbitals from Cr(1) to Cr(2) (or between dyz orbitals from Cr(2) to Cr(1)) correspond to hopping energies of 1.0 eV. 3.1 eV excitation drives a charge-transfer-type transition from O 2p to Cr eg orbitals. The relevant electronic structures are displayed along with photoexcitation at (c) 1.0 eV and (d) 3.1 eV. On-site transitions from O 2p to Cr eg states are possible at both Cr(1) and Cr(2) sites.

Full size image

In this context, ultrafast optical spectroscopy (UOS) is a powerful tool for providing insight into the intertwined spin and orbital DOFs in TM compounds14. By using femtosecond (fs) photoexcitation to drive the system out of equilibrium, the interplay among the competing charge, spin and orbital DOFs can be disentangled via their different timescales for returning to the initial ground state, as exemplified in previous studies of various TM oxides15,16,17,18,19,20,21,22. However, to the best of our knowledge this technique has not yet been used to study α-Sr2CrO4, providing an exciting opportunity to shed light on the origin of the various order parameters present in this system.

In this work, we thus investigate the non-equilibrium dynamics of spin and orbital order in α-Sr2CrO4 by measuring the transient changes in reflectivity at 1.55 eV after femtosecond optical photoexcitation. By varying the pump photon energy, we can selectively drive specific microscopic processes that trigger clear T-dependent anomalies across the spin and orbital order temperatures. Photoexcitation at 1.0 eV directly perturbs spin and orbital order by inducing spin hopping between neighboring Cr4+ ions. In contrast, 3.1 eV photons excite carriers through a charge-transfer-type transition (which does not directly affect spin/orbital order), yet the resulting relaxation dynamics are still influenced by the existing spin and orbital ordered states. Our results thus show that UOS is sensitive to all three of the spin and orbital ordering transitions that have been previously measured via other techniques8,10 through their distinct timescales14. Furthermore, we provide experimental evidence for the existence of a phase transition at TO, with a close relation to the stripe-type spin-orbital order below TS.

Results and discussion

Experimental description

We measured the time-resolved photoinduced changes in reflectivity on an epitaxially grown, 100 nm thick c-axis oriented film of α-Sr2CrO4, which is usually hard to synthesize in bulk single crystalline form8. Our experiments were based on a 250 kHz femtosecond (fs) regenerative amplifier producing ~ 100 fs pulses at 1.55 eV, used to probe the transient response and also to pump an optical parametric amplifier that generated the 1.0 eV pump pulses. A beta-barium borate (BBO) crystal was used to obtain the 3.1 eV pump pulses by frequency doubling the fundamental 1.55 eV pulses. We used a near normal incident geometry for both pump and probe beams, which were linearly cross-polarized along the two equivalent in-plane a-axes (since α-Sr2CrO4 has tetragonal symmetry). The fluence of the 1.0 eV (3.1 eV) pump pulses was 400 (800) μJ cm−2, generating 0.022 (0.034) carriers/Cr site and a lattice temperature increase < 5 K. We measured the time-resolved reflectivity data up to t = 250 picoseconds (ps), and verified that the measured response was linear with pump fluence up to ~ 1 mJ cm−2 for both 1.0 eV and 3.1 eV pumping.

To observe non-equilibrium spin and orbital ordering dynamics, we used our 1.0 eV and 3.1 eV pump pulses to drive specific transitions in the electronic structure of α-Sr2CrO4. Two electrons occupy Cr4+t2g states in α-Sr2CrO4, leading to a reversed crystal splitting effect that lifts their degeneracy9,23. This results in a lower energy for the dxy orbital compared to those of the dyz/dzx orbitals (Fig. 1(b)). Theoretical calculations of the ground state orbital structure also revealed an AF pattern in the occupancy of dzx and dyz orbitals on neighboring Cr4+ ions (Cr(1) and Cr(2)) below TO, in addition to AF spin ordering below TN12,23. These AF spin and orbital orderings produce different partial densities of states on neighboring Cr ions, resulting in an energy scale of 1.0 eV for inter-site spin hopping from Cr(1) to Cr(2) (Cr(2) to Cr(1)) sites between dzx (dyz) orbitals, as indicated by the orange arrows in Fig. 123 (see the supplementary material for additional experimental details in Supplementary Note 1). Additionally, charge transfer-type transitions between neighboring oxygen 2p and Cr eg orbitals occur at higher energy scales (~3 eV). We note that these assignments also agree with previous optical conductivity data11 and our data (see the supplementary material for additional experimental details in Supplementary Note 2 with Fig. S2), showing clear peaks at these photon energies. In our experiments, therefore, 1.0 eV photoexcitation directly perturbs spin and orbital order, while 3.1 eV photoexcitation creates carriers whose dynamics are influenced by the existing spin and orbital orders as they relax from higher energy states. We tracked the resulting dynamics with a probe photon energy of 1.55 eV, set below the charge transfer (CT) gap energy of 2.0 eV11 to give general sensitivity to dynamics in all t2g orbitals. Even though the CT transition can contribute to the dynamics measured at 1.55 eV, it too is sensitive to spin and orbital order, as 2 eV corresponds to the transition from O 2p to Cr t2g states (Fig. 4 in ref. 23).

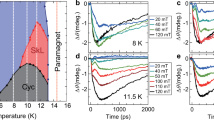
Figure 2 shows T-dependent transient reflectivity (ΔR/R) data for both pump photon energies, revealing dynamics on both fast (sub-ps) and relatively slow timescales. After 1.0 eV photoexcitation, a step-like feature appears immediately after time t ~ 0 ps at high temperatures, as exemplified at 180 K, while an additional decaying component arises at low temperatures, as seen at 20 K. In contrast, while the 1.0 eV pump data shows a monotonic decay after t ~ 0 ps (Fig. 2(a)), the dynamics are more complicated after 3.1 eV photoexcitation, displaying a sharp peak at t = 0.2 ps as well as a slowly rising component up to t ~ 4 ps (Fig. 2(b)). Finally, there is a slow decay at low temperatures and long time delays after both 1.0 eV and 3.1 eV photoexcitation. We note that the periodic oscillations at a frequency of 22 GHz in the transient reflectivity after 3.1 eV photoexcitation are due to optically driven acoustic phonons (see the supplementary material for additional experimental details)24; this is well established and will not be discussed further here.

Fig. 2: Photoinduced time-resolved changes in reflectivity (ΔR/R) in α-Sr2CrO4.
figure 2

We measured ΔR/R at 1.55 eV after (a) 1.0 eV and (b) 3.1 eV photoexcitation at various temperatures.

Full size image

Dynamics after 1.0 eV photoexcitation

For more insight, we plotted the T-dependence of the ΔR/R signal at different time delays after 1.0 eV pumping in Fig. 3(a). ΔR/R at the peak (t = 0.2 ps) and t = 4 ps clearly deviates from the low-T linear behavior across TN. In contrast, at longer timescales of t = 100 ps, we observe an increase in the ΔR/R signal below the stripe-type ordering temperature (TS = 50 K). This suggests that the dynamics at short and long timescales after 1.0 eV photoexcitation are related to Néel spin order and stripe-type spin-orbital order, respectively.

Fig. 3: Analysis of the temperature-dependent reflectivity transients (ΔR/R) after 1.0 eV photoexcitation.
figure 3

a ΔR/R at time delays of 0.2 ps (black circles), 4 ps (red squares), and 100 ps (blue diamonds). b Transient reflectivity data at temperature T = 20 K (blue circles) and 120 K (purple circles) along with fits using bi-exponential decay functions (dashed lines). The temperature dependence of the (c) amplitude A1 and (d) decay time τ1 of the fast component extracted from our fits. The solid grey lines indicate the transition temperatures of the stripe-type order (TS), antiferro-type spin order (TN), and antiferro-type orbital order (TO), respectively. The error bars were calculated as described in Methods.

Full size image

To quantify the timescale for the recovery of magnetic order, we fit our data with a bi-exponential decay function, \(\Delta R(t)/R={A}_{1}\exp (-t/{\tau }_{1})+{A}_{2}\exp (-t/{\tau }_{2})\), from t = 0.2 ps to 200 ps, as shown in Fig. 3(b) (see Supplementary Note 3 for the detail and Fig. S3 for the fitting results at all measured temperatures.) Both the amplitude A1 (Fig. 3(c)) and decay time τ1 (Fig. 3(d)) of the fast component clearly show a gradual increase below TN. Near the lowest temperatures, τ1 ~ 10 ps, revealing the timescale on which AFM order recovers after 1.0 eV excitation. Previous work on antiferromagnetic TM oxides has demonstrated that this time constant is linked to spin-lattice relaxation, i.e. photoexcited electrons rapidly transfer their energy to the lattice, which in turn equilibrates with spins on a timescale given by τ119,25; this is consistent with our data, and indicates that AFM order restricts carrier hopping below TN (Fig. 1(a)). Such dynamics of τ1 does not appear in the ΔR/R data following 3.1-eV pump, as the spin order is not likely to be destroyed by photoexcitation to Cr eg bands. We also found that τ2 exhibits a slower decay time (~200 ps) above TS (see Fig. S4(b)), likely due to residual lattice heating. However, below TS, τ2 increases up to ~ 500 ps, which may be linked to a structural change occurring concurrently with the appearance of stripe-type spin-orbital order (see Fig. S5 in Supplementary Note 4).

Dynamics after 3.1 eV photoexcitation

In contrast with the transient reflectivity measured after 1.0 eV photoexcitation, which exhibited a relatively simple exponential recovery, the dynamics after 3.1 eV photoexcitation are more complex. Fig. 2(b) reveals three distinct timescales, including (1) the initial sharp peak at t = 0.2 ps, followed by (2) an increase up to t ~ 4 ps and (3) a subsequent decay on longer timescales. Fig. 4(a) shows ΔR/R as a function of T at time delays corresponding to these features. While the initial dynamics at t = 0.2 ps shows only small T-dependent anomalies, ΔR/R at 4 ps and 100 ps changes across TS, similar to the results after 1.0 eV excitation.

Fig. 4: Analysis of the temperature-dependent reflectivity transients (ΔR/R) after 3.1 eV photoexcitation.
figure 4

a ΔR/R at time delays of 0.2 ps (black circles), 4 ps (red squares), and 100 ps (blue diamonds). We also plot the amplitude B1 (orange circles) obtained from our curve fits. b Transient reflectivity data at temperature T = 20 K (blue circles) and 180 K (red circles), along with fits using the model described in the text. The data and fit curve at 180 K are scaled up by a factor of four for clear comparison. c The rise time (τ3) and (d) decay time (τ4) obtained from the ultrafast dynamics in (b), revealing a clear anomaly across the antiferro-type orbital ordering temperature TO = 140 K. The error bars were calculated as described in Methods.

Full size image

For a more quantitative analysis, we fit the data up to 25 ps with a model function:

$$\frac{\Delta R}{R}(t)=\, S(t)\times \left(1-\exp \left(-\frac{t}{{\tau }_{3}}\right)\right)\\ \times \left({B}_{1}\exp \left(-\frac{t}{{\tau }_{4}}\right)\right)+C\exp \left(\frac{-{(t-{t}_{0}^{{\prime} })}^{2}}{{\tau }_{p}}\right).$$
(1)

While a simple two-exponential decay model was sufficient to fit the 1.0 eV data, for the 3.1 eV data we used equation (1), particularly to account for the relatively slow rising dynamics. In this model, S(t) = (1 + erf(t/τ0))/2 is a step-function representing the convolution of the material response with the pulse duration of τ0 ~ 100 fs. We use \(1-\exp (-t/{\tau }_{3})\) to fit the slow rising dynamics with a rise time τ3, and \(B\exp (-t/{\tau }_{4})\) to fit the subsequent decay with amplitude B and decay time τ4. The remaining part, \({C}_{1}\exp {(-(x-{t}_{0}^{{\prime} })/{\tau }_{p})}^{2}\)), is used to fit the initial peak at \({t}_{0}^{{\prime} } \sim 0.2\) ps. The fitting results at T = 10 and 180 K are displayed in Fig. 4(b) with the raw data, showing that our model can accurately represent the complex dynamics triggered by 3.1 eV pumping (see Supplementary Note 5 for the fitting detail and Fig. S6 for the fitting results at all temperatures).

The initial sharp peak may originate from several different processes, including electron-electron scattering among the photoexcited carriers26 and two-photon absorption; additional measurements are required to conclusively determine its origin. Regardless, the initial charge transfer-type excitation between O 2p to Cr eg states on neighboring ions driven by 3.1 eV photoexcitation should not directly influence magnetic or orbital order on ultrafast timescales, because neither the initial nor the final state are involved with the spin and orbital order in the Cr t2g states (Fig. 1(d)). This is why the dynamics after 1 eV photoexcitation characterized by τ1 do not appear in the ΔR/R data following 3.1 eV pumping, as spin order is not destroyed by photoexcitation to Cr eg bands.

After the initial peak, the slow rise denoted by τ3 (Fig. 4(b)) is due to relaxation of the photoinduced carriers from their initial eg levels into the t2g states examined by our 1.55 eV probe pulse, as indicated by the upper black arrow in Fig. 1(d)). This slow rising component does not appear in the 1.0 eV data (Fig. 2(a)), since our 1.55 eV probe energy is higher than that of the 1.0 eV pump. Despite a gradual change in the amplitude B1 (Fig. 4(c)), the relevant rise time, τ3, shows a clear anomaly across TO = 140 K (Fig. 4(d)), a transition temperature that has been observed only once before via specific heat measurements10. This suggests that the orbital configuration changes below TO, which can influence carrier relaxation into the conduction band minima originating from Cr t2g orbitals.

For further insight into the orbital configuration, we refer to previous theoretical calculations based on a Kugel-Khomskii model (Fig. 4(a) in8). Considering the exchange interactions between the neighboring spins and orbitals within t2g states, two different antiferro-type orbital orderings in the dyz and dzx states with Néel-type and stripe-type patterns can exist (Fig. 1(a)), depending on the next-nearest-neighbor exchange coupling. These calculations confirmed that the stripe-type orbital order has a lower energy, which should be accompanied by a reconfiguration of the spin degrees of freedom. This agreed with RXS data showing a scattering signal consistent with stripe-type order at the lowest temperatures8, as well as muon spin rotation data showing a second oscillatory component that may be due to coexisting stripe-type spin order27. These results therefore suggested that stripe-type spin-orbital order is the ground state, but AF-type orbital order can also exist in α-Sr2CrO4, depending on inter-site interactions between Cr ions.

The appearance of stripe-type spin-orbital order below TS causes the amplitude A1, associated with the spin demagnetization dynamics triggered by 1.0 eV pumping, to be suppressed (Fig. 3(c)). This occurs because the probability of inter-site transitions driven by 1.0 eV photoexcitation between the same spin-polarized dyz (or dzx) orbitals at the nearest Cr ions in the stripe-type spin-orbital ordered phase is half of that at higher temperatures, as with τ4 (Fig. 1(a)). However, the relevant decay time τ1 for spin relaxation does not change abruptly across TS, suggesting a persistent nature of the Néel-type spin order that is stable at all temperatures below TN, though it may be accompanied by stripe-type spin order below TS27. This corresponds to the previous RXS results, showing a gradual development of the Néel-type magnetic Bragg peak across TS8.

Finally, at higher temperatures, the T-dependent anomalies in τ3 and τ4 across TO = 140 K most likely originate from the phase transition into the AF-type orbital ordered state. Assuming that there is no orbital order above TO, the electronic structure for T > TO will differ from the orbital-ordered state below TO. This is supported by the fact that the c-axis lattice constant in the CrO6 octahedral structure decreases below TO, as shown in Fig. S59(See the supplementary material for additional experimental details). Such distortions in the octahedral structure can change the hybridization strength between t2g and eg orbitals28, which in turn affects the on-site relaxation of photoinduced carriers from eg states to t2g states after 3.1 eV photoexcitation (Fig. 1(d)). In other words, an increase in t2g-eg hybridization will enable photoexcited electrons in the eg bands to scatter into the t2g bands more effectively, decreasing τ3 below TO. Simultaneously, the photoexcited holes will hop from the O2p oxygen states to either Cr(1) or Cr(2) ions, facilitating both on-site and inter-site recombination with the excess electrons in the t2g bands (both processes contribute to τ4). These considerations thus give us a general picture of carrier dynamics in α-Sr2CrO4 (and its sensitivity to orbital order) after 3.1 eV photoexcitation.

Conclusions

In conclusion, we used femtosecond optical spectroscopy to track non-equilibrium carrier dynamics in α-Sr2CrO4, revealing clear temperature-dependent anomalies across the spin and orbital ordering temperatures. These experimental results are consistent with a theoretical prediction8 of two possible orbital configurations in the dyz and dzx states, i.e. Néel-type order below TO that turns into stripe-type order below TS. Overall, our results underline the ability of ultrafast optical spectroscopy to distinguish spin and orbital orders through their timescales for coupling to the electronic structure in complex materials.

Methods

The time-resolved photoinduced changes in reflectivity were measured on an epitaxially grown 100 nm thick c-axis oriented film of α-Sr2CrO4. We used a 250 kHz femtosecond regenerative amplifier producing ~100 fs pulses at 1.55 eV to probe the transient response. The 1.55 eV pulses were also used to pump an optical parametric amplifier that generated the 1.0 eV pump pulses. We used a beta-barium borate (BBO) crystal to obtain the 3.1 eV pump pulses by frequency doubling the fundamental 1.55 eV pulses. We used a near normal incident geometry for both pump and probe beams, which were linearly cross-polarized along the two equivalent in-plane a-axes of tetragonal α-Sr2CrO4. We measured the time-resolved reflectivity data up to t = 250 ps. We used an UV-VIS spectrometer to obtain the reflectivity data at room temperature. The light polarization was set to be perpendicular to the c-axis. We then transformed the reflectivity to optical conductivity using a Kramers-Kronig analysis. The error bars in (Figs. 3a and 4a) are calculated by using the deviations between the raw data taken at the neighboring time delays within 100 fs. The error bars in (Figs. 3c, d and Fig. 4c, d) in the main text and Fig. S4a, b, Fig. S7a–d and Fig. S8c–f were calculated by curve fitting to the raw data with 95% confidence bounds. We also observed coherent oscillatory signals in the 3.1 eV pump and 1.55 eV probe measurements due to acoustic phonons (Fig. S8.) However, we did not any obvious change across the spin and orbital ordering transitions (Supplementary Note 6). Both 1.0 eV and 3.1 eV pumping induce negative changes in the reflectivity change of 1.55 eV probe (Supplementary Note 7). The temperature rise due to our 1.0 eV and 3.1 eV pumping is less than 5 K29 (Supplementary Note 8). Interestingly, we also found that the specific heat data10 show T-dependent anomalies at all of the three spin and orbital ordering temperatures after extracting the magnetic contribution using the explicit Debye model30 (Supplementary Note 9).