Introduction

Polycrystals are usually deformed via dislocation motion and grain boundary (GB) sliding. The former dominates when GB density is low, and the latter dominates in fine-grained polycrystals. Consequently, the flow stress σf increases as the mean grain diameter l decreases for large-grained polycrystals because GBs impede the dislocation-mediated plasticity. This Hall–Petch behaviour1,2,3 gives way to inverse Hall–Petch behaviour when grain size is reduced to around 10–15 nm, where the GB sliding dominates the plasticity and softens the materials4,5. Recently, GBs are stabilised through relaxation and segregation6 or through high pressure7 so that the inverse Hall–Petch softening effect is staved off, and the Hall–Petch behaviour can extend to 3 nm7. However, the effect of grain diameter on material strength at l < 3 nm has been rarely explored because ultrafine-grained polycrystals are usually unstable and undergo grain coarsening8.

We expect that the inverse Hall–Petch softening4,5,6,9 breaks down, and a Hall–Petch-like strengthening restores in the ultrafine-grained regime (Fig. 1) because polycrystals will become amorphous solids (i.e. glasses) when grains are small enough9,10 and glasses usually exhibit higher strength than their polycrystalline counterparts11,12,13. In contrast to polycrystal whose plasticity is controlled by dislocation motion (Hall–Petch) or GB sliding (inverse Hall–Petch)4, glass deforms and flows in the form of nanoscale shear band14,15,16, which is due to the propagation of localised shear transformation zones (STZs)17,18,19. To search for the expected strengthening regime and investigate its mechanism, solids with ultrafine crystalline grains are needed.

Fig. 1: Three regimes of flow stress σf(l).
figure 1

As grain diameter l decreases, σf exhibits the Hall–Petch relationship (green curve) and the inverse Hall–Petch softening (grey line) in polycrystal regime1,2,3,4,5,6,10, and a power-law strengthening (magenta curve) in the glass-crystal composite (GCC) regime. Symbols refer to the measured results at mixing ratio x = 0.5. The fitted lc = 1.89 ± 0.01. The boundary (dashed line) between the inverse Hall–Petch softening and power-law strengthening coincides with the polycrystal–glass transition (see Supplementary Note 1 for the details). The mechanisms of the three regimes: dislocation motion, grain boundary (GB) sliding, and grain blocked shear transformation zone (STZ) are shown in the bottom.

Full size image

In recent years, nanocrystallites embedded in an amorphous matrix have attracted considerable interest because these materials possess advantages of both polycrystal and glass. For example, such structure can produce ultrahigh strength20 and world-record fatigue resistance21 and thereby shows promising applications21,22. These materials are known as the dual-phase glass-crystal structure20 or nanocomposite21, and lack of a standard terminology. Here, we call them glass-crystal composites (GCCs). How the grain size affects the strength of such material and whether the inverse Hall–Petch softening gives way to a strengthening behaviour in ultrafine-grained materials remain unclear.

Polycrystals and GCCs with mean grain diameter l < 3 nm are difficult to fabricate. In the previous study, we found that the grain size of a polycrystal composed of hard and soft particles (Fig. 2a–c) can be continuously reduced to a few particles by compression (Fig. 2d and Supplementary Figs. 1 and 2)10. This system provides an ideal platform to study whether the inverse Hall–Petch strengthening breaks down and a Hall–Petch-like strengthening restores in the finer-grained regime. The microstructure change in solids is difficult to resolve in situ because of the fast dynamics and localised nature of STZs11,15,23, and thus it has primarily been studied by simulations24,25.

Fig. 2: Compression reduces the grain size in the glass-crystal composites (GCCs).
figure 2

a The interaction potentials for hard and soft particles. Soft particle has a square-shoulder potential with an outer diameter of 1.3 and inner hardcore diameter of 1. b Compressed bonds between soft–soft (SS) and soft–hard (SH) particles. c Example local packing structures for crystal (packing fraction ϕ = 0.65) and glass (ϕ = 0.82) without and with compressed bonds, respectively. d GCCs at different ϕ and mixing ratio x = 0.5. Each crystalline particle is coloured according to its angle of the bond-orientational order parameter ψ6 as shown by the colour wheel. Disordered particles are in white. e The enlarged views of the dash-boxed regions in d. Crystallites (as coloured in d) are primarily composed of hard particles (black-rim circles). f, g The contour plots of crystallinity X and grain size Ng in the ϕ–x plane, respectively. Their colour bars are shown in the right. Three structural quantities at x = 0.5 are shown in (h–j). h Ng decreases with ϕ. Ng ≈ 3 when ϕ is extrapolated to the random close-packing density ϕRCP = 0.842 for binary-disk systems66. i 〈∣ψ6∣〉 averaged over hard and soft particles. j Δα = α(ϕ) − α(0.79) for four types of bonds, which reflect particles' aggregation propensity (Eq. (1)). The changes in slope at ϕ = 0.80 in (h, j) correspond to a glass–glass transition (see Supplementary Note 2 for the details).

Full size image

Here, we perform the event-driven molecular dynamics simulation26 on binary mixtures of hard and soft particles in two dimensions (see details in “Methods”) for which the continuously tunable grain size has been achieved10. The system is compressed from a single crystal to polycrystals and to GCCs with continuously decreasing of l (Supplementary Figs. 1, 2c), which enables us to study the strength of the ultrafine-grained regime and its microstructure change and mechanism. The grain diameter is usually in unit of particle number in simulations and nanometer in experiments. The diameter of a typical metallic atom, e.g. Cu or Ni4,7, is about 0.25 nm. The measured stress–strain curves at different packing fraction ϕ and mixing ratio x, the flow stress σf and shear modulus K as a function of crystalline grain size all show not only the conventional Hall–Petch strengthening and inverse-Hall–Petch softening, but also a power-law strengthening in the ultrafine-grained regime. The mechanisms of the mechanical behaviours are analysed from the microstructural deformations upon shear. The observed softening–hardening transition in Fig. 1 coincides with the polycrystal–glass transition identified in the previous work10.

Results

Structures of the GCCs

The area fraction ϕ increases with pressure (see “Methods” and Supplementary Fig. 2a). At ϕ = 0.62, a random mixture of soft and hard particles with the mixing ratio x: (1 − x) forms a single crystal (Supplementary Fig. 1) because their sizes are the same. As pressure increases, more soft particles are compressed and more size mismatches are produced, which leads to amorphisation (Fig. 2d, e) with the reduced crystallinity X (Fig. 2f) and grain size Ng (Fig. 2g, h). X is the fraction of crystalline particles, and Ng is the mean number of particles per crystalline grain (see the definition in “Methods”). Figure 2e shows that hard particles are highly apt to participate in crystalline grains. For systems with large x, less hard particles are available for grain formation, thereby decreasing the crystallinity (Fig. 2f). The crystalline order of particle i is characterised by its bond-orientational order parameter ψ6i (see details in “Methods”). ∣ψ6i∣ = 1 for a perfect hexagonal lattice and is close to zero for a disordered structure. As ϕ increases (i.e. the grain size decreases in Fig. 2h), 〈∣ψ6∣〉 gradually decreases for hard particles but maintains constant for soft particles (Fig. 2i), demonstrating that the structure primarily changes near hard particles.

For binary systems, the chemical short-range order (SRO) is characterised by the Warren-Cowley parameter27,28

$${\alpha }_{{{{{{{{\rm{AB}}}}}}}}}=1-\frac{{Z}_{{{{{{{{\rm{AB}}}}}}}}}}{{x}_{{{{{{{{\rm{B}}}}}}}}}{Z}_{{{{{{{{\rm{A}}}}}}}}}},$$
(1)

where ZA is the coordination number of A-type particle; ZAB is the number of B-type particles neighbouring surrounding A, and xB is the fraction of B-type particles. αAB = 0, >0 and <0 correspond to random mixture, favoured, and unflavoured AB bonds, respectively. Δα of four types of bonds relative to the values at ϕ = 0.79 (Fig. 2j) show that the same type particles have a higher affinity, which increases with ϕ. This demixing in binary solid can enhance the local packing efficiency29 and result in a stable GCC.

Mechanical behaviours

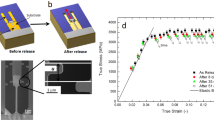
The stress-strain curves at different ϕ in Fig. 3a exhibit a linear increase (i.e. elastic regime) at strain γ < 0.025 (Supplementary Fig. 3), a nonlinear increase (i.e. strain-hardening) at 0.025 < γ < 0.2, and a plateau (i.e. steady flow) at γ > 0.2. The plateau height, which refers to the flow stress σf, increases as the grain size decreases at Ng < 170, i.e. \(l\simeq \sqrt{170}\simeq 14\) particles. This behaviour is qualitatively different from the inverse Hall–Petch behaviour, and can neither be fitted by the Hall–Petch relationship1,2 (Fig. 3b). Instead, σf(Ng) satisfies a power law,

$${\sigma }_{{{{{{{{\rm{f}}}}}}}}}({N}_{{{{{{{{\rm{g}}}}}}}}})\propto {({N}_{{{{{{{{\rm{g}}}}}}}}}-{N}_{{{{{{{{\rm{g1}}}}}}}}})}^{-{\eta }_{1}}$$
(2)

with the fitted η1 = 0.63 ± 0.09 and Ng1 = 3.24 ± 0.17 (Fig. 3b). The shear modulus exhibits a similar power law

$$K({N}_{{{{{{{{\rm{g}}}}}}}}})\propto {({N}_{{{{{{{{\rm{g}}}}}}}}}-{N}_{{{{{{{{\rm{g2}}}}}}}}})}^{-{\eta }_{2}},$$
(3)

with the fitted η2 = 0.72 ± 0.14 and Ng2 = 3.07 ± 0.27 (Fig. 3c). The σf and K diverge at Ng ≃ 3, indicating that the minimum grain size is at least 3 particles, which is consistent with the extrapolated Ng value at the random close-packing density in Fig. 2h where the stress diverges30. The divergence is caused by the hard-core interactions between particles which render the system incompressible when the shells of soft particles collapse. Systems composed of soft-core particles can be infinitely compressed. In real systems, atoms exhibit hard cores under high pressures.

Fig. 3: Mechanical properties.
figure 3

a Stress–strain curves for glass-crystal composites (GCCs) with 50% soft particles at different packing fraction ϕ, corresponding to different grain size Ng. b The flow stress σf averaged over the strain range 0.3 < γ < 0.4 in (a). Black curve: the fitting of Eq. (2) with Ng1 = 3.24 ± 0.17 (vertical dashed line) and η1 = 0.63 ± 0.09. The Hall–Petch relation (green-dashed curve) cannot well fit the data. c The shear modulus K measured from the slope of σ(γ) in the elastic regime of γ < 0.025 in (a). Black curve: the fitting of Eq. (3) with Ng2 = 3.07 ± 0.27 and η2 = 0.72 ± 0.14. Inset: σf(K). d σf fitted by Eq. (2) (dashed curves) at different x. e Rescaling of (d) collapses all the data on a straight line. f The fitted minimum grain sizes from σf(Ng) (solid symbols) and K(Ng) (open symbols) at different x.

Full size image

σf(Ng) and K(Ng) derived from the plastic and elastic regimes are strikingly similar. Thus σf(K) is linear (Fig. 3c inset). This indicates that the solids with different grain sizes yield at the same strain, as confirmed in Supplementary Fig. 3 in which the slope of σf(γ) always changes around γ = 0.025. The linear behaviour of σf(K) is often observed in glasses28,31.

The data for x = 0.5 in Fig. 3b and d are from different trials of simulation, and both well fit Eq. (2). σf(Ng) at other mixing ratios can also be well fitted by Eq. (2) (Fig. 3d) and can collapse well onto the master line after being rescaled by the fitting parameters (Fig. 3e). K(Ng) at other mixing ratios also exhibit similar results as Fig. 3c. The minimum grain sizes Ng1,2 fitted from σf(Ng) and K(Ng) are very close and can be reduced to three particles when the fraction of soft particles x ≥ 0.5 (Fig. 3f).

This power-law strengthening holds at Ng < 170 particles (Fig. 3b), i.e. l < 3.5 nm for typical alloys. At l > 3.5 nm, we observe the conventional inverse Hall–Petch behaviour, see section “Polycrystal-glass transition” for details. A similar inverse pseudo Hall–Petch to pseudo Hall–Petch transition has been recently reported at 3.1 nm in nanocrystalline graphene32, but there are only two data points at < 3.1 nm which can hardly provide a quantitative fitting.

Microstructure changes under shear

The structural deformation around particle i is characterised by the mean squared nonaffine displacement17,33,

$${D}_{i}^{2}=\frac{1}{{N}_{i}}\mathop{\sum }\limits_{j=1}^{{N}_{i}}| {{{{{{{{\bf{d}}}}}}}}}_{ij}-{{{{{{{{\bf{F}}}}}}}}}_{i}{{{{{{{{\bf{d}}}}}}}}}_{ij}^{0}{| }^{2}$$
(4)

which describes its neighbours’ average deviation from the linear strain field. dij = rj − ri is the distance vector between atom i and its neighbour j in the current state, \({{{{{{{{\bf{d}}}}}}}}}_{ij}^{0}\) is for the initial undeformed state, and Fi is the transformation matrix for all distances between particle i and its Ni neighbours in a strain interval. Under shear (Fig. 4a–f), particles whose D2 > 0.6 usually signature local plastic deformations33, i.e. STZs, which are labelled in yellow in Fig. 4h–k. These yellow particles are mainly found in amorphous regions and anti-correlate with crystalline regions (Fig. 4o). The Pearson correlation coefficients between quantities A and B is defined as \(C(A,B)=\frac{\mathop{\sum }\nolimits_{i}^{N}({A}_{i}-\langle A\rangle )({B}_{i}-\langle B\rangle )}{\sqrt{\mathop{\sum }\nolimits_{i}^{N}{({A}_{i}-\langle A\rangle )}^{2}}\sqrt{\mathop{\sum }\nolimits_{i}^{N}{({B}_{i}-\langle B\rangle )}^{2}}}\), where 〈〉 averages over all the N particles. In the elastic regime γ < 0.025, plastic flows are absent (Fig. 4g). In the strain-hardening regime (0.025 ≤ γ ≤ 0.2), the high-D2 yellow particles form small stripes with a typical thickness of 2–4 particles. These localised plastic flows, i.e. STZs, homogeneously occur in space (Fig. 4h–j) because scattered crystallites interrupt their growth (Fig. 4a–f and Supplementary Fig. 4b). By contrast, the plastic flows in normal glasses usually form extreme localised shear bands because no crystallite blocks the growth of STZs (Supplementary Fig. 4a). The extremely localised plastic flows in normal glasses often cause strain softening and even catastrophic failure, which limit their applications11,12. By contrast, the homogeneous distribution of STZs in GCCs prevents the extreme localisation of plastic flow and leads to strain-hardening and associated strengthening effect (Fig. 3a, b)34. As γ increases, the yellow deformation zones grow and percolate the whole sample (Fig. 4k and Supplementary Fig. 4c) in the steady flow regime γ > 0.25. Crystalline grains rotate (Fig. 4l), split (Fig. 4m), and rebuild (Fig. 4n) during the deformation process (see Supplementary Movies 1–3), which continuously affect the plastic flow.

Fig. 4: Shear-induced deformations at packing fraction ϕ = 0.81 with 50% soft particles.
figure 4

a The initial state without a strain. Black arrows denote the shear along the x direction. b–f The structures at γ = 0.02, 0.05, 0.1, 0.2, and 0.3, respectively. Crystalline particles are coloured in the same way as Fig. 2d. g–k Mean squared nonaffine displacements D2 corresponding to (b–f), respectively. Particles strongly deviate from linear affine strain field are colour in yellow. The black (1), blue (2), and red (3) ellipses in (a) show crystalline grain that rotates (l), divides (m), and rebuilds (n) under shear, respectively. l The [01] lattice direction of the crystalline grain in the black ellipses 1 in (a–f) rotates from 30∘ to 9∘. This grain retains during the shear and impedes the spreading of STZ as shown by the white ellipse in (j). m A crystalline grain in the blue ellipses 2 in (a–f) disintegrates into two grains. n A crystalline grain becomes amorphous and then recrystallises into a new one in the red ellipses 3 in (a–f). o The Pearson correlation coefficients C between D2 and crystalline order ∣ψ6∣ (squares) and between D2 and disorderness 1 − ∣ψ6∣ (circles).

Full size image

Crystallites (high-∣ϕ6∣ regions) not only spatially anticorrelate with strong-local-rearrangement (large D2) regions (Figs. 4o and 5a, b), but also tend to rotate clockwise, leading to more red clusters than blue clusters in Fig. 5c. This rotation is consistent with the shear direction. The long-live neighbour particles can characterize the local structural rearrangement and reflect the macroscopic rheological response of glasses from the microscopic structure35. Such analysis has been applied in colloidal gel36 and glass35, but rarely in GCCs or polycrystals. We find that plastic flows with high D2 (Fig. 5a) strongly correlate with particles having less long-lived neighbours (Fig. 5b). Crystalline particles have more long-lived neighbours than amorphous particles particularly at high γ (Fig. 5d), indicating that more bond breakings occur in amorphous regions. Since the plastic deformations mainly occur in amorphous regions, the yield strain is a constant regardless of the crystalline grain size (Fig. 3a and Supplementary Fig. 3).

Fig. 5: Microstructure changes during plastic deformation at strain γ = 0.25.
figure 5

a The spatial distribution of nonaffine displacement D2. b The spatial distribution of the number of long-lived neighbours of each particle nA,B normalised by the average number 〈nA,B〉, which anticorrelates with (a). c The rotation angle of crystalline particles when γ increases from 0 to 0.25. Clockwise rotations (red) dominate. Amorphous particles are in black. The green ellipses in (a–c) mark a crystalline grain that clockwise rotates (Fig. 4l) to accommodate the plastic flow. d The mean number of long-lived neighbours n for crystalline and disordered particles.

Full size image

The shear-induced structure changes are shown in Fig. 6. The average crystalline order 〈∣ψ6∣〉 are nearly constant during plastic deformation (Fig. 6a). The average 〈D2〉 of soft particles are greater than that of hard particles (Fig. 6b) and their ratio is constant in the plastic regime of γ > 0.08 (Fig. 6c), implying that a fixed large portion of deformation is obtained from the soft particles under shear. The deformation participation ratio \({P}_{r}=\frac{1}{{N}_{{{{{{{{\rm{S,H}}}}}}}}}}\mathop{\sum }\nolimits_{i}^{{N}_{{{{{{{{\rm{S,H}}}}}}}}}}{{\Theta }}({D}_{i}^{2}-0.6)\), where NS,H is the numbers of soft or hard particles and Θ is Heaviside function, i.e., the fraction of particles whose D2 > 0.6. Soft particles show larger Pr than hard particles (Fig. 6d), which confirms their dominating contribution to plastic flows. The spatially uniform distribution of soft particles (Supplementary Fig. 1) accounts for the homogeneity of STZs (Fig. 4e–k and Supplementary Fig. 4b, c) that mitigate the extreme localisation of plastic flows (Supplementary Fig. 4a–c). The number of long-lived neighbouring particles n(γ) at different ϕ or Ng are almost the same for hard particles, but different for soft particles (Fig. 6e). This finding is consistent with that shown in Fig. 5d, indicating that the plasticity mainly occurs on the soft particles distributed in amorphous regions (Fig. 2e). n(γ) of soft particles decreases more rapidly in larger-grained GCCs (lower ϕ), implying that their local cages can be easily broken, and the stress can be effectively released. Therefore, large-grained GCCs show weaker strain-hardening and strengthening effects (Fig. 3b, d).

Fig. 6: Shear-induced changes for hard and soft particles at different packing fractions ϕ.
figure 6

a The average order parameter 〈∣ψ6∣〉 for hard and soft particles remain constant during the deformation at each density. The legend in (a) is for panels (a–f). b The average nonaffine displacement 〈D2〉 for hard and soft particles. c The ratio of 〈D2〉 for hard to soft particles. d Deformation participation ratios Pr67. e Mean number of long-lived neighbours n is insensitive to density for hard particles and more sensitive for soft particles as shear increases. n for soft particles are lower than that of hard particles because some soft particles are compressed smaller, and thus they have fewer neighbouring particles. f The average potential energy per particle under shear.

Full size image

In contrast to strain softening in normal glasses, rejuvenated glasses exhibit strain-hardening similar to our GCCs because they both exhibit uniform flow stresses. However, we find that their underlying mechanisms are different. For rejuvenated glasses, the stored strain reduces the activation energy of STZ and causes uniform plastic flow with the decrease of energy34. For GCCs, however, the crystallites block the shear banding, thereby producing a uniform plastic flow (Supplementary Fig. 4c) associated with a constant energy (Fig. 6f).

Polycrystal-glass transition

As grain size decreases small enough, a polycrystal or a GCC will eventually become an amorphous glass. It is not clear whether an ultrafine grained polycrystal or GCC should be called as polycrystal or amorphous glass, or it is just a matter of terminology without a clear distinction. This basic question has been rarely asked and poorly explored. Crystal-glass transition has been observed in colloidal37,38, granular39,40, and atomic systems41,42, but these studies are neither about ultrafine-grained solids nor about the polycrystal-glass transition. Nanoindentation in Ni-W alloy shows that the deformation morphology becomes similar to those in glasses when the grain size decreases to approximately 3 nm in the inverse Hall–Petch regimes9. However, whether this difference in deformation morphology indicates a polycrystal-to-glass transition remains unclear9. For the hard–soft binary systems, surprisingly we find that polycrystal–glass transition occurs at a sharp point rather than a gradual crossover10. Various quantities peak at l ≃ 14 particles, i.e. ϕ = 0.7 (Supplementary Fig. 5)10, which indicates a sharp polycrystal-glass transition. Therefore, GCCs with l < 14 particles can also be considered as dual-phase glasses (Fig. 1). The polycrystal–glass transition coincides with the transition between the inverse Hall–Petch softening and the power-law strengthening regimes in Fig. 1. The maximum residual specific heat at l = 14 particles (Supplementary Fig. 5a) implies the maximum fluctuation of compressed SS or SH bonds, which is in accordance with the strongest fluctuations of structure and dynamics (Supplementary Fig. 5b, c). The maximum fluctuations of a structure parameter about crystallinity (Supplementary Fig. 5b) and a dynamic parameter about vibration amplitude (Supplementary Fig. 5c) at l = 14 particles imply the maximum compressibility as confirmed in Supplementary Fig. 5d, which is in accordance with the minimum strength at the boundary between the inverse Hall–Petch softening and power-law strengthening regimes (Fig. 1). Therefore, the features of the polycrystal–glass transition10 can explain the transition between the inverse Hall–Petch softening and the power-law strengthening. In turn, the transition provides an additional signature of the poorly explored polycrystal–glass transition.

The system can be compressed into a glass when \((x-0.193)(0.786-\frac{1}{{\lambda }^{2}})\, > \,0.02\)10, i.e., the shoulder width λ and fraction of soft particles x must be large enough to provide sufficient size mismatches for glass formation. The power-law strengthening regime (Fig. 1) can exists only in samples whose λ and x satisfy the above inequality. For example, systems with small λ or x do not exhibit the strengthening regime because it is a polycrystal instead of a glass even under the highest pressure (i.e. ϕ = 0.83) in our simulation (see Supplementary Fig. 6).

The classical Hall–Petch strengthening and inverse Hall–Petch softening indicate that the strongest strength occurs at their boundary state. However, we observe the strength of GCCs can be six times higher than the boundary state between the Hall–Petch and inverse Hall–Petch regimes (Fig. 1). At l ≃ 2, σf = 0.3 in the reduced unit (Figs. 3b and 1) corresponds to σf = 125 GPa for graphene, whose energy and distance units are U0 = 525 kJ mol−1 and σ = 0.128 nm43, respectively. Such σf is higher than the strength of polycrystal graphene32,44,45,46. Therefore, the ultrafine-grained GCCs have the potential to achieve extremely high strength.

Discussion

Our simple system can model binary experimental systems whose components have different softness, such as alloys, granular and colloidal particles with different stiffness. For instance in Al–Ce alloy, the 4f-electrons of Ce atom are localised and thus Ce atoms interact via shoulder potentials47, and their diameters can be reduced by 20% using cutting edge high-pressure technologies48. Such large deformation is sufficient to induce the polycrystal–glass transition. In such binary systems, the grain size can be continuously decreased to a few particles because the size-mismatched particles, i.e. the compressed soft particles, are gradually ‘added’ through the interior of the bulk by compression10. It is well known that adding size-mismatched particles, i.e. solute particles, can reduce polycrystalline grain size8, but adding excessive solutes will produce glasses instead of ultrafine-grained polycrystal49. By contrast, the solutes in our system are not added to the solution all at once, but incrementally added to the interior of the polycrystal, which hinders the glass formation. Thus, the soft–hard binary system provides a full spectrum of grain size, which bridges the polycrystal and glass and enables to explore how the strength changes with grain size beyond the Hall–Petch and inverse Hall–Petch regimes. We find that the inverse Hall–Petch softening terminates at l ≃ 14 particles, i.e. 3.5 nm in typical alloys, and a strengthening regime develops at l < 14 particles. The power-law strengthening regime in GCCs complements to the Hall–Petch and inverse Hall–Petch regimes for the grain size effect on solid strength (Fig. 1).

We observe that the strain-hardening and power-law strengthening arises from grain-mediated STZ, which is qualitatively different from the dislocation-mediated strengthening in the Hall–Petch relationship (Fig. 1). The uniformly distributed crystalline grains in the amorphous matrix impede the growth of STZs, which suppress the formation of extreme localised shear band. Therefore, GCCs avoid sudden stress drop that usually exists in normal glasses, and exhibit dramatic strengthening and strain-hardening which are absent in normal glasses. Moreover, we find that plastic deformation arises from bond-breaking in the amorphous regions and collective cluster rotation in the crystalline regions. Crystalline grain rotations often lead to good ductility, which explains the observed high ductility in dual-phase aluminium alloy22. This hardening mechanism avoids the inverse Hall–Petch softening in nanocrystal and the shear-band softening in glass, thereby providing a route to improve the strength of materials.

Low-dimensional systems are much softer because there are more long-wavelength fluctuations50 and particles have fewer neighbour-provided constraints51. Consequently, the space dimension could affect the nature of phase transition such as crystal melting50,51 and glass dynamics52. For example, the transient localization of particles on approaching the glass transition is absent in 2D, but very pronounced 3D52. Analysis based on local coordinates can avoid long-wavelength fluctuations so that the glassy behaviours are similar in 2D and 3D53,54,55. We expect the strengthening beyond the inverse Hall–Petch (Fig. 1) remains valid in 3D because a completely disordered solid has a higher strength than the polycrystals in the inverse Hall–Petch regime in 3D. This expectation is independent of the dimensionality.

Various quantities of this binary system simultaneously peak at the same ϕ (Supplementary Fig. 5), which indicates a sharp polycrystal-to-glass transition point. In addition, we find that this polycrystal-glass transition point coincides with the transition between the inverse Hall–Petch softening and power-law hardening. The features at the polycrystal-glass transition can qualitatively explains the softening–hardening transition, and in turn, the softening-hardening transition provides an additional feature for the polycrystal-glass transition. The thermally induced transition and the nonequilibrium shear-induced transition are qualitatively different and the shear could shift the transition point. However, the polycrystal-glass transition without shear coincides with the softening–hardening transition with shear, which suggests deep connections between the material properties with and without shear. These results provide insights into the poorly explored polycrystal-glass transition and the discovered softening–hardening transition.

Methods

Model and simulation details

The soft particle is described by square-shoulder potential

$$U(r)=\left\{\begin{array}{ll}\infty ,\quad &r\le \sigma \\ {U}_{0},\quad &\sigma\, < \,r\le \lambda \sigma \\ 0,\quad &\lambda \sigma\, < \,r\end{array}\right.$$
(5)

where σ and λσ are the diameters of the inner hard core and outer shoulder, respectively. In this work, λ = 1.3. The energy unit U0 is the height of the shoulder. The pair potential for hard particles is characterised as follows:

$$\begin{array}{r}U(r)=\left\{\begin{array}{ll}\infty ,\quad &r\le \lambda \sigma \\ 0,\quad &\lambda \sigma\, < \,r.\end{array}\right.\end{array}$$
(6)

The square-shoulder potential has been used to describe cerium and cesium atoms, water and silica molecules, micelle and granular particles, and to study self-assembly, glasses, quasicrystals, and photonic crystals47,56,57,58,59,60.

We simulate N = 12,800 particles under periodic boundary conditions with the fraction of soft particles x ranging from 0.35 to 0.6. The packing fraction ϕ is defined as the area fraction of hard particles and the hard cores of soft particles:

$$\phi =\frac{N\pi {\sigma }^{2}}{4A}[(1-x){\lambda }^{2}+x],$$
(7)

where A is the area of the simulation box. Particles are randomly distributed in a low-density fluid (ϕ = 0.5) state and then relaxed at temperature T = 2.0U0/kB. The relaxed systems are then compressed into polycrystal and glass (Supplementary Fig. 1) by using the Lubachevsky-Stillinger algorithm61. The resultant systems are sufficiently equilibrated at T = 0.13U0/kB for a time period of 105t0, where kB is the Boltzmann constant, \({t}_{0}=\sqrt{m{\sigma }^{2}/{U}_{0}}\) is the mean time for a particle moving a distance σ, and m is the unit of mass for hard and soft particles. All the results are measured at T = 0.13U0/kB. After the system is compressed to the desired ϕ and its corresponding Ng, a shear is applied along the x direction by using the Lees-Edwards periodic condition in y direction with a strain rate of 10−5. All figure and movies are about samples with 50:50 soft–hard mixing ratio. Samples with other mixing ratios range from 35:65 to 60:40 exhibit similar results. Each simulation is repeated ten times for sufficient statistics.

Identification of crystalline grains

The local hexagonal order of particle j is characterised by the weighted bond-orientational order parameter62

$${\psi }_{6j}=\frac{1}{{l}_{{{{{{{{\rm{tot}}}}}}}}}}\mathop{\sum }\limits_{k=1}^{{N}_{j}}{l}_{jk}{e}^{i6{\theta }_{jk}},$$
(8)

where θjk is the orientational angle of the bond between particle j and its neighbour k. i2 = − 1. The Voronoi polygon has Nj edges with perimeter ltot, and the length of the edge between j and k is ljk. A higher ∣ψ6j∣ represents a higher 6-fold crystalline order. A crystalline bond is defined as \(| {\psi }_{6j}\cdot {\psi }_{6k}^{* }|\, > \,0.6\). A particle with three or more crystalline bonds is defined as a crystalline particle63,64. Two neighbouring crystalline particles belong to the same grain if the difference between their orientational angle is less than 6∘. Non-crystalline particles and single isolated crystalline particles are defined as disordered.

The weighted mean grain size10,65

$${N}_{{{{{{{{\rm{g}}}}}}}}}=\sum \frac{{n}_{s}{s}^{2}}{{N}_{{{{{{{{\rm{x}}}}}}}}}},$$
(9)

where ns is the number of grains with s crystalline particles; Nx is the total number of crystalline particles; and \(\frac{{n}_{s}s}{{N}_{{{{{{{{\rm{x}}}}}}}}}}\) is the probability that a particle belongs to the s-sized grains. The grain diameter \(l=\sqrt{{N}_{{{{{{{{\rm{g}}}}}}}}}}\).