Introduction

The recent emergence of 2D magnetic materials with their potential applications in spin-logic circuitry and memory devices has triggered experimental research to find methods for detection and control of their magnetic ordering1. This has been a challenge for the past decade because of the low magnetic moment of these magnets at the 2D limit, compared with their bulk counterpart. There have been many techniques introduced so far, commonly used for the detection of magnetic behavior and quantitative study of the magnetism in the 2D magnets, such as magneto-transport measurements2,3,4 and electron tunneling5,6, magnetic circular dichroism and magneto-optical Kerr effect measurements7,8,9, optical second harmonic generation10,11,12, magnetic force microscopy13,14,15, scanning superconducting quantum interference device (SQUID) microscopy16,17, angular electron spin resonance18 and nitrogen-vacancy (NV) magnetometry19,20,21,22,23,24,25,26,27,28. Among them, NV-magnetometry provides high sensitivity and nano-precision in the detection of magnetic ordering at a large temperature range from 0.35 to 600 K29,30. By this technique, we can detect weak static and dynamic magnetic stray fields that provide quantitative information about the magnetization of a 2D magnet down to the monolayer limit, providing insights into the magnetic domains and localized magnetic defects27.

A central challenge for achieving high spatial resolution and extracting quantitative results on material magnetization using NV magnetometry is to achieve a nanoscale and well-defined distance between the sample and the NV centers21. A powerful method is to embed a single NV spin into a diamond scanning probe, which enables imaging with 50 nm spatial resolution and quantitative determination of monolayer magnetizations22,24. A second approach is to deposit a 2D magnet directly onto a diamond chip hosting a high density of near-surface NV spins23,31,32,33,34,35. This approach benefits from a strong signal due to a large number of NV spins. Furthermore, it enables large-area magnetic imaging with 100 μm-scale field-of-views at diffraction-limited resolution36, but requires the ability to fabricate the sample onto the diamond.

For the NV-magnetometry of 2D materials, here we develop a method based on a deterministic placement of a diamond membrane onto the target magnetic flake on a substrate with micrometer lateral precision. We demonstrate a pick-and-place diamond transfer procedure similar to the “dry-transfer” technique commonly used in assembling stacks of 2D materials37. Using this technique we achieve close proximity between the diamond and the sample that is crucial for detecting the weak magnetic fields of atomically thin magnetic layers with high spatial resolution. By using micron-sized diamond membranes as done in ref. 38, we strongly increase the probability to achieve nanoscale stand-off distance between diamond and sample with respect to using millimeter-sized diamonds39. Such large diamonds generally lead to micron-scale diamond-sample distances because of the ~3 orders of magnitude larger probability to capture spurious particles (e.g., dust) between diamond and sample. Moreover, our transfer technique positions the diamond at a target location with a micrometer lateral precision while being compatible with 2D materials assembly techniques. This high degree of control also precludes an incorrect orientation of the diamond, as well as the need to further push/drag the diamond to a target location using micromanipulators, which can damage sensitive samples such as 2D materials. Furthermore, thinning the diamond membrane to a few microns enhances the collection of the NV photoluminescence because of reduced optical aberrations and yields a flexible membrane that can conform more readily to a target surface, which facilitates pickup with the PDMS/PMMA stamp. An additional benefit of our approach is that it enables placing a diamond sensor onto commonly used substrates such as SiO2/Si that facilitates optical detection and thickness determination of 2D materials. Moreover, these substrates and materials can be equipped with electronic circuitry (e.g., for the microwave resonator) to study and control the various spins in the system.

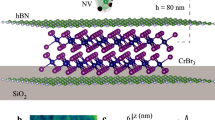
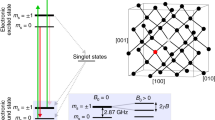
We use the diamond transfer technique to characterize the magnetization of a 2D interlayer antiferromagnet, Chromium Sulfur Bromide (CrSBr) (Fig. 1a). The diamond membrane contains a layer of NV centers implanted at about 70 nm below the surface (see Methods). Each NV has an S = 1 electron spin with a zero-field quantization axis (\({\hat{S}}_{{{{\rm{NV}}}}}\)) that is along the diamond [111] axis, angled by α = 54.7° relative to the sample-plane normal (Fig. 1a). The Zeeman splitting of the NV spin states ms = ± 1 is induced by a small external field (Bex ~ 5.6 mT) and is modulated by the projection of the local magnetic stray field (BNV) along \({\hat{S}}_{{{{\rm{NV}}}}}\)40. We detect this field by measuring the NV electron spin resonance (ESR) transitions frequencies through the application of a microwave magnetic field via a stripline and readout of the NV’s spin-dependent photoluminescence (PL)40,41.

Fig. 1: NV magnetometry of the interlayer antiferromagnet CrSBr.
figure 1

a Schematics of the sample. A diamond membrane with a shallowly implanted layer of NV centers (at the depth of about 70 nm, shown with the layer in red) is placed onto the CrSBr crystal. The NV centers consist of a substitutional nitrogen atom adjacent to a vacancy in the diamond lattice. They are oriented along the [111] directions in the diamond crystal, at α = 54.7° with respect to the sample normal. We use the subset of NVs oriented along \({\hat{S}}_{{{{\rm{NV}}}}}=\sin \!\alpha \,\hat{x}+\cos \!\alpha \,\hat{z}\) for magnetometry. A small external magnetic field Bex = 5.6 mT along \({\hat{S}}_{{{{\rm{NV}}}}}\) enables selective driving of the ms = 0 ↔ − 1 electron spin resonance (ESR) transition of the target NV subset using microwaves applied via the stripline. A green laser (520 nm) excites the spin-dependent NV photoluminescence (PL). b Illustration of the modulation of the NV ESR frequency by the stray fields (purple arrows) generated by the uncompensated CrSBr magnetization at the CrSBr edges. The CrSBr magnetic stacking order is indicated by black arrows. The plot shows the expected spatial dependence of the CrSBr stray fields and the corresponding change of the NV ESR frequency (fESR = f0 − γdBNV) sensed by the selected NV family, where f0 = D − γBex with D = 2.87 GHz the NV zero-field splitting.

Full size image

As illustrated in Fig. 1b, each CrSBr layer is ferromagnetically ordered along its in-plane magnetic easy-axis (y-axis) below its Néel temperature12,42. Therefore, an odd number of CrSBr layers leads to a net magnetic moment that generates a magnetic stray field (purple arrows) at the CrSBr edges (Fig. 1b). We determine the projection of this field onto the NV axis (dBNV) by measuring the corresponding shift in the NV ESR frequency dfESR = γNVdBNV, with γNV = 28.053 GHz/T the NV gyromagnetic ratio40. From the stray field, we quantify the monolayer magnetization of the CrSBr flake and extract the NV-sample distance. We note that the small bias field Bex of 5.6 mT used in our measurements is negligible compared to the crystal anisotropy and exchange fields of CrSBr43, such that the CrSBr flakes preserve their interlayer antiferromagnetic ordering along the easy axis. Thus, depending on their thickness, the total stray field can have zero vs. finite value for even vs. odd numbers of the CrSBr layers.

Results and discussion

Diamond membrane transfer

The main steps for the sample preparation are shown in Fig. 2 with further details in the Methods section. The diamond membrane used in this work is fabricated by ion implantation at a depth of about 70 nm below the diamond surface with an NV density of 103 NVs/μm2 (see Methods). As shown in Fig. 2a, a large diamond chip is etched by O2 plasma into squares of 50 × 50 μm2 with a thickness of 5 μm, which remain connected to the surrounding diamond by small holding bars. Next, the diamond frame is attached to a metallic tip using a UV-curing adhesive. The metallic tip is held by micro-manipulators of a probe station that facilitates a controllable movement of the diamond chip. With that, the diamond chip is brought above a flexible 0.5 mm-thick polydimethylsiloxane (PDMS) layer held on a substrate. As shown in Fig. 2b, another metallic sharp tip (width ≈ 10–20 μm in diameter) is then used to break the connecting rod and tip out one of the square diamond membranes onto the PDMS (No. 1). To detach the diamond membrane from the diamond frame, we first bring a target membrane to (almost) touch the PDMS surface, then push the target membrane into contact with the (sticky) PDMS polymer, then lift the frame to detach it from the membrane, and then retract the tip. This procedure eliminates the chance of the membrane flipping upside down. The reason for choosing PDMS is to provide the diamond membrane with a rather flexible substrate with low adhesion to ease the diamond pick-up procedure that follows in the next step.

Fig. 2: Fabrication of the diamond membrane and transfer on 2D magnets.
figure 2

a An SEM image of the diamond membrane etched into the 50 × 50 × 5 μm3 squares by O2 plasma. b Detaching a single square of the diamond-membrane by a metallic tip (shown in blue) that is controlled by micro-manipulators. After the detachment, the membrane drops on a polydimethylsiloxane (PDMS) layer that is held on a substrate (here called PDMS 1). c A PMMA-PDMS stamp (prepared separately by suspension of PMMA membrane, described in the Methods section) is vertically brought in contact with the diamond membrane by a micro-manipulator. Adhesion of the diamond to the PMMA allows for the pick-up of the diamond membrane by retracting the PMMA-PDMS stamp. d Transfer of the diamond on top of a CrSBr flake that is located next to the Au stripline on a SiO2-Si substrate. The optical micrograph shows the region defined by the black dashed line (the scale bar is 10 μm). e By melting the PMMA at 180 °C the PMMA and diamond membranes are released on top of the SiO2 substrate, leaving the diamond on the target CrSBr flake within a few micron precision. As shown in the optical micrograph, the PMMA membrane is removed by e-beam lithography at the region of interest.

Full size image

To pick up the diamond (Fig. 2c), we use a stamp that is made of a layer of poly-methyl methacrylate (PMMA) and PDMS (No. 2) held on a glass slide (see Methods section for the preparation of the PMMA membrane and the stamp). The PDMS-PMMA stamp is then brought in contact with the diamond membrane (held on PDMS 1), using a transfer stage that is equipped with micromanipulators. The good adhesion of the diamond and PMMA helps with the diamond pick-up when retracting the stamp (when in contact, the stack can additionally be annealed up to 80 °C to promote the adhesion). In the next step (Fig. 2d), the diamond membrane is transferred on top of a CrSBr flake previously placed next to the Au stripline (see Methods for details).

When aligned, the diamond membrane and CrSBr flake are brought in contact while heating up the stage to 100 °C. After cooling down the stage to 30 °C and retracting the PDMS, the PMMA and diamond get locally detached from the PDMS in the central area and stay on the SiO2 substrate. At this step, the stage is heated up to 180 °C to melt the PMMA which relaxes the PMMA-diamond on the CrSBr-substrate and allows for full detachment of PMMA from the PDMS stamp (Fig. 2e). The PMMA in the region of interest is then removed by e-beam lithography, leaving an overlap between the unexposed part of the PMMA and the diamond membrane to avoid diamond displacement in the PMMA-removal procedure. The PMMA removal is not necessary and is done to avoid the possibility of light scattering. We note that the presence of the PMMA has minimal effect on the detected NV response (see Supplementary Fig. 5). Thus, the last step could be omitted, especially to avoid air exposure in the case of air-sensitive magnetic materials. Note that the dark shadow around the central area of the diamond (in Fig. 2e) is a signature of the diamond membrane being directly in touch with the CrSBr flake44 which is essential for detecting the magnetization. The fringes observed in the optical image are related to the slight gradual variation of the diamond thickness due to the deep etching process of the diamond top surface (see Supplementary Fig. 1) which does not change the NV-CrSBr distance.

The direct contact with the intact interface between the diamond and the 2D magnet is one of the main advantages of this technique. The method minimizes the chance of contamination (e.g., dust particles) at the interface that has been affecting measurements in previous reports with a wet transfer of the diamond39. Moreover, this diamond transfer method can be used in the inert atmosphere of a glove box which makes it suitable for air-sensitive 2D magnetic materials. In addition, with the full coverage of the 2D flakes with the diamond and PMMA membranes, further encapsulation of air-sensitive flakes can be avoided.

NV electron spin resonance measurements

The CrSBr flake that we study here consists of regions with various thicknesses that can be distinguished by their optical contrast with respect to the SiO2/Si substrate (Fig. 3a). The atomic force microscope (AFM) image of the flake (Fig. 3b) and the corresponding AFM height profile (Fig. 3c) show the thickness of different regions of the CrSBr flake across its width. Over the same region, we measure the NV ESR transition frequency (Fig. 3d). The spatial alignment of Fig. 3a–d along the width of the CrSBr flake guides us to determine the ESR signal corresponding to each step in the CrSBr flake. The non-zero modulation of the ESR frequency at some of the edges is a signature for an odd number of CrSBr flakes that would give rise to an uncompensated stray field. For such measurements, as described earlier, we are able to selectively detect the PL response from the NV centers and the CrSBr flake because of their distinct PL spectrum (Fig. 3e and Supplementary Fig. 1).

Fig. 3: Stray field detection of CrSBr.
figure 3

a Optical micrograph of the studied region of the CrSBr flake (scale bar is 5 μm). The black arrow shows the direction of the magnetization easy axis of the CrSBr flake. The gray dashed line highlights the edge of the 2.4 nm CrSBr layer. b Atomic-force microscope (AFM) image of the CrSBr flake. c Height profile of the CrSBr flake, measured along its width. d Electron spin resonance frequency measured at T = 10 K along the width of the CrSBr flake. The ESR signal is measured along the white dashed lines shown in Supplementary Figs. 1 and 3. e Photoluminescence (PL) measurements of the NV-diamond and CrSBr, performed at 10 K, with excitation wavelength and power of 520 nm and 10 μW, respectively. Due to the high density of the NV centers, the PL spectrum between 600 and 800 nm is dominated by the PL signal from the NV centers. f Spatial map of the PL and ESR contrast, measured at T = 70 K, corresponding to the CrSBr region shown in the AFM image in this panel (the AFM image is presented in an adaptive nonlinear color range to highlight the small steps). g AFM height profile of the 2.4 nm step in the CrSBr flake. The data is collected from 15 individual height profiles collected along the edge of the CrSBr step. The height of 2.43 ± 0.3 nm is extracted by subtraction of the mean height values at the two height levels. h Estimated stray field at the 2.4 nm CrSBr edge (solid black line) and fit (dotted red line, see Supplementary Note 3). The error bars represent the fit uncertainty of the ensemble ESR frequency (±1 s.d.).

Full size image

In Fig. 3f, we show the spatial map of the PL and ESR contrast measured at 70 K for the regions shown in the AFM image in this panel. The PL intensity map indicates a noticeable contrast as the CrSBr thickness changes considerably. On the contrary, the measured ESR signal shows insignificant variation at the large step height of CrSBr (~ 28 and 72 nm) and changes considerably across the other edges with the thickness of ~ 2.4 and ~ 15 nm. This is also confirmed by the same magnitude of the ESR signal measured at another 2.4 nm CrSBr step in the middle of the flake (see panels c, d, and g) which corresponds to a tri-layer CrSBr edge12,45. Moreover, our AFM characterization indicates two more steps in the CrSBr flake with 1.1 ± 0.23 nm and 1.71 ± 0.19 nm thicknesses associated with monolayer and bilayer of CrSBr (shown in Supplementary Fig. 2). We observe a finite modulation of the ESR signal at the monolayer CrSBr step and no ESR modulation at the bilayer CrSBr. We conclude that the ESR measurement is indeed detecting only the uncompensated stray field generated by the steps in the CrSBr thickness corresponding to an odd number of CrSBr layers, as expected for an antiferromagnetic interlayer stacking order46. The same magnitude of the ESR modulations at different steps is consistent with the detected stray field being generated by an uncompensated magnetic moment of a single layer of the CrSBr.

At the positions 35 and 42 μm (Fig. 3d), we observe a modulation of fESR of approximately double the amplitude as the modulations observed at the other steps discussed above. These positions are located in a region where the AFM image shows strong topography changes. In particular, the higher-contrast AFM image in Supplementary Fig. 2 shows that the CrSBr in the region between 36 and 45 μm is broken into multiple smaller pieces. If two such neighboring pieces have opposite magnetic order, the stray fields generated at their edges would add, which could explain the observed doubling of the ESR shift.

To extract the magnetization, we focus on the central peak in the NV-ensemble-measured stray field of Fig. 3d, because it is well isolated from other peaks and is located in a region where the CrSBr shows a clear, small and isolated step in its height of 2.4 nm (Fig. 3g). This enables an accurate analysis of the stray field. By the NV ESR measurements, we extract a stray magnetic field of dBNV ~ 60 μT generated at the edge of the 2.4 nm CrSBr step (Fig. 3h). For quantitative magnetometry, we need to know the direction of the magnetization of the 2D magnet with respect to the NV axis (\({\hat{S}}_{{{{\rm{NV}}}}}\)). For the case of CrSBr, the direction of the magnetic easy axis can be readily distinguished optically, as the mechanical exfoliation of the crystals results in elongated rectangular flakes following the in-plane magnetic anisotropy axes47. As shown earlier in Fig. 1b, the direction of the CrSBr magnetization and the NV axis in our sample is such that the CrSBr stray fields have a finite projection only along the z-component of the NV spins. Thus, knowing the projection of the \({\overrightarrow{M}}_{{{{\rm{CSB}}}}}\) on \({\hat{S}}_{{{{\rm{NV}}}}}\), we can extract the uncompensated saturated magnetization of CrSBr. By fitting the stray-field peak of Fig. 3h (see Supplementary Figure 3), we find Ms = 0.46(2) T, consistent with the Ms = 0.48(2) T saturation magnetization reported by SQUID measurements in a magnetic field-polarized bulk CrSBr crystal45. In contrast to ref. 45, the Ms value in our work is extracted from the stray field of an uncompensated magnetic layer on top of a multi-layer CrSBr crystal. Furthermore, we extract an NV-sample distance z0 = 0.13(4) μm (see Supplementary Note 3). This is larger than the ~ 70 nm NV implantation depth expected from the stopping range of ions in matter (SRIM)45, corroborating previous work48 that demonstrated that the SRIM underestimates NV implantation depth.

Detection of magnetic phase transition

For bulk CrSBr, the transition temperature from the antiferromagnetic to paramagnetic state is about 130 K, as measured by SQUID magnetometry45,47. Here we evaluate the thermal fluctuations of magnetic moments in the CrSBr flake by measuring the NV ESR frequency at various temperatures over the width of the CrSBr flake. In Fig. 4a, we show the stray field modulation across the width of the CrSBr flake measured below the phase transition temperature and in panel b we show the modulation of the stray field as a function of temperature. From there, we extract the temperature-dependence of the magnitude of the stray field at the three studied CrSBr edges, normalized by their maximum value estimated for T = 0 K (dBT0), shown in panel c. The dBT0 is estimated by the extrapolation of dBNV to 0 K. As expected, the stray fields from the three CrSBr edges (with thicknesses of 15 and 2.4 nm) show a gradual decay as the temperature is increased towards the critical temperature (Tc). We find the temperature at which the net stray fields from the edges of the CrSBr disappear to be 130 K. The extracted Tc from these measurements agrees well with previously reported values45,47.

Fig. 4: Stray-field detection of the CrSBr phase transition.
figure 4

a Stray field as a function of the position below the phase transition temperature. b Stray field vs temperature and position showing the magnetic phase transition. For each temperature, the measured stray field at T = 157 K was subtracted to compensate for a background variation in the ESR frequency caused by the static field inhomogeneity (also see Supplementary Fig. 6). c Normalized stray field vs temperature. The error bars represent the fit uncertainty of the peak amplitude (± 1 s.d.). To extract the critical temperature Tc, we use a simple polynomial equation \(\propto 1-{(T/{T}_{c})}^{\beta }\) to fit the data, finding a phase transition temperature of Tc = 130(1) K in reasonable agreement with ref. 45 (see Supplementary Fig. 4 for the measurement at various microwave and laser powers).

Full size image

The key benefits of NV magnetometry are its magnetic sensitivity, its well-understood level structure and interaction with auxiliary nuclear spins, and the precisely tunable NV density and implantation depth. Our method integrates these advantages with 2D materials assembly methods. The developed method for the pick-up/transfer of NV-diamond membranes allows for high precision in alignment and direct contact of the diamond and magnetic target, facilitating NV-ensemble magnetometry to detect stray fields down to the monolayer limit. The compatibility of this method with the conventionally used transfer stages and glove-box inert atmosphere will pave the way for further easy and fast exploration of sensitive 2D magnetic materials. Using this technique we have obtained an intact interface at the 2D magnet-diamond interface, resulting in a spatially resolved magnetization profile. By the NV ESR measurements, we have quantified the magnetization of a single layer of the CrSBr without the need for exfoliation of a monolayer of the crystal or applying a large external magnetic field. These measurements performed on various CrSBr thicknesses resolve the uncompensated magnetization of the crystal, determining an even versus an odd number of CrSBr layers. Moreover, the temperature dependence of the measured ESR signal shows that the net stray fields from the edges of the CrSBr vanish close to the Néel temperature. These experimental realizations enabled by the diamond transfer technique open the way for more applications of NV-ensemble magnetometry of 2D magnetic materials, enabling large-area and fast readout of magnetic configurations in 2D spintronic devices.

Methods

Diamond membrane preparation

We fabricate the 50 × 50 × 5 μm3 diamond membrane (shown in Fig. 2a, e) from a 4 × 4 × 0.5 mm3 electronic-grade diamond chip acquired from Element 6 Inc. We start by having the chip cut and polished into 2 mm × 2 mm × 50 μm membranes by Almax Easylabs. After cleaning in nitric acid, we have nitrogen ions implanted by Innovion at a density of 1013/cm2 and an energy of 54 keV, yielding an estimated implantation depth of 70 ± 10 nm49. To create NVs, we vacuum anneal the diamond at a pressure of 3 × 10−6 mBar by a 6 h ramp to 400 °C, 4 h hold, 6 h ramp to 800 °C, 2 h hold and cool down to room temperature. Assuming a nitrogen-to-NV conversion efficiency of 1%49 during the anneal, we estimate the resulting NV density to be 103 NVs/μm2.

We etch the microsquares into the NV-side of the diamond using a Ti mask and reactive ion etching (RIE). We deposit 50 nm of Ti using e-beam evaporation, define its shape in a PMMA resist using e-beam lithography, and etch it into shape by 3 min. of reactive ion etching in a SF6/He plasma at PRF = 30 W RF power. We then transfer the Ti mask 5 μm into the diamond using RIE in an O2 plasma (PRF = 90 W, PICP = 1100 W, etch rate 0.25 μm per min). As the final step, we flip the diamond and etch from the backside using O2 RIE and a quartz hard mask with a square 1.4 mm opening until microsquares are released and only remain attached to the bulk diamond via a small holding bar. The Ti is removed using HF50.

PMMA-PDMS stamp preparation

For the preparation/suspension of the PMMA membrane, first, we spin-coat a layer of a water-soluble polymer, Electra 92 (AR-PC 5090, All-resist) at the rate of 1000 rpm for 3 min. The Electra is then backed on a hotplate at 100 ∘C for 1 min. Then two layers of PMMA (4%, 950 K) are successively spin-coated on top of the Electra layer with 1000 rpm for 3 min. After each spin-coating step, the PMMA layer is annealed on the hot plate at 180 ∘C for 45 s. At this stage, the layer PMMA (≈ 0.7−1 μm thick) is solidified and is ready for suspension. For that, we use a Scotch tape and cut an open window (7 × 7 mm2) in its center. We attach the tape to the PMMA-Electra-SiO2 sample and immerse the sample in water. The tape holds the PMMA membrane and gives some control over the movement of the sample, while the Electra layer gets dissolved in water. By that, the SiO2 sample gets detached and the PMMA layer stays on the water surface. In the next step, we take the tape and the PMMA out of the water beaker, let it dry in air for about 10 min, and put it on top of a PDMS layer held on a grass slide51.

Sample preparation

Before using the described technique for the transfer of the diamond membrane on the CrSBr flake, there are a few steps taken for the sample preparation. The Au-stripline is made by e-beam lithography and deposition of the Ti (5 nm) and Au (100 nm) using e-beam evaporation at ultra-high vacuum (<10−6 mbar), followed by liftoff in acetone and O2 plasma treatment to remove the PMMA layer and its residues, respectively. The CrSBr flakes are cleaved from their bulk crystals using Nitto tape and are directly exfoliated on a PDMS layer. Then they are transferred from the PDMS on the target substrate distanced by <5 μm from the Au stripline using micro-manipulators of a transfer stage. The sample preparation could also be done by the lithography of the Au stripline directly on the substrate where the CrSBr flake is exfoliated on.

CrSBr synthesis

CrSBr crystals are prepared by the direct reaction of their components in a stoichiometric ratio, mixing chromium (99.99%, Alfa-Aesar), sulfur (99.99%, Sigma-Aldrich), and bromine (99.9%, Sigma-Aldrich), with a 3% in mass excess of bromine, which acts as a transport agent. Crystals are characterized by powder and crystal X-Ray diffraction, energy dispersive X-Ray analysis, high-resolution TEM, SQUID magnetometry, and temperature-dependent single crystal, as reported in ref. 42.

Photoluminescence microscope setup

We detect the NV photoluminescence (PL) using a home-built cryogenic microscope setup. The cryostat is a Montana S100 hosting a room-temperature-stabilized NA = 0.85 microscope objective. We position and focus the sample using cryogenic slip-stick positioners (ANPx101 and ANPz101, Attocube), and use a fast steering mirror (FSM300, Newport) to make spatial NV PL maps (Fig. 3e, f). We excite the PL using a continuous-wave 520 nm laser (Obis LX 520, Coherent) and detect it using an avalanche photodiode (Excelitas, SPCM-AQRH-13) after suppressing the laser and the CrSBr PL by band-pass filtering (600–800 nm). The NV+CrSBr PL spectrum shown in Fig. 3e is recorded with an Andor Kymera spectrometer equipped with an Ivac CCD camera using a 550 nm long-pass filter. A Windfreak SynthHD v2 generates the microwaves used for driving the NV spins.