Introduction

Maximum electric fields typically measured in thunderclouds (see Table 3.2 of ref. 1 and references therein) are \((1-2)\times 1{0}^{5}\) V/m (the highest measured value is \(4 \, \times 1{0}^{5}\) V/m), which is lower than the expected conventional breakdown field, of the order of \(1{0}^{6}\) V/m. Two main scenarios of lightning initiation have been suggested. One relies on the emission of positive streamers from hydrometeors when the electric field exceeds \((2.5-9.5)\times 1{0}^{5}\) V/m,2 and the other involves cosmic ray particles and the relativistic runaway breakdown that occurs in a critical field, calculated to be of the order of \(1{0}^{5}\) V/m at altitudes of 4–6 km (e.g., ref. 3). More details on the lightning initiation scenarios proposed to date can be found in reviews by Solomon et al.,4 Petersen et al.,5 Rakov6, Dwyer and Uman,7 and in references therein. Whatever the scenario, the formation of “lightning seed” (\(1{0}^{-4}\) S/m, \(\sim 10\) m; ref. 4) is required, except for the most recent model of Attanasio et al.8 The latter was inspired by the work of Rison et al.,9 who suggested that many or possibly all lightning flashes are initiated by the so-called fast (\(3\times 1{0}^{7}-1{0}^{8}\) m/s) positive breakdown in virgin air. This breakdown does not create a hot channel and its electromagnetic signature is similar to the narrow bipolar pulse (NBP), although most of the flashes do not exhibit an NBP-like signature (either wideband or VHF) at their onset. Rison et al.9 ruled out the role of runaway electron avalanches in the formation of fast positive breakdown and, hence, in lightning initiation. On the other hand, not in support of the Rison et al.’s inference on the universal nature of fast positive breakdown, lightning initiation by fast negative breakdown was reported by Tilles et al.10 The latter observation was unexpected, because the critical electric field for propagation of negative streamers is about a factor of 2 higher than that for positive streamers. Finally, recent interferometric observations11 demonstrated the possibility of lightning initiation without any form of fast breakdown of the type observed by Rison et al.9 and Tilles et al.10 Clearly, the mechanism of lightning initiation remains the subject of intense debate.

Thunderstorm electric field structure is highly inhomogeneous and extremely complex, in particular due to the presence of hydrometeors, i.e., airborne water particles in liquid and solid states (droplets, snowflakes, graupel, hail, etc.) moving in the air flow. The presence of hydrometeors is the main difference between the cloud medium and the clear air. Importantly, the above two scenarios of lightning initiation either fully ignore the existence of charged hydrometeors in the thundercloud or focus on the analysis of one or a few particles. In our view, the collective dynamics of charged hydrometeors that are involved in the turbulent motion play a fundamental role in the lightning discharge initiation. The idea to consider collective effects in the plasma-like cloud medium—the charged hydrometeor ensemble—was first suggested by Trakhtengerts12, who introduced a simple bi-disperse model for beam instability, which leads to cloud medium stratification and the electrical discharge initiation. In subsequent studies,13,14 it was shown that under typical thundercloud conditions the collective modes of space charge can form and become unstable for wavelengths from 10 to 100 m. The influence of the collective field of hydrometeors on electron runaway effects in a thundercloud was studied by Trakhtengerts et al.15,16 More recently, Iudin17 established that even a statistically uniform distribution of charged hydrometeors produces enormously strong fluctuations of mesoscale (0.1–1 m) electric field. It was also pointed out there that the level of mesoscale electric field fluctuations can be greatly enhanced by the effects of clustering of hydrometeors in thundercloud turbulent flow (see e.g., ref. 18 and refs 19,20). Di Renzo and Urzay21 introduced the aerodynamic mechanism of electric field generation in turbulence laden with bi-disperse suspensions of oppositely charged particles. The turbulence preferentially concentrates small particles in interstitial regions between vortices, where the strain rate is large. Conversely, the larger, oppositely charged particles are more ballistic, and, as a result, they are more uniformly distributed than the smaller particles. The characteristic length associated with the resulting electric fields is much larger than the mean inter-particle distance and the smallest size of the turbulent eddies.21 Although these turbulence-driven electric fields are expected to be small compared with the breakdown field in the atmosphere, they can lead to strong polarization of colliding (or nearly colliding) hydrometeors due to their high permittivity22 and to initiation of small-scale discharges.

In the course of cloud electrification, large but short electric field spikes (bursts) always exist on a small spatial scale, but they are averaged out on a larger scale. Such highly localized field bursts generally cannot be detected with the traditional in-cloud field measuring instruments (for example, in the case of balloon soundings the electric field measurement spatial resolution makes 10 m), but their occurrence is evidenced by observations of corona discharge at the time of collisions or nearly collisions of water drops and ice particles (see ref. 23 and references therein). Another possible piece of evidence is the electromagnetic radiation recorded from thundercloud by Zonge and Evans24, 10–15 min prior to the first lightning discharge. Also, Harvey and Lewis25 reported the UHF/VHF noise from clouds that was emitted over extended periods of time in the absence of lightning.

Characteristic parameters of the processes leading to the formation of EICRs are presented in Table 1, where \(E\) is the typical longitudinal electric field leading to the initiation of the process and \(\sigma\) is the electrical conductivity of the resultant formations, occurring in the cloud in the course of it electrification.

Table 1 Characteristic parameters of processes involved in the formation of EICRs.
Full size table

In this paper, we will show how highly localized electric field bursts facilitate electron avalanches in the vicinity of colliding (or nearly colliding) hydrometers and eventually lead to formation of decimeter-scale, long-lived elevated-ion conductivity regions (EICRs) in thunderclouds. New theory describing transitions from IPCs to RICSs and from RICSs to EICRs is presented in the Results section followed by Discussion and conclusions. The Methods section contains the background material.

Results

Ion production centers

In the vicinity of individual hydrometers the external electric field represented by superposition of the large-scale and mesoscale electric fields increases at least (for a spherical shape) threefold due to polarization charges on particle surfaces. When droplets collide (or nearly collide, i.e., come in close proximity of each other), the discharge occurs at even a lower external field strength than for the case of non-interacting particles. As pointed out by Sartor and Atkinson,26 when two equal and oppositely charged spheres converge to a distance equal to one-tenth of their radius, the intensity of the field on their surfaces increases by a factor of 14 compared with the case when the charges are distributed uniformly over the spheres. Collisions or nearly collisions of water drops and ice particles are known to cause corona-type discharges (see ref. 23 and references therein). According to Shishkin27, corona between water drops with 400–600 \(\upmu\)m radius occurred for separation distances up to 1.5 mm (up to 2.3 mm for ice particles). It follows from his Fig. 1 that for a rainfall intensity of 10 mm/h, the rate of water drops coming within 1.5 mm of each other is a factor of 10 higher than their collision rate.

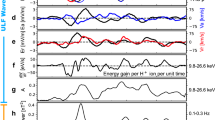
Fig. 1: Determination of the breakdown electric field (Ec or Enc).
figure 1

a Dependence of the conventional (\({E}_{c}\)) and nonconventional (\({E}_{nc}\)) reduced breakdown electric fields on the altitude (\(h\)) above sea level. b Dependence of the positive increment (eigenvalue) of the conventional (broken line) and nonconventional (solid line) breakdown electric fields on the magnitude of the electric field for different (color-coded) altitudes. c Dependencies of the relative concentrations of different (color-coded) species (components of the eigenvector) on the altitude above sea level for electric field equal to 1.5 MV/m.

Full size image

Ion production centers are defined here as space-time regions in which the small-scale electric field magnitude exceeds the effective breakdown level \({E}_{nc}\). The latter corresponds to the condition when the effective ionization frequency \({{\mathfrak{J}}}_{i}=\frac{{\nu }_{i}{\nu }_{d}}{{\nu }_{a}}\) (first introduced in ref. 28) exceeds the frequency \({\nu }_{h}\) of ion loss to hydrometeors, where \({\nu }_{i}\) is the ionization frequency, \({\nu }_{d}\) is the electron detachment frequency, and \({\nu }_{a}\) is the electron attachment frequency (see the Methods section). Clearly, the ion production centers exist on time scales substantially exceeding the inverse frequency of electron attachment \({\nu }_{a}^{-1}\). Since strong electric fields \(E({\bf{r}},t)\,>\,{E}_{c}\) are produced with the participation of polarization charges on the surface of hydrometeors, the ion production centers have linear scales of the order of the size (radius) of large hydrometeors of \({r}_{0}\). The pattern of the local electric field changes as hydrometeors move in a turbulent air flow. The large hydrometeors are dominated by their inertia and are more ballistic, so the lifetime of the ion production center can be estimated as

$${\tau }_{0}\approx \frac{{r}_{0}}{u}\approx 2\times 1{0}^{-4}\,\text{s}\,,$$
(1)

where \(u\approx 10\) m/s is the characteristic velocity of updraft in the active region of thundercloud and \({r}_{0}\approx 2\) mm. According to Zipser and Lutz,29 lightning is absent or highly unlikely if the vertical updraft speed does not exceed a threshold of roughly 6–7 m/s (mean) or 10–12 m/s (peak), regardless of cloud depth.

The random field of the effective ionization frequency \({{\mathfrak{J}}}_{i}({\bf{r}},t)\) is independent of the concentration distribution for negative ions \({n}_{n}({\bf{r}},t)\) and can be represented as the sum of identical impulses \({\mathfrak{I}}({\bf{r}},t)\) at random points \(({{\bf{r}}}_{k},{t}_{k})\) of the space-time domain:

$${{\mathfrak{J}}}_{i}({\bf{r}},t)=\sum _{k}{\mathfrak{I}}({\bf{r}}-{{\bf{r}}}_{k};t-{t}_{k})$$
(2)

with the average number of pulses per unit time and per unit volume (occurrence rate of ion production centers) \({\mathfrak{M}}\) being constant. The function \({\mathfrak{I}}({\bf{r}},t)\) has the following general form:

$${\mathfrak{I}}({\bf{r}},t)=J\psi ({\bf{r}})\theta (t),$$
(3)

where \(J\) characterizes the intensity of ion production+ center, \(0\,<\,\psi\, ({\bf{r}})\le 1\) for \(r\le {r}_{0}\) and \(\psi ({\bf{r}})=0\) for r > r0; \(0\,<\,\theta (t)\le 1\) for \(0\,<\,t\,<\,{\tau }_{0}\) and \(\theta (t)=0\) when \(t\,<\,0\) and \(t\,>\,{\tau }_{0}\), so that \({r}_{0}\) and \({\tau }_{0}\) give the characteristic spatial dimension of the individual center and its lifetime (see Eq. (1)), respectively.

The active intra-cloud environment can be viewed as a system with stochastic deposition of electric charges: the ion production centers make spatial variations of charge density more pronounced, while the recombination and ion absorption by hydrometeors diminish those fluctuations. It is important to note that, due to the ion drift in the local electric field, the ion production centers are each represented by a pair of spots: one is dominated by positive ions and the other by negative. Positive and negative spots move in opposite directions mainly along the ambient large-scale field direction, thus reducing the probability of recombination losses. During the lifetime \({\tau }_{0}\) of the ion production center, positive and negative spots move away from each other by a distance of the order of \(l={\tau }_{0}\cdot {V}_{c}={\tau }_{0}\cdot {\mu }_{s}{E}_{c}\simeq 1\) cm, where \({V}_{c}\) is the characteristic ion drift velocity in breakdown electric field \({E}_{c}\). At times much greater than \({\tau }_{0}\), the enlargement of ion spots is mainly due to aerodynamic mixing in turbulent air flow.

We now discuss in more detail the dynamics of negative ions in thunderclouds. In the Methods section, we introduced the system (24) of drift-diffusion equations for the dynamics of charged species in thundercloud and investigated its simplification in the uniform case (30) to find the effective breakdown electric field \({E}_{nc}\). In general, the electric field magnitude \({\bf{E}}({\bf{r}},t)\) is a random function of spatial coordinates and time, which leads to the strong space-time inhomogeneities in the distribution of the effective ionization frequency \({{\mathfrak{J}}}_{i}\). The equation corresponding to the eigenvalue \({\lambda }^{+}={{\mathfrak{J}}}_{i}-{\nu }_{h}\) (see Eq. (38) in the Methods section) for negative ions with recombination losses and ion stochastic drift in the field \({\bf{E}}({\bf{r}},t)\) taken into account has the following form

$$\frac{\partial {n}_{n}}{\partial t}=({{\mathfrak{J}}}_{i}({\bf{r}},t)-{\nu }_{h}){n}_{n}-{\beta }_{np}{n}_{n}{n}_{p}-\nabla \cdot {{\bf{J}}}_{n},$$
(4)

where \({\nu }_{h}\) is the frequency of ion losses to hydrometeors; \({\beta }_{np}\) is the ion–ion recombination coefficient, \({{\bf{J}}}_{n}\) is the flux density of negative ions, and the effective ionization frequency \({{\mathfrak{J}}}_{i}({\bf{r}},t)\) is also represented by a random function of spatial coordinates and time. Using relation for the negative ion velocity \({{\bf{V}}}_{n}=-{\mu }_{n}{\bf{E}}\) (see Eq. (28)), and the Poisson equation (29) with \({n}_{n1}+{n}_{n2}+{n}_{n3}={n}_{n}\), for the negative ion flux divergence we obtain (neglecting the ion diffusion)

$$\nabla \cdot {{\bf{J}}}_{n}={{\bf{V}}}_{n}\nabla {n}_{n}-\frac{{\mu }_{n}}{{\varepsilon }_{0}}\left(\right.e({n}_{p}-{n}_{n})+{\rho }_{h}({\bf{r}},t)\left)\right.{n}_{n},$$
(5)

where \({\mu }_{n}\) is absolute value of negative ion mobility, \(e\) is the electron charge absolute value, \({\varepsilon }_{0}\) is the permittivity of free space and \({\rho }_{h}({\bf{r}},t)\) is the charge density associated with charged hydrometeors. Substituting expression (5) into Eq. (4), we obtain

$$\frac{\partial {n}_{n}}{\partial t}+{{\bf{V}}}_{n}({\bf{r}},t)\cdot \nabla {n}_{n}=\left({{\mathfrak{J}}}_{i}({\bf{r}},t)-{\nu }_{h}+\frac{{\mu }_{n}}{{\varepsilon }_{0}}{\rho }_{h}({\bf{r}},t)\right){n}_{n}+\left(\frac{e{\mu }_{n}}{{\varepsilon }_{0}}-{\beta }_{np}\right){n}_{n}{n}_{p}-\frac{e{\mu }_{n}}{{\varepsilon }_{0}}{n}_{n}^{2}.$$
(6)

Taking into account the inhomogeneities of the space charge distribution leads to the appearance on the right side of Eq. (6) of an additional linear term \(\frac{{\mu }_{n}}{{\varepsilon }_{0}}{\rho }_{h}({\bf{r}},t){n}_{n}\), the value of which is comparable with the ion losses to hydrometeors for \({\nu }_{h}\simeq 1\) s\({}^{-1}\) (see the Methods section) and for typical charge density in thundercloud at \({\rho }_{h}\simeq 1\) nCm\({}^{-3}\) (ref., 1 ch. 3). It can be seen that the prevalence of positively charged hydrometeors promotes an increase in the concentration of negative ions, while an excess of negatively charged hydrometeors prevents an increase in the concentration of negative ions. At the same time, it is important to note that the prevalence of positively charged hydrometeors contributes to the growth of negative ion losses due to their attachment to the surface of positively charged hydrometeors. These features can play a significant role in the charging processes of hydrometeors, which are outside the scope of this paper. Therefore, we will not further consider the term \(\frac{{\mu }_{n}}{{\varepsilon }_{0}}{\rho }_{h}({\bf{r}},t){n}_{n}\) in Eq. (6). Besides, speaking about negative ions, it is reasonable to assume that at the region of their maximum concentration (which is of the greatest interest) \({n}_{p}\ll {n}_{n}\) because of drift separation. In addition, \(\frac{e{\mu }_{n}}{{\varepsilon }_{0}}\,\gtrsim\, {\beta }_{np}\).30 Therefore, we can drop the term \(\left(\right.\frac{e{\mu }_{n}}{{\varepsilon }_{0}}-{\beta }_{np}\left)\right.{n}_{n}{n}_{p}\) from Eq. (6). In this case, Eq. (6) becomes:

$$\frac{\partial {n}_{n}}{\partial t}+{{\bf{V}}}_{n}({\bf{r}},t)\cdot \nabla {n}_{n}=({{\mathfrak{J}}}_{i}({\bf{r}},t)-{\nu }_{h}){n}_{n}-\frac{e{\mu }_{n}}{{\varepsilon }_{0}}{n}_{n}^{2}.$$
(7)

The last equation involves only the concentration of negative ions \({n}_{n}\) and describes their dynamics that essentially depends on the ratio of the reproduction rate of negative ions and the rate of their losses to hydrometeors. In its turn the ion reproduction rate is represented by the effective ionization frequency \({{\mathfrak{J}}}_{i}\), which is proportional to the product of two strong functions of the local electric field: \({{\mathfrak{J}}}_{i}({\bf{r}},t)\propto {\nu }_{i}({\bf{E}}({\bf{r}},t))\cdot {\nu }_{d}({\bf{E}}({\bf{r}},t))={\nu }_{i}({\bf{r}},t)\cdot {\nu }_{d}({\bf{r}},t)\).

The characteristic negative ion output from a separate ion production center can be estimated using Eq. (7) and assuming that the efficiency of ion production centers is relatively high \(J\gg {\nu }_{h}\). Then for a separate center we get the following nonlinear single-site equation:

$$\frac{{\rm{d}}{n}_{n}}{{\rm{d}}t}=J{n}_{n}-\frac{e{\mu }_{n}}{{\varepsilon }_{0}}{n}_{n}^{2},$$
(8)

where, \(\frac{{\rm{d}}}{{\rm{d}}t}=\frac{\partial }{\partial t}+{{\bf{V}}}_{n}({\bf{r}},t)\nabla\) is the Lagrangian derivative or the substantial derivative. The solution of the last equation, which is valid throughout the lifetime of a separate center \(0\,<\,t\,<\,{\tau }_{0}\), is as follows

$${n}_{n}(t)=\frac{{n}_{0}}{1+\left(\right.\exp (Jt)-1\left)\right.{n}_{0}/{\bar{n}}_{n}}\exp (Jt),$$
(9)

where

$${\bar{n}}_{n}=\frac{J{\varepsilon }_{0}}{e{\mu }_{n}}\simeq \frac{J}{{\beta }_{np}}$$
(10)

is the ion concentration saturation level that makes about \({\bar{n}}_{n}\simeq 1{0}^{20}\) m\({}^{-3}\) at \(J\simeq 1{0}^{9}\) s\({}^{-1}\) when the electric field is about twice the nonconventional breakdown value (see Fig. 1b). Of course, such a high concentration value in the ion production center rapidly decreases due to the ion stochastic drift. In this case, the characteristic absolute value of electric charge \({Q}_{s}\) concentrated in ion spot reaches approximately \({Q}_{s}\simeq 4\pi e{r}_{0}^{3}{\bar{n}}_{n}/3\simeq 5\times 1{0}^{-7}\) C. Note that characteristic charge of the plasma spot by several orders of magnitude exceeds the peak charge values \({Q}_{h}\) of large hydrometeors that only reaches about \({Q}_{h}\simeq 2\times 1{0}^{-10}\) C.31 Even at a distance of 10 cm from the center of spot charge \({Q}_{s}\) the electric field exceeds the critical field \({E}_{s}^{+}\simeq 500\) kV/m for positive streamer propagation. Thus, the appearance of ion spots with charges at the level of \({Q}_{s}\) provides a significant increase in the level of electric field fluctuations on the \(\sim \! 0.1-1\) m scale.

Cumulative effect of new ion production centers and residual ion concentration spots

If the rate of occurrence of ion production centers is sufficiently high, some of the newly-created centers will necessarily overlap (fully or partially) the remnants of previously created (and decaying) center (residual ion concentration spot). Note that the characteristic size of residual ion concentration spot (tens of centimeters–meters) is considerably larger than that of the ion production center (millimeters). In the case of overlap (in the space-time continuum), the electric field burst giving rise to the new center, prior to exceeding the ionization level, will facilitate detachment of electrons from negative ions lingering in that location from the previous field burst. The resultant increase of the number of seed electrons will enhance the electron avalanching process and lead to accumulation of energy in some of the residual ion concentration spots.

The mutual influence of ion production centers is significant when collisions of hydrometeors producing electron avalanches become abundant, so that the space-time regions occupied by two or more residual ion concentration spots begin to overlap. The spatio-temporal volume \({\mathfrak{S}}\) occupied by a RICS left by a single ion production center is approximately equal to the product of ion lifetime \({\tau }_{n}\) during which the ion concentration \(n({\bf{r}},t)\) remains noticeable above the background, and the spatial volume occupied by the RICS at that time. In turn, the volume occupied by a RICS by time \({\tau }_{n}\) is determined by the distance of the stochastic drift of negative ions (see the second term on the left side of Eq. (7)) coupled with their aerodynamic mixing during this time, that is, by the quantity \({L}_{\perp }=\sqrt{{{\mathfrak{D}}}_{n}{\tau }_{n}}\), where the effective diffusion coefficient of negative ions \({{\mathfrak{D}}}_{n}\approx {\langle {({{\bf{V}}}_{n}({\bf{r}},t)-{{\bf{V}}}_{na})}^{2}\rangle }^{\frac{1}{2}}\cdot {N}_{h}^{-1/3}\) is expressed in terms of the large hydrometeors number density \({N}_{h}\), and stochastic (\({{\bf{V}}}_{n}({\bf{r}},t)=-{\mu }_{n}{\bf{E}}({\bf{r}},t)\)) and average (\({{\bf{V}}}_{na}=-{\mu }_{n}{{\bf{E}}}_{a}\)) drift velocities of negative ions.17 Note, that at times much greater than \({\tau }_{0}\), enlargement of RICSs is mainly due to aerodynamic mixing in turbulent air flow.

The geometrical problem of RICSs overlapping amounts to 4D objects being introduced at random into a space-time continuum. The average number of the 4D spots per unit spatio-temporal volume is the same as the rate of occurrence of ion production centers \({\mathfrak{M}}\). Two 4D spots are assumed to be connected in the following two cases: (1) if the spots have common points, i.e., overlap in the space-time continuum; (2) if spots do not touch each other, but are connected by a chain of overlapping spots; that is, if spot A is connected to spot B, and spot B is connected to spot C, then A is connected to C. It is important to note that the 4D spots forming geometrically connected chains of events in the space-time continuum can be disconnected in the system snapshot, i.e., when viewed at a fixed instant of time in the spatial continuum only. We are interested in finding out how many spots can form a cluster of connected spots, such that the conductivity of the equivalent spatial spot, whose shape/size and position in space will be changing as a result of random acts of overlapping, will be steadily increasing with time to a value characteristic of EICR (see Table 1). It should be noted that, when passing in the space-time continuum from one spot to another, one must always move in the positive direction of the time axis to preserve the causality principle.

The control parameter of the overlapping problem is the product of the rate of occurrence \({\mathfrak{M}}\) of the 4D spots and their 4D-volume \({\mathfrak{S}}\), i.e., the dimensionless filling factor:

$${\mathfrak{V}}={\mathfrak{S}}{\mathfrak{M}}\simeq \frac{{\pi }^{2}}{2}{L}_{\perp }^{3}{\tau }_{n}{\mathfrak{M}}=\frac{{\pi }^{2}}{2}{{\mathfrak{D}}}_{n}^{3/2}{{\tau }_{n}}^{5/2}{\mathfrak{M}}.$$
(11)

The criterion of the formation of elevated ion conductivity regions can be related, via the directed percolation theory (see ref. 32 and references therein), to the minimum value of concentration (e.g., the rate of occurrence \({\mathfrak{M}}\)) for which the cluster spans the specified 4D region. For the characteristic values of the ion mobilities \({\mu }_{n}\approx 2\times 1{0}^{-4}\) ·m2 V−1 ·s\({}^{-1}\),33 we obtain \({{\mathfrak{D}}}_{n}\approx 1\) m\({}^{2}\) s\({}^{-1}\). Substituting values \({{\mathfrak{D}}}_{n}\simeq 1\) m \({}^{2}{{\rm{s}}}^{-1}\) and \({\tau }_{n}\approx 1\) s, we get \({L}_{\perp }\approx 1\) m and \({\mathfrak{S}}\simeq 1\) m\({}^{3}{\rm{s}}\). In the above, the mobility of ions is assumed to be constant. Actually, the ion mobilities can significantly vary with electric field and can double near the breakdown threshold34 in the vicinity of IPCs. However, when the dependence of mobility on electric field is taken into account, the value of \({\mathfrak{S}}\) increases only slightly because the main dynamics of spots unfolds in relatively weak electric fields.

Critical rate of occurrence of ion production centers leading to formation of EICRs

As the filling factor \({\mathfrak{V}}\) increases, space-time chains or clusters of 4D spots appear on the background of low and initially equal concentrations of positive and negative ions. Spatio-temporal scales of these clusters diverge (in the sense of aiming for infinity) when the parameter \({\mathfrak{V}}\) tends to some critical value, depending strongly on the dimension of space (see Table 2). In the case of the four-dimensional space-time continuum of interest, the dimensionless filling factor critical value is \({{\mathfrak{V}}}_{c}\approx 0.13\).35 The condition \({\mathfrak{V}}\,>\,{{\mathfrak{V}}}_{c}\) means that, with a high probability, the specified spatio-temporal region is bridged by a chain or cluster of overlapping 4D spots when the filling factor exceeds 0.13 (percolation threshold); that is, the elevated ion density spots in that region occupy more than 13% of that region. Thus, the cumulative effect of the overlapping of new ion production centers and RICS becomes significant (that is, the overlapping occurs often enough to ensure a steady conductivity growth) when the rate of occurrence of ion production centers exceeds the critical value given by:

$${{\mathfrak{M}}}_{c}=\frac{{{\mathfrak{V}}}_{c}}{{\mathfrak{S}}}\approx 0.1\,{{\rm{m}}}^{-3}\,{{\rm{s}}}^{-1}.$$
(12)

The obtained estimate is at least three orders of magnitude lower than the maximum observed rate of hydrometeor collisions (discussed below). This means that the proposed mechanism begins to work when only 1 out of 1000 collisions or nearly collisions of hydrometeors leads to production of electron avalanches.

Table 2 The dimensionless filling factors for different space dimensions.
Full size table

There are a number of publications in which collision rates based on in situ measurements and modeling are presented. Note that the collision rate is proportional to the product of concentrations of colliding particles (usually millimeter-scale graupel and small ice crystals or snow) and cross-sectional area and fall speed of larger particles (graupel) (e.g., see ref. 36).

Gardiner et al.37 reported a collision rate of 25 m\({}^{-3}\) s\({}^{-1}\) for large graupel and small ice crystals, observed in a small isolated thunderstorm in Montana. A similar collision rates, up to 30 m\({}^{-3}\) s\({}^{-1}\), were reported for graupel and snow by Ziegler et al.36 (Fig. 17) who compared measurements during the early stage of a thunderstorm in New Mexico with predictions of their cloud electrification model. At their maximum rate, the computed mean diameter of snow reached about 0.3 mm and that of graupel was about 2 mm. Further, Ziegler and MacGorman38 (p. 841 and Fig. 5) reported a graupel-snow collision rates of 50–250 m\({}^{-3}\) s\({}^{-1}\) for a tornadic storm. Ziegler et al.36 (p. 12,848) reported very high observed ice particle concentrations, about 1000 per liter, that were not consistent with their model predictions. Such high ice concentrations are expected to yield very high collision rates, several orders of magnitude higher than their model values of up to 30 m\({}^{-3}\) s\({}^{-1}\). Ziegler et al.36 interpreted this difference as being due to their data containing a large fraction of ice particles smaller than a few hundred micrometers in diameter, which apparently do not significantly contribute to charge transfer in collisions. It is not clear if collisions of the smaller ice particles produce corona (most of the laboratory data are for water drops with diameters exceeding 150 \(\upmu\)m or so).

Dye et al.,39 who studied the initial stage in two small thunderstorms in New Mexico, reported hydrometeor collision rates exceeding 102 m−3 s−1 (see their Fig. 9) and up to about 103 m−3 s−1 (see their Fig. 8). It the latter case, ice particle concentrations up to several thousand per liter were observed (particles larger that about 50 μm in diameter were detectable). The authors noted potential problems with the measurements and adjusted the collision rates presented in their Fig. 8, which we cited above, in an attempt to account for possible overestimation of particle concentrations.

In summary, hydrometeor collision rates of the order of tens to a few hundred per cubic meter per second are apparently considered “normal”, while the rates of the order of \(1{0}^{3}\) m\({}^{-3}\) s\({}^{-1}\) or higher have been reported, but are considered excessive.

Because of the cumulative effect of new and decaying ion production centers, described in the section “Cumulative effect of new ion production centers and residual ion concentration spots”, the conductivity of ion concentration spots will be gradually increasing17. When the average conductivity of the ion spots rises to about \(\sigma \simeq 1{0}^{-9}\) S/m (that drastically exceeds the background cloud conductivity), the characteristic time of Maxwellian relaxation \({\varepsilon }_{0}/\sigma\), where \({\varepsilon }_{0}\) is the permittivity of free space, becomes ~\(1{0}^{-2}\) s. We refer to these relatively high conductivity ion spots as elevated ion conductivity regions (EICRs). EICRs will polarize in the ambient electric field faster than they can be destroyed by cloud aerodynamic flow. As a result, the streamer initiation process may begin. For a hydrometeor located near the positive pole of EICR, there is a two-level electric field amplification on its surface: three times in the immediate vicinity of the positive pole of the EICR and three times near the pole of the hydrometeor itself. In this way, polarization effects due to the ambient field facilitate initiation of positive streamers from hydrometeors entering the immediate vicinity of the positive pole of EICR. Note that due to the ion drift in the ambient electric field EICRs have an elongated shape oriented along the ambient electric field, with one end being dominated by positive ions and the other by negative ions.

It should be emphasized that there is a significant asymmetry in the ways of positive and negative ion concentration spots development: when a new ion production center arises on the background of the negative spot, this facilitates positive and negative ions production in the new center. On the contrary, as positive ion spots are unable to provide appreciable quantity of electrons, they do not facilitate ions multiplication.

Discussion

The present paper is devoted to the mechanism, by which an essentially non-conducting thundercloud becomes seeded by decimeter-scale, long-lived elevated ionic conductivity regions (EICRs). Formation of EICRs involves a sequence of processes that is launched by electron avalanches produced by highly localized electric field bursts in the vicinity of colliding (or nearly colliding) hydrometeors. As a result, ion production centers (IPCs) with dimensions of the order of \(1{0}^{-3}-1{0}^{-2}\) m and lifetimes of the order of \(1{0}^{-4}-1{0}^{-3}\) s are formed. IPCs evolve into what we call residual ion concentration spots (RICSs) whose dimensions are of the order of 0.1–1 m and lifetimes of the order of 1–10 s. Some new IPCs will occur in electrically undisturbed parts of the cloud, while others will overlap (fully or partially) RICSs. When such overlapping occurs, there is cumulative effect in growth of ion concentration, which is enhanced by the release (detachment) of electrons previously captured and retained by the neutrals (primarily oxygen). This electron detachment is facilitated by electric field bursts giving rise to new IPCs. Clearly, if the rate of occurrence of IPCs is sufficiently high, the cumulative effect in the growth of ion concentration in RICS (or parts of RICS involved in the overlapping process) can lead to a significant increase in ionic conductivity. As a result, EICRs are formed. The dimensions and lifetimes of EICRs are similar to those of RICS (0.1–1 m and 1–10 s, respectively), but their conductivity is about 3 orders of magnitude higher (see Table 1).

At the time of electric field burst, the initial field rise promotes the electron detachment inside the RICS, increasing the seed electron population just before the field amplitude of the burst reaches the breakdown value. As a result, electron and positive ion production is intensified when the new IPC overlaps RICS. The steady increase in the local ion concentration in the course of multiple-overlap process is limited only by ion losses to hydrometeors and ion–ion recombination losses (see Eq. (10)). The resultant decimeter-scale, long-lived EICRs have relatively high conductivity, up to \(1{0}^{-9}\) S/m or so vs. <\(1{0}^{-13}-1{0}^{-12}\) S/m (conductivity of clear air at thundercloud altitudes, which is higher than the cloud conductivity, due to immobilization of charges residing on hydrometeors), background conductivity. This ensures the effective polarization of EICR in external electric field within a few milliseconds. Moreover, charge magnitudes inside EICRs can reach \(1{0}^{-7}\) C, which significantly exceeds the maximum values of charges observed on hydrometeors. The resultant stochastic distribution of the ionic volume charge density provides local electric field enhancements and pre-ionization level that may be sufficient for the initiation and development of streamers.

The EICR formation mechanism requires only one condition: the rate of occurrence of ion production centers per unit time in a unit volume should exceed the critical level of \(1{0}^{-1}\) m\({}^{-3}\) s\({}^{-1}\). Since hydrometeor collision rates three and even four orders of magnitude higher than this value have been reported from observations (ref., 39 Fig. 8), (ref., 36 Section 5.3), it is reasonable to expect that at least 1 out of 1000 collisions will produce electron avalanches that are needed for creation of ion production centers in the cloud.

In the case of overlapping IPC and RICS, the growth of ion concentration, is due to both the detachment of electrons from negative ions and the fact that the exponential increase of concentration of negative ions begins not from the level averaged over space at the current time, but from an elevated concentration in the RICS that has survived until the appearance of the new IPC. More complex additional contributions are also possible, due to overlapping clusters of three or more IPCs/RICSs.

In the framework of our proposed scenario, the essentially non-conducting cloud becomes seeded by elevated-ion-conductivity regions with spatial extent of 0.1–1 m and a lifetime of 1–10 s. These regions can serve to promote the initiation of streamers (more efficiently than much smaller hydrometeors) and eventually lead to the initiation of lightning. The proposed scenario can possibly lead to a paradigm shift in our approaches to the still unsolved mystery of lightning initiation, because it does not require the presence of super-energetic cosmic ray particles (\(>\!1{0}^{16}\) eV40, unrealistic potential difference inside the cloud (450 MV41), or unrealistically large (6 cm or more) hydrometeors42).

Methods

This is a theoretical study whose methodology is based on the plasma-chemical reactions and evolutionary equations presented below.

The conventional breakdown electric field \({E}_{c}\) in the air is classically determined by considering the balance between the production and loss of free electrons in the course of electron impact ionization. The rate of increase of free electron number density \({n}_{e}\) is given by the electron multiplication equation:

$$\frac{\partial {n}_{e}}{\partial t}=({\nu }_{i}-{\nu }_{a}){n}_{e},$$
(13)

where \({\nu }_{i}\) is the ionization frequency, defined as the number of ionization events performed by an electron per second, and \({\nu }_{a}\) is the frequency of electron attachment to neutrals (mostly to oxygen). Clearly, the multiplication of electrons is impossible in the frame of Eq. (13) when \({\nu }_{a}\,>\,{\nu }_{i}\), and the \({\nu }_{a}={\nu }_{i}\) condition corresponds to the threshold for exponential growth of \({n}_{e}\) in time. Each of the two frequencies is a function of applied field, and the threshold field \(E={E}_{c}\) can be found by equating the difference \(({\nu }_{a}-{\nu }_{i})\) to zero:43

$${\nu }_{i}({E}_{c})-{\nu }_{a}({E}_{c})=0.$$
(14)

The electron attachment to oxygen, which is the electronegative component of the air, is mainly responsible for the loss of free electrons in the lower atmosphere. Under normal conditions, the attachment frequency \({\nu }_{a}\) is of the order of \(1{0}^{8}\) s\({}^{-1}\);43 that is, the lifetime of free electrons is of the order of 10 ns. In the attachment process, the electrons form negative oxygen ions, whose very low mobility makes them unable to cause impact ionization. The breakdown field of air has a value of \({E}_{c}\simeq 2.6\)–3.2 MV/m at sea level43 and exponentially decreases with altitude due to exponential decrease in the air molecule density.

Basic reactions and basic equations

Free electrons in the high field region of thundercloud are needed to start an electric discharge. As noted above, in lower atmospheric layers free electrons almost instantaneously attach to oxygen molecules, forming negative ions. Therefore, background pre-ionization (conductivity) within the troposphere (that is produced by solar energetic particles, by cosmic rays and, at least within a few kilometers of the ground surface, by the decay of radioactive gases emitted from the ground) is determined almost exclusively by ions. The main processes of electron attachment in cold air are

$$e+{{\rm{O}}}_{2}\Rightarrow {{\rm{O}}}^{-}+{\rm{O}},$$
(15a)
$$e+2{{\rm{O}}}_{2}\Rightarrow {{\rm{O}}}_{2}^{-}+{{\rm{O}}}_{2},$$
(15b)
$$e+{{\rm{O}}}_{2}+{{\rm{N}}}_{2}\Rightarrow {{\rm{O}}}_{2}^{-}+{{\rm{N}}}_{2}.$$
(15c)

The three-body attachment reactions (15b) and (15c) dominate over the two-body attachment reactions (15a) at low electric fields (below 55 Td in air at atmospheric pressure34). In the subsequent changes in the state of negative ions, an essential role is played by the fast reactions of charge transfer to oxygen and ozone molecules

$${{\rm{O}}}^{-}+{{\rm{O}}}_{2}\Rightarrow {({{\rm{O}}}_{3}^{-})}^{* }\Rightarrow {\rm{O}}+{{\rm{O}}}_{2}^{-},$$
(16)
$${{\rm{O}}}^{-}+{{\rm{O}}}_{2}+M\Rightarrow {({{\rm{O}}}_{3}^{-})}^{* }+M\Rightarrow {{\rm{O}}}_{3}^{-}+M,$$
(17)

where \({\rm{M}}\) is any heavy species (usually \({{\rm{N}}}_{2}\) and \({{\rm{O}}}_{2}\)).

If the electron has sufficient energy during its collision with a neutral particle (generally \({{\rm{N}}}_{2}\) and \({{\rm{O}}}_{2}\) molecules), it can create a positive ion and an additional free electron:

$$e+{{\rm{N}}}_{2}\Rightarrow e+e+{{\rm{N}}}_{2}^{+},$$
(18a)
$$e+{{\rm{O}}}_{2}\Rightarrow e+e+{{\rm{O}}}_{2}^{+}.$$
(18b)

Free electron can also appear by detachment from a negative ion. Since the additional electron in a negative ion is associated with the neutral atom or molecule by some energy, it is necessary to expend energy that is at least equal to the energy of this bond for the reaction of electron detachment. The required energy can be supplied upon collision of \({{\rm{O}}}^{-}\) and \({{\rm{O}}}_{2}^{-}\) ions with heavy species causing collisional electron detachment from negative ions in \({{\rm{N}}}_{2}-{{\rm{O}}}_{2}\) mixtures.34 The main processes are

$${{\rm{O}}}^{-}+{{\rm{N}}}_{2}\Rightarrow e+{{\rm{N}}}_{2}{\rm{O}},$$
(19)
$${{\rm{O}}}_{2}^{-}+{\rm{M}}\Rightarrow e+{{\rm{O}}}_{2}+{\rm{M}},$$
(20)

where \({{\rm{O}}}^{-}\) and \({{\rm{O}}}_{2}^{-}\) negative ions are primarily created in processes (15a–c). The efficiency of collisional detachment of electrons from negative ions depends on translational temperature of ions that increases due to the drift of ions in the electric field and can significantly differ from the gas temperature. Unlike elastic collisions the charge-exchange collisions between ions and air are known to be dominant in the case of the drift of ions in elevated fields. Pancheshnyi34 has shown that for an inelastic process with the energy threshold \(\Delta\) (activation energy) the reaction constant rate \(k\) can be found as

$$k={k}_{0}\exp \left(-\frac{\Delta }{{\Theta }_{i}}\right)\!,$$
(21)

where \({k}_{0}\) is the energy-independent part of the reaction constant rate and \({\Theta }_{i}\) is an effective ion temperature in field direction. In Eq. (21), the ion temperature \({\Theta }_{i}\) is in energy units, i.e., it is multiplied by the Boltzmann constant (\({\Theta }_{i}={k}_{{\rm{B}}}{T}_{i}\), where \({k}_{{\rm{B}}}=1.38\times 1{0}^{23}\) J/K is the Boltzmann constant and \({T}_{i}\) is the absolute temperature of ions).

An electron can be liberated when an ozone ion is destroyed in the presence of atomic oxygen in the air:

$${{\rm{O}}}_{3}^{-}+{\rm{O}}\Rightarrow e+2{{\rm{O}}}_{2}.$$
(22)

The dissociative conversion

$${{\rm{O}}}_{3}^{-}+{\rm{O}}\Rightarrow {{\rm{O}}}_{2}^{-}+{{\rm{O}}}_{2}.$$
(23)

also occurs in the presence of atomic oxygen.

Basic reactions and their frequencies and rate parameters as a function of the reduced electric field \(\breve{E}=E/{N}_{a}\), gas temperature T, and electron temperature Te are summarized in Table 3 below. In accordance with Benilovand and Naidis,44 we assume that \(T_{{\mathrm{e}}}\)(\({\rm{eV}}\))\(=0.447\cdot {\breve{E}}^{0.16}\), when \(\breve{E}\,<\,50\) Td and \(T_{{\mathrm{e}}}\)(\({\rm{eV}}\))\(=0.0167\cdot \breve{E}\) when \(\breve{E}\ge 50\) Td. The effective breakdown electric field depends on many factors, including the composition of gas, its water content, temperature and pressure, and preceding energy deposition into gas. In the following, we will discuss those factors with emphasis on the ones pertinent to the effective breakdown field. In particular, we will show that electron detachment decreases the effective breakdown field. We start with the evolution of ions, primarily negative, and plasma-chemical interactions between charged species. Ionization and detachment increase the number of electrons whereas attachment and recombination decrease it. Similarly, these elementary kinetic processes change the number of positive and negative ions. Besides, fast charge transfer processes similar to reactions (16) and (17) change the variety (composition) of negative ions. In this consideration three types of negative ions are introduced: two types of light unstable ions (e.g., \({{\rm{O}}}^{-}\) and \({{\rm{O}}}_{2}^{-}\)) that effectively contribute to detachment and stable heavy ions (e.g., \({{\rm{O}}}_{3}^{-}\)) that hardly contribute to detachment at low concentration of atomic oxygen.34,47 Number densities of charged species in a thundercloud obey the following system of drift-diffusion equations:

$$\frac{\partial {n}_{e}}{\partial t}=({\nu }_{i}-{\nu }_{a1}-{\nu }_{a23}){n}_{e}+{\nu }_{du1}{n}_{nu1}+{\nu }_{du2}{n}_{nu2}+{\nu }_{ds}{n}_{n3}-{\beta }_{ep}{n}_{e}{n}_{p}+\Omega -\nabla \cdot {{\bf{J}}}_{e},$$
(24a)
$$\frac{\partial {n}_{n1}}{\partial t}={\nu }_{a1}{n}_{e}-{\nu }_{du1}{n}_{n1}-{\nu }_{cu}{n}_{n1}-{\nu }_{cs}{n}_{n1}-{\beta }_{n1p}{n}_{n1}{n}_{p}-\nabla \cdot {{\bf{J}}}_{n1},$$
(24b)
$$\frac{\partial {n}_{n2}}{\partial t}={\nu }_{a23}{n}_{e}+{\nu }_{cu}{n}_{n1}-{\nu }_{du2}{n}_{nu2}+{\nu }_{r}{n}_{n3}-{\beta }_{n2p}{n}_{n2}{n}_{p}-\nabla \cdot {{\bf{J}}}_{n2},$$
(24c)
$$\frac{\partial {n}_{n3}}{\partial t}={\nu }_{cs}{n}_{n1}-{\nu }_{ds}{n}_{n3}-{\nu }_{r}{n}_{n3}-{\nu }_{h}{n}_{n3}-{\beta }_{n3p}{n}_{n3}{n}_{p}-\nabla \cdot {{\bf{J}}}_{n3},$$
(24d)
$$\frac{\partial {n}_{p}}{\partial t}={\nu }_{i}{n}_{e}-{\nu }_{h}{n}_{p}-{\beta }_{ep}{n}_{e}{n}_{p}-{\beta }_{n1p}{n}_{n1}{n}_{p}-{\beta }_{n2p}{n}_{n2}{n}_{p}-{\beta }_{n3p}{n}_{n3}{n}_{p}+\Omega -\nabla \cdot {{\bf{J}}}_{p}.$$
(24e)

where \({n}_{e}\), \({n}_{p}\), \({n}_{n1}\), \({n}_{n2}\), \({n}_{n3}\) and \({{\bf{J}}}_{e}\), \({{\bf{J}}}_{p}\), \({{\bf{J}}}_{n1}\), \({{\bf{J}}}_{n2}\), \({{\bf{J}}}_{n3}\) are concentrations and flux densities of electrons, positive and negative ions, respectively; \({\nu }_{i}\) is the ionization frequency; \({\nu }_{a1}\) and \({\nu }_{a23}={\nu }_{a2}+{\nu }_{a3}\) are the electron two-body and three-body attachment frequencies (note that in (13) \({\nu }_{a}={\nu }_{a1}+{\nu }_{a23}\)); \({\nu }_{du1}\), \({\nu }_{du2}\), \({\nu }_{ds}\) are electron detachment frequencies defined for different negative ions (see Table 3); \({\nu }_{h}\) is the rate of ion loss to hydrometers; \({\beta }_{ep}\) is an electron-ion recombination coefficient; \({\beta }_{n1p}\), \({\beta }_{n2p}\), \({\beta }_{n3p}\) are ion–ion recombination coefficients; \(\Omega\) is the number of pairs of electrons and positive ions that are created per unit volume and per unit time due to collisions of neutrals and ionization of neutrals by photons and cosmic rays.

Table 3 Basic reactions.
Full size table

The frequencies of the various processes in the system of Eqs. (24a–e) are calculated using the information given in Table 3. The coefficients of electron-ion recombination \({\beta }_{ep}\) and ion–ion recombination \({\beta }_{n1p}\), \({\beta }_{n2p}\), \({\beta }_{n3p}\) are nearly the same; at sea level they are approximately equal to 10\({}^{-13}\) m\({}^{3}\)/s (10−12 m3/s for hydrated ions). The electron-ion recombination is as efficient as attachment in immobilizing electrons when \({\beta }_{ep}{n}_{p}\simeq {\nu }_{a}\simeq 1{0}^{8}\) s\({}^{-1}\); that is, for the positive ion number density \({n}_{p}\simeq 1{0}^{20}-1{0}^{21}\) m\({}^{-3}\). When the density of positive ions \({n}_{p}\lesssim 1{0}^{19}\) m\({}^{-3}\), the electron attachment surpasses electron-ion recombination as the electron-loss process.

To estimate the number of pairs of electrons and positive ions \(\Omega\) that are created per unit volume and per unit time in fine weather conditions we use the balance Eq. (24e), assuming that \({n}_{e}=0\), \({n}_{p}={n}_{n}={n}_{n1}+{n}_{n2}+{n}_{n3}\) and \({\beta }_{n1p}\simeq {\beta }_{n2p}\simeq {\beta }_{n3p}\):

$$\frac{\partial {n}_{p}}{\partial t}=\Omega -{\beta }_{np}{n}_{p}^{2},$$
(25)

where \({\beta }_{np}\simeq{\beta }_{n1p}\simeq{\beta }_{n2p}\simeq{\beta }_{n3p}\). As follows from Eq. (25), the stationary concentration of ions \({\bar{n}}_{n}\) in the absence of hydrometeors is determined by the following relation \({\bar{n}}_{p}=\sqrt{\Omega /{\beta }_{np}}\). The stationary concentration of ions in fine weather conditions is \({\bar{n}}_{p}\approx 1{0}^{9}-1{0}^{10}\) m\({}^{-3}\), which implies that \(\Omega \approx 1{0}^{5}-1{0}^{7}\) m\({}^{-3}\)s\({}^{-1}\). Raizer43 gives an estimate \(\Omega \approx 1{0}^{7}\) m\({}^{-3}\)s\({}^{-1}\). On the contrary, for low concentration of ions in the presence of cloud particles, one can obviously neglect recombination losses compared with the loss of ions to hydrometeors in Eq. (24e):

$$\frac{\partial {n}_{p}}{\partial t}=\Omega -{\nu }_{h}{n}_{p}.$$
(26)

Then the stationary value of the ion concentration in the cloud (in the presence of hydrometeors) is \({\breve{n}}_{p}=\Omega /{\nu }_{h}\). Chiu48 reported at least 2 orders of magnitude lower concentration of ions in the interior region of the cloud compared with those outside the cloud at the same height. This is apparently caused by the ion attachment to the water droplets (Chiu48 did not consider the presence of ice in the cloud), which makes the cloud conductivity lower than that of the surrounding air. So, if we take, following Chiu,48 even three orders of magnitude lower concentration of ions in the interior region of the cloud compared with those outside the cloud at the same height \({\breve{n}}_{p}=1{0}^{-3}{\bar{n}}_{p}\), we obtain \({\nu }_{h}\approx 1{0}^{-1}-1\) s\({}^{-1}\). Note that Eq. (26) is applicable to a non-thunderstorm cloud. Collisions of charged hydrometeors in thundercloud turbulent flow increase the ionization rate that leads to both the strong conductivity fluctuations in thunderclouds and to the strong inhomogeneities in the distribution of negative and positive ions, leading to violation of the local electroneutrality \({n}_{n}({\bf{r}},t)\,\ne \,{n}_{p}({\bf{r}},t)\).

The flux densities of the elementary charge carriers can be represented as follows:

$${{\bf{J}}}_{s}({\bf{r}},t)={n}_{s}{{\bf{V}}}_{s}({\bf{r}},t)-{D}_{n}\nabla {n}_{s},$$
(27)

where subscript “\(s\)” represents subscripts “\(e\)”, “\(p\)”, and “\(n1\)”, “\(n2\)”, “\(n3\)” that refer to electrons, positive ions and three types of negative ions, respectively, \({n}_{s}\), \({{\bf{V}}}_{s}\), and \({D}_{s}\) are the number density, drift velocity, and diffusion coefficient for species \(s\). In the atmosphere under normal conditions \({D}_{e}\simeq 0.1\) m2 s−1 and \({D}_{n1}\simeq {D}_{n2}\simeq {D}_{n3}\simeq {D}_{p}\simeq 2\times 1{0}^{-4}\) m2 s−1.33

In a weakly ionized gas, electrons and ions mainly collide with neutral molecules, and these collisions are mostly elastic. In atmospheric air under normal conditions, the mean free path of electrons and ions is of the order of \(1{0}^{-7}\) m (0.1 micron). On spatial scales exceeding the mean free path of electrons and ions and on time intervals that exceed the inverse collision frequency, the negative species, and positive ions move with velocities \({{\bf{V}}}_{s}\), and \({{\bf{V}}}_{p}\), respectively, which are represented by a superposition of the air flow velocity \({{\bf{V}}}_{A}({\bf{r}},t)\) and drift velocities in the local electric field:

$${{\bf{V}}}_{s}({\bf{r}},t)={{\bf{V}}}_{A}({\bf{r}},t)-{\mu }_{s}\cdot {\bf{E}}({\bf{r}},t);{{\bf{V}}}_{p}({\bf{r}},t)={{\bf{V}}}_{A}({\bf{r}},t)+{\mu }_{p}\cdot {\bf{E}}({\bf{r}},t),$$
(28)

where \({\mu }_{s}\), and \({\mu }_{p}\) are the absolute values of negative and positive ion mobilities, and subscript “\(s\)” represents subscripts “\(e\)”, “\(n1\)”, “\(n2\)”, and “\(n3\)” that refer to electrons and three types of negative ions. In the atmosphere under normal conditions the typical values of mobilities are \({\mu }_{e}\approx 0.1\) m\({}^{2}\)V\({}^{-1}\)s\({}^{-1}\) and \({\mu }_{p}\approx {\mu }_{n}\approx 2\times 1{0}^{-4}\) m\({}^{2}\)V\({}^{-1}\)s\({}^{-1}\).33 The local electric field \({\bf{E}}({\bf{r}},t)=-\nabla \varphi ({\bf{r}},t)\) satisfies Poisson equation

$${\nabla }^{2}\varphi =-\frac{e}{{\varepsilon }_{0}}({n}_{p}-{n}_{e}-{n}_{n1}-{n}_{n2}-{n}_{n3})-\frac{{\rho }_{h}({\bf{r}},t)}{{\varepsilon }_{0}},$$
(29)

where \(e\) is the absolute value of electron charge, \({\varepsilon }_{0}\) is the permittivity of free space, and \({\rho }_{h}({\bf{r}},t)\) is the charge density associated with charges residing on hydrometeors.

Homogeneous breakdown field determination

For low concentrations of charge carriers in the system of Eqs. (24a–e), inhomogeneity and nonlinearity can be neglected. Then, at the breakdown threshold, the following system of linear differential equations will be valid for the production of electrons and negative ions

$$\frac{\partial {n}_{e}}{\partial t}=({\nu }_{i}-{\nu }_{a1}-{\nu }_{a2}){n}_{e}+{\nu }_{du1}{n}_{nu1}+{\nu }_{du2}{n}_{nu2}+{\nu }_{ds}{n}_{n3}+\Omega ,$$
(30a)
$$\frac{\partial {n}_{n1}}{\partial t}={\nu }_{a1}{n}_{e}-{\nu }_{du1}{n}_{n1}-{\nu }_{cu}{n}_{n1}-{\nu }_{cs}{n}_{n1},$$
(30b)
$$\frac{\partial {n}_{n2}}{\partial t}={\nu }_{a2}{n}_{e}+{\nu }_{cu}{n}_{n1}-{\nu }_{du2}{n}_{nu2}+{\nu }_{r}{n}_{n3},$$
(30c)
$$\frac{\partial {n}_{n3}}{\partial t}={\nu }_{cs}{n}_{n1}-{\nu }_{ds}{n}_{n3}-{\nu }_{r}{n}_{n3}-{\nu }_{h}{n}_{n3}.$$
(30d)

Note that the system of Eqs. (30a–d) is no longer dependent on the concentration of positive ions whose production dynamics is described by the following equation

$$\frac{\partial {n}_{p}}{\partial t}={\nu }_{i}{n}_{e}-{\nu }_{h}{n}_{p}.$$
(31)

The complete system of Eqs. (30a–d) and (31) can be represented in the matrix form as:

$$\frac{d{\bf{n}}}{dt}=\widehat{{\bf{A}}}\cdot {\bf{n}}+\widehat{\Omega },$$
(32)

where \(\widehat{{\bf{A}}}\) is the coefficient matrix of the complete system; \(\hat{\Omega }={(\Omega ,0,0,0,\Omega )}^{{\rm{T}}}\); \({\bf{n}}\) is column vector of species concentrations, \({\bf{n}}={({n}_{e}(t),{n}_{nu1}(t),{n}_{nu2}(t),{n}_{n3}(t),{n}_{p}(t))}^{{\rm{T}}}\) and \({(\widehat{{\bf{X}}})}^{\rm{T}}\) is transposed matrix \(\widehat{{\bf{X}}}\). Matrix \(\widehat{{\bf{A}}}\) has the following form:

$$\widehat{{\bf{A}}}=\left(\begin{array}{ccccc}{\nu }_{i}-{\nu }_{a1}-{\nu }_{a2}&{\nu }_{du1}&{\nu }_{du2}&{\nu }_{ds}&0\\ {\nu }_{a1}&-{\nu }_{du1}-{\nu }_{cu}-{\nu }_{cs}&0&0&0\\ {\nu }_{a2}&{\nu }_{cu}&-{\nu }_{du2}&{\nu }_{r}&0\\ 0&{\nu }_{cs}&0&-{\nu }_{ds}-{\nu }_{r}-{\nu }_{h}&0\\ {\nu }_{i}&0&0&0&-{\nu }_{h}\end{array}\right).$$
(33)

The corresponding characteristic equation of the system is a polynomial equation of the fifth degree. By definition, the critical breakdown field corresponds to the appearance of a positive root \({\lambda }^{+}\) of the characteristic equation of a homogeneous system, which loses stability. Note that system (32) ignores positive and negative ions attached to hydrometeors, which leads to a slight violation of charge conservation principle. The corresponding solution of the complete system of Eqs. (30a–d) and (31) can be written as

$${\bf{n}}(t)={({n}_{e}(t),{n}_{n1}(t),{n}_{n2}(t),{n}_{n3}(t),{n}_{p}(t))}^{{\rm{T}}}={n}_{0}\cdot \widehat{{\bf{n}}}\cdot \exp ({\lambda }^{+}\cdot t),$$
(34)

where \(\widehat{{\bf{n}}}\) is an eigenvector of the complete system (30a–d) and (31), which corresponds to the eigenvalue \({\lambda }^{+}\). The dependence of the conventional and nonconventional breakdown electric fields on altitude above sea level is shown in Fig. 1, which was generated with the use of our custom code (see ref. 49). First of all, it is clearly seen from Fig. 1a that with the effects of electron detachment from negative ions in elevated electric field taken into account, the level of the nonconventional field noticeably decreases in comparison with the conventional one. The abrupt dependence of the increment (eigenvalue \({\lambda }^{+}\)) of the species concentration growth on electric field amplitude is shown in Fig. 1b. It can be seen that a slight increase in the field amplitude leads to a sharp increase in the increment \({\lambda }^{+}\). It is worth noting that the dependence of the increment on the field for the nonconventional case evolves more gradually compared with the conventional one. This means that electrical breakdown with the effects of electron detachment taken into account is realized at longer time intervals compared with the conventional case. The dependence of the eigenvector components on altitude shown in Fig. 1c characterizes the changes in the relative species concentrations for different electric field amplitudes as a function of altitude.

The effective ionization frequency

In order to clarify the physical meaning of the decrease in the critical electric field seen in Fig. 1a, let us consider a simplified version of system (30a–d)–(31), in which all three types of negative ions are lumped in a single category with concentration \({n}_{n}={n}_{n1}+{n}_{n2}+{n}_{n3}\). Then, at the breakdown threshold, the following system of linear differential equations will describe the production of electrons and negative ions:

$$\frac{\partial {n}_{e}}{\partial t}=({\nu }_{i}({\bf{r}},t)-{\nu }_{a}){n}_{e}+{\nu }_{d}({\bf{r}},t){n}_{n},$$
(35a)
$$\frac{\partial {n}_{n}}{\partial t}={\nu }_{a}{n}_{e}-{\nu }_{d}({\bf{r}},t){n}_{n}-{\nu }_{h}{n}_{n},$$
(35b)

where \({\nu }_{a}={\nu }_{a1}+{\nu }_{a23}\) and \({\nu }_{d}=({\nu }_{du1}{n}_{u1}+{\nu }_{du2}{n}_{u2}+{\nu }_{ds}{n}_{s})/{n}_{n}\) is an effective detachment frequency, which is determined by the eigenvector components of system (30a–d). Similar to system (30a–d), system (35a and b) is independent on the concentration of positive ions whose production dynamics is still described by Eq. (31). The characteristic equation of linear system (35a and b) has the following form

$${\lambda }^{2}-{\rm{tr}}({\bf{A}})\lambda +\det ({\bf{A}})=0,$$
(36)

where \({\bf{A}}\) is the coefficient matrix of linear system (35a, b); \({\rm{tr}}({\bf{A}})={\nu }_{i}-{\nu }_{a}-{\nu }_{d}-{\nu }_{h}\) is the matrix \({\bf{A}}\) trace, and \(\det ({\bf{A}})={\nu }_{a}{\nu }_{h}-{\nu }_{i}({\nu }_{d}+{\nu }_{h})\) is the determinant of matrix \({\bf{A}}\). The loss of stability of homogeneous system of linear differential equations of the first order (35a and b) and, correspondingly, the appearance of the positive root \({\lambda }^{+}>\,0\) of its characteristic Eq. (36) occurs even for \({\nu }_{i}\ll {\nu }_{a}\), when \(\det ({\bf{A}})\), i.e., the free term of Eq. (36) becomes negative. Assuming that the absolute value of the matrix \({\bf{A}}\) determinant is much smaller than the square of the matrix \({\bf{A}}\) trace, \(\det ({\bf{A}})\ll {\rm{tr}}{({\bf{A}})}^{2}\), for the eigenvalue \({\lambda }^{+}\), which is an increment of the exponential growth/decay, we get

$${\lambda }^{+}\approx \frac{\det ({\bf{A}})}{{\rm{tr}}({\bf{A}})}=\frac{{\nu }_{i}({\nu }_{d}+{\nu }_{h})-{\nu }_{a}{\nu }_{h}}{{\nu }_{a}+{\nu }_{d}+{\nu }_{h}-{\nu }_{i}}.$$
(37)

When the double inequality \({\nu }_{a}\gg {\nu }_{d}\gg {\nu }_{h}\) is satisfied, (37) reduces to the following:

$${\lambda }^{+}\approx \frac{{\nu }_{i}{\nu }_{d}}{{\nu }_{a}}-{\nu }_{h}={{\mathfrak{J}}}_{i}-{\nu }_{h},$$
(38)

where \({{\mathfrak{J}}}_{i}=\frac{{\nu }_{i}{\nu }_{d}}{{\nu }_{a}}\) is the effective ionization frequency first introduced in ref. 28 In other words, instability in the system occurs when the effective ionization frequency \({{\mathfrak{J}}}_{i}\) exceeds the frequency \({\nu }_{h}\) of ion losses to hydrometeors. This happens when the applied electric field exceeds the nonconventional breakdown field \({E}_{nc}\), which is determined by the condition

$${{\mathfrak{J}}}_{i}({E}_{nc})\approx \frac{{\nu }_{i}({E}_{nc}){\nu }_{d}({E}_{nc})}{{\nu }_{a}({E}_{nc})}\,>\,{\nu }_{h}.$$
(39)

Since for the conventional breakdown field \({E}_{\mathrm {c}}\)\({\nu }_{i}({E}_{c})={\nu }_{a}({E}_{c})\), and \({\nu }_{d}({E}_{c})\gg {\nu }_{h}\) even at sea level, it is evident that the nonconventional breakdown field is considerably lower then the conventional breakdown field (\({E}_{nc}\,<\,{E}_{c}\)).

The corresponding solution of the complete system of Eqs. (35a, b) and (31) in the matrix form is:

$${\bf{n}}(t)={({n}_{e}(t),{n}_{n}(t),{n}_{p}(t))}^{{\rm{T}}}={n}_{0}\cdot \widehat{{\bf{n}}}\cdot \exp ({\lambda }^{+}\cdot t),$$
(40)

where

$$\widehat{{\bf{n}}}=\left(\begin{array}{c}\frac{{\nu }_{d}\,+\,{\nu }_{h}\,+\,{\lambda }^{+}}{{\nu }_{a}}\\ 1\\ \frac{{\nu }_{i}({\nu }_{d}\,+\,{\nu }_{h}\,+\,{\lambda }^{+})}{{\nu }_{a}({\nu }_{h}\,+\,{\lambda }^{+})}\end{array}\right)\approx \left(\begin{array}{c}\frac{{\nu }_{d}}{{\nu }_{a}}\\ 1\\ 1\end{array}\right)$$
(41)

is an eigenvector of the complete system (35a, b) and (31), which corresponds to the eigenvalue \({\lambda }^{+}\). By means of reactions (15a–c), the charges of electrons pass to negative ions, which, in turn, become an important source of free electrons when the electric field increases to a critical level equal to \({E}_{nc}\). It follows from (41) that under quasi-equilibrium conditions and when

$$\frac{\partial E({\bf{r}},t)}{\partial t}\ll {\nu }_{a}\cdot E({\bf{r}},t),$$
(42)

the electron concentration is proportional to the ion concentration:

$${n}_{e}({\bf{r}},t)\approx \frac{{\nu }_{d}({\bf{r}},t)}{{\nu }_{a}}\cdot {n}_{n}({\bf{r}},t).$$
(43)

It is known that the role of detachment becomes decisive in the case of repeated discharges.43,50 Formally, electrons no longer participate in the game on time scales significantly exceeding the inverse frequency of electron attachment. However, under certain conditions (discussed above) they can return to the game via the detachment process.