Introduction

Biomass resources are a viable abundant, green, renewable, and sustainable alternative to conventional resources for chemical synthesis and energy delivery. Such a transition is intensified by reducing the amount of extractable fossil fuels, hardening environmental regulations, and stabilizing prices of biomass conversion1,2,3,4. The main avenues to achieving this milestone pass from the conversion of lignocellulosic biomass5,6,7. Since various substances can be synthesized by either direct or indirect lignocellulose conversion, among which sugars and sugar alcohols (SA) are of great interest8,9,10.

SAs, also known as polyols, are comprised of acyclic hydrogenated carbohydrates11. Thanks to their unique structures and the density of functional groups, SAs have found high popularity in pharmaceuticals, the food industry, and chemical processes12. Possessing similar or even better properties than conventional sugars, SAs also considered food ingredients13. Furthermore, they are increasingly utilized in pharmaceutical applications owing to their remarkable functional properties and health merits14. Despite existing in approximately small quantities, SAs were globally consumed up to 1.9 × 106 metric tons in 202211,14, which justifies the importance of developing reliable approaches to predict their properties and behavior. SA processing through biorefinery needs efficient solvents to pretreat or dissolve biomass, provide a suitable reaction medium, and enhance the conversion of sugars into either intermediates or ultimate products15,16.

To this end, many solvents with different characteristics, such as water, organic solvents, acids, bases, and ionic liquids (ILs)17 have been suggested. ILs not only offer liquid state and non-volatility in a broad range of temperatures but also benefit from high thermal stability and remarkable solubility strength. These characteristics make them potentially attractive tools to overcome various operational challenges18 associated with conventional solvents. The versatility of ILs allows their feature, thermochemical properties, and solvation power to be designed by adjusting the anion/cation pair appropriately19,20,21,22,23.

ILs offer high dissolving capacity for SAs due to the presence of various cations and anions, relatively low melting points, as well as ionic nature and non-volatility due to strong ionic-cationic interaction24,25,26,27,28,29. Xia et al. have recently reported the fabrication of cellulose- and lignin-obtained products employing ILs30. Accordingly, ILs have remarkable benefits in SAs extraction over conventional solvents. The solubilities of four sugar compounds (i.e., galactose, glucose, xylose, and fructose) in Aliquat®336 and 1-etyhl-3-methylimidazolium ethylsulfate ([Emim][EtSO4]) were measured (288–328 K) by Carneiro et al. and then correlated by two activity coefficient models (ACMs)31. Carneiro et al. also developed a theoretical and experimental study addressing the solubilities of sorbitol and xylitol in three ionic liquids in a wide range of temperatures (288–433 K) and evaluated some ACMs for thermodynamic modeling32. In another study, they measured the solubilities of sorbitol and xylitol in five different ILs namely 1-butyl-3-methylimidazolium dicyanamide ([Bmim][DCA]), 1-ethyl-3-methylimidazolium dicyanamide ([Emim][DCA]), 1-ethyl-3-methylimidazolium trifluoroacetate([Emim][TFA]), trihexyltetradecylphosphonium dicyanamide ([P6,6,6,14][DCA]), and Aliquat® dicyanamide at 288–339 K33. They also developed a thermodynamic model based on the perturbed-chain statistical associating fluid theory (PC-SAFT) equation of state (EoS). The solubility measurements of fructose and glucose in similar ILs were also done by the same research group34. Mohan et al. applied a molecular screening method based on the continuum solvation model to screen a large number of ILs for the solubility of xylose, glucose, fructose, and galactose over a somewhat wide temperature range (303.15 K to 373.15 K)35. They benefitted from the same approach to screen ILs for the solubility of sucrose, cellobiose, and maltose36. Paduszyński et al. measured solubility data and thermodynamic analysis of fructose, glucose, and sucrose in the presence of low-viscosity ILs composed of 1-butyl-3-methylimidazolium ([Bmim]+) cation and dicyanamide ([DCA]−) trifluoroacetate ([TFA]−) anions37. Their thermodynamic analysis was based on the PC-SAFT EoS. The same group investigated the solid–liquid equilibria of dicyanamide-based ILs and SAs (erythritol, xylitol, and sorbitol)38. A PC-SAFT modeling scheme was also employed to reproduce the measured data38. They also reported the impact of functionalized cations on the properties of ILs and their solubility strength for glucose39. The same thermodynamic approach utilizing the PC-SAFT approach was also developed in this system. The solubility of six monosaccharide SAs, namely glucose, mannose, fructose, galactose, xylose, and arabinose in different ILs composed of varied cations (1-butyl-3-methylimidazolium and trihexyltetradecylphosphonium) and anions (dicyanamide, dimethylphosphate, and chloride) were determined experimentally (288.2–348.2 K) and their solvation characteristics, as well as molecular-scale mechanisms, were studied by Teles et al.40. Asymmetric dicationic ILs have been recently introduced for this process and a pioneer study was developed by Yang et al., in which the impact of 1-(3-(trimethylammonio)prop-1-yl)-3-methylimidazolium bis(dicyanamide), 1-(3-(trimethylammonio)prop-1-yl)-1-methylpiperidinium bis(dicyanamide), and 1-(3-(trimethylammonio)prop-1-yl)pyridinium bis(dicyanamide) on the solubility of fructose and glucose was investigated at 323.15–353.15 K41. ACMs (Wilson, non-random two liquids (NRTL), and UNIQUAC) and semi-empirical equations (modified Apelblat and λh equation) were then applied to model the measured data. More recently, experimental investigations have addressed the solubility data of different compounds in numerous ILs42,43,44. Review studies also delve deeply into different aspects of this process7,17,30.

These thermodynamic-based calculations (i.e., semi-empirical equations, ACMs, and EoSs) are only applicable to a specific SA-IL system and it is not possible to use them for monitoring the phase equilibrium of several systems simultaneously. On the other hand, the artificial intelligence (AI) approaches can be simply applied to estimate the solubility of a wide range of SAs in different ILs. Hence, any effort leading to the simulating of the solubility of SAs in ILs with the use of machine learning (ML) tools is currently of great interest. ML-based tools have already been engaged in the accurate, fast, and easy-to-use estimation of the equilibrium data20,45,46,47,48,49, process assessment50,51, the properties of solvents22,52,53,54,55,56, oil reservoirs57, gas shales58, and biomass-derived materials59.

The solubility of SAs in ILs is a strong function of temperature and ILs type, which is identified by their properties. The type and properties of the SA compound also affect the solvation behavior. Early thermodynamic models utilizing EoSs33,38,39 and ACMs31,32,34,35 have several disadvantages. To elaborate on this, these models can accurately calculate solubility data only over a narrow and limited range of conditions. Moreover, they are component-specific, which results in the generation of too many parameters for various SA-IL systems. Consequently, a large number of component-specific parameters are found in the literature. On account of this, a universal ML model capable of covering a wide range of SA-IL systems, and temperatures is of paramount interest. From different standpoints, if the application of the ML models gains success, these models can possibly replace the conventional computation methods because of their facile usability and short computation period. ML is now widely utilized to address engineering issues, such as thermophysical property estimation60,61.

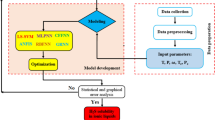
To benefit from a broad application of sugar alcohols in pharmaceuticals, the food industry, and chemical processes, it is necessary to extract them first. Feasible study, design, and optimization of SA extraction by ionic liquids require precise knowledge about the solubility data. Since the experimental measurement of SAs solubility in ILs is time-consuming and the literature introduces no comprehensive model for its estimation, the present study applies artificial intelligence tools for the considered task. The constructed intelligent model in this study can effectively engage in the simulation and optimization of the SA extraction by ILs.

Theory

Relevancy analysis

Before explaining ML models, it is essential to identify the direction and strength of the relationship between the system variables, namely solubility as the dependent variable and temperature, and SA and IL types, which are independent variables. This can be managed by facile and easy-to-interpret statistical analyses that measure the monotonic association between independent-dependent pairs of variables62. Pearson, Spearman, and Kendall's analyses benefit from a statistical notion known as covariance, which signifies the degree of correlation or the strength of the relationship between two variables. In other words, these analyses offer a straightforward criterion for how a pair of variables vary together63,64.

Pearson’s analysis [Eq. (1)] introduces a dimensionless parameter (− 1 to + 1) and Spearman’s criterion [Eq. (2)] offers the same range of the criterion and is actually the modified version of Pearson’s equation62. Even though the range of Spearman’s and Pearson’s parameters is the same, their quantitative and qualitative prediction of a single independent-dependent pair may differ62. For a system composed of a set of input (X) and output (Y) variables the Pearson (r) and Spearman (\({\mathrm{r}}^{{^{\prime}}}\)) coefficients can be calculated as follows:

$$\mathrm{r}=\frac{\sum_{\mathrm{i}=1}^{\mathrm{NDP}}\left({\mathrm{X}}_{\mathrm{i}}-{\mathrm{X}}_{\mathrm{av}}\right)\left({\mathrm{Y}}_{\mathrm{i}}-{\mathrm{Y}}_{\mathrm{av}}\right)}{\sqrt{\sum_{\mathrm{i}=1}^{\mathrm{NDP}}{\left({\mathrm{X}}_{\mathrm{i}}-{\mathrm{X}}_{\mathrm{av}}\right)}^{2}}\sqrt{\sum_{\mathrm{i}=1}^{\mathrm{NDP}}{\left({\mathrm{Y}}_{\mathrm{i}}-{\mathrm{Y}}_{\mathrm{av}}\right)}^{2}}}$$
(1)
$${\mathrm{r}}^{{^{\prime}}}=1-\frac{6\sum_{\mathrm{i}=1}^{\mathrm{NDP}}{\mathrm{d}}_{\mathrm{i}}^{2}}{{\mathrm{NDP}}^{3}-\mathrm{NDP}}$$
(2)

where NDP and d indicate the number of data points and the difference between the two ranks of each observation, correspondingly. Kendall’s criterion [Eq. (3)] benefits from a correlation coefficient that is based on the ranks of the observations64,65.

$${\mathrm{r}}^{{^{\prime}}{^{\prime}}}=\frac{2\left({\mathrm{N}}_{\mathrm{c}}-{\mathrm{D}}_{\mathrm{d}}\right)}{{\mathrm{NDP}}^{2}-\mathrm{NDP}}$$
(3)

By employing the correlation parameters (r, \({\mathrm{r}}^{{^{\prime}}}\), and \({\mathrm{r}}^{{^{\prime}}{^{\prime}}}\)), the relationship between the dependent variable (SAs solubility in ILs) and the independent variables (temperature, the molecular weights (MW) of SA and IL, the density of IL, and the fusion temperature and enthalpy) can be determined based on the regulations presented in Table 1.

Table 1 Range and interpretation of the correlation parameters62.
Full size table

The main idea of this study lies in the use of ML models with the simplest procedure. Other than that, the employed parameters can simply represent the nature of the materials in question and distinguish them, since the temperature is the main effective process variable in SA-IL solid–liquid equilibria; MWs can distinguish the compounds and somewhat representative of the molecular length; Fusion enthalpy and temperature are characteristics of the solubility of solids in liquids; And the density of IL shed light on the solubility power of the solvent (IL). These variables are easily available for the entire databank. Other variables mentioned by the reviewer are not available for all the whole compounds, and vaporization temperature does not make sense in this system as the evaporation of ILs is infinitesimal. On account of such a standpoint, these variables were selected for modeling the systems in question.

These analyses and further analysis of the ML models are implemented based on a solubility databank (647 data points of 19 SAs and 21 ILs). The databank is reported in Table 2. The properties of ILs and SAs are also summarized in Tables 3 and 4, respectively.

Table 2 The experimental data collected from the literature to develop machine-learning models.
Full size table
Table 3 The properties of ionic liquids utilized in machine-learning models.
Full size table
Table 4 The properties of sugar alcohols utilized in machine-learning models.
Full size table

Machine learning

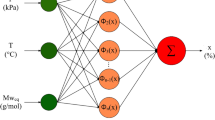
Artificial neural networks (ANN) have different variants, including multilayer perceptron (MLP), radial basis function (RBF), recurrent neural networks (RNN), general regression neural network (GRNN), and cascade feed-forward neural network (CFFNN)87,88. The smallest meaningful section of the ANN is the artificial neurons, which are assigned to performing calculations based on Eq. (4)89.

$$\mathrm{z}=\mathrm{\varphi }[\left(\sum_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{x}}_{\mathrm{i}}\times {\mathrm{w}}_{\mathrm{i}}\right)+\mathrm{b}]$$
(4)

In Eq. (4), z stands for the neuron’s output; while a particular artificial neuron received n inputs (\({\mathrm{x}}_{\mathrm{i}}\)), and each connection is adjusted by a corresponding weight (\({\mathrm{w}}_{\mathrm{i}}\)). Moreover, each neuron contains one extra adjusting parameter, which is called bias (\(\mathrm{b}\)). To overcome the restriction of only linear input–output mappings and propose a strategy to model nonlinear relationships, a frequently nonlinear activation function (\(\mathrm{\varphi }\)) is also incorporated in the neuron body. Linear, hyperbolic, tangent, logistic, and Gaussian activation functions can be implemented in the neuron structure90.

All of the ANN models include three types of layers: an input layer that receives the independent variables, the output layer that delivers the target prediction, and single or multiple hidden layers which have the task of data processing and recognition90. The number of independent features and dependent variables determines the number of elements in the input and output layers, respectively.

The training phase of ANN is responsible for obtaining appropriate values of the bias/weight that provide the best prediction accuracy for a dependent variable. This study applied the following ANN models to find the best one in the calculation of SAs solubilities in a variety of ILs.

MLP neural network (MLPNN)

This model utilizes a supervised learning technique called backpropagation for training and is a reliable model in many modeling fields. This study equips the hidden and output layers of the MLP model with the tangent hyperbolic [Eq. (5)] and logarithm sigmoid [Eq. (6)] activation functions, respectively90.

$${\varphi }\left(\mathrm{Z}\right)=\frac{1-\mathrm{exp}(-2\mathrm{Z})}{1+\mathrm{exp}(-2\mathrm{Z})}$$
(5)
$${\varphi }\left(\mathrm{Z}\right)=\frac{1}{1+\mathrm{exp}(-\mathrm{Z})}$$
(6)

RBF network (RBFN)

This model utilizes Gaussian or RBF as the activation function [Eq. (7)64] in the hidden layer, whereas its output is a linear combination of neuron parameters and RBF transformation of the inputs [Eq. (8)]. One of the best features of this model is its simplicity and fast-training nature47.

$${\varphi }\left(\mathrm{Z}\right)=\mathrm{exp}(\frac{{\mathrm{Z}}^{2}}{2{\upsigma }^{2}})$$
(7)
$${\varphi }\left(\mathrm{Z}\right)=\mathrm{Z}$$
(8)

where \(\upsigma\) is the spread factor.

To obtain the best RBF performance, the number of nodes in the hidden layer and the spread coefficient must determine carefully47.

Cascade feed-forward neural network (CFFNN)

This model generates a cascade configuration that links the nodes of the input to the hidden and output layers46. This model also utilizes the tangent hyperbolic and logarithm sigmoid transfer functions in the hidden and output layers, respectively.

It is worth noting that the learning step alters the connection weights and biases by a predefined optimization algorithm. This optimization algorithm continuously changes the model’s weights and biases to minimize the prediction error between the model output and the expected target (real data). This study employs the Levenberg–Marquardt (LM) algorithm to accomplish the training phase of the CFF and MLP models.

General regression neural network (GRNN)

Similar to the MLP and CFFNN, this ANN type also constitutes of the input, hidden, and output layers. The last two layers have the Gaussian and linear transfer functions, respectively. The only difference between GRNN and RBFN topologies is that the number of hidden neurons of the earlier is fixed and cannot be manipulated91.

Adaptive neuro-fuzzy inference systems (ANFIS)

ANFIS is designed by combining fuzzy logic and ANN to benefit from the strength of both models. This model consists of five successive layers, namely the first layer (fuzzy formation), the second layer (fuzzy rules), the third layer (normalization of membership functions), the fourth layer (fuzzy rule conclusion section), and the fifth layer (output calculation). By minimizing the observed error between the predicted and actual responses utilizing an appropriate scenario, the parameters of ANFIS can be adjusted92.

Least-squares support vector regression (LSSVR)

This method is capable of transferring the independent variables to a multi-dimensional space through the application of kernel functions (K)92. The most well-known and widely-employed kernel types that are employed in the LSSVR model are polynomial, linear, and Gaussian.

Uncertainty criteria

To check the reliability of the models, coefficient of determination (R2), mean squared error (MSE), root-mean-square deviation (RMSE), average absolute relative deviation percentage (AARD), mean absolute error (MAE), and relative absolute error (RAE), which are presented in Eqs. (9–14), are assessed. These variables are then employed in ranking the models.

$${R}^{2}=1- \left(\frac{\sum_{\mathrm{i}=1}^{\mathrm{NDP}}{({\mathrm{X}}_{\mathrm{i}}^{\mathrm{calc}.}-{\mathrm{X}}_{\mathrm{i}}^{\mathrm{exp}.})}^{2}}{\sum_{\mathrm{j}=1}^{\mathrm{NDP}}{({\mathrm{X}}_{\mathrm{j}}^{\mathrm{exp}.}-{\bar{\mathrm{X}} }^{\mathrm{exp}.})}^{2}} \right)$$
(9)
$${\mathrm{MSE}}=\frac{1}{\mathrm{NDP}}\sum_{\mathrm{j}=1}^{\mathrm{NDP}}{({\mathrm{X}}_{\mathrm{j}}^{\mathrm{calc}.}-{\mathrm{X}}_{\mathrm{j}}^{\mathrm{exp}.})}^{2}$$
(10)
$${\mathrm{RMSE}}=\sqrt{\frac{1}{\mathrm{NDP}}\sum_{\mathrm{j}=1}^{\mathrm{NDP}}{({\mathrm{X}}_{\mathrm{j}}^{\mathrm{calc}.}-{\mathrm{X}}_{\mathrm{j}}^{\mathrm{exp}.})}^{2}}$$
(11)
$${\mathrm{AARD}}=\frac{100}{\mathrm{NDP}}\sum_{\mathrm{j}=1}^{\mathrm{NDP}}\left|\frac{{\mathrm{X}}_{\mathrm{j}}^{\mathrm{calc}.}-{\mathrm{X}}_{j}^{\mathrm{exp}.}}{{\mathrm{X}}_{\mathrm{j}}^{\mathrm{exp}.}}\right|$$
(12)
$${\mathrm{MAE}}=\frac{1}{\mathrm{NDP}}\sum_{\mathrm{j}=1}^{\mathrm{NDP}}\left|{\mathrm{X}}_{\mathrm{j}}^{\mathrm{calc}.}-{\mathrm{X}}_{\mathrm{j}}^{\mathrm{exp}.}\right|$$
(13)
$${\mathrm{RAE}}=100\times \frac{\sum_{\mathrm{j}=1}^{\mathrm{NDP}}\left|{\mathrm{X}}_{\mathrm{j}}^{\mathrm{calc}.}-{\mathrm{X}}_{\mathrm{j}}^{\mathrm{exp}.}\right|}{\sum_{\mathrm{j}=1}^{\mathrm{NDP}}\left|{\mathrm{X}}_{\mathrm{j}}^{\mathrm{exp}.}-{\bar{\mathrm{X}} }^{\mathrm{exp}.}\right|}$$
(14)

Results and discussion

This section includes the results of relevancy analysis, ranking analysis, and a detailed investigation of determining the best model for predicting SAs solubility in ILs.

The correlation coefficients (relevancy factors) between dependent and independent variables are calculated by the 3 methods and presented in Fig. 1. To this end, 6 effective parameters, namely temperature, MWs and densities of solvents (ILs), MW of solute (SA), and the fusion temperature and enthalpy of the SA were assessed, among which temperature and fusion temperature have apparently the major impact on the solubility. The MW of SAs, as well as the enthalpy of fusion, also have a large impact on the SA solubility in ILs. The observed relevancy factors depict that while the temperature and properties of ILs (MW and density) enhance the solubility of SAs, the features of SAs (MW, fusion temperature, and enthalpy) have the opposite effect.

Figure 1
figure 1

The results of relevancy analysis for the solubility of sugar alcohols in ionic liquids.

Full size image

The next analysis presents a ranking test, which draws a comparison among the investigated models. This is addressed in Fig. 2. It is worth noting that this comparison is made at their best structures. The features of the models’ pre-assessment, as well as the best performance of each model, are addressed in Tables 5 and 6.

Figure 2
figure 2

Comparing the employed neural networks based on their best performance for the solubility of sugar alcohols in ionic liquids.

Full size image
Table 5 The features of the assessed artificial intelligence models.
Full size table
Table 6 The best features of the assessed artificial intelligence models.
Full size table

Based on their performance in the training, testing, and combined phases, the models are sorted and compared in this figure. The training phase included 85% of the entire databank. To do so, the rank was calculated based on Eq. (15) and the rank indices already calculated by Eqs. (9)–(14).

$$\mathrm{Rank}=\mathrm{Round}\left[\frac{1}{6}\sum_{\mathrm{i}=1}^{6}{\mathrm{Rank}}_{\mathrm{Index}}(\mathrm{i})\right],\mathrm{ i}:\mathrm{R},\mathrm{ MSE},\mathrm{ RMSE},\mathrm{AARD},\mathrm{MAE},\mathrm{ and RAE}$$
(15)

Results of the ranking test clarify that the ANFIS model offers the best estimations for the solubility data for the training, testing, and entire databank, while RBFNN presents the least accuracies in the same data distribution. As a consequence, the ANFIS model is introduced as the best model and applied to simulate different SA-IL systems in the following sections. This model predicts overall experimental data with the AARD = 7.43%, MAE = 0.017, RAE = 9.28%, MSE = 0.0009, RMSE = 0.03, and R2 = 0.98260.

Figure 3 depicts the calculated solubilities by the ANFIS model (Fig. 3A–C), as well as the relative deviations (Fig. 3D), against the experimental values. These figures approve that the calculated solubilities in the two training and testing steps are close to the real ones, which indicates the effectiveness of the model. The distribution of the relative deviations also confirms such a statement.

Figure 3
figure 3

The overall performance of the ANFIS model for the dissolution of sugar alcohols in ionic liquids in terms of the calculated results in the (A) training, (B) testing, and (C) entire datasets and (D) relative deviations utilizing the ANFIS model.

Full size image

The observations of this figure also depict that overfitting has not occurred in this system. Indeed, when a calculation procedure tends to learn every detail of a system in the training step, and the model then acts inaccurately to estimate the testing data, overfitting has occurred. An indication of overfitting in a system is a small error on the training dataset, while large errors on the test dataset. As a consequence of overfitting, the model is not capable of generalizing the features or patterns that have already been learned in the training phase. A reason for overfitting is often the insufficient distribution of the training and testing datasets viz a small training dataset, which was not the case in this study. The employed distribution of data in this study (85% for the training set) and also the accuracies in the training and testing datasets signify that the ANFIS model did not fall into the overfitting well. This issue can be understood by tracking the residuals and standard deviations in the training and testing categories.

The ingredients of Fig. 4, which depict the residuals (\({\mathrm{X}}_{\mathrm{i}}^{\mathrm{exp}.}-{\mathrm{X}}_{\mathrm{i}}^{\mathrm{calc}.}\)) distributions indicate that those of the major portion of the dataset in training, testing, and entire datasets fall within the range of ± 0.05 (molar fraction). To this end, the average residual values and standard deviations were calculated based on Eqs. (16) and (17)64, respectively. The ANFIS model presents 0.0020004, 0.0019553, and 0.0019937 residuals for the testing, training, and entire datasets, while the standard deviations are 0.029708, 0.031421, and 0.029946, respectively.

Figure 4
figure 4

The histograms of the ANFIS deviations in the (A) training, (B) testing, and (C) entire datasets.

Full size image
$$\mathrm{Average \, Residual}=\frac{1}{\mathrm{NDP}}\sum_{\mathrm{i}=1}^{\mathrm{NDP}}\left({\mathrm{X}}_{\mathrm{i}}^{\mathrm{exp}.}-{\mathrm{X}}_{\mathrm{i}}^{\mathrm{calc}.}\right)$$
(16)
$$\mathrm{Standard \, Deviation}=\sqrt{\frac{1}{\mathrm{NDP}}\sum_{\mathrm{j}=1}^{\mathrm{NDP}}{\left[\left({\mathrm{X}}_{\mathrm{i}}^{\mathrm{exp}.}-{\mathrm{X}}_{\mathrm{i}}^{\mathrm{calc}.}\right)-\mathrm{Average \, Residual}\right]}^{2}}$$
(17)

A quantitative measure of the applicability of the ANFIS model, which is presented in terms of standardized residuals [Eq. (18)] and Hat Index [Eq. (19)], is addressed in Fig. 5. In Eq. (19), M is an NDP × 6 matrix showing the experimental quantities of the independent variable. Then, the leverage method can explore the region a model is applicable with the use of standardized residual information when they are in the range of ± 3. In Fig. 5, this range is identified by dotted lines. Equation (20) is utilized to determine the quantity of critical leverage.

Figure 5
figure 5

The analysis of the leverage method for detecting the valid and suspect data points for the dissolution of the sugar alcohols in ionic liquids.

Full size image
$$\mathrm{Standardized \,residual \, of \, data \, point \, i}=\frac{{\mathrm{X}}_{\mathrm{i}}^{\mathrm{exp}.}-{\mathrm{X}}_{\mathrm{i}}^{\mathrm{calc}.}}{\mathrm{Standard \, deviation}};i=\mathrm{1,2},,\dots ,NDP$$
(18)
$$\mathrm{Hat \, Index}=\mathrm{M}{\left({\mathrm{M}}^{\mathrm{Transposed}}\times \mathrm{M}\right)}^{-1}{\mathrm{M}}^{\mathrm{Transposed}}$$
(19)
$$\mathrm{Critical \, leverage}=\frac{3}{\mathrm{NDP}}\left(1+\mathrm{the \,number \,of \,independent \,variables}\right)=0.0325$$
(20)

The applicability domain of the ANFIS model and the corresponding boundaries are defined in Fig. 5. In a nutshell, the leverage method confirms that the ANFIS model is readily capable of estimating the solubility of SAs in ILs based on the collected databank with high reliability. To elaborate on this, since only 20 data points among 647 solubility samples were identified as either good leverage (Hat Index > critical leverage) or outlier (standardized residuals out of the range of ± 3), the domain of applicability includes larger than 96.9% of the entire databank. On account of these findings, the ANFIS model is reliable owing to its high level of coverage and wide range of applicability.

The solubility of sorbitol in diverse ILs is presented in Fig. 6 and compared with the ANFIS calculations. Clearly, the model can represent the solubility data in the entire range of temperatures and can also distinguish the effect of solvent type as well. Figure 7, which addresses the impact of IL on the xylitol solubility, also depicts that the ANFIS results are accurate enough in the low-to-high solubility ranges. Similar observations for the solubility of fructose in different ILs have existed in Fig. 8. It is inferred from this figure that even sharp solubility changes with the temperature can be simulated by the ANFIS model with remarkable precision.

Figure 6
figure 6

Comparing the experimental solubilities of sorbitol in varied ionic liquids with the ANFIS model’s result.

Full size image
Figure 7
figure 7

Comparing the experimental solubilities of xylitol in varied ionic liquids with the ANFIS model’s result.

Full size image
Figure 8
figure 8

Comparing the experimental solubilities of fructose in varied ionic liquids with the ANFIS model’s result.

Full size image

The solubility behavior of fructose, glucose, and sucrose in [C4C1Im][CF3CO2] IL is presented in Fig. 9, which signifies that they are well estimated by the ANFIS model within the entire range of temperatures.

Figure 9
figure 9

Comparing the experimental solubilities of fructose, glucose, and sucrose in [C4C1Im][CF3CO2] ionic liquid and with the ANFIS model’s result.

Full size image

[C4C1Im][(OCH3)2PO4] IL that offers low-to-high solubility capacity for different SA compounds, including xylose, glucose, and fructose is assessed and compared to the ANFIS estimations in Fig. 10. It can be seen that the model can describe the solubility behavior of different IL-SA pairs, from low to high solubility range, with remarkable accuracy.

Figure 10
figure 10

Comparing the experimental solubilities of fructose, glucose, and sucrose in [C4C1Im][(OCH3)2PO4] ionic liquid with the ANFIS model’s result.

Full size image

The impact of the SA compound and temperature on the absorption capacity of [bmim][DCA] IL is compared in Fig. 11. Despite some minor discrepancies in the higher solubility range, the ANFIS model can represent the real data accurately. It is worth discussing that the collected dataset and the discrepancies of different datasets also affect the accuracy of the ANFIS model and a major portion of the observed error arises from these scattering. This issue is well magnified in Fig. 11B. As per the figure, there is more than one reference for the collected data of the solubilities of sorbitol, glucose, and fructose in [bmim][DCA], and the reported quantity and even trends in each case vary to a great extent, which generates uncertainties in the model behavior.

Figure 11
figure 11

Comparing the experimental solubilities of (A) xylose, mannose, and galactose, and (B) sorbitol, glucose, and fructose in [bmim][DCA] ionic liquid with the ANFIS model’s result.

Full size image

Table 7 summarizes the performance of the ANFIS model for predicting the phase equilibrium of various SA-IL pairs. The largest deviation is observed in the case of D-xylitol solubility in [bmim][C(CN)3] (ARD = 9.72% and AARD = 29.62%) and the largest relative deviations (Min RD = − 28.02% and Max RD = 75.23%) belong to a data point from the same system as well. Nevertheless, the maximum AARD% does not exceed 10% in the majority of SA-IL pairs, which signifies the accuracy of the ANFIS model in representing the solubility data of SAs in ILs. The ANFIS model can be further employed for the solubility data modeling in various solutions composed of SA compounds and ILs.

Table 7 The accuracy of the ANFIS model’s result for different SA-IL systems in terms of various deviation factors.
Full size table

Although ML studies, which consider the systems in question, cannot be for the time being found in the literature, a comparison between any available modeling approach with the one developed herein is of great interest and can then shed light on the quality of ML models. The previous calculation procedures for the solubility of SAs in ILs include thermodynamic modeling that benefits from the use of ACMs mainly including NRTL and UNIQUAC and EoS such as PC-SAFT.

To this end, PC-SAFT is a popular EoS that can benefit from either predictive or correlative schemes. Carneiro et al.33 developed calculations based on this method for the solubilities of xylitol and sorbitol in 1-ethyl-3-methylimidazolium dicyanamide, 1-butyl-3-methylimidazolium dicyanamide, Aliquat® dicyanamide, trihexyltetradecylphosphonium dicyanamide, and 1-ethyl-3-methylimidazolium trifluoroacetate at 288–339 K. In the whole systems investigated, they obtained 3.7–112.2% and 3.3–21.7% deviations when the predictive and correlative approaches were employed, respectively. The use of a fitting parameter in the calculations, which was determined based on the regression of the solubility data, notably improved the accuracy of calculations. Paduszynski et al.37 also benefitted from the same approach with some minor modifications for the system including 1-butyl-3-methylimidazolium dicyanamide 1-butyl-3-methylimidazolium trifluoroacetate ILs and glucose, fructose, and sucrose SAs. Then, they reported very poor agreement between the calculations and the measurements in the predictive mode. Benefitting from two adjustable parameters and the regression of solubility temperatures, they improved the accuracy of the model considerably. Their further study also reported the same trends38. Although this method of calculation was successful and is in many cases comparable to the ML calculations in this study, it demands a two-step regression procedure including the optimization of pure and binary data.

The solubilities of glucose, fructose, xylose, and galactose in two ILs namely the 1-etyhl-3-methylimidazolium ethylsulfate (also known as [emim][EtSO4]) and the Aliquat®336 at 288–328 K were modeled by Carneiro and co-workers31 by the use of NRTL and UNIQUAC equations. The AARD% obtained for the two equations did not exceed 4% (based on molar fractions) in almost all cases, and no significant difference between the two equations was observed. This team32 then utilized a similar methodology within the same ACMs and an e-NRTL equation for the systems composed of xylitol and sorbitol and several ILs. Their calculations based on NRTL, UNIQUAC, and e-NRTL ACMs resulted in 0.9–3.7%, 1.1–3.2%, and 0.7–2.6% deviations, respectively. Similar observations were reported in the further studies of the same research group34. Compared to the ML models, the thermodynamic models based on activity coefficient equations demand more sophisticated calculations as well as a regression-based procedure, which can lead to the accumulation of a large number of parameters for a vast number of SA-IL binary systems.

Conclusions

Ionic liquids have recently been introduced to enhance the development of sugar-derived compounds and their efficient extraction. This study is the first attempt to develop several machine learning models for predicting the solubility of sugar alcohols in ionic liquids. Machine learning models were implemented using 647 solubility samples of 19 sugar alcohols in 21 ionic liquids collected from the literature. After detecting the effective variables, i.e., temperature, molecular weight and density of ILs, the molecular weight of SAs, the fusion temperature, and enthalpy, artificial neural networks, least-squares support vector regression, and adaptive neuro-fuzzy inference system (ANFIS) was appraised among which, ANFIS was the superior one. The accuracy of this model was approved by an R2 of 0.98359 and an AARD of 7.43% for estimating the entire databank. On the contrary, the radial basis neural network is identified as the worst model with AARD = 18.21% and R2 = 0.93202. Checking the ANFIS model predictions by the leverage method showed that this model is reliable because of its broad range of applicability and a remarkable level of coverage. The results of this investigation can contribute to the screening of ionic liquid solvents for the appropriate extraction of sugar alcohols. Moreover, ANFIS models can be efficiently employed for solubility estimation in the investigated SA-IL systems.