Introduction

Since the concept of organic halide perovskite was proposed in 20131, it has drawn substantial interests for researchers from materials, chemistry and physics field2. In 2015, Nam-Gyu Park et al.3 used 10% cesium to substitute formamidine cation and got lower trap-density, higher open circuit voltage, respectful thermal property and enhanced stability. Recently, as the efficiency of formamidine based perovskite materials has reached more than 20% efficiency and 3000 min T80 lifetime (the time that the solar cell can run at 80% of its initial performance)4,5, they have been considered as promising candidates for new era perovskite materials.

Though researchers try hard to promote efficiency and improve stability of formamidine based perovskite materials, the mechanism for improving the efficiency and stability of perovskite materials and devices is still not clear. For instance, how the photoelectric properties and charge dynamics in perovskites be affected by specific mechanisms including the size, the interaction of organic cations and the interaction with the crystal structure. Some former study thought that the main function of organic cations is to stabilize the structure and will not change photoelectronic properties6. Mehdizadeh et al.7 studied that the rotation of the MA in Rz and Rx modes causes substantial changes in the band structure, density of states, electron density, dielectric function, and absorption spectrum. They found that these changes are greatly affected by the interaction of cation–cation (MA-Pb) and cation–anion (MA-X) and van der Waals radius of organic cations. Researchers had also done related studies on the FA system and compared the differences from the MA system due to ion size, charge distribution and hydrogen bonding. Besides, the inorganic PbI6 octahedral frame experienced Glazer tilt with a time of 0.2–1.5 ps in MAPbI3, and the FA cation at A-site in FAPbI3 rotates or rolls in the cage (2 − 3 ps), which indicates organic cations’ orientation plays an important role in halide perovskite8. To be more specific, the orientation of organic cation has relations with ferroelectricity9, ion transport10, phase transition temperature11, water molecule adsorption and device stability12.

Recently, some researchers paid attention to this and used density functional theory (DFT) to describe this phenomenon in detail. Carlo et al.13 revealed the role of organic cations in hybrid halide perovskite MAPbI3. Furthermore, Jonathon et al.14 considered the influence of the rotation of the MA cation along the coordinate axis and the coaxial precession on the performance of perovskite. Besides, Nathaniel et al.15 considered the coupling effect between cations and inorganic lattice, the different energy barrier between FA and MA cation rotation. Akhtarianfar et al.16 investigated the formamidine cation rotation in FAPbI3. But there is no one has studied the effect of cation orientation on inorganic ions, perovskite lattice and properties in the FA/Cs system of formamidine based perovskite. On the other hand, studies show that the rotation of cations decreases at low temperature and high pressure17,18, so it is possible to control the synthesis of cation-oriented cubic perovskite to bring vital different changes in this field.

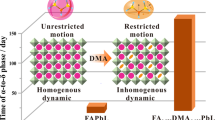
Hence, our work is the first time to investigate the complex coupling effect of organic orientation in formamidine based perovskite. We used DFT theory to build a supercell to study this problem, and tried to build a reasonable explanation of it. We found that the coupling effect of organic cations and cesium atom affected many properties of this mixing system, such as lattice constant, band structures, charge distribution, dielectric constant, optical absorption properties, and even the performance of solar cell device (Fig. 1). Our work not only expounds the mechanism of the role of cation orientation in the mixed system, but also points out a feasible way for the synthesis of electron and optically adjustable perovskite materials and devices.

Figure 1
figure 1

Schematic diagram of possible ways to change the orientation of organic cation and the result lead by it.

Full size image

Computational details

All of these first-principles calculations were performed by using the Vienna Ab initio Simulation Package (VASP)19,20. Perdew–Burke–Ernzerhof (PBE) exchange correlation functional was used within a generalized gradient approximation (GGA)21 and optB86b22 van der Waals force revision. We focused on the pseudo-cubic phase of formamidine based perovskite with the chemical structures of FAPbI3 and FA0.875Cs0.125PbI3. A cut-off energy of 400 eV was chosen to reach the desired accuracy. For the optimization of the geometric structure, the total energy convergence criterion was chosen as 10–5 eV, and the force on each atom was converged to an accuracy of 0.01 eV·Å−1. The size of the FAPbI3 supercell is 2 × 2 × 2, and one formamidine is substituted by a cesium atom to simulate the 12.5% doping. A reciprocal-space sampling with gamma center in an 8 × 8 × 8 Monkhorst–Pack k-point mesh23 was set in the Brillouin zone for the standard DFT calculations. The occupied and empty bands set in the DFT calculation are 240 for FAPbI3 and 224 for FA0.875Cs0.125PbI3. Molecular dynamics simulation used canonical ensemble (NVT). The temperature of simulation is 400 K. The total simulation time of each trajectory was 5 ps with a 2 fs timestep. Considering the computational accuracy and the enormous demands of calculation resources, the phase of perovskite will change from high to low temperature, and VASP calculations are performed at 0 K, we did not calculate phonon spectrum and elastic constants. And to mitigate the effect due to the 0 K calculation, we used the crystal constant from experiment as the basis to build our model. The VESTA software was used to visualize crystal structures and electron distribution24. The VASPKIT toolkit was used to post-process the band gap, density of state and dielectric constant data25.

For calculating cohesive energy \({E}_{c}\), the formula is as follows:

$${E}_{c}=\frac{E\left({A}_{m}{B}_{n}{C}_{p}{D}_{q}\right)-mE\left(A\right)-nE\left(B\right)-pE\left(C\right)-qE\left(D\right)}{The\, number\, of \,atoms \,in \,a \,conventional \,unit \,cell}$$
(1)

where \(E({A}_{m}{B}_{n}{C}_{p}{D}_{q})\) means the relaxed energy of structure, \(A, B, C, D\) are the elements in structure, \(m, n, p, q\) are the numbers of each element. \(E\left(A\right), E\left(B\right), E\left(C\right), E(D)\) are the energy of single atom of each element.

For evaluating the optical properties, we calculated the frequency-dependent complex dielectric function26.

$$\varepsilon \left(\omega \right)= 1+ \frac{8\pi }{\Omega {N}_{k}}\sum_{k,v,c}\frac{{\left|\langle {\varphi }_{kv}\left|\widehat{v}\right|{\varphi }_{kc}\rangle \right|}^{2}}{{\left({E}_{kc}-{E}_{kv}\right)}^{2}\left({E}_{kc}-{E}_{kv}-\omega -i\eta \right)}$$
(2)

where \(\Omega\) is the volume of the cell, \(\widehat{v}\) is the operator of velocity,\(\eta\) is an opportune broadening factor, \({N}_{k}\) is the total number of k-points in the Brillouin zone, and the indices \(c\) and \(v\) show the unoccupied and occupied states, respectively. The frequency-dependent absorption coefficient \(\alpha \left(\omega \right)\), is given by

$$\alpha \left(\omega \right)= \omega \sqrt{\frac{-\mathrm{Re}\varepsilon \left(\omega \right)+ \sqrt{{\mathrm{Re}}^{2}\varepsilon \left(\omega \right)}+{\mathrm{Im}}^{2}\varepsilon \left(\omega \right)}{2}}.$$
(3)

Results and discussion

Structural stability and adjustment

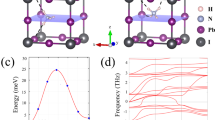
Figure S1 shows the initial 2 × 2 × 2 supercell of FAPbI3 and FA0.875Cs0.125PbI3 with formamidine cations facing the (100), (110) and (111) direction. Before all others, all the calculations have converged on the energy convergence standard 10–5 eV and the force convergence standard 0.01 eV·Å−1 per atom by using GGA-PBE exchange correlation functional21 with van der Waals force correlation22 without considering the spin–orbit coupling (SOC). We also calculated cohesive energy and ab-initio molecular dynamics (AIMD) in 400 K to confirm the dynamical stability of these hybrid perovskites27,28. The cohesive energy of all our structures is less than zero, which means these structures are stable in 0 K. The energy-time curves of AIMD of all our structures are straight, which means these structures are stable in 400 K (Table 1; Figure S2).

Table 1 Calculated lattice constant, cell volume, distortion index (bond length) and relaxed energy of FAPbI3 and FA0.875Cs0.125PbI3.
Full size table

In Table 1 and Fig. 2, the data of relaxed structures for the cubic phase of FAPbI3 and FA0.875Cs0.125PbI3 are displayed. Refer to previous research, PBE-vDW method can obtain the most accurate lattice constant than DFT-PBE and HSE06 methods in formamidine halide perovskite29. The lattice constant of FAPbI3 supercell we calculated in (100) direction is close to antecedent experiment30,31 and calculation29. We used the cell volume and lattice constant obtained by the cube root of cell volume for measuring the disorder of the structure due to the structure will turn from cubic phase to pseudo-cubic phase32. Therefore, we have reason to believe that our model effectively represents the specific case of an actual condition of perfectly aligned molecular dipoles.

Figure 2
figure 2

(a) Relative energy and relative cell volume in different FA cations orientation; (b) relative energy and distortion index (bond length) in different FA cations orientation.

Full size image

Firstly, let us separately discuss changes lead by orientation in FAPbI3 and FA0.875Cs0.125PbI3 system. From Fig. 2a, we can discover that the relaxed energy at each formamidine orientation is similar, and the energy barrier is 0.2–0.3 eV for each condition. It’s not a tremendous energy barrier, so formamidine cations can freely rotate in cage. According to previous research, the formamidine cations are indeed rapid rotating with a time period of 2–3 ps and PbI6 octahedral framework is undergoing Glazer tilting with a time period of about 0.2–1.5 ps17,33.

Besides the relaxed energy, the relative cell volume of (110) is the smallest in three rotation models, leading to the minimum of lattice constant. The change of lattice constant in FAPbI3 system is affected by the reorientation of formamidine cations because their atom arrangement and charge distribution are anisotropic. These factors cause Pb–I–Pb to be subject to different forces like N–H···I hydrogen bond and van der Waals force in different directions34. Furthermore, the contraction of perovskite lattice from FAPbI3 to FA0.875Cs0.125PbI3 is usually attributed to the substitution from formamidine to cesium because of the smaller radius of cesium35. In fact we indeed find that the lattice constant of FA0.875Cs0.125PbI3 in (100) direction has a 0.1% decrease than FAPbI3, which is consistent with the experiment36. But the phenomenon in (110) and (111) is different. This difference can be attributed to the coupling effect between the orientation of organic cations and the addition of cesium.

This coupling effect also influences the tilt of PbI6 octahedron. From Fig. 2b, both FAPbI3 and FA0.875Cs0.125PbI3 systems get the minimum value of distortion index (this index describes the degree of tilt of PbI6 octahedron) in (110) direction. We can also directly see the degree of deformation in Figure S3. The difference is that FAPbI3 gets the maximum value in (111) direction but FA0.875Cs0.125PbI3 gets it in (100) direction, which maybe lead by the cesium and formamidine cations co-effect.

All in all, the reorientation of formamidine cations and the entrance of cesium give the formamidine perovskite adjustment structural properties. Lots of researches before shows that organic cations will be ‘frozen’ in low temperature14,37,38. And the structural stability is also be closely bound up with the internal structure of perovskite. Therefore, our work indicate which low temperature state is good for the application in different areas.

Electronic properties

Figure 3 shows the 2D and 3D maps of electron charge density. This map reveals the interaction among the components of the perovskite and how electrons distribute in the lattice. We set the isosurface level 0.1 electrons/bohr3 to see the distribution more directly.

Figure 3
figure 3

Two-dimensional (2D) depiction of electron charge density in crystallographic plane of (001) in FAPbI3 (a) (100), (b) (110), (c) (111) and FA0.875Cs0.125PbI3, (d) (100), (e) (110), (f) (111). 3D charge map is also shown for each sub-figure.

Full size image

According to the non-doped FAPbI3 perovskite, the interaction of formamidine with PbI6 octahedron leads to a considerable disorder, which alters its volume (cell volume is changed as well) (refer to Table 1; Fig. 2). Interestingly, Table 1 tells us the distortion of PbI6 octahedron reaches a minimum in (110) direction. This phenomenon can be attributed to that the symmetrical interactions in (110) plane uniformly inflate the size of PbI6, which leads to a decrease of PbI6 distortion degree compared with other orientations7.

Moreover, the FA0.875Cs0.125PbI3 system shows some similarities and differences. Diverse directions indeed tilt the PbI6 octahedron and Pb–I–Pb bond angle, but the addition of cesium also affects them. It’s obviously that the cesium atom shows strong ionization because the light around the cesium atom is weak in 2D contour plot Fig. 3d–f. This is because the electronegativity of cesium is near the largest in periodic table, and the electron in Cs 6s orbit is easy to be seized and lose. Owing to this, the bond angle of Pb–I–Pb is strongly tilted when formamidine cations orient to (100) direction. In (110) direction, the distortion reduces than (100) orientation, and we can see the bond angle of Pb–I–Pb is tilting slightly than (100) orientation. This reduction maybe is the same reason like FAPbI3 we discussed below. But the FA0.875Cs0.125PbI3 system’s distortion index is larger than FAPbI3 system when orients to (110) direction, which is caused by the smaller radius of cesium. When turns to (111) direction, the Pb–I–Pb bond occurs inner fold on x–y plane with a 7.8° angle but the distortion is smaller than FAPbI3 in the same direction. This is because the substitution of cesium reduces the charge interaction lead by (111) direction of formamidine cations. To be more specific, the (111) orientation of formamidine causes a catercorner electronic interaction, but cesium atom also possesses a strong polarization force. The coupled effect of them leads to this result, and even affects the bandgap and density of state we will discuss after.

Now let’s focus on the role of formamidine orientation in electronic structure. Figures 4, 5 and 6 shows the band structure and density of state (DOS) of formamidine based perovskite. Figure 4 indicates the trends of band gap of FAPbI3 and FA0.875Cs0.125PbI3. Since spin–orbit coupling (SOC) will change the band gap, and GGA will underestimate the band gap, the effects of them coincidentally make the band gap calculated without considering the SOC close to the experimental value32,34,39. While using HSE06 + SOC can get a more accurate value, we just want to focus on the variation of band gap. Hence, it’s enough for us to use the result of PBE-vDW function.

Figure 4
figure 4

(a–c) Band gap of FAPbI3 with different FA cations orientation: (a) (100), (b) (110), (c) (111); (d–f) band gap of FA0.875Cs0.125PbI3 with different FA cations orientation: (d) (100), (e) (110), (f) (111).

Full size image
Figure 5
figure 5

Schematic energy level diagram of different formamidine orientations (black line: atom energy level; blue line: valence band minimum; orange line: conduction band maximum; black dotted line: fermi energy).

Full size image
Figure 6
figure 6

Total density of state (TDOS) and projected density of state (PDOS): (a–c) FAPbI3 with different FA cations orientation: (a) (100), (b) (110), (c) (111); (d–f) FA0.875Cs0.125PbI3 with different FA cations orientation: (d) (100), (e) (110), (f) (111).

Full size image

From Fig. 4, we can see that the band gap of FAPbI3 increases from (100) to (110) and to (111) direction, while the band gap of FA0.875Cs0.125PbI3 decreases first and then increases. In both models, the band gap in the (110) direction changes from direct to indirect. We propose that the reasons for these phenomena may be as follows: (1) the distortion of PbI6 octahedron; (2) the addition of cesium atom; (3) the dispersive force between the organic cations and the inorganic framework.

First and foremost, the lattice contraction is affected by the A-site cation radius. If the perovskite lattice contracts, the band gap will increase. That’s why the band gap of FA0.875Cs0.125PbI3 will increase from 1.3547 eV of FAPbI3 to 1.4802 eV in (100) direction. Moreover, metal-halide orbital overlap is a σ* interaction, decreasing the Pb–I–Pb bond angle will reduce the degree of overlap between the metal and halide orbitals40. The result is that when cesium substitution increases, the valence band moves to a slightly lower energy (see in Fig. 5; Table S1), thereby widening the band gap. This phenomenon is consistent with the Cs-doped experiment3,35,36.

Secondly, the tilt of the PbI6 octahedron can change the spatial distribution and overlap of electron orbits, and this tilting effect depends on the electronic interaction between ions. This condition is well known as the dipole coupling effect lead by the number of 1H-1H dipolar couplings on adjacent cations41. From Table S1 and Fig. 4b,c, the band gap increases though the lattice constant contract, which can be attributed to the turning of formamidine cations from (110) to (111) direction enhances the dipole–dipole interaction and the distortion index. Meanwhile, from Table 1 and Fig. 4d–f, the smaller size of cesium and the largest distortion index increase the band gap in (100) direction. But the reorientation decreases the distortion index, leading to the reduction of band gap in (110) and (111) directions. Besides, the addition of cesium decreases the number of N–H···I hydrogen bond14,33, and this influence may enlarge in (110) and (111) directions. Hence, the band gap reduces and even is smaller than the FAPbI3 system in these two directions.

Thirdly, the dispersive force between the organic cations and the inorganic framework leads to the gap transformation from direct to indirect in (110) direction of both systems (see in Fig. 4b,e). Carlo et al.13 firstly discovered and demonstrated this change when viewing the turning of methylamine cations in MAPbI3. Then Farshad et al.16 also found this phenomenon in FAPbI3. Besides, the static effects, such as Rashba splitting in the conduction band may play an effective role in VBM42. At our work, we also observed 10 meV and 25 meV departure of VBM in (110) direction of FAPbI3 and FA0.875Cs0.125PbI3. This change may have a potential impact on the transport and recombination of carriers.

From Fig. 5, we can see that the orientation of formamidine cations not only affect the band gap, but also turn the VBM, CBM and Fermi energy. They are rising first and then falling in general and the trend is accordant in both systems. Recently, band gap engineering is popular40,43,44. Researchers achieved high efficiency by turning perovskite band gap alignment with ETL or HTL layer. If we can control the band gap by turning the intrinsic organic cation, it’s a new idea to achieve higher carrier mobility, Jsc, Voc and efficiency.

As is well-known that the CBM is mainly contributed by the electrons of the Pb 6p orbitals, and the VBM mainly is contributed by the electrons of I 5p orbitals. From the PDOS result in Fig. 6, we indeed find that the frontier orbitals are composed of Pb atom and I atom.

In addition, the difference between energy state below and above the Fermi energy means the bang gap, and it’s consistent with the result of band gap in Fig. 4. Besides, comparing Fig. 6a–c and Fig. 6d–f, the addition of cesium atom makes the total DOS distribution more localized around the Fermi energy, which enhances ionic interaction though the electrons of cesium do not distribute in frontier orbitals (Fig. 6d–f). This is thought that the addition of cesium makes perovskite structure more stable8. Moreover, the turning of orientation from (100) to (111) in Fig. 6a–c makes the formamidine density of state in about 3 eV deep conduction band stronger. This condition is the same with Cs-doped system. This confirms the interaction between formamidine and PbI6 framework. Compared with the same direction of FAPbI3 and FA0.875Cs0.125PbI3, cesium atom exists in deeper conduction bands, and the energy state distribution is deep than 5 eV. Cesium ion exhibits strong ionization and this may contribute to other atoms’ charge distribution in space and the stability of the structure.

Optical properties

With the special electronic structure, FAPbI3 also has fantastic ability of optical absorption in the visible range used in solar cell and light emitting diode. Many features of FAPbI3, such as excellent stability under high humidity, sharper absorption edge, high charge mobility and low exciton binding energy can be attributed to the high dielectric constant of the material45. The coupling effect of organic cation orientation and the substitution of cesium can also be observed in optical properties. The reorientation of the organic cation and the addition of cesium with their correlated dipole moment dedicates to the dielectric response and throw a crystal field to formamidine based perovskite7. To study the role of organic cation with cesium atom, we calculated dielectric function in Fig. 7 and absorption spectrum in Fig. 8 for FAPbI3 and FA0.875Cs0.125PbI3 in (100), (110) and (111) direction.

Figure 7
figure 7

The real and imaginary part of dielectric function of (a) FAPbI3 and (b) FA0.875Cs0.125PbI3 with different FA cations orientation.

Full size image
Figure 8
figure 8

Optical adsorption spectrum of perovskite structures of (a) FAPbI3 and (b) FA0.875Cs0.125PbI3 with different FA cations orientation.

Full size image

Figure 7 shows the real and imaginary part of dielectric function. Generally speaking, the real part of dielectric function represents static dielectric constant at E = 0, which is calculated to be 6.50, 6.68 and 6.49 for FAPbI3 and 6.29, 6.63 and 6.43 for FA0.875Cs0.125PbI3 in (100), (110) and (111) direction (inset zoomed pictures of Fig. 7; Table S2). It’s obviously that the rotation of formamidine cations change the static dielectric constant in different orientation, and the entrance of cesium contracts the value of static dielectric constant compared with FAPbI3. This transformation definitely influences the optical properties like absorption in Fig. 8. The dashed curves in Fig. 7a,b display imaginary part of dielectric function. And it’s well known that the first peak represents as the direct optical transition, which is also called optical gap7. It can be seen in Fig. 7a that the rotation of formamidine cations from (100) to (111) leads to a blue shift in FAPbI3. But a red shift occurs when formamidine cations rotate from (100) to (111) in FA0.875Cs0.125PbI3. This is as well as the trends of band gap and absorption spectrum.

From Fig. 8, the inset zoomed pictures show band edge absorption condition, which has a strong correlation with band gap. All of these same trends prove the orientation of formamidine cations and the addition of cesium exist coupling effect. Besides, the after peak sometimes is thought as the exciton emission peak in quantum dot perovskite46.

Hence, the coupling effect of organic cation orientation and the substitution of cesium makes the optical performance of the mixed cation halide perovskite tunable. This is a crucial and promising method for manufacturing light-absorbing devices with variable intrinsic properties.

Conclusions

Today, the efficiency and stability of formamidine based perovskite materials have been rapidly improved, but there are still many unsolved mysteries in the theories used to explain its advantages over other materials. Our work suggests that the size of PbI6 octahedron, lattice constant, charge distribution, band gap, density of state and absorption spectrum are inseparable from the orientation of organic cations and its coupling with cesium atom.

To be more specific, when the cation rotates from (100) to (110) and then to (111), the lattice constant and distortion index of FA and FA/Cs systems both decrease first and then increase. Although the minimum point is the same, the distortion index of the (111) plane in the FA/Cs system is abnormally smaller than the FA system due to the interaction between FA orientation and Cs. These results are due to the orientation of cations and the addition of cesium atom, which change the forces between ions in the crystal lattice, such as van der Waals forces and N–H···I hydrogen bonds.

In regard to electronic and optical properties, the different orientations of FA lead to changes in the band gap. Particularly, in the (110) direction, the band gap of the formamidine based perovskite becomes indirect. The addition of Cs also changes the band gap. We summarize the reasons into the following three points: (1) the distortion of PbI6 octahedron; (2) the addition of cesium atom; (3) the dispersive force between the organic cations and the inorganic framework. Moreover, the orientation of FA changes the distribution of electrons in the frontal orbit, while the addition of Cs makes it more localized and concentrated near the band gap. Furthermore, the orientation of FA changes the energy level of CBM, VBM and Fermi energy, which can provide a new idea for the experiment of band gap adjustment and alignment. Eventually, the orientation of FA and the doping of Cs also change the dielectric constant and the peak of the optical absorption spectrum.

Overall, this work starts from the formamidine rotation and its interaction with cesium atom. We demonstrate a possible way to engineer lattice constant, band gap, density of state and absorption spectrum, which is a prerequisite for controllable variable high-efficiency optoelectronic device.