Introduction

Recently, micro/nano-electromechanical systems (M/NEMS) have attracted numerous attentions due to their ultra-small dimensions, favorable mechanical and electrical properties, and low power consumptions. These tiny structures represent the most promising contenders in numerous micro/nano-based applications in several fields. As a result, modelling and analysis of pull-in characteristics in the micro-scale have found significant industrial applications. However, as the pull-in instability restricts the operational range of tiny devices, obtaining system characteristics becomes important in numerous micro/nano-structures1,2,3,4,5,6,7,8,9,10,11.

In general, classical theories are not able to model the real behaviors of electromechanical systems in the nano-scale. That is because several effects, especially intermolecular interactions play significant roles in the submicron-scale. To predict the accurate response of different NEMS structures, several theoretical models have been developed and modified. For example, electric fringing-fields corrections (FFC)12,13, dispersion forces (Casimir and vdW)14,15, size-dependent theories (couple stress (CST), strain gradient (SGT), and so on)16,17, and surface layer elasticity models18,19 have been taken into account so far. Each of these models and theories has special applications based on the miniature system properties and circumstances. It has been demonstrated that without taking the fringing corrections and dispersion effects into account, the structure will behave harder14,20,21. As a result, the predicted NEMS responses may not be accurate enough. Moreover, the impacts of size-dependency and surface layer energy can be a hardening or softening factor at different conditions in submicron structures21,22,23. The role of all these effects on the behavior and stability of nano-systems will be considered and discussed by a set of parametric studies in this paper.

In order to be able to overcome the problems of conducting conscientious experimental examinations, researchers have been competing to improve the modelling tools capable of predicting the behavior of different types of NEMS. One of the most important issues is the electrostatic force, which acts an essential role in the pull-in instability of micro/nano-systems. On the other hand, it has been demonstrated that the electric FFC is an effective nonlinearity in investigating actuated small-scale systems24,25. Recently, the impacts of FFC on the response of several fully-clamped nano-beams have extensively been examined20. Ouakad20 found that FFC should be taken into account because this consideration improves the prediction of the critical voltage for the snap-through, and the overall behavior of arch nano-systems. Moreover, the experimental validation demonstrates that the fringing correction in nano-devices acts a key role that should be considered in the modelling.

Thermal sensitive nano-electromechanical manipulators have numerous industrial applications. Rokni and Lu26 studied the behavior of fully-clamped multi-layer nano-ribbons subjected to electric and Casimir forces at different temperatures without considering the size parameter. The stability of fully-clamped miniature beams under thermal, molecular and electromechanical effects was examined27 without modelling the surface energy. The static pull-in instability of a thermal nano-cantilever piezowire under vdW attraction was examined by SoltanRezaee and Ghazavi28 while the frequency analysis and investigation of different electric fringing-fields corrections were not carried out. Pradiptya and Ouakad29 investigated the size-dependent dynamic response of fixed-fixed carbon nano-tubes subjected to DC and AC fields by considering thermal effects using SGT. The impacts of Poisson’s ratio on structural behaviors of a nano-wire by considering high-temperature variations were studied using CST30. Recently, Tavakolian et al.31 analyzed the dynamic stability of size-dependent nano-cantilevers under electro-thermal actuation without taking the surface layer effects into account. It is worth noting that the pull-in parameters of clamped-clamped smart MEMS were extensively studied32,33,34; however, with numerous practical applications of micro-beams with the sliding end35,36, they have been less attentive. Overall, it can be concluded that temperature variation affects the instability considerably that should be taken into account.

In this research, the coupled contributions of molecular forces, surface layer energy, size-dependency, piezoelectricity, FFC, thermal expansion, and geometrical nonlinearity on the pull-in characteristics using modified CST and SGT are considered for the first time. All the mentioned parameters represent key roles in piezoNEMS and it is remarkable to account their effects on both static and dynamic results of nano-bridges simultaneously to develop an accurate model. The equilibrium differential equations are derived using the extended Hamilton’s principle and Galerkin decomposition is implemented to discretize the nonlinear equations. To improve the accuracy of the solution by consuming the lowest computations, the number of mode shapes and the size of voltage increments are optimized. Herein, free vibrations of the nano-beam incorporating influences of different system parameters are analyzed. Determining the critical voltage of thermomechanical piezoelectric nano-systems is the principal objective of this paper. This adjustable thermomechanical model is able to control the stability conditions at different temperatures. The results are expected to be instrumental in the analysis, design, and operation of several NEMS.

Theoretical Model

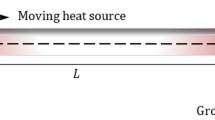
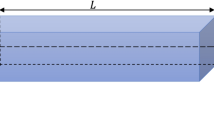
The schematic of a piezoelectric nano-beam fabricated from a movable rectangular arm and a stationary plate as the substrate is represented in Fig. 1. The deformable electrode deflects toward the substrate due to the attractions of Casimir and electric forces. Furthermore, the piezobeam is actuated by the direct current VP as the polarization voltage, which is applied along the thickness of the nano-beam and leads to a load in the longitudinal direction33. Such a configuration as an adjustable system is useful in several nano-bridges, tunable filters, thermal gates, cooling devices, and variable switches31,35,36. In this case, the boundary conditions (BCs) of the structure are such that the beam does not tolerate any traction along its neutral axis. There is not any rotation or vertical displacement at the right end.

Figure 1
figure 1

Schematic of a piezoelectric controllable nano-system with fixed-sliding boundary conditions under Casimir and electrostatic effects.

Full size image

Strain, potential, and kinetic energy

Based on the thermo-elasticity mechanics, the strain energy of a thermo-sensitive beam Ut is

$${U}_{t}=-\,\frac{EA\Delta T}{2}{\alpha }_{t}{\int }_{0}^{L}{(\frac{\partial w(x,t)}{\partial x})}^{2}dx,$$
(1)

where A, E, ΔΤ, and αt are the rectangular cross-sectional area, bulk Young’s modulus of the beam or modulus of elasticity, temperature variation, and thermal expansion coefficient, respectively. Furthermore, w is the beam displacement along z coordinate axis.

It should be mentioned that all the symbols used in this work are defined in the Nomenclature. The nonlinear curvature effect should be considered when the deformable beam undergoes distortion due to the external force. Therefore, we obtain the strain as

$${\xi }_{xx}(x,t)=\frac{ds-dx}{dx},$$
(2)

where s and ξxx are the actual length arched beam during deflection and beam axial strain at its neutral axis, respectively.

It should be mentioned that the energy of the linear spring can be given as

$${U}_{k}=\frac{1}{2}{K}_{s}{u}^{2}(x,t),$$
(3)

where Uk, Ks, and u are the spring potential energy, beam displacement along x coordinate axis, and linked spring stiffness, respectively.

The nonlinear curvature ζ is stated as37

$$\zeta (x,t)=\frac{d\theta }{ds},$$
(4)

where θ is the angle of arched element.

By taking the nonlinear curvature of the piezobeam into account, both of axial strain εxx and stress σxx can be expressed as19,38

$${\varepsilon }_{xx}(x,t)={\xi }_{xx}(x,t)-z\zeta (x,t);\,{\rm{all}}\,{\rm{other}}\,{\varepsilon }_{ij}=0,$$
(5)
$${\sigma }_{xx}(x,t)=E{\varepsilon }_{xx}(x,t)-{e}_{31}{E}_{z};\,{\rm{all}}\,{\rm{other}}\,{\sigma }_{ij}=0,$$
(6)

where e31 is the transversal piezoelectric coefficient (−6.4 C.m−2).

To model the electrostatic response of the piezobeam, the energy of the piezobeam Up is stated as38

$${U}_{P}=-\,{e}_{31}\frac{{V}_{P}}{h}\frac{A}{2}{\int }_{0}^{L}{(\frac{\partial w}{\partial x})}^{2}dx,$$
(7)

where h, L, and VP are the beam thickness, beam length, and the piezovoltage between top and bottom surfaces, respectively.

Moreover, the moment of the nano-beam by considering bulk and surface layer is expressed as

$$M={\int }_{A}{\sigma }_{xx}zdz+{\int }_{S}({\tau }_{0}+{E}^{s}{\varepsilon }_{xx}^{s})zdz=-\,\zeta (x,t)(\frac{Eb{h}^{3}}{12}+\frac{{E}^{s}b{h}^{2}}{2}+\frac{{E}^{s}{h}^{3}}{6}),$$
(8)

where b, Es, τ0, and εxxs are the beam width, surface Young’s modulus around the beam, surface strain around the beam (beam surface layer strain), and residual stress of the beam surface area, respectively.

Therefore, the energy of the nano-beam is derived as

$${U}_{m}=\frac{{E}_{eff}{I}_{eff}}{2}{\int }_{0}^{L}{\zeta }^{2}(x,t)dx,$$
(9)

where Um and Eeff Ieff are the mechanical strain energy and effective Young’s modulus and second moment of area of beam (bulk and surface layer), respectively.

The energy due to the surface layer tension Us is obtained as

$${U}_{s}={\tau }_{0}b{\int }_{0}^{L}\zeta (x,t)w(x,t)\,dx$$
(10)

Due to the nonclassical modified couple stress theory (MCST), the energy of a beam in the submicron-scale is given by17

$${U}_{l,{\rm{MCS}}}=\frac{bhE{\ell }^{2}}{4(1+\nu )}{\int }_{0}^{L}{(\frac{{\partial }^{2}w(x,t)}{{\partial }^{2}x})}^{2}dx,$$
(11)

where Ul, ℓ, and ν are the strain energy due to material size, material nano-scale factor or size-dependent parameter according to MCST, and Poisson’s ratio, respectively.

According to another nonclassical SGT17, the energy of a nano-beam is39

$${U}_{l,{\rm{SG}}}={\int }_{0}^{L}[\begin{array}{c}\frac{bhE}{4(1+\nu )}(2{l}_{0}^{2}+\frac{8{l}_{1}^{2}}{15}+{l}_{2}^{2}){(\frac{{\partial }^{2}w(x,t)}{\partial {x}^{2}})}^{2}\\ \,+\,\frac{b{h}^{3}E}{48(1+\nu )}(2{l}_{0}^{2}+0.8{l}_{1}^{2}){(\frac{{\partial }^{3}w(x,t)}{\partial {x}^{3}})}^{2}\end{array}]dx,$$
(12)

where ℓi (i = 0, 1, 2) are the additional length parameters (dilatation, deviatoric stretch, and rotation gradients).

Furthermore, the kinetic energy of the beam is

$${E}_{k}=\frac{1}{2}{\int }_{0}^{L}\rho A{(\frac{\partial w(x,t)}{\partial t})}^{2}dx,$$
(13)

where ρ is the beam density.

External work

In general, the work carried out by possible attractions can be given by

$${W}_{ext}={\int }_{0}^{L}{F}_{ext}w(x,t)dx,$$
(14)

where Wext and Fext are the external work and distributed external force (per unit length), respectively.

Considering two parallel plates (moveable electrode and substrate) without considering FFC, the electric attraction can be estimated as12,25

$${F}_{els}=\frac{{\varepsilon }_{0}b{V}^{2}}{2{(G-w(x,t))}^{2}},$$
(15)

where G, V, and ε0 are the initial separation or gap, external applied DC voltage or electric potential difference, and electrical permittivity constant of free space vacuum (8.854 × 10−12 F.m−1), respectively.

Although, Parallel-Plates (PP) model for electric force is the most common configuration in numerous applications; NEMS designers are turning the focus to the electric FFC. In order to complement this effect, different corrections can be suggested to the pure electric expression. Taking into account the simplest as well as the most extensively used FFC in the literature, which is known as Palmer’s (PM) model, the electrostatic attraction can be given by12

$${F}_{els,PM}=\frac{{\varepsilon }_{0}b{V}^{2}}{2{(G-w(x,t))}^{2}}+\frac{0.65{\varepsilon }_{0}{V}^{2}}{2(G-w(x,t))}.$$
(16)

In addition, Mejis-Fokkema (MF) model is another famous one, which can adjust the electrostatic force as follows13:

$${F}_{els,MF}=\frac{{\varepsilon }_{0}b{V}^{2}}{2{(G-w(x,t))}^{2}}(1+0.265{(\frac{G-w(x,t)}{b})}^{0.75}+0.53\frac{h}{b}{(\frac{G-w(x,t)}{b})}^{0.5}),$$
(17)

where the effects of both beam width and thickness have been reflected.

On the other hand, Casimir regime is important in nano-devices, which can be disregarded beyond this scale. Casimir force is given by40

$${F}_{cas}=\frac{{\pi }^{2}bc{h}_{p}}{240{(G-w(x,t))}^{4}},$$
(18)

where c and hp are the light speed (2.9979 × 108 m.s−1) and reduced Planck’s constant (1.055 × 10−34 J.s), respectively.

The studied nano-manipulator is under both Casimir Fcas and electric Fels forces by considering FFC, so the performed work by the mentioned forces is given by

$${W}_{ext}={\int }_{0}^{L}({\int }_{0}^{w}(\{\begin{array}{c}{F}_{els}\\ {F}_{els,PP}\\ {F}_{els,MF}\end{array}+{F}_{cas})dw(x,t))dx.$$
(19)

Governing equations according to MCST and SGT

To derive the nonlinear EOM of the presented nano-manipulator, the well-known extended Hamilton’s principle41 is applied as

$$\delta {\int }_{0}^{t}({U}_{t}+{U}_{k}+{U}_{p}+{U}_{m}+{U}_{s}+{U}_{l}-{E}_{k}-{W}_{ext})dt=0.$$
(20)

By replacing the potential, kinetic, and strain energy plus the performed work by other (corrected electrostatic as well as Casimir) forces considering the related supplementary relations into Eq. (20), using the variational approach, the following PDE for the piezoelectric size-dependent nano-beam can be obtained

$$\begin{array}{c}\{\begin{array}{c}\frac{bhE}{2(1+\nu )}{\ell }^{2}\frac{{{\rm{\partial }}}^{4}w}{{\rm{\partial }}{x}^{4}}(forMCST)\\ \frac{b{h}^{3}E}{24(1+\nu )}(2{l}_{0}^{2}+\frac{8{l}_{1}^{2}}{10})\frac{{d}^{6}w}{d{x}^{6}}+\frac{bhE}{2(1+\nu )}(2{l}_{0}^{2}+8{l}_{1}^{2}/15+{l}_{2}^{2})\frac{{{\rm{\partial }}}^{4}w}{{\rm{\partial }}{x}^{4}}(forSGT)\end{array}\\ +\,(E\frac{b{h}^{3}}{12}+{E}_{s}(\frac{b{h}^{2}}{2}+\frac{{h}^{3}}{6}))[\frac{{{\rm{\partial }}}^{4}w}{{\rm{\partial }}{x}^{4}}+\frac{{\rm{\partial }}}{{\rm{\partial }}x}(\frac{{\rm{\partial }}w}{{\rm{\partial }}x}\frac{{\rm{\partial }}}{{\rm{\partial }}x}(\frac{{{\rm{\partial }}}^{2}w}{{\rm{\partial }}{x}^{2}}\frac{{\rm{\partial }}w}{{\rm{\partial }}x}))]-b{\tau }_{0}\frac{{{\rm{\partial }}}^{2}w}{{\rm{\partial }}{x}^{2}}(4+{(\frac{{\rm{\partial }}w}{{\rm{\partial }}x})}^{2})\\ +\,(Ebh\varDelta T{\alpha }_{T}+{e}_{31}{V}_{{\rm{P}}}b-sign(\theta )\frac{{K}_{s}}{2}{\int }_{0}^{L}{(\frac{{\rm{\partial }}w}{{\rm{\partial }}x})}^{2}dx)\frac{{{\rm{\partial }}}^{2}w}{{\rm{\partial }}{x}^{2}}+\rho bh\frac{{{\rm{\partial }}}^{2}w}{{\rm{\partial }}{t}^{2}}={F}_{ext}.\end{array}$$
(21)

The boundary conditions (BC) of the considered system are

$$w(0)=w(L)=0,dw(0)/dx=dw(L)/dx=0.$$
(22)

The mentioned BC are not sufficient for the strain gradient model. Accordingly, they are written as

$$\begin{array}{c}w(0)=w(L)=0,dw(0)/dx=dw(L)/dx=0,\\ {d}^{2}w(0)/d{x}^{2}={d}^{2}w(L)/d{x}^{2}=0,OR\,{d}^{3}w(0)/d{x}^{3}={d}^{3}w(L)/d{x}^{3}=0.\end{array}$$
(23)

For the sake of the scalability of the problem, the nonlinear equations of motion are considered in the dimensionless form as

$$\begin{array}{c}\chi =\frac{x}{L},\,\varpi =\frac{w}{G},\,\tau =\frac{ht}{2{L}^{2}}\sqrt{\frac{E}{3\rho }},\,\phi =\frac{G}{b},\,\xi =\frac{{G}^{2}}{{L}^{2}},\,\beta =\frac{{L}^{2}}{{h}^{2}},\,\eta =\frac{2{E}^{s}}{E}(\frac{3}{h}+\frac{1}{b}),\\ \iota =\frac{6{\ell }^{2}}{(1+\nu ){h}^{2}},\,{\iota }_{0}=\frac{{l}_{0}^{2}}{(1+\nu ){L}^{2}},\,{\iota }_{1}=\frac{0.4{l}_{1}^{2}}{(1+\nu ){L}^{2}},\,{\iota }_{2}=\frac{6{l}_{2}^{2}}{(1+\nu ){h}^{2}},\,\lambda =\frac{48{\tau }_{0}{L}^{2}}{E{h}^{3}},\\ \vartheta =\frac{12{L}^{2}\varDelta T{\alpha }_{T}}{{h}^{2}},\,\varUpsilon =\frac{12{L}^{2}{e}_{31}{V}_{{\rm{P}}}}{E{h}^{3}},\,{c}_{cas}=\frac{{\pi }^{2}{h}_{p}c{L}^{4}}{20{h}^{3}{G}^{5}E},\\ \kappa =sign(\varDelta T)\frac{6L{G}^{2}{K}_{s}}{Eb{h}^{3}}{\int }_{0}^{L}{(\frac{\partial \varpi }{\partial \chi })}^{2}d\chi ,\,\upsilon =\frac{V{L}^{2}}{hG}\sqrt{\frac{6{\varepsilon }_{0}}{hGE}},\end{array}$$
(24)

χ: dimensionless length according to beam length (x/L); ϖ: dimensionless beam midpoint displacement (w/G); τ: dimensionless time; ϕ: ratio of initial gap to beam width (G/b); ξ: square ratio of initial gap to beam length; β: square ratio of beam length to thickness; η: surface elasticity dimensionless parameter; ι: material size dimensionless parameter according to MCST; ιi (i = 0, 1, 2): length dimensionless parameters according to SGT; λ: residual surface-induces normal stress dimensionless parameter; ϑ: thermal expansion dimensionless parameter; ϒ: piezoelectric voltage dimensionless parameter; ccas: Casimir dimensionless coefficient; κ: dimensionless spring coefficient; υ: dimensionless voltage.

Substituting the dimensionless terms Eq. (24) into Eq. (21), the equations of motion are derived from the equilibrium equation as

$$\begin{array}{c}\{\begin{array}{c}\iota \frac{{\partial }^{4}\varpi }{\partial {\chi }^{4}}\\ ({\iota }_{0}+{\iota }_{1})\frac{{\partial }^{6}\varpi }{\partial {\chi }^{6}}+(12{\iota }_{0}\beta +8{\iota }_{1}\beta +{\iota }_{2})\frac{{\partial }^{4}\varpi }{\partial {\chi }^{4}}\end{array}+(1+\eta )\frac{{\partial }^{4}\varpi }{\partial {\chi }^{4}}\\ +\,(\vartheta +\varUpsilon -\kappa -4\lambda )\frac{{\partial }^{2}\varpi }{\partial {\chi }^{2}}+\xi ((1+\eta )[\frac{\partial }{\partial \chi }(\frac{\partial \varpi }{\partial \chi }\frac{\partial }{\partial \chi }(\frac{{\partial }^{2}\varpi }{\partial {\chi }^{2}}\frac{\partial \varpi }{\partial \chi }))]-\lambda {(\frac{\partial \varpi }{\partial \chi })}^{2}\frac{{\partial }^{2}\varpi }{\partial {\chi }^{2}})\\ +\,\frac{{\partial }^{2}\varpi }{\partial {\tau }^{2}}=\frac{{\upsilon }^{2}}{{(1-\varpi )}^{2}}\{\begin{array}{c}1\\ 1+0.65\phi (1-\varpi )\\ 1+0.265{(\phi (1-\varpi ))}^{0.75}+0.53\sqrt{\xi /\beta }{\phi }^{1.5}{(1-\varpi )}^{0.5}\end{array}+\frac{{c}_{cas}}{{(1-\varpi )}^{4}}.\end{array}$$
(25)

Solution Methodology

In general, analytical techniques are not able to solve the nonlinear differential equations of excited thermal piezo NEMS. For that reason, the governing equation of motion is better to be linearized and solved by numerical methods. In this research, a computational method called SSLM is expended to estimate threshold characteristics. In the following, the term ϖ will be considered as a linear combination of a number of modes or a set of basic functions, which are defined independently from each other. In this condition, the approximate solution of the studied structure will be constructed as

$$\varpi ={A}^{{\rm{T}}}\varphi =\mathop{\sum }\limits_{i=1}^{N}{A}_{i}{\varsigma }_{i}(\chi ),$$
(26)

where Αi is the amplitude factor of the beam transverse displacement and φ is the non-normalized system mode shapes vector includes a set of harmonic functions ςi, e.g. as following for MCST case42

$${\varsigma }_{i}={B}_{i}((\sin ({\delta }_{i}\chi )-\,\sinh ({\delta }_{i}\chi ))\frac{\cosh \,{\delta }_{i}-\,\cos \,{\delta }_{i}}{\sinh \,{\delta }_{i}-\,\sin \,{\delta }_{i}}+\,\cosh ({\delta }_{i}\chi )-\,\cos ({\delta }_{i}\chi )),$$
(27)

where terms Bi signifies the displacement scaling and the values δi are the characteristic equation roots. For SGT also different solutions have been presented in several papers39,43.

Having the Eq. (27) and replacing the Eq. (26) into (25), multiplying both sides by φ(χ), ultimately the governing equation is converted as

$$n=m\ddot{B}+\{\begin{array}{c}\iota {K}_{1}B\\ (({\iota }_{0}+{\iota }_{1}){K}_{0}+(12{\iota }_{0}\beta +8{\iota }_{1}\beta +{\iota }_{2}){K}_{1})B\end{array}+(\begin{array}{c}(1+\eta ){K}_{1}+(\vartheta +{\Upsilon }-\kappa -4\lambda ){K}_{3}\\ \,+\,\xi (2(1+\eta ){K}_{2}-\lambda {K}_{4})\end{array})B,$$
(28)

where beam stiffness expressions Ki (i = 0, 1, 2, 3, 4) and the beam inertia expression m are obtained as

$$\begin{array}{c}{K}_{0}={\int }_{0}^{1}\frac{{\partial }^{3}\varphi }{\partial {\chi }^{3}}\frac{{\partial }^{3}{\varphi }^{T}}{\partial {\chi }^{3}}d\chi ,\,{K}_{1}={\int }_{0}^{1}\frac{{\partial }^{2}\varphi }{\partial {\chi }^{2}}\frac{{\partial }^{2}{\varphi }^{T}}{\partial {\chi }^{2}}d\chi ,\,{K}_{2}={\int }_{0}^{1}\frac{\partial \varphi }{\partial \chi }\frac{{\partial }^{2}{\varphi }^{T}}{\partial {\chi }^{2}}B\frac{\partial {\varphi }^{T}}{\partial \chi }B\frac{{\partial }^{2}{\varphi }^{T}}{\partial {\chi }^{2}}d\chi ,\\ {K}_{3}={\int }_{0}^{1}\varphi \frac{{\partial }^{2}{\varphi }^{T}}{\partial {\chi }^{2}}d\chi ,\,{K}_{4}={\int }_{0}^{1}\varphi \frac{\partial {\varphi }^{T}}{\partial \chi }B{B}^{T}\frac{\partial \varphi }{\partial \chi }\frac{{\partial }^{2}\varphi }{\partial {\chi }^{2}}d\chi ,\,m={\int }_{0}^{1}\varphi {\varphi }^{T}d\chi ,\end{array}$$
(29)

and

$$n={\int }_{0}^{1}(\frac{{\upsilon }^{2}}{{(1-B\varphi )}^{2}}\{\begin{array}{c}1\\ 1+0.65\phi (1-B\varphi )\\ 1+0.265{(\phi (1-B\varphi ))}^{0.75}+0.53\sqrt{\xi /\beta }{\phi }^{1.5}{(1-B\varphi )}^{0.5}\end{array}+\frac{{c}_{cas}}{{(1-B\varphi )}^{4}})\varphi d\chi .$$
(30)

Having the Eq. (28), the total stiffness of the nano-beam is expressed as

$$\begin{array}{c}K=\{\begin{array}{c}\iota {K}_{1}\\ ({\iota }_{0}+{\iota }_{1}){K}_{0}+(12{\iota }_{0}\beta +8{\iota }_{1}\beta +{\iota }_{2}){K}_{1}\end{array}+(1+\eta ){K}_{1}\\ \,+\,6\xi (1+\eta ){K}_{2}+(\vartheta +\varUpsilon -\kappa -4\lambda ){K}_{3}-3\xi \lambda {K}_{4}-dn(B)/dB,\end{array}$$
(31)

where

$$\frac{dn(B)}{dB}={\int }_{0}^{1}(\frac{2{\upsilon }^{2}}{{(1-B\varphi )}^{3}}\{\begin{array}{c}1\\ 1+0.325\phi (1-B\varphi )\\ 1+\frac{0.1656{\phi }^{0.75}}{{(1-B\varphi )}^{-0.75}}+\frac{0.3975\sqrt{\xi /\beta }{\phi }^{1.5}}{{(1-B\varphi )}^{-0.5}}\end{array}+\frac{4{c}_{cas}}{{(1-B\varphi )}^{5}})\,{\varphi }^{2}d\chi .$$
(32)

The static analysis

In actuated electromechanical systems, the movable arm cannot tolerate any external voltage. In this case, the response of nano-devices is achievable by considering Eq. (33) as

$$(\{\begin{array}{c}\iota {K}_{1}\\ ({\iota }_{0}+{\iota }_{1}){K}_{0}+(12{\iota }_{0}\beta +8{\iota }_{1}\beta +{\iota }_{2}){K}_{1}\end{array}+(\begin{array}{c}(1+\eta ){K}_{1}+(\vartheta +\varUpsilon -\kappa -4\lambda ){K}_{3}\\ \,+\,\xi (2(1+\eta ){K}_{2}-\lambda {K}_{4})\end{array}))B=n.$$
(33)

At the unstable conditions, the system stiffness will become singular or det(K) equals zero when the instability happens44. This method prepares a useful and practical way of computing the instability condition of the structures.

The nonlinear motion equations are solved numerically. In this research work, SSLM is employed45, and instability characteristics will be determined. Because of the nonlinear treatment of considered nano-beam, linearizing initial states may be a source of errors. To minimize the possible errors, SSLM is considered to increase the external electrostatic actuation slightly. Due to sufficient small increments of the external actuation, the beam deflection will also increase slightly. As a result, we will be able to model the nonlinear behavior of the thermal nano-switch accurately. Moreover, by accounting Taylor’s expansions, accuracy necessities are obtained. Considering Eq. (33), the equation of equilibrium at the ith step is derived as

$$(\{\begin{array}{c}\iota {K}_{1}^{i}\\ ({\iota }_{0}+{\iota }_{1}){K}_{0}^{i}+(12{\iota }_{0}\beta +8{\iota }_{1}\beta +{\iota }_{2}){K}_{1}^{i}\end{array}+(\begin{array}{c}(1+\eta ){K}_{1}^{i}+(\vartheta +\varUpsilon -\kappa -4\lambda ){K}_{3}^{i}\\ \,+\,\xi (2(1+\eta ){K}_{2}^{i}-\lambda {K}_{4}^{i})\end{array}))B={n}^{i}.$$
(34)

As an example, the term ni is achieved from Eq. (30) as

$${n}^{i}={\int }_{0}^{1}(\frac{{({\upsilon }^{i})}^{2}}{{(1-B{\varphi }^{i})}^{2}}\{\begin{array}{c}1\\ 1+0.65\phi (1-B{\varphi }^{i})\\ 1+\frac{0.265{\phi }^{0.75}}{{(1-B{\varphi }^{i})}^{-0.75}}+\frac{0.53\sqrt{\xi /\beta }{\phi }^{1.5}}{{(1-B{\varphi }^{i})}^{-0.5}}\end{array}+\frac{{c}_{cas}}{{(1-B{\varphi }^{i})}^{4}}){\varphi }^{i}d\chi .$$
(35)

The eigenvalue problem

To obtain the system frequencies at different voltages, the static solution can be substituted into the characteristic equation for the corresponding eigenvalues. To this end, the frequency of the structure equals zero, when the pull-in takes place. Consequently, the frequency of the manipulator can be achieved via the following equation.

$$\det \,(K-m{\omega }^{2})=0,$$
(36)

where “det” refers to the determinant operator and the terms K and m are presented in Eqs. (31) and (29), respectively. Accordingly, by considering the dynamic governing equation (Eq. (28)) as well as Eq. (36), the i-th step will be derived as

$${m}^{i}\ddot{B}+\{\begin{array}{c}\iota {K}_{1}^{i}\\ ({\iota }_{0}+{\iota }_{1}){K}_{0}^{i}+(12{\iota }_{0}\beta +8{\iota }_{1}\beta +{\iota }_{2}){K}_{1}^{i}\end{array}B+(\begin{array}{c}(1+\eta ){K}_{1}^{i}+(\vartheta +\varUpsilon -\kappa -4\lambda ){K}_{3}^{i}\\ +\xi (2(1+\eta ){K}_{2}^{i}-\lambda {K}_{4}^{i})\end{array})B={n}^{i}.$$
(37)

Results and Discussion

The taken step length of the solution procedure can meaningfully influence the accuracy of obtaining responses. Firstly, we will try to determine an appropriate length to increase the external electrostatic actuation in SSLM. For this purpose, responses of the prepared system in ref. 35 considering different voltage lengths are listed in Table 1. It can be concluded that the obtained responses will be converged by taking an adequately small step length into account.

Table 1 Convergence of system responses considering different voltage increases.
Full size table

In order to make validation, we have compared the threshold voltages with the experimental46, analytical 26, and numerical27 results reported in the literature for beams with different length (Table 2). The width and thickness of the deformable beam are 50 and 1 μm, respectively, and the initial gap is 3 μm. Furthermore, the modulus of elasticity and Poison’s ratio are 169 GPa and 0.6, respectively. As it can be seen, the results obtained from our model show a good correlation with experiments validating its high accuracy.

Table 2 Comparison of the pull-in voltage with experimental, analytical and numerical data.
Full size table

As another validation, a fixed-sliding micro-beam in the attendance of electrostatic is modeled and pull-in characteristics are obtained and compared with a micro-structure with similar BCs (Table 3). Koochi et al.35 examined a fixed-sliding micro-beam using the Modified Adomain decomposition and numerical solution as well as a lumped model, which assumes the uniform external forces along the beam. The available theoretical results, which are provided in Table 4, illustrate that the responses of the performed analysis are in an appropriate agreement with available data in the open literature.

Table 3 Comparison the obtained results with the available results35.
Full size table
Table 4 Properties and dimensions of the proposed manipulator.
Full size table

The dimensions and constants employed to model the nano-system are mentioned in Table 4. More details and explanations will be discussed in the subsequent section.

Static analysis

The relationships between the mid-beam deflections versus the voltage will be displayed in this section. Based on the figures, mid-beam deflections increase with an increase in the value of the applied voltage. In general, the actuated nano-beam is not able to endure relatively considerable voltages. Note that all reported results presented in this section (Static analysis) are according to MCST unless specified otherwise.

Figure 2 shows the static defection variation with respect to different expressions of the fringing correction when the DC voltage increases from zero. Two well-known models for FFC, which are PM and MF models in addition to the electrostatic PP model for the electric actuation, are assumed to correct the distributed electric force. It is recognized that the impacts of the FFC on the system stability are remarkable. The figures display that considering the FFC makes the electrode softer and causes the decline of instability voltages. Furthermore, it can be seen that the effects of FFC are more significant by taking MF than PM model. The obtained results completely agree with the results of clamped-clamped nano-beams for different types of electric FFC reported by Ouakad20. He found that the responses of MF model are generally in better agreement with the finite element method (FEM) and experimental data.

Figure 2
figure 2

The impacts of the electrostatic force and different fringing-fields on the system behavior.

Full size image

Figure 3 displays the deflection of the electrode, including the thermal variations and FFC (KS = 1 N/m). In this case, we consider the actuated system with (Fels,PP and Fels,MF) and without (Fels) fringing effects at the temperatures of 263 K and 283 K. It can be concluded that the effects of FFC on the stability are remarkable at different temperatures or when the system operates in thermally fluctuating conditions. The effect of the linear spring on the structural behavior should be explained with respect to the sign of the thermal expansion coefficient (Table 4). It is also seen that the nano-system becomes more stable (i.e., higher pull-in voltage is obtained) with increasing the temperature. This is due to the negative coefficient of the thermal expansion (i.e., the beam starts shrinking while heated) that causes increasing the tensile strength by applying a load in the x-direction. Moreover, the curves illustrate that an increase in the ambient temperature makes the system harder and increases the contributions of electric force corrections. It means that the effect of FFC becomes greater at higher temperatures and differences between instability voltages will increase.

Figure 3
figure 3

The impacts of the thermal force and different fringing-fields on the system behavior.

Full size image

In Fig. 4, the impact of Casimir force with (considering MF model) and without taking FFC (assuming PP model) on the system behavior are presented. Generally, the instability condition or pull-in phenomenon happens with a delay in nano-systems without considering Casimir force. In addition, when there is no electric force, the deformable electrode endures a primary displacement due to Casimir effect. On the other hand, the influence of this force on the critical applied voltage becomes more obvious in the Parallel-Plates model. Accordingly, differences between the instability voltages decrease slightly with considering electric FFC. Moreover, by using the relation \({c}_{cas}={\pi }^{2}{h}_{p}c{L}^{4}/20{h}^{3}{G}^{5}E\), it can be understood that the impact of Casimir force enhances with an increase in the nano-beam length, unlike the thickness. This also specifies that the impact of Casimir on the system behavior is more considerable for slender electrodes.

Figure 4
figure 4

The impacts of Casimir force and Mejis-Fokkema fringing-field on the system.

Full size image

Comparing the obtained graphs confirms that FFC is vital to be considered in evaluating the behavior of nano-switches. It can be computed in a relative error of almost 24–25% in predicting the instability parameters of the MEMS when neglecting this effect. Therefore, we have found reasonable agreement between the responses of this dimensionless nano-system and the numerically calculated values for arch MEMS in Ref. 20.

Figure 5 illustrates the variations of the mid-beam at different amounts of spring stiffness vs. the external voltage. Here, as the spring stiffness tends to zero, there exists no thermal force in this configuration. Therefore, the thermal effect is meaningless without considering the spring in such beams with the fixed-sliding BCs (since a fixed-sliding beam like a cantilever one is capable of moving in the longitudinal axis, the temperature variation results in changing its length and it will be free of stress). On the other hand, as the spring stiffness tends to ∞, the responses become close to those for a clamped-clamped block. The influence of spring stiffness is more considerable at lower temperatures due to the difference between the pull-in voltages of blue curves, which should be explained regarding the thermal expansion coefficient. Finally, as a practical point, it is notable that the influence of temperature variations increases while the stiffness enhances, so the difference between the pull-in voltages becomes greater in devices with doubly clamped BCs.

Figure 5
figure 5

The impacts of the thermal force and spring stiffness on the system behavior.

Full size image

Figure 6 shows the relationship between the curves and the excitation including/excluding the effects of FFC using different size theories. To investigate the impact of higher-order material size parameters, the achieved results have been compared using MCST and SGT. First, note that in this research, the higher-order bending rigidity of material is assumed 21 nm. As a result, the modified couple stress length-scale parameter is 15 nm17,47. Assuming three equal strain gradient length-scale parameters39, these parameters will be equal to 9 nm43,48. The results demonstrate that both MCST and SGT make the beam to be harder and cause an increase in the threshold voltage.

Figure 6
figure 6

The impacts of different size theories and fringing-fields on the system behavior.

Full size image

In Fig. 7, it can be found that the piezovoltage affects the system response significantly by changing the structural behavior. Based on the application, the piezovoltage can compress or stretch the beam by considering the polarity. The results show that the positive actuation increases the instability voltage by increasing the beam stiffness where the negative polarity produces a compression force in the x-direction. It is comprehended that piezoexcitations shift the equilibrium manifold and consequently the instability voltage. The results agree well with the reported ones in clamped-clamped piezobased bridges32,33.

Figure 7
figure 7

The impact of the piezoelectric voltage on the system behavior.

Full size image

The relationships between the mid-beam vs. the electrostatic excitation by considering different FFC models with both positive and negative piezoexcitation are shown in Fig. 8. It can be observed that the impact of piezoelectricity changes by taking different models to consider FFC. Generally, as the piezoelectric voltage increases, the difference between the results of FFC models becomes more considerable. Consequently, differences between the instability voltages in FFC models are increased by considering the positive piezoelectric excitation. On the other hand, differences between the results of piezovoltage will increase as the negative polarity considered.

Figure 8
figure 8

The impacts of the piezoelectric voltage and fringing-fields on the system behavior.

Full size image

It is interesting to note that by tuning the value of piezoexcitation, the bridge behavior is changeable, so the pull-in voltage is controllable. As a result, we can increase the stability range or decrease the critical voltage by taking positive or negative piezoelectric actuation. Therefore, improving the performance of several nano-switches are possible by considering piezomaterials and applying the piezovoltage as an important design parameter in numerous applications.

Dynamic analysis

Here, the vibrations of the rectangular electromechanical nano-system will be analyzed. It should be noted that for more accurate investigations of each parameter, these assumptions are taken into account unless specified otherwise (T = 273 K, λ = 0, η = 0, ι = 0, ιi = 0, VP = 0, ϕ = 0, and ccas = 0). In these cases, the system frequency decreases with an increase in the external voltage at first. After that, the system response tends to 0 promptly, when the DC voltage goes to a maximum amount (near the critical value).

Figure 9 shows the relationships between the mid-beam and the voltage parameter by considering all PP, PM, and MF models. It can be concluded, taking FFC affects pull-in characteristics more than system frequencies. In addition, the impacts of the electrostatic force corrections on the nano-system frequency become more obvious with increasing the voltage gradually. The responses for system frequencies are qualitatively agreeable by accounting numerical results of Ouakad20, including the electric fringing-fields effect (all models). Finally, note that without applying the DC voltage, there is no difference between the response frequencies with/without accounting FFC (Fig. 9). It means that the start points of curves are the same in this figure unlike other figures of dynamic behavior.

Figure 9
figure 9

The impacts of different fringing-fields on the system dynamic behavior.

Full size image

The impact of the residual tension in the surface layer on the nano-system frequency is shown in Fig. 10. It is comprehended that system frequencies and instability voltages change with variations of the tension. Here, response frequencies and critical voltages increase by considering positive surface stress. On the other hand, the values for the residual surface stress nano-materials may be negative. In this case, the results are exactly the opposite of the positive one, so considering the negative stress makes the fixed-sliding beams soften. Moreover, using the relation \(\lambda =24{\tau }_{0}{L}^{2}/E{h}^{3}\), it is recognized the influence of residual surface tension reduces with decreasing the nano-beam length and increasing the thickness. Therefore, this molecular surface effect will be more dominant in the slender nano-structures. It is necessary to mention that the effect of FFC becomes more significant by considering positive term; however, the difference between the positive and negative stress decreases, including FFC.

Figure 10
figure 10

The impacts of residual surface stress on the system dynamic behavior.

Full size image

Figure 11 displays the effect of different nonclassical size theories (MCST and SGT) on the dynamic behavior and response frequencies of the nano-beam. The curves illustrate that by considering the length-scale parameters, we have a stiffer nano-system. Therefore, both system frequencies and dynamic voltage will be increased by taking nonclassical theories into account. Moreover, differences between the results of SGT and classical theory is more considerable. Ultimately, from relations of material size parameters, it is found that the influence of size parameters becomes weak by increasing the beam thickness.

Figure 11
figure 11

The impacts of different nonclassical size theories on the system dynamic behavior.

Full size image

The obtained results of this research allow a better understanding of the instability of the nano-beam based tiny devices and can guide scientists to improve their general performance, appropriately. Moreover, the outcomes of this study explain the causes of differences obtained in the literature when comparing the responses of the nano-system without considering modified models including nonclassical theories, small-scale effects, and external force corrections to experimental data. There is still plenty of exploration to be discovered regarding the reliability of electro-thermo-mechanical nano-systems. Forthcoming investigations need to be established, including modelling the impacts of out‐of‐plane electrodes arrangement on the behavior of nano-devices with different BCs by considering both size and surface effects, which should be verified experimentally.

Conclusion

In order to investigate the pull-in phenomenon of adjustable intelligent systems, a nano-beam with a sliding end connected to spring was taken into account and a thermomechanical model was presented. In the model, the impacts of the surface layer, molecular forces, size-dependency, piezoelectricity, and temperature variations were included with consideration of the nonlinear curvature. Two famous models for the electric fringing corrections, which are PM and MF models, were assumed to correct the distributed electrostatic force. The PDEs were derived by the extended Hamilton’s principle. Galerkin decomposition was implemented to discretize the nonlinear equations. To improve the accuracy of responses by spending affordable computational calculations, the number of mode shapes and the size of voltage increments were optimized. Afterward, the structural behavior of the nano-system under Casimir and corrected electric attractions were analyzed numerically. Finally, the system vibrations with regard to the environment temperature, surface layer, and material size theories (MCST and SGT) were studied.

The obtained results reveal that the classical theory predicts lower values for instability voltages and system frequencies. It was also shown that considering the electric FFC is essential for accurate modelling of the nano-switches behavior. Moreover, the effect of MF model is more remarkable than the other one. In addition, this effect causes a significant change at higher temperatures as well as in cases of positive residual surface stress and positive piezoelectric voltage. As a practical point, the effect of temperature variation increases while the stiffness of the connected spring enhances, so differences between the critical voltage at different temperatures becomes greater in clamped-clamped beams. Finally, it should be mentioned that the piezoexcitation could be employed as a design parameter to improve the controllability and increase the performance range of adjustable smart devices.