Abstract
The interaction of a mechanical oscillator with the operation actions and environment fields will give rise to the splitting of normal modes. In this study, we investigate the normal mode splitting behaviour of a moving-particles-pumped single-span clamped-hinged elastic homogeneous beam based on the proposed multi-octave modal parametric oscillation model. Numerical experiments show the entangled and squeezed oscillations of the phase-conjugated waves near the resonance tongues. Theoretical analysis predicts the occurrence of multiple simple resonances and the squeezing of the twin waves modal oscillation in the region with a low speed of movement for the studied system.
Similar content being viewed by others
Introduction
The interaction of a mechanical oscillator with the time-varying operation actions and environment fields may give rise to twin waves entanglement and squeezing behaviours. Attached moving articles are the most general operation actions and environmental disturbances for different forms of mechanical oscillators from the nano-scale devices to the large-scale infrastructures1,2,3,4. Considering the moving inertial effect of the attached particle, structural normal mode oscillations are parametrically modulated5,6,7,8. Although the parametric modulation gives rise to normal mode splitting and twin waves oscillation behaviours that have been observed in different physical systems9,10,11,12, to the best of our knowledge based on a survey of the literature, these behaviours have not been reported for the system studied in this investigation. It appears that the classical analysis of the studied system is generally based on an implicit assumption that these twin waves behaviours are found in a squeezed form or are short-lived. However, many numerical and experimental studies on this type of system13,14,15,16 have reported colourful eccentric oscillation behaviours. Recent analytical work8,17 has shown that the moving particle pumping effect can be modelled as multi-octave parametric excitation of the structure modal oscillations. In this study, we investigate the moving-particles-pumped normal mode splitting and twin waves characteristics of a single-span clamped-hinged elastic beam around the parametric resonance tongues based on this model. Numerical experiments based on the finite element method (FEM) structure modelling are conducted.
The studied single-span structure is a clamped-hinged (CH) beam with uniform cross-section as shown in Fig. 1A. Its first two transverse vibration mode shapes are shown in Fig. 1B. Under a stream of moving particles with equal spacing distance, the governing equation of motion for the z-direction transverse vibration of the beam can be expressed as
where ρA, EI(x), L, and w(x, t) denote the mass per unit length, flexural rigidity, span length, and flexural deformation response of the supporting structure; x is the longitudinal coordinate of the supporting structure, with the origin at the left end-support of the structure; δ is the Dirac delta function; m, q i (t), v, and t i = t − (i − 1)T denote the mass, transverse displacement, travelling speed, and travelling time, respectively, of the i-th particle on the supporting structure; \(T=\frac{{l}_{{\rm{m}}}}{v}\); and lm is the spacing distance of the moving particle stream. In this study, the cases when lm = L are discussed. Considering the z-direction displacement compatibility at the instant of t for the i-th particle and the beam at the contact point of x = vt i
When the particle is light compared to the supporting structure, its inertial perturbation to beam normal modes is small. Structural vibrations can still be efficiently described using the unperturbed orthogonal basis as
where w r (t) is the response of the r-th structure modal coordinate; · denotes the differentiation with respect to time t; \(M={\int }_{{\rm{0}}}^{L}\rho Adx\); ω r are the natural frequencies of the r-th mode; and φ r is the mode shape of the r-th mode satisfying \({\int }_{{\rm{0}}}^{L}\rho A{\varphi }_{r}^{2}(x)dx=M\). Since \({\varphi }_{r}{\varphi }_{s},{\varphi }_{r}{\dot{\varphi }}_{s},{\varphi }_{r}{\ddot{\varphi }}_{s}\) are continuous periodic functions with period T that can be expressed as harmonic series, this system is essentially a coupled multi-octave modal parametric oscillation (MOMPO) system. The multi-octave parametric excitation will pump multiple parametric resonance tongues around ω ≈ 2ω r /n (r, n ∈ Z) along the frequency axis where ω = 2πv/L.
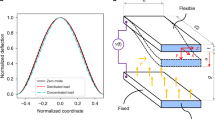
Tested structure and moving-particles-pumped amplitude modulation for the split fundamental mode around the principal resonance tongue. (A) Clamped-hinged beam-like structure transporting moving particle; (B) Mode shapes of the first two transverse flexural modes; (C) Tri-phase plots of the Floquet multiplier distribution on the μ − β plane for the studied case around the principal resonance tongues of the fundamental mode based on the MOMPO model analysis; (D) Numerically calculated amplitude-amplified-wave-dominated modal response phase trajectory (the magenta line) under w1(0) = 0, \({\dot{w}}_{1}\)(0)/ω1 = 1 and amplitude-suppressed-wave-dominated modal response phase trajectory (the azure line) under w1(0) = 1, \({\dot{w}}_{1}\)(0)/ω1 = 0 in the principal resonance of the fundamental mode when μ = 0.1 and β = 1.8 based on FEM structure modelling; (E) Numerically calculated modal response phase trajectories based on FEM structure modelling around the principal resonance tongue of the fundamental mode under initial disturbance of w1(0) = 1, \({\dot{w}}_{1}\)(0)/ω1 = 1 when μ = 0.1.
Focusing on the principal resonance tongue of the fundamental mode, the principal components of the modal oscillation around the transition curves are analysed according to the Floquet theory18 and are composed of twin modulated harmonic waves
where γ1, γ2 and Ω1ω, Ω2ω are the amplitude modulation characteristics of exponentials and modulated frequencies; A1, A2 and θ1, θ2 are the amplitudes and phase angles related to the given initial conditions as well as system characteristics. The determination of γ1, γ2 and ωΩ1, ωΩ2 is based on the numerical computation of the one-period response of the system to the unit initial displacement and velocity disturbances. If the computed one-period displacement response to the unit initial displacement disturbance is denoted as w1,1(T) and the computed one-period velocity response to the unit initial velocity disturbance is denoted as \({\dot{w}}_{1,2}\)(T), then \({\gamma }_{1},\,{\gamma }_{2}=\mathrm{Re}(\mathrm{ln}(\alpha \pm \sqrt{{\alpha }^{2}-1})/2\pi )\), \({\Omega }_{1}=\text{Im}(\mathrm{ln}(\alpha +\sqrt{{\alpha }^{2}-1})/2\pi )\), and \({\Omega }_{2}=1+\text{Im}(\mathrm{ln}(\alpha -\sqrt{{\alpha }^{2}-1})/2\pi )\), where \(\alpha =[{w}_{1,1}(T)+{\dot{w}}_{1,2}(T)]/2\).
For the system described by Eq. (1), the principal component around the resonance tongues is composed of twin modulated harmonic waves. Figure 1C presents the tri-phase and contour plots of the computed characteristics multiplier (λ1, λ2) distributions on the μ − β plane (μ = m/M, β = ω/ω1) for the twin waves of the fundamental mode around the principal resonance tongue. It can be seen that around this resonance tongue heading to β = 2.0 with an oblique angle, the amplitude modulation characteristics of exponentials (γ1, γ2) for the twin waves satisfy the conditions γ1 ≈ −γ2 for the in-resonance region and γ1 = γ2 for the out-of-resonance region. For μ = 0.1 and β = 1.8, which is found in the principal resonance tongue of the fundamental mode, the computed phase trajectories based on the FEM structure modelling (as shown in Fig. 1D) considering a stream of 50 particles passing the beam verify that the amplitude-amplified wave dominates the modal oscillation when w1(0) = 0, \({\dot{w}}_{1}\)(0)/ω1 = 1 and the amplitude-suppressed wave dominates the oscillation when w1(0) = 1, \({\dot{w}}_{1}\)(0)/ω1 = 0. To further check the oscillations near the transition curve out of the resonance tongues for μ = 0.1 and β = 1.70, 1.75, 1.85, 1.90, Fig. 1E presents the computed oscillation phase trajectories for the fundamental mode. It can be seen that in this degenerate characteristic exponential region, the twin modulated harmonics oscillation with close frequencies and similar amplitudes presents beats shape displacement and velocity oscillations.
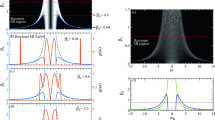
The results obtained in a detailed investigation of the frequency modulation characteristics around the principal resonance tongue for n = 1 are shown in Fig. 2. Figure 2A presents the tri-phase and the contour plots of Ω1 and Ω2 for the fundamental mode based on the MOMPO model analysis. It can be seen that Ω1 = Ω2 = n/2 for the in-resonance region and n/2 − Ω1 = Ω2 − n/2 for the out-of-resonance region. FEM structure modelling based calculated amplitude spectra of the fundamental modal displacement responses are presented in Fig. 2B. It can be seen that for the in-resonance region (μ = 0.1, β = 1.8), the two components show the same oscillation frequency and present a single peak at Ω = 0.50 in the amplitude spectrum. For the out of-the-resonance region, the oscillation amplitude spectrum peaks for the twin waves are symmetrically distributed with respect to the axis of Ω = 0.50. When β approaches 2.0, little variation is observed among the Ω1s and Ω2s computed from the MOMPO model considering the fundamental mode and from the FEM structure modelling-based numerical experiments. Considering that the 1/2 sum combination resonance tongue for modes 1 and 2 heading to β = 2.13 is placed nearby, the observed deviations are reasonable. Figure 2B also shows that among the twin waves, the modulated harmonics with the singularity red-shifted frequency in the region above the resonance tongue and the modulated harmonics with singularity blue-shifted frequency in the region below the resonance tongue dominate the modal oscillation when ω is away from the resonance tongues.
Moving-particles-pumped fundamental mode spectrum splitting of the CH beam near the principal resonance tongue. (A) Triphase and contour plots of the predicted frequency modulation characteristics distribution on the μ − β plane for clamped-hinged uniform beams carrying moving particles around the principal resonance of the fundamental mode based on MOMPO model analysis; (B) Numerically calculated amplitude spectrum based on FEM structure modelling for the fundamental mode response oscillation under a stream of 100 particles around the principal resonance tongue with initial disturbance of w1(0) = 1, \({\dot{w}}_{1}\)(0)/ω1 = 1 when μ = 0.1.
The variation trends of the twin-wave oscillation amplitudes on the μ − β plane are analysed according to the MOMPO model described by Eq. (1). Figure 3 presents the normalized oscillation amplitudes (\({\tilde{A}}_{1}\), \({\tilde{A}}_{2}\)) of the twin waves of the fundamental mode where \({\tilde{A}}_{1}=|{A}_{1}|/\sqrt{{A}_{1}^{2}+{A}_{2}^{2}}\) and \({\tilde{A}}_{2}=|{A}_{2}|/\sqrt{{A}_{1}^{2}+{A}_{2}^{2}}\), A1, A2 are the computed twin waves amplitudes. Figure 3A presents the tri-phase and contour plots of \({\tilde{A}}_{1}\) distribution on the μ−β plane. As shown, in the region below the resonance tongue, the normalized amplitude of the modulated harmonics with singularity red-shifted frequency quickly decreases from 0.99 to 0.01 along with the increase in the distance away from the resonance tongue. In the region above the resonance tongue, the plateau-shaped distribution around \({\tilde{A}}_{1}\) ≈ 0.99 demonstrates the dominance of this component in this region. Similarly, the \({\tilde{A}}_{2}\) distribution shown in Fig. 3B indicates that the modulated harmonics with the singularity blue-shifted frequency are vital in the region below the resonance tongue and are squeezed after going through the resonance tongue. The computed amplitude distribution surfaces determine the range where the modal oscillation can be approximated by single modulated harmonics.
Moving-particles-pumped twin waves normalized amplitudes around the principal resonance tongue for the fundamental mode of the CH beam based on the MOMPO model analysis. (A) Tri-phase and contour plots of the normalized amplitude of the singularity red-shifted components on the μ − β plane; (B) Tri-phase and contour plots of the normalized amplitude of the singularity blue-shifted components on the μ − β plane.
In addition to the principal resonance, the higher-order simple parametric resonances will also induce twin waves oscillation behaviours. Since these resonances are predicted to occur in the regions with low moving speed of the same scale of importance, the related parametric amplification and twin waves behaviours must be investigated. Fig. 4 presents the computed peak characteristics multipliers λ1 for the simple resonance tongues of the first two modes of the CH beams based on the multi-octave modal parametric oscillation model when μ = 0.1. It can be seen that with the increase in n, the computed λ1 s monotonically decreased to 1. Moreover, this figure also shows that the peak characteristic multipliers of the second mode are larger than those of the fundamental mode. If the resonances of the higher-order modes are excited either owing to the described auto-mode parametric modulation or owing to the cross-mode coherent coupling, important parametric amplification may occur.
In this study, we investigate the moving-particles-pumped structure normal mode splitting and twin waves oscillation for the single-span CH homogeneous beam structures. The analytical modelling of the system as a multi-octave parametric excited system predicts the occurrence of the parametric resonance when ω ≈ 2ω r /n and the twin waves oscillation characteristics around the resonance tongues. FEM-based numerical experiments show the in-resonance amplitude-modulated and out-of-resonance frequency-modulated twin waves oscillation characteristics around the principal parametric resonance tongue for the fundamental mode. Away from the parametric resonance tongues, the twin waves will be squeezed to show the classical single modulated harmonics modal oscillation. If multiple structural modes considering geometric configuration, higher dimension effects, supporting conditions, particle moving routes, and environmental disturbance patterns are important, the mode splitting and multi-wave oscillation phenomena with varying patterns around the simple and combination resonance tongues will be ubiquitous and need to be carefully discriminated.
Methods Summary
The analysis of twin waves oscillation for the system described by Eq. (1) is conducted based on the Floquet theory18. The tested CH beam-like structure was designed to be composed of steel with Young’s modulus E = 210 GPa, Poisson ratio υ = 0.3, and mass density ρ = 7800 kg/m3. The cross-section is a uniform rectangle along the x-axis with a length-height ratio L/h = 10 and a height-width ratio h/b = 10. The eigen-frequencies and mode shapes computation were conducted on an FEM model using the 12-DOFs Kirchhoff thin-plate element. Since the most important first three modes are the transverse flexural modes for this slender elastic continuum, the response computation was conducted on an FEM model using the 4-DOFs Euler/Bernoulli beam element, with a cross-section area of A = bh and a moment of inertia about the y-axis I = b3h/12, based on the Newmark method. Particle-structure interaction was simulated by updating the elemental stiffness, mass and damping matrices according to the particle mass and the shape function value at the particle on-element location.
Data availability
The datasets generated and analysed in the FEM numerical experiments are available from the corresponding author on reasonable request.
References
Li, G. H. et al. Bridge Structure Stability and Vibration (in Chinese), 12, 302–351. (China Railway Press, Beijing, 1992).
Abdel-Rahman, E. M., Nayfeh, A. H. & Masoud, Z. N. Dynamics and control of cranes: a review. Journal of Vibration and Control 9(7), 863–908 (2003).
Kiani, K. & Mehri, B. Assessment of nanotube structures under a moving nanoparticle using nonlocal beam theories. Journal of Sound and Vibration 329(11), 2241–2264 (2010).
Abe, K., Chida, Y., Quinay, P. E. B. & Koro, K. Dynamic instability of a wheel moving on a discretely supported infinite rail. Journal of Sound and Vibration 333(15), 3413–3427 (2014).
Siddiqui, S. A. Q., Golnaraghi, M. F. & Heppler, G. R. Dynamics of a flexible cantilever beam carrying a moving mass. Nonlinear Dynamics 15(2), 137–154 (1998).
Rao, G. V. Linear dynamics of an elastic beam under moving loads. Journal of Vibration and Acoustics 122(3), 281–289 (2000).
Ouyang, H. Moving-load dynamic problems: A tutorial. Mechanical Systems and Signal Processing 25(6), 2039–2060 (2011).
Sun, Z. Moving-inertial-loads-induced dynamic instability for slender beams considering parametric resonances. Journal of Vibration and Acoustics-ASME 138(1), 011014 (2016).
Thompson, R. J., Rempe, G. & Kimble, H. J. Observation of normal-mode splitting for an atom in an optical cavity. Physical Review Letters 68(8), 1132–1135 (1992).
Klinner, J., Lindholdt, M., Nagorny, B. & Hemmerich, A. Normal mode splitting and mechanical effects of an optical lattice in a ring cavity. Physical Review Letters 96(2), 023002 (2006).
Dobrindt, J. M., Wilson-Rae, I. & Kippenberg, T. J. Parametric normal-mode splitting in cavity optomechanics. Physical Review Letters 101(26), 263602 (2008).
Huang, S. & Agarwal, G. S. Normal-mode splitting in a coupled system of a nanomechanical oscillator and a parametric amplifier cavity. Physical Review A 80(3), 033807 (2009).
Siddiqui, S. A. Q., Golnaraghi, M. F. & Heppler, G. R. Dynamics of a flexible beam carrying a moving mass using perturbation, numerical and time-frequency analysis techniques. Journal of Sound and Vibration 229(5), 1023–1055 (2000).
Park, S. & Youm, Y. Motion of a moving elastic beam carrying a moving mass - analysis and experimental verification. Journal of Sound and Vibration 240(1), 131–157 (2001).
Bilello, C., Bergman, L. A. & Kuchma, D. Experimental investigation of a small-scale bridge model under a moving mass. Journal of Structural Engineering 130(5), 799–804 (2004).
Stancioiu, D., Ouyang, H., Mottershead, J. E. & James, S. Experimental investigations of a multi-span flexible structure subjected to moving masses. Journal of Sound and Vibration 330(9), 2004–2016 (2011).
Sun, Z. Multi-octave mode in a moving-particle-pumped structure: rectangular plate with clamped opposite boundaries. Scientific Reports, 2018 (submitted).
Nayfeh, A. H. & Mook, D. T. Nonlinear Oscillations (Wiley Classics Library Edition). 5, 258–364. (Wiley Interscience, New York, 1995).
Acknowledgements
This research was supported by the State Key Laboratory for Disaster Reduction in Civil Engineering Independent Research Fund (Grant No. SLDRCE14-B-24) of the Ministry of Science and Technology of China.
Author information
Authors and Affiliations
Contributions
Z. Sun conducted the analytical MOMPO modelling and derivation, FEM structural modelling based numerical experiments design, computation, and data processing, made the figures, and wrote the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The author declares no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sun, Z. Normal Mode Splitting in a Moving-Particles-Pumped Mechanical Oscillator: Clamped-Hinged Homogeneous Beam. Sci Rep 8, 9803 (2018). https://doi.org/10.1038/s41598-018-27989-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-27989-8
This article is cited by
-
Multi-harmonic forced vibration and resonance of simple beams to moving vehicles
Frontiers of Structural and Civil Engineering (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.