Abstarct
The stability and reactivity of clusters are closely related to their valence electronic configuration. Doping is a most efficient method to modify the electronic configuration and properties of a cluster. Considering that Cu and S posses one and six valence electrons, respectively, the S doped Cu clusters with even number of valence electrons are expected to be more stable than those with odd number of electrons. By using the swarm intelligence based CALYPSO method on crystal structural prediction, we have explored the structures of neutral and charged Cun+1 and CunS (n = 1–12) clusters. The electronic properties of the lowest energy structures have been investigated systemically by first-principles calculations with density functional theory. The results showed that the clusters with a valence count of 2, 8 and 12 appear to be magic numbers with enhanced stability. In addition, several geometry-related-properties have been discussed and compared with those results available in the literature.
Similar content being viewed by others
Introduction
Because of the peculiar electronic structure (3s 23p 63d 104s 1) of the Cu atom with one s electron outside a closed d shell, the small energy difference between the atomic s and d levels leads to strong hybridization effects, which may play an important role in determining the structures and electronic properties of copper clusters. In recent years, the structure and properties of copper clusters have received considerable attention from both the experimental and theoretical points of view1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21. Many experimental data such as the bond length, frequency, binding energy, vertical ionization potentials (VIP) and vertical electron affinities (VEA), adiabatic detachment energy (ADE) and vertical detachment energy (VDE) are reported for pure neutral and charged copper clusters1,2,3,4,5,6,7,8,9,10,11,12,13. With the development of rigorous calculation methods, numerous theoretical works have been performed by different programs, such as SIESTA, deMon-KS, ALLCHEM, Gaussian etc.14,15,16,17,18,19,20,21. For example, Jaque and Labbe14 studied the molecular structure, binding energy, electronic properties and reactivity descriptors using the GAUSSIAN09 package for nine neutral copper clusters. Ramirez et al.15 presented the minimum energy structures of Cun μ (μ =±1, 0, 2; n = 3–13) clusters through a joint gradient embedded genetic algorithm (GEGA) technique. Jug et al.16 investigated the structure and stability of neutral and ionic Cun clusters (n ≤ 10) using the DFT program ALLCHEM, calculations on the LDA level are proved to be a suitable mean for the determination of structure and frequency. GGA corrections are needed for correct prediction of the relative stability of isomers and the global minimum. Density functional theory calculations of copper cluster Cun (n = 2–10) are analyzed with respect to their molecular orbitals. Results showed that shell type orbitals of s, p and d character govern the electronic structure growth and have an influence on the geometric structure17. Using the demon-KS package, Calaminici et al.18 reported the LCGTO-DFT local and GGA first principles all-electron calculations for the structural and spectroscopic properties of neutral and charged Cun (n ≤ 5) clusters. On the basis of the first-principles code SIESTA, Fernandez et al.19 preformed a systematic study of the electronic properties and geometric structure of copper clusters Cun μ (n ≤ 13 and n = 20; μ = 0, ±1). The maximum size of planar clusters are determined at n = (5, 6, 4) for anionic, neutral and cationic copper, respectively. Moreover, the trends of the cohesive energy, ionization potentials, electron affinities, and highest occupied–lowest unoccupied molecular orbital (HOMO-LUMO) gap are studied in detail as the cluster size increase and charge state changes.
As we know that the structures and properties of clusters are very sensitive to the number of atoms, which can change dramatically with the addition or substitution of one atom. The introduction of a doped atom in copper clusters, such as a sulfur atom in our work, can undoubtedly change the clusters’ structure, which in further alters their physical and chemical properties significantly. Copper sulfides have attracted sustained research interests over the past decades due to their wide applications in solar cell devices, nonlinear optical materials, lithium ion batteries, nanometer-scale switches and gas sensors22,23,24,25. For example, the electronic structures of Cu2S cluster were calculated in the local density functional approximation26. Their theoretical results suggested that the structures closely resemble an S− bridging a Cu2 + as shown by the geometries and charge distributions. The potential energy surface minima of neutral copper sulfide clusters have been explored using the Coalescence Kick global optimization method and combined with a DFT approach27. The calculated HOMO-LUMO gap (1.3 to 3.3 eV) showed that the (CuS)n clusters can be considered as a suitable candidate for renewable energy sources. At last, Scott et al.’s results confirmed that Cu-S-Cu units can be found in an active site of some metalloproteinase like cytochrome c-oxidase28. The short Cu-Cu distance and small Cu-S-Cu bond angle play an essential role in the electron transport made by this protein.
It is well known that the Jellium model plays a significant role in the realm of cluster. It incorporates a positively charged (spherical or non-spherical) background potential, which results in discrete energy levels of the delocalized (“metallic”) electrons corresponding to angular momentum shells (in the spherical case the shells are labeled as: 1S2 1P6 1D10 2S2 1F14, 2P6, 1G18…)29. There are certain valence electronic configurations (2, 8, 18, 20, 40, 58…) know as magic numbers, that exhibit increased stability relative to their neighboring configurations. So, these clusters are generally resistant to reactivity with small clusters30,31,32,33,34. For example, Jaque et al.14 studied the molecular structures, binding energy, electronic properties and reactivity descriptors for the neutral copper cluster, and found that the large HOMO-LUMO energies gap, minimum polarizability and maximum hardness corresponding with the 2 and 8 valence electrons are operative for characterizing and rationalizing the electronic properties of copper clusters. However, other groups found that some clusters with the non-magic number total electrons can also exhibit an increased stability35, 36. For example, Rebere et al.36 reported that Ag15 +, Ag14 and Ag13 − clusters with 14 valence electrons are resistant to reactivity with oxygen, even though they do not have a magic number of electrons. This simulated further and more detailed investigations on the magic numbers.
Although the structural and electronic properties of copper and sulfur doped copper clusters have been investigated by both experiment and theory, some important question arises: (i) For different copper clusters with the small energy difference between the atomic s and d levels, how does hybridization effect from different molecular orbitals? (ii) How does the structural vary as a consequence in anionic and cationic CunS clusters? Furthermore, are their structures and properties greatly distinct from the neutral CunS clusters? (iii) In view of the fact that the electronic structure of Cu and Ag featuring a closed d shell and a singly occupied s shell (3d 104s 1 and 4d 105s 1), whether the Jellium model is in accordance with the pure copper clusters? With a doped sulfur, how does the magic number vary? (iv) For the charged CunS clusters, how does HOMO-LUMO gap change? Hence it is necessary to carry out a systematic investigation to reveal the magic number, structures and electronic properties of copper and sulfur doped copper clusters.
With this purpose in mind, we perform a systematic, in–depth study of the geometric structures and electronic properties for neutral Cun+1 and CunS (n = 1–12) clusters and their ions based on particle swarm optimization algorithm and density function theory. Thus, we are able to advance a fundamental understanding of the ground state geometric configurations. In addition, the magic numbers, HOMO-LUMO gaps, density of states (DOS), adaptive natural density partitioning (AdNDP), electron localization function (ELF) and Mayer bond order are also analyzed. Subsequently, the calculated values are compared with available experimental and theoretical data.
Results and Discussions
Structural properties
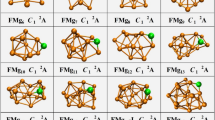
We performed unbiased searches for the global minima structures of neutral and charged Cun+1 and CunS (n = 1–12) clusters. Previously reported structures are successfully reproduced with CALYPSO method from experimentally and theoretically. The global minimum structures for each size are displayed in Fig. 1. The corresponding electronic states, symmetries, total energies are also determined and listed in Table S1 in the Supporting Information (S1).
As depicted in Fig. 1, it is clear that the charges have important influence on the structures of pure and doped clusters. We found nearly the same structure only in the cases of n = 1, 3 for Cun+1 and n = 1, 2 for CunS, respectively, while the remaining clusters contain different structures. For example, both Cu3 + and Cu3 have a triangular structure, while Cu3 − is composed of a linear structure. The same trend can be also observed for Cu3S+/0/− cluster, namely, Cu3S+ and Cu3S possess the same triangular structure, whereas Cu3S− has a rhombus structure. In addition, the transition from two-dimensional (2D) to three-dimensional (3D) configurations is closely related to their charge state. For non doped-cluster, the 2D-3D structure transition occurs at n = 4–5 for Cun +, n = 6–7 for Cun, and n = 5–6 for Cun −; while for S doped ones, n = 2–3 for CunS+, n = 2–3 for CunS, and n = 5–6 for CunS−, respectively. For neutral copper cluster, two growth patterns can be obtained here. One is to remain essentially two dimensional and grow by forming successive triangle faces for n = 2–6. From n > 7, the cluster forms a pentagon bipyramid structure with the two capping atoms forming a bond. And, it becomes more closely packed with the increasing atomic number of clusters. For charged copper cluster, the ground state structures exhibit a layer-like 3D configuration from n = 5 to 6, which display a preference for layered and pyramidal geometries. In addition, our structures for Cu2 +/− (\({D}_{\infty h}\), \({D}_{\infty h}\)), Cu3 +/− (D 3h, \({D}_{\infty h}\)), Cu4 +/− (D 2h, D 2h), Cu5 +/− (D 2d, C 2v), Cu6 +/− (C 2v, C 2v), Cu7 +/− (D 5h, C 3v), Cu8 +/− (C s, D 2d), Cu9 +/− (C 2v, C 2v), Cu10 +/− (D 2d, C s), Cu11 +/− (D 3h, C 2v), Cu12 +/− (C 1, C s) and Cu13 +/− (C s, C 2v) are consistent with previous computational values of reference20. Nevertheless, it should be mentioned that a new lowest energy structure of Cu9 cluster is identified, which is different from previous studies14,15,16. In present work, a C 2v symmetry Cu9 cluster is found as the lowest energy structure; however, different isomer with C s symmetry are reported by Jug (ALLCHEM), Jaque (B3PW91/LANL2DZ) and Ramirez et al. (BLYP/6-311+G(d)). The different lowest energy structures may be due to the fact that the different functional and basis sets may reverse the order of clusters in some cases. So, in order to confirm the lowest energy structure of Cu9 cluster, the same functional and basis sets (B3PW91/LANL2DZ) are performed based on the DFT calculations. Results showed that the Cu9 structure C s, reported in ref. 14 as a minimum, in our calculation is found to be the second one, at a relative energy of 0.02 eV above our minimum. In addition, it is also noted that the Gibbs free energy of Jaque et al.’s results is 6.3 × 103 J/mol higher than our calculated work. Above analysis indicated that that our results are energetically lower and structurally more stable than Jaque et al.’s results.
For the neutral and charged CunS clusters, different types of clusters possess the same growth pattern with rare exceptions. Practically speaking, the doped clusters are formed by adding a copper atom into the smaller sized Cun−1S clusters. Any additional S atom is just one more vertex to surround the Cu atom, and finally the cluster forms a triangular prism. In conclusion, the growth pattern of CunS+/0/− clusters are quite different from Cun +/0/− clusters. One Cu atom directly added on the Cun−1S clusters are dominant growth pattern for CunS+/0/− clusters.
To check the accuracy of the lowest energy structures, several available experimental and theoretical results are calculated and compared. For Cun clusters, the evolution of VIP, VEA and static mean polarizablity (α) values is plotted in Figure S1, together with available experimental and calculated results3,4,5, 13, 16. For Cun − clusters, the calculated ADE and VDE are listed in Table 1, which also includes the available experimental values taken from ref. 1. For Cu2S cluster, the calculated bond length (Cu-S, Cu-Cu) and bond angle (CuSCu) (2.14 Å, 2.67 Å and 77.5°) are close to the Boris and Mahe et. al’s. work (2.11 Å, 2.63 Å and 76.7°)37, 38. In addition, we found that our calculated results about the bond length and angles, dissociation energies and frequency are also in excellent agree with the experimental and theoretical results for CunS clusters26, 27, 37, 38. In conclusion, we can see that our calculated values are in good agreement with the experimental and theoretical results. Thus, we believe that the choice of functional and basis sets could be reasonably good to describe the present systems.
Stabilities and electronic properties
To analyze the relative stabilities of the lowest energy structures of Cun+1 +/0/− and CunS+/0/− (n = 1–12) clusters, the averaged binding energies E b(n) and second-order difference of energies ∆2 E(n) have been derived. E b(n) and ∆2 E(n) of each complex for CunS+/0/− clusters are calculated as follows:
For Cun +/0/− clusters, E b(n + 1) and ∆2 E(n + 1) are defined as:
The calculated E b (n) and \({{\rm{\Delta }}}_{2}E(n)\) as a function of the number n of copper atoms are plotted in Fig. 2. As by comparing E b (n) for both CunS+/0/− and Cun +/0/− clusters, the primary features are concluded: (i) The values of \({E}_{b}({{\rm{Cu}}}_{n}{{\rm{S}}}^{-/0/+})\) clusters are higher than those of \({E}_{b}({{\rm{Cu}}}_{n}^{-/0/+})\) clusters, implying that the doped S atom can enhance the stability of host Cun +/0/− clusters. (ii) For Cu n S clusters, there are six visible peaks in the curves at n = 2, 4, 6, 8, 10 and 12, indicating that Cu2, 4, 6, 8, 10, 12S are relatively more stable than its neighboring clusters. For Cu n S−/+ clusters, Cu3S−, Cu5S−, Cu7S−, Cu9S− and Cu3S+ have a higher relative stability than their neighbors, respectively. (iii) For Cun+1 +/0/− clusters, E b(n) have a monotonically increasing with an increase of copper atoms, revealing an enhanced effect on the stabilities of the Cun+1 +/0/− clusters with the cluster size increasing. In addition, the charged clusters have larger values for the binding energy than neutral ones, while ionic clusters possessing the largest values lie in between them. Another important parameter to evaluate the relative stabilities is the size-dependent second energy difference, the values of neutral and charged clusters exhibit obvious odd-even alternations as shown in Fig. 2. In which the charged and neutral clusters are more stable with even and odd cluster size n for non-doped Cun+1 +/0/−, respectively. Whereas the charged and neutral clusters are more stable with odd and even cluster size n for doped CunS+/0/−, respectively. The above analysis can be explained by this can be attributed to the presence or absence of unpaired electrons of the complex. In addition, we can easily point to some conspicuous peaks: n = 2, 7, 6 for Cun+1 +/0/− clusters as well as n = 3, 2, 5 for CunS+/0/− clusters. It suggests that these clusters are more stable compared with other clusters.
The HOMO-LUMO energy gaps (E gap) have been proved to be a powerful tool to represent the ability of the molecule to participate in the chemical reaction in some degree. Larger values of values indicate stronger chemical stability. The calculated of HOMO-LUMO energy gaps are shown in Fig. 3 for the lowest energy structures of Cun+1 +/0/− and CunS+/0/− (n = 1–12) clusters. It is interesting to notice that Cun+1 with even number of electrons are more stable than other clusters with odd number of electrons. Contrary, for Cun+1 + and Cun+1 − clusters, odd-even alteration behaviors of E gap curve present the opposite trend compared to the corresponding neutral clusters. This can be explained that even numbers electrons are always exist in pairs and can lead to a closed shell electronic structure. We also observe that E gap of cationic copper clusters are larger than their anionic counterparts, indicating that Cun+1 + clusters are less stable, which is in excellent agreement with the results of averaged binding energies shown in the Fig. 2. As for Cun+1 − clusters, four local maxima of E gap are found at n = 2, 6, 8 and 12, respectively, suggesting that Cu3, 7, 9, 13 − clusters are more stable than their neighbors. The local maxima of the E gap for Cun+1 and Cun+1 + clusters indicate that neutral Cu2, 6, 8 and cationic Cu3, 5, 9 + clusters possess enhanced relative stability. Similarly, for CunS+/− clusters, except Cu2S+, the results of E gap present the same odd-even oscillation. Moreover, the E gap of CunS− are always lower than their cationic counterparts with the exception of CuS+. Those results indicate that cationic clusters are more stable than corresponding anionic clusters. In the case of CunS+/0/− clusters, some local maxima E gap values are observed at Cu2S, Cu4S, Cu6S for neutral clusters, Cu3S+, Cu5S+, Cu9S+ for cationic clusters as well as Cu3S−, Cu5S−, Cu11S− for anionic clusters. Combining the above analysis on E b(n), ∆2 E(n) and E gap values of Cun+1 +/0/− and CunS+/0/− clusters, we can infer that Cu8, Cu3 +, Cu7 −, Cu2S, Cu3S+ and Cu5S− clusters exert a remarkable chemical stability. At the same time, we checked the valence electrons of above stable clusters, the number is 2 and 8 for Cu3 + and Cu8, Cu7 −, Cu2S, Cu3S+ respectively, which are magic numbers according to Jellium model. However, our theoretical predictions point out that the clusters of Cu5S− is particularly stable despite the cluster has 12 valence electrons and do not conform to the predictions of the Jellium model. Finally, for CunS+/0/− clusters, the calculated HOMO-LUMO gaps range from 1.01–4.29 eV, 0.8–2.96 eV, 1.26–2.53 eV, respectively. These are desirable band gaps of semiconductor nanomaterials, from an application point of view, it suitable for application in photocatalysis field (especially for CunS+ clusters). We expect that studies of the neutral and charged sulfur-copper clusters could provide favorable information in the searching functional design and application of the renewable energy sources.
To understand the nature of the chemical bonding and the formation mechanism of these various Cu-S compounds, the total density of states (TDOS) and partial density of states (PDOS) of Cu2S and CuS cluster are shown in Fig. 4. In addition, the Figures of Cu3S+ and Cu5S− clusters are discussed and plotted in Figures S2 and S3 (see S1). From Fig. 4, the band gaps of Cu2S are larger than that of CuS, and the TDOS of Fermi level for Cu2S clusters is higher than CuS clusters, indicating the metallicity of CuS cluster is weakened due to a Cu ejection. We can also note that the TDOS of Cu2S clusters mainly comes from copper atoms in the region from −0.4 to −0.2 a.u. and sulfur atom in the region from 0.05 to 0.15 a.u. As evidenced by the diagram, the HOMO level is dominated primarily by the S-p orbital and partially by the Cu-p, d orbitals, in which Cu-p energy level is lower than Cu-d and S-p orbital energy level is much higher than Cu-d. The contribution from Cu-s and S-s orbital is almost zero. At LUMO case, the level is composed of Cu-s, p, d orbitals and S-s, p orbitals. The major contributions come from Cu-s orbital. Moreover, the orbital energy levels of Cu-p and S-p are higher than that of S-s; the contribution from Cu-d orbital is very small. These results provide a certification for our discussion based on molecular orbital composition analysis.
In order to decipher the chemical bonding of cluster, we performed a detailed analysis based on the localized orbitals resulting from the AdNDP method. AdNDP method, which is developed by Zubarev and Boldyrev39, is a very efficient and visual approach to the interpretation of the molecular orbital because it is an extension of the natural bond orbital analysis. It represents the molecular electronic structure in terms of n-center two-electron (nc-2e) bonds, the familiar lone pairs (1c-2e) and localized 2c-2e bonds or delocalized nc-2e bonds (3 ≤ n ≤ total number of atoms in the system). Moreover, the occupation numbers (ON) are expected to be close to the maximum values (ON = 2.00|e|).
When performing AdNDP approach to characterize the chemical bonding in Cu2S, the full-filled 3d orbital of Cu are not shown in this figure with ON ranging from 1.96 to 1.99 |e|. Excluding Cu (3d) orbital, Cu2S has 8 valence electrons with each copper atom contributing one valence electron and each sulfur atom contributing six valence electrons. The results of Cu2S cluster are depicted in Fig. 5. AdNDP analyses find four electrons are localized along the two localized Cu-S two-center two-electron (2c-2e) σ-bonds (ON = 1.972|e|). The remaining 4 electrons contain two lone pairs (LPs) with one s-type (ON = 1.956 |e|) and one p-type (ON = 1.936 |e|) on the sulfur atom. More specifically, per 2c-2e bond possesses the atomic contribution of 39.28%Cu + 60.72%S. In Cu-S 2c-2e bond, Cu-s and p offer 34.22% and 2.67% contribution to the Cu-based orbital, the S-based orbital possess the contributions of S-p (52.57%) and S-s (7.76%). Evidently, the Cu-S 2c-2e σ-bond is mainly dominated by the components from Cu-s and S-p type orbitals.
For Cu3S+ cluster, the 8 valence pairs are localized as one LPs with one S-s (ON = 1.968 |e|) and three localized Cu-S 2c-2e σ-bonds (ON = 1.981 |e|). The atomic contributions come from 32.61%Cu + 67.39%S for per 2c-2e bond. In Cu-S 2c-2e bond, the Cu-based orbital consist of Cu-s (27.10%) and Cu-p (3.96%); the corresponding S-based orbital is composed of 51.18% S-p and 16.22% S-s. Obviously, Cu-s and S-p possess three localized Cu-S 2c-2e bond. In addition, there is no covalent bonding between Cu and Cu atoms, indicating that interaction between Cu and Cu atoms is a kind of non-Lewis interaction.
There are 12 valence pairs in Cu5S− cluster, analyses reveal two localized 2c-2e σ-bonds (ON = 1.969 |e|), two localized 2c-2e π-bonds (ON = 1.914 |e|), and two delocalized Cu-Cu-Cu 3c-2e σ-bonds (ON = 1.960 |e|). For the four localized 2c-2e bond, it attribute to the high symmetry structure and high atomization energy. And, each 2c-2e σ-bond involves the atomic contribution of 15.75%Cu + 84.25%S. For the bond, each Cu and S atoms can be considered as contributing Cu-s, -p (4.22%, 3.03%) and S-s, −p (74.14%, 9.9%), respectively. Furthermore, the atomic orbital composition from 2c-2e π-bond is obviously different from 2c-2e σ-bond. In 2c-2e π-bond, the Cu-S bond are consisted of 5.9%Cu + 94.1%S. Cu-based orbital is most from of 5.91% Cu-p. S-based orbital possess the atomic contribution of 94.08% S-p. In addition, there are two 3c-2e σ-bond exist in Cu5S− cluster, each of atomic contribution involve 15.93%Cu(2) + 47.75%Cu(3) + 24.91%Cu(5). In Cu(2)-Cu(3)-Cu(5) 3c-2e bond, bridged Cu(2)-s and p contribute 11.19% and 4.02% to the Cu(2)-based orbital, Cu(3)-based orbital is completely consistent with 46.93% Cu-s, whereas Cu(5)-s and p contribute 20.67% and 3.34% to the Cu(5)-based orbital, respectively. Evidently, Cu(3)-s and Cu(5)-s orbitals appear to be the major contribution to the Cu(2)-Cu(3)-Cu(5) bridging bond in C 2v Cu5S− cluster. For the Cu(1)-Cu(4)-Cu(5) 3c-2e bond, the atomic contribution are like as the results in Cu(2)-Cu(3)-Cu(5) 3c-2e bond.
For Cu3 + cluster, the results found that a pair of electrons is located inside of the copper triangle being delocalized over all three copper atoms. The occupation number of 3c-2e Cu-Cu-Cu σ-bonds is equal to the ideal value of 2.00 |e|. Due to the same contribution from the different three copper atoms, the corresponding atomic contribution is 33.33%Cu(1) + 33.33%Cu(2) + 33.33%Cu(3). Moreover, the 3c-2e Cu-Cu-Cu σ-bond possesses the orbital contribution of Cu-s (30.87%) and p (2.46%). The major contribution to the 3c-2e σ-bonds come from three Cu-s type orbital.
There exist 8 valence electrons in Cu7 − cluster. Analysis indicate that there are one delocalized 4c-2e σ-bond (ON = 1.862 |e|) in the trigonal pyramid structure and three delocalized 5c-2e σ-bonds (ON = 1.842 |e|) in three tetrahedral edges. For the 4c-2e Cu(1)-Cu(2)-Cu(4)-Cu(6) σ-bond, this bond can be viewed as contributing 17.54%Cu(1) + 33.22%Cu(2) + 17.55%Cu(4) + 17.55%Cu(6). Moreover, Cu(2)-s and p contribute 32.41% and 0.62% to the Cu(2)-based orbital; In Cu(1, 4, 6)-based orbital, each Cu atom possess the same contribution from Cu-s (13.78%) and Cu-p (3.33%). So, in 4c-2e Cu(1)-Cu(2)-Cu(4)-Cu(6) σ-bond, the major contribution is composed of Cu(1, 2, 4, 6)-s orbitals. For the 5c-2e σ-bond, the contribution from different copper atom is absolutely same. Cu(1)-Cu(4)-Cu(5)-Cu(6)-Cu(7) are chosen as representative examples. The corresponding atomic contribution is composed of 11.28%Cu(1) + 11.28%Cu(4) + 20.25%Cu(5) + 15.54%Cu(6) + 20.24%Cu(7). Moreover, Cu(1, 4)-s, -p offer 2.11% and 8.53% to the Cu(1, 4)-based orbital. Cu(5, 7)-s and p have 17.92% and 2.01% for the Cu(5, 7)-based orbital. At last, the contribution of Cu(6)-based orbital involves Cu-s (9.90%) and Cu-p (4.81%), respectively. In conclusion, in the 5c-2e σ-bond, Cu (5, 7, 6)-s provide the major contribution.
According to the AdNDP analysis of the bare Cu8 cluster, 8 valence electrons possess four delocalized 4c-2e σ-bonds (ON = 1.866 |e|). The corresponding atomic contribution from Cu(1)-Cu(2)-Cu(4)-Cu(6) is consistent with 17.54%Cu(1) + 33.22%Cu(6) + 17.55%Cu(7) + 17.54% Cu(8). Furthermore, Cu(1, 6, 7)-s, -p provide 11.91% and 2.89% to the Cu(1, 6, 7)-based orbital. Cu(8) -s, -p possess 30.23% and 0.84% for the Cu(8)-based orbital. Obviously, Cu-s provides the major contribution to four delocalized 4c-2e σ-bonds in Cu8 cluster.
In order to study the bond interactions of doped systems, we conducted the electron localization function (ELF) analysis using the Multiwfn program package40. The ELF is usually interpreted as the probability of finding an electron pair localized in some region of the real space. There are three special cases: ELF = 0 indicates that there is no electron density between atomic orbitals; ELF = 0.5 shows the regions with bonding of a metallic character; ELF = 1 corresponds to perfect localization, and means covalent bonds and inner shell or lone pair electrons. To elucidate the type of bonding in clusters, bond length and Mayer bond order and ELF cut planes for Cu2S, Cu3S+ and Cu5S− cluster are illustrated in Fig. 6. We can see that the ELF values near Cu atoms are very high which associated with 1s core electrons, whereas the ELF values of regions between copper atoms are very small (nearly zero), it means that the chemical bonding between Cu and Cu atoms can be neglected. The ELF values of bonds are small between Cu and S atoms, indicating that there exist typical of ionic bonding in Cu2S, Cu3S+ and Cu5S− clusters. In addition, the distribution of ELF value near the S atom is not spherically symmetric, and there is a region with higher localized degree. This implies that the S atom through sp hybridization from normal two-center σ bonds with the near copper atoms. The present results are in good agreement with AdNDP chemical bonding analysis. Moreover, in Cu5S− cluster, it is clear that electrons are mainly localized within the two outside triangles, corresponding to the three-center two-electron bond (3c-2e). Simultaneously, Mayer three-center bond order analyses show that the value of outside triangle is 0.071e. In addition, based on the two-center bond order analysis, the bond order of boundary Cu-Cu bond (0.521) is markedly larger than the inner one (0.290). Results indicate that the bond of boundary Cu-Cu is more stable than the inner ones; the bond of boundary Cu-S is more stable than that of Cu-Cu. At last, comparing the different bond lengths, we can find that short bond lengths lead to strong interatomic interactions, which play an important role in stabilizing structures.
Conclusions
In this paper, we have performed a global minimum search for the lowest energy structures of neutral, cationic and anionic Cun+1 and CunS (n = 1–12) clusters by using CALYPSO method in combination with density functional theory. The results are summarized as below:
-
(i)
The structure searches show that the lowest energy structures are sensitive to the charge states. A new global minimum state of Cu9 cluster is obtained, which is more stable than previous work. For CunS+/0/− clusters, Cu directly added on the Cun−1S clusters to form the CunS clusters is the dominant growth pattern.
-
(ii)
Sulfur atom doping has considerable influence on not only geometries and properties but also the valence electron count of copper clusters. Trends of the atomic binding energies, second-order difference of energies and HOMO-LUMO gaps showed that the clusters containing even number of electrons maintain greater stability than odd number of electrons. In addition, Cu3 +, Cu8, Cu7 −, Cu2S and Cu3S+ follow the trends predicted by the Jellium model with the 2, 8 valence electron systems being the most stable. However, Cu5S− cluster with 12 valence electrons does not correspond to the magic numbers also exhibit an increased stability.
-
(iii)
The calculated HOMO-LUMO gaps range from 1.01–4.29 eV, 0.8–2.96 eV, 1.26–2.53 eV, respectively, which make CunS+/0/− clusters suitable candidates for renewable energy sources (especially CunS+ clusters). Density of states reveals that the orbital contribution of HOMO level is dominated by the S-p and Cu-s, p, d, the orbital contribution from S-s is almost zero. In LUMO level, the orbital contributions are composed of Cu-s, p, d and S-s, p, respectively. Moreover, the structural symmetry effect corresponding orbital composition.
-
(iv)
AdNDP analyses show the chemical bonding patterns are in good agreement with the geometric structures and the ELF and Mayer Bond order analysis. The bond of boundary Cu-Cu is more stable than the inner ones. The bond of boundary Cu-S is more stable than that of Cu-Cu.
Methods
The lowest energy structures of neutral and charged Cun+1 and CunS clusters are searched by the swarm-intelligence based CALYPSO structure prediction method41,42,43. This method is based on globally minimizing potential energy surfaces, merging ab initio total energy calculations with CALYPSO cluster prediction through particle swarm optimization. It has been successful in correctly predicting structures for various systems44,45,46. In this prediction method, each generation contain 20 structures, 70% of which are generated by particle swarm optimization (PSO). PSO is a population approach based stochastic optimization technique developed by Eberhart and Kennedy in 199547, 48. The others are new and will be generated randomly. In process of searching, a sequence of 50 generations of structural candidates is followed to achieve convergence. So, we can achieve 1000 structurally different low-lying isomers. Among the 1000 isomers, the top fifty low-lying isomers are collected as candidates. Those structures with energy difference from the lowest energy isomers less than 0.3 eV are further optimized to identify the lowest energy structure. The further geometry optimizations are performed with no symmetry constraints at the level of the generalized gradient approximation (GGA) using the exchange-correlation functional B3P8649, 50 as implemented in the GAUSSIAN09 package51. The basis set labeled GENECP, i. e. the LanL2DZ basis set for Cu atom and 6-311 + G* basis set for S atom, respectively52, 53.
References
Leopold, D. G., Ho, J. & Lineberger, W. C. Photoelectron spectroscopy of mass selected metal cluster anions. I. Cu− n , n = 1–10. J. Chem. Phys. 86, 1715–1726, doi:10.1063/1.452170 (1987).
Rohlfing, E. A. & Valentini, J. J. UV laser excited fluorescence spectroscopy of the jet-cooled copper dimer. J. Chem. Phys. 84, 6560–6566, doi:10.1063/1.450708 (1986).
Knickelbein, M. B. Electronic shell structure in the ionization potentials of copper clusters. Chem. Phys. Lett. 192, 129–134, doi:10.1016/0009-2614(92)85440-L (1992).
Powers, D. E. et al. Supersonic copper clusters. J. Chem. Phys. 78, 2866–2881, doi:10.1063/1.445273 (1983).
Ho, J., Ervin, K. M. & Lineberger, W. C. Photoelectron spectroscopy of metal cluster anions: Cu− n, Ag− n, and Au− n. J. Chem. Phys. 93, 6987–7002, doi:10.1063/1.459475 (1990).
Spasov, V. A., Lee, T. H. & Ervin, K. M. Threshold collision-induced dissociation of anionic copper clusters and copper cluster monocarbonyls. J. Chem. Phys. 112, 1713–1720, doi:10.1063/1.480736 (2000).
Ingolifsson, O., Busolt, U. & Sugawara, K. Energy-resolved collision-induced dissociation of Cu− n(+) (n = 2–9): stability and fragmentation pathways. J. Chem. Phys. 112, 4613–4620, doi:10.1063/1.481017 (2000).
Moore, C. E. Atomic Energy Levels Vol. II of Nat Bur Standars (1971).
Winter, B. J., Parks, E. K. & Riley, S. J. Copper clusters: the interplay between electronic and geometrical structure. J. Chem. Phys. 92, 8618–8621, doi:10.1063/1.460046 (1991).
Krucheberg, S. et al. Decay pathways and dissociation energies of copper clusters, Cun + (2 ⩽ n ⩽25), Cun 2+ (15 ⩽n ⩽25). J. Chem. Phys. 114, 2955–2962 (2001).
Huber, K. P. & Herzberg, G. Molecular Spectra and Molecular Structure IV. Constants of Diatomic Molecular, Van Nostrand Reinhold. New York, (1979).
Sappey, A. D., Harrington, J. E. & Weisshaar, J. C. Cu+ 2 vibronic states at 0–1.4 eV from multiphoton ionization–photoelectron spectroscopy. J. Chem. Phys. 88, 5243–5245, doi:10.1063/1.454577 (1998).
James, A. M., Lemire, G. W. & Langridge-Smith, P. R. R. Threshold photoionisation spectroscopy of the CuAg molecule. Chem. Phys. Lett. 277, 503–510, doi:10.1016/0009-2614(94)00834-5 (1994).
Jaque, P. & Labbe, A. T. Characterization of copper clusters through the use of density functional theory reactivity descriptors. J. Chem. Phys. 117, 3208–3218, doi:10.1063/1.1493178 (2002).
Ramirez, G. G., Granja, F. A. & Robles, J. DFT and GEGA genetic algorithm optimized structures of Cun ν (ν = ±1,0,2; n = 3–13) clusters. Eur. Phys. J. D. 57, 49–60, doi:10.1140/epjd/e2010-00001-4 (2010).
Jug, K., Zimmermann, B., Calaminici, P. & Köster, A. M. Structure and stability of small copper clusters. J. Chem. Phys. 116, 4497–4507, doi:10.1063/1.1436465 (2002).
Karl, J., Bernd, Z. & Andresa, M. K. Growth pattern and bonding of copper clusters. Int. J. Quant. Chem. 90, 594–602, doi:10.1002/qua.976 (2002).
Calaminici, P., Köster, A. M., Russo, N. & Salahub, D. R. A density functional study of small copper clusters: Cun (n ≤ 5). J. Chem. Phys. 105, 9546–9556, doi:10.1063/1.472939 (1996).
Fernandez, E. M. et al. Trends in the structure and bonding of noble metal clusters. Phys. Rev. B. 70, 165403-1-14, 10.1103/PhysRevB.70.165403 (2004).
Jaque, P. & Labbe, A. T. Polarizability of neutral copper clusters. J. Mol. Model. 20, 2410-1-8, 10.1007/s00894-014-2410-6 (2014).
Massobrio, C., Pasquarello, A. & Corso, A. D. Structural and electronic properties of small Cun clusters using generalized-gradient approximations within density functional theory. J. Chem. Phys. 109, 6626–6630, doi:10.1063/1.477313 (1998).
Roseboom, E. H. An investigation of the system Cu-S and some natural copper sulfides between 250 and 700 °C. Econ. Geol. 61, 641–672 (1996).
Zhao, Y. X. & Burda, C. Development of plasmonic semiconductor nanomaterials with copper chalcogenides for a future with sustainable energy materials. Energy Environ. Sci. 5, 5564–5576, doi:10.1039/C1EE02734D (2012).
Sagade, A. A., Sharma, R. & Sulaniya, I. Enhancement in sensitivity of copper sulfide thin film ammonia gas sensor: effect of swift heavy ion irradiation. J. Appl. Phys. 105, 043701-1-8, doi:10.1063/1.3053350 (2009).
Sakamoto, T., Sunamura, H. & Kawuara, H. Nanometer-scale switches using copper sulfide. Appl. Phys. Lett. 82, 3032–3034, doi:10.1063/1.1572964 (2003).
Dixon, D. A. & Gole, J. L. Description of the ground state electronic structures of Cu2O, Cu2S, Ag2O and Ag2S. Chem. Phys. Lett. 189, 390–394, doi:10.1016/0009-2614(92)85220-5 (1992).
Sanchez, O. J. J. et al. Structures and electronic properties of neutral (CuS)N clusters (N = 1–6): A DFT approach. Chem. Phys. Lett. 570, 132–135, doi:10.1016/j.cplett.2013.03.072 (2013).
Scott, R. A. Functional significance of cytochrome c oxidase structure. Structure. 3, 981–986, 10.1016/S0969-2126(01)00233-7 (1995). Andrew, C. R. & Sanders-Loehr. Copper-sulfur proteins: using Raman spectroscopy to predict coordination geometry. J. Acc. Chem. Res. 29, 365–372 (1996). Williams, S. E. W. et al. Farred resonance Raman study of copper a in submie II of cytochrome c oxidase. J. Am. Chem. Soc. 118, 3986–3987 (1996).
de Heer, W. A. The physics of simple metal clusters: experimental aspects and simple models. Rev. Mod. Phys. 65, 611–676, doi:10.1103/RevModPhys.65.611 (1993).
Reber, A. C. et al. Spin accommodation and reactivity of aluminum based clusters with O2. J. Am. Chem. Soc. 129, 16098–16101, doi:10.1021/ja075998d (2007).
Luo, Z. et al. Probing the magic numbers of aluminum–magnesium cluster anions and their reactivity toward oxygen. J. Am. Chem. Soc. 135, 4307–4313, doi:10.1021/ja310467n (2013).
Luo, Z. et al. Spin accommodation and reactivity of silver clusters with oxygen: the enhanced stability of Ag13 −. J. Am. Chem. Soc. 134, 18973–18978, doi:10.1021/ja303268w (2012).
Luo, Z. X. et al. Reactivity of silver clusters anions with ethanethiol. J. Phys. Chem. A 118, 8345–8350, doi:10.1021/jp501164g (2014).
Burgert, R. et al. Primary reaction steps of Al13 − clusters in an HCl atmosphere: snapshots of the dissolution of a base metal. Science 319, 438–442, doi:10.1021/ja060613x (2008).
Henry, J. D. Structures and stability of Doped Gallium nanoclusters. J. Phys. Chem. C. 116, 24814–24823, doi:10.1021/jp307555r (2012).
Rebern, A. C., Gamboam, G. U. & Khannam, S. N. The oblate structure and unexpected resistance in reactivity of Ag15 + with O2. J. Phys.: Conf. Ser. 438, 012002 (2013).
Mahe, L., Boughdiri, S. F. & Barthelat, J. C. Electronic structures and energetics in the CuX and Cu2X Series (X) O, S, Se, Te, Po). J. Phys. Chem. A. 101, 4224–4230, doi:10.1021/jp963427u (1997).
Ni, B., Kramer, J. R. & Werstiuk, N. H. Atoms in molecules computational study on the molecular structure of (Cu2S)n clusters. J. Phys. Chem. A. 107, 2890–2897, doi:10.1021/jp027587j (2003).
Zubarev, D. Y. & Boldyrev, A. I. Developing paradigms of chemical bonding: adaptive natural density partitioning. Phys. Chem. Chem. Phys. 10, 5207–5217, doi:10.1039/b804083d (2006).
Lu, T. & Chen, F. W. Multiwfn: a multifunctional wavefunction analyzer. J. Comput. Chem. 33, 580–592, doi:10.1002/jcc.v33.5 (2012).
Wang, Y. C., Lv, J., Zhu, L. & Ma, Y. M. Crystal structure prediction via particle-swarm optimization. Phys. Rev. B. 82, 094116-1–20 (2010).
Wang, Y. C., Lv, J., Zhu, L. & Ma, Y. M. CALYPSO: A method for crystal structure prediction. Comput. Phys. Commun. 183, 2063–2070, doi:10.1016/j.cpc.2012.05.008 (2012).
Wang, Y. C. et al. An effective structure prediction method for layered materials based on 2D particle swarm optimization algorithm. J. Chem. Phys. 137, 224108-1-6 (2012).
Xing, X. D. et al. Insights into the geometries, electronic and magnetic properties of neutral and charged palladium clusters. SCI REP-UK. 9, 19656-1-11 (2016).
Jin, Y. Y. et al. Probing the structural evolution of ruthenium doped germanium clusters: photoelectron spectroscopy and density functional theory calculations. SCI REP-UK 6, 30116-1-9 (2016).
Shu, Y. et al. Coexistence of multiple metastable polytypes in rhombohedral bismuth. SCI REP-UK 6, 20337-1-8, 10.1038/srep20337 (2016).
Kennedy, J. & Eberhart, R. C. A discrete binary version of the particle swarm algorithm. IEEE 4105, 4104–4108, doi:10.1109/ICSMC.1997.637339 (1997).
Eberhart, R. C. & Shi, Y. Particle swarm optimization: developments, applications and resources. Proc. Congress on Evluationary Computation, IEEE, Piscataway, NJ, 81–86 (2001).
Becke, A. D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 98, 5648–5652, doi:10.1063/1.464913 (1993).
Perdew, J. P. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. B. 33, 8822–8824, doi:10.1103/PhysRevB.33.8822 (1986).
Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., Montgomery, J. A. Jr, Vreven, T., Kudin, K. N., Burant, J. C., Millam, J. M., Iyengar, S. S., Tomasi, J., Barone, V., Mennucci, B., Cossi, M., Scalmani, G., Rega, N., Petersson,G. A., Nakatsuji, H., Hada, M., Ehara, M., Toyota, K., Fukuda, R., Hasegawa, J., Ishida, M., Nakajima, T., Honda, Y., Kitao, O., Nakai, H., Klene, M., Li, X., Knox, J. E., Hratchian, H. P., Cross, J. B., Bakken, V., Adamo, C., Jaramillo, J., Gomperts, R., Stratmann, R. E., Yazyev, O., Austin, A. J., Cammi, R., Pomelli, C., Ochterski, J. W., Ayala, P. Y., Morokuma, K., Voth, G. A., Salvador, P., Dannenberg, J. J., Zakrzewski,V. G., Dapprich, S., Daniels, A. D., Strain, M. C., Farkas, O., Malick,D. K., Rabuck, A. D., Raghavachari, K., Foresman, J. B., Ortiz, J. V., Cui,Q., Baboul, A. G., Clifford, S., Cioslowski, J., Stefanov, B., Liu, G., Liashenko, A., Piskorz,P., Komaromi, I., Martin, R. L., Fox, D. J., Keith,T., Al-Laham, M. A., Peng, C. Y., Nanayakkara, A., Challacombe, M., Gill, P. M. W., Johnson, B., Chen, W., Wong, M. W., Gonzalez, C., Pople, J. A., Gaussian 09, Revision C.0, Gaussian:, Inc., Wallingford, CT, 2009.
Hay, P. J. & Wadt, W. R. Ab initio effective core potentials for molecular calculations. Potentials for K to Au including the outermost core orbitals. J. Chem. Phys. 82, 299–310, doi:10.1063/1.448975 (1985).
Krishnan, R., Binkley, J. S., Seeger, R. & Pople, J. A. Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions. J. Chem. Phys 72, 650–654, doi:10.1063/1.438955 (1980).
Acknowledgements
The authors are grateful to the National Natural Science Foundation of China (Nos U1404109 and 11504334), the Natural Science Foundation of China (Grant no. 11647030) and Sichuan University of Science and Engineering (Grant nos 2015RC41, 2015RC44 and 2013RC10), Colleges and Universities in Henan Province Key Scientific Research Project (17A140031). This work was supported by Sichuan University of Science & Engineering High Performance Computing Center of Science & Engineering provided computational.
Author information
Authors and Affiliations
Contributions
Zi-Gang Shen and Yan-Fei Hu conceived the idea. Ya-Nan Tang and Wei-Guang Chen performed the calculations. Cheng-Gang Li, Zi-Gang Shen, Yan-Fei Hu, Bao-Zeng Ren wrote the manuscript and all authors contributed to revisions.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Li, CG., Shen, ZG., Hu, YF. et al. Insights into the structures and electronic properties of Cun+1 μ and CunSμ (n = 1–12; μ = 0, ±1) clusters. Sci Rep 7, 1345 (2017). https://doi.org/10.1038/s41598-017-01444-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-01444-6
This article is cited by
-
Studies on the structural and electronic characteristics of alkaline-earth metal Mgn+1 and BaMgn (n = 2–10) clusters and their anions
Theoretical Chemistry Accounts (2022)
-
Probing the structural evolution and electronic properties of divalent metal Be2Mgn clusters from small to medium-size
Scientific Reports (2020)
-
Structure and optical properties of (CuAg)n (n = 1–6) nanoalloy clusters within density functional theory framework
Journal of Nanoparticle Research (2020)
-
Interaction of H2O with (CuS)n, (Cu2S)n, and (ZnS)n small clusters (n = 1–4, 6): relation to the aggregation characteristics of metal sulfides at aqueous solutions
Journal of Molecular Modeling (2019)
-
Copper signalling: causes and consequences
Cell Communication and Signaling (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.