Main

Global warming depends on Earth’s sensitivity to increased CO2, but this sensitivity is tied to how clouds ‘feedback’ on global warming1. While recent progress has been made in constraining low-cloud feedbacks2,3, anvil cloud feedbacks are still leading sources of uncertainty in quantifying climate sensitivity4,5 despite decades of study6,7,8,9,10,11,12. The question thus remains: how do anvil clouds respond to and affect warming?

Changes in anvils were once thought to produce a strong negative climate feedback by acting as a solar thermostat6, but the observations that led to this conclusion are no longer considered evidence of such an effect7. Then anvils were thought to act as an infrared iris8. Criticisms of this study’s methodology followed9,13,14, but recent comprehensive assessments still cannot rule out a modest anvil cloud feedback4,5.

These assessments refer to an anvil cloud area (or amount) feedback, but it should be more precisely referred to as the altitude-corrected anvil cloud feedback (hereafter, the anvil cloud feedback) since it results from changes in area and optical depth but not changes in altitude, which are considered in a separate feedback15. Such decompositions are arbitrary because climate is unchanged by how it is analysed, but the choice is important because it can simplify interpretations of uncertainty16. Further decomposition may help constrain the anvil cloud feedback by answering which individual feedback—area or optical depth—truly embodies the uncertainty that obscures estimates of climate sensitivity.

Anvil cloud area is controlled in part by unconstrained microphysics17,18,19 but also by robust thermodynamic principles20,21, which predict a decrease in anvil area with warming as atmospheric static stability increases21. This is consistent with observed variability22,23,24 and most simulations25. The resulting area feedback might be small because anvils are radiatively neutral7,11,26. But how neutral must anvil clouds be for the feedback to be small? What if their radiative effect changes with warming? Or if more of Earth is then exposed to the radiative effects of underlying low clouds? These questions limit our ability to constrain the anvil cloud area feebdack.

Less is known about how cloud optical depth changes with warming27, but it will manifest in optical properties such as anvil cloud albedo. Changes in albedo might produce an even stronger feedback than changes in area because anvils have a much stronger effect in the short wave than in the net11. But how much does cloud albedo change with warming? And by how much must it change to produce a substantial feedback? These questions call for more quantitative answers before we can conclude which feedback is more uncertain.

We need a physically motivated decomposition that addresses confounding factors such as cloud overlap and distinguishes feedbacks from changes in anvil area and albedo. Since models must contend with representing unconstrained microphysics17,18,19, we primarily use observations. This rules out using purely model-based cloud feedback decompositions28,29. Cloud-controlling factor analysis, an observation-based method used mostly for constraining low-cloud feedbacks30, requires further study before being suitable for confidently constraining anvil cloud feedbacks. The connection between anvil clouds and their cloud-controlling factors are not as well understood as for low clouds.

In this Article, we derive an analytical cloud feedback decomposition based on the essential physics of cloud radiative effects. When it is combined with cloud observations, we can identify, understand and constrain cloud feedbacks transparently. We adopt a storyline approach31 where we examine the driving factors that control a cloud feedback and judge the plausibility of these factors to produce a particular feedback value by comparing with observations and theory derived from process understanding. This approach shows which feedback is constrained and which obscures estimates of climate sensitivity.

Conceptualizing cloud radiative effects

Clouds are complex, but for simplicity we divide them into two types, high (h) and low (ℓ), and subsume their properties into a few parameters obtainable from observations and reanalysis (Extended Data Table 1). They include area fractions fh, fℓ, emission temperatures Th, Tℓ and albedos αh, αℓ. Long-wave emissivities are not considered because most clouds have an emissivity close to one32. Clear-sky radiation is distilled to the incoming solar radiation S↓, surface albedo αs and outgoing long-wave radiation for a given surface temperature \({R}_{{{{\rm{cs}}}}}^{{T}_{{\mathrm{s}}}}\). Neglecting atmospheric absorption will bias the surface and cloud albedos to be higher, but this permits the derivation of analytical expressions for cloud radiative effects from high clouds and low clouds Ch, Cℓ; cloud-overlap effects mℓh; and the top-of-the-atmosphere (TOA) energy balance N. See Fig. 1 for an illustration and Methods for the derivation.

Fig. 1: Conceptualizing cloud radiative effects.
figure 1

We idealize the vertical cloud profile into two distinct layers that represent anvil clouds and low clouds with random overlap. Equations indicate the domain-averaged contribution of high clouds, low clouds and the surface to TOA energy balance. Their sums in the long wave and short wave are given by Equations (14) and (16), respectively. See Extended Data Table 1 for symbol meanings and values.

Full size image

Analytic feedbacks and the storyline approach

Feedbacks are computed by differentiating Earth’s TOA energy balance (Equation (16) minus Equation (14); Methods) with respect to the surface temperature Ts (ref. 33). To start, we have:

$$\lambda \equiv \frac{{\mathrm{d}}N}{{\mathrm{d}}{T}_{{\mathrm{s}}}}=\frac{{\mathrm{d}}{N}_{{{{\rm{cs}}}}}}{{\mathrm{d}}{T}_{{\mathrm{s}}}}+\frac{{\mathrm{d}}C}{{\mathrm{d}}{T}_{{\mathrm{s}}}},$$
(1)

where Ncs is the clear-sky TOA energy balance and C = Ch + Cℓ + mℓh is the net cloud radiative effect from all clouds. Plugging in the expressions for C (Equations (15) and (17); Methods), we arrive at an equation for tropical climate feedbacks:

$$\lambda ={\lambda }_{0}+\mathop{\sum}\limits_{i={\mathrm{h}},\ell }\left({\lambda }_{i}^{{{{\rm{area}}}}}+{\lambda }_{i}^{{{{\rm{temp}}}}}+{\lambda }_{i}^{{{{\rm{albedo}}}}}\right),$$
(2)

where λ0 is the reference response assuming a fixed anvil temperature and fixed relative humidity12,34; and \({\lambda }_{i}^{{{{\rm{area}}}}}\), \({\lambda }_{i}^{{{{\rm{temp}}}}}\) and \({\lambda }_{i}^{{{{\rm{albedo}}}}}\) are the feedbacks from changes in cloud area, cloud temperature and cloud albedo. See Methods for the derivation.

These analytic expressions serve our storyline approach by transparently and quantitatively relating changes in cloud properties to their radiative feedbacks. A more formal Bayesian framework of hypothesis testing (used in refs. 4,31 to constrain climate sensitivity by reconciling diverse lines of evidence) will not be necessary here because we consider only a process perspective on anvil changes.

The anvil cloud area feedback, \({\lambda }_{h}^{{{{\rm{area}}}}}\), comes from collecting terms from equation (1) that involve changes in anvil area dfh/dTs:

$${\lambda }_{h}^{{{{\rm{area}}}}}=\frac{{\mathrm{d}}\ln {f}_{{\mathrm{h}}}}{{\mathrm{d}}{T}_{{\mathrm{s}}}}\left({C}_{{\mathrm{h}}}+{m}_{\ell {\mathrm{h}}}\right).$$
(3)

This physically based derivation shows that \({\lambda }_{h}^{{{{\rm{area}}}}}\) depends on the fractional change in anvil area with warming \({\mathrm{d}}\ln {f}_{{\mathrm{h}}}/{\mathrm{d}}{T}_{{\mathrm{s}}}\) and the sum of the present-day anvil cloud radiative effect Ch and cloud-overlap effect mℓh. This aids our storyline approach in two ways. Fractional changes in cloud area are easier to interpret and bound than absolute changes. And although we computed the change in cloud radiative effect with warming, our derivation reveals the area feedback does not depend on the change in radiative effect, but its present-day value.

This means it can be quantified and used to constrain the feedback—the smaller Ch + mℓh is, the larger \({\mathrm{d}}\ln {f}_{{\mathrm{h}}}/{\mathrm{d}}{T}_{{\mathrm{s}}}\) has to be to produce a given \({\lambda }_{h}^{{{{\rm{area}}}}}\) bound. We can probe the plausibility of a given bound by quantifying the observed anvil cloud radiative effect, calculating the change in anvil area required to produce the bound and then comparing the required change in anvil area with the amount expected from theory, simulations and observations. If the expected change in anvil area is much smaller than the required change, then that bound can be refined.

Climatology

Bounding the area feedback requires quantifying the tropically averaged anvil cloud radiative effect and cloud-overlap effect (Ch + mℓh). These quantities are not directly observed and must be inferred from our simple model of cloud radiative effects.

We do this by inputting observations of cloud fraction from CALIPSO, a dataset from a satellite with lidar remote sensing 35, clear-sky radiation from CERES, a dataset from radiometers flying on multiple satellites 36, surface temperature from HadCRUT5, a dataset based on measurements from ships, buoys, and weather stations 37, and atmospheric temperature from ERA5, a climate reanalysis dataset 38, into our expression for the net cloud radiative effect (equations (15) and (17); Methods). Similar to ref. 22, fh and fℓ are identified as the maximum of the observed cloud fraction profile above and below 8 km, respectively, and for an optical depth range between 0.3 and 5.0. This excludes the thickest and thinnest portions of anvil clouds, but the relationship between cloud area and surface warming is robust to the optical depth range considered22. Th and Tℓ are the atmospheric temperature at the height of fh and fℓ.

We ensure goodness of fit between the inferred and observed cloud radiative effects by adding a single scaling factor n to the anvil cloud fraction, which accounts for collapsing the anvil cloud fraction profile into a single level (Methods and Extended Data Fig. 1). We treat n as a constant because spatio-temporal variations in the vertical profile of anvil clouds affect the optical depth and hence αh and αℓ, which already capture this variability as they are allowed to vary from year to year. In summary, n, αh and αℓ are tunable parameters to ensure consistency with observations at TOA (see Methods for further details).

We test our idealizations by comparing the observed net, short-wave and long-wave cloud radiative effects (Cobs, \({C}_{{{{\rm{obs}}}}}^{{{{\rm{sw}}}}}\) and \({C}_{{{{\rm{obs}}}}}^{{{{\rm{lw}}}}}\)) with their counterparts from the simple model (Fig. 2), which take the spatial fields of cloud fraction, temperature, albedo and clear-sky radiation as inputs. Our model can reproduce spatial patterns of long-wave and short-wave cloud radiative effects, although there are small deviations throughout the tropics: an underestimate of C in the southeast of China and an overestimate of C in the eastern Pacific, next to South America (Fig. 2c). Given the overall close agreement, we consider our model fit for evaluating the tropical anvil cloud area feedback.

Fig. 2: Observed net, short-wave and long-wave cloud radiative effects from CERES compared with their inferred counterparts.
figure 2

a, Observed cloud radiative effects. b, Inferred cloud radiative effects. c, Observed – inferred radiative effects. Tropical mean values are shown in the upper left of each panel. The West Pacific Warm Pool and East Pacific regions are boxed in a. The colour bar is the same for all plots.

Full size image

The climatological values of tropical quantities used in our calculations are summarized in Extended Data Table 1, and the cloud properties of interest are plotted in Fig. 3. The fh is maximum in the West Pacific Warm Pool, and fℓ is maximum along the East Pacific. Decomposing C into its contributions from different layers reveals that the net C is dominated by Cℓ. By comparison, the overlap effect mℓh is much smaller and varies less. The same is true for the high-cloud radiative effect Ch, which exhibits strong cancellation between its short-wave and long-wave components not just in the warm pool24,39,40, but across the tropics.

Fig. 3: Climatological values of tropical quantities.
figure 3

a,b, Effective anvil cloud fraction (a) and low-cloud fraction (b) from CALIPSO. The West Pacific Warm Pool and East Pacific regions are boxed to indicate regions of maximum anvil and low-cloud coverage, respectively. c–h, Inferred cloud radiative effects from Equations (18), (19) and (21). c, Net cloud radiative effect. d, Low cloud radiative effect. e, Cloud overlap effect. f, Shortwave high cloud radiative effect. g, Longwave high cloud radiative effect. h, High cloud radiative effect. Tropical mean values and standard deviations are shown in the upper left of each panel. Refer to Extended Data Fig. 2 to see mℓh and Ch plotted with a finer colour scale.

Full size image

Constraining the anvil cloud area feedback

We can now constrain the tropical anvil cloud area feedback. To scale our estimate of \({\lambda }_{{\mathrm{h}}}^{{{{\rm{area}}}}}\) to the global average, we multiply by the area ratio of the tropics and the globe, 1/2.

$$\langle {\lambda }_{{\mathrm{h}}}^{{{{\rm{area}}}}}\rangle =\frac{1}{2}\frac{{\mathrm{d}}\ln {f}_{{\mathrm{h}}}}{{\mathrm{d}}{T}_{{\mathrm{s}}}}\left({C}_{{\mathrm{h}}}+{m}_{\ell {\mathrm{h}}}\right).$$
(4)

The plausible lower bound of \(\langle {\lambda }_{{\mathrm{h}}}^{{{{\rm{area}}}}}\rangle > -0.4\) W m−2 K−1 comes from assuming the anvil cloud feedback in ref. 4 is due to area changes alone. This bound allows the possibility of an overall negative cloud feedback, a necessary ingredient for a climate sensitivity below 1.5 K (ref. 31). Our inferred tropical mean value of Ch + mℓh ≈ −1.5 W m−2 implies that \({\mathrm{d}}\ln {f}_{{\mathrm{h}}}/{\mathrm{d}}{T}_{{\mathrm{s}}}\) must be ~50% K−1 to achieve this bound. Following our storyline approach, we assess how plausible these cloud changes are by comparing them with the changes expected from theory21 and observed interannual variability22.

The stability iris hypothesis21 states that anvil cloud fraction fh is proportional to detrainment from deep convection. Owing to mass conservation, this detrainment is equal to the clear-sky convergence, ∂pω, where ω is the subsidence vertical velocity (hPa day−1). If we make the ansatz that ∂pω is proportional to ω at the level of detrainment (h), then the fractional change in anvil area is equal to the fractional change in subsidence velocity at the anvil level:

$$\frac{{\mathrm{d}}\ln {f}_{{\mathrm{h}}}}{{\mathrm{d}}{T}_{{\mathrm{s}}}}=\frac{{\mathrm{d}}\ln {\omega }_{{\mathrm{h}}}}{{\mathrm{d}}{T}_{{\mathrm{s}}}}.$$
(5)

The subsidence velocity can be written as the quotient of the clear-sky radiative flux divergence in temperature coordinates (−∂TF) and the difference between actual and dry lapse rates19:

$$\omega =\frac{-{\partial }_{{\mathrm{T}}}F}{1/{{\Gamma }}-1/{{{\Gamma }}}_{{\mathrm{d}}}}.$$
(6)

Given that ∂TF does not vary with surface temperature41, if we further assume that Γh, the lapse rate at the anvil level, is moist adiabatic, then the change in cloud area can be computed with a few representative numbers. Assuming the surface warms from Ts = 298 K to 299 K and the anvil cloud warms from Th = 221 K to anywhere between 221 and 221.4 K (a typical range of anvil warming42, which affects the static stability the anvil finds itself in21), then we expect that anvils change in area at about

$$\begin{array}{ll}\displaystyle\frac{{\mathrm{d}}\ln {f}_{{\mathrm{h}}}}{{\mathrm{d{}}T}_{{\mathrm{s}}}}&=\displaystyle-\frac{{\mathrm{d}}\ln (1/{{{\Gamma }}}_{{\mathrm{h}}}-1/{{{\Gamma }}}_{{\mathrm{d}}})}{{\mathrm{d}}{T}_{s}}\,({{{\rm{stability}}}}\,{{{\rm{iris}}}})\\\displaystyle&\approx -1\,{{{\rm{to}}}}-4 \% \,{{{{\rm{K}}}}}^{-1},\end{array}$$
(7)

depending on anvil warming. Despite the simplifications, the result is similar to the mean and standard deviation of large-domain models in RCEMIP (Radiative–Convective Equilibrium Model Intercomparison Project) (−2 ± 5% K−1 for cloud-resolving models, −2 ± 4% K−1 for all models; table S5 of ref. 42).

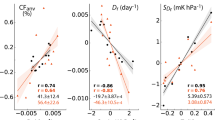
Now turning to ENSO- (El Niño/Southern Oscillation-) driven interannual variability, we compute annual averages of \(\ln {f}_{{\mathrm{h}}}\) and Ts (tropical mean surface temperature) from July to June, similar to ref. 22, and plot their scatter in Fig. 4. The line of best fit for this relation gives

$$\frac{{\mathrm{d}}\ln {f}_{{\mathrm{h}}}}{{\mathrm{d}}{T}_{{\mathrm{s}}}}\approx -7\,{{{\rm{to}}}}-11 \% \,{{{{\rm{K}}}}}^{-1}.\,({{{\rm{interannual}}}}\,{{{\rm{variability}}}})$$
(8)

This change is larger than our simple estimate and from RCEMIP; it is also larger than the change of −5% K−1 inferred from interannual variability in Atmospheric Model Intercomparison Project runs with the Institut Pierre Simon Laplace, Max Planck Institute and National Center for Atmospheric Research models (see figure S3 of ref. 21). However, since all of these estimates of anvil cloud changes are still much smaller than what is required to achieve the lower bound of \(\langle {\lambda }_{{\mathrm{h}}}^{{{{\rm{area}}}}}\rangle =-0.4\) W m−2 K−1, the bounds of the area feedback can be refined.

Fig. 4: Interannual changes in tropical mean anvil cloud area and anvil cloud albedo as a function of surface temperature.
figure 4

a, Area change. b, Albedo change. Each point represents one year from 2006 to 2016. In each subplot, the slope, correlation of the best fit line and its standard error are shown. Standard error in the slope due to limited sampling is indicated by shading. In b, the regression is calculated excluding the 2015--2016 El Niño. See Extended Data Fig. 4 for regression calculated including the El Niño and the regression calculated for low-cloud albedo.

Full size image

Care should be taken when inferring the long-term anvil cloud area change from present-day observations. Anvil area is better correlated with upper tropospheric stability than with surface temperature22,23, and surface- and upper-tropospheric warming (and thus changes in stability) do not always go hand in hand on interannual timescales23,43. ENSO-driven variability is associated with reorganization of deep convection44, which may further alter anvil area’s sensitivity to surface temperature. Anvil clouds are about half as sensitive for long-term warming as compared with interannual variability in the Institut Pierre Simon Laplace general circulation model23, the only model where such analysis has been done.

Given the evidence from theory (equation (7)), observations (equation (8)) and simulations21,23,25, we estimate that anvil cloud area changes at about

$$\frac{{\mathrm{d}}\ln {f}_{{\mathrm{h}}}}{{\mathrm{d}}{T}_{{\mathrm{s}}}}=-4\,\pm \,2\, \% \,{{{{\rm{K}}}}}^{-1}.\,({{{\rm{best}}}}\,{{{\rm{estimate}}}})$$
(9)

We found Ch + mℓh = − 1.5 W m−2, but other studies have estimated −4 W m−2 (ref. 40), 0.6 W m−2 (ref. 17) and 2 W m−2 (ref. 45). This is probably due to methodological differences and because anvil clouds have no precise definition. CERES TOA fluxes have their own small uncertainties36, and considering mid-level clouds as distinct entities from low clouds adds an additional uncertainty of 0.5 W m−2 (Methods). Therefore, we estimate the anvil cloud radiative effect and cloud-overlap effect to be,

$${C}_{{\mathrm{h}}}+{m}_{\ell {\mathrm{h}}}=-1\pm 3\,{{{{\rm{W}}\,{\rm{m}}}}}^{-2}.\,({{{\rm{best}}}}\,{{{\rm{estimate}}}})$$
(10)

Using these best estimates in equation (4), we get our best estimate of the anvil area feedback to within one standard deviation:

$$\langle {\lambda }_{{\mathrm{h}}}^{{{{\rm{area}}}}}\rangle =0.02\,\pm \,0.07\,{{{{\rm{W}}\,{\rm{m}}}}}^{-2}\,{{{{\rm{K}}}}}^{-1}.\,({{{\rm{best}}}}\,{{{\rm{estimate}}}})$$
(11)

Overlap effects with low-level clouds are accounted for (mℓh = 0.5 W m−2): they dampen the anvil cloud area feedback by about 25%. Our estimate for the anvil cloud area feedback is positive but ten times smaller in magnitude and three times more constrained than the World Climate Research Programme estimate of −0.2 ± 0.2 W m−2 K−1 for the anvil cloud feedback4. We deem the area feedback is now well constrained because its uncertainty is comparable to other assessed cloud feedbacks4,5. Our results provide a rigorous basis to qualitative arguments for a small area feedback7,11,26. What about the anvil cloud albedo feedback?

Uncertainty in the anvil cloud albedo feedback

A substantial feedback could be produced without any change in anvil area11,29. To see why, consider the anvil cloud albedo feedback,

$${\lambda }_{{\mathrm{h}}}^{{{{\rm{albedo}}}}}=\frac{1}{2}\frac{{\mathrm{d}}\ln {\alpha }_{{\mathrm{h}}}}{{\mathrm{d}}{T}_{{\mathrm{s}}}}\left({C}_{{\mathrm{h}}}^{{{{\rm{sw}}}}}+{m}_{\ell {\mathrm{h}}}^{{{{\rm{sw}}}}}\right).$$
(12)

It follows a form similar to the area feedback but depends on the fractional change in cloud albedo with warming \({\mathrm{d}}\ln {\alpha }_{{\mathrm{h}}}/{\mathrm{d}}{T}_{{\mathrm{s}}}\), the short-wave anvil cloud radiative effect \({C}_{{\mathrm{h}}}^{{{{\rm{sw}}}}}\) and the short-wave cloud-overlap effect \({m}_{\ell {\mathrm{h}}}^{{{{\rm{sw}}}}}\) (see Methods for derivation).

Given that \({C}_{{\mathrm{h}}}^{{{{\rm{sw}}}}}+{m}_{\ell {\mathrm{h}}}^{{{{\rm{sw}}}}}\approx -25\) W m−2 (Extended Data Table 1), producing \({\lambda }_{{\mathrm{h}}}^{{{{\rm{albedo}}}}}=-0.2\) W m−2 K−1 requires a fractional change in cloud albedo of only 1–2% K−1. How plausible is such a change?

Computing the anvil cloud albedos for each year (Methods), we find \({\mathrm{d}}\ln {\alpha }_{{\mathrm{h}}}/{\mathrm{d}}{T}_{{\mathrm{s}}}\approx\) 6–16% K−1 and a particularly large increase in albedo during the 2015–2016 El Niño (Fig. 4b) for reasons that are unclear—anvil height and temperature are not as sensitive to El Niño (Extended Data Fig. 3); and changes in low-cloud albedo are more ambiguous than anvil cloud albedo (Extended Data Fig. 4). Such a change implies \({\lambda }_{{\mathrm{h}}}^{{{{\rm{albedo}}}}}\approx 1/2\times 10 \%\) K−1 × −25 W m\({}^{-2} \sim {{{\mathcal{O}}}}(-1)\) W m−2 K−1, a large negative feedback, but this should be interpreted carefully.

First, our diagnosed values of cloud albedo may be biased by ignoring clear-sky atmospheric absorption, assuming a spatially uniform cloud albedo, excluding the thickest (τ > 5) and thinnest (τ < 0.3) portions of anvil clouds and assuming a cloud emissivity of 1. We have shown an increase in anvil cloud albedo with warming, whereas another observational study showed anvil cloud thinning with warming and thus a decrease in cloud albedo46. Yet another observational study showed ice-water path, a proxy for optical depth, to be non-monotonic with sea surface temperatures47.

Second, there is no guarantee that long-term warming will follow interannual warming.

Third, there is no compelling, quantitative understanding of cloud condensate or albedo changes. The cloud albedo response in simulations warrants caution because of large intermodel spreads in climatology of cloud condensate and cloud radiative effects42. A precise answer may depend on disentangling the uncertain response of precipitation efficiency with warming24,27.

Fourth, if anvil cloud optical depth is increasing, then long-wave emissivity εh will increase too and produce a countervailing positive long-wave feedback,

$${\lambda }_{{\mathrm{h}}}^{{{{\rm{emissivity}}}}}=\frac{1}{2}\frac{{\mathrm{d}}\ln {\epsilon }_{{{h}}}}{{\mathrm{d}}{T}_{{\mathrm{s}}}}\left({C}_{{\mathrm{h}}}^{{{{\rm{lw}}}}}+{m}_{\ell {\mathrm{h}}}^{{{{\rm{lw}}}}}\right),$$
(13)

but with an uncertain magnitude (see Methods for further discussion). The net result of these competing components of the optical depth feedback are unclear, although they might account for the negative anvil cloud feedback found in the observation study48 that forms the basis of estimates in comprehensive assessments4,5.

Given the lack of understanding of albedo changes, conflicting observational evidence and a potentially countervailing long-wave anvil emissivity feedback, we conclude the magnitude and uncertainty of the anvil cloud feedback in these previous assessments is embodied primarily by optical depth changes. Convective aggregation may also contribute some uncertainty if it changes anvil optical depth49.

Implications of uncertainty

A rigorous assessment of the anvil cloud area feedback was lacking because the confounding factors of cloud overlap and a changing cloud radiative effect on the feedback could not be accounted for. We leveraged the arbitrary nature of feedback decompositions to derive a physically based decomposition that could address these challenges. With it, we constrained the bounds on the anvil cloud area feedback by creating a physical storyline for its previous bounds and then refuting that storyline with observations and theory.

Much attention has been devoted to changes in anvil cloud area, but optical depth changes are now the most uncertain aspect of the anvil cloud response to warming. Focusing on them will promise enhanced returns for constraining climate sensitivity, but doing so with observations alone will be hard because detecting fractional change in cloud albedo at the precision of 1% K−1 nears the limit of active sensor global cloud observing systems50.

Constraining these feedbacks will require a mechanistic understanding of how anvil clouds partition themselves into their convective and stratiform components11,17. Pursuing such an understanding would benefit other approaches to constraining anvil cloud optical depth feedbacks, including emergent constraints, model intercomparisons, cloud-controlling factor analysis, process studies and climatological predictors, because confidence in these methods ultimately derives from understanding the physical relationships among environmental changes, cloud changes and the TOA response.

Such a physically transparent approach has even broader implications. Communicating with the public about our confidence (or lack thereof) in clouds and climate change is hard. However, a physical theory of cloud feedbacks that can constrain, quantify and interpret models and observations, like the one proposed here, could help clear the cloud of uncertainty.

Methods

Conceptualizing cloud radiative effects

We start with an idealized model of cloud radiative effects at the TOA. Although tropical cloudiness is expected to be trimodal51, for simplicity we will consider a domain containing two cloud types: high clouds (h) and low clouds (ℓ). (Many assessments of cloud feedbacks also use this bi-modal decomposition4.) Each type has an emission temperature (Th, Tℓ), an optically thick cloud fraction (fh, fℓ) and an albedo (αh, αℓ) (Fig.1). Mid-level clouds will be considered in our error analysis.

The TOA energy balance is N = S − R, where S is the absorbed short-wave radiation and R is the outgoing long-wave radiation. The cloud radiative effect C is the difference in N between all-sky and clear-sky (cs) conditions, C = N − Ncs (ref. 52); C can be decomposed into long-wave and short-wave components: C = Csw + Clw.

In the long-wave component, clear-sky regions with a surface temperature Ts will emit to space with an outgoing long-wave radiation of \({R}_{{{{\rm{cs}}}}}^{{T}_{{\mathrm{s}}}}\), but a portion will be blocked by clouds. Long-wave emissivity will not be considered because most clouds have an emissivity close to one32. Assuming random overlap between high clouds and low clouds53, the domain-averaged clear-sky contribution is \({R}_{{{{\rm{cs}}}}}^{{T}_{{\mathrm{s}}}}(1-{f}_{{\mathrm{h}}})(1-{f}_{\ell })\). Low clouds are so close to the surface that we treat their emission to space like clear-sky surface emission but at Tℓ. Their domain-averaged contribution is \({R}_{{{{\rm{cs}}}}}^{{T}_{\ell }}{f}_{\ell }(1-{f}_{{\mathrm{h}}})\). Since \({R}_{{{{\rm{cs}}}}}^{{T}_{s}}\) is an approximately linear function of temperature54, \({R}_{{{{\rm{cs}}}}}^{{T}_{\ell }}\approx {R}_{{{{\rm{cs}}}}}^{{T}_{s}}+{\lambda }_{{{{\rm{cs}}}}}({T}_{s}-{T}_{\ell })\), where λcs ≡ −dRcs/dTs ≈ −2 W m−2 K−1 is a representative value for the long-wave clear-sky feedback34. We assume that high clouds are so high that they emit directly to space33 with a value \(\sigma {T}_{{\mathrm{h}}\,}^{4}{f}_{{\mathrm{h}}}\). Summing these contributions, the domain-averaged outgoing long-wave radiation is

$$R={R}_{{{{\rm{cs}}}}}^{{T}_{{\mathrm{s}}}}(1-{f}_{{\mathrm{h}}})+\sigma {T}_{{\mathrm{h}}\,}^{4}{f}_{{\mathrm{h}}}+{\lambda }_{{{{\rm{cs}}}}}({T}_{{\mathrm{s}}}-{T}_{\ell })(1-{f}_{{\mathrm{h}}}){f}_{\ell },$$
(14)

and the long-wave cloud radiative effect −(R − Rcs) is

$$\displaystyle{C}^{{{{\rm{lw}}}}}={R}_{{{{\rm{cs}}}}\,}^{{T}_{{\mathrm{s}}}}{f}_{{\mathrm{h}}}-\sigma {T}_{{\mathrm{h}}\,}^{4}{f}_{{\mathrm{h}}}-{\lambda }_{{{{\rm{cs}}}}}({T}_{{\mathrm{s}}}-{T}_{\ell })(1-{f}_{{\mathrm{h}}}){f}_{\ell }.$$
(15)

In the short-wave component, there is an incoming solar radiation S↓, and we assume that there is no absorption except at the surface. High clouds reflect a portion αhfh back to space. The transmitted radiation then hits low clouds, which reflect a portion αℓfℓ back to space (ignoring secondary reflections with the anvils above). The transmitted radiation then hits the surface, which reflects a portion αs back out to space and absorbs the rest. Summing these contributions, the domain-averaged absorbed short-wave radiation at TOA is

$$\displaystyle S={S}^{\downarrow }(1-{\alpha }_{{\mathrm{h}}\,}{f}_{{\mathrm{h}}})(1-{\alpha }_{\ell }{f}_{\ell })(1-{\alpha }_{{\mathrm{s}}}).$$
(16)

The TOA-absorbed short-wave in clear skies is Scs = S↓(1 − αs), so the short-wave cloud radiative effect (S − Scs) is:

$$\displaystyle{C}^{{{{\rm{sw}}}}}={S}_{{{{\rm{cs}}}}}\left(-{\alpha }_{{\mathrm{h}}\,}{f}_{{\mathrm{h}}}-{\alpha }_{\ell }{f}_{\ell }+{\alpha }_{{\mathrm{h}}}{\alpha }_{\ell }{f}_{{\mathrm{h}}}{f}_{\ell }\right).$$
(17)

It will prove helpful to separate the contribution of isolated high clouds and isolated low clouds to the net cloud radiative C. Setting fℓ = 0 yields the isolated high-cloud radiative effect:

$$\displaystyle{C}_{{\mathrm{h}}}=\left(-{S}_{{{{\rm{cs}}}}}{\alpha }_{{\mathrm{h}}}+{R}_{{{{\rm{cs}}}}}^{{T}_{{\mathrm{s}}}}-\sigma {T}_{{\mathrm{h}}}^{4}\right){f}_{{\mathrm{h}}}.$$
(18)

Setting fh = 0 yields the isolated low-cloud radiative effect:

$$\displaystyle{C}_{\ell }=\left(-{S}_{{{{\rm{cs}}}}}{\alpha }_{\ell }-{\lambda }_{{{{\rm{cs}}}}}({T}_{{\mathrm{s}}}-{T}_{\ell })\right){f}_{\ell }.$$
(19)

The total cloud radiative effect C in terms of each cloud is:

$$C={C}_{{\mathrm{h}}}+{C}_{\ell }+{m}_{\ell {\mathrm{h}}},$$
(20)

where

$${m}_{\ell {\mathrm{h}}}=\left({S}_{{{{\rm{cs}}}}}{\alpha }_{\ell }{\alpha }_{{\mathrm{h}}}+{\lambda }_{{{{\rm{cs}}}}}({T}_{{\mathrm{s}}}-{T}_{\ell })\right){f}_{\ell }{f}_{{\mathrm{h}}},$$
(21)

represents the cloud-overlap masking effect. Note that Ch ∝ fh, Cℓ ∝ fℓ and mℓh ∝ fℓfh.

Feedback decomposition

We will now derive various cloud feedbacks from these equations and assume a fixed relative humidity. The lapse-rate feedback has been shown to be small when using this reference response16,55, so it will be ignored here.

$$\begin{array}{l}\lambda \equiv \displaystyle\frac{{\mathrm{d}}N}{{\mathrm{d}}{T}_{{\mathrm{s}}}}\\ =\displaystyle\frac{{S}_{{{{\rm{cs}}}}}}{{\mathrm{d}}{T}_{{\mathrm{s}}}}-\displaystyle\frac{{\mathrm{d}}{R}_{{{{\rm{cs}}}}}^{{T}_{{\mathrm{s}}}}}{{\mathrm{d}}{T}_{{\mathrm{s}}}}+\displaystyle\frac{{\mathrm{d}}C}{{\mathrm{d}}{T}_{{\mathrm{s}}}}\\ ={\lambda }_{{{{\rm{cs}}}}}(1-{f}_{{\mathrm{h}}})\\\quad +({R}_{{{{\rm{cs}}}}}^{{T}_{{\mathrm{s}}}}-\sigma {T}_{{\mathrm{h}}}^{4}+{\lambda }_{{{{\rm{cs}}}}}({T}_{{\mathrm{s}}}-{T}_{\ell }){f}_{\ell }-{S}_{{{{\rm{cs}}}}}{\alpha }_{{\mathrm{h}}}+{S}_{{{{\rm{cs}}}}}{\alpha }_{{\mathrm{h}}}{\alpha }_{\ell }{f}_{\ell })\displaystyle\frac{{\mathrm{d}}{f}_{{\mathrm{h}}}}{{\mathrm{d}}{T}_{{\mathrm{s}}}}\\\quad +(-{\lambda }_{{{{\rm{cs}}}}}({T}_{{\mathrm{s}}}-{T}_{\ell })(1-{f}_{{\mathrm{h}}})-{S}_{{{{\rm{cs}}}}}{\alpha }_{\ell }+{S}_{{{{\rm{cs}}}}}{\alpha }_{{\mathrm{h}}}\,{f}_{{\mathrm{h}}}{\alpha }_{\ell })\displaystyle\frac{{\mathrm{d}}{f}_{\ell }}{{\mathrm{d}}{T}_{{\mathrm{s}}}}\\\quad +-4\sigma {T}_{{\mathrm{h}}}^{3}\,{f}_{{\mathrm{h}}}\displaystyle\frac{{\mathrm{d}}{T}_{{\mathrm{h}}}}{{\mathrm{d}}{T}_{{\mathrm{s}}}}\\\quad +-{\lambda }_{{{{\rm{cs}}}}}(1-{f}_{{\mathrm{h}}}){f}_{\ell }\displaystyle\frac{{\mathrm{d}}({T}_{{\mathrm{s}}}-{T}_{\ell })}{{\mathrm{d}}{T}_{{\mathrm{s}}}}\\\quad +(-{S}_{{{{\rm{cs}}}}}\,{f}_{{\mathrm{h}}}+{S}_{{{{\rm{cs}}}}}\,{f}_{{\mathrm{h}}}{\alpha }_{\ell }{f}_{\ell })\displaystyle\frac{{\mathrm{d}}{\alpha }_{{\mathrm{h}}}}{{\mathrm{d}}{T}_{{\mathrm{s}}}}\\\quad +(-{S}_{{{{\rm{cs}}}}}\,{f}_{\ell }+{S}_{{{{\rm{cs}}}}}{\alpha }_{{\mathrm{h}}}\,{f}_{{\mathrm{h}}}\,{f}_{\ell })\displaystyle\frac{{\mathrm{d}}{\alpha }_{\ell }}{{\mathrm{d}}{T}_{{\mathrm{s}}}}\\\quad -{S}^{\downarrow }(1-{\alpha }_{{\mathrm{h}}}\,{f}_{{\mathrm{h}}})(1-{\alpha }_{\ell }{f}_{\ell })\displaystyle\frac{{\mathrm{d}}{\alpha }_{{\mathrm{s}}}}{{\mathrm{d}}{T}_{{\mathrm{s}}}}\\\quad -({T}_{{\mathrm{s}}}-{T}_{\ell })(1-{f}_{{\mathrm{h}}}){f}_{\ell }\displaystyle\frac{{\mathrm{d}}{\lambda }_{{{{\rm{cs}}}}}}{{\mathrm{d}}{T}_{{\mathrm{s}}}}.\end{array}$$
(22)

Recognizing that many of these terms can be rewritten as cloud radiative effects, we get:

$$\begin{array}{l}\lambda ={\lambda }_{{{{\rm{cs}}}}}(1-{f}_{{\mathrm{h}}})\\ \quad\ +\left({C}_{{\mathrm{h}}}+{m}_{\ell {\mathrm{h}}}\right)\displaystyle\frac{{\mathrm{d}}\ln {f}_{{\mathrm{h}}}}{{\mathrm{d}}{T}_{{\mathrm{s}}}}\\ \quad\ +\left({C}_{\ell }+{m}_{\ell {\mathrm{h}}}\right)\displaystyle\frac{{\mathrm{d}}\ln {f}_{\ell }}{{\mathrm{d}}{T}_{{\mathrm{s}}}}\\ \quad\ -\,4\sigma {T}_{{\mathrm{h}}\,}^{3}\;{f}_{{\mathrm{h}}}\displaystyle\frac{{\mathrm{d}}{T}_{{\mathrm{h}}}}{{\mathrm{d}}{T}_{{\mathrm{s}}}}\\ \quad\ -\,{\lambda }_{{{{\rm{cs}}}}}(1-{f}_{{\mathrm{h}}})\;{f}_{\ell }\displaystyle\frac{{\mathrm{d}}({T}_{{\mathrm{s}}}-{T}_{\ell })}{{\mathrm{d}}{T}_{{\mathrm{s}}}}\\ \quad\ +\left({C}_{{\mathrm{h}}}^{{{{\rm{sw}}}}}+{m}_{\ell {\mathrm{h}}}^{{{{\rm{sw}}}}}\right)\displaystyle\frac{{\mathrm{d}}\ln {\alpha }_{{\mathrm{h}}}}{{\mathrm{d}}{T}_{{\mathrm{s}}}}\\ \quad\ +\left({C}_{\ell }^{{{{\rm{sw}}}}}+{m}_{\ell {\mathrm{h}}}^{{{{\rm{sw}}}}}\right)\displaystyle\frac{{\mathrm{d}}\ln {\alpha }_{\ell }}{{\mathrm{d}}{T}_{{\mathrm{s}}}}\\ \quad\ +\,{C}_{{\mathrm{s}}}\displaystyle\frac{{\mathrm{d}}\ln {\alpha }_{{\mathrm{s}}}}{{\mathrm{d}}{T}_{{\mathrm{s}}}},\end{array}$$
(23)

where we have assumed that dλcs/dTs is negligible, and Cs = −S↓(1 − αhfh)(1 − αℓ)αs is the surface albedo radiative effect, which is equivalent to the ‘cryosphere radiative forcing’56.

Now we name and then describe each term:

$$\displaystyle\lambda ={\lambda }_{0}+{\lambda }_{{\mathrm{h}}}^{{{{\rm{area}}}}}+{\lambda }_{\ell }^{{{{\rm{area}}}}}+{\lambda }_{{\mathrm{h}}}^{{{{\rm{temp}}}}}+{\lambda }_{\ell }^{{{{\rm{temp}}}}}+{\lambda }_{{\mathrm{h}}}^{{{{\rm{albedo}}}}}+{\lambda }_{\ell }^{{{{\rm{albedo}}}}}+{\lambda }_{{\mathrm{s}}}^{{{{\rm{albedo}}}}}$$
(24)

where λ0 is the anvil cloud-masked long-wave clear-sky feedback. It is our null hypothesis for the climate response to warming because it assumes fixed relative humidity; fixed anvil temperature, area and albedo; fixed low-cloud temperature difference, area and albedo; and fixed surface albedo; \({\lambda }_{{\mathrm{h}}}^{{{{\rm{area}}}}}\) and \({\lambda }_{\ell }^{{{{\rm{area}}}}}\) are the feedbacks from a changing anvil cloud and low-cloud area, respectively; \({\lambda }_{{\mathrm{h}}}^{{{{\rm{temp}}}}}\) is the feedback from a changing anvil cloud temperature; \({\lambda }_{\ell }^{{{{\rm{temp}}}}}\) is the feedback from a changing temperature difference between low clouds and the surface; \({\lambda }_{{\mathrm{h}}}^{{{{\rm{albedo}}}}}\), \({\lambda }_{\ell }^{{{{\rm{albedo}}}}}\) and \({\lambda }_{{\mathrm{s}}}^{{{{\rm{albedo}}}}}\) are the feedbacks from a changing albedo of anvil clouds, low clouds and surface, respectively. We omit the surface albedo feedback from equation (2) because we are interested in tropical climate.

For simplicity, we have assumed that cloud emissivities of high clouds and low clouds (εh, εℓ) are equal to one32. However, if we relax this assumption for completeness, one can show this leads to a high-cloud and low-cloud emissivity feedback with the following forms:

$$\begin{array}{ll}{\lambda }_{{\mathrm{h}}}^{{{\displaystyle{\rm{emissivity}}}}}&=\displaystyle\left({C}_{{\mathrm{h}}}^{{{{\rm{lw}}}}}+{m}_{\ell {\mathrm{h}}}^{{{{\rm{lw}}}}}\right)\displaystyle\frac{{\mathrm{d}}\ln {\epsilon }_{{{h}}}}{{\mathrm{d}}{T}_{{\mathrm{s}}}},\\ {\lambda }_{\ell }^{{{\displaystyle{\rm{emissivity}}}}}&=\left({C}_{\ell }^{{{{\rm{lw}}}}}+{m}_{\ell {\mathrm{h}}}^{{{{\rm{lw}}}}}\right)\displaystyle\frac{{\mathrm{d}}\ln {\epsilon }_{\ell }}{{\mathrm{d}}{T}_{{\mathrm{s}}}},\end{array}$$
(25)

which closely resemble the form of the cloud albedo feedback. Some of the other feedbacks will have small modifications, but they are unimportant here.

Climatology

We combine monthly mean satellite observations, surface temperature measurements and reanalysis and re-grid all datasets onto a common 2° latitude × 2.5° longitude grid over the tropical belt (30° N−30°S) from June 2006 to December 2016. Although anvil clouds populate the globe57, it is less clear how extratropical anvils change with warming. Most cloud feedback assessments consider only tropical anvil clouds, so we will follow this convention.

From the CALIPSO lidar satellite dataset35, we obtain vertical profiles of cloud fraction for optical depths of 0.3 ≤ τ ≤ 5.0. This range excludes both deep convective cores and optically thin cirrus unconnected to deep convection22. We then vertically smooth the native vertical 60 m resolution profiles with a 480 m running mean. For anvil detection, we consider ice-cloud data above 8 km. For shallower clouds, we consider the sum of ice and liquid cloud fraction data below 8 km. The diagnosed cloud fractions are the absolute maximum of the profile in their respective domains, but if the identified maximum does not exceed a cut-off (fcut = 0.03), then that region is considered to be clear sky (f = 0). This algorithm is applied to every grid point and then tropically averaged. Our approach thus far resembles that of ref. 22, just extended to include low clouds.

To match the inferred cloud radiative effects with the observed, we consider an effective cloud fraction \({f}_{{\mathrm{h}}}=n\times {{{\rm{Max}}}}(\,f(z))\) for high clouds, where n is a single tuned parameter to account for collapsing the high-cloud profile into one level. This accounting is more important for high clouds, as their profile’s full width–half maximum is ~5 km (Extended Data Fig. 1), whereas low clouds are already localized with a full width–half maximum of ~1 km (Extended Data Fig. 1). While n could be more rigorously derived from detailed considerations of cloud overlap53, we opt to determine n by fitting the predicted tropical- and time-averaged long-wave cloud radiative effect Clw to its observed counterpart \({C}_{{{{\rm{obs}}}}}^{{{{\rm{lw}}}}}\) from CERES (see Cloud fraction section). Doing so yields a spatially and temporally constant value of n = 1.7. This value lies between that from assuming maximum overlap between each layer of the anvil cloud, which yields n = 1, and random overlap, which yields n ≈ 5.

The height of the diagnosed maximum cloud fraction is then used to diagnose the cloud temperatures Th, Tℓ at each space and time by selecting the corresponding atmospheric temperature in ERA5 reanalysis38. We use the HadCRUT5 dataset37 to diagnose the surface temperature Ts.

We use monthly mean TOA radiative fluxes, both clear sky and all sky, from the CERES satellite EBAF Ed4.1 product36,58. We diagnose the surface albedo αs as the ratio of upwelling clear-sky short-wave radiation \({S}_{{{{\rm{cs}}}}}^{\uparrow }\) to incoming short-wave radiation S↓. However, because short-wave absorption and scattering occurs in the real atmosphere, our surface albedo is more accurately characterized as the planetary clear-sky albedo59. We diagnose the cloud albedos by assuming that they are constant in space and by fitting the predicted tropical- and time-averaged short-wave cloud radiative effect Csw to its observed counterpart \({C}_{{{{\rm{obs}}}}}^{{{{\rm{sw}}}}}\) from CERES. With two unknowns, we must provide two constraints. We do this by splitting the tropics into two distinct dynamical regimes on the basis of a threshold of 500 hPa midtropospheric velocity ω500 = 25 hPa day−1 obtained from monthly ERA5 reanalysis data. These regions are treated as independent so that they provide two constraints. The regime-averaged short-wave radiative effect is then fitted to its observed counterpart by using the fsolve function from the scipy.optimize python module. (The precise threshold of 25 hPa day−1 was chosen because it resulted in the smallest root mean square error between Csw and \({C}_{{{{\rm{obs}}}}}^{{{{\rm{sw}}}}}\)).

Cloud fraction

We use the CALIPSO Lidar Satellite CAL_LID_L3_Cloud_Occurence-Standard-V1-00 data product60, the same dataset used in ref. 22. While the high-cloud fraction could simply be diagnosed as the maximum cloud fraction of the profile (t\({f}_{{\mathrm{h}}}={{{\rm{Max}}}}(\,f(z))\)), the calculated long-wave cloud radiative effect Clw will not match with observations. To rectify this, we consider using a single tuning parameter, n. That is, we have an effective cloud fraction \({f}_{{\mathrm{h}}}=n\times {{{\rm{Max}}}}(\,f(z))\) that accounts for representing a cloud profile with a single level.

We first demand that n be constant with space and time to ensure that areal changes (changes in fh) are not artificially convolved with vertical changes that relate to optical depth and albedo (α). This decision projects the spatio-temporal variability in the vertical extent of anvils more onto α than onto fh.

We then fit the predicted tropically and temporally averaged long-wave radiative effect Clw to its observed counterpart \({C}_{{{{\rm{obs}}}}}^{{{{\rm{lw}}}}}\) from CERES. Given these constraints, and the inputs to equation (15), n can be solved for as

$$\displaystyle n=\displaystyle\frac{\langle {C}_{{{{\rm{obs}}}}}^{{{{\rm{lw}}}}}+{\lambda }_{{{{\rm{cs}}}}}({T}_{{\mathrm{s}}}-{T}_{\ell }){f}_{\ell }\rangle }{\langle {R}_{{{{\rm{cs}}}}}\max (f(z))-\sigma {T}_{{\mathrm{h}}}^{4}\max (\,f(z))+{\lambda }_{{{{\rm{cs}}}}}({T}_{{\mathrm{s}}}-{T}_{\ell }){f}_{\ell }\max (\,f(z))\rangle },$$
(26)

where 〈⋅〉 denotes a tropical and temporal average.

When plotting the scatter of \(\ln {f}_{{\mathrm{h}}}\) against Ts in Fig. 4, grid cells with fh = 0 are excluded to avoid logarithmic divergences.

Uncertainty analysis for area feedback

Uncertainty in our estimates of \({\mathrm{d}}\ln {f}_{{\mathrm{h}}}/{\mathrm{d}}{T}_{{\mathrm{s}}}\) and Ch + mℓh translate to uncertainty in \({\lambda }_{{\mathrm{h}}}^{{{{\rm{area}}}}}\). As stated in the main text, we estimate \({\mathrm{d}}\ln {f}_{{\mathrm{h}}}/{\mathrm{d}}{T}_{{\mathrm{s}}}=-4\pm 2{{{ \% \,{\rm{K}}}}}^{-1}\). For the anvil cloud radiative effect, we found Ch + mℓh = −1.5 W m−2. However, other observational studies have found it to be −4 W m−2 (ref. 40), 0.6 W m−2 (ref. 17) and 2 W m−2 (ref. 45). This is probably due to methodological differences and the fact that anvil clouds have no precise definition. Furthermore, CERES TOA monthly fluxes have a stated uncertainty of 2.5 W m−2 (ref. 36).

Another source of error comes from neglecting mid-level clouds, a fairly common cloud type51, as their own identities. Let us assume that emissions from mid-level congestus clouds (c) experience a clear-sky greenhouse effect. By symmetry with low clouds, they should contribute an additional cloud-overlap masking term that appears in our expression for λarea: mch = (Scsαcαh + λcs(Ts − Tc))fcfh. Assuming that fc = 0.1, fh = 0.17, αc = αh = 0.45, Tc = 250 K, Ts = 298 K, Scs = 347 W m−2, λcs = −2 W m−1 K−1 yields mch ≈ −0.5 W m−2.

We therefore estimate Ch + mℓh = −1 ± 3 W m−2. This results in our best estimate of the anvil cloud area feedback:

$$\begin{array}{ll}\displaystyle\langle {\lambda }_{{\mathrm{h}}}^{{{{\rm{area}}}}}\rangle &=\displaystyle1/2\times (-4\pm 2{{{ \% \,{\rm{K}}}}}^{-1})\times (-1\pm 3\,{{{{\rm{W}}\,{\rm{m}}}}}^{-2})\\\displaystyle &=0.02\pm 0.07\,{{{{\rm{W}}\,{\rm{m}}}}}^{-2}\,{{{{\rm{K}}}}}^{-1}.\end{array}$$
(27)

Further uses of our framework

Our feedback expressions might also provide a quick, quantitative and physically transparent way to interpret how model biases influence feedbacks. For example, if members of a General Circulation Model ensemble simulate Ch between ±10 W m−2 but they all simulate the same \({\mathrm{d}}\ln {f}_{{\mathrm{h}}}/{\mathrm{d}}{T}_{{\mathrm{s}}}=-4 \% \,{{{{\rm{K}}}}}^{-1}\), then their area feedbacks will range between ∓0.2 W m−2 K−1. If all ensemble members simulate Ch = 1 Wm−2, but simulate \({\mathrm{d}}\ln {f}_{{\mathrm{h}}}/{\mathrm{d}}{T}_{{\mathrm{s}}}=\pm 5 \%\) K−1, then their area feedbacks will range between ±0.03 W m−2 K−1. This quantitative yet clear diagnostic could provide testable hypotheses that advance our understanding and development of models.