Origins of the open-circuit voltage in ternary organic solar cells and design rules for minimized voltage losses

Abstract

The power conversion efficiency of ternary organic solar cells (TOSCs), consisting of one host binary blend and one guest component, remains limited by large voltage losses. The fundamental understanding of the open-circuit voltage (V_OC) in TOSCs is controversial, limiting rational design of the guest component. In this study, we systematically investigate how the guest component affects the radiative and non-radiative related parts of V_OC of a series of TOSCs using the detailed balanced principle. We highlight that the thermal population of charge-transfer and local exciton states provided by the guest binary blend (that is, the guest-component-based binary blend) has a significant influence on the non-radiative voltage losses. Ultimately, we provide two design rules for enhancing the V_OC in TOSCs: high emission yield for the guest binary blend and similar charge-transfer-state energies for host/guest binary blends; high miscibility of the guest component with the low gap component in the host binary blend.

Main

The power conversion efficiencies of organic solar cells (OSCs) have increased rapidly in recent years, mainly benefiting from the development of novel non-fullerene acceptors^1,2,3,4,5. State-of-the-art record efficiencies of OSCs are obtained from ternary organic solar cells (TOSCs), where a guest component is added to a host binary blend^{6,7,8,9,10,11}. The guest component was initially designed to broaden the absorption range of the active layer and hence increase the photocurrent^12,13; however it was later found that the guest component can also improve the open-circuit voltage (V_OC) in some cases, although the mechanisms are still heavily debated^14,15,16. Despite these advances, voltage losses (ΔV), defined as the difference between the optical gap (E_g^opt) of the ternary blend and the experimentally determined V_OC, remain much larger than those in other high-efficiency photovoltaic technologies, presenting a key limiting factor for the efficiency of TOSCs¹⁷. Because light absorption and charge transport are nearly optimized in state-of-the-art TOSCs^10,11, further decrease of the ΔV probably represents the only avenue to notably improve the efficiency of TOSCs, such that they can be competitive with other photovoltaic technologies.

The understanding of the V_OC of TOSCs is much more complicated than that of their binary counterparts, as the guest component introduces extra complexity in the morphology and working principles. Currently, there is no single model which can rationalize the tunability of the V_OC in different TOSCs (summary in Supplementary Table 1)^{18,19,20,21,22,23}. The two widely used models to explain the tunable V_OC in the literature (that is, the ‘alloy’ and ‘parallel’ models) are distinguished by the assumption that a different type of morphology is formed upon the addition of the guest component^18,20,24; the former assumes a good miscibility with the host blend components, while the latter assumes a poor miscibility. Despite success in some cases, these two models frequently face challenges to explain the V_OC evolution in ternary systems. For example, on one hand, the ‘alloy’ model failed to explain the tunable V_OC in some two fullerene derivative-based TOSCs, where a fullerene ‘alloy’ was expected because of their similar molecular structures^19,21,25,26; while on the other hand, though the ‘parallel’ model was widely used to explain the linearly tunable V_OC (refs. ^18,27,28,29), it was reported that the V_OCs of some ‘parallel-like’ TOSCs were pinned to the smaller values of two binary devices^22,30,31, making the ‘parallel’ model puzzling. More importantly, both models correlate the V_OC exclusively with the energy of charge-transfer states (E_CT), without considering the effect of the guest component on the recombination processes^20,27, which are key to the ΔV. Particularly, the voltage loss due to the non-radiative recombination (ΔV_nr) has been a major part in state-of-the-art OSCs³² and it has not been taken into consideration in both models. A rational understanding of the V_OC in TOSCs is thus required to aid in the design of the guest component, which is essential to further improvement of TOSC efficiencies.

In this work, by investigating the radiative and non-radiative processes that determine the solar cell V_OC, we sketch a comprehensive picture for the composition-dependent V_OC of a variety of ternary blends in which the guest component induces different morphological effects on the host binary blend. In ternary blends where the guest component has a negligible effect on the host binary blend’s morphology (termed as Case-1), the radiative limit of the open-circuit voltage (V_OC^rad) can be predicted by the linear combination of the photovoltaic external quantum efficiency (EQE_PV) of two constituent binary devices (that is, the host binary device and the guest-component-based binary device). The prediction shows that there is little room to improve the V_OC^rad upon the addition of the guest component (within a ratio range practically relevant for efficient TOSCs); however, the V_OC improvement in Case-1 can still be achieved by reducing the ΔV_nr. More specifically, the ΔV_nr can be reduced by exploiting the thermal population of relatively more emissive charge-transfer (CT) and local exciton (LE) states in the guest-component-based binary blend (termed as guest binary blend) with respect to the initial CT states in the host binary blend. In the ternary systems where the guest component can significantly affect the host binary morphology (termed as Case-2), V_OC^rad can be improved, for example, when aggregation of binary components is suppressed upon the addition of the guest component. In addition, the ΔV_nr in this case can also be suppressed as aggregation-caused quenching (ACQ) is inhibited. As such, we not only provide a rational explanation of improved V_OC of TOSCs in different cases but also delineate two key design rules to further improve the V_OC in TOSCs: (1) a high emission yield for the guest binary blend and similar CT-state energies between the two binary blends; (2) a high miscibility between the guest component and the low gap component in the host binary blends.

Material systems and general description of the V _OC

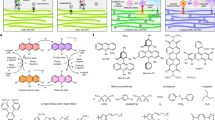
Whereas the guest component in principle can be either a donor, an acceptor or even an insulator material, state-of-the-art TOSCs are mostly based on systems where the guest component is an acceptor. Among these, fullerene derivatives have been widely used as the guest components and have had great success in enhancing the efficiency of OSCs^{33,34,35,36,37,38}. We therefore investigate a wide range of dual-acceptor TOSCs incorporating fullerene derivatives as their guest components (that is, PM6: Y6: PC₇₁M, PBDB-T: Y1: PC₇₁BM, PM6: IT-M: Bis-PC₆₂BM, PM6: ITCC: PC₇₁BM, PM6: IT-M: PC₇₁BM and PBDB-T: IEICO-4F:PC₇₁BM, with molecular structures depicted in Fig. 1a). The absorbance spectra of these materials are depicted in Supplementary Fig. 1, and the energy levels of these materials determined by the cyclic voltammetry (CV) (Supplementary Fig. 2) are summarized in Supplementary Table 2. These different combinations include representative situations where the guest component can increase, pin or decrease the V_OC of the host binary blends (Fig. 1b). The device fabrication details can be found in Methods and Supplementary Table 3, where the guest component (Acceptor 2) gradually replaces the acceptor in the host binary blend (Acceptor 1). All the photovoltaic parameters measured under the standard solar spectrum (the AM1.5g 100 mW cm⁻² spectrum) (Supplementary Fig. 3) are summarized in Supplementary Table 4.

Fig. 1: Molecular structures and composition-dependent V_OC.

a, Molecular structures of the donors (PM6 and PBDB-T), non-fullerene acceptors (Y6, Y1, IT-M, ITCC and IEICO-4F) and fullerene derivatives (PC₇₁BM and Bis-PC₆₂BM) studied in this work. b, V_OC measured under AM1.5g 100 mW cm⁻² conditions (which are the average values of at least two devices and plotted with bright-red spheres) and V_OC calculated by equation (1) (plotted with dark-red circles). The insets are the energetic levels of the materials approximated from cyclic voltammetry measurements (Supplementary Fig. 2 and Supplementary Table 2). The variations of V_OC for the same binary blends in different ternary systems (for example, different V_OC values of PBDB-T: PC₇₁BM in PBDB-T: Y1: PC₇₁BM and PBDB-T: IEICO-4F: PC₇₁BM) are due to the fact that different fabrication recipes are used (Supplementary Table 3).

Source data

On the basis of the detailed balance principle and assuming near thermal equilibrium conditions to hold, the V_OC of solar cells (including OSCs) is determined by the V_OC^rad (which is the open-circuit voltage assuming the absence of non-radiative decay pathways) and the ΔV_nr (refs. ^39,40). It can be written as:

$${V}_{{\rm{OC}}}={V}_{{\rm{OC}}}\!^{{\rm{rad}}}-{\Delta V}_{{\rm{nr}}}.$$

(1)

V_OC^rad is determined by the short-circuit current density J_SC and the radiative-limited saturation current density J_0,rad, both of which can be calculated from the EQE_PV:

$${V}_{{\rm{OC}}}\!^{{\rm{rad}}}=\frac{{kT}}{q}{\rm{ln}}\left(\frac{{J}_{{\rm{SC}}}}{{J}_{0,{\rm{rad}}}}+1\right)\approx \frac{{kT}}{q}{\rm{ln}}\left(\frac{{J}_{{\rm{SC}}}}{{J}_{0,{\rm{rad}}}}\right),$$

(2)

$${J}_{{\rm{SC}}}=q\int {{\rm{EQE}}}_{{\rm{PV}}}{{{\varnothing }}}_{{\rm{AM}}1.5{\rm{g}}}{\rm{d}}E{{;}}\,{J}_{0,{\rm{rad}}}=q\int {{\rm{EQE}}}_{{\rm{PV}}}{{{\varnothing }}}_{{\rm{BB}}}{\rm{d}}E.$$

(3)

Here k is the Boltzmann constant, T is the absolute temperature, q is the elementary charge, Ø_AM1.5g and Ø_BB are the photon flux spectra of AM1.5g and black-body radiation at 300 K, respectively (Supplementary Fig. 4).

The difference between the measured V_OC and the V_OC^rad is the voltage loss due to ΔV_nr, which can be quantified by measuring the external quantum efficiency of the electroluminescence (EQE_EL) of the device:

$${\Delta V}_{{\rm{nr}}}=-\frac{{kT}}{q}{\rm{ln}}\left({{\rm{EQE}}}_{{\rm{EL}}}\right).$$

(4)

On the basis of these equations, we can calculate the V_OC^rad and ΔV_nr (as summarized in Supplementary Table 5) by using experimentally determined EQE_PV spectra and EQE_EL values and then further calculate V_OC of the TOSCs (Fig. 1b). We notice that for all the ternary systems, the calculated V_OC trends (using equations (1)–(4)) match well with the values obtained from the current density–voltage curves. These results indicate that we can quantify the effects of the guest component on V_OC^rad and ΔV_nr, respectively.

Composition-dependent V _OC ^rad

We investigate the effects of the guest component on V_OC^rad by understanding how the guest component affects the EQE_PV (Supplementary Fig. 5) of which the absolute value in turn determines J_SC and the tail region determines J_0,rad (equations (2),(3)). We consider the guest component to form an additional binary blend with the donor material (that is, the guest binary blend) and compare the experimentally determined ternary EQE_PV (denoted as EQE_PV^E) with the linearly weighted sum of EQE_PV (denoted as EQE_PV^L) of two binary blends. Figure 2a,b depicts the EQE_PV^Eand EQE_PV^L in three representative ternary systems, that is, PM6: Y6: PC₇₁BM, PM6: ITCC: PC₇₁BM and PBDB-T: IEICO-4F: PC₇₁BM at a certain composition; the EQE_PV^E and EQE_PV^L in other ternary systems are depicted in Supplementary Fig. 6. We find that the EQE_PV^E matches well with the EQE_PV^L in most ternary systems (termed as Case-1) except for the PBDB-T: IEICO-4F: PC₇₁BM ternary blend (termed as Case-2); for the latter case, the EQE_PV^E edge exhibits a more distinct blue shift with increasing the PC₇₁BM composition, as compared to EQE_PV^L.

Fig. 2: The effect of the guest composition on the V_OC^rad.

a,b, EQE_PV^E(solid lines) and linearly rebuilt EQE_PV^L (dashed lines) of two binary devices match in PM6: Y6: PC₇₁BM and PM6: ITCC: PC₇₁BM (a) but deviate in PBDB-T: IEICO-4F: PC₇₁BM (b). c,d, V_OC^rad calculated from the EQE_PV^E (symbols) and predictions from equation (5) (grey dashed lines) match in PM6: Y6: PC₇₁BM, PBDB-T: Y1: PC₇₁BM and PM6: IT-M: Bis-PC₆₂BM (c) and PM6: ITCC: PC₇₁BM and PM6: IT-M: PC₇₁BM (d) but deviate in PBDB-T: IEICO-4F: PC₇₁BM (e). For the fullerene composition of 83.3 wt% in the PM6: Y6: PC₇₁BM ternary system, we notice a discrepancy between the EQE_PV^L and EQE_PV^E (Supplementary Fig. 6) and between the V_OC^rad calculated from the EQE_PV^E and predictions from equation (5). Because the composition of 83.3 wt% is well beyond the regular optimum composition, the PM6: Y6: PC₇₁BM ternary system is still classified as the Case-1. f,g, Prediction results via equation (5) for Case-1 TOSCs with parameter a fixed to 1 and parameter b varied from 10⁻⁵ to 1 (f) and 10¹ to 10⁵(g). V_OC^rad,T and V_OC^rad,H are the V_OC^rad of the ternary and the host binary devices, respectively.

Source data

The matched EQE_PV^L and EQE_PV^E in the Case-1 ternary system indicates that these ternary blends can be approximated as a linear combination of two binary blends without additional significant morphology changes during mixing (details in Supplementary Note 1). This is evidenced by the nearly unchanged melting endotherm, obtained using differential scanning calorimetry (DSC), and the grazing-incidence wide-angle X-ray scattering (GIWAXS) diffractogram of PM6: Y6: PC₇₁BM with respect to those of PM6: Y6 (Supplementary Figs. 7 and 8). The matched EQE_PV^L and EQE_PV^E also indicates that the J_SC and J_0,rad of the Case-1 TOSCs can be reproduced using the linearly weighted values of two binary devices (refer to equation (3)), as evidenced in Supplementary Fig. 9. In contrast, the blue-shifted EQE_PV^E edge in Case-2 points towards suppressed aggregation of the component with the smallest E_g^opt (that is, IEICO-4F in this case) upon adding the PC₇₁BM. The impact of PC₇₁BM on the aggregation of IEICO-4F is further evidenced by the absence of a melting endotherm at about 325 °C in the DSC heating thermograms of the ternary blend, which is readily observed for both neat IEICO-4F and the PBDB-T: IEICO-4F binary blend (Supplementary Fig. 7). Instead, an endotherm below 300 °C emerges, which may result from both PC₇₁BM and/or IEICO-4F crystallites. Moreover, GIWAXS diffractograms of the ternary blend feature a broadened diffraction peak at 3.27 Å⁻¹ compared to neat IEICO-4F or the binary blend (Supplementary Fig. 8), consistent with a reduction in the size of ordered IEICO-4F domains. The blue-shifted EQE_PV^E edge results in considerable changes of J_0,rad without changing J_SC much, as the former is determined by the Ø_BB, which exponentially increases with decreasing energy, while the latter is determined by Ø_AM1.5g, which is almost flat in the relevant energy range. As a result, in IEICO-4F-based ternary systems, the J_0,rad calculated from the EQE_PV^E is smaller than the linearly weighted values, and the J_SC calculated from the EQE_PV^E matches well with the linearly weighted values of two binary devices (Supplementary Fig. 9).

Because the J_SC and J_0,rad can be reproduced by the linearly weighted values of two binary devices for Case-1 TOSCs, we can calculate V_OC^rad of TOSCs simply using the J_SC and J_0,rad values of two binary devices. Assuming J_SC^G= aJ_SC^H and J_0,rad^G = bJ_0,rad^H, we can obtain the following equation from equation (2) (details in Supplementary Note 1):

$${V}_{{\rm{OC}}}\!^{{\rm{rad}},{\rm{T}}}-{V}_{{\rm{OC}}}\!^{{\rm{rad}},{\rm{H}}}=\frac{{kT}}{q}{\rm{ln}}\left(\frac{1-x+{ax}}{1-x+{bx}}\right).$$

(5)

Here the superscripts H, G and T denote the host binary, guest binary and the ternary devices, respectively, and x is the composition of the guest component. The calculated V_OC^rad values for the Case-1 ternary systems in this work based on equation (5) are plotted as dashed lines in Fig. 2c,d and match well with the values directly calculated from the EQE_PV (plotted as scatters). In contrast, for the Case-2 TOSCs, there is a distinct discrepancy between the V_OC^rad calculated from the EQE_PV^E and the values predicted from equation (5), as shown in Fig. 2e, which is due to the suppressed aggregation of IEICO-4F in ternary blends.

In all our ternary systems, the parameter a varies from 0.5 to 1.5 and the parameter b varies from 10⁻⁵ to 10¹, as summarized in Supplementary Table 6. The wide range of the parameter b indicates the possibly significant difference between the J_0,rad values of two binary devices; because Ø_BB decreases exponentially with increasing photon energy, the J_0,rad can be orders of magnitude different for the OSCs with EQE_PV edges in different photon energy range (refer to equation (3)). Thus, we can further make a general prediction on the V_OC^rad in Case-1 ternary systems by fixing the parameter a as 1 and varying the parameter b from 10⁻⁵ to 10⁵ (Fig. 2f,g). With the parameter b < 1, that is, J_0,rad^H > J_0,rad^G, the V_OC^rad is almost pinned to the value of host binary devices within a practically relevant composition (for example, at most ~20 mV when the composition is 50%) in TOSCs. With the parameter b = 1, that is, J_0,rad^H = J_0,rad^G, the V_OC^rad of the TOSCs is completely pinned to that of host binary device. With the parameter b > 1, that is, J_0,rad^H < J_0,rad^G, the V_OC^rad of the TOSCs drops rapidly upon the addition of the guest component. Therefore, in Case-1 TOSCs, the prediction shows that V_OC^rad has little room to improve by adding a guest component within a practically relevant composition (for example, <50%). In contrast, the V_OC^rad cannot be predicted in Case-2 TOSCs and it can be possibly improved by adding a guest component because of, for example, the significantly suppressed aggregation of the low optical gap component in the host binary blend.

Composition-dependent voltage loss due to the non-radiative recombination

In this section, we investigate how the guest component affects the ΔV_nr in TOSCs by investigating the composition-dependent EQE_EL (refer to equation (4)). Figure 3a–c depicts the EQE_EL (determined at the injection current density approximately equalling to J_SC, as shown in Supplementary Fig. 10) of the TOSCs as a function of composition. The starting and ending points are the EQE_EL of the host binary and the guest binary devices, and the former is at least one order of magnitude larger than the latter in all studied ternary systems, the reason for which will be discussed later. The EQE_EL as a function of the composition in all our ternary systems can be categorized into three different trends: (1) in the Case-1 ternary systems of PM6: Y6: PC₇₁BM, PBDB-T: Y1: PC₇₁BM and PM6: IT-M: Bis-PC₆₂BM, the EQE_EL values are almost pinned to those of the host binary devices until the guest composition reaches ~80% and drops down rapidly afterwards (Fig. 3a); (2) in the Case-1 ternary systems of PM6: ITCC: PC₇₁BM, PM6: IT-M: PC₇₁BM, the EQE_EL values demonstrate continuous decrease with increasing guest (PC₇₁BM) composition (Fig. 3b); (3) in the Case-2 ternary system of PBDB-T: IEICO-4F: PC₇₁BM, the EQE_EL values initially increase with increasing guest (PC₇₁BM) composition until the guest composition reaches ~80%, followed by decreasing EQE_EL values afterwards (Fig. 3c).

Fig. 3: The effect of the guest composition on non-radiative recombination losses.

a–c, EQE_ELas a function of the composition: in the practically relevant range (usually <80% PC₇₁BM), the EQE_ELvalues are almost constant (a), continuously decreasing (b) and rising (c). d–f, EL spectra of three representative ternary systems: upon adding PC₇₁BM, the EL spectra of the host binary blend remain almost identical (d, PBDB-T: Y1: PC₇₁BM), gradually show the guest binary EL (e, PM6: ITCC: PC₇₁BM) or blue shift (f, PBDB-T: IEICO-4F: PC₇₁BM); the dashed arrows on the EL spectra in e,f are guides for the eyes to indicate the gradual change of the EL spectra; the insets in d–f depict the relative energy levels (exact values in Supplementary Table 7) and the relatively high luminescence quantum yields of the host CT states (indicated by the thicker arrows) and the relatively low luminescence quantum yields of the guest CT states (indicated by the thinner arrows). g, Illustration of the energetic levels in the multi-state simulation studying the thermal population effects on the EQE_EL versus compositions by changing the energy of the guest CT state $({E}_{{\mathrm{CT}}_{\mathrm{G}}})$ from 1.60 eV to 1.30 eV (indicated by the dashed arrow). h, Simulation results of the thermal population effects on the EQE_EL versus compositions by changing the ${E}_{{\mathrm{CT}}_{\mathrm{G}}}$ from 1.60 eV to 1.30 eV (indicated by the dashed arrow) and fixing the energy levels of the other states. i, Simulation results of the increased photoluminescence quantum yields (PLQYs) (related to the LE_H states) affecting the EQE_EL versus compositions (plotted with blue symbols); to make a direct comparison, the experimentally measured EQE_EL values in the PBDB-T: IEICO-4F: PC₇₁BM are also plotted in i. In all figures, the lines connecting the points are the guides for eyes.

Source data

To gain insights into the EQE_EL evolution, we measured the EL spectra of all ternary blends studied in this work (Supplementary Fig. 11). We start the analysis by comparing the EL spectra of the two constituent binary blends and their corresponding neat films (that is, the species with smaller E_g^opt values), as depicted in Supplementary Fig. 12. For the host binary blends, the EL spectra considerably overlap with those of their corresponding neat films, which can be ascribed to small energetic offsets between the CT and LE states (~30–80 meV; Supplementary Fig. 13 and Supplementary Table 7) and have been widely observed in other low-offset systems⁴¹. In contrast, EL spectra of guest binary blends demonstrate ‘pure’ CT emissions compared to those of the corresponding neat films, ascribed to large energetic offsets between the CT and LE states (~150 –340 meV; Supplementary Fig. 13 and Supplementary Table 7). The small energetic offset in the host binary blends enhances the hybridization between the CT and LE states and increases the thermal population of the LE states that are much more emissive compared to the CT states^32,41,42. This is why the EQE_EL of the host binary blend is at least one order of magnitude higher than that of the guest binary blend.

We then move to the EL spectra of ternary systems (Supplementary Fig. 14). In line with three different trends of the EQE_EL evolution, the EL spectra of ternary devices also exhibit three different situations. We plot one representative system for each situation in Fig. 3d–f, that is, PBDB-T: Y1: PC₇₁BM (Case-1), PM6: ITCC: PC₇₁BM (Case-1) and PBDB-T: IEICO-4F: PC₇₁BM (Case-2). In the PBDB-T: Y1: PC₇₁BM ternary system, the EL spectra of ternary devices are almost identical to that of the host binary device for most compositions, and the emission from the guest binary is missing in the EL spectra of the ternary devices. In contrast, in the EL spectrum of the PM6: ITCC: PC₇₁BM ternary system, the emission from the guest binary gradually appears and finally dominates the EL spectrum of the ternary devices. In the EL spectra of the PBDB-T: IEICO-4F:PC₇₁BM, the emission from the guest binary device is also missing (similar to the PBDB-T: Y1: PC₇₁BM case). What is different from the PBDB-T: Y1: PC₇₁BM case is that the EL peaks of the ternary devices demonstrate a more distinct blue shift compared with that of the host binary device, which can be ascribed to the suppressed aggregation of IEICO-4F and is consistent with the blue-shifted EQE_PV edge.

Comparing two different situations in Case-1 ternary blends, we notice that the appearance of the emission from guest binary blends, which have much lower EQE_EL than that of the host binary blends, correspond to a reduction of the EQE_EL in PM6: ITCC: PC₇₁BM and PM6: IT-M: PC₇₁BM. In addition, the appearance of the emission from the guest binary blends is correlated with the relative energetic levels of two CT states in host and guest binary blends. For instance, the energetic levels of the guest binary CT states in these Case-1 ternary systems, where the emission from guest binary appears, are lower than those of the host binary CT states. In contrast, in the other Case-1 ternary systems, where the emission from the guest binary blend is invisible, the energetic levels of guest CT states are higher than those of host CT states. The correlation between the appearance of the guest CT states in the EL spectra (and thus the EQE_EL reduction) and their energetic levels with respect to the host CT states implies a near thermal equilibrium condition within and between the excited states of the guest binary blends and those of the host binary blends, which is in line with the assumption needed for the validity of equation (1). Because carrier population in potential energy surfaces under thermal equilibrium follows the Boltzmann distribution, the EQE_EL evolution is dependent on the relative energetic levels between different states.

To rationalize the EQE_EL evolution under near thermal equilibrium, we extend our previously developed three-states model to incorporate the electronic states of the guest binary blends (details in Methods)³². Our extended ‘multi-states’ model includes four diabatic electronic states, that is, CT states in host binary and guest binary blends and their corresponding LE states of the low optical gap component, denoted as CT_H, CT_G, LE_H and LE_G, respectively, with the energies of ${E}_{{\mathrm{CT}}_{\mathrm{H}}}$, ${E}_{{{\rm{CT}}}_{{\rm{G}}}}$, ${E}_{{{\rm{LE}}}_{{\rm{G}}}}$ and ${E}_{{{\rm{LE}}}_{{\rm{G}}}}$ (Fig. 3g). Because the blends in our experiments show a small offset between ${E}_{{{\rm{LE}}}_{{\rm{H}}}}$ and ${E}_{{{\rm{CT}}}_{{\rm{H}}}}$ and a relatively large value between ${E}_{{{\rm{LE}}}_{{\rm{G}}}}$ and ${E}_{{{\rm{CT}}}_{{\rm{G}}}}$, we set the former to be 0.05 eV and the latter to be 0.20 eV in the simulation, with an ${E}_{{{\rm{LE}}}_{{\rm{H}}}}$ of 1.50 eV and an ${E}_{{{\rm{LE}}}_{{\rm{G}}}}$ of 1.80 eV. As a result, the host binary blend shows a much higher EQE_EL than that of the guest binary blend in our simulation, matching well with the ternary systems studied by our experiments in this research.

As indicated by the experimental results above, the relative energetic levels of the ${E}_{{{\rm{CT}}}_{{\rm{H}}}}$ and ${E}_{{{\rm{CT}}}_{{\rm{G}}}}$ have an important impact on EQE_EL of the ternary blends. Here we thus exploit our ‘multi-states’ model to first examine thermal population effects by gradually shifting ${E}_{{{\rm{CT}}}_{{\rm{G}}}}$ from 1.60 eV to 1.30 eV with a step of 0.05 eV and meanwhile fixing the other excitation energies, as illustrated in Fig. 3g. The modelling results are depicted in Fig. 3h, matching well with the EQE_EL evolution in the Case-1 ternary systems (Fig. 3a,b). With ${E}_{{{\rm{CT}}}_{{\rm{G}}}} > {E}_{{{\rm{CT}}}_{{\rm{H}}}}$, the radiative and non-radiative recombination processes at the highly emissive host binary blend are dominant in the ternary blends due to the dominant thermal population of the CT_H and LE_H states. As a result, the simulated EQE_EL is almost pinned to that of the host binary blends, as in the experimental cases of the PM6: Y6: PC₇₁BM, PBDB-T: Y1: PC₇₁BM and PM6: IT-M: Bis-PC₆₂BM. With ${E}_{{{\rm{CT}}}_{{\rm{G}}}} < {E}_{{{\rm{CT}}}_{{\rm{H}}}}$, the simulated EQE_EL evolution shows similar trends as the experimental results of PM6: ITCC: PC₇₁BM and PM6: IT-M: PC₇₁BM. This is because of the dominant thermal occupation of the CT_G states (which are less emissive compared with the host binary blend), leading to the continuous reduction of the EQE_EL with the increasing composition. Particularly, when the ${E}_{{{\rm{CT}}}_{{\rm{G}}}}={E}_{{{\rm{CT}}}_{{\rm{H}}}}$, the simulated EQE_EL of TOSCs are approximately the linear combination of those of two binary blends, which is due to equal thermal population of two CT states.

Our simulation—which exclusively considers the thermal population effect—can accurately explain how the guest component affects EQE_EL in the Case-1 ternary systems. However, the EQE_EL evolution in the PBDB-T: IEICO-4F: PC₇₁BM ternary system in the Case-2 is not observed in Fig. 3h, indicating that further parameters are required when the guest component affects the aggregation of the host binary blend. A straightforward effect of the suppressed aggregation is on the quantum yields of the photoluminescence (PLQY) due to the suppressed ACQ. Therefore, we examine the PLQY and the exciton lifetime of IEICO-4F: PC₇₁BM blends with different compositions, finding that the PLQY and exciton lifetime of the IEICO-4F increase with increasing PC₇₁BM components (Supplementary Figs. 15–17). In other words, the enhanced PLQY and the associated reduction of non-radiative recombination should also be taken into consideration. Therefore, using our ‘multi-states’ model, we also simulate how the PLQY (related to LE_H) affects the EQE_EL by fixing the energetic level of each state to their initial values as shown in Fig. 3g. The flat region in the simulated EQE_EL curves rises with the increasing PLQY (Fig. 3i). Therefore, when the PLQY of IEICO-4F continually increases with the increasing PC₇₁BM ratio, the EQE_EL evolution of PBDB-T: IEICO-4F: PC₇₁BM increases first and reduces subsequently as depicted in Fig. 3i. In addition to suppressing the ACQ, the guest PC₇₁BM in principle could also eliminate the trap states and hence enhance the PLQY. We rule out this possibility in our ternary blends by performing space-charge-limited current measurements (details in Supplementary Fig. 18)⁴³.

Discussion and conclusions

With the comprehensive picture of the effects of the guest component on the V_OC^rad and ΔV_nr, we now provide rational approaches to improving the V_OC in TOSCs based on our new understanding.

For Case-1 ternary system, where the guest component cannot substantially change the morphology of host binary blends (Fig. 4a), there is little room for improving the V_OC^rad within a reasonable composition range of the guest component, that is, at most ~20 meV improvement when the composition of the guest component is up to 50% (Fig. 2f). In contrast, the ΔV_nr can be considerably reduced by introducing the guest component with more emissive CT and LE states (with respect to the CT states in the host binary blend) and exploiting these states by the thermal population. This holds true for all our Case-1 systems if we look at them in a different way (that is, we consider that we add guest non-fullerene acceptors to the polymer: fullerene blends). This is also the reason why the V_OC can be either tunable or pinned to that of the host binary blend in the previously reported ‘parallel-like’ ternary systems^18,30. To introduce highly emissive guest CT and LE states (with respect to CT states in the host binary blend), the guest component should have high luminescent efficiency and the energetic offset between the guest CT and LE states should be minimized. Namely, the EQE_ELof the guest binary device should be higher with respect to that of the host binary device from a macroscopic perspective. Increasing the thermal population of these highly emissive states requires relatively low energetic levels with respect to those of the host CT states. However, the absorption from these states with lower energetic levels can make J_0,rad^G much larger than J_0,rad^H (that is, parameter b > 1) due to the exponential dependence of Ø_BB on the photon energy (refer to equation (3)). This leads to significant reduction of V_OC^rad as calculated in Fig. 2j. If the decreased ΔV_nr cannot compensate the reduction of V_OC^rad, the total V_OC can be decreased as in the cases of PM6: Y6: PC₇₁BM and PM6: IT-M: Bis-PC₆₂BM; hereby, once more Y6 and IT-M are considered as the guest acceptor. Therefore, to increase the thermal population of these highly emissive states and meanwhile avoid sacrificing the V_OC^rad, the energetic levels of the guest acceptor and host acceptor are preferably close to each other (Fig. 4b,c).

Fig. 4: Design rules to improve the V_OC in TOSCs.

a, Schematic illustration of the morphologic effect of the guest component on the host binary blends in TOSCs. b,c, Strategies to improve the V_OC in Case-1 TOSCs: the changes on the V_OC^rad should be minimized, and the improved V_OC can be reached by reducing the ΔV_nr (b); under the thermal equilibrium (described by the black arrows), reduced ΔV_nr can be realized by exploiting the thermal population of the more emissive states related with the guest component, where the luminescent efficiencies of different states are represented by the thickness of the coloured arrows (c). From the perspective of the device performance, the guest binary device should have higher EQE_EL than the host binary device (that is, EQE_EL^G > EQE_EL^H). In addition, to fully make use of the CT_G and LE_G without sacrificing the V_OC^rad, the CT_G energy should be close to the CT_H energy (that is, ${E}_{{{\rm{CT}}}_{{\rm{H}}}}\cong{E}_{{{\rm{CT}}}_{{\rm{G}}}}$). d,e, Strategies to improve the V_OC in Case-2 TOSCs: the improved V_OC can result from both increased V_OC^rad and reduced ΔV_nr (d); the guest component suppresses the aggregation of the host binary blends, leading to increased LE_H and CT_H energies and thus increased V_OC^rad (e). In addition, suppressed aggregation of the host binary blend also reduces the ACQ effect, enhancing the luminescent efficiencies of both LE_H and CT_H and thus reducing the ΔV_nr. Black arrows in e describe the thermal equilibrium condition; the thickness of the coloured arrows represents the luminescent efficiencies of different states; the dashed lines represent the initial conditions of the host binary blend; and the solid lines represent the conditions of the host binary blend after adding the guest component.

For Case-2 ternary systems, where the guest component significantly changes the morphology of host binary blends (Fig. 4a), both V_OC^rad and ΔV_nr can be optimized considerably to improve the V_OC by, for example, the suppressed aggregation as depicted in Fig. 4d,e. To reduce the ACQ, it is desirable to design the guest component with high miscibility with the low optical gap component of the host binary blends. The guest component in this case is not necessarily a semiconductor; it can even be an insulator⁴⁴, as long as the electronic properties of the solar cells are not negatively affected.

In addition, we note that Case-1 and Case-2 are not mutually exclusive; in reality, we can have TOSCs that meet the optoelectronic requirements in Case-1 and also the miscibility (morphology) requirement in Case-2. We notice that improving the V_OC by the criteria for Case-1 or Case-2 TOSCs has actually been realized in refs. ^7,8,34,38,45, although the mechanisms were not explicitly illustrated. Finally, we would also like to mention that while our design rules rationalize the V_OC evolutions in the ternary systems studied in this work as well as in some previous reports^7,8,34,38,45, we do not exclude the possibilities of other mechanism(s) to improve the V_OC in TOSCs, considering the wide range of possible materials combinations and associated complexities.

In summary, this work paints a comprehensive picture of how the guest component affects the radiative and non-radiative parts of the V_OC in TOSCs. Our results demonstrate that the V_OC can be improved in different ternary systems, regardless of whether the guest component can significantly alter the morphology of the host binary blend. On the basis of our new understanding, we provide design rules for enhancing V_OC of TOSCs: (1) use the guest binary blend with higher EQE_EL and similar CT-state energy with respect to that of the host binary; (2) use the guest component that has high miscibility with the low optical gap component in the host binary blend. Our design rules are in line with recent development of high-efficiency TOSCs and provide a rational guide to reach the next efficiency level of organic solar cells.

Methods

Materials

The materials used for fabricating the devices were either purchased from the company or synthesized by coauthors. PM6, PBDB-T, ITCC, IT-M, IEICO-4F and PFN.Br were purchased from the Solarmer (Beijing). PEDOT: PSS 4083 was purchased from Heraeus. PC₇₁BM and Bis-PC₆₂BM were purchased from Sigma Aldrich. Y6 and Y1 were synthesized by J. Yuan.

CV measurements

The CV measurements were performed on an Autolab PGSTAT10 with a three-electrode set-up. Glassy carbon electrodes were used as the working electrode. A platinum wire was used as the counter electrode and a silver wire as pseudo-reference electrode. The reference electrode was calibrated with ferrocene, whereas 0.1 M tetrabutylammonium hexafluorophosphate (BuNPF6) in anhydrous acetonitrile solution was used as the supporting electrolyte. The polymers and non-fullerene acceptors were drop cast onto the working electrodes from corresponding chloroform solutions (~2–5 mg ml⁻¹) for the measurements. The fullerene derivatives were directly measured in their 1,2-Dichlorobenzene solutions (5 mg ml⁻¹). During the measurements, the systems were bubbled with argon. Cyclic voltammetry was measured at a scan rate of 100 mV s^–1.

Device fabrication and characterization

All the devices were fabricated with the conventional structure: indium tin oxide (ITO)-coated glass/PEDOT: PSS (~30 nm)/active layer (~90 nm)/PFN.Br (~0.2 nm)/Al (100 nm). PEDOT: PSS 4083 was deposited by spin coating (3,500 r.p.m., 40 s) and afterwards annealed for 15 min at 150 °C. The active layer was deposited by spin coating as well, and the recipes for preparing the active layers are listed in the Supplementary Table 3. After depositing the active layer, the PFN.Br (dissolved in the methanol with a concentration of 0.5 mg ml⁻¹) was spin coated onto the active layer (2,500 r.p.m., 30 s). Finally, the devices were transferred into the vacuum chamber for depositing the aluminium electrodes. The area of tested solar cells is 4.8 mm². All the devices were encapsulated in a glovebox and afterwards measured in air. The current density–voltage (J–V) curves (measured in the forward direction, namely, from negative to positive bias with a step of 0.04 V) were recorded using a Keithley 2400 Source Meter under AM1.5g illumination provided by a solar simulator (LSH-7320 ABA light-emitting diode (LED) solar simulator) with an intensity of 100 mW cm⁻² after spectral mismatch correction. The light intensity for the J–V measurements was calibrated with a reference silicon cell (certified by National Renewable Energy Laboratory).

EQE_PV measurements

The EQE_PV spectra were measured by a regular EQE_PV set-up (EQE_PV above gap) combining a Fourier-transfer photocurrent spectroscopy (FTPS) (EQE_PV below gap). The FTPS curves were carried out using the Vertex 70 equipped with a quartz tungsten halogen (QTH) lamp, quartz beam splitter from Bruker optics. A current amplifier was used to amplify the photocurrent. The output voltage of the amplifier was fed back to the Vertex 70 and analysed by the software to obtain the photocurrent spectrum information. The final FTPS spectra were calibrated with a crystalline silicon photovoltaic cell. The EQE_PV spectra above gap were recorded by an integrated quantum efficiency measurement system named QE-R3011 (Enli Technology), which was also calibrated with a crystalline silicon photovoltaic cell before use.

DSC measurements

Experiments were performed under nitrogen with a DSC2 from Mettler Toledo equipped with a gas controller GC 200 system at a heating/cooling rate of 10 °C min⁻¹. Samples were prepared by drop casting solutions onto glass slides followed by drying and then transferring 2–4 mg of the material into 40 µl Al crucibles. The thermograms were extracted from the first heating scans.

GIWAXS measurements

GIWAXS data were recorded at NCD-SWEET beamline (ALBA synchrotron in Cerdanyola del Vallès, Spain) with a monochromatic X-ray beam (with a wavelength of 0.9603 Å) of 80 × 30 µm² (horizontal × vertical), using a Si (111) channel cut monochromator. The scattered signal was recorded using a Rayonix LX255-HS area detector placed at 241.1 mm from the sample position. The reciprocal q space and sample-to-detector distance were calculated using Cr₂O₃ as calibrant. A near-critical angle of incidence of 0.13° was used to maximize the thin film signal, and the collected 2D images were azimuthally integrated using PyFAI⁴⁶.

EQE_EL measurements

The EQE_EL measurements were performed on the home-built set-up. A source meter Keithley 2400 was used to inject and record the current densities into the devices, and a Hamamatsu silicon photodiode 1010B combined with a Keithley 485 were used to measure the EL intensities.

EL and PLQY measurements

The EL and PL spectra were recorded using the Andor spectrometer (Shamrock sr-303i-B equipped with a Newton EMCCDs). A source meter (Keithley 2400) was used to inject the current into the solar cells in the EL experiments. A continuous wavelength laser (532 nm) was used as the excitation source for the PL and PLQY experiments. The details of the PLQY method can be found in ref. ⁴⁷.

Theoretical model describing the composition-dependent EQE_EL behaviour

On the basis of purely diabatic states |G〉, |LE_H〉, |LE_G〉, |CT_H〉 and |CT_G〉, corresponding to the ground (G) state, the highly emissive local exciton states of the low optical component in host binary (LE_H) and guest binary (LE_G) blends, charge-transfer states in host binary (CT_H) and guest binary (CT_G) blends, the effective model Hamiltonian (H_eff) for excited states of the ternary system is written as:

(6)

where ${{{E}}}_{{{\rm{LE}}}_{{\rm{H}}}/{{\rm{LE}}}_{{\rm{G}}}/{{\rm{CT}}}_{{\rm{H}}}/{{\rm{CT}}}_{{\rm{G}}}}$ denotes the excitation energy from |G〉 to |LE_H〉 / |LE_G〉 / |CT_H〉 / |CT_G〉 states; ${{{t}}}_{{{\rm{LE}}}_{{\rm{H}}}-{{\rm{CT}}}_{{\rm{H}}}}$ and ${{{t}}}_{{{\rm{LE}}}_{{\rm{G}}}-{{\rm{CT}}}_{{\rm{G}}}}$ denote the electronic couplings of LE state with CT state in host binary and guest binary blends; ${{{t}}}_{{{\rm{CT}}}_{{\rm{H}}}-{{\rm{CT}}}_{{\rm{G}}}}$ denotes the electronic coupling between |CT_H〉 and |CT_G〉 states. In fact, the whole Hamiltonian of the ternary system shown in equation (6) consists of the two-block Hamiltonian corresponding to host- and guest-based binary blends and incorporates the interaction (${{{t}}}_{{{\rm{CT}}}_{{\rm{H}}}-{{\rm{CT}}}_{{\rm{G}}}}$) between the CT states of the two binary systems. The αth eigenstate $|{\Psi }_{\alpha }\rangle$ of the system Hamiltonian can be expressed as:

$$|{\Psi }_{\alpha}\rangle ={{{c}}}_{{{\rm{LE}}}_{{\rm{H}}}}|{{\rm{LE}}}_{{\rm{H}}}\rangle +{{{c}}}_{{{\rm{CT}}}_{{\rm{H}}}}|{{\rm{CT}}}_{{\rm{H}}}\rangle +{{{c}}}_{{{\rm{LE}}}_{{\rm{G}}}}|{{\rm{LE}}}_{{\rm{G}}}\rangle +{{{c}}}_{{{\rm{CT}}}_{{\rm{G}}}}|{{\rm{CT}}}_{{\rm{G}}}\rangle .$$

(7)

Here c denotes the expansion coefficients. Through the diagonalization of the system Hamiltonian, the expansion coefficients of the adiabatic eigenstate $|{\Psi }_{\alpha }\rangle$ with the eigenenergy ${{{E}}}_{{{\alpha }}}$ can be obtained.

To estimate the rates (k_r and k_nr) of the radiative and non-radiative recombination of the hybrid state for the ternary blends, the effects of the hybridization between these electronic states and the thermal population of the hybrid state are considered in an effective way:

$$\begin{array}{l}{k}^\mathrm{T}_{{\rm{r}}/{\rm{nr}}}={\sum }_{{{\alpha}}}{{P}}({{{E}}}_{{{\alpha }}}){({{{c}}}^{{{\alpha }}}_{{{\rm{LE}}}_{{\rm{G}}}})}^{2}{{{k}}}^{{{\rm{LE}}}_{{\rm{G}}}}_{{\rm{r}}/{\rm{nr}}}+ x{\sum }_{{{\alpha }}}{{P}}({{{E}}}_{{{\alpha }}}){({{{c}}}^{{{\alpha }}}_{{{\rm{CT}}}_{{\rm{G}}}})}^{2}{{{k}}}^{{{\rm{CT}}}_{{\rm{G}}}}_{{\rm{r}}/{\rm{nr}}}\\ +(1-x){\sum }_{{{\alpha }}}{{P}}({{{E}}}_{{{\alpha }}}){({{{c}}}^{{{\alpha }}}_{{{\rm{LE}}}_{{\rm{H}}}})}^{2}{{{k}}}^{{{\rm{LE}}}_{{\rm{H}}}}_{{\rm{r}}/{\rm{nr}}}+(1-x){\sum }_{{{\alpha }}}{{P}}({{{E}}}_{{{\alpha }}}){({{{c}}}^{{{\alpha }}}_{{{\rm{CT}}}_{{\rm{H}}}})}^{2}{{{k}}}^{{{\rm{CT}}}_{{\rm{H}}}}_{{\rm{r}}/{\rm{nr}}}.\end{array}$$

(8)

where $x$ denotes the composition of guest component; ${{{k}}}_{{\rm{r}}/{\rm{nr}}}\!^{{{\rm{LE}}}_{{\rm{H}}}}$, ${{{k}}}_{{\rm{r}}/{\rm{nr}}}\!^{{{\rm{LE}}}_{{\rm{G}}}}$, ${{{k}}}_{{\rm{r}}/{\rm{nr}}}\!^{{{\rm{CT}}}_{{\rm{H}}}}$ and ${{{k}}}_{{\rm{r}}/{\rm{nr}}}\!^{{{\rm{CT}}}_{{\rm{G}}}}$ denote the radiative/non-radiative recombination rates of the diabatic LE and CT states in host and guest binary blends, respectively; following our previous work, the radiative and non-radiative recombination rates of both LE_H and LE_G states are set to 10⁸ and 10¹⁰ s⁻¹, leading to a PLQY of 1% commonly found in experiment; those values of the weakly emissive CT_H and CT_G states are set to 10⁴ and 10¹⁰ s⁻¹; ${{P}}({{{E}}}_{{{\alpha }}})$ stands for the thermal (Boltzmann) population of the hybrid state ${{{E}}}_{{{\alpha }}}$. Thus, the EQE_EL values of these ternaries are quantified via:

$${{\rm{EQE}}}_{{\rm{EL}}}={{{\eta }}}_{{\rm{b}}}{{{\eta }}}_{{\rm{e}}}{{{\eta }}}_{{\rm{out}}}{\rm{PLQY}}.$$

(9)

where η_b is the current balance factor, η_e is the singlet exciton formation efficiency and η_out is the out-coupling efficiency, and PLQY ($={{{k}}}_{{\rm{r}}}/({{{k}}}_{{\rm{r}}}+{{{k}}}_{{\rm{nr}}})$) is the photoluminescence quantum yield efficiency of the active layer. Here η_b is assumed to be 1, η_e is assumed to be 0.25 and η_out is set to 0.2; the absolute values of these values do not change our qualitative conclusions.

Transient absorption spectroscopy measurements

Ultra-fast transient absorption spectroscopy was conducted on 10⁻¹⁵–10⁻⁹ s timescales using a commercial transient absorption system (HELIOS, Ultrafast Systems Inc.). Pump and probe pulses were generated by means of a regeneratively amplified Ti:Sapphire laser system (Solstice, SpectraPhysics Inc.), which generates 800 nm laser pulses with a nominal temporal width of ~100 fs at a repetition rate of 1 kHz. To generate the narrow band visible pump pulses, a fraction of the 800 nm beam was directed first through an optical parametric amplifier and thereafter a frequency mixer (TOPAS Prime, SpectraPhysics Inc.) to tune the excitation wavelengths. The intensity of the pump (pump energy) was modulated using neutral density filters and measured using a power meter (VEGA, P/N 7Z01560, OPHIR Photonics). Pump energies of 20 (±2) nJ and a pump spot diameter of 1 mm were employed for all measurements, resulting in an excitation fluence of 2.5 (±0.3 µJ cm⁻²).

A broadband near infrared (NIR) pulse (~850–1,400 nm), produced by means of bulk supercontinuum generation, was used as the probe. Generation of the supercontinuum was achieved by focusing a fraction of the 800 nm pulse into a ~5 mm yttrium aluminium garnet (YAG) crystal. The probe beam was delayed with respect to the pump beam using a motorized delay stage. To reduce the noise, the NIR white light probe was split into two beams, one of which is passed through the sample and the other used as a reference. Both beams were subsequently focused onto separate fibre-optic coupled, multichannel spectrometers. The probe beam was aligned with the pump pulse and focused on the sample, which was placed in a nitrogen-purged cuvette during measurements. Alternate pump pulses were blocked using a synchronized chopper (500 Hz). The transient absorption signals were collected by means of a pair of imaging spectrographs (HELIOS, Ultrafast Systems Inc.).

To verify that our observed dynamics did not arise from bimolecular effects, we performed a set of measurements on IEICO-4F, in which the excited state dynamics arising from pump fluences of 1.51 and 3.08 µJ cm⁻² were compared. We directly probe the total excited state population by monitoring the ground state bleach of IEICO-4F. We find that the 1/e recovery time of the ground state bleach varies by approximately 1 ps when decreasing the fluence from 3.08 µJ cm⁻² to 1.51 µJ cm⁻². By contrast, the 1/e lifetimes observed for the PC₇₁BM: IEICO-4F blends vary by approximately 6 ps across our range of blend ratios, strongly suggesting that multimolecular effects are unlikely to be the proximate cause of our observed dynamics.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.