Introduction

Two-dimensional (2D) spin models are one of the most well-studied magnetic systems in condensed matter physics. The pioneering solution by Onsager in 19441 revealed that the 2D ferromagnetic (FM) Ising model, characterized by nearest neighbor coupling J, undergoes a magnetic phase transition at kBTC = 2.269J, exhibiting an order parameter critical exponent β = 1/8. The 2D XY model, on the other hand, lacks long-range order, but it exhibits the ability to undergo a Berezinskii-Kosterlitz-Thouless transition, during which the correlation function transitions from an exponential decay to a power-law behavior as a function of distance2,3. In real magnetic materials, spins exhibit free 3D rotation rather than adhering to binary orientations or 2D rotations, and the Hamiltonian for actual magnetic systems will take the form of a Heisenberg model plus magnetic anisotropy4. According to the Mermin-Wagner theorem, in the case of an isotropic Heisenberg Hamiltonian with short-range magnetic exchange couplings, the thermal fluctuations are strong enough to prevent long-range magnetic order in the 2D limit at any finite temperature5, with the correlation length diverging only at absolute zero. Conversely, in the presence of easy-axis/easy-plane anisotropy, the renormalization group flow will favor the selection of the anisotropic component of the Hamiltonian as the relevant parameter, resulting in critical behavior that aligns with predictions from the Ising/XY models6.

The discovery of long-range magnetic order at non-zero temperatures in the 2D monolayer of several honeycomb lattice van der Waals (vdW) ferromagnets and antiferromagnets suggests a suppression of the thermal fluctuations, most likely due to the formation of an Ising-type magnetic anisotropy gap in these materials7,8,9,10,11,12. To understand the microscopic origin of the long-range magnetic order in the 2D limit for different classes of vdW materials, it is therefore important to determine the magnetic properties of their 3D bulk compounds. While the FM Ising Hamiltonian on a 2D square lattice has been solved1, the situation for Ising spin systems in 2D honeycomb lattices is more complicated. As a non-Bravais lattice, the honeycomb structure can host a few different collinear magnetic structures, including simple ferromagnets, Néel antiferromagnet with c-axis aligned moments, stripy antiferromagnet, and zig-zag antiferromagnet [Fig. 1e], depending on the relative strengths of nearest J1 (NN), next nearest J2 (NNN), and next-next nearest neighbor J3 (NNNN) magnetic exchange interactions [Fig. 1a]13. The first two magnetic structures have the same in-plane ordering wavevectors as the lattice vectors, and respect the three-fold rotational (C3) symmetry of the honeycomb lattice. The stripy and zig-zag antiferromagnetic (AF) structures, however, break the C3 rotational symmetry of the honeycomb lattice to C1 and fold the first Brillouin zone (FBZ) into a smaller rectangular magnetic FBZ. In these structures, there will be three magnetic domains separated by 60°, meaning that the overall magnetism still obeys the underlying C3 lattice symmetry. The magnetic order parameter is not a direct measure of the ordered or staggered moment because it has multiple components. For example, the order parameter for the zig-zag AF order is composed of three components (Ψ1, Ψ2, Ψ3), each reflecting the staggered moment along one of the three C3 axes14. By probing the static magnetic order and spin excitations across the magnetic phase transition, one can obtain information concerning the behaviors of the phase transition and compare the results with the expectations of the conventional Ising or XY models.

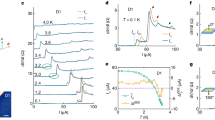
Fig. 1: Real/reciprocal space of FePSe3 and spin waves along in-plane and c-axis directions.
figure 1

a Schematics of the intralayer AF magnetic structure and exchange interactions. b Interlayer magnetic structure and coupling Jc. c Local Fe2+ environment in FePSe3, with the 3d6 spin configuration in an octahedral environment. d Neutron intensity of magnetic Bragg peak (1/2 0 1/2) as a function of temperature. e The in-plane zig-zag magnetic structure. The bold black rhombus shows the lattice unit cell and the dashed red rectangle shows the magnetic unit cell. f The reciprocal space with black hexagons shows the lattice FBZ and the dashed red rectangle shows the magnetic FBZ. The blue dots are the magnetic Bragg peaks from the magnetic structure shown in (e). g Out-of-plane spin wave dispersion along [1/2 0 L] from the experiment. All error bars indicate one standard deviation.

Full size image

For the FM honeycomb system CrSiTe3, the critical behavior of the magnetic phase transition exhibits 2D Ising characteristics15,16, with a dimensional crossover from 2D to 3D near TC17. For other honeycomb lattice ferromagnets such as CrI3, VI3, and CrGeTe3, the critical behavior is more reminiscent of the tricritical mean field model18,19,20,21,22. For AF-ordered MnPS3, NiPS3, and CoPS3, the critical behavior near TN shows 3D XY or Ising characteristics23,24,25. However, none of these AF materials with Ising-type anisotropy follow the genuine 2D Ising model due to the limited strength of the anisotropy, along with interlayer interactions that impact the magnetic phase transition26,27.

FePS3 and FePSe3 constitute a potential material family for exploring an Ising-type antiferromagnetic phase transition accompanied by C3 symmetry breaking. This study specifically centers on FePSe3 [Fig. 1a, c]. FePSe3 belongs to the rhombohedral \(R\bar{3}\) space group, with hexagonal layers stacked through weak vdW interactions along the c-axis [Fig. 1b]28. Compared with FePS3 in the monoclinic C/2m symmetry group, FePSe3 preserves the C3 symmetry and therefore is ideal to study any possible magnetic order induced in-plane C3 symmetry breaking without significant interlayer coupling effects29. Since FePSe3 has an in-plane zig-zag AF structure below TN = 110 K, we expect an FM exchange interaction J1 between NN, and AF exchange interactions in J2 and J3 between NNN and NNNN, respectively [Fig. 1a]28. In the 3D bulk limit, the AF ordering wavevector is QAF = (1/2, 0, 1/2) [Fig. 1b, f] due to a weak AF interlayer coupling Jc [Fig. 1b]28. The magnetic Fe2+ ion has a 3d6 electronic orbital with four unpaired spins, giving S = 2. A strong spin-orbit coupling (SOC) induces a large magnetic anisotropy with the c-axis as the easy axis28,30. Raman scattering experiments on bulk and monolayer FePSe3 have observed a ~ 15 meV spin gap, suggesting that the system is Ising-like11,12.

In this work, we use elastic and inelastic neutron scattering (INS) to study the magnetic order and spin dynamics in bulk single crystal FePSe3. The temperature dependence of the magnetic order parameter from elastic neutron scattering experiments suggests that the AF phase transition is first-order in nature [Fig. 1d]. In the AF ordered state, our INS experiments reveal that spin waves are gapped below ~15 meV, consistent with Raman scattering results11,12, and are highly 2D with weak dispersion along the c-axis [Fig. 1g]. By fitting the spin-wave dispersion spectra using linear spin wave theory (LSWT)31, we determine magnetic exchange couplings, magnetic anisotropy, and find evidence for a biquadratic term in the spin Hamiltonian. On warming above TN, we find dispersive spin excitations that can be explained by AF and FM excitations from honeycomb lattice clusters with the C3 symmetry. These results are different from the expectation of a conventional AF second-order phase transition, suggesting that the long-range AF order in FePSe3 is replaced by C3 magnetic honeycomb lattice clusters as the temperature is raised above TN. The uncorrelated paramagnetic scattering from individual Fe ions is only established at temperatures well above TN.

Results

Neutron diffraction experiments

Single crystal neutron diffraction experiments are performed at 6 K and 125 K to refine crystal and magnetic structures. From neutron diffraction experiments, the magnetic ordering wavevector observed at QAF = (1/2, 0, 1/2) as well the refinement at 6 K (see Supplementary Fig. 2) confirms the zig-zag magnetic structure, and the temperature dependence of the order parameter is shown in Fig. 1d. A power law fit of the order parameter with \(I={I}_{0}(1-{(T/{T}_{{{{\rm{N}}}}})}^{2\beta })\) yields a critical exponent β = 0.063, which is much smaller than the 2D Ising model prediction β = 1/8, suggesting a first-order nature of the phase transition. This is further supported by measurements of correlation lengths which jump abruptly at TN30.

INS experiments and linear spin wave theory fits

Figures 1g and 2b show the measured spin wave dispersions of FePSe3 at 5 K along the c axis and within the 2D honeycomb lattice plane, respectively. The overall dispersion has a band top of ~40 meV, with an anisotropy gap of ~15 meV at the Γ and M points. The large anisotropy gap value is also observed in the sister compound FePS3, which is due to the combined effects of SOC in the 3d6 orbital of Fe2+ and the distortion of the FeSe6 octahedron [Fig. 1c]. For comparison, the isostructural compounds MnPSe3 and MnPS3 do not exhibit such large gaps because their 3d5 electrons have quenched orbital moments26,32. The spin waves propagating along the c-axis exhibit significantly less dispersion in contrast to the in-plane spin waves, featuring a bandwidth of ~1 meV for the former as opposed to a 20 meV bandwidth for the latter, indicating the presence of a very weak interlayer coupling Jc [Fig. 1g]. This is consistent with the fact that the TN of FePSe3 changes little as a function of layer numbers, suggesting that the interlayer exchange interactions have minimal effect on the magnetic phase transition in FePSe39,11.

Fig. 2: Spin waves in FePSe3.
figure 2

a Calculated spin wave dispersion with (black) and without (red) biquadratic interactions. The inset shows the Q scan path. b LSWT fit of the experimental data with (white) and without (red) biquadratic interactions. All error bars indicate one standard deviation.

Full size image

To describe the in-plane spin wave dispersion, we first use LSWT to calculate the spin waves with the spin Hamiltonian

$${H}_{0}=\mathop{\sum}\limits_{ < i,j > }{J}_{ij}{{{{\bf{S}}}}}_{i}\cdot {{{{\bf{S}}}}}_{j}+\mathop{\sum}\limits_{i}{D}_{z}{({S}_{i}^{z})}^{2}$$
(1)

where the bilinear (Heisenberg) exchange interaction Jij is summed over the 1st, 2nd, and 3rd NN, and Dz is the single-ion anisotropy with the z-axis as its easy axis. It is worth noting that within the actual system, magnetic anisotropy may stem from either single-ion effects or Ising-type exchanges. Therefore, the Hamiltonian can encompass Ising exchange terms JzSizSjz in addition to the single-ion anisotropy. Nevertheless, within the framework of linear spin wave theory, the Ising term’s impact on dispersion will be identical to that of single-ion anisotropy, provided that the respective parameters are appropriately adjusted33 (see Supplementary Table III). For the sake of simplicity, we have chosen to solely include the single-ion anisotropy term here. Using a least-square-error fitting method with S = 2, we extract the magnetic exchange coupling parameters as shown in Table 1. However, the best fitting using this model with uniform J1 does not precisely reproduce the measured dispersion, especially the low-energy part perpendicular to the zig-zag direction. In fact, the exact same scenario is observed in the sister compound FePS334 where a simple Heisenberg model plus anisotropy cannot account for the spin excitations accurately. In the case of FePS3, two approaches have been utilized to resolve this problem, and here we apply them to FePSe3 as well. The first is to introduce bond-dependent J1 with J1a bonding the parallel spins and J1b for anti-parallel spins; The second is to introduce a biquadratic interaction

$$H={H}_{0}+\mathop{\sum}\limits_{ < i,j > }{K}_{ij}{({{{{\bf{S}}}}}_{i}\cdot {{{{\bf{S}}}}}_{j})}^{2}$$
(2)

where the biquadratic exchange Kij is summed over the 1st NN only. Both methods stabilize the zig-zag AF order, and with proper fitting parameters in Table 1, they yield nearly identical dispersions that can accurately reproduce the experimental data. For the J1a-J1b model, the difference between J1a and J1b is large, indicating that a lattice distortion should accompany the magnetic phase transition as in the case of FePS3. However, no obvious lattice parameter change is observed across TN, indicating that the J1a-J1b model is unlikely to be correct(see Supplementary Fig. 3 and Fig. 4). On the other hand, The existence of a biquadratic interaction has been theoretically proposed in many such 2D magnetic systems with edge-shared octahedron structures35,36, and therefore may be the more suitable model for describing the spin waves in FePSe3. The situation is similar in the case of iron-based superconductors, where a biquadratic interaction has been used to account for the observed in-plane spin wave dispersions37,38. A noteworthy fact is that the low-energy magnons at the Γ point are linearly coupled to phonons, which introduces a magnon-polaronic gap that lifts the twofold degeneracy of the AF magnons11,12. This suggests the necessity of introducing a magnon-phonon coupling term into the spin Hamiltonian. However, the impact of this term is minimal, exhibiting a gap of ~0.6 meV, a value below the resolution of the instruments. Hence, it is omitted from equation (2). Furthermore, the required strength of the Kitaev interaction (0.03 meV) to induce the magnon-phonon gap is significantly less than that of the Heisenberg exchanges, and thus, these are not taken into account in the fitting parameters.

Table 1 Magnetic exchange interaction strength in different models in FePSe3
Full size table

Thermal evolution of the spin excitations

The first-order nature of the AF phase transition also displays itself in the spin fluctuations in the neighborhood of TN. Figure 3 shows a summary of the INS spectrum near TN = 110 K. At T = 101 K, in-plane spin excitations are well-defined and similar to spin waves at 5 K [Fig. 3a]. On warming to T = 107 K, spin excitations remain well defined, but become broader with an anisotropy spin gap above 10 meV (Fig. 3b). Upon further warming to 110 K, the spin gap drastically decreases to zero at the M point, while keeping a non-zero value at the Γ point [Fig. 3c]. A cut along the [H, 0] direction at E = 5 ± 1 meV shows clearly that the M point spin fluctuations are enhanced from 110 K to 125 K, different from the expectation of critical magnetic scattering associated with a second-order phase transition. Although the spin gap closing at the M point may arise from the vanishing static magnetic moment across TN, the differences in the temperature dependence of the spin gap at Γ and M points cannot be explained by a second-order AF phase transition since the Γ and M points are equivalent within the spin wave theory which requires long-range AF order and folding of the Brillouin zone below TN. This is consistent with the observed first-order transition in the AF order parameter [Fig. 1d]. In the paramagnetic state, the rectangular magnetic Brillouin zone unfolds to the hexagonal lattice Brillouin zone. However, we find similar spin excitations as in the AF-ordered state [Fig. 3d–f].

Fig. 3: Spin excitations in FePSe3 at different temperatures.
figure 3

Spin excitations in FePSe3 in (a) 101 K, (b) 107 K, (c) 110 K, (d) 113 K, and (e) 125 K. f A constant-E cut of the intensity in (a–e) with E integrated between 4 and 6 meV. The incident neutron energy used here is Ei = 35 meV. All error bars indicate one standard deviation.

Full size image

Discussion

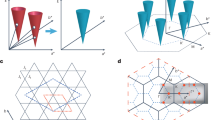
Although the AF phase transition in FePSe3 is first-order, the short-range zig-zag order may still persist near the phase transition. A natural way to reconcile the existence of the zig-zag order and the C3 symmetry is to combine all the zig-zag domains with equal weight [Fig. 4a], while the size of the fluctuation domains determines the correlation lengths of the short-range order. To understand the nature of the dispersive paramagnetic spin excitations in FePSe3, we plot constant-E slices in the [H K] plane at E = 5 ± 2 meV [Fig. 4c] and 11 ± 2 meV [Fig. 4d] at 110 K, which shows the spin excitations at the M points and their connections, respectively. The low-energy spin excitations show diffusive hexagonal patterns which are hollow at the Γ point, and the high-energy excitations show plate-like hexagonal patterns. Inspired by the spin cluster methods used in refs. 39,40,41, we apply a similar analysis on FePSe3. Assuming that the spins form clusters of hexagons with zig-zag order [Fig. 4a], we calculate the neutron intensity I(Q) with

$$I({{{\boldsymbol{Q}}}})\propto {f}^{2}({{{\boldsymbol{Q}}}})\mathop{\sum}\limits_{\langle m,n\rangle }{e}^{i{{{\boldsymbol{Q}}}}({{{{\boldsymbol{r}}}}}_{m}-{{{{\boldsymbol{r}}}}}_{n})}\left(1-\frac{{Q}_{z}^{2}}{{Q}^{2}}\right)\langle {S}_{m}^{z}{S}_{n}^{z}\rangle$$
(3)

where f2(Q) is the magnetic form factor, m, n ∈ 1,...,6 is the index for spins in Fig. 4a and b. The calculated I(Q) is then averaged over six zig-zag spin configurations. Figure 4d, f shows the calculated intensity from the zig-zag clusters [Fig. 4a], which matches well with the experimental result at low energy. For the higher energy part at 11meV, due to the enhanced Γ point spin fluctuations, an additional FM cluster is required [Fig. 4b] in order to reconstruct the plate-like excitation pattern.

Fig. 4: Simulation on spin fluctuations at Néel temperature in FePSe3.
figure 4

a, b Zig-zag AF and FM clusters were used to simulate the spin fluctuation, respectively. c Experimental data at T = 110 K and E = [3,7] meV. d Calculated neutron intensity of the AF cluster in (a). e Experimental data at T = 110 K and E = [9,13] meV. f Calculated neutron intensity of the AF cluster (a) plus the FM cluster (b). The AF clusters and FM clusters are weighted with a ratio of 2:1 in (f). g Experimental data at T = 4 K and E = [14,18] meV. h Calculated neutron intensity at the same energy range as (g) by LSWT with parameters from Table 1.

Full size image

The spin fluctuations observed at 110 K encode substantial information regarding the spin correlations in FePSe3. The pillar-like feature of the spin excitations at the M point in Fig. 3c indicates that the Q-dependence of low-energy spin excitations remains unchanged below ~8 meV. This implies that an integral over the low-energy excitations can reasonably approximate the instantaneous spin correlations. Consequently, despite our zig-zag cluster calculation is used to reproduce the spin fluctuation in the energy range E = [3,7] meV, it is reasonable to infer that this zig-zag arrangement effectively reflects the nature of these instantaneous spin correlations.

A noteworthy observation is that even in the AF state at 4 K, the dynamical spin-spin correlation centers around the FM wavevector located at Γ, rather than the AF wavevector at M [Fig. 4g, h]. The reason is that as the magnetic anisotropy grows, the AF spin wave excitations are gradually replaced by local spin-flip excitations. In an isotropic AF Heisenberg model, the magnetic excitations are spin waves that give zero structure factor at the FM wavevector, while in a pure AF Ising model, the spin-flip excitations will introduce a non-zero intensity centered at the Γ point. In the case of FePSe3, the robust magnetic anisotropy shifts the primary spin excitations from AF spin waves to spin-flip excitations. As the temperature rises to TN, the local spin-flip excitation remains gapped, indicating that the dynamic susceptibility associated with spin-flip scattering remains non-zero. Consequently, it cannot be the primary driving force behind the first-order magnetic phase transition. Instead, the excitations of zig-zag clusters at TN become gapless, implying that the dominant component of spin configurations near TN is the zig-zag short-range order. It can be speculated that the magnetic phase transition is driven by a discontinuous condensation of these zig-zag hexagonal clusters, corresponding to the C3–C1 symmetry breaking. This distinguishes it from the fluctuations observed in conventional Ising magnets that break the Z2 time-reversal symmetry through spin-flip scatterings.

In summary, we utilized neutron scattering to study the spin excitations and spin fluctuations in FePSe3 across TN. By analyzing the spin wave dispersion, we find evidence for biquadratic magnetic exchange interactions in the effective spin Hamiltonian terms. The microscopic origin of the biquadratic term remains to be determined. In addition, our magnetic order parameter measurements indicate that the AF phase transition is first-order in nature. From measurements of the temperature-dependent spin excitations across TN, we infer that the AF phase transition may be driven by the C3 to C1 symmetry breaking from low-energy spin clusters associated with zig-zag AF honeycomb lattice. Our results provide an enriched perspective on the intricate interplay between magnetic interactions and structural symmetries in the Ising magnetic systems with additional C3 symmetry breaking.

Methods

Sample synthesis and the reciprocal lattice

Single crystals of FePSe3 were synthesized using the chemical vapor transport method described in ref. 42. Around 2g stoichiometric starting materials (Fe, P, Se) were sealed in a quartz tube together with around 0.1 g iodine as a transport agent. The tube was then kept in a tube furnace for a week with a temperature gradient from 650 °C to 600 °C. FePSe3 flakes were collected at the cold end of the tube with typical masses of 5–10 mg. The momentum transfer Q is referenced in reciprocal lattice units with respect to the hexagonal unit cell of FePSe3 with a = b = 6.26 Å, c = 19.71 Å. The high symmetry points Γ, M, K in the reciprocal space are specified in Fig. 1f.

Neutron diffraction

Neutron diffraction experiments were performed at the CORELLI spectrometer at the Spallation Neutron Source, Oak Ridge National Laboratory43 on a single crystal sample. The overall diffraction patterns were collected at 6 K and 125 K. Order parameter scans were then performed at the (1/2 0 1/2) magnetic Bragg peak together with scans on the (3 0 0) and (3 3 0) Bragg peak which track the temperature dependence of the lattice parameters. The data collected at CORELLI was used to refine the crystallographic parameters through the JANA2006 software44 (See Supplementary Tables I and II).

Inelastic neutron scattering

Inelastic neutron scattering experiments were performed at the ARCS spectrometer45 on ~0.5 g of co-aligned crystals at the Spallation Neutron Source, Oak Ridge National Laboratory. The inelastic neutron spectra were plotted using DAVE-Mslice46. For linear spin wave theory fitting, we utilized the SpinW package47 to reconstruct the neutron structure factor S(Q, E). The gradient descent method was used to extract the best-fitting parameters.