Probing octupolar hidden order via Janus impurities

Abstract

Quantum materials with non-Kramers doublets are a fascinating venue to realize multipolar hidden orders. Impurity probes which break point group symmetries, such as implanted muons or substitutional impurities, split the non-Kramers degeneracy and exhibit a Janus-faced influence in such systems: they can destroy the very order they seek to probe. Here, we explore this duality in cubic osmate double perovskites which are candidates for exotic d-orbital octupolar order competing with quadrupolar states. Using ab initio computations, Landau theory, and Monte Carlo simulations, we show that Janus impurities induce local strain fields, nucleating quadrupolar puddles and suppressing the octupolar T_c. At the same time, strains mix the non-Kramers doublet with an excited magnetic triplet, creating parasitic dipole moments which directly expose the hidden octupolar order parameter. Our work unravels this Janus duality in recent impurity nuclear magnetic resonance (NMR) experiments, with important implications for uncovering hidden order in diverse multipolar materials.

Introduction

The idea of “hidden order”, or subtle broken symmetries which are difficult to detect, has a long history in f-electron heavy fermion materials, with notable examples such as NpO₂ and URu₂Si₂^{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20}. The intricacy of these orders stems from their spin-orbital entanglement and complex multipolar character. Understanding the origin of such multipolar orders and devising probes to characterize them remain important challenges in this field. Recent work has discovered multipolar orders in metallic and insulating d-orbital systems^{21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37}, opening up the exploration of distinct classes of materials and probes to shed light on these complex orders.

The simplest nontrivial multipolar order involves the ordering of quadrupoles, and it is intimately tied to the breaking of crystalline rotational symmetry, i.e. ‘nematic order’. Such nematic phases and nematic quantum critical points are of great interest in cuprate, iron pnictide, and iron chalcogenide materials^38,39. Experiments on heavy Mott insulators with strong spin-orbit coupling (SOC) have also revealed candidates hosting quadrupolar orders. For Mott insulators with one electron in the t_2g orbital, SOC leads to a j = 3/2 pseudospin which supports higher multipole operators^21,22,26. High-resolution X-ray diffraction experiments on a candidate material, Ba₂MgReO₆, have found compelling evidence for separate phase transitions associated with ordering of the associated quadrupole and dipole moments on Re^29,40. Earlier NMR experiments had proposed such successive broken symmetries in Ba₂NaOsO₆^27,28. Glassy valence-bond states, possibly with short-range multipolar orders, may be relevant to j = 3/2 Ba₂LuMoO₆⁴¹.

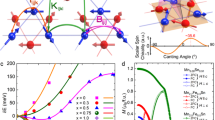
Going one step further, octupolar ordering corresponds to a pattern of loop current order which breaks time-reversal symmetry and leads to an octupolar magnetization density as depicted in Fig. 1a, b. Ferro-octupolar order is a spin-orbit coupled variant of ‘altermagnetism’^42,43,44, which has received a lot of recent attention. Closely related loop currents have been discussed in cuprates^45,46,47, manganites⁴⁸, iridates^49,50, and the recent kagome superconductors^51,52; however, smoking-gun signatures of these currents remain to be observed. Chiral-lattice antiferromagnets such as Pb(TiO)Cu₄(PO₄)₄ may also host octupoles⁵³.

Fig. 1: Ising octupolar order.

a Schematic view of octupolar order as arising from an alternating pattern of orbital currents around transition metal octahedra. b Octupolar order for t_2g orbitals, with a shape corresponding to the electron charge density cloud (which preserves cubic symmetry) and colors denoting the magnetization density due to orbital currents. c Microscopic origin of multipole orders in J = 2 magnets with SOC. The octahedral crystal field weakly splits the J = 2 levels into a low energy many-body E_g non-Kramers doublet and an excited T_2g magnetic triplet. We highlight the charge density in the real eigenfunctions (“orbitals”) $\left\vert {\psi }_{g,\uparrow }\right\rangle$ and $\left\vert {\psi }_{g,\downarrow }\right\rangle$ of the E_g levels; see text for details. The octupolar order in (b) is a complex superposition of these real wavefunctions. The time-reversed partner $\left\vert {\psi }_{g,\uparrow }\right\rangle -i\left\vert {\psi }_{g,\downarrow }\right\rangle$ (not shown) has reversed loop currents and magnetization densities.

Quantum materials that host non-Kramers doublets provide the most promising venue to search for multipolar orders^{54,55,56,57,58,59,60}. Unlike Kramers doublets, the degeneracy of non-Kramers doublets is protected by crystalline point group symmetries. These pseudospin-1/2 degrees of freedom thus cannot reflect pure dipoles since their degeneracy can be lifted by breaking crystal symmetries while preserving time-reversal symmetry. The ordering of these non-Kramers doublets, facilitated by exchange interactions, results in multipolar symmetry breaking.

An important route to sleuthing broken symmetries in quantum materials is via local probes such as NMR of doped impurity ions or muon spin rotation (μSR) of implanted muons. In the context of multipolar orders, we coin the term ‘Janus impurities’ to refer to such probes since they are two-faced like the Roman God Janus: while they may act as local probes of multipolar order, these impurities also break the local point group symmetry and split the non-Kramers degeneracy, thus destroying the very order they seek to detect. In this work, we ask whether Janus impurities can nevertheless be useful probes of multipolar orders.

As an example, recent work has shown that non-Kramers doublets naturally appear in heavy d-orbital Mott insulators, with strong SOC, which host two electrons in the t_2g orbital^30,31,32,36. In these systems, the j-j coupling between the two j = 3/2 electrons leads to a J = 2 multiplet, which splits in the cubic environment to yield a low energy non-Kramers doublet, as shown in Fig. 1c; we denote these doublet wavefunctions by $\left\vert {\psi }_{g,\uparrow }\right\rangle$ and $\left\vert {\psi }_{g,\downarrow }\right\rangle$ For these doublets, the pseudospin-1/2 operators (τ_x, τ_z) transform as a two-dimensional electric quadrupole, while τ_y transforms as a magnetic octupole^30,31,32. Ordering of (τ_x, τ_z) and of τ_y thus correspond respectively to quadrupolar and Ising-type octupolar orders. Ferro-octupolar order with 〈τ_y〉 ≠ 0 naturally explains^30,31,32,36 the time-reversal breaking transition seen via μSR in the osmium double perovskite (DP) Mott insulators, Ba₂CaOsO₆, Ba₂MgOsO₆, and Ba₂ZnOsO₆^{30,61,62,63,64} where Os⁶⁺ ions host a 5d² configuration.

Microscopic support for ferro-octupolar order in the cubic osmate DPs comes from recent density functional and dynamical mean field theory (DFT+DMFT) calculations³⁴, as well as model tight-binding calculations which extract the intersite exchange in the presence of electron interactions and SOC^36,37. Raman scattering from crystal field levels is one proposed route to probe such octupolar order³¹; however, smoking gun experimental signatures of this exotic order are still lacking. Furthermore, while octupolar order is the most likely broken symmetry state in these DPs, there can be competing quadrupolar orders^35,36,37. Such competing orders are important at crystal surfaces where the cubic symmetry is naturally broken by uniaxial strain fields, favoring quadrupolar order³⁶.

While ‘hidden order’ has been discussed in the literature, most efforts to date are theoretical studies of toy models, and clear evidence of hidden octupolar order has so far remained elusive. Here, we use ab initio calculations of the crystal structure, Landau theory analysis, Monte Carlo (MC) simulations, and modelling of NMR spectra, to explore the competition between octupolar and quadrupolar orders in the osmate double perovskites. Our work uncovers the evidence for octupolar order by making direct contact with recent experimental studies.

For Ba₂CaOsO₆, our ab initio computation of the phonon modes shows that the cubic $Fm\bar{3}m$ structure is stable against deformations. This bolsters the case for the possibility of octupolar ordering which preserves cubic symmetry, since non-cubic lattice distortions are otherwise likely to favour competing quadrupolar orders³⁵. We find a low energy peak in the phonon density of states (DOS) which is in good agreement with inelastic neutron scattering experiments³⁰. Upon substituting Ca²⁺ with Na⁺ or Sr²⁺, we find that these Janus impurities lead to local distortions in the crystal which break the octahedral point group symmetry around Os. Such strain fields acts as local transverse fields on the octupolar order, creating droplets of pinned quadrupolar order.

Our Monte Carlo simulations show that these quadrupolar droplets strongly suppress the ferro-octupolar T_c, and lead to an inhomogeneous and temperature-dependent distribution of octupolar and quadrupolar moments. Furthermore, we show that these strain fields can reveal the intrinsic octupolar order through the generation of parasitic dipole moments below the ferro-octupolar T_c. Finally, by explicitly modelling the ²³Na NMR spectrum, we show how our work allows us to capture all the key features observed in recent ²³Na NMR experiments on Ba₂Ca_1−δNa_δOsO₆⁶⁵, and to propose future experiments on Ba₂Ca_1−δSr_δOsO₆ and Ba₂Ca_1−δMg_δOsO₆.

Results

Phonon modes in Ba₂CaOsO₆

First principles density functional theory (DFT) calculations are carried out to explore the phonon dispersion and structures of Ba₂Ca_1−δNa_δOsO₆ and Ba₂Ca_1−δSr_δOsO₆. Our motivation here is two-fold: to examine the intrinsic stability of the cubic $Fm\bar{3}m$ phase of Ba₂CaOsO₆, and to explore how an impurity induces local strain fields. We study phonon properties within the formulation of density functional perturbation theory (DFPT) as implemented in the Vienna Ab-initio Simulation Package (VASP)^66,67. Total energy and force calculations for structure optimization are carried out using VASP in the plane wave pseudo-potential basis, and choosing the generalized gradient approximation (GGA) to describe the exchange-correlation functional, and incorporating the effects of Hubbard U and spin-orbit coupling (GGA+U+SOC) on Os (see Methods).

The computed phonon dispersion of Ba₂CaOsO₆ in its $Fm\bar{3}m$ structure, plotted along the high-symmetry points of the Brillouin zone (BZ) of its primitive unit cell, is shown in Fig. 2 for low energy E < 25 meV. We find three acoustic modes and nine optical branches in this energy window; as seen from the right panel of Fig. 2, this leads to a significant peak in the phonon density of states at E ≈ 10 meV, consistent with inelastic neutron scattering results at large momentum transfer³⁰. We observe no negative phonon frequencies, which thus confirms the intrinsic dynamical stability of the $Fm\bar{3}m$ structure with respect to any local non-cubic distortions. This shows that although the Os is in a d² configuration, with partially filled t_2g orbitals, it can be stable against Jahn-Teller distortions from orbital-lattice couplings⁶⁸. The absence of any non-cubic distortions lends support to the scenario that a low energy non-Kramers doublet is realized in the cubic structure of Ba₂CaOsO₆^30,31,32. The irreducible representations of the phonon modes at the Γ-point, as well as phonon spectra extending to higher energies, are given in Supplementary Note 1.

Fig. 2: Phonon dispersion.

Ab initio results for the low energy phonon dispersion of Ba₂CaOsO₆ shown along high symmetry paths in the BZ of the primitive unit cell. All modes have positive energy reflecting the stability of the cubic $Fm\bar{3}m$ structure. Right panel shows the corresponding phonon density of states (DOS). Inset: Crystal structure of Ba₂CaOsO₆, with shaded purple and cyan octahedra depicting the checkerboard arrangement of OsO₆ and CaO₆ units, and red balls indicating O atoms.

Local strains induced by impurities

Having confirmed the stability of the cubic $Fm\bar{3}m$ structure in Ba₂CaOsO₆, we next consider the influence of substitutional impurities like Na or Sr in place of Ca in the structure. Since the ionic radius of Na⁺ and Sr²⁺ in octahedral coordination of DP structure are 1.02Å and 1.18Å, as compared to 1.00Å for Ca²⁺, this substitution is expected to cause a local lattice distortion and a lowering of the local point group symmetry. This propensity to distortion is signalled by an optical phonon instability in the $Fm\bar{3}m$ structure (see Supplementary Note 1).

To investigate, in more detail, the effect of substitutional impurities and impurity clustering, we next study a Ba₂CaOsO₆ supercell of dimension 2 × 2 × 1 in terms of a cubic four formula unit cell. This results in 16 Ca sites in the supercell. We replace two of these Ca by Na or Sr, amounting to an effective impurity concentration δ = 1/8 for Ba₂Ca_1−δNa_δOsO₆ and Ba₂Ca_1−δSr_δOsO₆, respectively. We consider two configurations in the supercell: (i) the far configuration shown in Fig. 3a and (ii) the near configuration shown in Fig. 3c.

Fig. 3: Optimized structures showing impurity-induced local strains.

a Optimized Ba₂Ca_1−δNa_δOsO₆ structure in a supercell (with 16 formula units) corresponding to δ = 1/8, having two impurity Na atoms substituting for Ca at farthest sites. Deep cyan, yellow and red colored balls represent Ca, Na and O atoms, respectively. The optimized structure contains four inequivalent Os sites (colored differently). The Os sites exhibiting maximum distortion (Os1) are highlighted using shaded green octahedra. b Detailed view of the maximally distorted Os1O₆ octahedron which have 90^∘ O–Os–O bond angles, but with variations in the bond length, together with the local site-symmetry (4/mmm), and D parameter (D = 0.0107) which measures the degree of octahedral distortion (see text for details). This leads to an effective E_g strain field on the Os1 site. c Same as (a), but with two Na atoms substituting for nearest pairs of Ca. In this case six different inequivalent Os sites are created and depicted with different colored balls; Os sites exhibiting maximum distortion Os1 are highlighted with grey octahedra. d Same as (b) but shown for maximally distorted Os1 site in near configuration (see text for details). In this case, the site symmetry is lowered to m2m, D = 0.0104, and O-Os-O bond angles deviate from 90^∘ which leads to an additional T_2g strain field on Os1. Similar results are found for Ba₂Ca_1−δSr_δOsO₆.

In the far configuration, shown in Fig. 3a, we substitute two distant Ca atoms in the supercell with the substitutional impurity. Full structure optimization of this configuration leads to four inequivalent Os sites marked by different colors and labelled Os1–Os4, in Fig. 3a, b (see Supplementary Notes 1 and 2 for details). Of these four inequivalent Os sites, the maximal distortion occurs at sites that have two Na atoms at its nearest neighbour shell (depicted as green octahedra). The site symmetry of this Os site, marked Os1 and shown in Fig. 3b, is found to be 4/mmm. As discussed below, this leads to an E_g strain on the Os1 d orbitals. The distortion of OsO₆ octahedra can be measured by the distortion index, $D=\frac{1}{6}\mathop{\sum }\nolimits_{i = 1}^{6}\frac{| {l}_{i}-{l}_{av}| }{{l}_{av}}$ where l_i is the bond length of the ith Os-O bond, and l_av is the average bond length; for Os1O₆ we find D ≈ 0.01. We show in Supplementary Note 5 that this 1–2% E_g strain translates to a 5-10 meV splitting of the non-Kramers doublet.

We next turn to the near configuration shown in Fig. 3c, with two Na atoms substituting for neighbouring Ca atoms. In this case, full structure optimization leads to six inequivalent Os sites marked Os1–Os6 (for details see Supplementary Note 2). We find that the maximum distortion of Os–O bond lengths and bond angles occurs at the site marked Os1 which is adjacent to both Na atoms, with its site symmetry being lowered from 4/mmm to m2m (depicted as grey octahedra), and D ≈ 0.01. As discussed below and in Supplementary Note 2, this leads to an additional T_2g strain at this Os site. Finally, the distortion index D for sites further from the impurity site are an order of magnitude smaller (see Supplementary Note 2). As discussed later, the presence of this T_2g strain is crucial for theoretically modelling the experimentally observed NMR spectra.

Landau theory of multipole-strain coupling

Our next goal is to understand how the impurity-induced strain, discovered in our ab initio structure calculations, can impact multipolar orders. We resort here to a symmetry-based approach, beginning with a brief review of the multipoles and their symmetries for a d² electron configuration. We next turn to a Landau theory for the coupling of the multipoles to strain fields, and discuss a microscopic basis for this Landau theory where strain fields are shown to arise from impurity-induced deformations.

For two electrons in the t_2g orbital, the naively expected ground state is a J = 2 moment, which we can view as arising from spin-orbit locking of a total orbital angular momentum L = 1 and total spin S = 1. This gets split into a non-Kramers ground state doublet, and an excited triplet with a gap Δ ~ 10-20 meV³², in reasonable agreement with the spin gap observed in inelastic neutron scattering experiments³⁰ (see Supplementary Note 3). Working in the $\left\vert {J}_{z}=m\right\rangle$ basis, the non-Kramers doublet wavefunctions are given by

$$\left\vert {\psi }_{g,\uparrow }\right\rangle =\frac{1}{\sqrt{2}}(\left\vert 2\right\rangle +\left\vert -2\right\rangle );\quad \left\vert {\psi }_{g,\downarrow }\right\rangle =\left\vert 0\right\rangle .$$

(1)

Within this non-Kramers doublet space, the Pauli matrices τ_x, τ_y, τ_z refer to multipole operators, given by ${\tau }_{x}\equiv ({J}_{x}^{2}-{J}_{y}^{2})/2\sqrt{3}$, ${\tau }_{y}\equiv \overline{{J}_{x}{J}_{y}{J}_{z}}/6\sqrt{3}$, and ${\tau }_{z}\equiv (3{J}_{z}^{2}-J(J+1))/6$, with overline denoting symmetrization. Here, τ_x, τ_z are electric quadrupoles while τ_y is a magnetic octupole. The ground state doublet manifold has vanishing matrix elements for the dipole operators J, precluding magnetic dipole ordering. However, the ground state doublet can lead to broken time-reversal symmetry below T_c (while preserving cubic symmetry) if 〈τ_y〉 ≠ 0 which corresponds to ferro-octupolar ordering.

To examine the impact of strain, we note that the non-Kramers doublet degeneracy is protected by the crystalline point group symmetry. We thus expect that (random) local strains will break this degeneracy. Such strains may be produced by impurities, which can locally suppress the octupolar order while favoring quadrupolar orders. Landau theory provides a useful symmetry-based approach to study the coupling of strain to multipoles¹⁹. To explore this here, we begin by considering time-reversal invariant perturbations acting in the J = 2 space, focussing on the simplest E_g and T_2g strain fields. When we later discuss the microscopic basis for this Landau theory, our focus will be on strain fields localized at Os sites directly adjacent to the impurity site. While our previously discussed ab initio calculations yield a more complex distortion pattern of OsO₆ octahedra even far away from the impurity site, those longer range distortions are found to be the order of magnitude smaller; this will justify our simplified microscopic viewpoint.

The E_g strain perturbations act as fields (h_x, h_z) which couple to the low energy quadrupolar degrees of freedom (τ_x, τ_z) within the non-Kramers doublet. On symmetry grounds, these couplings take the form

$$\delta {H}_{x}=-{d}_{1}\int\,{{\rm{d}}}^{3}{{{\bf{r}}}}({\varepsilon }_{xx}({{{\bf{r}}}})-{\varepsilon }_{yy}({{{\bf{r}}}})){\tau }_{x}({{{\bf{r}}}})$$

(2)

$$\delta {H}_{z}=-{d}_{2}\int\,{{\rm{d}}}^{3}{{{\bf{r}}}}\frac{1}{\sqrt{3}}(2{\varepsilon }_{zz}({{{\bf{r}}}})-{\varepsilon }_{xx}({{{\bf{r}}}})-{\varepsilon }_{yy}({{{\bf{r}}}})){\tau }_{z}({{{\bf{r}}}})$$

(3)

We expect that these E_g strain fields can suppress the octupolar transition temperature since they act as transverse fields on the Ising octupolar order. We confirm this later using Monte Carlo simulations. For a sufficiently strong local strain field, it may be possible to locally kill the octupolar order. The strain-induced local quadrupolar order can lead to the broadening of NMR spectra via the generation of electric field gradients.

By contrast, the T_2g strain tensor components, such as ε_xy(r), lead to a coupling between the low-energy non-Kramers doublet and the excited magnetic triplet. This set of Hamiltonian perturbations takes the form

$$\begin{array}{lll}\delta {H}_{{{{\rm{od}}}}}\,=\,-\,{d}_{3}\displaystyle\int{{\rm{d}}}^{3}{{{\bf{r}}}}\left[{\varepsilon }_{xy}({{{\bf{r}}}}){Q}_{xy}({{{\bf{r}}}})+{\varepsilon }_{yz}({{{\bf{r}}}}){Q}_{yz}({{{\bf{r}}}})\right.\\ \qquad\qquad+\,\left.{\varepsilon }_{xz}({{{\bf{r}}}}){Q}_{xz}({{{\bf{r}}}})\right]\end{array}$$

(4)

where Q_αβ = (J_αJ_β + J_βJ_α)/2 has no matrix elements in the non-Kramers doublet subspace. In an octupolar ordered state with nonzero 〈τ_y(r)〉, taking into account the first-order perturbative correction to the wavefunction due to mixing with the excited magnetic triplet, these couplings induce weak dipole moments in the ground state. Defining ε ≡ (ε_yz, ε_zx, ε_xy), we arrive at

$$\langle {{{\bf{J}}}}({{{\bf{r}}}})\rangle =\frac{2{d}_{3}}{\Delta }{{{\boldsymbol{\varepsilon }}}}({{{\bf{r}}}})\langle {\tau }_{y}({{{\bf{r}}}})\rangle$$

(5)

The T_2g strain fields thus reveal the hidden octupolar order by generating ‘parasitic’ dipole moments. If the correlation length of these strain fields, and thus the parasitic dipole moments is short-ranged, these moments may provide a dephasing mechanism for oscillations in μSR experiments in the octupolar ordered state. We note that these parasitic dipole moments may also be observable in NMR experiments via their hyperfine coupling to nuclear dipole moments, an effect we will later model carefully.

One way such local strain fields could appear in a material is via a small density of impurities, such as antisite impurities, oxygen vacancies, or impurities induced by intentional chemical substitution. Our ab initio results show that when a single Ca²⁺ is replaced with Na⁺ or Sr²⁺, the six Os⁶⁺ ions neighbouring the impurity site will have their oxygen octahedra get uniaxially distorted from their original equilibrium positions. A schematic picture of the ideal cubic structure and a simplified model of the strain field in the xy plane induced by a single impurity is shown in Fig. 4a and b. The depicted distortions are based on our ab initio results, but have been simplified, as justified above, to only focus on distortions immediately adjacent to the impurity site. With Os⁶⁺ at the centre of the distorted octahedra as the local centre of inversion, such an octahedral distortion can be decomposed into odd-parity and even-parity modes, with only the latter having matrix elements in the d-orbital space; see Supplementary Note 5. This leads to E_g strain fields for the d-orbitals on the Os⁶⁺ site. With increasing impurity concentration, there is a higher probability of neighbouring pairs of Na⁺ or Sr²⁺ impurities. In this case, the local symmetry around Os⁶⁺ ions is further reduced, as found from our ab initio calculations, and shown in Fig. 4c. The strain fields at the Os⁶⁺ site then also include a T_2g component; we derive this in Supplementary Note 5. Thus, impurities induce both E_g and T_2g strain fields, providing a firm microscopic basis for our Landau theory.

Fig. 4: Schematic strain field configurations.

Simplified schematic crystal structure in single xy plane of the osmate cubic double perovskites. a Ideal crystal structure in the absence of impurities. b A_1g breathing distortion around an isolated impurity (Na⁺ or Sr²⁺) site. The light dashed lines and light red dots mark the original positions of oxygens in the undistorted cubic structure. This leads to an effective E_g octahedral distortion acting on d-orbitals for the six neighbouring Os sites as discussed in Supplementary Note 5. (Note that there is an additional pair of Os atoms above and below the impurity, not shown, that are affected in a similar way). c Modified distortion in the case of a pair of nearby impurities. In this case, the breaking of an additional mirror symmetry (vertical xz or yz plane passing through Os–Na–Os axis) leads to further symmetry lowering. This induces effective T_2g strain fields on d-orbitals on the six neighbouring osmiums (see Supplementary Note 5).

Impurity-induced T _c suppression

To study how impurities suppresses the octupolar T_c, we have carried out MC simulations for the pseudospin Hamiltonian H₀ + H_imp describing Os⁶⁺ non-Kramers doublets on the face-centred cubic (fcc) lattice. Here H₀ is the nearest-neighbour pseudospin Hamiltonian in the absence of impurities which has been previously obtained using microscopic calculations^36,37, and H_imp incorporates the transverse fields adjacent to the randomly located impurity sites. We note that such classical MC simulations for a spin-1/2 system, while not capturing the effects of quantum fluctuations, can nevertheless provide a useful guide to the physics, and has been used to explore 2D Kitaev materials^69,70 and 3D spin-ice compounds⁷¹.

The most general symmetry allowed H₀ is given by

$$\begin{array}{lll}{H}_{0}\,=\,\mathop{\sum}\limits_{\langle i,j\rangle }\left[{K}_{{{{\rm{o}}}}}{\tau }_{iy}{\tau }_{jy}+\left({K}_{1}{\cos }^{2}{\phi }_{ij}+{K}_{2}{\sin }^{2}{\phi }_{ij}\right){\tau }_{ix}{\tau }_{jx}\right.\\ \qquad\quad+\,\left({K}_{1}-{K}_{2}\right)\sin {\phi }_{ij}\cos {\phi }_{ij}\left({\tau }_{ix}{\tau }_{jz}+{\tau }_{iz}{\tau }_{jx}\right)\\ \qquad\quad+\,\left.\left({K}_{1}{\sin }^{2}{\phi }_{ij}+{K}_{2}{\cos }^{2}{\phi }_{ij}\right){\tau }_{iz}{\tau }_{jz}\right]\end{array}$$

(6)

where ϕ_ij = {0, 2π/3, 4π/3} correspond to nearest neighbours (i, j) in the {xy, yz, zx} planes. K_o and K_1,2, respectively, correspond to the octupolar exchange and quadrupolar couplings. We consider two sets of model exchange couplings as shown in Table 1. While Model A has exchange couplings motivated by our previous study³⁶, Model B explores the case of significantly enhanced quadrupolar exchange interactions.

Table 1 Exchange model parameters.

We next incorporate the effect of impurities. When we replace a fraction δ of Ca²⁺ by Sr²⁺ or Na⁺, the six Os⁶⁺ neighbours of the substituted site experience an E_g octahedral distortion as discussed above. This leads to local quadrupolar fields which couple as

$${H}_{{{{\rm{imp}}}}}=\mathop{\sum}\limits_{i,\alpha =x,z}{{{{\bf{h}}}}}_{{{{\rm{imp}}}}}^{\alpha }(i)\,{\tau }_{i\alpha }$$

(7)

where the quadrupolar fields h_imp(i) ≠ 0 only for sites adjacent to an impurity. These fields point along distinct directions for the Os⁶⁺ neighbours of the impurity site:

$$\pm x\,{{{\rm{neighbors}}}}:\,{{{{\bf{h}}}}}_{{{{\rm{imp}}}}}=h(\sqrt{3}\hat{x}-\hat{z})/2$$

(8)

$$\pm y\,{{{\rm{neighbors}}}}:\,{{{{\bf{h}}}}}_{{{{\rm{imp}}}}}=h(-\sqrt{3}\hat{x}-\hat{z})/2$$

(9)

$$\pm z\,{{{\rm{neighbors}}}}:\,{{{{\bf{h}}}}}_{{{{\rm{imp}}}}}=h\hat{z}$$

(10)

The field strength h is proportional to the distortion induced by the impurity. If there are adjacent impurities, we add up the corresponding quadrupolar fields on the neighbouring Os⁶⁺ sites to get the total h_imp(i). These quadrupolar fields act as transverse fields on the Ising octupolar order. We note that the transverse field strength and orientations are not random - however, the locations in space where they act is dictated by the random impurity positions. Using the ~1–2% strain inferred from our ab initio calculations, we estimate h to be on the order of ~5–10 meV; see Supplementary Note 5 for details on this estimate of h. Below we will explore a range of values in our MC simulations.

We ignore the T_2g strains for the MC simulations; since these strains do not act directly within the non-Kramers doublet subspace, their impact on octupolar ordering is weaker. While T_2g strain field induces parasitic dipole moments to first order in the strain (in the octupolar broken symmetry phase), they modify the pseudospin Hamiltonian itself only at second order in strain.

We have carried out MC simulations of the Hamiltonian H₀ + H_imp for different impurity concentrations and a range of local quadrupolar pinning field strengths h (see Methods). At zero impurity concentration (δ = 0), our model yields a ferro-octupolar transition temperature T_c ≈ 40 K, comparable with experiments on the undoped osmate double perovskites^{30,61,62,63,64}. As seen from Fig. 5, the octupolar T_c decreases nearly linearly with increasing impurity concentration δ. For larger h, the slope (dT_c/dδ) increases but eventually becomes independent of h since the local quadrupolar order gets perfectly pinned at large h. The exchange parameter sets for model A and model B are found to lead to similar results, with no significant differences either in the octupolar T_c or in the evolution of T_c with impurity concentration.

Fig. 5: Impurity induced T_c suppression.

Evolution of the ferro-octupolar T_c with increasing impurity concentration (at the Ca²⁺ site) for different values of the distortion-induced quadrupolar field h induced on neighbouring Os⁶⁺ sites. We show results for both model A (solid line) and model B (dashed line) with exchange parameters listed in Table 1.

The impact of impurities on local quadrupolar order may also be indirectly deduced from the components of the multipolar susceptibility tensor χ_ab(T) in the clean δ = 0 limit. The uniform susceptibility is given by

$${\chi }_{ab}(T)=\beta \left(\left\langle {M}_{a}{M}_{b}\right\rangle -\left\langle {M}_{a}\right\rangle \left\langle {M}_{b}\right\rangle \right)$$

where a, b ∈ (x, y, z), and ${M}_{a}={\sum }_{i}{\tau }_{i}^{a}/2$. Figure 6 shows the temperature evolution of the octupolar χ_oct(T) ≡ χ_yy and quadrupolar susceptibility χ_Q(T) ≡ χ_xx = χ_zz. The octupolar susceptibility diverges at the ferro-octupolar T_c. By contrast the quadrupolar components exhibit a Curie–Weiss type behaviour at high temperature, but this growth eventually get cutoff at T_c and it decreases slightly due to the onset of octupolar order. Model B with a larger antiferro-quadrupolar exchanges leads to a smaller uniform χ_Q(T). In the presence of a strain-induced perturbation h, we expect the induced local Os quadrupole moments in the vicinity of the impurity to qualitatively track the temperature dependence of χ_Q(T). This will play a role below in our understanding of the impurity NMR spectra.

Fig. 6: Octupolar and quadrupolar susceptibilities.

MC results in the clean case for (i) the octupolar χ_Oct(T) susceptibility which exhibits a divergence at the ferro-octupolar T_c, and (ii) the uniform quadrupolar χ_Q(T) susceptibility which has a Curie–Weiss form at high temperature but gets cut off at T_c and drops as we further cool into the ferro-octupolar symmetry broken phase. Results are shown for both model exchange parameters in Table 1.

Thermodynamic and μSR measurements on the osmate DPs Ba₂CaOsO₆, Ba₂MgOsO₆, and Ba₂ZnOsO₆ have found evidence for a single phase transition which does not involve a change in crystal symmetry but at which time-reversal symmetry is broken^{30,61,62,63,64}. These results are consistent with a ferro-octupolar ordering transition. Recent μSR and NMR results on Ba₂Ca_1−δNa_δOsO₆⁶⁵ show that T_c gets nearly linearly suppressed with increasing impurity concentration δ, as we go away from the clean limit δ = 0. Our model results in Fig. 5 showing the change of T_c with impurity concentration are consistent with these experimental results. For h = 10 meV, we find (1/T_c)(dT_c/dδ) ≈ − 2, which is in agreement with experiments on Ba₂Ca_1−δNa_δOsO₆ which find (1/T_c)(dT_c/dδ) ≈ − 2.2⁶⁵. With increasing impurity concentration, this model is expected to yield a disordered quantum critical point (QCP) where the octupolar T_c vanishes. Naively extrapolating our low doping results, this QCP is expected to occur at large dopant concentrations δ ≳ 0.5; however, quantum fluctuations may shift this QCP to smaller dopant concentrations.

NMR spectra

We next turn to modelling the ²³Na NMR spectra. Since the ²³Na nucleus has spin I = 3/2, we consider symmetry allowed terms for the interaction of this nuclear spin with the applied Zeeman field and the neighbouring Os multipole moments:

$$\begin{array}{lll}{H}_{{{{\rm{Na}}}}}\,=\,-\mathop{\sum}\limits_{i}\gamma (i)\,\hat{{{{\bf{I}}}}}(i)\cdot {{{\bf{B}}}}+{g}_{1}\mathop{\sum}\limits_{\langle i,j\rangle }\hat{{{{\bf{I}}}}}(i)\cdot {\tilde{\varepsilon }}_{j}\langle {\tau }_{j}^{y}\rangle \\ \qquad\qquad+\mathop{\sum}\limits_{\langle i,j\rangle }{\hat{{{{\bf{Q}}}}}}^{{{{\rm{Na}}}}}(i)\cdot {{\mathbb{A}}}_{ij}\cdot \langle {{{{\boldsymbol{{{{\mathcal{Q}}}}}}}}}_{j}\rangle \end{array}$$

(11)

Here, γ(i) is the gyromagnetic ratio (units: MHz/Tesla), which can be renormalized by the A_1g distortion around the Na site leading to a Knight shift. We define it as

$$\gamma (i)={\gamma }^{{{{\rm{Na}}}}}\left(1+{g}_{0}\mathop{\sum}\limits_{j\in {{{\rm{nbr}}}}(i)}\langle {{{{\mathcal{Q}}}}}_{j}^{{A}_{1g}}\rangle \right)$$

(12)

where γ^Na ≈ 11.262 MHz/T is the bare gyromagnetic ratio, and the A_1g distortion on the Na site is constructed as a sum of specific quadrupole moments the Os neighbours j, namely:

$$\langle {{{{\mathcal{Q}}}}}_{j}^{{A}_{1g}}\rangle =\left\{\begin{array}{ll}\frac{\sqrt{3}}{2}\langle {\tau }_{j}^{x}\rangle -\frac{1}{2}\langle {\tau }_{j}^{z}\rangle \quad &\,{{\mbox{for}}}\,\langle ij\rangle \,{{\mbox{along}}}\,\hat{x}\\ -\frac{\sqrt{3}}{2}\langle {\tau }_{j}^{x}\rangle -\frac{1}{2}\langle {\tau }_{j}^{z}\rangle \quad &\,{{\mbox{for}}}\,\langle ij\rangle \,{{\mbox{along}}}\,\hat{y}\\ \langle {\tau }_{j}^{z}\rangle \quad &\,{{\mbox{for}}}\,\langle ij\rangle \,{{\mbox{along}}}\,\hat{z}.\end{array}\right.$$

(13)

For an isolated Na⁺ ion, this sum over the six neighbours preserves the octahedral point group symmetry at the Na site, and thus it only leads to a temperature-dependent renormalization of the Knight shift.

The second term in Eq. (11) is the effect of the dipole moments on the Os atoms generated via T_2g distortions, as explained previously. This term only contributes when there are two neighbouring impurity Na ions, causing T_2g distortions on two of the Os atoms which are adjacent to both Na. We assume an Ising-like interaction between the parasitic dipole component produced by the T_2g strain and the dipole moment of the Na; here, ${\tilde{\varepsilon }}_{j}$ is a unit vector obtained by normalizing the T_2g distortion vector ε_j defined earlier. For instance, for a nearby pair of Na in the xy plane, ${\tilde{\varepsilon }}_{j}=\pm \hat{z}$ (see Supplementary Note 5). The magnitude of the T_2g distortion, which is not known in detail, is absorbed into the coupling constant d₁.

The third term accounts for the quadrupolar couplings between the Na and Os atoms. Since the Os atom only has E_g quadrupolar moments in the low energy doublet, we only consider, for simplicity, interactions between those and E_g quadrupoles of the Na nuclear spin. The local operators in this term are defined as

$${\hat{{{{\bf{Q}}}}}}^{{{{\rm{Na}}}}}=\left(\begin{array}{c}{\hat{I}}_{x}^{2}-{\hat{I}}_{y}^{2}\\ \left(3{\hat{I}}_{z}^{2}-I(I+1)\right)/\sqrt{3}\end{array}\right)$$

(14)

and

$$\langle {{{\mathcal{Q}}}}\rangle =\left(\begin{array}{c}\langle {\tau }_{x}\rangle \\ \langle {\tau }_{z}\rangle \end{array}\right)$$

(15)

Along the $\hat{x}$ bonds, we assume a diagonal interaction, i.e.

$${{\mathbb{A}}}_{ij}=\left(\begin{array}{cc}{a}_{1}&0\\ 0&{a}_{2}\end{array}\right)\quad \,{{\mbox{for}}}\,\langle ij\rangle \,{{\mbox{along}}}\,\hat{x}$$

(16)

We can then use rotations to infer the corresponding transformed ${\mathbb{A}}$ matrix for Na-Os bonds along the $\hat{y}$ and $\hat{z}$ directions. For simplicity, we set a₁ = a₂ = a.

We choose to measure the various couplings used in the Hamiltonian H_Na in Eq. (11) in units of γ^NaB ≡ ω₀. For a typical field B = 10T, we get ω₀ ≈ 112.6MHz. The couplings we use for illustrative NMR plots are given by (g₀, g₁, a) = (1, 5, − 1) × 10⁻³ω₀. This choice of couplings is found to provide a reasonable semi-quantitative description of the experimental NMR data⁶⁵; however, the key spectral features discussed below are not extremely sensitive, at a qualitative level, to the precise values of these couplings. Previous analyses of such spectra often focus only on the average quadrupole-quadrupole couplings. This misses the subtle effects of the remaining terms in Eq. (11), specifically the couplings (g₀, g₁).

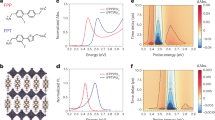
Figure 7 presents our results for the ²³Na NMR spectrum where we have averaged over external Zeeman field orientations as appropriate for a powder sample (see Methods and Supplementary Note 6 for details). These results are for an impurity concentration δ = 0.1 which is the smallest value of Na concentration which has been experimentally explored⁶⁵. This puts us close to the clean end point Ba₂CaOsO₆, so our starting point of assuming a dilute concentration of impurities is a valid approximation.

Fig. 7: Temperature-dependent NMR spectra.

a. Computed ²³Na NMR spectra over a wide temperature range. At high temperature (red: T = 5T_c), there is a narrow peak due to motional narrowing as we sample many fluctuating Os moment configurations. The shift of this peak upon cooling reflects the growth of quadrupolar susceptibility, while its broadening and asymmetry arises from moments getting locally pinned at low symmetry sites (yellow: T = 3T_c, 2T_c, T_c). The additional extremely large broadening below T_c (blue: T = 0.75T_c, 0.5T_c, 0.1T_c) reflects the formation of inhomogeneous parasitic dipole moments from the interplay of strain and octupolar order. b. Top: Inverse Knight shift obtained from the first moment 〈ω〉 of the theoretical NMR spectrum as $1/{K}_{s}^{{{{\rm{FM}}}}}={\omega }_{0}/(\langle \omega \rangle -{\omega }_{0})$. Bottom: Skew of the NMR spectrum showing the growth of spectral asymmetry upon cooling, with a singular increase below T_c which arises due to coupling of the ²³Na octupole to the ordered Os ferro-octupolar moment 〈τ_y〉.

Figure 7 a shows the calculated NMR spectra (see Methods) over a range of temperatures, ranging from high temperatures T = 5T_c to low temperatures within the octupolar ordered state T = 0.1T_c. Figure 7b shows the inverse Knight shift (associated with the first moment) and the skew of the spectrum as a function of temperature. We describe below key features of the theoretically calculated NMR spectra which capture the experimental observations⁶⁵ remarkably well.

• i. At high temperatures, e.g. T = 5T_c in Fig. 7a, the NMR spectrum exhibits a single narrow peak consistent with motional narrowing since the effect of the thermally fluctuating neighbour Os multipole moments average to zero. This single peak shifts upon cooling, with the inverse Knight shift (1/K_s) scaling approximately linearly with T. The systematic temperature dependence of the first moment of the spectrum is shown in Fig. 7b. We attribute this observed temperature dependence to the temperature-dependent quadrupolar susceptibility χ_Q(T) of Os shown in Fig. 6. Our scenario is that the impurity induces quadrupolar moments on the six neighbouring Os atoms, which scale as ~ χ_Q(T)h, where h is the impurity induced pinning field. We note that in this high T regime, we expect no difference between the uniform and local quadrupolar susceptibilities. These induced quadrupoles around the impurity site preserve the local point group symmetry, but lead to symmetry allowed renormalization of the effective gyromagnetic ratio for ²³Na, causing a temperature-dependent Knight shift. The inverse Knight shift thus scales as ${\chi }_{Q}^{-1}(T)$, which has a linear T dependence in the Curie-Weiss regime.

• ii. At intermediate temperatures (T = 3T_c, 2T_c, T_c in Fig. 7a), we find that in addition to the temperature-dependent Knight shift of the dominant peak, the NMR spectrum exhibits broadening as we cool, and further develops an asymmetry. This asymmetry may be seen via the growing skewness shown in Fig. 7c (see Methods). These effects arise due to the development of a growing inhomogeneous distribution of static quadrupolar droplets in the presence of the pinning due to impurity Na⁺ sites. As seen from Fig. 4, an isolated Na⁺ impurity only leads to an A_1g deformation of the surrounding oxygen octahedron; as discussed above, this does not lead to NMR peak splitting but only to a Knight shift. Instead, the broadening and asymmetry in our theory arises from regions harbouring pairs (or more) of neighbouring Na impurities which lowers the point group symmetry at the Na site and leads to peak splittings.

• iii. Finally, as we cool below T_c (T = 0.75T_c, 0.5T_c, 0.1T_c in Fig. 7a, the Knight shift as defined through the first moment changes its slope, having a weaker temperature dependence below T_c. We can understand this as the growth of χ_Q(T) getting cut off below T_c due to the onset of octupolar order as seen from Fig. 6, while the weaker impact of the octupolar order leads to a smaller slope. In addition, as we go below T_c, the NMR spectrum becomes extremely broad. In our calculations, this broadening reflects the presence of parasitic dipoles induced by the octupolar symmetry breaking. The impact of octupolar ordering is also reflected in the asymmetry of the spectrum. As shown in Fig 7c, the skew of the spectrum, defined as the third moment of the distribution, shows a singular increase below T_c, so that the octupolar ordering below T_c leads to a more asymmetric spectrum. This is in good agreement with recent experiments⁶⁵. We thus conclude that these NMR experiments are indirectly probing the onset of ferro-octupolar symmetry breaking.

Discussion

In summary, our work introduces the key concept of Janus impurities to refer to local impurity probes of non-Kramers doublets and their ordering. We have carried out a comprehensive study of how such Janus impurities break the non-Kramers degeneracy by inducing local strains, and how they can nevertheless serve as useful probes of multipolar orders.

As an example, we have studied the osmate double perovskites which feature competing octupolar and quadrupolar moments. Our work goes beyond previous studies in several respects, and makes direct contact with a body of recent experiments. (1) We have presented DFT computed phonon spectra in the osmates which are in good agreement with neutron scattering results, making the case that these osmates are intrinsically stable cubic materials. (2) We showed DFT results for how a doped impurity modifies the local structure and lowers the point group symmetry, leading to not only E_g strain but also T_2g strains, and presented the associated Landau theory for its impact on the local non-Kramers moment. (3) The above progress led us to a simplified one-parameter model for doped impurities. The resulting impact on Tc suppression, computed using Monte Carlo simulations, was shown to explain the data from recent μSR experiments. (4) Our Landau theory also showed that the T_2g strains, found in DFT, can nucleate local dipole moments in the ground state even though the cubic system has no ground state dipole moments (only quadrupolar and octupolar). (5) Finally, we presented a symmetry-based approach to modelling the NMR spectra of doped ²³Na, keeping track of the full inhomogeneous distribution of the local Os moments. This allows us to make direct contact with the temperature evolution of the NMR Knight shift and spectral features seen in the osmates both above and below Tc. In a broader sense, our work sets the framework for understanding NMR in an inhomogeneous multipolar environment in diverse quantum materials.

By combining ab initio methods, Landau theory, MC simulations, and modelling of NMR spectra, we have thus shown how local impurity strains can suppress the ferro-octupolar T_c, and how our work explains recent ²³Na NMR results on Ba₂Ca_1−δNa_δOsO₆ for doping δ ≪ 1. Our results lends further support to the scenario of octupolar order below T_c in these d-orbital materials, and show that Janus impurities can reveal useful information about multipolar orders.

We note that the Na⁺ impurity (i.e., the substitution of Ca²⁺ by Na⁺) not only produces strong local strain fields, but would also lead to local charge doping: each impurity could potentially dope 1/6-hole onto each of the six neighbouring Os. Our proposal here is that the local strain can play a highly significant role in accounting for the drop in T_c; the detailed exploration of charge doping effects and longer-range strain fields is a subject for future study. Our ab initio computations find that similar local strain fields are generated in Ba₂Ca_1−δSr_δOsO₆ due to isovalent substitution of Ca²⁺ by Sr²⁺. Experimental studies of Ba₂Ca_1−δSr_δOsO₆ and Ba₂Ca_1−δMg_δOsO₆, perhaps using ⁸⁷Sr NMR or ²⁵Mg NMR, would thus provide a route to distinguish the effects of strain from charge doping. Sr or Mg doping may also allow one to study the QCP where the octupolar T_c is suppressed to zero. The impact of charge doping with Na⁺ substitution going from δ = 0 to δ = 1⁶⁵ deserves a separate careful investigation. In addition, NMR studies on the undoped d² osmate double perovskites would also be extremely valuable to explore spectral signatures in the absence of strain fields. Finally, while we have focussed here on d-orbital multipoles, most of our results can also be directly translated to f-orbital candidates with ordered multipole moments such as PrV₂Al₂₀^{9,10,14,16,17,18,19}, or to systems with fluctuating multipoles such as spin-ice materials⁷¹.

Methods

Ab initio calculations

The ab initio calculations are carried out in the plane wave pseudo-potential basis, as implemented in Vienna ab-initio Simulation Package^66,67, choosing the generalized gradient approximation (GGA) to describe the exchange-correlation functional. We have also examined the effect of correlation beyond the GGA level by doing calculations within Hubbard U supplemented GGA+U calculations, with U value of 1–2 eV applied at Os site; we have found that the results are qualitatively unchanged. The effect of SOC which is especially important at the 5d Os sites is taken into account through GGA+U+SOC calculations. The cutoff energy of the plane-wave basis is chosen to be 600 eV which is found to be sufficient to achieve convergence in self-consistent field (SCF) calculations. Converged k-mesh of 8 × 8 × 8 is used for SCF calculation with a tight energy convergence threshold of 10⁻⁸ eV. Relaxations of the crystal structures are carried out with respect to internal atomic coordinates as well as cell volume using a convergence threshold of 10⁻⁵ eV for total energy and 10⁻³ eV/Å for maximum force/atom. Phonon properties are studied within the formulation of density functional perturbation theory (DFPT) as implemented in VASP. The phonon band structures were obtained by Fourier interpolation of the real-space force constants using PHONOPY⁷² code, and plotted along the high-symmetry momentum points of the BZ.

Monte Carlo Simulations

Monte Carlo (MC) simulations were carried out on a 14 × 14 × 14 fcc lattice (2744 spins) with periodic boundary conditions. The spins on the fcc sites form one sublattice of a cubic lattice which represents the Os pseudospins. Impurity sites are randomly selected from the second sublattice of the cubic lattice, representing substitution of Ca by Na or Sr, and the effect of this impurity in the simulations was mimicked by applying strain fields on the six neighbouring Os atoms (in accordance with Eqs. (7)-(10)). For Os sites that happen to be adjacent to multiple impurities, the corresponding strain fields are (vectorially) added. The MC simulations were thermalized over 10⁶ MC sweeps, and measured over 5 × 10⁵ sweeps. Results for each impurity concentration are averaged over 20 disorder realizations for T_c. For computing the NMR spectra for δ = 0.1, we average over 100 disorder configurations to capture the spectra over many Na nuclei.

NMR spectrum calculation

To obtain the spectrum shown in Fig. 7a, we solve for the eigenvalues of Eq. (11) (a 4 × 4 matrix), and associate the differences between successive eigenvalues as the observed frequencies in an NMR measurement. We thus have three frequencies associated with a given impurity atom. We collect the frequencies from all the impurity atoms in 100 disorder configurations (total 27440 impurity spectra for δ = 0.1), averaged over 300 Zeeman field directions to produce a data set that mimics that obtained through a powder sample NMR measurement. To obtain a simulated spectrum, the binned data are then smoothed using a Kernel Density Estimate (KDE) with a bandwidth of 2 × 10⁻⁴ω₀. The mean is defined as the first moment of the distribution, 〈ω〉, and the skew is defined as the third moment, 〈(ω−〈ω〉)³〉. The histogram from the raw data that was used to produce Fig. 7 is given in Supplementary Note 6.