Introduction

The zero temperature (T) superfluid density, ns(0), of the cuprate high-temperature superconductors is several orders of magnitude smaller than that of conventional superconductors1,2,3. Indeed (when translated into energy units) it is comparable to the critical transition temperature (Tc)3. This has led to the probably inescapable inference that Tc, itself, is determined, at least to a significant degree, by the condensation scale (i.e. the phase ordering temperature, Tθ ∝ ns(0)), rather than by the pairing scale (~Δ0/2), in contrast to the case in the Bardeen-Cooper-Schrieffer (BCS) theory of conventional superconductors. There is also compelling evidence that some degree of clearly identifiable superconducting fluctuations—colloquially referred to as ‘pairing without phase coherence’—persists for a substantial range (at least 20% or so) above Tc4,5,6,7,8,9,10,11,12,13,14. This has been known for some time for the underdoped cuprates, but it has recently become increasingly clear that the same is true for many or all overdoped cuprates as well (Fig. 1)8,13,15. Indeed, as a function of doping, the onset temperature (however defined) of superconducting fluctuations more closely parallels Tc than it does the conventionally defined pseudo-gap crossover.

Fig. 1: Cuprates phase diagram.
figure 1

Phase diagram of two representative cuprates, (a) La2−xSrxCuO4 (LSCO) and (b) Bi2Sr2CaCu2O8+δ (Bi-2212), as a function of doped hole concentration and temperature. Open black markers indicate Tc for bulk crystals, while the solid black line is the same for crystalline films from Ref. 10. The other symbols indicate crossover lines below which the existence of significant superconducting fluctuations are inferred from various different experiments that are directly sensitive to Cooper pair formation. Data, including error bars where applicable, are reproduced from Refs. 4,5,6,7,8,9,10,70,71,72, see also Supplementary Note 8. The quantitative identification of any crossover depends on the criterion used, and moreover distinct probes should have different sensitivity to superconducting correlations, so it is reasonable that the various lines do not coincide.

Full size image

However, what is unclear is why this occurs, and what we should learn from this. One proposal is that this should be taken as evidence that the system is approaching a strong pairing situation, referred to as the Bose–Einstein condensation (BEC) limit, in which the electrons form non-overlapping charge 2e bosons at a scale far above Tc16,17,18,19,20,21,22,23,24,25,26 (see also Supplementary Note 1). However, as we will discuss below, there are other conceptually distinct, yet equally well understood circumstances in which Tc is determined by phase ordering and in which Cooper pairing persists above Tc. The purpose of this work is to analyze the behavior that would be expected of a system either in the BEC limit or approaching the BCS to BEC crossover from the BCS side, and to present direct experimental evidence that this is not the case for the cuprates.

Framing the issue

BCS theory is a weak coupling theory that is built on a starting point that is the electronic structure from band theory. The BEC limit invokes electronic bound states. In the former case, the pairing is highly collective and the chemical potential, μ, is only weakly affected by the advent of pairing. In the latter, the chemical potential—by the definition of a bound state—must approach a value that lies below the band bottom as T → 0. These differences do not refer to subtle low-energy phenomena but rather to entirely different regimes of microscopic physics on energy scales of the order of the Fermi energy, EF, or larger27.

From this perspective, the fact that the Fermi surface and general features of the electron dispersion seen in ARPES experiments across the superconducting dome of the cuprates are more or less in agreement with expectations from band-structure calculations appears to be inconsistent with any large excursions toward the BEC limit. (This is illustrated in Fig. 2.) Emergent features of the low energy physics, such as a normal state pseudo-gap that competes with superconductivity (apparent below some generally relatively ill-defined T⋆)7,28,29,30,31,32,33,34 and various low energy kinks in the dispersion relations are certainly interesting and important, but occur on energy scales small compared to EF35,36,37,38. The fact that the application of magnetic fields large enough to quench superconductivity produces quantum oscillations39 is further evidence that pairing is a collective property of the superconducting state rather than a microscopic feature associated with bound-state formation, see Supplementary Note 2.

Fig. 2: Electronic structure of Bi-based cuprates along high symmetry directions.
figure 2

a Schematic Fermi surface and momentum cut trajectory in the tetragonal Brillouin zone of a CuO2 plane. b Low energy electronic structure near (π,0) in Bi-2212 (p = 0.22, Tc = 66 K) in the normal state. Data are reproduced from Ref. 8. c Electronic structure along Γ − X direction in LSCO (x = 0.23, Tc = 24 K) and Bi-2212. Light green lines are density functional theory (DFT) calculated band structure. For Bi-2212 only the antibonding band is shown. Deviations from the first principles dispersion apparent at low energies represent mass renormalization due to additional interaction effects, see Supplementary Note 9. Data are adapted from Refs. 8,73,74,75.

Full size image

One important feature of the superconducting state in the cuprates is that it has d-wave symmetry and gapless, nodal quasi-particle excitations, see Supplementary Note 3. There can be no nodal quasi-particles in the BEC limit. (See Ref. 40.) Thus, for this d-wave case, the BCS to BEC crossover24,26 would constitute a (Lifshitz) phase transition from a nodal to a nodeless state40,41. The existence of well-defined nodes is, of itself, proof that the cuprates are on the BCS side of the transition. This leaves only the question of how far on the BCS side they are from the point at which a BCS to BEC transition would have occurred, see Supplementary Note 4. In the language of effective field theories, the question we consider is not one concerning the correct infrared description (i.e. phases of matter) but rather concerns the ultra-violet (high energy ‘microscopic’) description consistent with experimental data.

Experimental perspective

We will focus our attention on the behavior of the chemical potential, μ, as this is a fundamental thermodynamic quantity that exhibits qualitatively different behavior in the two limits. Since by definition, in the BEC limit the chemical potential is below the band bottom, on approach to the BEC limit from the BCS side one should see that the chemical potential is significantly depressed from its band theory value toward the bottom of the band. Moreover, it should show strong T dependencies for temperatures of order Tc.

A number of fortuitous features of the electronic structure of the cuprates make it possible to stringently bound the evolution of the chemical potential from the electron dispersion measured in ARPES along the ‘nodal direction’ in the Brillouin zone. Specifically, it is possible to determine the value of the Fermi momentum, \({k}_{F}=| \overrightarrow{{k}_{F}}|\), as a function of temperature with a high degree of precision. In the superconducting state, since the gap vanishes along this direction, it is possible to measure the quasi-particle dispersion to where it crosses the chemical potential. Moreover, since the pseudo-gap—where it exists—also has a d-wave structure (see Supplementary Note 3), it also vanishes along this direction. Working further to our advantage is the fact that this is the trajectory through the Brillouin zone along which the spectral peaks seen in ARPES are the sharpest. Indeed, in bilayer cuprates (such as Bi-2212), the quantum chemistry results in a vanishing bilayer splitting at the node, so there is no need to worry about this complication either.

While knowledge of the temperature evolution of nodal kF does not permit an absolute measure of μ, it does allow a direct measure of changes in the chemical potential relative to a reference value,

$$\delta \mu (T)={v}_{F}\delta {k}_{F}(T),$$
(1)

where vF is the nodal velocity (which, conveniently, appears to be minimally dependent on T and on doped hole concentration, x, on the 10–100 meV energy scale36,37). It should be noted that a cascade of nodal dispersion kinks can affect the temperature dependent shift of the nodal kF up to 1% of the reciprocal lattice unit35,36,37,38, which is comparable to experimentally observed values, but at least 2 orders of magnitude smaller than what is expected in the crossover regime.

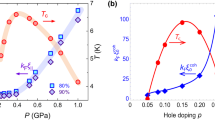
In Fig. 3 we show kF(T) from ARPES data in Bi-2212 for several different values of p. The measured changes in kF are sufficiently small that, within the uncertainties of interpretation, they are consistent with a temperature-independent chemical potential. (Specifically, minute but difficult to quantify shifts of kF are expected to arise from temperature dependent low-energy band renormalizations due to electron-electron or electron-phonon interactions, even in the absence of any T dependence of μ.) This is our primary finding. Indeed below, and in Fig. 4, we show that the very small changes in the chemical potential expected on the basis of BCS theory are order-of-magnitude consistent with these findings, assuming reasonable values of the T = 0 gap, Δ0 ≈ 40 meV. By contrast, even on the BCS side of the transition, in the regime proximate to a BEC limit a large shift in the chemical potential toward the band bottom would be expected.

Fig. 3: Temperature dependence of kF along the nodal direction.
figure 3

a Bi-2212 nodal momenta normalized to \(\frac{2\pi }{{a}_{0}}\), where a0 = 3.8 Åis the in-plane Cu–Cu separation under tetragonal approximation. Data are reproduced from Refs. 73,76,77. (Note that if these materials were in the crossover regime, the chemical potential would drop to the band bottom, and consequently kF would shift to zero.) b Chemical potential shifts δμ = vFδkF, evaluated by multiplying the kF shifts by the Fermi velocity37 in absolute energy units and in units of EF = 1.25 eV. In both panels, arrows indicate the corresponding values of Tc. Solid triangles (which correspond to the solid symbols in Fig. 1(b)) represent the superconducting gap opening temperature as determined from ARPES7,8. Dashed lines are guides to the eye. Typical error bars (not shown) are ≤4 meV (momentum resolution multiplied by Fermi velocity).

Full size image
Fig. 4: Thermal evolution of the chemical potential in the BCS limit.
figure 4

Thermal evolution of (a) δμ(T) = μ(T) − EF and (b) kF computed for the model of a d-wave BCS superconductor discussed in the text. The gray dashed line is for the normal state Δ0 = 0, and the blue and red solid lines are, respectively, for Δ0 = 0.1t and Δ0 = t. We have taken a density of doped holes x = 0.2 (n = 0.8) and Tc = 0.025t. Temperatures are shown in units of Tc and energies in units of EF = 1.7t.

Full size image

There are a few aspects of the result that merit closer inspection. As can be seen in Fig. 2c, EF (defined to be the position of the band-bottom at the Γ point relative to the chemical potential) is between 1 and 2 eV, which is large enough compared to Δ0 that it would seem obvious that the system is deep in the BCS limit. However, the band is relatively shallow near the van-Hove point. The energy at the M point, (0, π), is no more than 0.1 eV below μ (Fig. 2b)42,43. This is only a few times Δ0, so that if we focused exclusively on this near ‘antinodal’ region of the Brillouin zone, we might have anticipated more in the way of a shift in the chemical potential. The idea that the anti-nodal ‘heavy electrons’ can be viewed as somehow distinct from the near-nodal ‘light electrons’, however, runs up against the experimental fact that the chemical potential does not show any of the T dependence across Tc or T* that should be a corollary of such a two-patch theory (see next section). Indeed, the bound we have obtained on the chemical potential shifts are so stringent so that ∣δμ∣ < Δ0. In addition, near the BCS-BEC crossover, the backbending momenta of the Bogoliubov quasiparticle dispersion in the superconducting state should shift towards zero, which is not observed in the cuprates at any hole doping8,44,45.

Theory of the BCS to BEC crossover

As in the experimental discussion, we focus our theoretical analysis on the thermal evolution of the chemical potential μ. Specifically, we illustrate the fact that variations of μ are small in the BCS limit, increase upon approach to the BCS to BEC crossover, and are large whenever the BEC perspective is relevant, see Supplementary Note 5.

The BCS analysis

Given that the existence of nodal quasi-particles places the cuprates on the BCS side of the transition, it is reasonable to consider signatures of the approach to the BEC limit in the context of BCS theory. It is an often neglected feature of BCS theory that, in addition to the familiar gap equation, there is a second self-consistency equation that determines the chemical potential as the implicit solution to

$$n=2\int\frac{d\vec{k}}{{(2\pi )}^{d}}\left[| {u}_{\vec{k}}{| }^{2}(1-{f}_{\vec{k}})+| {v}_{\vec{k}}{| }^{2}{f}_{\vec{k}}\right]$$
(2)

where n is the electron density, \({f}_{\vec{k}}={[{e}^{\beta E(\vec{k})}+1]}^{-1}\) is the Fermi function, \(E(\vec{k})=\sqrt{{[\epsilon (\vec{k})-\mu ]}^{2}+| \Delta (\vec{k}){| }^{2}}\) and \(\epsilon (\vec{k})\) are the quasi-particle energies in the superconducting and normal state respectively, \(\Delta (\vec{k})\) is the gap function, with the coherence factors \(| {u}_{\vec{k}}{| }^{2}=[E(\vec{k})-\epsilon (\vec{k})+\mu ]/2E(\vec{k})\) and \(| {v}_{\vec{k}}{| }^{2}=[E(\vec{k})+\epsilon (\vec{k})-\mu ]/2E(\vec{k})\), and β = 1/T. If there are multiple bands, then this expression needs to be generalized to include a sum over bands. Naturally, Δ depends implicitly on T and on the nature of the interactions through the usual self-consistency relation.

To illustrate why this equation is safely neglected in most cases, consider the illustrative example of free electrons \((\epsilon (\vec{k})={\hslash }^{2}{k}^{2}/2m)\) in two dimensions (d = 2) with a \(\vec{k}\) independent (s-wave) gap function. Because the density of states is constant, the integrals above can be performed readily, with the result that μ(T, Δ) is obtained as the implicit solution to

$${E}_{F}=\frac{1}{2}\left[{E}_{\mu }+\mu \right]+T\ln \left[1+{e}^{-\beta {E}_{\mu }}\right]$$

where the Fermi energy EF = πℏ2n/m such that μ(T, Δ = 0) → EF as T → 0 and \({E}_{\mu }=\sqrt{{\mu }^{2}+{\Delta }^{2}}\). The second term in this equation is typically exponentially small, \(\sim {e}^{-\beta {E}_{F}}\), and hence

$$\mu (T,\Delta )={E}_{F}\left[1-| \Delta (T)/2{E}_{F}{| }^{2}\right]+{{{\mathcal{O}}}}(T{e}^{-\beta {E}_{F}}).$$
(3)

If we define the BCS to BEC crossover as the point at which μ(0, Δ) = 0, this occurs when Δ0 ≡ Δ(0) = 2EF—the shift of the chemical potential relative to its normal state, [μ(T > Tc) − μ(0)]/μ(T > Tc) ≈ [EF − μ(0)]/EF, thus is directly a measure of how closely we have approached this crossover.

In more general circumstances, band-structure effects result in an energy dependent density of states. In the small Δ0 (BCS) limit, this leads to a (logarithmically) larger shift in the chemical potential δμ = μ(0, Δ0) − μ(0, 0) of the form

$$\delta \mu \sim -\frac{1}{2}\frac{{\rho }^{{\prime} }(\mu (0,0))}{\rho (\mu (0,0))}| {\Delta }_{0}{| }^{2}\ln \left(\frac{2W}{{\Delta }_{0}}\right),$$
(4)

where \({\rho }^{{\prime} }(\mu )\) is the derivative of ρ with respect to μ and W is the electronic bandwidth. On the other hand, if we continue to follow the evolution of μ according to the BCS equations for a single band to the large Δ0 limit (where, of course, BCS theory is not in any way justified) the result is asymptotically independent of the band-dispersion:

$$\mu =\left[\frac{(n-1)}{\sqrt{n(2-n)}}\right]| {\Delta }_{0}| \left[1+{{{\mathcal{O}}}}\left(\frac{W}{| {\Delta }_{0}| }\right)\right].$$
(5)

For a cuprate-like band-structure, these two asymptotic forms typically give rise to a non-monotonic dependence of μ on Δ0. The presence of a van-Hove point below the Fermi energy implies that \({\rho }^{{\prime} }(\mu )\) is negative, meaning that for small Δ0, the superconductivity induced changes in the chemical potential are expected to be positive. On the other hand, for a hole-doped cuprate (with (n − 1) < 0), the chemical potential must drop toward the band bottom for large enough Δ0.

To make closer contact with experimental reality, we have numerically carried through the BCS analysis for a two-dimensional (2D) model that incorporates significant features of the electronic structure of the cuprates. Here, we take \(\epsilon (\vec{k})=4(t+{t}^{{\prime} })-2t(\cos ({k}_{x})+\cos ({k}_{y}))-4{t}^{{\prime} }\cos ({k}_{x})\cos ({k}_{y})\) (the zero of energy has been chosen to coincide with the band bottom, i.e. such that \(\epsilon (\vec{0})=0\) and we have set the lattice constant a = 1) with \({t}^{{\prime} }=-0.3t\) (obtained from a fit to low binding energy ARPES data8,45, see Supplementary Note 6) and \(\Delta (\overrightarrow{k})=\Delta (T)[\cos ({k}_{x})-\cos ({k}_{y})]/2\), where we further assume that \(\Delta (T)={\Delta }_{0}\sqrt{1-{(T/{T}_{c})}^{2}}\) for all T < Tc. We perform the calculation for hole concentration x = 0.2 (n = 1 − x = 0.8) and we use Tc = 0.025t. The results are shown in Fig. 4 for two values of Δ0: 1) Δ0 = 0.1t, which is a reasonable value for the cuprates; 2) Δ0 = t, which is far larger than is plausible, included for illustrative purposes. Not only is the thermal evolution of μ(T) very weak relative to EF, but also it appears that it is very small relative to Δ(T). Note that this analysis is not meant to quantitatively explain the experimental results, but rather to provide an estimate of the expected magnitude shift in μ and kF across Tc in the BCS limit.

The BEC limit

To develop intuition concerning the thermal evolution of μ in the BEC limit, we can carry out the same analysis for the case of a 2D non-interacting Bose gas. While this problem has no actual phase transition, in the presence of weak repulsive interactions, the superfluid transition occurs at a number of order 1 (which depends on the log-log of the interaction strength46) times the characteristic energy T0 ≡ 2πℏ2nB/mB. (If we identify the areal density of the bosons, nB with 1/2 the density of Fermions, n, and their mass mB as twice the electron effective mass, m, then T0 = EF/2, where EF is what would have been the Fermi energy in the absence of pair-binding.) Again, the fact that the density of states is a constant permits us to derive an analytic expression

$$\mu =T\ln [1-{e}^{-{T}_{0}/T}].$$
(6)

This result is shown in Fig. 5. From Eq. (6), it is easy to see that the chemical potential shifts by approximately a factor of 4 as the temperature changes from T = T0 (roughly Tc) to T = 2T0; a result that is qualitatively unchanged by weak interactions.

Fig. 5: Thermal evolution of the chemical potential in the BEC limit.
figure 5

Thermal evolution of δμ(T) = μ(T) − μ(0) in the BEC limit (black thick line) contrasted with its behavior in the BCS limit for Δ0 = 0.1t (light gray thin line) and Δ0 = t (dark gray thin line). As in Fig. 4, in the BCS calculation we have taken Tc = 0.025t and a density of doped holes x = 0.2 (n = 0.8), which yields EF = 1.7t. In comparing the BEC and BCS results we identified energy scales according to Tc ≡ T0, EF ≡ 2T0, and scaled up the BCS results by a factor of 50 in order to make the T dependence visible.

Full size image

Mixture of heavy bosons and light fermions

Motivated by the proposal of heavy antinodal electron pairs mixing with light nodal quasiparticles in cuprates, it is interesting to consider a two component system in which a 2D Bose gas is in equilibrium with a BCS superconductor16. One could imagine this arising in a two-band system, in which one band is in a BCS and the other in a BEC limit. Now the chemical potential must simultaneously satisfy Eqs. (3) and (6)—which in turn means that the fraction of particles that are bosonic must be determined self-consistently according to

$${n}_{tot}=n+2{n}_{B}=(1/\pi {\hslash }^{2})\left[m{E}_{F}+{m}_{B}{T}_{0}\right]$$
(7)

where ntot is the total electron density, and the factor 2 encodes the assumptions that two electrons can combine to form one boson. The result is a generally complicated thermal evolution of μ. However, in the limit that mB ≫ m (i.e. where the bosonic density of states is large compared to the fermionic density of states), the result simplifies; here, the density of fermions does not change significantly over the relevant range of μ, so the T dependence of μ reduces to the same expression as for the pure bosonic problem, Eq. (6), with an approximately constant value of nB.

Quantifying Cooper pair overlap

One line of analysis that is sometimes invoked in support of proximity to a BEC limit is based on an estimate of the number of Cooper pairs in a Cooper pair area26,47. This is estimated as N ≡ nπ∣ξ0∣2, where n is the density of conduction electrons per unit area and π∣ξ0∣2 represents the area associated with a given pair (ξ0 is the correlation length). It is then proposed that N is a reasonable metric, such that N ≫ 1 in the BCS limit and N ≲ 1 in the BEC limit.

However, neither n nor ξ0 is well defined. For instance, in the cuprate context, there is an order of magnitude uncertainty concerning what value of n is appropriate—whether it is proportional to x, the density of ‘doped holes’ relative to the undoped insulator, or (1 + x), the area enclosed by the Fermi surface, see Supplementary Note 7. ∣ξ0∣2 is even more uncertain, given that this is a nodal superconductor. The Fermi surface average of ∣ξ0∣2 is infinite due to its divergence in the nodal direction. Taking this at face value it suggests (not without reason) that a nodal SC can never approach the BEC limit. On the other hand, it is the Fermi surface average of ξ−2 that enters the mean-field estimate of Hc2, and this is dominated by the portions of the Fermi surface where the gap is maximal and/or the Fermi velocity is minimal. If one makes an estimate of N taking the shortest possible estimate of ∣ξ0∣2 (obtained from the largest experimentally inferred values of the mean-field Hc2) and the smallest possible value for n ~ x, the result suggests N ~ 1−10 for optimally doped cuprates—small enough that it might justify conjectures of a nearby BCS to BEC crossover. However, because of the uncertainties that lead to this estimate, we consider this analysis far less reliable than the analysis based on measurements of μ.

Further issues

To complete our analysis of the physics of pairing in the cuprates, it is important to ask whether there are any alternatives to the BEC perspective that can account for the experimental observations of an intimate relation between Tc and Tθ and a corresponding persistence of pairing without phase coherence in an usually large range of temperatures above Tc. Three theoretically understood examples of systems that exhibit these properties are:

  • A granular superconductor or Josephson junction array where Tθ (and hence Tc) is determined by the magnitude of the Josephson coupling between superconducting grains, while the pairing within a grain can be well described in the context of BCS theory48,49.

  • A quasi-1D superconductor, where the pairing (gap formation) can occur in a BCS-like manner on a single superconducting wire, while Tc is small in proportion to a positive power of the coupling between wires50.

  • A lightly doped spin-liquid of an appropriate variety, where the pairing scale is inherited from the spin correlations of the undoped insulator, while the superfluid density grows linear with doping, x51,52.

Which, if any of these possibilities is essential in the cuprates is still open to debate. There is surely considerable evidence of significant inhomogeneity in the electronic structure revealed by local probes53,54,55,56,57, so much so that there are suggestions that the cuprates should be viewed as electronic glasses15,58,59,60,61,62,63. In this light, it certainly is worth considering whether the materials might in some ways behave like granular superconductors. While there is no direct evidence of either quasi-1D electronic structure, or of any spin-liquid phases—doped or otherwise, it is not obvious (in the sense of adiabatic continuity) that these examples are totally irrelevant. At the very least, the existence in the cuprate phase diagram of a variety of ‘intertwined orders’ (see Supplementary Note 3), especially charge-density-wave order, likely plays a role in reducing the fraction of the electrons that contribute to ns.

In concluding, we address two points of perspective concerning the present results that could easily be misinterpreted:

  • The fact that the lack of substantial chemical potential shift with temperature is consistent with BCS theory does not prove that BCS theory is adequate to treat the emergent low energy properties of the cuprates. It resolves the high energy microscopic issue of what are the constituent degrees of freedom one should include in a theoretical treatment—they are roughly the quasi-particles of a Fermi liquid and not preformed Cooper pairs. However, the unusually large degree of superconducting fluctuations and the many other strange low energy behaviors of these materials certainly require more elaborate theoretical approaches than the simple BCS mean-field theory that works so well in conventional superconductors.

  • The idea that a BCS to BEC crossover may be at play has been mooted64,65,66,67,68,69 in the context of a variety of other unusual superconductors, including the Fe-based superconductors and more recently twisted bilayer graphene. Obviously, the evidence that this crosser is not relevant in the cuprates does not prove that it is not significant in other materials. Conversely, we propose that clear evidence can be obtained one way or the other from careful measurements of the evolution of μ as a function of T and other properties that affect the superconducting state.