Abstract
We demonstrate the photonic spin Hall effect in a system comprising designable liquid crystal materials. The photoalignment technique provides an effective approach to control the directors of the liquid crystal molecules. Twisting structures with different transverse distributions are conveniently introduced into the liquid crystal plates for tailoring the spin–orbit coupling process to present various photonic spin Hall effect phenomena. The light–matter interaction in the twisting mediums is described with a Schrödinger-like equation. The photonic spin Hall effect considered in the study is explained as the result of an effective magnetic field acting on a pseudospin. Moreover, owing to the designability of the liquid crystal system, it is a potential platform for Hamiltonian engineering. Several valuable multiple quantum systems are possible to be presented in classical analogies.
Similar content being viewed by others
Introduction
Spintronics becomes an attractive field of condensed matters in recent years and shows its immense potential in quantum information applications.1, 2 Various spintronic devices have been demonstrated to play important roles in quantum information processing and quantum computation.3, 4 The central theme of spintronics is manipulation of the spin degrees of freedom. The spin Hall effect (SHE) provides an effective approach for controlling the electron spin, and a large number of interesting investigations have been demonstrated.5, 6 Although considerable progress has been made, the electronic systems always face the problem of decoherence and decay.7 In this aspect, the photonic quantum system has obvious advantages. Moreover, the photon is also an ideal spin carrier. The discovery of photonic spin Hall effect (PSHE) provides a powerful approach for controlling and manipulating the spin photons.8 Therefore, the photonic systems can be alternative choices for designing spin-based devices, thus raising an increasing research interest.7, 9,10,11,12,13,14,15,16,17,18,19,20,21,22,23
The liquid crystal (LC) is a special state of certain matter that is intermediate between the crystalline solid and the amorphous liquid.24 Owing to its unique optical properties, the LC has been widely used for liquid crystal display and changes our daily life. Upon the development of novel manipulating techniques, the potentiality of LC materials in fabricating photonic devices is continuously released, and the tunable characteristic becomes an advantage of the LC-based devices.24 In this work, we investigate the PSHE via light–matter interaction in LC-based twisting structures which are made through the photoalignment technique.25, 26 The physical mechanism of such a system is discussed in detail. The light–matter interaction in the LC medium is described by the Maxwell–Schrödinger equation,27, 28 and the interaction Hamiltonian is obtained and shown to be similar with those of the Rashba and Dresselhaus types of electronic systems. Owing to the photoalignment technique, it is convenient to control the LC directors locally,25, 26 and thus the spin–orbit interaction process in the LC twisting structures can be flexibly tailored to present various PSHE phenomena. As regards the experimental verification, we prepare several representative samples, and the obtained results are consistent with our theoretical analyses. The value of the LC-based systems in designing photonic quantum devices is further discussed. The redistribution of photon spin is controllable through manipulating the distributions of LC directors, which offers a way to manipulate the photonic spin states. It provides a potential platform for Hamiltonian engineering, thus more valuable multiple quantum systems are possible to be presented.
Results
For PSHE, several types of systems have been demonstrated, and the corresponding mechanisms are respectively different. In our system, the proposed PSHE is the result of an effective “magnetic field” acting on a pseudospin. The pseudospin vector is defined according to the Stokes parameters;29 the values of its three components correspond to S 1, S 2, and S 3, respectively, while S 0 denotes the normalized vector modulus. The effective magnetic field (or pseudo-magnetic field) is provided by the LC-based inhomogeneous medium. The orientation of the local optical axis can be suitably controlled to form special transverse distributions with a “twisting” feature for effective spin-to-orbital angular momentum conversion,30, 31 and thus the pseudo-magnetic field is driven to become helical due to the strong spin–orbit interaction. Tailoring the transverse distribution can result in different pseudo-magnetic fields for realizing various PSHE phenomena. A classical distribution involves varying the orientation of the optical axis linearly with the azimuthal angle. The structure that achieves such a variation is known as the q-plate.31 In addition, other distributions with non-uniform azimuthal changes and/or additional radial changes are also investigated and demonstrated in our study.
The Stokes vector is associated with the polarization state of the photon. To study the evolution of the Stokes parameters, we begin from the Schrödinger-like equation for polarized light, which could be obtained through a simple transformation of the Jones matrix equation as32
In this equation, γ is equal to 2/k 0 Δn, and Δn denotes the birefringence of the LC material. The 2 × 1 row vector ψ representing the polarization state is expressed as ψ = [ψ + , ψ - ]T = ψ + e + + ψ - e - , where e ± denotes the basis of circular polarization. For the interaction Hamiltonian H, according to the hermiticity, its general form is H = [ζ, ε − κi; ε + κi, ζ]. In our system, the parameters are calculated to be \(\varepsilon =\,\cos \,[2\alpha (\overrightarrow{r})],\) \({\rm{\kappa }}=\,\sin \,[2\alpha (\overrightarrow{r})],\) ζ = 0, thus we have
In this equation, \(\alpha (\overrightarrow{r})\) denotes the angle between the transverse-position-dependent optical axis and the system coordinate axis. Through a simple transformation, the Hamiltonian corresponding to Eq. (2) can be expressed as
where
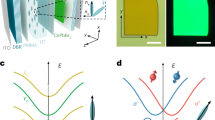
In the equations above, \(\overrightarrow{\sigma }\) is the Pauli matrix vector, while \({\overrightarrow{\Omega }}_{{\rm{eff}}}\) represents the effective magnetic field. It is obvious that \({\overrightarrow{\Omega }}_{{\rm{eff}}}\) is directly related to the distribution of the angle α. Three typical examples depicting the \(\alpha (\overrightarrow{r})\) functions are shown in Fig. 1. Figure 1a–c are plots of \(2\alpha (\overrightarrow{r})\), while Fig. 1d–f describe the corresponding effective magnetic field. The function α in Fig. 1(a) is given as α(r, φ) = 0.5φ. In this case, the orientation of the effective field changes regularly with respect to the angle α, as shown in Fig. 1(d). Moreover, if the azimuthal variation of α is non-uniform with the expression α(r, φ) = 2φ·H(φ − π)H(2π − φ)+10φ·H(φ)H(π − φ) (H(φ) represents the Heaviside step function) (Fig. 1b), the orientation distribution of \({\overrightarrow{\Omega }}_{{\rm{eff}}}\) is driven to be different in the respective angular regions (Fig. 1e). Besides variation along the azimuthal direction, a radial discontinuity can be introduced into \(\alpha (\overrightarrow{r})\), as is the case in Fig. 1c. The relevant formula in this case is α(r, φ) = 1.5φ + 0.5π·H(r − r 0) (r 0 = 260 μm), and the orientations of \({\overrightarrow{\Omega }}_{{\rm{eff}}}\) corresponding to the same polar angle in the two circular regions are opposite (Fig. 1f). The redistribution processes of photon spin are driven to be distinct according to different \(\alpha (\overrightarrow{r})\).The form of the interaction Hamiltonian for the LC-based PSHE system is similar with those of the intrinsic electronic SHE systems, but the detailed forms are different. As a result, the corresponding properties and phenomena have clear differences. In electronic systems, the main contributions to the interaction Hamiltonian are the Dresselhaus and Rashba terms. Due to the characteristics of the solid electronic systems, it is relatively hard to change the form of Hamiltonian in a specific system by certain methods. In our system, the critical factor of the interaction Hamiltonian is the distribution function \(\alpha (\overrightarrow{r})\). It is easy to control the form of Hamiltonian through tuning the \(\alpha (\overrightarrow{r})\). Correspondingly, various PSHE phenomena can be presented with our LC twisting structures. Previously, the optical SHE has been demonstrated in the exciton scattering systems, which is the result of the coherent precession of the photon pseudo-spin about a wave vector dependent effective magnetic field.7, 17 In the present work, the effective magnetic field is dependent of the spatial distribution of the LC directors, thus is tunable in the transverse plane.
Illustrations of the \(\alpha (\overrightarrow{r})\) functions that describe the distributions of the optical axis. The corresponding expressions of \(\alpha (\overrightarrow{r})\) are a α(r,φ) = 0.5φ, b α(r,φ) = 2φ·H(φ − π)H(2π − φ)+10φ·H(φ)H(π − φ), and c α(r,φ) = 1.5φ+0.5π·H(r − r 0) (r 0 = 260 μm). The spin–orbit interaction processes are tailored correspondingly to form different effective magnetic fields (d–f), which drive the pseudospin to present respective PSHE patterns
The effective magnetic field \({\overrightarrow{\Omega }}_{eff}\) originating from the spin-orbit interaction drives the pseudospin vectors to realign for forming the spin-dependent splitting effects. In our system, the pseudospin corresponds to the Stokes vector, so its precession can be intuitively described within the Poincaré sphere. The points on the sphere surface represent different pseudospin states. For an optimal spin-dependent splitting phenomenon, the initial state should be located on the equator of the Poincaré sphere denoting a linear superposition of σ+ and σ- states with equal probability amplitude, which indicates linearly polarized incident light. The direction of the effective magnetic field also lies in the x–y plane, and thus, the pseudospin vectors deviate from the equatorial plane and move towards the two poles under its influence. Further details can be obtained via the evolution equation for pseudospin, which is derived from Eq. (1). The components of the pseudospin vector, i.e., the Stokes parameters, can be expressed as average values of the Pauli matrices, namely, \({S}_{i}={\psi }^{\dagger }{\sigma }_{i}\psi\) (i = 1, 2, 3).28 Using the commutation relation for the Pauli spin, [σ 1, σ 2] = 2iσ 3 (and cyclic permutations),20, 27 the equation is deduced to be
wherein we set ν = γ/2. For simplification, the incident light is set to be horizontally polarized which is parallel to the x-axis. The direction of the effective magnetic field is anisotropic and dependent of the azimuthal angle. The redistribution of photon spin is controlled by \({\overrightarrow{\Omega }}_{{\rm{eff}}}\). If \({\overrightarrow{\Omega }}_{{\rm{eff}}}\) lies along the clockwise direction of \(\overrightarrow{S}({\overrightarrow{\Omega }}_{{\rm{eff}}}\cdot {\hat{e}}_{y} < 0)\), the pseudospin state should change towards the σ- state; on the contrary, when \({\overrightarrow{\Omega }}_{{\rm{eff}}}\) lies along the counterclockwise direction of \(\overrightarrow{S}({\overrightarrow{\Omega }}_{{\rm{eff}}}\cdot {\hat{e}}_{y} >0)\), the corresponding state changes oppositely and tends to the σ+ state. From Eqs. (1) and (2), it can be clearly observed that the off-diagonal elements of the Hamiltonian are different, and thus the σ+ and σ- states experience asymmetric interaction processes in the mediums. Based on such a mechanism, a splitting effect is expected to occur between the σ+ and σ- components of the output light. Moreover, as \({\overrightarrow{\Omega }}_{{\rm{eff}}}\) exhibits multifold rotational symmetry according to the coefficient q of the azimuthal coordinate, deduced from Eq. (5), the phenomenon of PSHE is supposed to present the characteristics of multiple azimuthal splitting. For a more distinct description, Eq. (5) is further solved, and analysis formulae of the pseudospin are obtained. Among the three components of \(\overrightarrow{S}\), S 3 which is associated with the helicity (or handedness) of light directly depicts the splitting between the σ+ and σ- states.21 The corresponding evolution equation is obtained through Eq. (5) as
For horizontally polarized incident light, the initial condition is S 1 = 1, S 2 = S 3 = 0. The equivalent length of the LC-based twisting medium is π/2k 0 Δn. Substituting these parameters into Eqs. (5) and (6), the expression for S 3 is derived as
Here, E 0 (r, φ) describes the transverse profile of the pump field, and ξ denotes the corresponding normalization parameter. Based on Eq. (7), considering the simplest case with α(r, φ) = 0.5φ, the output light is expected to result in two states corresponding to the σ+ and σ- components, respectively. As the coefficient q becomes larger, the number of splitting states should also increase. According to the symmetry of the system, this number can be predicted to be 4q. These states correspond to the σ+ and σ- components, respectively, and they distribute along the azimuthal direction in turn. If the function α(r, φ) becomes more complex, the distribution of the states is further modulated. Through controlling the formula of α(r, φ), various PSHE patterns could be observed.
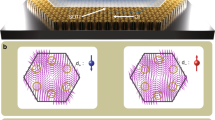
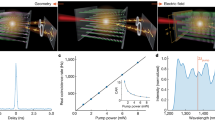
To demonstrate the intrinsic PSHE, we perform experiments based on the set-up shown schematically in Fig. 2. A continuous-wave laser at 671 nm is utilized as the pump light. After passing through the polarizer (P1), it is transformed into linearly polarized light. A half-wave plate is used for modulating the polarization direction. The samples with LC-based twisting structures are prepared by means of digital micro-mirror device (DMD) based micro-lithography,25, 26, 33 whose micrographs are shown in the left column of Fig. 3a–d]. The corresponding formulae of α(r, φ) for each of the illustrated cases are α 1 (r, φ) = 0.5φ, α 2 (r, φ) = 1.5φ, α 3 (r, φ) = 2φ·H(φ − π)H(2π − φ) + 10φ·H(φ)H(π − φ), and α 4 (r, φ) = 1.5φ + 0.5π·H(r − r 0 ) (r 0 = 260 μm), respectively. Beyond the twisting medium, a combination of a quarter-wave plate and a polarizer (P2) is positioned for measuring S 3, and the output light is detected by a CCD camera. The experimental results are shown in Fig. 3e–h. As the CCD camera locates in the far-field, the measurement distributions actually correspond to the Fourier transforms of those in the near-field. Combining the Fourier theory and the theory discussed above, the theoretical results are obtained and shown in Fig. 3i–l. It is seen that the observation results are in excellent agreement with the calculations.
Experimental set-up for PSHE measurement. A continuous-wave (CW) pump laser (671 nm) passes through the polarizer (P1) and becomes linearly polarized light. The half-wave plate (HWP) is used for modulating the polarization direction. Spin–orbit interaction processes in the LC twisting samples result in the PSHE phenomena. The pseudospin is measured with a combination of a quarter-wave plate (QWP) and a polarizer (P2). The output patterns are detected by a CCD camera
Micrographs of four representative samples with the distribution functions of optical axis as a α 1 (r, φ) = 0.5φ, b α 2 (r, φ) = 1.5φ, c α 3 (r, φ) = 2φ·H(φ − π)H(2π − φ) + 10φ·H(φ)H(π − φ), and d α 4 (r, φ) = 1.5φ + 0.5π·H(r − r 0 ), respectively. It is obvious that the measured PSHE patterns (e–h) are in excellent agreement with theoretical simulations (i–k). For α 1 (r, φ) and α 2 (r, φ), the number of splitting states is equal to 4q (q = 0.5 or 1.5), and these states locate along the azimuthal direction regularly. In the case of α 3 (r, φ), twenty states are on the upper half plane while four ones are on the lower half. If an additional circular discontinuity is introduced in as α 4 (r, φ), there are both six states locate within and outside of the circle. The two states in one radial orientation correspond to the σ+ and σ- components, respectively
When the distribution of the optical axis is α 1 (r, φ) = 0.5φ, two states are observed Fig. 3e and i, which originate from the splitting of the σ+ and σ- components. In comparison with the PSHE on the interface between two conventional dielectrics,9,10,11 there is an increase in the displacement of splitting owing to the inhomogeneity of the spin–orbit coupling system.21 Moreover, through tailoring the inhomogeneity to present the twisting feature, the phenomenon of PSHE is enhanced and the number of the splitting states is not limited to two. For α 2 (r, φ) = 1.5φ, the splitting states form a pattern of a flower with six petals (Fig. 3f and j). The system exhibits a C 3 rotational symmetry. In the case of α 3 (r, φ) = 2φ·H(φ − π)H(2π − φ) + 10φ·H(φ)H(π − φ), the splitting pattern shows symmetry breaking arising from the azimuthal asymmetry characteristic (Fig. 3g and k). Twenty states distribute in the upper half space, while four ones distribute in the lower half. For further consideration, we introduce radial variation into the function α as α 4 (r, φ) = 1.5φ + 0.5π·H(r − r 0 ). The subsequent distribution of states becomes increasingly complex (Fig. 3h and l). There are six states located both within and outside of the dislocation ring. As the directions of the effective magnetic field for r < r 0 and r > r 0 with the same azimuthal angle are opposite, the two splitting states along one radial orientation correspond to the σ+ and σ- components, respectively. Through designing the distribution of the optical axis, tunable PSHE with any desired splitting pattern could be realized.
Discussion
Owing to the characteristics of photonic systems, the transverse splitting is complete only in certain cases, so it is necessary to investigate the intensity of PSHE quantitatively. In the present system, we consider that the intensity of the PSHE is better to be measured by the splitting degree of the σ+ and σ- light spot. It is influenced by two aspects. For one aspect, the coupling process is critical. Owing to the periodic characteristic of the photonic systems in the longitudinal direction, the splitting degree does not increase with the coupling constant linearly, which differs from the situation in the electronic systems. The maximum is obtained when the relative phase retardation is equal to π/2. This point is determined by the thickness of the sample and the coupling constant k 0 Δn/2 in the Schrödinger-like equation jointly. For the other aspect, it should be referred to the function \(\alpha (\overrightarrow{r})\). As the observation is carried out in the far-field, that is to say that the splitting is measured in reciprocal space. We choose the spin-dependent shift of wave vector \(\Delta \overrightarrow{k}\) to describe the splitting degree (The first condition is set to be optimal). The expression is
When the distribution function is α(r, φ) = qφ + α 0 , the \(\Delta \overrightarrow{k}\) is derived to be \(\Delta {\overrightarrow{k}}_{\varphi }=-{\sigma }^{\pm }q{\hat{e}}_{\varphi }\,(\Delta {\overrightarrow{k}}_{r}=0).\) The splitting in the real space can be acquired by the equation
We can see that the splitting becomes larger with the value of q. This point can also be confirmed in the case α(r, φ) = 2φ·H(φ − π)H(2π − φ) + 10φ·H(φ)H(π − φ). From the measured pattern, it is obvious that the splitting corresponding to the portion of q = 10 is larger than that of q = 2. In addition, in the case α(r, φ) = 1.5φ + 0.5π·H(r − r 0 ), we have \(\Delta {\overrightarrow{k}}_{r}=-0.5\pi {\sigma }^{\pm }\cdot \delta (r-{r}_{0}){\hat{e}}_{r}\). As a result, the splitting appears in the radial direction.
In fact, more than the tunable PSHE, the LC-based systems possess greater value for quantum photonic applications. A direct consideration is to engineer the Hamiltonian. In several quantum information applications, controlling the evolution of the quantum systems is an important task. This can be carried out through appropriate Hamiltonian engineering. In the LC-based photonic systems, referring to Eq. (2), the form of interaction Hamiltonian is determined by the function \(\alpha (\overrightarrow{r})\). Utilizing photo-alignment technique, the function \(\alpha (\overrightarrow{r})\) can be flexibly steered, thus it is easy to realize the local and fine tuning of the interaction Hamiltonian. That is difficult to achieve previously. A representative example is the programmable optical vortex lattice.34, 35 Choosing \(\alpha (\overrightarrow{r})\) to be an appropriate periodic function, the LC medium can be designed for the analog of an arbitrary two-dimensional crystal lattice. If the considered system is more complex, we can divide it into small elements and tailor the corresponding sub-Hamiltonians, respectively. The control task of the entire system is realized through contenting the engineered sub-Hamiltonians in series. A useful application is the quantum random walk based on the spin–orbital angular momentum space of photons.36, 37 In such systems, the spin states of photon play the role of the coin in the typical model of discrete-time quantum walk. The spin–orbit coupling process in the q-plate is utilized for Hadamard operation together with suitable modulations provided by waveplates, thus the spin coin is tossed to determine how a step is taken. The walk of a photon is presented through increase or decrease in the orbital angular momentum (OAM). The change of OAM is ±ħ for one step. The quantum walk can be implemented step by step. The technique of Hamiltonian engineering opens possibilities for simulating the dynamical evolution of certain valuable multiple quantum systems.
In conclusion, we have demonstrated the photonic SHE based on spin–orbit coupling in LC-based twisting structures. The pseudospin states of photons are driven to split by the anisotropic effective magnetic field arising from the inhomogeneous light–matter interaction process in the LC medium. The interaction Hamiltonian of such a system is shown to be similar with that of the intrinsic SHE in electronic systems. Owing to the micro-lithography technology based on DMD device, the distribution of the directors of LC molecules could be designed with very high flexibility, thus the spin–orbit coupling process in the twisting mediums could be arbitrarily tailored to present various PSHE phenomena. Four representative samples are prepared for experimental observation, and the results are in excellent agreement with theoretical predictions. The tunable LC system may provide a potential platform for controlling the redistribution of photon spin and shed new light on photonic quantum simulations.
Methods
The samples are fabricated through the following method. The LC material we used for the samples is the sulphonic azo-dye SD1 (Dai-Nippon Ink and Chemicals, Japan). The director of LC molecule which corresponds to the optical axis can be locally controlled through several techniques. In the present work, we choose the photoalignment technique. Through suitably controlling the exposure process, the distribution of the LC directors can be flexibly desiged to form the twisting microstructures.
The details about preparing the samples are as follows: The first procedure is to fabricate the LC cells. Indium-tin-oxide coated glass substrates are ultrasonic bathed, UV-ozone cleaned and then spin-coated with 0.5% solution of sulphonic azo-dye SD1 in dimethylformamide, and then the LC cell is infiltrated with LC mixture E7. Following, the photo-alignment technique is applied to obtain the twisting microstructures. Spurt 6 μm spacers over one substrate then put the counter substrate over it. The two substrates are assembled together and sealed by epoxy glue. Afterwards the cell was placed at the image plane of the DMD based microlithography system to record the designed patterns, which correspond to the desired distribution function \(\alpha (\overrightarrow{r})\). Each area is exposed with a dose of ca. 1 J/cm2 each time, and after the eighteen-step five-time-partly-overlapping exposure with a total exposure dose of 5 J/cm2, a quasi-continuous space-variant orientation of SD1 was carried out. After LC capillarily filled, the samples with various twisting microstructures are achieved.
References
Zutic, I., Fabian, J. & Das Sarma, S. Spintronics: fundamentals and applications. Rev. Mod. Phys. 76, 323–410 (2004).
Awschalom, D. D., Bassett, L. C., Dzurak, A. S., Hu, E. L. & Petta, J. R. Quantum spintronics: engineering and manipulating atom-like spins in semiconductors. Science 339, 1174–1179 (2013).
Morton, J. J., McCamey, D. R., Eriksson, M. A. & Lyon, S. A. Embracing the quantum limit in silicon computing. Nature 479, 345–353 (2011).
Awschalom, D. D., Loss, D. & Samarth, N. Semiconductor Spintronics and Quantum Computation (Springer, Berlin, 2002).
Dyakonov, M. I. & Perel, V. I. Current induced spin orientation of electrons in semiconductors. Phys. Lett. A 35, 459–460 (1971).
Sinova, J. et al. Universal intrinsic spin Hall effect. Phys. Rev. Lett. 92, 126603 (2004).
Leyder, C. et al. Observation of the optical spin Hall effect. Nat. Phys 3, 628–631 (2007).
Onoda, M., Murakami, S. & Nagaosa, N. Hall effect of light. Phys. Rev. Lett. 93, 083901 (2004).
Hosten, O. & Kwiat, P. Observation of the spin Hall effect of light via weak measurements. Science 319, 787–790 (2008).
Qin, Y., Li, Y., He, H. Y. & Gong, Q. H. Measurement of spin Hall effect of reflected light. Opt. Lett. 34, 2551–2553 (2009).
Hermosa, N., Nugrowati, A. M., Aiello, A. & Woerdman, J. P. Spin hall effect of light in metallic reflection. Opt. Lett. 36, 3200–3202 (2011).
Luo, H. L. et al. Spin Hall effect of a light beam in left-handed materials. Phys. Rev. A 80, 043810 (2009).
Kong, L. J. et al. Spin Hall effect of reflected light from an air–glass interface around the Brewster’s angle. Appl. Phys. Lett. 100, 071109 (2012).
Bliokh, K. Y., Gorodetski, Y., Kleiner, V. & Hasman, E. Coriolis effect in optics: unified geometric phase and spin-Hall effect. Phys. Rev. Lett. 101, 030404 (2008).
Haefner, D., Sukhov, S. & Dogariu, A. Spin Hall effect of light in spherical geometry. Phys. Rev. Lett. 102, 123903 (2009).
Aiello, A., Lindlein, N., Marquardt, C. & Leuchs, G. Transverse angular momentum and geometric spin Hall effect of light. Phys. Rev. Lett. 103, 100401 (2009).
Kavokin, A., Malpuech, G. & Glazov, M. Optical spin Hall effect. Phys. Rev. Lett. 95, 136601 (2005).
Bliokh, K. Y. & Bliokh, Y. P. Conservation of angular momentum, transverse shift, and spin Hall effect in reflection and refraction of an electromagnetic wave packet. Phys. Rev. Lett. 96, 073903 (2006).
Kang, M. et al. Spatial splitting of spin states in subwavelength metallic microstructures via partial conversion of spin-to-orbital angular momentum. Phys. Rev. A 85, 035801 (2012).
Kammann, E. et al. Nonlinear optical spin Hall effect and long-range spin transport in polariton lasers. Phys. Rev. Lett. 109, 036404 (2012).
Yin, X. B., Ye, Z. L., Rho, J., Wang, Y. & Zhang, X. Photonic spin Hall effect at metasurfaces. Science 339, 1405–1407 (2013).
Li, G. et al. Spin-enabled plasmonic metasurfaces for manipulating orbital angular momentum of light. Nano Letters 13, 4148–4151 (2013).
Ling, X. H., Zhou, X. X., Luo, H. L. & Wen, S. C. Steering far-field spin-dependent splitting of light by inhomogeneous anisotropic media. Phys. Rev. A 86, 053824 (2012).
Khoo, I. C. & Wu, S. T. Optics and Nonlinear Optics of Liquid Crystals (World Scientific, 1993).
Hu, W. et al. Polarization independent liquid crystal gratings based on orthogonal photoalignments. Appl. Phys. Lett. 100, 111116 (2012).
Wei, B. Y. et al. Generating switchable and reconfigurable optical vortices via photopatterning of liquid crystals. Adv. Mater. 26, 1590–1595 (2014).
Kuratsuji, H. & Kakigi, S. Maxwell-Schrödinger qquation for polarized light and evolution of the Stokes parameters. Phys. Rev. Lett. 80, 1888–1891 (1998).
Botet, R. & Kuratsuji, H. Polarization of an electromagnetic wave in a randomly birefringent medium: a stochastic theory of the Stokes parameters. Phys. Rev. E 81, 036602 (2010).
Kavokin, A., Lagoudakis, P. G., Malpuech, G. & Baumberg, J. J. Polarization rotation in parametric scattering of polaritons in semiconductor microcavities. Phys. Rev. B 67, 195321 (2003).
Tamburini, F., Thidé, B., Molina-Terriza, G. & Anzolin, G. Twisting of light around rotating black holes. Nat. Phys 7, 195–197 (2011).
Marrucci, L., Manzo, C. & Paparo, D. Optical spin-to-orbital angular momentum conversion in inhomogeneous anisotropic media. Phys. Rev. Lett. 96, 163905 (2006).
Yariv, A. & Yeh, P. Optical Waves in Crystals (Wiley, 1984).
Wu, H. et al. Arbitrary photo-patterning in liquid crystal alignments using DMD based lithography system. Opt. Express 20, 16684–16689 (2012).
Barboza, R. et al. Harnessing optical vortex lattices in nematic liquid crystals. Phys. Rev. Lett. 111, 093902 (2013).
Barboza, R. et al. Vortex induction via anisotropy stabilized light-matter interaction. Phys. Rev. Lett. 109, 143901 (2012).
Goyal, S. K., Roux, F. S., Forbes, A. & Konrad, T. Implementing quantum walks using orbital angular momentum of classical light. Phys. Rev. Lett. 110, 263602 (2013).
Zhang, P. et al. Implementation of one-dimensional quantum walks on spin-orbital angular momentum space of photons. Phys. Rev. A 81, 052322 (2010).
Acknowledgements
National Natural Science Foundation of China (61225026, 61322503, 61490714); China Postdoctoral Science Foundation Funded Project (2016M590443); Program for Changjiang Scholars and Innovative Research Team at the University (IRT13021).
Author's contributions
Y. M., W. H. and Y. L. contributed to the original idea. P. C., C. L. and Y. M. prepared the samples. Y. M. and W. J. performed the PSHE experiments. B. W. and T. L. provided helpful discussions. Y. M., W. H. and Y. L. wrote the manuscript. Y. L. and W. H. supervised the project.
Competing interests
The authors declare no competing interest.
Author information
Authors and Affiliations
Corresponding authors
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Ming, Y., Chen, P., Ji, W. et al. Tailoring the photon spin via light–matter interaction in liquid-crystal-based twisting structures. npj Quant Mater 2, 6 (2017). https://doi.org/10.1038/s41535-017-0011-1
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-017-0011-1