Introduction

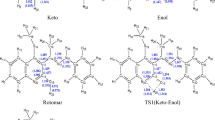
Tautomers are constitutional isomers that spontaneously convert to one another in dynamic equilibrium. The process of this interconversion is called tautomerization. Typical tautomerization involves the movement of a proton from one position to another and rearrangement of a double bond within the molecule. Other types of tautomerisms include annular, ring-chain, and valence tautomerisms1,2,3. One well-known example of tautomerization, and quite often involved in the field of drug development, is the keto-enol tautomerism, in which the carbonyl double bond (keto form) is interconverted to an alkene double bond (enol form). This is accompanied by the shift of the alpha proton in the keto form to the hydroxyl group in the enol form, as illustrated in Fig. 1.

Fig. 1: Keto-enol tautomerization in acetone.
figure 1

This schematic represents keto-enol tautomerization in acetone, highlighting the transfer of a proton (depicted in magenta) and the movement of a double bond (in red). The staggered equilibrium arrows indicate a preference for the keto form.

Full size image

Tautomerization plays an important role in biological systems. Non-Watson-Crick base pairing can occur due to tautomerization of nucleic acid base pairs. Such nucleic acid mismatches induced by tautomerization result in spontaneous mutagenesis and hence genetic instability4,5. In the case of drug molecules, the movement of proton within the molecules will lead to the conversion from a hydrogen bond donor to a hydrogen bond acceptor or vice versa, which is essential for the analysis of structure-activity relationship (SAR). Moreover, it has been estimated that more than a quarter of marketed drugs can exhibit tautomerism6 and analysis of chemical databases showed that 10-30% of potential drug molecules have potential tautomers7,8,9,10,11. Prediction of tautomeric states of compounds of interest is therefore an important subject in the field of computer-aided drug design.

State-of-the-art algorithms for tautomeric prediction usually involve enumeration of possible tautomers, followed by prediction of the dominant form or estimation of the tautomer populations12,13,14,15,16. The estimation of tautomeric ratios in aqueous medium can be achieved by pKa calculations. Such algorithms usually aim to provide a list of possible tautomeric forms with ratios of the corresponding species, since it is important to estimate the population of the tautomers due to the small differences in their free energies that could be easily compensated by the interaction with proteins. Previous efforts on pKa estimation rely on empirical pKa prediction models. For example, Epik Classic utilizes Hammett-Taft linear free energy relationship (LFER)17. However, such empirical methods are known to have limited accuracy, partly due to the under-coverage of chemical space in the database18,19. This could be problematic as the lack of experimental parameterization for novel chemical scaffolds prevents accurate prediction against novel compounds. Moreover, experimental challenges in obtaining the relative tautomer stability as well as isolating the distinct tautomeric forms could also be the cause of prediction uncertainty15. One potential rational solution to this would be prediction methods based on electronic structures. Indeed, more recent focuses have shifted to quantum-mechanics-based (QM) pKa prediction20,21,22. Such QM-based methods, however, are computationally demanding and may not be practical for applications like large-scale virtual screening. It should also be noted that solvent is another important factor in determining tautomeric ratios in solution.

Computational quantum chemistry provides a more accurate approach to describing molecular structures in drug design than classical force field-based molecular mechanics methods. QM calculations play a critical role for certain problems in the field, such as metal binding in metalloenzymes, reaction mechanism study, covalent inhibitor design23. Other applications of QM methods include calculation of molecular properties, QM-based descriptor for QSAR, parameterization of forcefields, and estimation of protein-ligand binding affinities23,24,25,26. Major QM methods used in the field of computer-aided drug discovery (CADD) can be classified to semi-empirical QM methods, Hatree-Fock (HF), post-Hatree-Fock (pHF) methods, and density functional theory (DFT). While quantum chemistry approaches have brought accuracy to the calculations, their computational cost makes them unsuitable as a daily tool in CADD except for the semi-empirical methods. Depending on the level of theory, the integral transformation could scale as high as \({{{\mathcal{O}}}}({M}^{5})\), where M is the number of atomic basis functions (AOs)27.

Therefore, even though the aforementioned classical quantum chemistry algorithms are well-designed, they still have unreasonable time and space requirements for medium and large molecules28. More often, applications of quantum chemistry methods are used in specific drug design scenario and the implementation of the QM methods is hard to generalize. This poses severe limitations on the general use of quantum chemistry methods in drug discovery, e.g., prediction of dominant product in tautomerism, understanding the dynamics of protein folding, and ligand binding free energy calculations.

Quantum simulation is considered one of the most promising applications of quantum technology since it has the potential of overcoming the exponential barrier of solving electronic structure problems29,30. Jordon-Wigner (JW) transformation31 was found to give mappings from fermionic creation and annihilation operators to qubit operators32. This result paved the road to generically simulate physical systems on well-controlled quantum computers. Moreover, the quantum phase estimation (QPE) algorithm33,34,35,36,37,38,39,40,41,42 provides accurate spectral calculations for molecular Hamiltonian with the potential of exponential speedup. However, the QPE method is not applicable on current quantum devices because it requires long coherence time and high gate fidelity. Instead, several variational methods37,43,44,45,46,47,48,49,50,51,52,53 suitable for noisy intermediate-scale quantum (NISQ) devices were proposed. One of the most practical approaches is the variational quantum eigensolver (VQE) algorithm43,44. VQE is a hybrid quantum-classical method that approximates ground states of molecular Hamiltonian by variationally tuning the ansatz parameters and is expected to give better accuracy than CCSD results with polynomial costs.

Quantum simulation of small molecules has since then been widely implemented. Researchers have worked towards molecules (BeH2, H2O, and H12) with improved algorithms and hardware design45,54,55. Others also provide strategies to simulate slightly larger systems, such as CO2, C2H4, C18, and the nitrogenase iron-sulfur molecular clusters56,57,58, using symmetries, fragmentation of molecules, spin-model simplifications, or qubit encoding methods59,60,61,62,63,64. However, these quantum simulation results are still quite limited in the problem size and often lack real world applications.

In this work, we aim to design a general methodology for a pharmaceutical application, namely, the prediction of preferred tautomeric states. We expect that our scheme could work for both current and future quantum devices. Specifically, we presented a hybrid quantum chemistry-quantum computation approach to predict the dominant form of tautomers, where quantum chemistry methods are used to construct the system of interest and reduce the size of the Hamiltonian to meet current quantum hardware requirement, and the reduced Hamiltonian was mapped to qubits using qubit-efficient encoding (QEE)64 and subsequently simulated with variational quantum eigensolver (VQE). We focus on predicting the preferred tautomeric states by considering the energetics of the states using quantum chemistry approaches to make the system applicable on current quantum computing schemes. This approach was practiced on two illustrative examples, acetone and Edaravone. Our quantum simulation results showed reasonable agreement with CCSD calculations.

Results

To compare the relative stability of tautomers, one would need to calculate the energies of the systems. Before jumping into detailed calculation of the electronic structures, the most straightforward and hand-wavy way to estimate tautomers’ relative stability is by considering the difference in bond dissociation energy for a simple system like the case of acetone tautomerism. The bond dissociation enthalpy65 difference between C=O, C-C, C-H (keto form, 745 + 347 + 413 = 1505 kcal/mol) and O-H, C-O, C=C (enol form, 467 + 358 + 614 = 1439) is 66 kJ/mol (15.8 kcal/mol), favoring the keto form. However, as the complexity of the molecules increases, the relative stability could not be attributed so easily. Factors like electrostatic effect, steric hindrance from the other parts of the molecule and intra-molecular hydrogen bonds need careful consideration as well. Commercial or publicly available CADD tools deal with the tautomerism problem using empirical or rule-based chemoinformatics methodologies, e.g., scoring tautomers based on the prediction of microstate and microstate pKa values. There is, however, still room for improvement with such an approach due to the lack of extensive databases and over-parameterization of the prediction models.

In principle, two important factors decide the tautomeric equilibrium. The relative potential energy difference, which determines the equilibrium direction, accounts for the stability between the isomers. On the other hand, the rate of isomer interconversion depends on the activation energy. As tautomerism involves bond breaking and bond formation, the best way to handle this problem should be quantum mechanics-based approaches by considering the energetics of the individual tautomeric forms. Indeed, methods involving implicit solvent density functional theory calculations have been implemented in the tautomer enumeration and scoring workflow66. However, such first-principle calculations are impractical for some of the CADD tasks even with the computation resources nowadays. For example, the enumeration of the tautomers and prediction of dominant species of the compound library is an essential step at the very beginning of a virtual screening campaign. A computational bottleneck on DFT calculations prevents practical applications of such algorithms from processing large databases. Here, we suggest an alternative method by a quantum mechanics-based computational scheme with current quantum computing simulators to predict the relative stability of the tautomeric forms. With the advent of quantum computing technologies, quantum chemical approaches could play an important and applicable role for tautomer predictions and computer-aided drug discovery when implemented on future large-scale quantum devices.

In the following, we first present the quantum chemistry overview of the two tautomeric systems: (1) acetone and its enol form, and (2) Edaravone’s keto, enol, and amine forms in the STO-3G basis set. Next, we introduce current challenges of simulating medium-to-large molecules and our workflow that could contribute to resolving the problems. Besides, we provide the background of the qubit-efficient encoding methods for quantum simulation. Lastly, we show the numerical results for the implementation of our workflow with quantum simulations of the two tautomeric systems.

Overview of systems

Acetone

We start with a relatively simple example of tautomerization. Acetone exhibits keto-enol tautomerization, in which the acetone and its enol form, propen-2-ol, interconvert to each other (Fig. 2a). The relative stability of these two isomers can be easily assessed by comparing their bond energy, and the keto from is more stable than the enol form by about 16 kcal/mol. Figure 2a shows the optimized geometries of the keto and enol forms of the acetone at the level of 6-311++G(d,p) using B3LYP in the Gaussian 16 program67. To enable quantum computing of the system at a reasonable computational cost, we reconstituted the molecules with the minimal STO-3G at the second-order Møller-Plesset perturbation theory (MP2) level with 52 spin-orbitals. The corresponding energy diagrams of the molecular orbitals near HOMO/LUMO are shown in Fig. 2b for the keto and enol form, respectively. The keto form is more stable than the enol form in most cases because the C=O double bond is stronger than the C=C bond. Polarization of the C=O double bond, as depicted in electrostatic potential surface of the acetone, gives it a relatively higher bond energy. The rearrangement of the double bond between the keto and enol form is apparent from the shift of the π bonding patterns of the HOMOs for the corresponding tautomers.

Fig. 2: Acetone tautomers and orbital energies.
figure 2

a Tautomeric isomers of acetone. The geometries were optimized at the B3LYP/6-311++G(d,p) level and the electrostatic potential surface generated by ESP_DNN93. b Hartree-Fock orbital energy levels around HOMO/LUMO as calculated using the STO-3G basis set. The full list of molecular orbital eignevalues can be found in Supplementary Information.

Full size image

Edaravone

Edaravone is an FDA-approved drug for the treatment of amyotrophic lateral sclerosis (ALS). The mechanism of the action of Edaravone involves its radical scavenging activity. The idea originated from a research program in Mitsubishi Yuka Pharmaceutical Corporation, in which the scientists try to utilize the radical-scavenging activity of phenol and avoid related toxicity. The researchers believed that an aromatic heterocyclic system with the potential of keto-enol tautomerization could exist in the form with a hydroxyl group68. Edaravone exists in three forms of tautomeric isomers - keto, enol, and amine (Fig. 3a), with varying physicochemical properties. Moreover, the three forms of Edaravone exhibit different antioxidant activity. Therefore, it is important to know which form among the three dominates to better understand the pharmacological effect of Edaravone. Estimation of relative stability among the three tautomers for Edaravone is not as trivial as for acetone, since the molecular structure of Edaravone is much more complicated. For example, the aromaticity of the N-substituted pyrazolone core in the three isomers varies. Moreover, the surface charge distribution of the three tautomers differs quite a lot and the twisted angles between the pyrazolone and the N-substituted benzene are distinct among the three according to the optimized geometries of the forms (at the level of B3LYP/6-311++G(d,p) theory) as depicted in Fig. 3a. Reconstitution of the electronic configuration using the minimal STO-3G basis at MP2 level yields 150 molecular orbitals. Energy diagrams of the molecular orbitals near HOMO/LUMO and the HOMOs and LUMOs of the three tautomeric species do not provide clear pictures for the relative stabilities of the three species as in the case of acetone (Fig. 3b).

Fig. 3: Edaravone tautomers and orbital energies.
figure 3

a Tautomeric isomers of Edaravone. The geometries were optimized at the B3LYP/6-311++G(d,p) level and the electrostatic potential surface generated by ESP_DNN93. b Hartree-Fock orbital energy levels around HOMO/LUMO as calculated using the STO-3G basis set. The full list of molecular orbital eignevalues can be found in Supplementary Information.

Full size image

Notice that it is already computationally expensive to construct the electronic structures of Edavarone at the MP2/STO-3G level of theory. However, in the field of medicinal chemistry, there are more compounds with larger sizes. It is therefore not an efficient way to predict the thermodynamic stability of different tautomer states by comparing the energies of the isomers using such quantum chemistry calculation directly. Calculations based on wave function approaches for pharmaceutical molecules remains impractical even if the sizes of the system can be recused using methods such as complete active space (CAS) approaches because CI expansion scales exponentially and the affordable active size is generally considered to be limited to 18 electrons in 18 orbitals69, although the limit had been pushed to 22 electrons in 22 orbitals with parallel multiconfigurational SCF implementation70.

In order to leverage the power of quantum computation, we proceed as follows. Firstly, the second-quantized electronic Hamiltonian can be written as

$$H=\mathop{\sum}\limits_{pq}{h}_{pq}{a}_{p}^{{\dagger} }{a}_{q}+\frac{1}{2}\mathop{\sum}\limits_{pqrs}{h}_{pqrs}{a}_{p}^{{\dagger} }{a}_{q}^{{\dagger} }{a}_{r}{a}_{s},$$
(1)

where hpq and hpqrs are the overlap and exchange integrals. The indices of the spin-orbitals are represented by p, q, r, and s in the summation of Eq. (1). For example, the indices run from 0 to 51 for acetone and from 0 to 149 for Edaravone because the molecules in the STO-3G basis set have 52 and 150 spin-orbitals respectively. To simulate electronic structure problems on quantum computers, the creation and annihilation operators and the electronic states have to be mapped to qubits.

Common qubit encoding methods are Jordan-Wigner, parity, and Bravyi-Kitaev encoding where the qubit requirements are \({{{\mathcal{O}}}}(N)\) where N is the number of spin-orbitals. For example, Jordan-Wigner (JW) encoding uses N qubits to store the N spin-orbital occupation number. In this encoding scheme, the \(\left\vert 0\right\rangle\) qubit state represents that the spin-orbital is not occupied while the \(\left\vert 1\right\rangle\) qubit state represents that the spin-orbital is occupied. The mappings of the creation and annihilation operators for JW are

$${a}_{p}^{{\dagger} }=\frac{1}{2}({X}_{p}-i{Y}_{p})\otimes {Z}_{p-1}\otimes \cdots \otimes {Z}_{0},$$
(2)
$${a}_{p}=\frac{1}{2}({X}_{p}+i{Y}_{p})\otimes {Z}_{p-1}\otimes \cdots \otimes {Z}_{0},$$
(3)

where the Z Pauli strings address the fact that electronic wavefunctions are anti-symmetric. For acetone and Edaravone in the STO-3G basis set, JW encoding will map the electronic structure problems to 52 qubits and 150 qubits. No meaningful data would be collected for VQE using that many qubits on NISQ devices because of decoherence. It is, therefore, important to reduce the problem size.

Workflow

Here we propose a hybrid computational scheme for the prediction of the preferred tautomeric state, comprising classical quantum chemistry (using classical computers) and quantum computation. The workflow involves (1) geometry optimization of the isomers using density functional theory, (2) reconstruction of the molecular orbital space in a minimal basis set, (3) reduction of the MO space, (4) single point energy calculations of active MO sets, (5) selection of the most representative active MO set, and finally (6) energy calculation in Quantum computing scheme using QEE, as illustrated in Fig. 4. We use the CCSD energies of the full systems as the benchmark of our workflow performance.

Fig. 4
figure 4

Proposed workflow of preferred tautomeric state prediction.

Full size image

Specifically, to reduce the problem size, we use quantum chemistry methods to select active molecular orbitals (MOs) and map the Hamiltonian onto fewer qubits using a qubit-efficient encoding method. The geometries of the tautomeric isomers are prepared and initially optimized using Avogadro71 with the MMFF94 force field72,73,74,75,76 and further optimized at the level of 6-311++G(d,p) using B3LYP77,78 in the Gaussian 16 program. Due to limited resources for quantum computing, the molecules are reconstituted with the minimal STO-3G at the MP2 level79, followed by the calculation of occupancies of natural orbitals (NOs) using Gaussian 16. The STO-3G basis set has been widely used in several pioneering works of computation chemistry with quantum computing scheme45,54,55. Although the computational cost has been greatly reduced with the minimal basis set, the number of required qubits still exceeds the affordable amount of current QC simulators or real quantum devices.

The reduction of the MO space is then achieved by considering the occupation numbers and quantum hardware limitations. The selection of active space was achieved mostly by excluding the inner core and the outer virtual orbitals. In practice, the natural orbitals with occupancy closest to 0 (completely virtual) or 2 (fully occupied) were frozen or removed. Besides, quantum hardware constraints and the efficiencies of the qubit-efficient encoding method are also considered in the selection process. The reduced second-quantized Hamiltonian is then encoded onto qubits.

The natural orbitals for Acetone and Edaravone tatutomers calculated at the MP2/STO-3G level can be found in Supplementary Information. Selected combinations of active MOs are listed in Supplementary Information for acetone and Edaravone, respectively. After the active space selection from quantum chemistry methods, we have 12 spin-orbitals (6 molecular orbitals) for acetone, propen-2-ol, and the three tautomers of Edaravone. With Jordan-Wigner (JW) encoding, the qubit count to simulate the quantum systems is 12 qubits which is still a difficult task for noisy intermediate-scale quantum devices without error mitigation. Therefore, we use qubit-efficient encoding (QEE) to encode the systems onto 8 qubits shown in Table 1 because it provides fewer qubit counts and renders the systems to be suitable for the use of hardware-efficient ansatzes. We then use a hardware-efficient ansatz to simulate the systems with variational quantum eigensolver (VQE).

Table 1 Comparison of qubit counts for Jordan-Wigner encoding and qubit-efficient encoding for the tautomers of acetone and Edaravone.
Full size table

Even though the qubit requirement is reduced by classical active space selection methods, it is still hard to be implemented on a quantum device as the circuit depth would not permit. For JW encoding, some unphysical (e.g. not particle conserving or violating other symmetries) electronic configurations are also encoded. This necessitates the usage of chemical-inspired ansatzes (e.g. the unitary couple cluster (UCC) ansatz) that often have larger circuit depth so that the trial wavefunction only represents the states in the chemical subspace. It is still possible to use a hardware-efficient ansatz for JW encoded problems, but the number of entangling layers has to be large. With more entangling layers, the ansatz circuit would have better expressibility80 and entanglement to include the solution space81, but it may suffer from the vanishing gradient and the barren plateau problem82,83,84. Thus, we resort to a qubit-efficient encoding (QEE) method proposed in64 which provides an logarithmic saving of qubit counts (8 qubits for QEE). Additionally, QEE only encodes the physical (significant) electronic configurations such that low depth hardware-efficient ansatzes are suitable for QEE encoded problems.

Variational quantum circuits and parameter initialization

After obtaining the qubit Hamiltonian from QEE, we employ two different hardware-efficient ansatz, as illustrated in Fig. 5, for the VQE algorithm. The first hardware-efficient ansatz consists of four two-qubit entangling building blocks, and the layers are arranged in a staggered form where Fig. 5a gives an example of two hardware-efficient layers. The first ansatz used in this work consists of at most 20 layers and eight parameterized Ry rotations at each layer in the end. Therefore, the largest circuit in this form has 80 CNOT gates and 168 parameters. While for the second/alternative ansatz, each layer consists of seven CNOT gates and eight parameterized Ry rotations shown in Fig. 5b. The largest circuit in this form consists of 10 layers and has 70 CNOT gates and 80 parameters. We have also run this alternative ansatz circuit on a noisy simulator where the circuit consists of four layers and has 28 CNOT gates and 32 parameters.

Fig. 5: The hardware-efficient ansatz circuit layers used in this work.
figure 5

a Two hardware-efficient layers of the 8-qubit ansatz circuit. Note that there are single-qubit parametrized Ry rotations on all the qubits at the end of this ansatz circuit. b One hardware-efficient layer of the alternative 8-qubit ansatz circuit. Note that there is no single-qubit rotation at the end of this ansatz circuit.

Full size image

For the initial state, we have compared two initialization strategies. First, we have used the Hartree-Fock (HF) state as the initial state where all the parameters are set to zero initially64. We have also compared HF initialization with the Gaussian initialization strategy proposed in ref. 85. Zhang et al.85 proposed this Gaussian initialization strategy to escape from barren plateau where the initial parameters are sampled from a Gaussian distribution. The Gaussian distribution used in this work has a mean of 0 and a variance of 0.3.

Numerical results

We investigate the performance of our workflow with several numerical experiments. First, the CCSD energies for the full systems of the tautomers in the STO-3G basis set are calculated and are considered our benchmark for energy estimation performance. Second, energy calculations of VQE with hardware-efficient ansatz on a noiseless quantum simulator are performed for both the acetone and the Edaravone tautomers. Third, VQE energies on a noiseless quantum simulator for the acetone system using an alternative ansatz circuit are obtained. Lastly, a noisy simulation (with the noise model detailed in Supplementary Information) of the acetone system has been done using four layers of the alternative ansatz circuit.

The CCSD energies of the full systems and the active-space systems in the STO-3G basis set are computed. For the acetone system (Table 2), the full system CCSD energy of the enol form relative to the keto form is 24.070 kcal/mol, and the active-space system CCSD energy of the enol form relative to the keto form is 23.766 kcal/mol. For the Edaravone system (Table 3), the full system CCSD energy of the enol form relative to the keto form is 13.726 kcal/mol and the CCSD energy of the amine form relative to the keto form is 25.947 kcal/mol. While for active-space system of Edaravone, the CCSD energy of the enol form relative to the keto form is 9.197 kcal/mol and the CCSD energy of the amine form relative to the keto form is 25.398 kcal/mol.

Table 2 Relative ground state energies of acetone and propen-2-ol in kcal/mol calculated by CCSD and with the VQE results calculated on a noisy simulator.
Full size table
Table 3 Relative ground state energy of the keto, enol, and amine form of Edavarone in kcal/mol.
Full size table

For the VQE results of acetone shown in Fig. 6, we use two different parameter initialization strategies (Gaussian and HF) and investigate how different number of ansatz circuit layers affect VQE calculations. For acetone in Fig. 6a with 20 circuit layers using Gaussian initialization, the keto form has an error of 0.135 kcal/mol and the enol form has an error of 0.258 kcal/mol which are well below chemical accuracy (1 kcal/mol). It can be seen that more entangling ansatz layers provides lower VQE error (see Fig. 6a) and better estimations of the relative energy gaps between the keto and enol forms of acetone (see Fig. 6b). Besides, VQE calculations of active-space systems have the same trends with CCSD calculations of the full systems for the predictions of stability between the tautomers (see the dotted lines in Fig. 6b). However, for the case where initial states are HF states, the VQE results are often found to be trapped in local minimum or barren plateau. This can be clearly observed from the keto form of acetone in Fig. 6c where the final states are almost the same as the initial HF state. While for the case where Gaussian initialized parameters are used, the VQE shows faster convergence to chemical accuracy (require lower circuit depth) where only 12 circuit layers are needed to reach chemical accuracy. Also, the relative energy gaps between the keto and enol forms of acetone are not accurate when using HF intialization (see Fig. 6d).

Fig. 6: The relationship between acetone VQE results and the number of hardware-efficient ansatz layers.
figure 6

a, b are the results when Gaussian-initialized parameters are used while c and d are the results when initial states are the HF states. All the x-axes represent the number of hardware-efficient circuit layers. For a and c, the y-axes represent VQE energy errors of the keto or enol form of acetone, and the dashed lines represent chemical accuracy (Chem. Accu.). For b and d, the y-axes represent the energies relative to the keto form (so VQE energies, CCSD energies, and exact energies of the keto form are set to zero). Note that the exact energies (Exact in the legend) are the results from exact diagonalization of the active-space Hamiltonian for each tautomer, and CCSD full in the legend represents the CCSD energy of the full system relative to the keto form.

Full size image

Similar VQE results can be found in Fig. 7 for the Edavarone system. For Edaravone in Fig. 7a with 20 circuit layers, the keto form has an error of 0.730 kcal/mol, the enol form has an error of 1.006 kcal/mol, the amine form has an error of 1.168 kcal/mol which are fairly close to chemical accuracy. Figure 7a also shows that more entangling ansatz layers often provides lower VQE error and better estimations of the relative energy (Fig. 7b). For the case of HF initialization for Edavarone, the VQE errors and calculations of relative energy gaps also reach similar accuracy in Fig. 7c and Fig. 7d. However, it can still be observed that Gaussian initialization has a better convergence with respect to the number of circuit layers.

Fig. 7: The relationship between Edaravone VQE results and the number of hardware-efficient ansatz layers.
figure 7

a, b are the results when Gaussian-initialized parameters are used while c and d are the results when initial states are the HF states. All the x-axes represent the number of hardware-efficient circuit layers. For a and c, the y-axes represent VQE energy errors of the keto, enol, or amine form of Edaravone, and the dashed lines represent chemical accuracy (Chem. Accu.). For b and d, the y-axes represent the energies relative to the keto form (so VQE energies, CCSD energies, and exact energies of the keto form are set to zero). Note that the exact energies (Exact in the legend) are the results from exact diagonalization of the active-space Hamiltonian for each tautomer, and CCSD full in the legend represents the CCSD energies of the full systems relative to the keto form.

Full size image

Additionally, we tested the performance of an alternative ansatz (see Fig. 5b for a single layer) on the acetone system. The results in Fig. 8 show that the energy gap estimation has reached chemical accuracy with just 4 entangling layers (28 two-qubit gates). The circuit depth and the two-qubit gate count are reasonable for near-term quantum devices. Thus, we have run the circuit with the parameters being set at the optimal point on a noisy simulator (the noise model is based on the thermal relaxation channel with specific values listed in Supplementary Information). The results for noisy simulation can be found in Table 2 where the VQE errors and the energy gaps are found to be close to chemical accuracy.

Fig. 8: The relationship between acetone VQE results and the number of the alternative ansatz layers from the main text.
figure 8

Gaussian-initialized parameters are used. All the x-axes represent the number of hardware-efficient circuit layers. For a, the y-axis represents VQE energy errors of the keto or enol form of acetone, and the dashed line represents chemical accuracy (Chem. Accu.). For b, the y-axis represents the energies relative to the keto form (so VQE energies, CCSD energies, and exact energies of the keto form are set to zero). Note that the exact energies (Exact in the legend) are the results from exact diagonalization of the active-space Hamiltonian for each tautomer, and CCSD full in the legend represents the CCSD energy of the full system relative to the keto form.

Full size image

Discussion

In this work, we have proposed a hybrid quantum-classical workflow for the prediction of the relative stability of tautomers. It is of the pharmaceutical industry’s interest to accurately predict the preferred tautomeric state of a given molecules and its computation methodology. However, the computational requirements using classical approaches for quantum chemistry are too expensive, so we have made use of quantum simulation for electronic structure calculations.

We are aware of some studies that are making the effort to realize quantum simulation as a practical application for quantum chemistry. Recently, Tazhigulov et al.58 simulated strongly-correlated molecules that are more relevant to real world problems on Google’s Sycamore quantum processor. They mapped the electronic structures of iron-sulfur molecular clusters and α-RuCl3 into low-energy spin models using the results from theoretical and spectroscopic studies. This simplification reduced the qubit requirements and rendered the possibility of simulating larger molecules. They then used the finite-temperature version of quantum imaginary time evolution to capture physical observables. However, the circuit depth for the evolution were too large for the quantum device. Thus, they recompiled the circuit on a classical noiseless emulator, and numerous error mitigation techniques were employed. One of their experiments that used 9 qubits and 82 two-qubit gates achieved acceptable accuracy, while the data for the experiment that used 11 qubits and 310 two-qubit gates were not quantitatively meaningful. This research benchmarked the performance and limitation of quantum simulation on quantum hardware. It is, therefore, important to reduce hardware requirements of physical simulation to this limitation (e.g. using similar qubit and two-qubit gate counts).

Instead of utilizing empirical information, we have used ab initio quantum chemistry methods to reduce quantum hardware requirements. Besides, the problem of interest is to find the relative ground state energy differences rather than absolute energies or other observables, so there are more rooms for orbital reduction. First, we optimize the geometry using B3LYP. Next, we use the natural orbitals from MP2 to select active orbitals. The selection criteria includes the occupation numbers and hardware limitation. To exploit as much quantum resources, we map the reduced Hamiltonian onto fewer qubits using QEE. Finally, we simulate the molecules/tautomers with 12 active spin-orbitals using VQE with 8 qubits and 80 two-qubit gates, which is fairly close to the quantum hardware limitation from58 (9 qubits and 82 two-qubit gates). In this work, not much efforts were done on exploring the best ansatz circuit for the VQE simulation, but we have found that an alternative ansatz circuit with 28 two-qubit gates can sufficiently provide accurate VQE calculations for the acetone system. This two-qubit gate count is much fewer than the quantum hardware limitation from58 which shows the applicability of our methodology.

The VQE results for predicted stability agrees with those from full system CCSD results. For the prediction of acetone, its keto form is more stable than its enol form. For the case of Edaravone, its keto form is the most stable and its amine form is the most unstable. Note that these results did not incorporate solvent effects, which is an important factor in consideration of tautomerism in biological systems. Continuum solvation models, such as Polarizable Continuum Model (PCM)86, the Solvation Model based on Density (SMD)87 or the Conductor-like Screening Model (COSMO)88, can be used to take into account the solvent effects. For example the PCM-VQE algorithm provides a self-consistent way to include the solvent effect which does not require extra quantum resources.

The CCSD results are considered to be the solution for the comparison with VQE results since FCI is too expensive for such large systems. Nevertheless, there could be even larger systems where CCSD starts becoming intractable. This is where our hybrid quantum-classical workflow could come into play because MP2 (which provides natural orbital occupancy) is computationally cheaper than CCSD and quantum simulation has the potential of becoming a more advantageous approach.

Note that even though the VQE data are from noiseless simulator, there are still some VQE errors. The reasons could be that either the ansatz circuit could not capture the numerically true ground states or the parameter optimization stopped at local minimum or got stuck on barren plateau. Nevertheless, the errors are within chemical accuracy and does not affect the stability prediction.

The inclusion of active space selection process in this work alleviates the burden on quantum resources. Not too much has been emphasized on the selection of active space in this work. The selection of CAS is itself a sophisticated work and remains a challenge in the field89. Future work will focus on generalization of active space selection for the tautomerization process. Potential focuses could be placed on the π-orbitals since the process involves the migration of double bonds or on the atom types that are heavily involved in the tautomerization process such as N or O. Similar complete active space concept has been used for generation of tautomers by mirco-pKa predictions90. Of course a quantum device with more qubits that are less error-prone can bring value into quantum chemistry, but we are not close to achieving large-scale fault-tolerant in any architecture. As quantum computers will certainly be improved, the active orbital selection criteria can be adjusted such that more orbitals can be included. Such versatility stems from the fact that the limitation of quantum hardware is included in the selection criteria.

Given the importance of tautomerism in pharmaceutical research, our work aims to extend the applications of quantum computing in drug discovery and predictions of chemical events. To realize useful applications for quantum computers in near term, hybrid methods and reasonable classical preprocessing are necessary. On the other hand, the classical methods should be adaptable to the advancement of future quantum computers. Certain modifications on the quantum subroutines can also be done to improve the whole picture. We have employed QEE to increase the maximal number of spin-orbitals that can be simulated on limited quantum resources. Besides, to avoid the local minimum/barren plateau problem seen in this work, one could employ some parameter optimization strategies such as the initialization strategy proposed in refs. 85 and 91. One could also change the VQE subroutine to methods such as imaginary time evolution92 for better convergence or quantum algorithms with better scaling when future hardware admits.

Methods

Qubit efficient encoding

As we want to work on a larger electronic system, an encoding scheme using \({{{\mathcal{O}}}}(N)\) qubits (like JW encoding) would not be practical on current and near-future devices. Therefore, it would be suitable to resort to encoding methods using fewer qubits. Here, we choose Qubit Efficient Encoding (QEE) from ref. 64 where the qubit scales logarithmically with respect to N. This is done by only mapping particle conserving or other eletronic configurations with certain symmetries to the qubit basis states which exploits the exponential growth of qubit Hilbert space.

Since the encoding scheme works in a subspace of the space spanned by the occupation basis, we will not be able to map a single creation or annihilation operator as the operators change the number of electrons in the system. Nevertheless, the second-quantized Hamiltonian can be written as a linear combination of excitation operators, which conserve the number of particles, \({E}_{pq}\equiv {a}_{p}^{{\dagger} }{a}_{q}\) yielding

$$H=\mathop{\sum}\limits_{pq}{h}_{pq}{E}_{pq}+\frac{1}{2}\mathop{\sum}\limits_{pqrs}{h}_{pqrs}({\delta }_{qr}{E}_{ps}-{E}_{pr}{E}_{qs})$$
(4)

by using the anti-commutation relations of fermionic operators. Any excitation operator Epq can be written as \({E}_{pq}=\mathop{\sum }\nolimits_{k,k{^\prime} = 0}^{| {{{{\mathcal{F}}}}}_{m}| -1}{c}_{k{^\prime} k}^{pq}{\left\vert {{{{\bf{f}}}}}_{{{{\bf{k}}}}{^\prime} }\right\rangle }_{{{{\rm{f}}}}}{\left\langle {{{{\bf{f}}}}}_{{{{\bf{k}}}}}\right\vert }_{{{{\rm{f}}}}}\), where \({{{{\mathcal{F}}}}}_{m}\) is the set of all particle conserving (or with other symmetries) electronic configurations \({\left\vert {{{{\bf{f}}}}}_{{{{\bf{k}}}}}\right\rangle }_{{{{\rm{f}}}}}\) and \({c}_{k{\prime} k}^{pq}={\left\langle {{{{\bf{f}}}}}_{{{{\bf{k}}}}^{\prime} }\right\vert }_{{{{\rm{f}}}}}{E}_{pq}{\left\vert {{{{\bf{f}}}}}_{{{{\bf{k}}}}}\right\rangle }_{{{{\rm{f}}}}}\). \({c}_{k{^\prime} k}^{pq}\) is zero if the transition from \({\left\vert {{{{\bf{f}}}}}_{{{{\bf{k}}}}}\right\rangle }_{{{{\rm{f}}}}}\) to \({\left\vert {{{{\bf{f}}}}}_{{{{\bf{k}}}}{^\prime} }\right\rangle }_{{{{\rm{f}}}}}\) via excitation operator Epq is impossible. The coefficient \({c}_{k{\prime} k}^{pq}\) can be ± 1 according to the antisymmetric property of fermions where \({c}_{k{^\prime} k}^{pq}=\mathop{\prod }\nolimits_{i = \min (p,q)+1}^{\max (p,q)-1}{(-1)}^{{f}_{i}}\). With a transformation \({{{\mathcal{E}}}}\) that maps the selected electronic configurations one-to-one to qubit basis states in an arbitrary order, the corresponding qubit operator of Epq can be written as

$${\tilde{E}}_{pq}={{{\mathcal{E}}}}\circ {E}_{pq}\circ {{{{\mathcal{E}}}}}^{-1}=\mathop{\sum }\limits_{k,k{^\prime} =0}^{| {{{{\mathcal{F}}}}}_{m}| -1}{c}_{k{^\prime} k}^{pq}{\left\vert {{{{\bf{q}}}}}_{{{{\bf{k}}}}{^\prime} }\right\rangle }_{{{{\rm{q}}}}}{\left\langle {{{{\bf{q}}}}}_{{{{\bf{k}}}}}\right\vert }_{{{{\rm{q}}}}},$$
(5)

where \({\left\vert {{{{\bf{q}}}}}_{{{{\bf{k}}}}}\right\rangle }_{{{{\rm{q}}}}}={{{\mathcal{E}}}}{\left\vert {{{{\bf{f}}}}}_{{{{\bf{k}}}}}\right\rangle }_{{{{\rm{f}}}}}\) is the encoded qubit state of \({\left\vert {{{{\bf{f}}}}}_{{{{\bf{k}}}}}\right\rangle }_{{{{\rm{f}}}}}\) under the map \({{{\mathcal{E}}}}\). The transition between the two basis states \({\left\vert {{{\bf{q}}}}\right\rangle }_{{{{\rm{q}}}}}={\left\vert {q}_{Q-1},...,{q}_{0}\right\rangle }_{{{{\rm{q}}}}}\) and \({\left\vert {{{\bf{q}}}}^{\prime} \right\rangle }_{{{{\rm{q}}}}}={\left\vert q^{{\prime} }_{Q-1},...,{q}_{0}^{\prime} \right\rangle }_{{{{\rm{q}}}}}\) can be factorized as \({\vert {{{\bf{q}}}}^{\prime} \rangle }_{{{{\rm{q}}}}}{\langle {{{\bf{q}}}}\vert }_{{{{\rm{q}}}}}= {\bigotimes}_{k = 0}^{Q-1}{\vert q^{{\prime} }_{k}\rangle }_{{{{\rm{q}}}}}{\langle {q}_{k}\vert }_{{{{\rm{q}}}}}\). Therefore, the encoded excitation operator can be expressed as

$${\tilde{E}}_{pq}=\mathop{\sum }\limits_{k,k^{\prime} =0}^{| {{{{\mathcal{F}}}}}_{m}| -1}{c}_{k^{\prime} k}^{pq}{\left\vert {\bf{q}}_{{\bf{k}}^{\prime}} \right\rangle }_{{{{\rm{q}}}}}{\left\langle {{{{\bf{q}}}}}_{{{{\bf{k}}}}}\right\vert }_{{{{\rm{q}}}}}=\mathop{\sum }\limits_{k,k^{\prime} =0}^{| {{{{\mathcal{F}}}}}_{m}| -1}\mathop{\bigotimes }\limits_{w=0}^{{Q-1}}{c}_{k^{\prime} k}^{pq}{T}_{k^{\prime} k,w},$$
(6)

where \({T}_{k{^\prime} k,w}\) could be one of the following operators

$${Q}^{+}={\left\vert 1\right\rangle }_{{{{\rm{q}}}}}{\left\langle 0\right\vert }_{{{{\rm{q}}}}}=\frac{1}{2}(X-iY),$$
(7)
$${Q}^{-}={\left\vert 0\right\rangle }_{{{{\rm{q}}}}}{\left\langle 1\right\vert }_{{{{\rm{q}}}}}=\frac{1}{2}(X+iY),$$
(8)
$${N}^{(0)}={\left\vert 0\right\rangle }_{{{{\rm{q}}}}}{\left\langle 0\right\vert }_{{{{\rm{q}}}}}=\frac{1}{2}(I+Z),$$
(9)
$${N}^{(1)}={\left\vert 1\right\rangle }_{{{{\rm{q}}}}}{\left\langle 1\right\vert }_{{{{\rm{q}}}}}=\frac{1}{2}(I-Z)$$
(10)

according to the qubit basis state transitions.

As each operator \({T}_{k{^\prime} k,w}\) is a sum of two Pauli operators, this allows us to express the qubit Hamiltonian

$${H}_{{{{\rm{q}}}}}=\mathop{\sum}\limits_{pq}{h}_{pq}{\tilde{E}}_{pq}+\frac{1}{2}\mathop{\sum}\limits_{pqrs}{h}_{pqrs}({\delta }_{qr}{\tilde{E}}_{ps}-{\tilde{E}}_{pr}{\tilde{E}}_{qs})$$
(11)

as a sum of Pauli operator strings. With the Hamiltonian in Pauli strings, the energy expectation value can be obtained using a quantum computer. In this work, we select electronic configurations that are particle-conserving and singlet so we reduce the qubit requirement from 12 qubits to 8 qubits. In the original QEE paper, the authors discovered that the number of qubit Hamiltonian terms is bounded as follows: when \(m\le \frac{N}{2}\), the upper bound is \({{{\mathcal{O}}}}(\frac{{N}^{2m+1}}{(m-1)!\,m!})\) and when \(m\, > \frac{N}{2}\), the upper bound is \({{{\mathcal{O}}}}(\frac{{N}^{2(N-m)+1}}{(N-m-1)!\,(N-m)!})\) Here, N represents the number of spin-orbitals, and m represents the number of electrons. It is worth noting that this scaling is generally higher than \({{{\mathcal{O}}}}({N}^{4})\) for JW encoding. Nevertheless, the authors present several scenarios in which QEE yields significant reductions in qubit counts while maintaining similar or even fewer numbers of Hamiltonian terms. The QEE paper provides use cases where 4 to 8 qubits are utilized after obtaining the QEE Hamiltonian, which is also the case for this work.

Variational parameter optimization

For noiseless VQE simulation, the statevector simulator from Qiskit was used, and the classical optimization of the variational parameters was done using the Sequential Least Squares Programming (SLSQP) method with 50k iterations. For noisy VQE simulation, the statevector simulator from Qiskit was used with 100k measurement shots per circuit. There is no classical optimization of the variational parameters for noisy simulation as we use the optimal circuit parameters from noiseless simulation.