A holographic duality from lifted tensor networks

Abstract

Tensor networks provide an efficient classical representation of certain strongly correlated quantum many-body systems. We present a general lifting method to ascribe quantum states to the network structure itself that reveals important new physical features. To illustrate, we focus on the multiscale entanglement renormalization ansatz (MERA) tensor network for 1D critical ground states on a lattice. The MERA representation of the said state can be lifted to a 2D quantum dual in a way that is suggestive of a lattice version of the holographic correspondence from string theory. The bulk 2D state has an efficient quantum circuit construction and exhibits several features of holography, including the appearance of horizon-like holographic screens, short-ranged correlations described via a strange correlator and bulk gauging of global on-site symmetries at the boundary. Notably, the lifting provides a way to calculate a quantum-corrected Ryu–Takayanagi formula, and map bulk operators to boundary operators and vice versa.

Introduction

In recent years, there has been a push to understand the celebrated anti-de Sitter/conformal field theory (AdS/CFT) correspondence^1,2, a concrete realization of the so-called holographic principle, from the perspective of quantum information theory. In particular, some aspects of the AdS/CFT have been realized using tensor network descriptions of ground states of critical quantum many-body systems. It was first suggested by Swingle in ref. ³ that the multiscale entanglement renormalization ansatz (MERA)^4,5, a particular tensor network suited to describing critical ground states, might also be viewed as a spatial slice of a holographic AdS spacetime. Since then, several other holographic interpretations have been presented both of the MERA and other related tensor networks, see e.g. refs. ^{6,7,8,9,10,11,12,13,14,15}. Even in the absence of general consensus yet on how the MERA realizes holography, one basic lesson is more or less apparent: a given MERA representation can be interpreted in dual (even several) ways.

Several approaches have been suggested to realize the construction of bulk quantum mechanical states that are dual to boundary theories and carry bulk degrees of freedom (DOFs). Most of these programmes can be fit into one of three approaches: (1) holographic codes, including matchgate tensor networks^10,16, (2) random tensor network/random stabilizer bulk states¹⁷ or (3) exact holographic mappings^11,12,18. Each of these approaches carry their own advantages and disadvantages; however, a particular limitation of the first two approaches is that neither of them allow you to dial in an arbitrary CFT on the boundary (matchgate tensor networks do allow for encoding fermionic CFTs). On the other hand, since the third approach is an exact mapping, it is not an efficient representation of the boundary CFT. We focus on a method that naturally allows for both of these features, a programme we began in our recent work^14,15, and demonstrate how we may modify our lifting procedure to obtain several missing features that are required for a unified description of the holographic principle through tensor networks.

In this work, we describe how the MERA description of $\left|\Psi \right\rangle$ can be ‘lifted’ to a 2D quantum state $\left|{\Psi }^{({\rm{lift}})}\right\rangle$. In this lifting construction, two new physical bulk DOFs are introduced on each bond of the tensor network using a lifting tensor. If this is done with lifting tensors that simply copy virtual bonds to the new bulk DOFs (Such as was done in our prior work^14,15), one obtains a bulk state that is dependent on the basis of the copy tensor in which the information is promoted to the bulk. Our key insight is to choose the lifting tensor to be an intertwiner. This means that equivalent MERA representations related by a basis change along a bond give rise to lifted states that vary only by on-site unitary transformations—thus, they all have the same entanglement properties. Therefore, we may associate a unique 2D entanglement structure to each 1D critical MERA state, and thus obtain a strict correspondence between the boundary/bulk entanglement properties.

By virtue of our construction defining a unique 2D entanglement structure, we can analytically derive the Ryu–Takayanagi formula $\left|{\Psi }^{{\rm{(lift)}}}\right\rangle$ from bulk entropic quantities. (In our previous work this was only done numerically). In addition, this insight gives rise to a mapping of bulk operators to boundary operators and vice versa.

Finally, the original MERA, $\left|\Psi \right\rangle$ can be recovered from our lifted MERA, $\left|{\Psi }^{({\rm{lift}})}\right\rangle$, by a series of local projections. Due to the lifted MERA having only short-ranged entanglement, this process can be viewed as a strange correlator. Namely, this is an overlap between a 2D quantum state $\left|{\Psi }^{({\rm{lift}})}\right\rangle$ with short-range entanglement and a 2D product state, suggesting that the strange-correlator construction could be useful as a bulk description in a holographic interpretation of the MERA.

Results

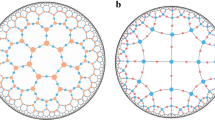
We consider a MERA tensor network that defines a class of a quantum many-body states on an infinite one-dimensional lattice, see Fig. 1a. The MERA is particularly well suited to describe critical ground states¹⁹. Given a critical Hamiltonian, the approximate MERA representation of its ground state can be obtained, e.g. by a variational energy minimization algorithm²⁰, and the approximation can be made more accurate by increasing $\chi$ (which increases the number of variational parameters). Given the MERA representation of a 1D critical ground state $\left|\Psi \right\rangle$, we lift it to a 2D quantum state $\left|{\Psi }^{({\rm{lift}})}\right\rangle$ by inserting a 4-index lifting tensor $t$ in the middle of each bond of the MERA, as shown in Fig. 1c. During this insertion, one pair of indices from $t$ are connected to the ends of the split bond, while the other pair add new DOFs in the bulk. Note that this construction is quite general and in fact can be done for any tensor network rather than just the MERA tensor network (However, many of the holographic features to follow rely on additional structure from the MERA, and so will not appear for an arbitrary tensor network.). We require that the lifting tensor $t$ fulfils some reasonable axioms that are depicted in Fig. 1d. The first axiom allows us to reverse the lifting and recover a properly normalized boundary state: $\left|{\Psi }^{({\rm{lift}})}\right\rangle \to \left|\Psi \right\rangle$ by local bulk projectors onto unnormalized singlets $\left|+\right\rangle ={\sum }_{j = 1}^{\chi }\left|j\right\rangle \left|j\right\rangle$, that is

$$|\Psi \rangle =\left(\mathop{\otimes }\limits_{{\rm{all}}\,{\rm{bulk}}\,{\rm{sites}}}\eta {\sqrt{\chi }}^{-1}\langle +|\right)|{\Psi }^{({\rm{lift}})}\rangle .$$

(1)

We have introduced a new parameter $\eta \,\ne\, 0$, which we call the tuning parameter, to capture the rescaling freedom that is not fixed by any of our physical considerations. The second axiom ensures $\left|{\Psi }^{({\rm{lift}})}\right\rangle$ is a normalized quantum state. It corresponds to demanding that the lifting tensor is isometric (Therefore, just like the MERA, the lifted MERA may also be expressed as a quantum circuit with a bounded-width causal cone. This, in particular, implies that the expectation value of local observables can be computed efficiently from the lifted MERA, along with being the basis of the holographic screen property). The third axiom, additional to the axioms assumed in refs. ^14,15, ensures that $\left|{\Psi }^{({\rm{lift}})}\right\rangle$ is covariant under a change of basis of the original tensor representation of the MERA by a unitary $U$ acting on the fundamental representation of $U(\chi )$. This axiom implies that the lifting tensor is an intertwiner of $U(\chi )$ that heavily constrains the structure of the lifting tensor to a canonical form (see the section ‘Proof of canonical form for the lifting tensor’ in Methods).

(2)

The numbers at the end of each index, including those with tildes, are simply labels here for each index. Taking this solution, the other two lifting axioms imply

$$\sqrt{\chi }\alpha +{(\sqrt{\chi })}^{3}\beta =\sqrt{\chi }{\eta }^{-1},$$

(3)

$$(| \alpha {|}^{2}+| \beta {|}^{2}){\chi }^{2}+(\alpha {\beta }^{* }+{\alpha }^{* }\beta )\chi =1,$$

(4)

where $\eta$ is the tuning parameter from the first lifting axiom, Fig. 1d(i). Assuming $\alpha$ and $\beta$ are real and positive yields solutions

$$\alpha =\sqrt{\frac{1-{\eta }^{-2}}{{\chi }^{2}-1}},\qquad \beta =\frac{\sqrt{{\chi }^{2}-1}-\eta \sqrt{1-{\eta }^{-2}}}{\eta \chi \sqrt{{\chi }^{2}-1}}.$$

(5)

where we find that the parameters are bounded by the bond dimension $\chi$: $1\le \eta \le \chi$ and $0\le \alpha ,\beta \le {\chi }^{-1}$. These values correspond to a legitimate choice ${t}^{(\alpha ,\beta )}$ for the lifting tensor. A 2D bulk state is defined by choosing a lifting tensor from this domain; different lifting tensors correspond to different bulk states.

Fig. 1: The MERA and lifted MERA tensor networks.

a A patch of an infinite MERA tensor network, which describes a quantum-critical ground state $\left|\Psi \right\rangle$ on an infinite lattice ${\mathcal{L}}$ as follows. Each open index $i$ at the boundary of the tensor network is associated with a site of ${\mathcal{L}}$ and labels an orthonormal basis $\left|i\right\rangle$ on the site. For a given basis state of the lattice, the open indices are fixed to the corresponding values, which yield a closed tensor network. The latter can be contracted to obtain a complex number, which is the amplitude of the basis state in $\left|\Psi \right\rangle$. For simplicity, we assume that each index of the tensor network runs over $\chi$ values. The tensor network is made of two types of tensors, illustrated here $u$ and $w$. b All tensors are isometries and fulfil the constraints shown here. c The lifted MERA—that describes a 2D quantum state $\left|{\Psi }^{({\rm{lift}})}\right\rangle$—is obtained by inserting a 4-index ($\chi \times \chi \times \chi \times \chi$) lifting tensor $t$ on each bond of the MERA. d The lifting tensor $t$ is required to satisfy the axioms shown described in the text.

As is well known, the MERA description of a quantum state of size $| {\mathcal{L}}|$ can be described as a unitary circuit of depth $\mathrm{log}\,(| {\mathcal{L}}| )$ acting on input ${\left|0\right\rangle }^{\otimes |{\mathcal{L}}|}$, where the unitary tensors are unitary gates and the isometric tensors can be extended to a unitary gate with fixed input $\left|0\right\rangle$ or ${\left|0\right\rangle }^{\otimes 2}$ for the trinary MERA, see Fig. 1a⁵. The same is true for the lifted MERA. The reason being that by the second lifting axiom, see Fig. 1d(ii), the lifting tensor is an isometry from index $\tilde{1}$ to indices 1, 2, 3, see Eq. (2). Thus, any unitary extension, adding axillary indices $\tilde{2}$ and $\tilde{3}$, of the map ${\left|j\right\rangle }_{\tilde{1}}{\left|0\right\rangle }_{\tilde{2}}{\left|0\right\rangle }_{\tilde{3}}\,\mapsto\, \chi \alpha {\left|j\right\rangle }_{1}{\left|{\Phi }^{+}\right\rangle }_{2,3}+\chi \beta {\left|{\Phi }^{+}\right\rangle }_{1,2}{\left|j\right\rangle }_{3}$, where $\left|{\Phi }^{+}\right\rangle$ is the Bell state, will suffice. From this, one may construct a quantum circuit generating the lifted MERA with the same circuit complexity as the MERA.

Correlation functions

Now, we turn to the physical properties of the lifted MERA state that are distinct from the MERA. The MERA has polynomially decaying correlation functions; this behaviour is one of the reasons that the MERA is viewed as a good tensor network to approximate critical theories. In contrast, the lifted MERA has exponentially decaying correlation functions. To see this first, consider the bulk correlator ${\langle \langle {O}_{A}{O}_{B}\rangle \rangle }_{\text{spine}}$ of two operators ${O}_{A}$ and ${O}_{B}$ (each acts on a pair of bond sites) that are located deep in the bulk along the ‘spine’ of the lifted MERA, see Fig. 2a. Thanks to the facts that MERA tensors $u,w$ are isometries by construction⁵, and by the second lifting axiom, the tensor $t$ is also an isometry (from index $\tilde{1}$ to indices 1, 2, 3), ${\langle \langle {O}_{A}{O}_{B}\rangle \rangle }_{\text{spine}}$ will depend only on the tensors that are located along the spine of the lifted MERA (and the corresponding tensors along the spine of the conjugate-lifted MERA). All the remaining tensors cancel out with their complex conjugate transpose, see Fig. 2b. Thus, we obtain the closed-form expression

$${\langle \langle {O}_{A}{O}_{B}\rangle \rangle }_{\text{spine}}\equiv {\text{Tr}}\,\left({\rho }^{({\rm{1}})}{T}_{A}[{T}^{\ell }[{T}_{B}]]\right)-\langle {O}_{A}\rangle \langle {O}_{B}\rangle$$

(6)

where ${T}_{A},\,{T}^{\ell },\,{T}_{B}$ are defined as shown in Fig. 2c–e, operators ${O}_{A}$ and ${O}_{B}$ act on bulk sites that are separated by $\ell$ sites and ${\rho }^{({\rm{1}})}$ is the reduced density matrix of one bulk site, $s$, located below a spine in the MERA. For any chosen $w$ the transfer matrix $T$ has dominated eigenvalue ${\lambda }_{\max }=1$. The corresponding eigenvector, $\left|{\lambda }_{\max }\right\rangle$, we may now use in place of the spine and everything above. In addition, for large $\ell$, ${(T)}^{\ell }\approx \left|{\lambda }_{\max }\right\rangle \left\langle {\lambda }_{\max }\right|$ is a projector onto this dominant eigenvector. This means that the decay of correlations is controlled by the largest eigenvalue <1, most commonly the second largest eigenvalue ${\lambda }_{2}\,<\,1$, and we have ${\langle \langle {O}_{A}{O}_{B}\rangle \rangle }_{\text{spine}}=O({\lambda }_{2}^{\ell })$. Thus, correlations decay exponentially along the spine with a correlation length $\xi =1/\mathrm{ln}\,({\lambda }_{2}^{-1})$.

Fig. 2: The two-point correlation function in the bulk along the horizontal and vertical directions.

a A ‘spine’ of the lifted MERA, comprising a 1D chain of $w$-tensors. An infinite number of arbitrarily long spines can be located in the infinite lifted MERA. b Tensor network expression, Eq. (6), for the 2-point correlator of two operators ${O}_{A}$ and ${O}_{B}$ (each acts on a pair of bond sites) that are located deep along the spine. c–e Definitions of $T,\,{T}_{A},\,{T}_{B}$ that appear in Eq. (6). f Tensor network expression, Eq. (7), excluding subtraction for local terms $\langle {O}_{rmA}\rangle \langle {O}_{rmB}\rangle$. In this expression, operators ${O}_{A}$ and ${O}_{B}$ are located at the same depth in the bulk, but are now separated along the horizontal direction by a geodesic distance $L=2\ell$. Here also ${O}_{A}$ and ${O}_{B}$ are each located at the base of a spine section of the tensor network.

Next, consider a 2-point correlator ${\langle \langle {O}_{A}{O}_{B}\rangle \rangle }_{\text{horizontal}}$ of operators ${O}_{A}$ and ${O}_{B}$ that are located at the same depth in the bulk, but are now separated by a distance $L$ along the horizontal direction. Here $L$ is the length of the geodesic between ${O}_{A}$ and ${O}_{B}$. For simplicity, let us also assume that ${O}_{A}$ and ${O}_{B}$ are each located at the base of a spine section of the tensor network, and the two spines converge to two neighbouring sites $s,s+1$ as we look deeper into the bulk. Once again, the correlator has a closed-form expression (see Fig. 2f where $L=2\ell$)

$$\begin{array}{l}{\langle \langle {O}_{A}{O}_{B}\rangle \rangle }_{\text{horizontal}}\equiv \,{\text{Tr}}\,\left({\rho }^{(2)}\left[({T}^{\ell }[{T}_{A}])\otimes ({T}^{\ell }[{T}_{B}])\right]\right)\,-\,\langle {O}_{A}\rangle \langle {O}_{B}\rangle \end{array}$$

(7)

where ${\rho }^{(2)}$ is the reduced density matrix of a pair of bulk sites located at neighbouring sites $s$ and $s+1$, and $T$ is the same transfer matrix that appears in Eq. (6). Once again, we find that the correlator ${\langle \langle {O}_{A}{O}_{B}\rangle \rangle }_{\text{horizontal}}$ decays exponentially as ${\langle \langle {O}_{A}{O}_{B}\rangle \rangle }_{\text{horizontal}}=O({\lambda }_{2}^{\ell })$.

Here we considered bulk sites located along spines for convenience. The above arguments can be easily generalized for any pair of bulk locations; the closed-form expressions for 2-point correlators away from spines are more complicated and also involve the $u$-tensors. Thus, we find that the bulk correlations decay exponentially in any direction. Note that the reason for the polynomial decaying correlations in the MERA is due to the correlation functions decaying exponentially with respect to the tensor network length (going roughly as the logarithm of the boundary distance); this is equivalent to a polynomial decaying correlation function in the boundary distance.

Strange correlators

The qualitatively different structure of correlations in the MERA and lifted MERA can be understood in terms of a strange correlator. As introduced in ref. ²¹, a strange correlator is a classical partition function with algebraically decaying correlations that are obtained as the overlap of a quantum state with exponentially decaying correlations and a product state. By construction, Eq. (1), the critical MERA state $\left|\Psi \right\rangle$ is recovered by taking the overlap of the short-range correlated lifted MERA state $\left|{\Psi }^{({\rm{lift}})}\right\rangle$ with the product state $({\otimes }_{{\rm{all}}\,{\rm{bulk}}\,{\rm{sites}}}\left\langle +\right|)$. Thus, the MERA viewed in this way bears a striking resemblance with a strange correlator. The difference is that a strange correlator is a partition function, a number, while the MERA is a critical quantum state. However, an infinite critical MERA, which we have considered here, can also be understood as a critical partition function: either as a Euclidean path integral on a 2D light-cone geometry of a 1D critical quantum system^22,23, or as a 2D classical partition function ${Z}_{{\rm{crit}}}$, albeit with complex Boltzmann weights²⁴, once we take an additional overlap with a fixed 1D product state $({\otimes }_{{\rm{all}}\,{\rm{boundary}}\,{\rm{sites}}}\left\langle {+}_{x}\right|)$, where $\left|{+}_{x}\right\rangle ={\sum }_{j = 1}^{\chi }\left|j\right\rangle$; for sites with bond dimensions less than $\chi$ we sum only upto the bond dimension in $\left|{+}_{x}\right\rangle$. Thus, we obtain

$$\left(\mathop{\otimes }\limits_{{\rm{all}}\,{\rm{boundary}}\,{\rm{sites}}}\langle {+}_{x}|\right)\left(\mathop{\otimes }\limits_{{\rm{all}}\,{\rm{bulk}}\,{\rm{sites}}}\langle +|\right)|{\rm{\varPsi}} {\rangle }^{({\rm{lift}})}\propto {Z}_{{\rm{crit}}}.$$

(8)

Holographic screens

In the rest of the paper, we show that the lifted MERA encapsulates the essential properties of holography. First, we demonstrate that a novel feature of the lifted MERA, first observed in ref. ¹⁴, is the appearance of holographic screens. A holographic screen is a codimension one surface (the ‘screen’) in the bulk that carries all information contained in the region enclosed between the surface and the boundary. (Even if DOFs inside this region are lost, all its information remains intact on the enclosing screen.) Consider, for example, the path ${\gamma }_{A}^{{\rm{virtual}}}$ shown in Fig. 3, which encloses the two-dimensional wedge $W[A]$. We have

$${\rho }_{W[A]}^{{\rm{bk}}}={R}^{\dagger }{\rho }_{A}^{{\rm{virtual}}}R.$$

(9)

where ${\rho }_{W[A]}^{{\rm{bk}}}$ is the reduced state of all the bulk sites inside the wedge $W[A]$, $R$ is the tensor obtained by contracting all the tensors inside the wedge and ${\rho }_{A}^{{\rm{virtual}}}$ is the reduced density matrix of the virtual DOFs associated with the bonds that are intersected by the path ${\gamma }_{A}^{{\rm{virtual}}}$. Here $R$ is an isometry, namely $R{R}^{\dagger }={1}_{d}$ where $d={\chi }^{\left|{\gamma }_{A}^{{\rm{virtual}}}\right|}$ (since all the tensors inside the wedge are isometries). Equation (9) also implies that the traces of moments of the two reduced states are equal; thus, there Von Neumann entropies are equal: $S({\rho }_{{\gamma }_{A}}^{{\rm{virtual}}})=S({\rho }_{W[A]}^{{\rm{bk}}})$. While this illustrates how the information in a two-dimensional wedge is encoded on a codimension one surface ${\rho }_{{\gamma }_{A}}^{{\rm{virtual}}}$, the latter is not physically accessible from the bulk. Thus, we refer to ${\rho }_{{\gamma }_{A}}^{{\rm{virtual}}}$ as a virtual holographic screen.

Fig. 3: The path ${\gamma }_{A}$ indicates DOFs of a holographic screen on a lifted state $\left|{\Psi }^{({\rm{lift}})}(\eta )\right\rangle$ that follows a dual geodesic connecting the end points of the boundary region $A$.

The bulk DOFs located just outside the 1D path carry all the information contained within the wedge $W[A]$ when $\eta ={\eta }_{{\rm{Holo}}}$, but are also recovered for any $\eta$ if the corresponding bulk sites along ${\gamma }_{A}$ are slightly modified by applying a simple filtering operation, as described in the section ‘Holographic screen’ in Methods. On the other hand, virtual holographic screens, such as ${\gamma }_{A}^{{\rm{virtual}}}$, exist in the lifted MERA for any value of $\eta$ with no modification. But because these screens are associated with virtual DOFs associated with the bonds of the lifted MERA, they are not physically accessible.

Remarkably, for the unique value $\eta ={\eta }_{{\rm{Holo}}}\equiv \sqrt{2\chi }/\sqrt{\chi +1}$, which corresponds to fixing $\alpha =\beta$ in Eq. (2), the inaccessible state ${\rho }_{{\gamma }_{A}}^{{\rm{virtual}}}$ is exactly equal to the reduced state ${\rho }_{{\gamma }_{A}}^{{\rm{bk}}}$ of the physical sites located along a path ${\gamma }_{A}$ that closely follows the virtual screen as shown in Fig. 3. See the section ‘Holographic screen’ in Methods for details. Thus we have

$$S\left({\rho }_{{\gamma }_{A}}^{{\rm{bk}}}\right)=S\left({\rho }_{{\gamma }_{A}}^{{\rm{virtual}}}\right)=S\left({\rho }_{W[A]}\right),$$

(10)

Furthermore, for any physical local observable ${O}_{W[A]}$ in $W[A]$ one can determine a local observable ${O}_{{\gamma }_{A}}^{{\rm{bk}}}\equiv R{O}_{W[A]}{R}^{\dagger }$ that clearly has the same expectation value as ${O}_{W[A]}$ but is supported only on the sites located along ${\gamma }_{A}$. We refer to ${\gamma }_{A}$ as the physical holographic screen, or simply holographic screen.

More generally, a holographic screen is any path through the lifted network between the end points of a boundary interval that is generated by the greedy algorithm introduced in the section ‘Holographic screen’ in Methods. A holographic screen cuts through only lifting tensors, separating the two DOFs associated with each lifting tensor site; however, only the outside DOFs constitute the physical DOFs of the holographic screen ${\gamma }_{A}$. The greedy algorithm ensures that all the tensors inside the wedge constitute an isometry mapping from ${\gamma }_{A}^{{\rm{virtual}}}$ to $W[A]$, which leads to the holographic screen property. We remark that the construction of screens via this greedy algorithm and the ability to map bulk operators onto the enclosing screen appears similar to the construction of holographic codes by Harlow et al.¹⁰.

For a given boundary interval A, we can use a greedy algorithm to construct a maximal holographic screen, the screen with the maximal number of tensors in $W[A]$ for some region $A$. We find that the length of the maximal screen can be bounded by a constant multiple of the traditional geodesic path between the end points of region $A$ (see Supplementary Methods Sec. II). Later, we will exploit this property as motivation to assign a physical distance between bulk sites through the maximal holographic screen and to derive a Ryu–Takayanagi-like formula.

Bulk-boundary correspondence

Second, we show that bulk operators can be mapped to boundary operators and vice versa via a series of tensor contractions and expansions. The conceptual idea is illustrated by the invertible maps in Fig. 4. Using this, it becomes clear that any operator on the boundary can be slowly shifted with an effective boundary towards the centre of the MERA, making use of type (ii) to (iii) conversions and contractions with the original MERA tensors. After moving the effective boundary to just below the point of interest, we can move the operator on the effective boundary to the bulk sites, using a type (i) to (iii) conversion, then reconstruct everything below to recover the original bulk MERA quantum state (We exploit the isometry properties of the MERA and lifting tensors in order to reconstruct the spatial region that was contracted over as the boundary operator was inched up into the bulk.). Similarly, we may reverse the process by first contracting the effective boundary upto the bulk site before slowly reconstructing the bulk MERA above the operator of interest. The reconstruction was done via insertions of identity (of the original MERA tensors and their inverses), the unwanted tensors are then contracted with the operators, which act to smear the operator out and conversions of type (ii) to (i) are used to insert $t$ tensors. This process smears the bulk operator out across the region of the boundary that was reconstructed.

Fig. 4: Graphical equations indicating interconvertability of operators: (i) boundary type with lifting $A$, (ii) boundary type without lifting $B$ and (iii) bulk type $C$.

Arrows indicate that the operator of one type may be transformed into the other type, the top row of these is obvious where any $A$ or $C$ there exists as an operator $B$ (via tensor contraction). The opposite directions are less obvious but turn out to be possible using the basis-independent lifting tensors (which was not the case in refs. ^14,15 because of the fixing of the basis).

This method can be used to compute bulk operators corresponding to scaling field operators of the boundary CFT. Consider a scale-invariant, single-site, operator $B$ with scaling dimension $\Delta$ on the original trinary MERA. The scale invariance means that ${C}_{W}[B]={3}^{-\Delta }B$, where ${C}_{W}[\cdot ]$ denotes the contraction map with a single copy of both the scale-invariant isometric tensor of the MERA, $w$, and its dual, ${w}^{\dagger }$. This map is sometimes referred to as the single-site scaling super-operator in the literature¹⁹. This operator can be modified to retain this property on the bulk sites by first defining the analogous boundary operator for the lifted MERA, ${O}^{(B)}=B+bI$ where $b=\frac{{3}^{-\Delta }{\rm{Tr}}(B)| \alpha {|}^{2}\chi }{{3}^{-\tilde{\Delta }}-1}$. This operator is scale invariant with respect to the composition of contraction by the same MERA isometries followed by the contraction map, $L$, which contracts the operator with lifting tensors. This leads to $L\circ {C}_{W}[{O}^{B}]={3}^{-\tilde{\Delta }}{O}^{B}$ where the shifted scaling dimension is

$$\tilde{\Delta }=\Delta -{\mathrm{log}\,}_{3}(1-| \alpha {|}^{2}{\chi }^{2}).$$

(11)

Using a type (i) to (iii) conversion, the corresponding bulk operator is

$${O}_{{\rm{bulk}}}^{(B)}=\frac{{O}^{(B)}-{\beta }^{2}\chi {\rm{Tr}}({O}^{(B)})I}{1-| \beta {|}^{2}{\chi }^{2}}.$$

(12)

This bulk operator can be moved a distance $k$ vertically along the spine of the lifted MERA, leaving the expectation value with respect to $\left|{\Psi }^{({\rm{lift}})}\right\rangle$ invariant up to a factor ${3}^{-k\tilde{\Delta }}$. Supplementary Methods Sec. III contains the full details for mapping operators in either direction of this bulk-boundary operator correspondence.

Gauge symmetries

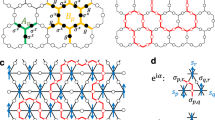
In AdS/CFT, a global on-site symmetry in the boundary description generally corresponds to a local gauge symmetry in the bulk. Here we show how our construction can be generalized to implement this feature by introducing a symmetric lifting tensor. Our construction follows closely that presented in ref. ¹⁵, but here we additionally incorporate basis independence on subspaces that are left unconstrained by the symmetry. Consider that the state $\left|\Psi \right\rangle$, which is represented by a MERA, has a global on-site symmetry described by group ${\mathcal{G}}$, namely, $\left|\Psi \right\rangle =({\otimes }_{s\in {\mathcal{L}}}{U}_{g}^{[s]})\left|\Psi \right\rangle$ for all $g\in {\mathcal{G}}$ where ${U}_{g}^{[s]}$ is a unitary representation of group element $g$ acting on-site $s$ of the lattice and ${U}_{g}^{[s]}={U}_{g}$ for all $s$. It turns out that under reasonable assumptions²⁵, if the global on-site symmetry is to be preserved at all renomalization scales, then the MERA representation of $\left|\Psi \right\rangle$ necessarily consists of tensors that commute with ${\mathcal{G}}$ as depicted in Fig. 5a (for sufficiency see also refs. ^26,27). It is natural to express the MERA tensors and the lifting tensor in the symmetry basis, in which ${U}_{g}$ (or equivalently the vector space ${\mathbb{V}}$ on which it acts) decomposes as the direct sum of irreducible representations (irreps) as in ref. ²⁶

$${\mathbb{V}}={\mathop \oplus\limits_{j}}{{\mathbb{D}}}_{j}\otimes {{\mathbb{V}}}_{j},\ \ {U}_{g}={\mathop\oplus \limits_{j}}{I}_{\text{dim}({{\mathbb{D}}}_{j})}\otimes {U}_{g,j}.$$

(13)

Here ${{\mathbb{D}}}_{j}$ is the degeneracy space of irrep space ${{\mathbb{V}}}_{j}$, ${U}_{g,j}$ denotes the unitary corresponding to group element $g$ acting on the irrep space ${{\mathbb{V}}}_{j}$. (Notice that the symmetry acts as the identity ${I}_{\text{dim}({{\mathbb{D}}}_{j})}$ on the degeneracy space.) In order to make the symmetry manifest in our construction, we fix the symmetry basis $\left|j,{t}_{j},{m}_{j}\right\rangle =\left|j{t}_{j}\right\rangle \otimes \left|j{m}_{j}\right\rangle$ on each bond, where $\left|j{t}_{j}\right\rangle$ and $\left|j{m}_{j}\right\rangle$ are the basis in the degeneracy space ${{\mathbb{D}}}_{j}$ and irrep space ${{\mathbb{V}}}_{j}$, respectively. We are still free to choose any basis in the degeneracy spaces since the symmetry acts trivially there. In order to generalize our construction to lift a symmetric MERA (a symmetric MERA representation of a ground state can be obtained by using the variational energy minimization algorithm adapted to the presence of the symmetry. This algorithm outputs a MERA composed of symmetric tensors and the bond irreps, and their degeneracies, that characterize the ground state, see, e.g. ref. ²⁷)—a MERA composed of tensors that commute with ${\mathcal{G}}$—we replace the lifting tensor $t$ with the symmetric lifting tensor ${t}^{{\rm{sym}}}$ as defined in Fig. 5b. It can be readily checked that ${t}^{{\rm{sym}}}$ satisfies the symmetries depicted in Fig. 5c, which in turn imply that the bulk state has a local gauge symmetry—as generated by the elementary gauge transformations depicted in Fig. 5d, e. When the symmetry group ${\mathcal{G}}$ is set to identity, the symmetric lifting tensor ${t}^{{\rm{sym}}}$ reduces to the non-symmetric version $t$.

Fig. 5: The local bulk gauging of a global on-site symmetry around a vertex.

a In a MERA representation of a state that has a global on-site symmetry ${\mathcal{G}}$, all the tensors can be chosen to commute with the symmetry as shown here; g succinctly denotes a unitary representation of $g\in {\mathcal{G}}$. b We use the symmetric lifting tensor defined as shown here for lifting a symmetric MERA (composed from tensors satisfying panel a). Here within a given irrep $j$, ${t}_{j}^{{\rm{sym}}}$ is a non-symmetric lifting tensor tuned by a parameter ${\eta }_{j}$, ${\varkappa }_{j}$ is the Frobenius–Schur indicator and ${d}_{j}$ is the dim(${{\mathbb{V}}}_{j}$) in Eq. (13). c Symmetries of the symmetric lifted tensor. d An elementary $w$-gauge transformation—e.g. tensor product of group unitaries acting on bulk sites located immediately around a $w$ tensor—leaves the bulk state invariant as shown. The left and right equalities are obtained by applying panels c and a, respectively. e Similarly, an elementary $u$-gauge transformation leaves the bulk state invariant.

Ryu–Takayangi formula

In the AdS/CFT correspondence, the celebrated Ryu–Takayanagi formula²⁸ relates the entanglement entropy of a region in the boundary vacuum to the area of the minimal surface that subtends from the region into the bulk. In particular, for 1+1D CFTs, the entanglement entropy of a region $A$ in the vacuum is proportional to the length ${L}_{{\gamma }_{A}^{{\rm{geo}}}}$ of the geodesic path ${\gamma }_{A}^{{\rm{geo}}}$ between the end points of $A$ through a spatial slice of the dual bulk AdS${}_{2+1}$ spacetime:

$$S({\rho }_{A}^{{\rm{CFT}}})=\frac{c}{3}{\log}\,(| A| )=\frac{{L}_{{\gamma }_{A}^{{\rm{geo}}}}}{4{G}^{(2)}}.$$

(14)

Here $c$ is the CFT central charge, ${G}^{(2)}$ is Newton’s constant in 2-space dimensions and $| A|$ is the length of region $A$ in the flat metric of the boundary CFT. It is important to note that Eq. (14) is the semi-classical Ryu–Takayanagi formula. If instead we have quantum gravity in the bulk Eq. (14) is replaced with $S({\rho }_{A}^{{\rm{CFT}}})=\frac{{L}_{{\gamma }_{A}^{{\rm{geo}}}}}{4{G}^{(2)}}+Q$ where $Q$ is the 1-loop additive correction given by the entanglement entropy between the DOFs located inside and outside of the geodesic²⁹.

Previous work using unlifted MERA³ has connected boundary entropy and bulk geodesics via the quantity $| {\gamma }_{A}| \mathrm{log}\,(\chi )$, which depends exclusively on the numerical parameter $\chi$. However, from the result of Brown and Henneaux³⁰, the radius of curvature of semi-classical AdS${}_{3}$ space is proportional to the central charge according to $c=3R/2{G}^{(2)}$ and so we would expect the geodesic lengths to vary with theoretical quantity $c$ rather than parameter $\chi$. We now derive a formula analogous to the quantum-corrected Ryu–Takayanagi formula using our lifting construction. First recall that when $\eta ={\eta }_{{\rm{Holo}}}$ we find $S({\rho }_{{\gamma }_{A}}^{{\rm{bk}}})=S({\rho }_{W[A]}^{{\rm{bk}}})$. Therefore we define

$$\frac{{\ell }_{{\gamma }_{A}}}{4{G}^{(2)}}\equiv S({\rho }_{{\gamma }_{A}}^{{\rm{bk}}}).$$

(15)

For this reason, the function ${\ell }_{{\gamma }_{A}}$, a measure of entanglement entropy, is a bonafied measure of length as it is positive, symmetric in boundary points and satisfies the triangle inequality. The full proof is included in Supplementary Methods Sec. I.

Next consider the state $\left|{\Psi }^{({\rm{lift}})}(\eta =1)\right\rangle$, in which the bulk DOFs are completely decoupled from the boundary. Thus $S({\rho }_{W[A]}^{{\rm{bk}}}(\eta =1))=S({\rho }_{A}^{{\rm{CFT}}})$, where $S({\rho }_{A}^{{\rm{CFT}}})$ is the entanglement entropy of the boundary CFT. Using this fact and extending the definition Eq. (15) away from $\eta ={\eta }_{{\rm{Holo}}}$ (see the section ‘Holographic screen’ in Methods) we find

$$S({\rho }_{A}^{{\rm{CFT}}})=\frac{{\ell }_{{\gamma }_{A}}}{4{G}^{(2)}}-Q(W[A]),$$

(16)

where the subtracted term is

$$Q(W[A])=S({\rho }_{W[A]}^{{\rm{bk}}})-S({\rho }_{W[A]}^{{\rm{bk}}},\eta =1)\,>\,0.$$

(17)

To it, Eq. (16) equates the entropy of the boundary CFT to an entropic property of DOFs along the geodesic of the bulk quantum state $\left|{\Psi }^{({\rm{lift}})}(\eta ={\eta }_{{\rm{Holo}}})\right\rangle$ minus a correction term $Q(W[A])$ corresponding to the additional entanglement between the wedge $W[A]$ and the rest of the bulk state. In fact, Eq. (16) can be generalized to all valid lifted states $\left|{\Psi }^{({\rm{lift}})}(\eta )\right\rangle$ but it is necessary to apply a pre-filtering operation along the screen, which is an identity operation in the special case $\eta ={\eta }_{{\rm{Holo}}}$ (see the section ‘Holographic screen’ in Methods).

Numerical calculation

The above discussion holds for the non-symmetric lifted MERA. When using symmetric lifting tensors, there is additional entanglement between bulk sites within and without the wedge due to coupling between charge DOFs. To better understand Eq. (16) in the symmetric case, we consider the MERA representation of ground states of unitary minimal model CFTs, realized in anionic Heisenberg models³¹ (see also the section ‘Details for the numerics’ in Methods). Each such CFT is specified by an integer $k\ge 2$ and an associated Hamiltonian, $H(k)$, acting on a chain of non-Abelian anyons. The anyons are spin$-1/2$ irreps of the quantum group $SU{(2)}_{k}$, which is a deformation of the usual $SU(2)$ group such that there are no spin projection quantum numbers associated to the anyons and total angular momentum is truncated at $k/2$. The Hamiltonian is

(18)

where the ${h}_{i}$ term (depicted here in the anyon fusion basis) projects onto the state $\left|{\frac{1}{2}}_{i}\times {\frac{1}{2}}_{i+1}\to 0\right\rangle$, i.e. physically the projection onto the spin 0 fusion space of two (deformed) spin 1/2 particles at sites $i$ and $i+1$. The Hamiltonian is described by a unitary minimal model CFT with central charge $c(k)=1-\frac{6}{(k+1)(k+2)}$³² and in the limit $k\to \infty$ the deformation disappears and the model becomes the bosonic CFT from the usual $SU(2)$ symmetric antiferromagnetic spin $\frac{1}{2}$ Heisenberg model.

We considered Hamiltonians with the values of $k=2,\,4,\,5,\ldots ,10$ and also $k=\infty$ (We have excluded $k=3$ due to convergence issues when calculating it, see the section ‘Details for the numerics’ in Methods.). For each of these, we obtained the MERA representation of the ground state by using the anyonic version of the MERA energy minimization algorithm³³ implimented with ref. ³⁴. We then lifted each MERA representation by using the symmetric lifting tensor defined in Fig. 5b—where $j$ now labels anyon charges—to obtain the dual bulk states. For each of these, we computed the Réyni-2 entropy, ${S}^{(2)}(\rho )=-\mathrm{log}\,\left({\rm{Tr}}\left[{\rho }^{2}\right]\right)$ (We use the Reyni-2 entropy as it is easier to compute than the von-Neumann entropy for the lifted MERA.), along the holographic screen illustrated in Fig. 3. Details about our numerical simulations are described in the section ‘Details for the numerics’ in Methods. Figure 6 shows a plot of this bulk entanglement entropy density (This density is taken with respect to the number of bulk sites in the maximal holographic screen (the path taken through the bulk) as opposed to the boundary size.) vs the central charge of the boundary state. These results demonstrate a linear dependence of bulk entropy density on central charge $c$ for ${\eta }_{j}=1$, and passes through 0 at $c=0$. However, the computed slope of 1.131 is roughly six times greater than expected. We attribute this increase in entropy density to the charge DOFs along the bonds in the original MERA, as while the degeneracy DOFs are decoupled between bulk and boundary sites, this is not true for charge DOFs. We therefore find $S({\rho }_{W[A]}^{{\rm{bk}}})$ is >$S({\rho }_{A}^{{\rm{CFT}}})$, which would be an interesting prediction to test in other examples of the Ryu–Takayanagi formula. For $\eta ={\eta }_{{\rm{Holo}}}$, achieved by setting ${\eta }_{j}=\sqrt{2{\chi }_{j}}/\sqrt{{\chi }_{j}+1}$ for each charge sector, the entropy density tends to grow with the central charge similar to the $\eta =1$ case. (We have excluded the $k=4$ point for ${\eta }_{j}={\eta }_{{\rm{Holo}},j}$ here as the lifting procedure for $\eta ={\eta }_{{\rm{Holo}}}$ appears to amplify numerical instabilities. We have included the full dataset in the section ‘Details for the numerics’ under Methods which includes the $k=4$ point for a variety of $\eta$ values. We also exclude the $k=3$ point since it did not appear to numerically converge to a particular value in our calculations, this point is also excluded from the dataset given in the section ‘Details for the numerics’ under Methods.) We also note that there appears to be a constant offset for ${\eta }_{j}={\eta }_{{\rm{Holo}},j}$ (and for other values of $\eta$), for which the entropy density monotonically increase with $\eta$. But since the entropy density at ${\eta }_{j}={\chi }_{j}$ is fixed by the numerical parameter ${\chi }_{j}$ we expect the bond dimensions to contribute to the entropy density with similar importance to the underlying boundary model from which that the lifted MERA arises, understanding these contributions for both non-symmetric and symmetric models would be useful for future work. These results suggest that even for the symmetric lifted MERA we can interpret the shifts in entropy density for lifted MERA states with ${\eta }_{j}\,>\,1$ arising from additional entanglement between DOFs from inside and outside the wedge.

Fig. 6: The second Rényi entropy density ${S}^{(2)}({\rho }_{{\gamma }_{A}}^{{\rm{bk}}}(\eta ))/| {\gamma }_{A}|$ of bulk sites on the maximal holographic screen ${\gamma }_{A}$ (see Fig. 3).

This is computed for lifted ground state approximations of the anyonic symmetric Hamiltonian $H(k)$ with $k=5,\,6,\,7,\,8,\,9,\,10,\,\infty$, describing unitary minimal model CFTs with central charge $c(k)$. Results shown for lifted states with ${\eta }_{j}=1$ and ${\eta }_{j}=\sqrt{2{\chi }_{j}}/\sqrt{{\chi }_{j}+1}$ (holographic limit), where we use the same charge sectors $j=1/2,\,3/2$ and same degeneracy dimensions ${\chi }_{1/2}=5,\,{\chi }_{3/2}=3$ for all $k$. The linear fit ${S}^{(2)}({\rho }_{{\gamma }_{A}}^{{\rm{bk}}}(1))/| {\gamma }_{A}| =1.131\times c(k)-0.003$, is calculated also using the $k=2,\,4$ points (not shown).

Discussion

In this work we have started with a tensor network, which is a classical description of a quantum system, and promoted it to a bona fide quantum state using a new lifting method. By virtue of applying our construction to the MERA network we obtained a lifted MERA state which exhibits several key features of the holographic duality. (i) A bulk-boundary operator mapping, (ii) the appearance of holographic screens, (iii) the gauging of global boundary symmetries, and (iv) an analogue of the quantum-corrected Ryu–Takayanagi formula. A key aspect of this construction is that it yields a unique bulk state (up to on-site unitary transformations) for a given MERA state, which allows a strict correspondence between the entanglement properties of the boundary and the bulk. In particular, we exploited this to use the bulk entanglement entropy as a measure of geodesic lengths, which when compared with the boundary entropy led to a Ryu–Takayanagi like formula. More broadly, our work illustrates a possible way to build a holographic description of the MERA from ground up, by only assuming a reasonable set of input conditions (the lifting axioms and gauging of boundary symmetries).

An interesting feature that this tensor network approach to the holographic principle uncovers is a relation to strange correlators. Strange correlators were first introduced in ref. ²¹ to map 2D symmetry protected quantum phases of matter to 1D critical systems. Using the PEPS tensor network ref. ³⁵ extended strange correlators to map 2D topologically phases, described by a topological quantum field theory (TQFT), to 1D critical systems, thus also explicitly realizing the TQFT${}_{2+1}$/CFT${}_{1+1}$ correspondence. While the lifted MERA does not immediately satisfy the TQFT${}_{2+1}$/CFT${}_{1+1}$ correspondence, it does satisfy the conditions of a strange correlator as the reverse lifting procedure.

This leads to an interesting open question is: under what conditions does the lifted (symmetric) MERA, dual to a critical MERA, describe a state with topological order? If this is possible, then our construction could yield a TQFT${}_{2+1}$/CFT${}_{1+1}$ correspondence—similar to the topological PEPS-based construction presented in ref. ³⁵—but approached from the CFT side. From this property the lifting procedure we have discussed suggests that the perspective of the TQFT/CFT correspondence and strange correlators would be an enlightening perspective from which to approach holography.

Methods

Proof of canonical form for the lifting tensor

Starting with just the third axiom (basis independence) from Fig. 1d, depicted below:

(19)

we show that all tensors that obey this axiom can be described by a tensor of the form of Eq. (2).

Here $t$ is the $\chi \times \chi \times \chi \times \chi$ lifting tensor, and the above equation holds for all unitaries $U$ of the group $U(\chi )$, where each bond is labelled by a fundamental representation (or its dual). The group $U(\chi )$ can be decomposed into $U(1)\times SU(\chi )$, a phase times the special unitary from the group $SU(\chi )$. Since Eq. (19) involves two copies of $U$ and two copies of its adjoint (either ${U}^{\dagger }$ or ${U}^{* }$) the phase contributions cancel out. Therefore, we may restrict ${U}_{g}$ only to the subgroup $SU(\chi )$. The tensor product (or fusion) of a fundamental and anti-fundamental representations ($f$ and $\bar{f}$, respectively) of $SU(\chi )$ is isomorphic to the direct sum of the trivial representation 0 and the anti-symmetric representation $A$. Equation (19) then implies that the lifting tensor is an intertwiner of the group $SU(\chi )$ (and therefore an intertwiner of the group $U(\chi )$). But since we can achieve this with two different choices of fusion pathway we obtain the following two possible fusion decompositions (in accordance with the Wigner-Eckart theorem) of the lifting tensor:

(20)

(21)

there is an ambiguity. We can also write this as

$$t={a}_{1}{V}_{1}+{b}_{1}{A}_{1},$$

(22)

$$t={a}_{2}{V}_{2}+{b}_{2}{A}_{2}.$$

(23)

where ${V}_{i}$ and ${A}_{i}$, respectively, correspond to the diagrams shown in Eq. (20) for $i=1$, and, respectively, to the diagrams shown in Eq. (21) for $i=2$. Specifically, ${V}_{i}$ denotes the projection onto the trivial (vacuum) representation, and ${A}_{i}$ denotes the projection onto the anti-symmetric representation. Of course since ${V}_{2}$ is itself a symmetric $SU(\chi )$ tensor, we can write it as

$${V}_{2}=\gamma {V}_{1}+\delta {A}_{1}\Rightarrow {A}_{1}={\delta }^{-1}{V}_{2}-{\delta }^{-1}\gamma {V}_{1},$$

(24)

where the second equality follows after assuming there is a non-zero contribution of ${A}_{1}$ to ${V}_{2}$. If this is not the case and $\delta =0$ then this indicates that ${V}_{1}\propto {V}_{2}$. With the exception of the $\chi =1$ case (where there is no anti-symmetric representation) this is obviously never true. Lastly, we can substitute this into the first representation of $t$ to get a basis in terms of ${V}_{i}$:

$$t={a}_{1}{V}_{1}+{b}_{1}{A}_{1}={a}_{1}{V}_{1}+{b}_{1}({\delta }^{-1}{V}_{2}-{\delta }^{-1}\gamma {V}_{1})=\tilde{a}{V}_{1}+\tilde{b}{V}_{2}$$

(25)

The final step, required for completeness, is to show that for any pair $(a,b)$ there exists a pair $(\tilde{a},\tilde{b})$ and vice versa. We have already shown one direction:

$$\tilde{a}=a+b{\delta }^{-1}$$

(26)

$$\tilde{b}=b{\delta }^{-1}\gamma$$

(27)

Clearly this implies that there is a unique $(\tilde{a},\tilde{b})$ pair for each $(a,b)$ pair. To show the opposite we invert the equations to obtain:

$$a=\tilde{a}-\tilde{b}{\gamma }^{-1}$$

(28)

$$b=\tilde{b}\delta {\gamma }^{-1}$$

(29)

This indicates that if $\gamma \,\ne\, 0$ then we also have a unique $(a,b)$ for each $(\tilde{a},\tilde{b})$. To show this is the case note that if $\gamma =0$ then we have that tensor ${V}_{2}\propto {A}_{1}$. But from Eq. (21) it is clear (when bending the top-right most leg down) that ${V}_{2}$ is the identity on a ${\chi }^{2}$ dimensional vector space, while ${A}_{1}$ is a projector onto the ${\chi }^{2}-1$ dimensional anti-symmetric representation. Therefore, $\gamma \,\ne\, 0$.

Holographic screen

In the results we pointed out that in our quantum bulk state there are a number of regions of the bulk/boundary of the lifted MERA, $W[A]$, that are equivalent to the DOFs on a corresponding screen, ${\gamma }_{A}$, of one dimension lower in the bulk. This relationship is key to our analogous Ryu–Takayanagi formula. A key step in this process is to exploit the fact that the lifted MERA is constructed from isometries and unitaries. This then gives rise to a state which we will call ${\hat{\rho }}_{{\gamma }_{A}}^{{\rm{virtual}}}$, constructed by contracting all tensors outside the virtual screen, ${\gamma }_{A}^{{\rm{virtual}}}$. This then allows us to connect the states in the wedge $W[A]$, ${\rho }_{W[A]}^{{\rm{bk}}}$, and ${\hat{\rho }}_{{\gamma }_{A}}^{{\rm{virtual}}}$ by an isometry $R$ (where $R{R}^{\dagger }=1$):

$${\rho }_{{\gamma }_{A}}^{{\rm{virtual}}}=R{\rho }_{W[A]}^{{\rm{bk}}}{R}^{\dagger }.$$

(30)

The intuition behind how the virtual screen works is best illuminated by a constructive greedy algorithm, from which we can construct viable wedges $W[A]$. This greedy algorithm is essentially the same as the greedy algorithm defined in ref. ¹⁰, but slightly restricted here due to us using ordinary isometries rather then perfect or block perfect tensors³⁶. To perform this algorithm, first choose a boundary $A$, from which we will define a ‘wedge’ ${W}_{0}[A]$ as the empty set of tensors/the set of physical sites on the boundary $A$. Associated to this is the holographic screen ${\gamma }_{A,0}^{{\rm{virtual}}}$ which is just the boundary $A$. Next define a new wedge ${W}_{1}[A]$ by choosing a subset of tensors from the original MERA connected to the holographic surface ${\gamma }_{A,0}^{{\rm{virtual}}}$ (the boundary $A$). This subset must include only tensors $u,w:{{\mathcal{H}}}_{{\rm{in}}}\,\mapsto\, {{\mathcal{H}}}_{{\rm{out}}}$ where the entire space ${{\mathcal{H}}}_{{\rm{in}}}$ is on the surface ${\gamma }_{A,0}$, i.e. all legs leading down of the chosen $u$ and $w$ must be on ${\gamma }_{A,0}^{{\rm{virtual}}}$ (or directly above a tensor $t$ that is on ${\gamma }_{A,0}^{{\rm{virtual}}}$). ${{\mathcal{H}}}_{{\rm{out}}}$ is then the resulting space that the selected $u$ and $w$ map ${{\mathcal{H}}}_{{\rm{in}}}$. This is then specified by ${\gamma }_{A,1}^{{\rm{virtual}}}$ that agrees with ${\gamma }_{A,0}^{{\rm{virtual}}}$ except where a selected tensor remains above it, in that case it passes above the tensor instead. This then defines a new wedge ${W}_{1}[A]$ as the set of tensors $u$ and $w$ selected, denoted $\{T\}$. It may also be viewed as the boundary sites $A$ and all bulk sites directly below the tensors $\{T\}$. The associated holographic surface ${\gamma }_{A,1}^{{\rm{virtual}}}$ is then the effective boundary for region $A$ when excluding tensors $\{T\}$. This processes can then be repeated any number of times, building ${W}_{n+1}[A]$ out of ${W}_{n}[A]$ and ${\gamma }_{A,n+1}^{{\rm{virtual}}}$ out of ${\gamma }_{A,n}^{{\rm{virtual}}}$ by selecting tensors with ${{\mathcal{H}}}_{{\rm{in}}}$ only along the effective boundary ${\gamma }_{A,n}^{{\rm{virtual}}}$ (again ignoring $t$ tensors). This generates all holographic surfaces, and we will call the surface associated to the maximal sized set $W[A]$ as the maximal holographic surface. As discussed in Supplementary Methods Sec. II, this is closely related to the dual graph geodesic. This construction makes it is clear that $R$ is an isometry from the effective boundary ${\gamma }_{A}^{{\rm{virtual}}}$ to the sites in wedge $W[A]$ (including boundary sites in $A$), where $\dim (W[A])\ge \dim ({\gamma }_{A}^{{\rm{virtual}}})$.

Reaching Eq. (30) only requires the MERA begin constructed from isometries and the second lifting axiom holds, see Fig. 1d(ii), meaning the lifting tensor may be interpreted as an isometry.

The final step in making the connection between sites in ${\rho }_{W[A]}^{{\rm{bk}}}$ and on holographic screen ${\gamma }_{A}$ is to connect the virtual screen to the true holographic screen. This is done by relating the two tensor sums that appear on the right hand sides of Fig. 7a and b. If this can be done then we have said that ${\rho }_{{\gamma }_{A}}^{{\rm{virtual}}}$ is equal to the holographic screen ${\rho }_{{\gamma }_{A}}^{{\rm{bk}}}$. The support of ${\rho }_{{\gamma }_{A}}^{{\rm{bk}}}$ is defined as a subset of the DOFs generated by the lifting tensors along the holographic screen, in particular the DOF that is deeper into the bulk for each lifting tensor. Then because ${\rho }_{{\gamma }_{A}}^{{\rm{virtual}}}$ is equal to ${\rho }_{W[A]}^{{\rm{bk}}}$ by an isometry, so is ${\rho }_{{\gamma }_{A}}^{{\rm{bk}}}$.

Fig. 7: A graphical demonstration of the mapping from virtual bonds to bulk degrees of freedom.

Expanding the lifting tensor below for a single site given states a ${\rho }_{{\gamma }_{A}}^{{\rm{virtual}}}$ and b ${\rho }_{{\gamma }_{A}}^{{\rm{bk}}}$. We contract everything besides these sites into ${\rho }^{(1)}$ everything else being the same we see that these two states are very similar, only differing by an exchange of $\alpha$ and $\beta$. This diagram is for a single site but can be extended to other multi-site cases by similar equivalences (exchanging $\alpha$ and $\beta$ for each lifting tensor along the cut one at a time).

The tensor network described by Fig. 7a refers to ${\rho }_{{\gamma }_{A}}^{{\rm{virtual}}}$ and Fig. 7b refers to ${\rho }_{{\gamma }_{A}}^{{\rm{bk}}}$. Comparing the two right hand sides of Fig. 7a and b it is possible to see that the diagrams associated with coefficient $\alpha {\beta }^{* }$ (or its complex conjugate) are isotropically equivalent between Fig. 7a and b. We can also see that the diagrams with coefficients $| \alpha {|}^{2}$ and $| \beta {|}^{2}$ are also isotopically equivalent, but require the two diagrams also be swapped (i.e. the diagram for $| \alpha {|}^{2}$ in one sum is the same as the diagram for $| \beta {|}^{2}$ in the other, and vice versa). Therefore to equate these two diagrams we need to generate a method to swap $\alpha$ and $\beta$.

To do this we define a completely positive operator ${\mathcal{F}}$ which acts on all DOFs arising from the lifting tensors along ${\gamma }_{A}$. It is obvious that when $\alpha =\beta$ then this operator is the identity, thus earning this limit of $\eta$ its designation as the holographic limit of lifting, $\eta ={\eta }_{{\rm{Holo}}}=\frac{\sqrt{2\chi }}{\sqrt{\chi +1}}$. When we extend $\eta$ away from the holographic limit this ${\mathcal{F}}={\otimes }_{j\in {\gamma }_{A}}{F}_{j}^{(\alpha ,\beta )}$ takes the form of a filtering operation constructed from local operators ${F}_{j}^{(\alpha ,\beta )}$:

(31)

Where we set $a=\beta {\alpha }^{-1}$ and $b=({\alpha }^{2}-{\beta }^{2}){\alpha }^{-1}{(\alpha +\chi \beta )}^{-1}$, with these parameters the operator is completely positive. Graphically the action of this on a lifting tensor is

(32)

where the renormalisation of the CP map, given in Eqs. (35) and (36), has been ignored.

Since this operation swaps $\alpha$ and $\beta$ then we can view it as converting $\eta$ to $\tilde{\eta }$:

$$\tilde{\eta }(\eta )=\frac{\eta \chi }{1+\sqrt{{\chi }^{2}+1}\sqrt{{\eta }^{2}-1}}$$

(33)

We will use ${\mathcal{F}}$ to indicate the flip of $\alpha$ and $\beta$ for the lifting tensors along the holographic screen sites, therefore we define a modified density matrix ${\widetilde{\rho }}_{{\gamma }_{A}}^{{\rm{bk}}}$ with the same support as ${\rho }_{{\gamma }_{A}}^{{\rm{bk}}}$ by:

$${\widetilde{\rho }}_{{\gamma }_{A}}^{{\rm{bk}}}={{\rm{Tr}}}_{{\rm{bt}}}\left({\mathcal{F}}\left[{\rho }_{{\gamma }_{A}}^{{\rm{bk}},(2)}\right]\right)={\rho }_{{\gamma }_{A}}^{{\rm{virtual}}}=R{\rho }_{W[A]}^{{\rm{bk}}}{R}^{\dagger }$$

(34)

Here we apply the filtering operation ${\mathcal{F}}$ to the quantum state ${\rho }_{{\gamma }_{A}}^{{\rm{bk}},(2)}$ reduced to only (the pair of) DOFs generated by all the lifting tensors along ${\gamma }_{A}$. Having applied the filter we then trace out the bottom DOF of each lifting tensor along ${\gamma }_{A}$ by ${{\rm{Tr}}}_{{\rm{bt}}}$ and reduce the support back to that of ${\rho }_{{\gamma }_{A}}^{{\rm{bk}}}$. By the previous arguments this is equal to ${\rho }_{{\gamma }_{A}}^{{\rm{virtual}}}$ and therefore also equal to $R{\rho }_{W[A]}^{{\rm{bk}}}{R}^{\dagger }$. So when we extend our Ryu–Takayanagi formula to $\eta$ other than the holographic limit, we replace $S({\rho }_{{\gamma }_{A}}^{{\rm{bk}}})$ with $S({\widetilde{\rho }}_{{\gamma }_{A}}^{{\rm{bk}}})$ in Eq. (15).

Beginning with the completely positive operator from Eq. (31), from which we constructed the filtering operators, we can construct a local POVM on each site such that one of the measurement outcomes corresponds to successfully flipping $\alpha$ and $\beta$. For $a\,>\,| a+b\chi |$ we find the POVM to be:

$$\begin{array}{l}{M}_{1}=\displaystyle\frac{{F}^{(\alpha ,\beta )}}{a}\\ {M}_{2}=\displaystyle\sqrt{1-{\left(\frac{a+b\chi }{a}\right)}^{2}}{{\mathcal{P}}}^{S}\end{array}$$

(35)

Where ${{\mathcal{P}}}^{S}=\frac{1}{\chi }{\sum }_{j = 1}^{\chi }\left|jj\right\rangle \left\langle jj\right|$ is the projector onto the singlet. Otherwise we find the POVM to be:

$$\begin{array}{l}{M}_{1}=\displaystyle\frac{{F}^{(\alpha ,\beta )}}{| a+b\chi | }\\ {M}_{2}=\displaystyle\sqrt{1-{\left(\frac{a}{a+b\chi }\right)}^{2}}{{\mathcal{P}}}^{S}\end{array}$$

(36)

The probability of success for measurement outcome 1 (successfully flipped $\alpha$ and $\beta$) can also be computed making use of the fact that it is acting on a bulk lifted state. Therefore the probability of outcome 1 for a local operator at some site can be worked out by realising that the expectation value of the identity term is 1 (as the lifted MERA is a pure quantum state). Further when computing the expectation value of the projector ${{\mathcal{P}}}^{S}$ on a single site the outcome will be ${\eta }^{-2}$. This can be observed from the first lifting axiom, which states the expectation value of the bulk state times the singlet is equal to the ${\eta }^{-1}$ times the norm of a lifted state where we have the decoupled lifting tensor at that site (i.e. the lifting tensor generated by $\eta =1$). Since this lifting is again a pure state that gives expectation value ${\eta }^{-2}$. Therefore for a lifted tensor on any single site, the probability of success of the filtering operation is:

$$P=\left\{\begin{array}{ll}\frac{{a}^{2}+(2ba\chi +{b}^{2}{\chi }^{2}){\eta }^{-2}}{{a}^{2}}&a\,>\,| a+b\chi | \\ \frac{{a}^{2}+(2ba\chi +{b}^{2}{\chi }^{2}){\eta }^{-2}}{| a+b\chi {|}^{2}}&a\,<\,| a+b\chi | \end{array}\right.$$

(37)

Finally, it is important to note how this changes when we consider symmetries. For Abelian symmetries nothing changes except that we define the flip operator separately on each charge $j$ based on the tuning ${\eta }_{j}$ of that charge (or equivalently ${\alpha }_{j}$ and ${\beta }_{j}$). For non-Abelian symmetries we choose to flip only the degeneracy DOFs and leave the gauge DOFs alone.

As discussed in the main text the limit $\eta =1$ is also a special limit where the geometric definition of the length $\ell \propto S({\widetilde{\rho }}_{{\gamma }_{A}}^{{\rm{bk}}})=S({\rho }_{A}^{{\rm{CFT}}})$. The opposite limit is also of interest as the state ${\widetilde{\rho }}_{{\gamma }_{A}}^{{\rm{bk}}}\propto {I}_{{\gamma }_{A}}$ and so the definition of length is $\ell \propto S({\widetilde{\rho }}_{{\gamma }_{A}}^{{\rm{bk}}})=\mathrm{log}\,(\chi )| {\gamma }_{A}|$. For values of $\eta$ between these extremes (including the holographic limit) we expect a contribution from both the model as observed when $\eta =1$ (and therefore dependent on central charge for CFTs) and the bond dimension as observed when $\eta =\chi$. We cannot make any more predictions other then we expect an increase in entropy with central charge and with bond dimension, finer details require numerical analysis due to the highly non-linear interaction between $\eta$ and the model occurring at sites deeper into the bulk then the sites of ${\gamma }_{A}$ which does not occur when $\eta =1$ or $\eta =\chi$. Finally even these limits break down due to non-linearities occurring arising from gauge DOFs coupling all DOFs with charges in the bulk. This is expected to increase the entropy when ${\eta }_{j}=1$ as we no longer recover the CFT and also decrease the entropy when ${\eta }_{j}={\chi }_{j}$ as we do not end up with a maximally mixed state.

Details for the numerics

In the results we discussed the symmetric lifted MERA, focusing on a family of anyonic Heisenberg models³¹ which generated a complete set of unitary minimal model CFTs. Here we will give further details regarding the calculations and results.

Each CFT from this family of unitary minimal models is specified by an integer $k\ge 2$ and an associated Hamiltonian, $H(k)$, acting on a chain of non-Abelian anyons. Without exploiting the anyonic symmetry the family of Hamiltonians $H(k)$ of Eq. (18) is the anyonic analogue of the standard spin $\frac{1}{2}$ antiferromagnetic Heisenberg model. These deformed Heisenberg models exist as points, labelled by integers $k\ge 2$, along the XXZ spin chains:

$$\begin{array}{l}H(k)=-\frac{1}{2d(k)}{\sum }_{i}\left[({\sigma }_{i}^{x}{\sigma }_{i+1}^{x}+{\sigma }_{i}^{y}{\sigma }_{i+1}^{y})\right.\\\left.+\,\frac{d(k)}{2}\left(1-{\sigma }_{i}^{z}{\sigma }_{i+1}^{z}\right)+i\sqrt{1-\frac{{d}^{2}(k)}{4}}({\sigma }_{i+1}^{z}-{\sigma }_{i}^{z})\right].\end{array}$$

(38)

where $d(k)=2\cos \left(\frac{\pi }{k+2}\right)$. While the total Hamiltonian is hermitian (up to boundary terms), the local interaction terms are non-hermitian. These local non-hermitian contributions are important as when they are removed $H(k)$ no longer corresponds to unitary minimal models, instead each Hamiltonian becomes a bosonic CFT with central charge $c=1$.

Irrespective of if we explicitly include the non-hermitian local interaction terms, the ground state energy density is:

$$\frac{E(k)}{N}=\frac{{d}^{2}(k)-4}{4d(k)}{\int }_{-\infty }^{\infty }dx\frac{{\rm{{\rm{sech}} }}(\pi x)}{\cosh \left[2x\arccos \left(\frac{d(k)}{2}\right)\right]-\frac{d(k)}{2}}$$

(39)

and if we keep the non-local terms then the central charge is

$$c(k)=1-\frac{6}{(k+1)(k+2)}.$$

(40)

Associated to each CFT are a number of conformal dimensions:

$${h}_{r,s}=\frac{{\left((k+2)r-(k+1)s\right)}^{2}-1}{4(k+2)(k+1)},$$

(41)

with parameters $1\le r\le k$ and $1\le s\le k+1$. From these conformal dimensions the scaling dimensions (for the primary fields) of our CFT models can be computed and are simply the sum of two allowable conformal dimensions for the model, each corresponding to a particular representation of the CFT algebra with this particular central charge. The remaining scaling dimensions (associated to descendent fields) are just the other scaling dimensions positively displaced by an integer value. As can be seen from the results of ref. ³³ not all possible scaling dimensions will appear, and in fact only a few of them will. Therefore as we have no prior knowledge of which representations will appear in our model we compute the error in scaling dimensions with respect to the closest possible scaling dimension of the model.

As shown in ref. ³², and used in the main text, $H(k)$ can also be understood as a deformed Heisenberg model (for $k\ge 2$). In which case the anyons are spin$-1/2$ irreps of the quantum group $SU{(2)}_{k}$. This group is a deformation of the standard $SU(2)$ symmetry group, restricting to a finite number of possible spin values, eliminating those half integers with values >$\frac{k}{2}$, truncating the total angular momentum to $k/2$. If we choose to exploit these anyonic symmetries then the Hamiltonian may be presented as:

(42)

where the ${h}_{i}$ term (depicted here in the anyon fusion basis) projects onto the state $\left|{\frac{1}{2}}_{i}\times {\frac{1}{2}}_{i+1}\to 0\right\rangle$, i.e. physically it is the projection onto the spin 0 fusion space of two (deformed) spin 1/2 particles at sites $i$ and $i+1$. In the limit $k\to \infty$ the deformation disappears and the model becomes the bosonic CFT from the usual $SU(2)$ symmetric antiferromagnetic spin $\frac{1}{2}$ Heisenberg model. This can be observed in both Eqs. (38) and (42) (noting that $d(\infty )=2$).

The presence of these non-hermitian terms is also the reason that we cannot use the usual, non-symmetric, MERA for spin chain to simulate this family of models. Instead, we must resort to the anyonic version of the MERA³³. We studied the $k=2,\cdots \ ,10$ models and the $k=\infty$, the last of which corresponds to the standard spin $\frac{1}{2}$ antiferromagnetic Heisenberg model. We obtained the anyonic MERA representation of each ground state via a variational energy minimisation computation, as described in ref. ³³, and implemented with ref. ³⁴. In the simulations, we kept five transition layers and an additional scale-invariant layer. We assigned degeneracy 5 and 3 to irreps $\frac{1}{2}$ and $\frac{3}{2}$, respectively, on each bond index of the MERA, and zero degeneracy to all other irrep labels. (Except in the $k=2$ case, where spin $\frac{3}{2}$ does not exist.) The relative errors in ground state energy, central charge, and first couple (non-trivial) scaling dimensions are listed in Table 1.

Table 1 The relative errors in energy density $E(k)$, central charge $c(k)$ and the first three non-trivial scaling dimensions ${\Delta }^{(1,2,3)}$, for the numerical ground state calculations for the Hamiltonian given in Eqs. (38) and (42).

We then lifted the resulting MERA tensor network representation using the symmetric lifting tensor defined in Fig. 5b—where $j$ now labels anyon charges—to obtain the dual bulk states. For each of these we computed the Réyni-2 entropy, ${S}^{(2)}(\rho )=-\mathrm{log}\,\left({\rm{Tr}}\left[{\rho }^{2}\right]\right)$, along the holographic screen illustrated in Fig. 3. We use the Reyni-2 entropy as it is easier to compute than the von-Neumann entropy for the lifted MERA. In the main text, Fig. 6 showed a plot of this bulk entanglement entropy density vs the central charge of the boundary state. This density is taken with respect to the number of bulk sites in the maximal holographic screen (the path taken through the bulk) as opposed to the boundary size.

In addition, to the results presented in plot Fig. 6 we studied the $k=2$ and $k=4$ ground states, excluding the $k=3$ ground state due to convergence issues that arose during the lifting procedure. For each value of $k$ we studied six additional values of tuning parameters—corresponding to six further dual bulk states for each critical ground state—focusing on the ${\eta }_{j}\to 1$ limit. We considered ${\eta }_{j}=\{1,\,1.01,\,1.03,\,1.1,\,1.2,\,1.5\}$ where ${\eta }_{j}$ takes the same value for all $j$. In addition we considered the holographic limit ${\eta }_{j}=\frac{\sqrt{2{\chi }_{j}}}{\sqrt{{\chi }_{j}+1}}\mathop{\to }\limits_{{\chi }_{j}\to \infty }\sqrt{2}$which is roughly between the $\eta =1.2$ and $\eta =1.5$ cases but with a $j$ dependent tuning parameter. We also considered the maximal entropy limit where ${\eta }_{j}={\chi }_{j}$. In these last two values of $\eta$ we have set $\eta$ separately on each charge sector, $j$, based on the bond dimension, ${\chi }_{j}$, associated to said sector.

The results for all values of $k$ and $\eta$, excluding values for $k=3$, are plotted in Fig. 8. We restrict ourselves to regions $A$ between two spines (sequences of isometries connected via the middle sites) which eventually are neighbouring at some renormalisation scale. This means that the region $A$ corresponds to the boundary sites between the middle sites of the spine. This then means that the geodesic ${\gamma }_{A}$ corresponds to only paths which are of the form of shown in Supplementary Methods Fig. 2a, and therefore is both the maximal holographic screens and the graph geodesic paths.

Fig. 8: The second Rényi entropy density ${S}^{(2)}({\rho }_{{\gamma }_{A}}^{{\rm{bk}}}(\eta ))/| {\gamma }_{A}|$ of bulk sites on the geodesic holographic screen ${\gamma }_{A}$ (see Fig. 3) for ground states of the Hamiltonian $H(k)$ for various values of $\eta$ for each $k$, and ${\eta }_{{\rm{holo}}}\equiv \frac{\sqrt{2\chi }}{\sqrt{\chi +1}}$.

The connections for different models for a given tuning parameter is not to indicate a predicted model that the authors propose, but rather to aid the reader in separating the different sets of lifting results based on the values of $\eta$ used.

To compute the entropy density of this we compute the eigenvalues ${\{{\lambda }_{i}\}}_{i = 0,\cdots }$ of the transfer matrix shown in Fig. 9. By doing this we have computed the asymptotic entropy density ${S}^{(2)}({\rho }_{{\gamma }_{A}}^{{\rm{bk}}})/| {\gamma }_{A}| ={\mathrm{log}\,}_{2}({\lambda }_{1})$ as $| A| \to \infty$ and so only the scale-invariant layer contributes to this calculation. In each of these ground states we see a complete ordering of the entropy density growing with the tuning parameter $\eta$ just as we would expect in the non-symmetric case. We may find this complete order breaks down and a partial order emerges if we had tuned the ${\eta }_{j}$ parameters separately for each $j$ so that we may have ${\eta }_{j}^{(1)}\,<\,{\eta }_{j}^{(2)}$ but ${\eta }_{{j}^{\prime}}^{(1)}\,>\,{\eta }_{{j}^{\prime}}^{(2)}$.

Fig. 9

The transfer matrix that was used to compute the entropy density.

Given this observation we can now consider the two limits of $\eta$ and compare them to the non-symmetric case. The first limit of $\eta =\chi$, which for the symmetric case becomes ${\eta }_{j}={\chi }_{j}$. In the non-symmetric case we expect the entropy density to be the maximal possible entropy density of $\mathrm{log}\,(\chi )$. For the symmetric case the analogue would be expected to be $\mathrm{log}\,({\sum }_{j}{\chi }_{j}{D}_{j})$ where ${D}_{j}$ is the quantum dimension of the charge $j$ which is defined for $SU{(2)}_{k}$ as:

$${D}_{j}=\frac{\sin \left(\frac{(2j+1)\pi }{k+2}\right)}{\sin \left(\frac{\pi }{k+2}\right)}$$

(43)

In Table 2 we compare the computed entropies for when ${\eta }_{j}={\chi }_{j}$ for all values of $k$. Based on the non-symmetric results, where the state should be a maximally mixed state we expect this to go as $S({I}_{{\gamma }_{A}})/| {\gamma }_{A}| =-{\mathrm{log}\,}_{2}\left(\frac{{\sum }_{j}{\chi }_{j}{D}_{j}}{{({\sum }_{j}{\chi }_{j}{D}_{j})}^{2}}\right)$ (using base 2 for all entropy calculations) where $j$ is summed over all possible charge labels. We find that the entropy for the symmetric models does not completely saturate this bound as there is additional information which is encoded in the probability of existing in the different gauge sectors. As confirmation that this is the case we see that when $k=2$ and we have only stored a single gauge DOF, this bound perfectly predicts the entropy density.

Table 2 Entropy densities for computed results for ${\eta }_{j}={\chi }_{j}$, $S\left({\widetilde{\rho }}_{{\gamma }_{A}}^{{\rm{bk}}}\right.$, and the expected maximal entropy density, $S({I}_{{\gamma }_{A}})/| {\gamma }_{A}|$. In addition to this the differences between the computed and predicted entropy densities, $\Delta S$, are given as well as the relative difference ${\Delta }_{{\rm{Rel}}}S$.

We also wish to study the other limit, where ${\eta }_{j}=1$, and compare it with the prediction of describing the entropy of the original CFT theory. For Renyi-2 entropy the relationship between the entropy of the CFT on region $A$, ${\rho }_{A}^{{\rm{CFT}}}$ and the central charge $c$ and the subsystem size $| A|$, is:

$${S}^{(2)}({\rho }_{A}^{{\rm{CFT}}})=\frac{c}{4}{\mathrm{log}\,}_{2}(| A| ).$$

(44)

For the path that we are considering there is a relationship between $| A|$ and the path length through the bulk $| {\gamma }_{A}| =2N$ given by:

$$| A| =2\frac{{3}^{N}-1}{3-1}\Rightarrow | {\gamma }_{A}| =2\,{\mathrm{log}\,}_{3}\left(| A| +1\right)$$

(45)

This means that we expect our entropy density to take the form:

$${S}^{(2)}({\rho }_{A}^{{\rm{CFT}}})/| {\gamma }_{A}| \approx \frac{c}{8}{\mathrm{log}\,}_{2}(3)\approx 0.20c.$$

(46)

To study this we first perform linear regression on our $\eta =1$ limit to compare to the prediction from Eq. (46) for a linear regression to ${S}^{(2)}({\rho }_{A}^{{\rm{CFT}}})/| {\gamma }_{A}| =mc+{x}^{(0)}$. We then compare the regression to linear, quadratic and cubic models and consider the t-statistics of the coefficients of these models to determine the most appropriate model. The t-statistic in this case is a measure of the probability that the results (the entropy density) are completely uncorrelated to the other variables (the central charge). In particular this probability is the chance that a random Gaussian distribution could give rise to this distribution. The t-statistic has an associated p-value which is interpreted as the probability of having sampled random points to generate a correlation of this magnitude or greater. Further we work out the t-statistics for comparing the higher order models to the linear model, in this case we repeat the analysis on the difference between the entropy density an the linear model.

Doing this we get $m=1.131\pm 0.095$ with a t-statistic of 11.9 (p-value of $6.8\times 1{0}^{-6}$) and ${x}^{(0)}=-0.003\pm 0.083$ with a t-statistic of −0.0384 (p-value of 0.97). This states that the deviation of the intercept away from the theoretically predicted value of 0 is extremely likely ($\sim 97 \%$) to be simply due to random noise (here due to the fact that the MERA with finite bound dimension is only an approximation to the ground state). The linear contribution is highly unlikely to be due to random noise ($<1{0}^{-3} \%$). Further the value we find is that the slope is about five times greater then what we predicted and this is attributed to be due to additional decoherence that occurs due to the coupling of the charge sectors to the bulk DOFs.

For completeness we also study the likelihood of this data being described by a higher order polynomial in the central charge. This was done by computing the t-statistics for the coefficients when performing regression to the quadratic and cubic models. Here we find that the Gaussian random noise is highly likely to be able to generate data with a quadratic fit which is just as significant as the one we found. For the cubic model each coefficient has a $\sim 8 \%$ chance of having being generated by the random noise, this is better then the quadratic model but in the linear case the probability of the observed relation arising from random noise is a factor of 1000 smaller then any polynomial relationship from the cubic regression. For completeness we also compare this to the linear model of ${S}^{(2)}({\rho }_{A}^{{\rm{CFT}}})/| {\gamma }_{A}| =1.131\times c-0.003$ and find similar results (where here we say the null model is Gaussian noise plus the observed linear model). These results are given in Table 3.

Table 3 Table of coefficients for polynomial fits to the $\eta =1$ data.

At the extreme points of $\eta$ (${\eta }_{j}=1$ and ${\eta }_{j}={\chi }_{j}$) we see there is an almost linear relationship between the entropy density and the central charge. For ${\eta }_{j}=1$ we expected this based on non-symmetric results, for ${\eta }_{j}={\chi }_{j}$ this observation is likely coincidental since the quantum dimension tends to grow as the central charge. Between these extreme points we see a deviation from linearity which becomes most extreme around $\eta ={\eta }_{{\rm{Holo}}}$. These deviations are most noticeable for $k=4,\,5,\,6$. There are two possible reasons that this may be the case, the first is that we should use a different tuning parameter for the different charge sectors. However, the behaviour of the deviation is consistent between the constant tuning parameter ${\eta }_{j}=1.2$ and a the holographic tuning ${\eta }_{j}=\sqrt{2{\chi }_{j}}/\sqrt{{\chi }_{j}+1}$, roughly $\eta =(1.29,\,1.22)$ for the two non-zero charge sectors, are the same. This suggests that the behaviour has to do with the average tuning values (or average tuning values relative to the charge sector bond dimension) as opposed to arising due to relative tunings between charge sectors.

The abnormal behaviour could also arise from the fact that as $\eta$ varies between 1 and $\chi$ we get a mixture of behaviours arising in the lifted MERA state. Drawing from our intuition in the non-symmetric case, when $\eta =1$ we find that the state along the maximal holographic screen should behave as a section of the boundary CFT. On the other hand, in the $\eta =\chi$ limit this gives rise to a maximally mixed state. In between these limits we expect there to be both mixed state contributions as well as the pure state contribution. Notwithstanding, since the mixing of $\alpha$ and $\beta$ contributions to the lifting tensor occurs not only at the holographic screen, but also above it, this suggest that should be some form of non-linear feedback as we transition between the $\eta =1$ and $\eta =\chi$ extremes which could be important. For this reason the anomalous behaviour around $\eta ={\eta }_{{\rm{Holo}}}$ may be indicative of some kind of transition from CFT like behaviour to a mixed state like behaviour. This non-linearity with respect to the central charge may just be the true behaviour around these parameters, however, the authors suspect the lifting procedure simply exacerbates the numerical instabilities in the original MERA tensor network state. For this reason it may be worthwhile exploring this for a possible transition and any associated order parameters in future work.