Introduction

The thermodynamic implications of quantum dynamics are currently helping us build new architectures for the super-efficient nano- and micro-engines, and design protocols for the manipulation and management of work and heat above and beyond the possibilities offered by classical processes,1,2,3,4 including steps towards the formulation of a coherent framework for caloritronics5,6,7,7 and the demonstration of Maxwell’s daemon with elementary working media.8, 9 Exciting experimental progress towards the achievement of such paramount goals is currently ongoing.10, 11 Quantum coherences are believed to be responsible for the extraction of work from a single heat bath12 and the enhanced performance of quantum engines,13 while weakly driven quantum heat engines are known to exhibit enhanced power outputs with respect to their classical (stochastic) versions.14

Despite such evidences, the identification of the specific features of quantum systems that might influence their thermodynamic performance is currently a debated point. In particular, the role that quantum correlations and coherences in schemes for the extraction of work from quantum systems appears to be quite controversial.15,16,17,18,19,20 Yet, the clarification of the relevance of genuinely quantum features would be key for the grounding of quantum thermodynamics as a viable route towards the construction of a framework for quantum technologies.1,2,3,4 Indeed, the very tight link between thermodynamics and quantum entanglement21 cries loud for the clarification of the role of quantum correlations as a resource for coherent thermodynamic processes and transformations.22

In this paper, we make steps towards the clarification of the role of quantum correlations in work extraction processes by investigating a simple ancilla-assisted protocol. We address the concept of ergotropy, i.e., the maximum work that can be gained from a quantum state, with respect to some reference Hamiltonian, under cyclic unitaries.23 We consider the joint state of a system and an isodimensional ancilla, which can be measured in an arbitrary basis, and show that quantum correlations are related to a possible increase of the extracted work. More precisely, we demonstrate that if system and ancilla share no quantum quantum discord,24,25,26 then the information gathered through the measurements performed on the state of the ancilla cannot help in catalyzing the extraction of work from the system. We extend this result to the case of quantum entanglement, thus establishing a tight link between enhanced work-extraction performances and a clear-cut resource in quantum information processing. We illustrate our findings for the relevant case where system and ancilla are both embodied by qubits, showing the existence of a families of states that provide attainable (upper and lower) bounds to the gain in extractable work at a set degree of quantum correlations between system and ancilla. Not only do our results shed light on the core role that quantum correlations have in thermodynamically relevant processes they also open up the pathway towards the study of the implications of the structure of generally quantum correlated resources for ancilla-assisted work extraction schemes and the grounding of the technological potential of the thermodynamics of quantum systems.

Results

Ergotropy

We start by introducing the ergotropy, which is the maximum amount of work that can be extracted from a quantum system in a given state by means of a cyclic unitary transformation.23 Consider a system S with Hamiltonian \({\hat H_S}\) and density matrix \({\hat \rho _S}\) given by,

$${\hat H_S} = \mathop {\sum}\limits_k {\epsilon _k}\left| {{\epsilon _k}} \right\rangle \left\langle {{\epsilon _k}} \right|,\quad {\hat \rho _S} = \mathop {\sum}\limits_k {r_k}\left| {{r_k}} \right\rangle \left\langle {{r_k}} \right|,$$
(1)

with \({\epsilon _k} \le {\epsilon _{k + 1}} (k = 1,2,..)\) the energy of the \({k^{{\rm{th}}}}\) eigenstate \(\left| {{\epsilon _k}} \right\rangle\) of \({\hat H_S}\) and \({r_k} \ge {r_{k + 1}}\) the population of the eigenstate \(\left| {{r_k}} \right\rangle\) of \({\hat \rho _S}\). If \({\rho _S}\) is a passive state (i.e., if \([{\hat \rho _s},{\hat H_S}] = 0\) and \({r_n} \ge {r_m}\) whenever \({\epsilon _n} < {\epsilon _m}\)), no work can be extracted by means of a cyclical variation of the Hamiltonian parameters (\({\hat H_S}(0) = {\hat H_S}(\tau ) = {\hat H_S}\)) over a fixed time interval \([0,\tau ]\).27,28,29 If the initial state \({\hat \rho _S}\) is not passive with respect to \({\hat H_S}\), then work (defined here as the difference in energy between initial and final state of the system) may be extracted cyclically, and its maximal amount, the ergotropy \({\cal W}\), has been shown in ref. 23 to be given by

$${\cal W} = \mathop {\sum}\limits_{j,k} {r_k}{\epsilon _j}\left( {{{\left| {\left. {\left\langle {{\epsilon _j}} \right|{r_k}} \right\rangle } \right|}^2} - {\delta _{jk}}} \right).$$
(2)

The ergotropy \({\cal W}\) vanishes for passive initial states. It is upper-bounded by the work \({{\cal W}_{{\rm{th}}}}\) extracted when the final state of the system is the Gibbs state \({e^{ - \beta {{\hat H}_S}(0)}}/{\rm{Tr}}{\kern 1pt} [{e^{ - \beta {{\hat H}_S}(0)}}]\) with the same entropy as \({\hat \rho _S}\) (here \(\beta\) is an effective inverse temperature determined by imposing that initial and final states have the same entropy).23 The preparation of S in pure initial states entails the reachability of such upper bound.

Daemonic work and quantum correlations

In order to connect with the theory of quantum correlations, we extend the framework for maximal work extraction by introducing a non-interacting ancilla A and assume that system and ancilla are initially prepared in the joint state \({\hat \rho _{SA}}\). The intuition behind the protocol, that will be discussed below, is that should \({\hat \rho _{SA}}\) contain correlations between S and A, a measurement performed on the ancilla would give us information about the state of S, which could then be used to enhance the amount of work that can be extracted from its state.

Within such a generalized framework, the amount of extractable work crucially depends on the measurements performed on A, that we describe through a set of orthogonal projectors \(\{ \hat {\Pi}_a^A\}\). Upon the measurement of A with outcome \(a\), the state of the system collapses onto the conditional density matrix \({\hat \rho _{S|a}} = {\rm{T}}{{\rm{r}}_A}[\hat {\Pi}_a^A{\hat \rho _{SA}}\hat {\Pi}_a^A]/{p_a}\) with probability \({p_a} = {\kern 1pt} Tr{\kern 1pt} [\hat {\Pi}_a^A{\hat \rho _{SA}}]\). The time evolution of state \({\rho _{S|a}}\) then follows a cyclic unitary process \({\hat U_a}\) conditioned on the outcome of the measurement. By averaging over all of the possible outcomes of the measurement, the work extracted from the state of \(S\) reads

$${W_{\{ \hat {\Pi}_a^A\} }} = {\rm{Tr}}\left[ {{{\hat \rho }_S}{{\hat H}_S}} \right] - \mathop {\sum}\limits_a {p_a}{\rm{Tr}}\left[ {{{\hat U}_a}{{\hat \rho }_{S|a}}\hat U_{a}^{\dag} {{\hat H}_S}} \right]$$
(3)

with \({\hat \rho _S} = {\rm{T}}{{\rm{r}}_A}[{\hat \rho _{SA}}]\). This quantity explicitly depends on the specific control strategy determined by the outcomes of the measurements \(\{ \hat {\Pi}_a^A\}\). We can thus proceed to maximize the extracted work by performing the optimal ergotropic transformation for each of the \({\hat \rho _{S|a}}\) such that

$${{\cal W}_{\{ \hat {\Pi}_a^A\} }} = {\rm{Tr}}\left[ {{{\hat \rho }_S}{{\hat H}_S}} \right] - \mathop {\sum}\limits_a {p_a}\mathop {\sum}\limits_k r_k^a{\epsilon _k}$$
(4)

with \(\{ \hat {\Pi}_a^A\}\) a set of orthogonal projective measurements, and \(r_k^a\) the eigenvalues of \({\hat \rho _{S|a}}\). We call this quantity the Daemonic Ergotropy. The optimization procedure due in order to derive Eq. (4) echoes the one presented in ref. 23 for the case of a single spin.

On the other hand, if we do not use the information obtained upon measuring the ancilla, and thus control the system in the same way, independently of the measurement outcomes (i.e., \({\hat U_a} = \hat U\) for any \(a\)), the maximum extractable work would be given by the ergotropy \({\cal W}\) associated with state \({\hat \rho _S} = {\rm{T}}{{\rm{r}}_A}\{ {\rho _{SA}}\} = \mathop {\sum}\nolimits_k {r_k}\left| {{r_k}} \right\rangle \left\langle {{r_k}} \right|\). In the “Methods” section we have shown that the information acquired through the measurements allows to extract more work than in the absence of them, that is \({{\cal W}_{\{ \hat {\Pi}_a^A\} }}{\rm{ \ge }}{\cal W}\).

In what follows the main object of our attention will be the difference \({{\cal W}_{\{ {\Pi}_a^A\} }} - {\cal W}\), which is expected to be related to the (nature and degree of) correlations between S and A. For instance, should S and A be initially statistically independent, i.e., \({\hat \rho _{SA}} = {\hat \rho _S} \otimes {\hat \rho _A}\), the measurements on the ancilla would not bring about any information on the state of S, as we would have \({\hat \rho _{S|a}} = {\hat \rho _S}\) for any set \(\{ \hat {\Pi}_a^A\}\) and outcome \(a\). Consequently, there would be no gain in work extraction and \({{\cal W}_{\{ {\Pi}_a^A\} }} = {\cal W}\). However, besides such a rather extreme case, other instances of no gain in work extraction (from correlated \({\hat \rho _{SA}}\) states) might be possible, and our goal here is to characterize such occurrences.

In order to achieve this goal, we introduce the quantity

$$\delta {\cal W} = {\rm{ma}}{{\rm{x}}_{\{ \hat {\Pi}_a^A\} }}{{\cal W}_{\{ \hat {\Pi}_a^A\} }} - {\cal W},$$
(5)

which we dub, from now on daemonic gain in light of its ancilla-assisted nature. Clearly, \(\delta {\cal W} \ge 0\) because of the considerations above and the optimization entailed in Eq. (5).

Our aim is to connect \(\delta {\cal W}\) to quantum correlations. To this end, we notice that \(\delta {\cal W}\) is invariant under local unitary transformations: any unitary transformation on S can be incorporated in the transformations used for the extraction of work, while any unitary on A is equivalent to a change of measurement basis. Then, we consider quantum discord24,25,26 as the figure of merit to quantify the degree of quantum correlations shared by system and ancilla. For measurements performed on the system S, discord is defined as

$${{\overrightarrow {\cal D}}_{SA}} = {{\cal I}_{SA}} - \mathop {{\max }}\limits_{\left\{ {\hat \Phi _a^{\cal S}} \right\}} {{\overrightarrow {\cal J}} _{SA}},$$
(6)

where \({{\cal I}_{SA}} = {S_A} + {S_B} - {S_{AB}}\) is the mutual information between S and A (here S is the von Neumann entropy), and \({\overrightarrow {\cal J} _{SA}}\) is the one-way classical information associated with an orthogonal measurement set \(\{ \hat \Phi _a^S\}\) performed on the system.24,25,26 Explicit definitions are given in the “Methods” section. We believe the choice of Eq. (6) is well motivated in light of the explicit asymmetry of both \(\delta {\cal W}\) and \({\overrightarrow {\cal D} _{SA}}\) with respect to the subject of the projective measurements. We are now in a position to state one of the main results of our work, which we present in the form of the following Theorem:

Theorem 1

For any system S and ancilla A prepared in a state \({\hat \rho _{SA}}\) , we have

$$\delta {\cal W} = 0 \Rightarrow {\overrightarrow {\cal D} _{SA}} = 0$$
(7)

with \(\delta {\cal W}\) and \({\overrightarrow D _{SA}}\) as defined in Eq. (5) and (6), respectively.

The asymmetry of the daemonic gain is well reflected into the impossibility of linking \(\delta {\cal W}\) to the discord associated with measurements performed on the ancilla. That is

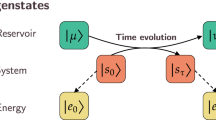
$$\delta {\cal W} = 0\not\Rightarrow {{\overleftarrow {\cal D}} _{SA}} = 0.$$
(8)

The proof of both Theorem 1 and the corollary statement in Eq. (8) are presented fully in the “Methods” Section, while a scheme of principle is presented in Fig. 1. It is important to observe that, in general, the inverse of Theorem 1 does not hold, i.e., \({{\overleftarrow {\cal D}} _{SA}} = 0 \,{\rm{or}}\,{\overrightarrow {\cal D} _{SA}} = 0 \,\not\Rightarrow \,\delta {\cal W} = 0\) as there can well be classically correlated states associated with a non-null daemonic gain. However, a remarkable result is found when \({\hat \rho _{SA}}\) is pure, for which the only possible quantum correlations are embodied by entanglement.

Fig. 1
figure 1

a In our ancilla-assisted protocol, a null daemonic gain gain [i.e., \(\delta {\cal W}\) = 0, cf. Eq. (5)] implies the absence of quantum correlations between the system S and the ancilla A [as measured by the discord associated with measurements on S, cf. Eq. (6)]. b A non-null value of \(\delta {\cal W}\), on the other hand, implies the possible existence of quantum correlations between S and A. For pure bipartite states (in arbitrary dimensions), the nullity of the daemonic gain is a necessary and sufficient condition for separability

Full size image

Theorem 2

For any system S and ancilla A prepared in a pure state \({\hat \rho _{SA}} = \left| \psi \right\rangle {\left\langle \psi \right|_{SA}}\) we have

$$\delta W = 0 \Leftrightarrow {\left| \psi \right\rangle _{SA}} is\,separable,$$
(9)

and \(\delta {\cal W} = \mathop {\sum}\nolimits_k {r_k}{\epsilon _k} - {\epsilon _1}\) , where \({r_k}\) are the Schmidt coefficients of \({\left| \psi \right\rangle _{SA}}\) and \({\epsilon _k}\) are the eigenvalues of \({\hat H_S}\) , ordered such that \({r_k} \ge {r_{k + 1}}\) and \({\epsilon _k} \le {\epsilon _{k + 1}}\) .

Theorem 2 is a thermodynamically motivated separability criterion for pure bipartite states in arbitrary dimensions and an explicit quantitative link between the theory of entanglement and the thermodynamics of information.

Illustrations in two-qubit systems

The statements in Theorems 1 and 2 are completely general, and independent of the nature of either S or A, which could in principle live in Hilbert spaces of different dimensions. However, in order to illustrate their implications and gather further insight into the relation between the introduced daemonic gain and both discord and entanglement, here we focus on the smallest non-trivial situation, which is embodied by a two-qubit system.

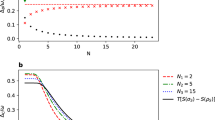
We start with the implications of Theorem 1 and compare \(\delta {\cal W}\) with discord \({\overrightarrow {\cal D} _{SA}}\). Since both these quantities are invariant under local unitary transformations on \({\hat \rho _{SA}}\), without loss of generality we can consider the system Hamiltonian \({\hat H_S} = - {\sigma _z}\) (throughout the remainder of the manuscript we measure energy in units of the Bohr frequency of the system and set \(\hbar = 1\)). This choice of Hamiltonian sets the energy difference between the logical state of the system and allows for an agile evaluation of the extractable work without unnecessary complications (the choice of sign is immaterial as far as our results are concerned). In Fig. 2 we show the distribution of randomly generated two-qubit states over the \(\delta {\cal W}\)-vs.-\({\overrightarrow {\cal D} _{SA}}\) plane. Such an extensive numerical analysis reveals that, for any state \({\hat \rho _{SA}}\) with discord \({\overrightarrow {\cal D} _{SA}} = {\cal D}\), we have

$$\delta {\cal W} \ge \delta {{\cal W}_{{\rm{min}}}}({\cal D}) = h\left( {1 - {\cal D}/2} \right),$$
(10)

where \(h(x) = - x\mathop {{\log }}\nolimits_2 (x) - (1 - x)\mathop {{\log }}\nolimits_2 (1 - x)\). The monotonicity of \(h(x)\) implies that growing values of quantum correlations are associated with a monotonically increasing daemonic gain: for the states lying on such lower bound, quantum correlations form a genuine resource for the catalysis of thermodynamic work extraction. Moreover, as \(\mathop {{\lim }}\nolimits_{x \to 1} h(x) = 0\), a two-qubit system with \({\overrightarrow {\cal D} _{SA}} = 0\) (i.e., a classically correlated state) can achieve, in principle, any value of daemonic gain up to the maximum that, for this case, is \(\delta {\cal W}\) = 1. On the other hand, the daemonic ergotropy is maximized by taking pure two-qubit states with growing degree of entanglement. As \({\cal D} \to 1\) the gap between lower and upper bounds closes as only pure states achieve maximum discord.

Fig. 2
figure 2

Distribution of two-qubit states in the daemonic gain-vs.-discord plane. We have generated 3 × 103 general random states of system and ancilla, evaluating the discord and daemonic gain for each of them (blue dots). The blue curves enclosing the distribution correspond to the boundaries discussed in the body of the paper. Notice that states with no quantum correlations may correspond to arbitrarily large values of the daemonic gain \(\delta {\cal W}\)

Full size image

The analysis of Fig. 2 reveals that the availability of discord-like quantum correlations in the joint system-ancilla state forces the daemonic gain to exceed a minimum bound, washing out a whole range of values of \(\delta {\cal W}\) that are, instead, achievable in principle using classical-quantum states (i.e., states such that \({\overrightarrow {\cal D} _{SA}} = 0\)): A minimum amount of quantum correlations in the state \({\rho _{SA}}\), as quantified by discord, is needed in order to be sure to have a gain \(\delta {\cal W}\) bigger or equal to \(\delta {{\cal W}_{{\rm{min}}}}({\cal D})\). Within the context of this work, this defines the advantage towards enhanced work extraction provided by quantum correlations.

We can now address Theorem 2 and its consequences for two-qubit states. Similarly to what was done above, we have studied the distribution of random two-qubit states in the daemonic ergotropy-vs.-entanglement plane, choosing quantum concurrence \({\cal C}\) as a measure for the latter.30 The results are illustrated in Fig. 3. As before, a lower bound to the amount of daemonic ergotropy at set value of concurrence can be identified. We have that, for any state \({\hat \rho _{SA}}\) with concurrence \({\cal C}\)

$$\delta {\cal W} \ge \delta {{\cal W}_{{\rm{min}}}}({\cal C}) = 1 - \sqrt {1 - {{\cal C}^2}} ,$$
(11)

a lower bound that is achieved by Bell-diagonal states that are fully characterized in the “Methods” section. The upper bound, on the other hand, is achieved by maximally ergotropic (in our daemonic sense) states \({\hat \rho _{SA}} = [\left| {00} \right\rangle {\left\langle {00} \right|_{SA}} + \left| {11} \right\rangle {\left\langle {11} \right|_{SA}} + {\cal C}(\left| {00} \right\rangle {\left\langle {11} \right|_{SA}} + h.c.)]/2\).

Fig. 3
figure 3

Distribution of two-qubit states in the daemonic gain-vs.-concurrence plane. We have generated 104 general random states of system and ancilla, evaluating the concurrence C and daemonic gain \(\delta {\cal W}\) for each of them (red dots). The blue curves enclosing the distribution correspond to boundary families discussed in the body of the paper. Notice that states at \({\cal C} = 0\) may correspond to arbitrarily large values of the daemonic gain \(\delta {\cal W}\)

Full size image

Discussion

We have illustrated an ancilla-assisted protocol for work extraction that takes advantage of the sharing of quantum correlations between a system and an ancilla that is subjected to suitably chosen projective measurements. Our approach allowed us the introduction of a new form of information-enhanced ergotropy, which we have dubbed daemonic, that acts aptly as a witness for quantum correlations in general, and serves as a necessary and sufficient criterion for separability of bipartite pure states. We have characterized fully the distribution of quantum correlated two-qubit states with respect to the figure of merit set by the daemonic ergotropy, finding that quantum correlations embody a proper resource for the work-extraction performances of the states that minimize \(\delta {\cal W}\). Our work opens up interesting avenues for the thermodynamic interpretation of quantum correlations, clarifies their resource-role in ancilla-assisted information thermodynamics and opens up possibilites to understand the role of correlations in the charging power of quantum batteries.31

Methods

Here, we define the notion of discord used in the paper, present details of the core results discussed in the main body of the paper and the formal proofs of both Theorem 1 and 2.

Discord

We recall the definition of quantum discord \({{\overleftarrow {\cal D}}_{SA}}\) associated with orthogonal measurements \(\hat \Phi _a^A\) performed over the ancilla24,25,26

$${{\overleftarrow {\cal D}} _{SA}} = {{\cal I}_{SA}} - {\rm{ma}}{{\rm{x}}_{\{ \hat \Phi _a^A\} }}{{\overleftarrow {\cal J}} _{SA}},$$
(12)

where \({{\cal I}_{SA}}\) is the mutual information \({{\cal I}_{SA}} = S({\hat \rho _A}) + S({\hat \rho _S}) - S({\hat \rho _{SA}})\), \({{\overleftarrow {\cal J}} _{SA}} = S({\hat \rho _S}) - \mathop {\sum}\nolimits_a {p_a}S({\hat \rho _{S|a}})\) is the so-called one-way classical information and \(S(\hat \rho ) = - {\rm{Tr}}[\hat \rho \,\mathop {{\log }}\nolimits_2 \,\hat \rho ]\) is the von Neumann entropy of the general state \(\hat \rho\). The maximization inherent in Eq. (12) is over all the possible orthogonal measurements on the state of A. Similarly, we define the discord \({\overrightarrow D _{SA}}\) associated with measurements performed over the state of the system S as Eq. (12) with the role of S and A being swapped.

Theorem 1

In order to provide a full-fledged assessment of Theorem 1, we should first discuss the following Lemma.

Lemma 1

For any set of orthogonal projective measurements \(\{ \hat {\Pi}_a^A\}\) performed over an ancilla A prepared with a system S in a state \({\hat \rho _{SA}}\) , we have \({{\cal W}_{\{ \hat {\Pi}_a^A\} }} \ge {\cal W}\) .

Proof

In order to show this statement, we observe that

$$\begin{array}{*{20}{l}}\\ {{{\hat \rho }_S}} \hfill & { = \mathop {\sum}\limits_k {r_k}\left| {{r_k}} \right\rangle \left\langle {{r_k}} \right| = \mathop {\sum}\limits_a {\rm{T}}{{\rm{r}}_A}[\hat {\Pi}_a^A{{\hat \rho }_{SA}}]} \hfill \\ \\ {} \hfill & { = \mathop {\sum}\limits_a {p_a}{{\hat \rho }_{S|a}} = \mathop {\sum}\limits_a {p_a}\mathop {\sum}\limits_k r_k^a\left| {r_k^a} \right\rangle \left\langle {r_k^a} \right|.} \hfill \\ \end{array}$$
(13)

Eq. (13) implies that \({r_k} = \mathop {\sum}\nolimits_a {p_a}\mathop {\sum}\nolimits_j r_j^a|\left. {\left\langle {{r_k}} \right|r_j^a} \right\rangle {|^2}\). As \({{\cal W}_{\{ \hat {\Pi}_a^A\} }} - {\cal W} = <$> <$>\mathop {\sum}\nolimits_k {\epsilon _k}\left( {{r_k} - \mathop {\sum}\nolimits_a {p_a}r_k^a} \right)\), we have that

$${{\cal W}_{\{ \hat {\Pi}_a^A\} }} - {\cal W} = \mathop {\sum}\limits_a {p_a}\mathop {\sum}\limits_{k,j} r_j^a{\epsilon _k}\left( {|\left. {\left\langle {{r_k}} \right|r_j^a} \right\rangle {|^2} - {\delta _{kj}}} \right) \ge 0$$
(14)

due to the fact that \(\mathop {\sum}\nolimits_{k,j} r_j^a{\epsilon _k}(|\left. {\left\langle {{r_k}} \right|r_j^a} \right\rangle {|^2} - {\delta _{k{\kern 1pt} j}}) \ge 0\), as this is the ergotropy of \({\hat \rho _{S|a}}\) relative to the Hamiltonian \(\mathop {\sum}\nolimits_k {\epsilon _k}\left| {{r_k}} \right\rangle \left\langle {{r_k}} \right|\), which is non-negative by definition.

We are now in a position to provide the full proof of Theorem 1, which we restate here for easiness of consultation: Theorem 1. For any system S and ancilla A prepared in a state \({\hat \rho _{SA}}\) , we have

$$\delta {\cal W} = 0 \Rightarrow {\overrightarrow {\cal D} _{SA}} = 0$$
(15)

with \(\delta {\cal W}\) and \({\overrightarrow {\cal D} _{SA}}\) as defined in Eq. (5) and (6), respectively.

Proof

In light of Lemma 1, we have that \({{\cal W}_{\{ \hat {\Pi}_a^A\} }} - {\cal W} = 0 \Leftrightarrow \delta {\cal W} = 0\) for any set \(\{ \hat {\Pi}_a^A\}\). Then, in order to prove the statement of the Theorem, it is enough to show that, regardless of the choice of projective set \(\{ \hat {\Pi}_a^A\} ,\quad {{\cal W}_{\{ \hat {\Pi}_a^A\} }} - {\cal W} = 0 \Rightarrow {\overrightarrow {\cal D} _{SA}} = 0\). Let assume that \({\overrightarrow {\cal D} _{SA}} \ne 0\). Then, there is at least a set \(\{ \hat {\Pi}_a^A\}\) such that \({{\cal W}_{\{ \hat {\Pi}_a^A\} }} - {\cal W} \ne 0\). Two cases are possible:

  1. (i)

    There is a measurement outcome \(\bar a\) such that \({\hat \rho _{S|\bar a}} \ne \mathop {\sum}\nolimits_k r_k^{\bar a}\left| {{r_k}} \right\rangle \left\langle {{r_k}} \right|\) with \(r_k^{\bar a} \ge r_{k + 1}^{\bar a}\). Then

    $${{\cal W}_{\{ {\Pi}_a^A\} }} - {\cal W} \ge {p_{\bar a}}\mathop {\sum}\limits_{k,j} r_j^{\bar a}{\epsilon _k}\left( {|\left. {\left\langle {{r_k}} \right|r_j^{\bar a}} \right\rangle {|^2} - {\delta _{kj}}} \right) >0,$$
    (16)

    given that \(\mathop {\sum}\nolimits_{k,j} r_j^{\bar a}{\epsilon _k}\left( {|\left. {\left\langle {{r_k}} \right|r_j^{\bar a}} \right\rangle {|^2} - {\delta _{kj}}} \right)\) is the ergotropy of \({\hat \rho _{S|\bar a}}\) relative to the Hamiltonian \(\mathop {\sum}\nolimits_k {\epsilon _k}\left| {{r_k}} \right\rangle \left\langle {{r_k}} \right|\), and is zero if and only if \({\hat \rho _{S|\bar a}} = \mathop {\sum}\nolimits_k r_k^{\bar a}\left| {{r_k}} \right\rangle \left\langle {{r_k}} \right|\).

  2. (ii)

    For every \({\rm a \ }\) \({\rho _{S|a}} = \mathop {\sum}\nolimits_k r_k^a\left| {{r_k}} \right\rangle \left\langle {{r_k}} \right|\) with \(r_k^a \ge r_{k + 1}^a\). In this case \({{\cal W}_{\{ {\Pi}_a^A\} }} - {\cal W} = 0\). However, as \({\hat \rho _{SA}}\) is such that \({\overrightarrow {\cal D} _{SA}}\, \ne\, 0\), it is always possible to identify another set \(\{ {\hat{\Pi}'}{}_a^A\}\) such that \({{\cal W}_{\{ {{\Pi}'}_a^A\} }} - {\cal W} >0\). In order to show how this is possible, we note that \({\hat \rho _{SA}}\) can be written as

    $${\hat \rho _{SA}} = \mathop {\sum}\limits_{a,a'} \mathop {\sum}\limits_{k,k'} C_{kk'}^{aa'}\left| {{r_k}} \right\rangle {\left\langle {{r_{k'}}} \right|_S} \otimes \left| a \right\rangle {\left\langle {a'} \right|_A}$$

with the condition \({p_a}C_{kk'}^{aa} = r_k^a{\delta _{kk'}}\). As \({\overrightarrow {\cal D} _{SA}} \ne 0\), there are two measurement outcomes \(\bar a\) and \(\bar a\prime\) such that \(C_{kk\prime }^{\bar a \, \bar a} \,\ne\, C_k^{\bar a\,\bar a\prime }{\delta _{kk\prime }}\). Should this be not true, we would have \({\overrightarrow {\cal D} _{SA}} = 0\), and thus a contradiction. Therefore, as \({\overrightarrow {\cal D} _{SA}} \ne 0\), the matrix \(_A\left\langle {\bar a} \right|{\hat \rho _{SA}}{\left| {\bar a\prime } \right\rangle _A}\) cannot be diagonal in the basis \(\{ {\left| {{r_k}} \right\rangle _S}\}\) (here \(\left| {{{\bar a}_A}} \right\rangle\) is the eigenstate of \(\hat {\Pi}_a^A\) with eigenvalues \(\bar a\)). If \(\bar a = \bar a'\), case \((ii)\) cannot occur.

However, if \(\bar a \, \ne \, \bar a\prime\), we can define the new set of projectors \(\{ \hat {{\Pi}'}_{\!\!a}^A\}\) with elements \(\hat {\Pi}\prime _{\!\!\bar a}^A = (\left| {\bar a} \right\rangle + \left| {\bar a\prime } \right\rangle )(\left\langle {\bar a} \right| + \left\langle {\bar a\prime } \right|)/2\), \(\hat {\Pi}\prime _{\!\!\bar a'}^A = (\left| {\bar a} \right\rangle - \left| {\bar a\prime } \right\rangle )(\left\langle {\bar a} \right| - \left\langle {\bar a\prime } \right|)/2\) and \(\hat {\Pi}\prime_{\!\!a}^A = \hat {\Pi}_a^A\) for \(a \, \ne \, \bar a,\bar a'\). Then, the density matrix \(\hat \rho {\prime _{S|\bar a}} = {\rm{T}}{{\rm{r}}_A}\{ \hat {\Pi}\prime _{\!\!\bar a}^A{\hat \rho _{SA}}\} /p{\prime _{\!\!\bar a}}\) reads

$$\begin{array}{ccccc}\\ \hat \rho {\prime _{\!\!S|\bar a}} = & \frac{1}{{2p{\prime _{\!\!\bar a}}}}\left[\mathop {\sum}\limits_k ({p_{\bar a}}r_k^{\bar a} + {p_{\bar a'}}r_k^{\bar a'})\left| {{r_k}} \right\rangle {\left\langle {{r_k}} \right|_S} + \left( {{\,}_A\left\langle {\bar a} \right|{{\hat \rho }_{SA}}{{\left| {\bar a\prime } \right\rangle }_A}{ + _A}\left\langle {\bar a\prime } \right|{{\hat \rho }_{SA}}{{\left| {\bar a} \right\rangle }_A}} \right)\right],\\ \end{array}$$
(17)

which shows that \(\hat \rho {\prime _{\!\!\!S|\bar a}}\) is not diagonal in the basis \(\{ {\left| {{r_k}} \right\rangle _S}\}\). Therefore, \(\rho {\prime _{\!\!\!S|\bar a}} \ne \mathop {\sum}\nolimits_k r\prime _{\!\!\!k}^{\bar a}\left| {{r_k}} \right\rangle {\left\langle {{r_k}} \right|_S}\) with \(r\prime _{\!\!k}^{\bar a} \ge r\prime _{\!\!\!k + 1}^{\bar a}\). So, proceeding in a similar way as for case \((i)\), we conclude that

$${{\cal W}_{\{ {{{\Pi}'}_a^A}\} }} - {\cal W} >0.$$
(18)

If \(_A\left\langle {\bar a} \right|{\hat \rho _{SA}}{\left| {\bar a\prime } \right\rangle _A}{ + _A}\left\langle {\bar a\prime } \right|{\hat \rho _{SA}}{\left| {\bar a} \right\rangle _A} = 0\), it is enough to consider \(\hat \rho {\prime _{\!\!S|\bar a\prime }}\) instead of \(\hat \rho {\prime _{\!\!S|\bar a}}\).

Having proven Theorem 1, we can provide a justification of two important Corollaries

Corollary 1

Under the premises of Theorem 1, \(\delta {\cal W} = 0 \,{\Rightarrow} {{\overleftarrow {\cal D}} _{SA}} = 0\)

Proof.

It is enough to consider the state

$${\hat \rho _{SA}} = \mathop {\sum}\limits_{k,a} {q_{ak}}\left| {{r_k}} \right\rangle {\left\langle {{r_k}} \right|_S} \otimes \left| {{\phi _a}} \right\rangle {\left\langle {{\phi _a}} \right|_A},$$
(19)

where \(\{ {\left| {{\phi _a}} \right\rangle _A}\}\) is a non orthogonal set of states. Under such conditions, we have \({{\overleftarrow {\cal D}} _{SA}}\, \ne \, 0\). If we choose \({q_{ak}}\) such that \({q_{ak}} \ge {q_{ak + 1}}\), we have \({{\cal W}_{\{ \hat {\Pi}_a^A\} }} - {\cal W} = 0\) for any set \(\{ \hat {\Pi}_a^A\}\), as \({\hat \rho _{S|a}} = \mathop {\sum}\nolimits_k r_k^a\left| {{r_k}} \right\rangle {\left\langle {{r_k}} \right|_S}\) with \(r_k^a = \mathop {\sum}\nolimits_{a'} {q_{a'{\kern 1pt} k}}{\left| {\left. {\left\langle {{\phi _{a'}}} \right|{a_A}} \right\rangle } \right|^2}/{p_a} \ge r_{k + 1}^a\)).

Corollary 2

Under the premises of Theorem 1, we have that \({{\overleftarrow {\cal D}} _{SA}} = 0\,{\rm{or}}{\overrightarrow {\,{\cal D}} _{SA}} = 0 \, {\not \Rightarrow}\, \delta {\cal W} = 0\) .

Proof.

We consider the state \({\hat \rho _{SA}} = \mathop {\sum}\nolimits_k {r_k}\hat {\Pi}_k^S \otimes \hat {\Pi}_k^A\), where \(\hat {\Pi}_k^A\) and \(\hat {\Pi}_k^S\) are orthogonal projectors of rank one. Although such state has zero discord, the quantity \({{\cal W}_{\{ {\Pi}_k^A\} }} - {\cal W}\) is positive since

$${{\cal W}_{\{ {\Pi}_k^A\} }} - {\cal W} = \mathop {\sum}\limits_k {r_k}{\epsilon _k} - {\epsilon _1} >0.$$
(20)

Therefore, \(\delta {\cal W} >0\).

Theorem 2

We can now provide a proof of Theorem 2, which we state again for easiness of consultation.

Theorem 2

For any system S and ancilla A prepared in a pure state \({\hat \rho _{SA}} = \left| \psi \right\rangle {\left\langle \psi \right|_{SA}}\) we have

$$\delta W = 0 \Leftrightarrow {\left| \psi \right\rangle _{SA}} \, is\,separable,$$
(21)

and \(\delta {\cal W} = \mathop {\sum}\nolimits_k {r_k}{\epsilon _k} - {\epsilon _1}\) , where \({r_k}\) are the Schmidt coefficients of \({\left| \psi \right\rangle _{SA}}\) and \({\epsilon _k}\) are the eigenvalues of \({\hat H_S}\) , ordered such that \({r_k} \ge {r_{k + 1}}\) and \({\epsilon _k} \le {\epsilon _{k + 1}}\).

Proof

We make use of the instrumental result embodied by Corollary 2 and consider the pure state \({\hat \rho _{SA}} = \left| {{\psi _{SA}}} \right\rangle \left\langle {{\psi _{SA}}} \right|\) whose Schmidt decomposition reads \(\left| {{\psi _{SA}}} \right\rangle = \mathop {\sum}\nolimits_k \sqrt {{r_k}} {\left| {{r_k}} \right\rangle _S} \otimes {\left| {{\phi _k}} \right\rangle _A}\) with \({r_k} \ge {r_{k + 1}}\). Corollary 2 has shown that \(\delta {\cal W} = \mathop {\sum}\nolimits_k {r_k}{\epsilon _k} - {\epsilon _1}\). Therefore, \(\delta {\cal W}\) = 0 it must be \({\epsilon _1} = \mathop {\sum}\nolimits_k {r_k}{\epsilon _k}\), which implies \({r_k} = {\delta _{1k}}\). This implies that the state has a single Schmidt coefficient, and is thus separable. The proof of the reverse statement is trivial.

Analysis of the two-qubit case

We provide additional details on the analysis performed on the two-qubit case illustrated in the main body of the paper.

In what follows, with no loss of generality, we choose the system Hamiltonian \({\hat H_S} = - {\hat \sigma _z}\). As stated in the main body of the paper, we choose concurrence as the entanglement measure to be used in our analysis. For a bipartite qubit state, concurrence is defined as30

$${\cal C} = {\rm{max}}[0,{\lambda _1} - \mathop {\sum}\limits_{j >1} {\lambda _j}],$$
(22)

where \({\lambda _k}\) are the square roots of the eigenvalues of \({\hat{\rho}} {\hat{\tilde{\rho}}}\) with \({\hat{\tilde{\rho}}} = ({\hat \sigma _y} \otimes {\hat \sigma _y}){\hat \rho ^*}({\hat \sigma _y} \otimes {\hat \sigma _y})\), ordered so that \({\lambda _k} \ge {\lambda _{k + 1}}\). In the main body of the paper we have proven that the ergotropic gain of any state \({\hat \rho _{SA}}\) with concurrence \({\cal C}\) is larger than, or equal to

$$\delta {{\cal W}_{{\rm{min}}}}({\cal C}) = 1 - \sqrt {1 - {{\cal C}^2}}.$$
(23)

The states locally equivalent to

$${\hat \rho _{SA}} = \left( {\begin{array}{*{20}{l}}\\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ \\ 0 \hfill & x \hfill & {{\cal C}/2} \hfill & 0 \hfill \\ \\ 0 \hfill & {{\cal C}/2} \hfill & {1 - x} \hfill & 0 \hfill \\ \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array}} \right)$$
(24)

with \(x = (1 \pm \sqrt {1 - {{\cal C}^2}} )/2\), which have concurrence \({\cal C}\), are such that \(\delta {\cal W} = \delta {{\cal W}_{{\rm{min}}}}({\cal C})\). These states belong to the class parametrized as \(p\left| {\phi _ + ^\eta } \right\rangle <$> <$>\left\langle {\phi _ + ^\eta } \right| + \frac{{1 - p}}{2}(\left| {01} \right\rangle \left\langle {01} \right| + \left| {10} \right\rangle \left\langle {10} \right|)\) where \(\left| {\phi _ + ^\eta } \right\rangle = \sqrt \eta \left| {01} \right\rangle + \sqrt {1 - \eta } \left| {10} \right\rangle \). On the other hand, the states locally equivalent to

$${\hat \rho _{SA}} = \left( {\begin{array}{*{20}{c}}\\ {1/2} & 0 & 0 & {{\cal C}/2} \\ \\ 0 & 0 & 0 & 0 \\ \\ 0 & 0 & 0 & 0 \\ \\ {{\cal C}/2} & 0 & 0 & {1/2} \\ {} & {} & {} & {} \\ \\ \end{array}} \right),$$
(25)

which also have concurrence \({\cal C}\), are such that \(\delta {\cal W} = 1\), and thus embody the upper bound to the daemonic ergotropy at set value of concurrence.

In order to show this, we parameterize the projectors \(\hat {\Pi}_1^A\) and \(\hat {\Pi}_2^A\) that are needed to calculate the daemonic ergotropy in terms of the angles \(\theta \in [0,\pi ]\) and \(\phi \in [0,2\pi )\) such that

$${\Pi}_1^A = \left( {\begin{array}{*{20}{c}}\\ {\mathop {{\cos }}\nolimits^2 \left( {\theta /2} \right)} & {{e^{ - i\phi }}\sin (\theta /2)} \\ \\ {{e^{i\phi }}\sin (\theta /2)} & {\mathop {{\sin }}\nolimits^2 \left( {\theta /2} \right)} \\ \\ {} & {} \end{array}} \right)$$

and \({\Pi}_2^A = 1 - {\Pi}_1^A\). An extensive numerical analysis of the distribution itself has shown that the states lying on the lower boundary belong to the class of so-called \(x\) -states of the form

$${\rho _{SA}} = \left( {\begin{array}{*{20}{l}}\\ a \hfill & 0 \hfill & 0 \hfill & z \hfill \\ \\ 0 \hfill & b \hfill & w \hfill & 0 \hfill \\ \\ 0 \hfill & w \hfill & c \hfill & 0 \hfill \\ \\ z \hfill & 0 \hfill & 0 \hfill & {1 - a - b - c} \hfill \\ \end{array}} \right),$$
(26)

where \(a,b,c,w,z\) are positive numbers such that \(bc \ge {w^2}\), \(ad \ge {z^2}\). This class plays a key role in the characterization of the states that maximize quantum correlations at set values of the purity of a given bipartite qubit state.32,33,34,35,36 The ergotropy \({\cal W}\) for such class of states is

$${\cal W} = \left\{ {\begin{array}{*{20}{l}}\\ 0 \qquad{{\rm{for}}\;a + b \ge \frac{1}{2},}\qquad \\ \\ {2 - 4(a + b)} \quad{{\rm{otherwise}}.} \\ \end{array}} \right.$$
(27)

On the other hand, we have \({{\cal W}_{\{ {\Pi}_a^A\} }} = 1 - 2(a + b) + ({X_ + } + {X_ - })/2\) with

$$\begin{array}{ccccc}\\ {X_ \pm } = & \left\{ {{{\left[ {2(a + b) - 1 \pm (1 - 2b - 2c)\cos \theta } \right]}^2}} \right. \left. + \, 4\left[w{e^{ - i\phi }}\right. + z{e^{i\phi }}{{|}^2}{{\sin }^2}\theta \right\}^{\frac{1}{2}}\\ \end{array}$$
(28)

The associated concurrence is \({\cal C} = 2{\rm{max}}\{ 0,z - \sqrt {bc} ,w - \sqrt {ad} \}\). We make the ansatz that a state as in Eq. (24) with \(x\) real and positive, minimizes \(\delta {\cal W}\) at a fixed value of \({\cal C}\). Then, from the positivity of the density matrix, \(x\) must satisfy the condition \({\cal C} \le 2\sqrt {x(1 - x)}\) with \(x \in [0,1]\).

For such state, we have \(\delta {\cal W} = 2 - 2x - {\rm{max}}\{ 0,2 - 4x\}\). If we consider \(x \ge 1/2\), then \(\delta {\cal W} = 2 - 2x\), which is minimum when \(x\) is maximum, i.e., for \(x = (1 + \sqrt {1 - {{\cal C}^2}} )/2\). For \(x \le 1/2\) we have \(\delta {\cal W} = 2x\), which is minimum when \(x\) is minimum, i.e., for \(x = (1 - \sqrt {1 - {{\cal C}^2}} )/2\). In both cases, \(\delta {\cal W}\) takes the expression in Eq. (23).

In order to show that the class in Eq. (25) is such that \(\delta {\cal W} = 1\), it is enough to observe that, for such state, \({\cal W} = 0\). In fact, we trivially have \({\rho _S} = {1}/2\) and, by choosing for instance \(\hat {\Pi}_1^A = \left| 0 \right\rangle {\left\langle 0 \right|_A}\), we get pure post-measurement states, and thus \({{\cal W}_{\{ \hat {\Pi}_a^A\} }} = 1\). Therefore, \(\delta {\cal W} = 1\) regardless of the value taken by \({\cal C}\).

As mentioned above, the validity of the ansatz used here is justified by an extensive numerical investigation based on 106 random bipartite states generated uniformly according to the Haar measure.