Introduction

Nonlinear phenomena are of great interests and particularly useful for applications. One important example in spintronics is the spin torque nano-oscillator (STNO)1,2,3,4,5,6,7,8,9,10,11, where the magnetic dissipation is fully compensated by the current-induced spin torque12,13, exhibiting persistent oscillations of particular magnetic textures, such as uniform magnetization1,14,15,16, magnetic vortices2,3,17,18,19,20, skyrmions7,21,22,23, etc. Potential applications of STNOs include microwave generators in communication technology and core elements in recently developed neuromorphic spintronics24,25,26,27,28,29. For a multi-STNO system, the interactions between different STNOs can give rise to additional intriguing nonlinear dynamics, for instance, the mutual synchronization, which corresponds to the situation where all STNOs oscillate with the same frequency and the same phase30 so that the radiation power of the STNOs can be significantly enhanced, compared to an individual single-STNO-based microwave generator. Another interesting nonlinear phenomenon of interacting oscillators, the so-called frequency comb characterized by equally spaced discrete frequencies in the spectrum31,32, has received increasing research attention33,34,35 and been predicted also in magnetic systems36,37,38,39,40,41.

Among the reported proposals, the synchronization and frequency comb based on spatially separated STNOs coupled through dipolar field require the fabrication of a patterned magnetic working layer39, which might reduce the quality of the devices and cause additional cost. The weak strength of the dipolar-induced coupling not only limits the window of frequency mismatch between the oscillators, but also hinders the synchronization of multiple oscillators42. Those STNOs coupled through spin waves within one magnetic working layer36,37,38, on the other hand, inevitably suffer from energy inefficiency due to the large dissipation in form of spin waves irrelevant to the coupling between the STNOs. Moreover, owing to the mutual disturbance of the dynamical magnetizations in the neighboring STNOs, there is a critical distance between the STNOs, below which neither the frequency comb nor the synchronization can be stabilized by the spin-wave-induced coupling37, which hinders the device miniaturization for related applications. Recent theoretical proposal of individual boundary-free ferrimagnetic (FiM)-skyrmion-based STNO43 sheds some light to overcome these problems and stimulates the present study.

In this work, we demonstrate theoretically both synchronization and frequency comb in the dynamics of two coupled FiM-skyrmion-based STNOs, where the repulsive coupling strength between skyrmions results from the instantaneous spatial overlap between their magnetic texture and therefore depends on not only the distance of the STNOs but also the trajectories of the skyrmion motion44,45,46. An explicit analysis on the interacting energy and the current-induced potential well interprets the condition of the transition between synchronization and frequency comb obtained from micromagnetic simulations. The extension of these nonlinear dynamical behaviors to a STNO array and their tunability by the applied currents are also demonstrated.

Results and discussion

Theoretical model

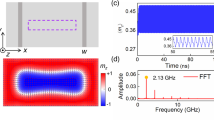
Figure 1a depicts our model with two skyrmion-based STNOs, where the magnetic working layer is a synthetic ferrimagnetic (SFiM) film composed of two ferromagnets with different magnetizations (parameterized by Mt and Mb), which are coupled by a relatively strong antiferromagnetic Ruderman–Kittel–Kasuya–Yosida (RKKY) interaction47,48. The skyrmion textures in the two ferromagnets are therefore bound together to behave as a single SFiM skyrmion (see Fig. 1b for the magnetic structure). Current injectors constructed by the spacer and fixed layer are placed on top of the SFiM film in order to generate spin transfer torques to trigger the SFiM-skyrmion dynamics, more explicitly, a stable orbital motion around the edge of each current injector43 (see Fig. 1c).

Fig. 1: Nonlinear dynamics in coupled SFiM-skyrmion-based STNOs.
figure 1

a Sketch of two coupled skyrmion-based STNOs. b Magnetic texture of the SFiM skyrmion. The color bar represents the z component of magnetization. c Definitions of the quantities to describe the rotational motion of the skyrmions. The blue and orange dashed circles indicate the current injection areas. d–f Fast Fourier transformation (FFT) spectra of the recorded magnetizations \({m}_{x,{{{{\rm{A}}}}}_{1}}^{{{{\rm{t}}}}}\) and \({m}_{x,{{{{\rm{A}}}}}_{2}}^{{{{\rm{t}}}}}\) averaged separately over Area1 and Area2 indicated in a, with oscillator spacing d12 = 70, 50 and 40 nm. The insets show the time evolution of magnetizations. In the calculation, we take the diameters of the circular injectors d1 = d2 = 30 nm, saturation magnetizations \({M}_{{{{\rm{s}}}}}^{{{{\rm{t}}}}}=600\) kA m−1 and \({M}_{{{{\rm{s}}}}}^{{{{\rm{b}}}}}=580\) kA m−1, and driving currents j1 = 40 MA cm−2 and j2 = 80 MA cm−2.

Full size image

To investigate the consequences of the dynamical interactions between the SFiM skyrmions, we employ the open-source micromagnetic software MUMAX349 to simulate the magnetization dynamics (see “Methods” section for the details). With the magnetic structure from micromagnetic simulations, we also evaluate the parameters in the phenomenological equation of skyrmion motion, i.e., the Thiele’s equation43,50,51,52,53, which could provide a comprehensive understanding of the coupled skyrmion dynamics. Specifically, as derived in Supplementary Note 1, the Thiele’s equation of ith skyrmion can be written as

$${{{{\bf{m}}}}}_{{{{\rm{eff}}}},i}\cdot {\ddot{{{{\bf{r}}}}}}_{{{{\rm{c}}}},i}={{{{\bf{G}}}}}_{i}\times {\dot{{{{\bf{r}}}}}}_{{{{\rm{c}}}},i}-\alpha {{{{\bf{L}}}}}_{i}\cdot {\dot{{{{\bf{r}}}}}}_{{{{\rm{c}}}},i}+{{{{\bf{F}}}}}_{j,i}+{{{{\bf{F}}}}}_{{{{\rm{ss}}}},i},$$
(1)

where meff is the effective mass tensor, G the gyrovector, α the damping constant, and L the dissipative tensor. The instantaneous location rc of the SFiM skyrmion, with respect to the center of the corresponding current injector, is defined by its guiding center54, as shown in Fig. 1c. Fj and Fss correspond to the current-induced force and the one from skyrmion-skyrmion interaction, respectively. More details of Eq. (1) are presented in Supplementary Note 1.

Synchronization and frequency comb

We consider different values of the injected currents through the two STNOs to drive them with a small free-running frequency difference. The dynamic properties of the two STNOs are read out by the local magnetizations averaged over the detection areas (Area1 and Area2 in Fig. 1a), \({m}_{x,{{{{\rm{A}}}}}_{1}}^{{{{\rm{t}}}}}\) and \({m}_{x,{{{{\rm{A}}}}}_{2}}^{{{{\rm{t}}}}}\), which reflect the output signals in magnetoresistance measurement. The micromagnetic simulation with different values of oscillator spacing (d12) shows distinct dynamic properties. Specifically, when the spacing is too large, as shown by Fig. 1d with d12 = 70 nm, the two STNOs simply present individual oscillations. At a moderate spacing, they interfere with each other, resulting in a nice frequency comb (see Fig. 1e with d12 = 50 nm). Once d12 becomes sufficiently small, the oscillations of the two STNOs are forced to share a common frequency, corresponding to a synchronization (Fig. 1f with d12 = 40 nm). Supplementary Movies 1 and 2 show the dynamic behavior of skyrmions in frequency comb and synchronization situations, respectively.

To gain a deeper understanding of the evolution of the above dynamics with varying d12, the trajectories of the skyrmion motion, which are responsible for the time-dependent \({m}_{x,{{{{\rm{A}}}}}_{i}}^{{{{\rm{t}}}}}\), are calculated from both the MUMAX3 and Thiele’s equation and presented in Supplementary Fig. 2 with different values of d12. Accordingly, FFT spectra of the x components of the skyrmion locations, rcx,1 and rcx,2, are plotted in Fig. 2, which exhibits exactly the same frequency characteristics as those in Fig. 1. Namely, before entering the synchronization situation, the FFT spectrum experiences a frequency comb due to nonlinear effects55. The equal spacing in the frequency comb scenario can be clearly recognized in Fig. 2c, d with d12 = 50 nm. As seen, the results from the Thiele’s equation nicely reproduce all features obtained from MUMAX3, except a slightly larger difference between the two free-running frequencies, which might be introduced by the approximation in the phenomenological parameters in Thiele’s equation. Therefore, our further calculation and analysis on synchronization and frequency comb will be mainly based on the Thiele’s equation.

Fig. 2: Frequency spectra for different oscillator spacings.
figure 2

FFT spectra of rcx,1 (blue curve) and rcx,2 (orange curve) from a MUMAX3 and b Thiele’ s equation. c, d Details of frequency spectrum at d12 = 50 nm. The parameters in this calculation are the same as those used in Fig. 1.

Full size image

Figure 3a shows the frequencies of the peaks in the FFT of rcx,1 and rcx,2 as functions of d12. The color of the data points stands for the amplitude of the corresponding FFT peaks. A transition between the synchronization and frequency comb is clearly observed at \({d}_{12}^{* }\simeq 41.4\) nm. This behavior is similar to the previous prediction from the classical Kuramoto model31. However, after a close comparison with the results of Kuramoto model, we find that the frequencies in Fig. 3a systematically increase when the oscillator spacing approaches \({d}_{12}^{* }\) from both sides, whereas those in Kuramoto model are always distributed symmetrically around the average of the two free-running frequencies55.

Fig. 3: Nonmonotonic variation of oscillation frequency with the oscillator spacing.
figure 3

a FFT spectra of rcx,1 (open symbols) and rcx,2 (solid symbols), b temporal-averaged orbit radius rc,i and c azimuthal component Fjθ,i of current-induced forces, with different oscillator spacings d12. The color bars in a represent the amplitude in Fourier transformation. The light yellow and green backgrounds indicate the synchronization and non-synchronization regions, respectively. The curves in a are the plots of Eq. (2), while the symbols in a–c represent the results of the Thiele’ s equation with the same parameters as those used in Fig. 1.

Full size image

To analyze this behavior, we derive the expressions of major frequencies in both synchronization and non-synchronization regions by ignoring the minor inertia term of Eq. (1) (see derivations in Supplementary Note 2), which are found to be in the same form as

$${\omega }_{i}=\frac{{{{{\bf{F}}}}}_{j,i}\cdot {{{{\bf{e}}}}}_{\theta ,i}}{\alpha L\left\vert {{{{\bf{r}}}}}_{{{{\rm{c}}}},i}\right\vert },$$
(2)

with i = 1, 2 for the two STNOs in the non-synchronization region and i = syn for an effective oscillator after synchronization. For the latter, we define rc,syn = rc,1 + rc,2 and Fj,syn = Fj,1 + Fj,2. The unit vector eθ,i is along the azimuthal direction perpendicular to rc,i and L denotes the diagonal component of the dissipative tensor L. In Fig. 3b, c, we present the temporal-averaged values of rc,i and Fjθ,i, respectively, as functions of d12, from which we see that rc,i and Fjθ,syn (Fjθ,1 and Fjθ,2) decrease (increase) in the vicinity of \({d}_{12}^{* }\). The decrease of Fjθ,syn with increasing d12 results from the change of the angle between Fj,1 and Fj,2. By substituting these quantities into Eq. (2), we calculate ωi and plot them as solid curves in Fig. 3a, which match well with FFT spectrum.

It is noteworthy that in the synchronization region below \({d}_{12}^{* }\), as shown in Supplementary Fig. 3, the relative phase Δ (=φ1 − φ2) of the two STNOs displays a small variation around a certain value with time, forming a dancing synchronization56. In addition, as seen from Fig. 3a, there is a weak signal at the double synchronization frequency, which is caused by the deviation of the skyrmion trajectory from a perfect circular orbit (see Supplementary Fig. 2b, g)55,57. Above \({d}_{12}^{* }\), the relative phase changes over the 2π range (see Supplementary Fig. 3), as expected for a non-synchronization state.

Transition condition from synchronization to frequency comb

The distinct behaviors of the relative phase in synchronization and frequency comb regions inspire us to derive the condition between the two cases from the evolution equation of the relative phase. In practice, we write the evolution equation in the form of two effective potential energies as58 (see Supplementary Note 2 for the details)

$$\frac{d\Delta }{dt}=-\frac{\partial {V}_{j}}{\partial \Delta }-\frac{\partial {V}_{{{{\rm{ss}}}}}}{\partial \Delta },$$
(3)

where the effective potential Vj is generated by the current-induced driving forces and can be expressed as

$${V}_{j}=-\left(\frac{{F}_{j\theta ,1}}{\alpha L{r}_{{{{\rm{c}}}},1}}-\frac{{F}_{j\theta ,2}}{\alpha L{r}_{{{{\rm{c}}}},2}}\right)\Delta ,$$
(4)

depending linearly on Δ. The other potential energy Vss is associated with the skyrmion-skyrmion interaction force, which, under the condition of rc,1 ≈ rc,2 in our simulation, can be approximately described by

$${V}_{{{{\rm{ss}}}}}\,\approx\, F{\lambda }_{{{{\rm{ss}}}}}\left(\frac{1}{\alpha L{r}_{{{{\rm{c}}}},1}^{2}}+\frac{1}{\alpha L{r}_{{{{\rm{c}}}},2}^{2}}\right){{{{\rm{e}}}}}^{{\lambda }_{0}-{r}_{12}/{\lambda }_{{{{\rm{ss}}}}}},$$
(5)

where r12 is the distance between the skyrmion centers (see Fig. 1c). The fitting of the numerical results for the interaction potential energy reveals that the three characteristic parameters F, λ0 and λss equal to 2.3 × 10−12 N, 9.68 and 4.348 nm, respectively (see Supplementary Note 1). Equation (5) suggests a higher interacting potential when the skyrmions are close with each other.

In the dancing synchronization region, the relative phase between the two oscillators only shows a small-amplitude vibration around a finite value. The temporal average of Eq. (3) over a period thus gives the vanishing of its left side, leading to ∂(〈Vj〉 + 〈Vss〉)/∂Δ = 0. The specific value of the average relative phase 〈Δ〉 can be determined from the extremum problem of the total potential energy 〈Vj〉 + 〈Vss〉 with respect to Δ. Accordingly, we calculate 〈Vj〉 and 〈Vss〉 (see Supplementary Note 2 for the details), and plot 〈Vj〉 + 〈Vss〉 as a function of Δ with different values of d12 in Fig. 4a. As one can see, for d12 = 35 nm (far below the critical value \({d}_{12}^{* }=\) 41.4 nm in Fig. 3), the potential curve has a local minimum value at Δ ~ 39 degrees. As shown in Fig. 4b, the relative phases extracted from this way show reasonable agreement with those based on the Thiele’s equation in the whole synchronization region. In the opposite limit with a sufficient large d12, there is no local minimum in the total potential anymore (see the yellow curve in Fig. 4a with d12 = 50 nm), reflecting the breakdown of synchronization.

Fig. 4: Phase difference from effective potentials.
figure 4

a The temporal-averaged total effective potential energy as a function of the relative phase between the two oscillators, with different values of d12. b The phase difference at the local minimum of the potential energy and that from the Thiele’ s equation in the synchronization region. In this calculation, the parameters are the same as those used in Fig. 1.

Full size image

The condition of the synchronization thus corresponds to the appearance of the local minimum point in the Δ dependence of the total potential energy. The potential curve with \({d}_{12}^{* }=41.4\) nm, as shown by the red solid curve in Fig. 4a, however, still has a clear local minimum feature. This can be attributed to approximations in the estimation of the potential energy, for example, rc,1 ≈ rc,2. Considering the relatively weak dependence of 〈Vj〉 on d12 and taking its value at d12 = 41.4 nm, we calculate the total potential with Eq. (5) and find that the local minimum feature starts around \({\tilde{d}}_{12}^{* }=44.9\) nm, which is slightly larger than \({d}_{12}^{* }=41.4\) nm from the Thiele’s equation.

Figure 5a, b summarize the variations of \({\tilde{d}}_{12}^{* }\), as well as those of \({d}_{12}^{* }\) from the Thiele’s equation and MUMAX3, with the increase of current density j1 and saturation magnetization \({M}_{{{{\rm{s}}}}}^{{{{\rm{t}}}}}\), respectively. The results from different approaches show nice agreement. The increase of the critical distance in Fig. 5a and the nonmonotonic behavior in Fig. 5b can therefore be understood from the perspective of potential energy. Since the current-induced potential Vj changes linearly with Δ, according to Eq. (4), the formation of the energy minimum state observed in Fig. 4a then relies on the ratio \(\left\vert {V}_{j}\right\vert /\Delta\). A larger \(\left\vert \langle {V}_{j}\rangle \right\vert /\Delta\) requires a stronger interaction potential 〈Vss〉 and thus a smaller distance d12 to synchronize the two STNOs. For a quantitative estimation, we compute \(\left\vert \langle {V}_{j}\rangle \right\vert /\Delta\) from the Thiele’s equation for different current densities j1 (saturation magnetizations \({M}_{{{{\rm{s}}}}}^{{{{\rm{t}}}}}\)), as shown in the inset of Fig. 5a (Fig. 5b), where we neglect the weak d12-dependence of 〈Vj〉 and choose a small oscillator spacing d12 = 40 nm (34 nm) to ensure the STNOs always in a synchronization state for all adopted parameters. As expected, \(\left\vert \langle {V}_{j}\rangle \right\vert /\Delta\) decreases with j1 and shows a nonmonotonic dependence on \({M}_{{{{\rm{s}}}}}^{{{{\rm{t}}}}}\), explaining well the change of the critical distance. The influences of the damping constant and RKKY coupling coefficient on \({d}_{12}^{* }\) are summarized in Supplementary Fig. 4. While the critical distance is found to show a nonmonotonic dependence on the RKKY coupling coefficient, it decreases with the increase of damping constant, which can be interpreted by the variation of \(\alpha \left\vert \langle {V}_{j}\rangle \right\vert /\Delta\). As shown in Supplementary Fig. 5, the values of 〈rc,i〉 (〈Fjθ,i〉) involved in \(\left\vert \langle {V}_{j}\rangle \right\vert\) become smaller (larger) for a higher damping, giving rise to a larger \(\alpha \left\vert \langle {V}_{j}\rangle \right\vert /\Delta\) and hence a smaller critical distance.

Fig. 5: Tunability of critical distance.
figure 5

a The critical distance \({d}_{12}^{* }\) as a function of the current density j1 (with fixed magnetization \({M}_{{{{\rm{s}}}}}^{{{{\rm{t}}}}}=600\) kA m−1) and b its dependence on the saturation magnetization \({M}_{{{{\rm{s}}}}}^{{{{\rm{t}}}}}\) (with j1 = 60 MA cm−2). The insets show the calculated values of \(\left\vert \langle {V}_{j}\rangle \right\vert /\Delta\) with d12 = 40 nm and 34 nm for a and b, respectively. Other parameters are the same as those in Fig. 1.

Full size image

In contrast to the previous proposals based on dipolar interactions between spatially separated STNOs, the coupling between our SFiM-skyrmion-based STNOs originates mainly from the short-range exchange interactions, while the demagnetization effect of the dipolar interactions is found to play a marginal role (see Supplementary Fig. 6). In addition, the FiM resonance frequency is about 140 GHz for our adopted parameters, which is much higher than the working frequency of our STNOs (about 2 GHz). Thus, the spin-wave excitation and the energy dissipation through it can be neglected in our oscillator system.

Extension to a two-dimensional STNO array

In this section, we take a 3 × 3 STNO array (see Fig. 6a) as an example in our micromagnetic simulation to demonstrate the extension of the foregoing synchronization and frequency comb, as well as their current control, in multiple STNOs with a fixed geometry. In the simulation, we tune the current density of the central STNO (Osc5), j5, and choose the other driving currents randomly within the range of 65–75 MA cm−2 to introduce different working frequencies of the STNOs. Figure 6b shows the FFT spectra of the recorded magnetizations averaged over 45 × 45 nm2 areas, with different values of j5. As one can see, the synchronization and frequency comb features do show up for j5 = 70 MA cm−2 and j5 = 55 MA cm−2, respectively. Interestingly, for j5 = 60 MA cm−2 between them, chaotic peaks appear, implying the loss of the periodicity of skyrmion motion. For a rather smaller current j5 = 40 MA cm−2, on the other hand, we surprisingly find a clear synchronized main frequency accompanying with relatively weak signals at fractional frequencies (1/3 and 2/3 of the main frequency), which might be generated by the strong nonlinearity of the system59.

Fig. 6: Current control in STNO array.
figure 6

a Structure of our 3 × 3 STNO array under consideration. The dashed circles indicate the current injection areas (labeled Osc1-Osc9) with the identical diameters of 30 nm and center-to-center distance of 70 nm. The current densities are adopted to be 67, 66, 66, 71, 75, 68, 69 and 72 MA cm−2 for j1-j4 and j6-j9. b FFT spectra of the recorded magnetizations averaged over 45 × 45 nm2 areas, with different values of j5 injected into the central STNO (Osc5). The curves in b have been shifted vertically for clarity. c The time evolution of the phase difference (θ1 − θ5) and order parameter (ζ) with different values of j5.

Full size image

The motion of each skyrmion can be read out from the direction of the total magnetization below the corresponding current injection area60. In practice, we define the angle between the in-plane magnetization component of the mth STNO and the x axis as θm and plot the time evolution of the phase difference between Osc1 and Osc5 in the top panel of Fig. 6c with different values of j5. We can see that the two oscillators are indeed in synchronization states for j5 = 40 and 70 MA cm−2, but not for j5 = 55 and 60 MA cm−2 (see Supplementary Fig. 3 of the two-STNO case). For a full analysis of all STNOs, we compute the order parameter42,

$$\zeta =\frac{1}{N}\left\vert \mathop{\sum}\limits_{m}{{{{\rm{e}}}}}^{{{{\rm{i}}}}{\theta }_{m}}\right\vert ,$$
(6)

where N = 9 is the total number of STNOs. As ζ = 0 and 1 correspond to disordered state and perfect synchronization, respectively, the finite value ζ > 0.5, shown in the bottom panel of Fig. 6c, reflects the strong correlation between our STNOs even in the non-synchronization states. The good phase coherence for the synchronization state at j5 = 70 MA cm−2 leads to ζ ~ 0.92. It should be pointed out that the choice of the central STNO is essential for the current control, according to Supplementary Fig. 7, where the manipulation of the input currents at Osc1 and Osc2 does not introduce qualitative change in the dynamics. In this work, the thermal effects are not taken into account. One could expect that the trajectories of skyrmions will be affected by the thermal fluctuation, which results in a noisy frequency spectrum and may prevent the observation of the synchronization and frequency comb at high temperatures. However, such effect could be too weak to play a relevant role at low temperatures, so that the nonlinear dynamical phenomena predicted here should remain identifiable in the frequency spectra.

In conclusion, we investigated the current-induced magnetization dynamics in both coupled FiM-skyrmion-based double STNOs and a multi-STNO array, and found nonlinear dynamical phenomena, including dancing synchronizations and frequency combs. The conditions of the transition between them were systematically calculated through numerical simulations and explicitly analyzed based on the effective potential energies. The switching of different dynamical behaviors by tuning the driving currents was demonstrated.

Methods

Micromagnetic simulations

Micromagnetic simulations of a synthetic ferrimagnet are performed by employing the open-source software MUMAX349 to solve the Landau-Lifshitz-Gilbert (LLG) equation61,

$${\dot{{{{\bf{m}}}}}}^{\tau }=-\gamma {{{{\bf{m}}}}}^{\tau }\times {{{{\bf{H}}}}}_{{{{\rm{eff}}}}}^{\tau }+\alpha {{{{\bf{m}}}}}^{\tau }\times {\dot{{{{\bf{m}}}}}}^{\tau }+\gamma {H}_{j}^{\tau }\left({{{{\bf{m}}}}}^{\tau }\times {{{\bf{p}}}}\right)\times {{{{\bf{m}}}}}^{\tau },$$
(7)

where the layer index τ = t and b for the top and bottom ferromagnets, respectively. mτ, γ and α are the reduced magnetization, the gyromagnetic ratio and the damping constant, respectively. \({{{{\bf{H}}}}}_{{{{\rm{eff}}}}}^{\tau }\) denotes the effective field,

$${{{{\bf{H}}}}}_{{{{\rm{eff}}}}}^{{{{\rm{t(b)}}}}}=\frac{{{{\rm{2}}}}{J}_{{{{\rm{RKKY}}}}}}{{\mu }_{0}{M}_{{{{\rm{s}}}}}^{{{{\rm{t(b)}}}}}{t}_{z}^{{{{\rm{t(b)}}}}}}{{{{\bf{m}}}}}^{{{{\rm{b(t)}}}}}+{{{{\bf{H}}}}}_{{{{\rm{ex}}}}}^{{{{\rm{t(b)}}}}}+{{{{\bf{H}}}}}_{{{{\rm{DMI}}}}}^{{{{\rm{t(b)}}}}}+{{{{\bf{H}}}}}_{{{{\rm{an}}}}}^{{{{\rm{t(b)}}}}},$$
(8)

where the four terms on the right side of Eq. (8) represent the RKKY exchange field47, Heisenberg exchange field, Dzyaloshinskii-Moriya exchange field62,63 and magneto-crystalline anisotropy field, respectively. JRKKY, μ0 and \({M}_{{{{\rm{s}}}}}^{\tau }\) stand for the RKKY coupling coefficient, the vacuum permeability constant and the saturation magnetization, respectively. \({t}_{z}^{{{{\rm{t}}}}}\) (\({t}_{z}^{{{{\rm{b}}}}}\)) is the thickness of the top (bottom) ferromagnet and we set \({t}_{z}^{{{{\rm{t}}}}}={t}_{z}^{{{{\rm{b}}}}}={t}_{z}\). To save computational cost, the effective field does not include the contribution of the demagnetization, mainly resulting in a modification in the skyrmion size, which can be corrected approximately by modulating the Dzyaloshinskii-Moriya interaction (DMI) strength or introducing an effective anisotropy field64. \({H}_{j}^{\tau }\) in Eq. (7) is the strength of dampinglike spin torque, expressed as \({H}_{j}^{\tau }={j\hslash P}/(2{\mu }_{0}{e{t}_{z}{{M}}_{{{{\rm{s}}}}}^{\tau }})\) with j being the current density, ℏ the reduced Planck constant, P the spin polarization efficiency and e the elementary charge65. The polarization vector p is set to be along the −z direction.

In our simulations, we take a Co/Pt/Ru/Co/Pt multilayer as the working synthetic ferrimagnet, where the size of each Co layer is 512 × 512 × 1 nm3 discretized by 1 × 1 × 1 nm3 unit cells. The material parameters66 are taken to be the exchange coefficient At(b) = 15 pJ m−1, the magnetic anisotropy constant Kt(b) = 0.8 MJ m−3 and the DMI constant Dt(b) = 4 mJ m−2. The saturation magnetization \({M}_{{{{\rm{s}}}}}^{{{{\rm{b}}}}}\) of the bottom Co layer is fixed to be 580 kA m−1, while \({M}_{{{{\rm{s}}}}}^{{{{\rm{t}}}}}\) of the top one is slightly different from \({M}_{{{{\rm{s}}}}}^{{{{\rm{b}}}}}\) in order for the magnetizations to exhibit intriguing ferrimagnetic dynamics. Such a difference in the values of \({M}_{{{{\rm{s}}}}}^{\tau }\) has been experimentally reported in SFiM systems67. In addition, we set P = 0.4, α = 0.05 and JRKKY = − 1 mJ m−2 (it is experimentally achievable48). Note that in our calculations, current-induced spin torques are applied to the local magnetizations of both the top and bottom ferromagnets, so our results of a synthetic ferrimagnet can be directly transferred to a monolayer ferrimagnet.

While the regular (anti)ferromagnet does not allow self-confined skyrmion oscillator in a continuous working layer, both a synthetic ferrimagnet and a single FiM film can be used as the platform for boundary-free skyrmion oscillators43. We consider a synthetic ferrimagnet here because of its tunability of RKKY coupling strength via the spacer thickness and the accessibility of the MUMAX3 software for micromagnetic simulations. As an initialization process in magnetic simulations, we start from a homogeneous magnetic state and apply a relatively strong current (with the intensity of 600 MA cm−2 and duration of 1.16 ns) into the current injector (Fig. 1a) to generate one SFiM skyrmion in each oscillator. The simulation results are presented in Supplementary Fig. 8.