Fe₃GeTe₂: a site-differentiated Hund metal

Abstract

Magnetism in two-dimensional (2D) van der Waals (vdW) materials has lately attracted considerable attention from the point of view of both fundamental science and device applications. Obviously, establishing a detailed and solid understanding of their magnetism is the key first step toward various applications. Although Fe₃GeTe₂ is a representative ferromagnetic (FM) metal in this family, many aspects of its magnetic and electronic behaviors still remain elusive. Here, we report our new finding that Fe₃GeTe₂ is a special type of correlated metal known as “Hund metal”. Furthermore, we demonstrate that Hund metallicity in this material is quite unique by exhibiting remarkable site dependence of Hund correlation strength, hereby dubbed “site-differentiated Hund metal”. Within this new picture, many of the previous experiments can be clearly understood, including the ones that were seemingly contradictory to one another.

Introduction

Fe₃GeTe₂ has been a focus of the recent surge of 2D magnetic material research^{1,2,3,4,5,6,7,8,9,10,11,12}. On the one hand, it displays many fascinating properties such as high critical temperature (T_c ≃ 220 K)^6,8, heavy fermion behavior⁹, and the relative ease of exfoliation^5,7. Its great potential has also been highlighted by recent experiments showing that T_c can be increased even up to room temperature^10,11 and that the large anomalous Hall current is originated from the unique band topology¹². On the other hand, its electronic and magnetic properties are far from being clearly understood. The very basic picture for the magnetic moment is still under debate^9,13,14. The measured quasiparticle masses are not consistent with each other and exhibit an order-of-magnitude difference depending on experimental probes^9,12,13,14. These puzzles are posing a challenge to the current theory of this material.

In this work, we suggest a new physical picture for Fe₃GeTe₂. We first provide convincing evidence that Fe₃GeTe₂ is a “Hund metal”. The term Hund metal was coined to refer to an intriguing type of correlated (not necessarily magnetic) metals^{15,16,17,18,19} in which Hund coupling J_H, rather than Hubbard U, plays the main role in determining the electronic properties¹⁹. Hund metals can host various interesting phenomena such as spin freezing^20,21, spin-orbital separation^{22,23,24,25,26}, orbital differentiation^27,28, and unconventional superconductivity^21,29. This concept has been providing a compelling view for many of multiorbital systems^{15,19,20,21,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44}, most prominently for iron-based superconductors^{15,19,29,30,32,33,37,45}, ruthenates^{20,21,31,36,40}, and presumably also for recently discovered nickelate superconductors^46,47. Our analysis demonstrates that Fe₃GeTe₂ is a new member of this family.

Further, we show that Hund metallicity of this material is distinctive from other known Hund metals by exhibiting the remarkable site dependence of correlation strengths; dubbed “site-differentiated” Hund metal (see Fig. 1). This intriguing site dependence is originated from the microscopic details of underlying band structure. The suggested new picture is an important key to understand experiments including the ones that are seemingly contradictory to each other.

Fig. 1: Overview figure.

Left panel: A schematic illustration of “site-differentiated Hund metal” physics in Fe₃GeTe₂. Colored areas highlight different regimes or phases; Mott insulator (dark green; i.e., whose charge gap is opened due to Hubbard U), Mott metal (light green; i.e., whose correlated metallic behavior is governed by U), weakly correlated metal (yellow; electronic correlation is weak enough), and Hund metal (red; i.e., whose correlated metallic behavior is governed by Hund J_H). For more details to define each region of the phase diagram, we refer to refs. ^35,42,61. While both Fe sites fall into the Hund metal regime, they are clearly differentiated in terms of electron scattering rate Γ, quasiparticle effective mass m^*/m^b, and Sommerfeld coefficient γ (as depicted along z axis) which are attributed to the electronic structure details (see the schematic DOS). In parentheses shown are the calculated spin-orbital-averaged values of (Γ, m^*/m^b, γ) taken at T = 100 K. The unit of Γ is meV. The x- and y axis corresponds to J_H/U and U/W, respectively. U = 5.0 and J = 0.9 eV (J_H/U = 0.18) were used for both Fe-I and Fe-II; see “Methods” for a more detailed discussion. The effective bandwidth W_Fe-I for Fe-I is found to be smaller than that of Fe-II through the analysis of the hybridization function (see the main text). A rough estimation of their difference based on the integrated DOS yields ~1.6 eV (see the main text). Right panel: Crystal structure of Fe₃GeTe₂.

Results and discussion

Fe₃GeTe₂ is a Hund metal

Fe₃GeTe₂ is a vdW material with a layered Fe₃Ge substructure sandwiched by two Te layers. Five Fe-3d levels of both Fe-I and Fe-II are split into three groups, namely ${d}_{{{{\rm{{z}}}^{2}}}},{d}_{{{{{\rm{x}}}}}^{2}-{{{{\rm{y}}}}}^{2}/{{{\rm{xy}}}}}$ and d_xz/yz. More details can be found in Supplementary Note 1 of Supplementary Information (SI).

We firstly demonstrate that all the key features defining Hund metal are well identified in Fe₃GeTe₂via density functional theory plus dynamical mean-field theory (DFT+DMFT) calculations (see “Methods”). In order to concentrate on the intrinsic nature of correlation (separately from magnetism), we suppress magnetic ordering unless otherwise specified. The result of U = 5 and J_H = 0.9 eV will be presented as our main parameter choice. Computation methods, including the parameter dependence and other details, are given in “Methods”.

First, we examine so-called two-faced or “Janus” effect which represents the physics governed by J_H distinctively from that of Mott correlation U^18,19. The straightforward way is to see the simultaneous increase of both U_c (the critical value of U at which the metal-to-Mott-insulator transition occurs) and “correlation strength” as measured typically by the inverse of quasiparticle weight Z (or equivalently, the quasiparticle scattering rate Γ) as J_H increases^18,19.

Let us uncover the “first face” of this effect, namely, the U_c increase by J_H. To avoid the demanding computations scanning the large parameter space, here we simply examine the atomic gap Δ_at ≡ E_N+1 + E_N−1 − 2E_N (E_N: the atomic ground state energy of N-electron subspace). According to the original Mott–Hubbard picture, the gap opening is associated with Δ_at > W (W: bandwidth), and the system gets closer to Mott transition as Δ_at increases. This analysis, albeit simple, is well justified by the observations that the actual DMFT phase diagrams are consistent with the behavior of Δ_at in the large J_H regime^19,42. We found that Δ_at ≈ U − 1.52J_H from a five-degenerate-orbital model with 6 electrons, which guarantees that ∂Δ_at/∂J_H < 0 (see the inset of Fig. 2a). Note that J_H drives the system away from being a Mott insulator; hereby the Janus' first face is unveiled.

Fig. 2: Quasiparticle scattering rate Γ, local susceptibilities multiplied by temperature k_BTχ and the spin susceptibilities with no factor k_BT.

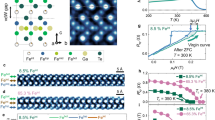
a The J_H dependence of quasiparticle scattering rate Γ for each orbital in Fe-I (orange) and Fe-II (blue) at T = 300 K. Inset in (a) shows the J_H dependence of Δ_at for a degenerate five-orbital model with six electrons. b, c Temperature dependence of the susceptibilities (b) k_BTχ^spin/orb and (c) χ^spin of Fe-I (orange) and Fe-II (blue). The filled and open symbols refer to the spin and orbital susceptibility, respectively. Two arrows in (b) indicate the onset temperature of spin screening below which χ^spin deviates from the Curie law of free local moment. The inset in (c) is an enlarged view of ${\chi }_{{{{\rm{Fe-II}}}}}^{{{{\rm{spin}}}}}$ in the low-temperature region.

To see its “second face”, the calculated Γ is presented in Fig. 2a. Here, ${\Gamma }_{l}={Z}_{l}{{{\rm{Im}}}}{\Sigma }_{l}({{{\rm{i}}}}{\omega }_{n}){| }_{{\omega }_{n}\to {0}^{+}}$, where Z_l is the quasiparticle weight and Σ_l(iω_n) the local self-energy on the imaginary frequency (ω_n) axis for a given orbital l (see Supplementary Note 2 of SI for additional discussion). It is clear that the Γ is enhanced as J_H increases. Also, the scattering rate is strongly orbital-dependent as depicted by different symbols, and the differences become more pronounced as J_H increases. This feature, often called orbital differentiation, has been regarded as one of the key pieces for identifying iron-based superconductors as a Hund metal^27,28.

Having evidenced Janus behavior, we now turn to another defining feature of Hund metallicity, namely, spin-orbital separation^{22,23,24,25,26}. As discussed in previous works, the electronic behavior of Hund metals follows the local-atomic and Landau-quasiparticle picture in the high- and low-enough energy region, respectively, due to the gradual development of screenings. Deng et al. suggested that the much higher onset screening temperature for the orbital degree of freedom (${T}_{{{{\rm{onset}}}}}^{{{{\rm{orb}}}}}$) than that of spin (${T}_{{{{\rm{onset}}}}}^{{{{\rm{spin}}}}}$) is a key signature of Hund metals; i.e., ${T}_{{{{\rm{onset}}}}}^{{{{\rm{orb}}}}}\gg {T}_{{{{\rm{onset}}}}}^{{{{\rm{spin}}}}}$²⁶. Following the literature, we tracked local susceptibilities up to high enough temperature. Figure 2b shows the calculated local spin and orbital susceptibilities multiplied by k_BT (k_B: Boltzmann constant). The spin susceptibility with no prefactor k_BT is presented in Fig. 2c. The onset screening temperatures for spin (below which k_BTχ^spin starts to deviate from the Curie law) are indicated by the vertical orange arrows; ${T}_{{{{\rm{onset}}}}}^{{{{\rm{spin}}}}}\approx 3000$ K and 9000 K for Fe-I and Fe-II, respectively. Importantly, the onset temperatures for orbital screenings are much higher; ${T}_{{{{\rm{onset}}}}}^{{{{\rm{orb}}}}} > 20000$ K for both Fe-I and Fe-II; see the empty symbols. The well-separated ${T}_{{{{\rm{onset}}}}}^{{{{\rm{spin}}}}}$ and ${T}_{{{{\rm{onset}}}}}^{{{{\rm{orb}}}}}$ provide further evidence that Fe₃GeTe₂is a Hund metal.

We also investigated the long-time correlators, C^spin/orb(τ = 1/2k_BT) (τ: imaginary time); see Supplementary Note 3 of SI for its definition and the related discussion. These quantities were recently used as another useful proxy to measure the degree of spin-orbital separation⁴². The results also clearly show that Fe₃GeTe₂is well classified as a Hund metal.

We finally note that the ferromagnetic transition temperature (T_c ≃ 220 K) of Fe₃GeTe₂ is much lower than the characteristic temperature scales of T_onset for spin and orbital. It indicates that the Hund metal character is developed well above the ferromagnetic transition temperature and the magnetic order itself is not immediately relevant to Hund metallicity.

Site-differentiated Hund metallicity

Hund metallicity in Fe₃GeTe₂is unique in that its Hund physics is clearly differentiated at two sites. Note that the scattering rate Γ is an order-of-magnitude larger in Fe-I. Γ of Fe-I ${d}_{{{{\rm{{x}}}^{2}-{y}^{2}/xy}}}$ (orange triangles in Fig. 2a) reaches 0.6 at J_H = 1.3 eV, whereas that of Fe-II ${d}_{{{{\rm{{z}}}^{2}}}}$ only 0.05 (blue circles) for example. The orbital-dependent correlation is also more pronounced in Fe-I (Fig. 2a).

χ^spin also shows remarkable site dependence as presented in Fig. 2c: As the temperature is lowered, χ^spin of Fe-I (orange line) well follows ~1/T behavior in sharp contrast to Fe-II (blue line) which almost saturates at ~100 K (see inset of Fig. 2c). It implies that, below this temperature, the spin moments of Fe-II tend to be itinerant. For Fe-I, on the other hand, we could not find any indication of susceptibility saturation down to the lowest temperature we reached (~100 K), indicative of the persistent local moment character. See also Supplementary Note 3 of SI for further analysis based on long-time correlators.

What is the origin of this site-dependent Hund physics? First of all, we note that the d-orbital occupations are almost the same in both sites; the calculated electron occupancy is 6.431 ± 0.001 at U = 0 and 6.18 ± 0.05 at U = 5 eV (−/+ corresponding to Fe-I/Fe-II). It is largely attributed to the strong covalency in this chalcogenide material. Although the electron number depends on the charge-counting method, this level of coincidence can effectively exclude the possibility of the site-differentiated Hund physics being originated simply from the different charge status or valence. Rather, it indicates the more subtle electronic origins. Second, the calculated density of states (DOS) does not show significant difference between Fe-I and Fe-II other than the more pronounced van Hove singularity (vHS) for Fe-I d_x2-y2/xy (see Supplementary Note 4 of SI).

Highly useful insights are obtained from the calculated “one-shot” hybridization function Δ(iω_n) for each orbital. For its definition and the related figures, refer to Sec. S4 of SI. $-{{{\rm{Im}}}}\Delta ({{{\rm{i}}}}{\omega }_{n})$ at high energy (which approximately scales as the square of the bandwidth) is smaller for Fe-I than Fe-II (see Supplementary Fig. 4a in SI). It shows that the effective bandwidth for Fe-I is smaller than Fe-II, indicative of the stronger correlation at Fe-I. This feature of smaller bandwidth for Fe-I is also seen in the integrated DOS analysis (see Supplementary Fig. 4b). It is therefore consistent with the larger Γ (discussed above; see Fig. 2a) and the greater mass of Fe-I (to be discussed below; see Fig. 3d). Also, in the low-frequency regime, $-{{{\rm{Im}}}}\Delta ({{{\rm{i}}}}{\omega }_{n})$ of Fe-I d_x2-y2/xy is smallest and exhibits a downturn as ω_n → 0. Note that $-{{{\rm{Im}}}}\Delta ({{{\rm{i}}}}{\omega }_{n}){| }_{{\omega }_{n}\to 0} \sim 1/\{(\pi D({E}_{{{{\rm{f}}}}}))\}$. Here, D(E_f) is the DOS at the Fermi level E_f. Thus, this downturn of $-{{{\rm{Im}}}}\Delta ({{{\rm{i}}}}{\omega }_{n})$ is most likely due to the well-developed vHS (i.e., the divergence of DOS), which in turn suppresses the low-energy effective hopping processes³¹. That is, electron scattering and mass enhancement of Fe-I d_x2-y2/xy are further boosted by vHS.

Fig. 3: Comparison with reported experiments.

a The momentum-dependent spectral function A(k, ω) calculated from FM phase in comparison with ARPES data. The two figures on the left (expressed with black and white intensity) are the ARPES results measured with differently polarized photons of linear horizontal (LH) and linear vertical (LV) polarization taken from ref. ¹⁴. The rightmost figure is the k_z-integrated DFT+DMFT result at T = 100 K. It is found that each band has the significantly mixed characters of Fe-I, Fe-II, and other anions. b Fermi surfaces in the k_x--k_y plane. The two left plots are the ARPES results (black and white)¹⁴. The right three plots (colored) show the k_z-integrated DFT+DMFT results: FM at T = 100 and 200 K, and paramagnetic at T = 300 K. ARPES data in (a) and (b) are presumably measured below 25 K¹⁴. c The calculated Γ/k_BT as a function of temperature. A vertical dotted line indicates the experimentally reported incoherence-coherence crossover temperature^9,48, and the colored areas highlight the regions for which Γ≤k_BT³¹ (yellow) and T≤T_c (skyblue). The upper- and the lower-filled symbols refer to the values of the majority and minority spin, respectively in the FM phase, and the fully filled symbols represent the values of the paramagnetic phase. d The calculated m^*/m^b of each orbital at T = 100 K for Fe-I (orange) and Fe-II (blue). The filled and empty stars indicate the values of the majority and minority spin, respectively in the FM phase, and the circles represent the values from paramagnetic phase. The horizontal dash-dotted and dashed line indicates the values from specific heat¹³ and ARPES experiments^12,14, respectively. e The calculated orbital-decomposed Sommerfeld coefficient in FM phase at T = 100 K. Here “total” denotes the sum of all orbital contributions, and “the rest” the contributions from the other states than Fe d-orbitals. The experimentally measured values are represented by horizontal dashed lines^6,13,62.

Understanding the experiments

The new picture for Fe₃GeTe₂ as a “site-differentiated Hund metal” provides useful insights to understand the experiments. Before discussing those features in detail, let us take a look at the spectral function A(k, ω) which can be directly compared with angle-resolved photoemission spectroscopy (ARPES) results, thereby enabling us to check the reliability of our parameter choices for interactions and the correlated electronic structure. Figure 3a shows the excellent agreement between theory and experiment. For example, the pronounced spectral features, namely the bands assigned as γ, ζ and ω in ref. ¹⁴ are well identified in our A(k, ω). The near-Fermi-level states are also well reproduced; see, e.g., α, δ and η bands.

The first experimental quantity we want to revisit is the large quasiparticle mass; m^*/m^b = γ/γ^b ≃ 13 reported from specific heat measurement¹³ (i.e., taken from the measured Sommerfeld coefficient γ and its DFT estimate γ^b). This value remains as a puzzle especially because ARPES data was deemed to be in fair agreement with band calculations m^*/m^b ≃ 1.6^12,14. This large discrepancy has been highlighted throughout the literature^9,13,14, but the issue remains still unresolved.

Here, we argue that these seemingly contradictory experimental results can be understood as a natural manifestation of the site-differentiated Hund physics. In multiorbital systems, the mass enhancement measured by specific heat is mainly determined by the more correlated orbital²⁷. In fact, our calculation shows m^*/m^b ≈ 7–23 for the more correlated site Fe-I, which is comparable to the value from specific heat experiment (dash-dotted line in Fig. 3d). It is due to that Sommerfeld coefficient γ extracted from specific heat is a sum of each orbital contribution ${\gamma }_{l} \sim {({m}^{* }/{m}^{{{{\rm{b}}}}})}_{l}$; see Supplementary Note 5 in SI for more details. As discussed in ref. ²⁷, it is comparable to the series resistor in a circuit for which total resistance is given by the direct sum, and the total voltage can be approximated by the one applied to the large resistor. Indeed, the site- and orbital-decomposed values (Fig. 3e) clearly show that the Fe-I contributions dominate the total value γ_tot, whereas those of Fe-II are much smaller. The sum over all orbitals γ_tot eventually gives rise to good agreement with experiments.

The ARPES situation is quite different on the other hand. The mass enhancement of a given “band” is a weighted sum of each orbital contribution therein. In fact, the previous study revealed that most bands in this material have both Fe-I and Fe-II characters (see, e.g., Supplementary Fig. 3 of ref. ¹⁴). As inferred from m^*/m^b ≈ 2–4 of Fe-II being comparable to an ARPES estimate (Fig. 3d), we presume that, at least in some bright bands captured by ARPES, the weaker correlated Fe-II d-orbitals as well as the other itinerant Ge and Te states possibly have the larger portion than Fe-I, which can result in the small m^*/m^b (see Supplementary Note 6 in SI for the related analysis).

Now let us examine the heavy fermion behavior and the incoherence-coherence crossover observed at T ~ 100 K^9,48. Figure 3c presents Γ/k_BT as a function of temperature for both paramagnetic (fully filled symbols) and FM phases (partially filled). Here, the coherence temperature T^* is defined by Γ/k_BT^* = 1 (see the yellow region in which Γ≤k_BT), namely the temperature below which quasiparticle lifetime exceeds the timescale of thermal fluctuation^31,42. We note that the sizable site dependence of correlation makes electron scattering very different at two Fe sites: Whereas Γ/k_BT of Fe-II remains less than 1 even well above the experimental T^*, that of Fe-I is much greater. The larger contribution from Fe-I, particularly ${d}_{{{{\rm{{x}}}^{2}-{y}^{2}/xy}}}$ orbitals, and its significant temperature dependence as T → T^* indicate that the experimentally observed incoherence-coherence crossover around T ~ 100 K^9,48 is mainly attributed to the corresponding orbitals residing in Fe-I.

For comparison, we also investigate the isostructural material Ni₃GeTe₂ whose γ ~ 9 mJ/mol ⋅ K² is much smaller¹³. Our calculation reasonably well reproduces the experiment and the mass enhancements m^*/m^b≤1.5 with no appreciable site differentiation (see Supplementary Note 6 in SI for our calculation results). This contrasting behavior, attributed to the absence of vHS and the different valence (see Supplementary Fig 6c in SI), renders Fe₃GeTe₂ as a unique example of site-differentiated Hund metal.

Finally, another important issue for Fe₃GeTe₂ is related to the nature of its magnetic moment. While in the early works it was understood or discussed within itinerant Stoner picture^9,13, more recent studies emphasized the local nature of spin. For example, Xu et al. observed the nearly unchanged exchange splitting in their ARPES data even up to T > T_c¹⁴. The situation is therefore reminiscent of a prototypical FM Hund metal SrRuO₃ whose exchange splitting persists above T_c due to the enhanced local spin character whereas the very low-temperature behavior is well described within Stoner theory^49,50. Note that, near T_c ≃ 220 K, χ^spin of Fe-I clearly indicates the local moment behavior (Fig. 2c), and as a consequence, Γ is large. As temperature decreases, on the other hand, Γ gets reduced by the enhanced spin screenings, which eventually result in the long-lived quasiparticles well below T ~ 100 K (Fig. 3c). Therefore, our current study provides a unified picture for Fe₃GeTe₂ within which its spin moment can be described as being localized above and itinerant well below T_c.

We demonstrated that Fe₃GeTe₂ is a Hund metal with intriguing site dependence originated from the microscopic details in the underlying band structure. The proposed new picture of “site-differentiated Hund metal” not just makes this representative metallic vdW ferromagnet an even more exciting material platform, but also provides useful insights to understand the previous experiments including the ones that are seemingly contradictory to each other. Our results hopefully stimulate further experimental and theoretical investigations of the related systems. For example, the direct experimental observations of the site- or orbital-selective correlation effects can be an interesting research direction.

Methods

Computation details of DFT+DMFT calculations

The DFT electronic structure of Fe₃GeTe₂ was obtained by using FLAPWMBPT package⁵¹, which is based on the full-potential linearized augmented plane wave plus local orbital method, employing the local density approximation (LDA). We used experimental lattice parameters as reported in ref. ⁵. On top of this non-spin-polarized DFT band structure, 108 maximally localized Wannier functions were constructed with a wide energy window of [−15:10] eV containing Fe-s, Fe-p, Fe-d, Ge-s, Ge-p, Ge-d, Te-s, Te-p, and Te-d characters, and its tight-binding Hamiltonian was built through the J_X interface⁵². We performed single-site dynamical mean-field theory (DMFT)^53,54 calculations for d-orbitals of Fe-I and Fe-II by employing COMCTQMC⁵⁵ implementation of the hybridization-expansion continuous-time quantum Monte Carlo (CTQMC) algorithm⁵⁶ as an impurity solver. Namely, we solved two impurity problems, one for Fe-I and one for Fe-II, per DMFT self-consistency loop. Within our DFT+DMFT scheme, electronic self-energy is momentum-independent (i.e., local in space)⁵³, and is assumed to be diagonal in cubic harmonics basis to avoid a sign problem by omitting the off-diagonal elements of hybridization functions whose values are actually small. The self-energy on the real frequency axis was obtained from the analytic continuation of imaginary axis data using the maximum entropy method⁵⁷. For the magnetically ordered phase of Fe₃GeTe₂, we used EDMFTF package⁵⁸ for DFT+DMFT calculations.

For the double counting (DC) self-energy, we adopted the nominal DC scheme which reads ${\Sigma }_{{{{\rm{DC}}}}}({n}_{0})=U({n}_{0}-\frac{1}{2})-\frac{J_{\rm H}}{2}({n}_{0}-1)$⁵⁹, where n₀ is the nominal charge. We took n₀ = 6.0 for both Fe-I and Fe-II, which is close to the d-orbital occupancy obtained from DFT (n_DFT ≃ 6.4). Note also that this DC scheme with n₀ = 6.0 was used for this material in a previous study¹³, which yields good agreement of magnetic moment with experimental data. While we mainly present the results obtained from n₀ = 6.0, we found that varying n₀ in a range of [5.4:6.6] does not lead to any qualitative changes; e.g., see Supplementary Note 7 of SI for spin and orbital susceptibilities obtained from different Σ_DC(n₀) values.

The Hubbard U and Hund coupling J_H of Fe-d were chosen to be U ≡ F⁰ = 5.0 eV and J_H ≡ (F² + F⁴)/14 = 0.9 eV for both Fe-I and Fe-II, which were used in a previous study on Fe₃GeTe₂¹². These values are also comparable to the theoretically estimated values for iron chalcogenide family⁶⁰. Here, F⁰, F², and F⁴ are Slater integrals, and the ratio F⁴/F² = 0.625 was used for parametrization of on-site Coulomb interaction tensor. For Ni₃GeTe₂ which will be discussed in Supplementary Note 6 of SI, the same computation scheme was used except for the use of a larger nominal charge (n₀ = 8.0) for the DC self-energy and a larger Hubbard U of U ≡ F⁰ = 6.0 eV, considering its chemical environment on Ni sites. Note also that, for Ni₃GeTe₂, we did not consider any magnetic order due to its absence even at very low temperatures^5,13. We used experimental lattice parameters of Ni₃GeTe₂⁵.