Main

In opto-electronic devices energy dissipation can be highly undesirable or very much needed, depending on the foreseen application. Photon detectors and solar cells are the prototypical semiconductor components belonging to the second category: the incoming electromagnetic energy must be mostly transferred and dissipated within the active region for optimized operation13. The same condition holds for most microwave and radio systems: an antenna must efficiently deliver/extract the signal to/from the receiving/emitting circuit. The crucial concept here is the critical coupling between input channel and load. It is nothing else than the so-called impedance matching condition, which, once expressed in terms of losses, indeed states that radiative and material losses must be equal1. On one hand, the critical coupling provides a common framework to the efforts aiming at developing perfect absorbers and optimal thermal emitters14. On the other hand, it is noticeably similar to the lasing condition, on exchanging losses with gain. Indeed, the link between perfect absorbers and lasers has been recently pointed out in terms of time reversal within the coherent perfect absorption framework (CPA; ref. 11).

In all the aforementioned examples, the material loss mechanisms feature a much larger bandwidth than the energy exchange rate with the electromagnetic field. Therefore, independently of the presence of a resonator and its radiative losses, light–matter interaction can be described under a perturbative approach, simply in terms of absorption and spontaneous emission. In contrast, when a material excitation is coupled to an optical resonator having a similar bandwidth and a sufficiently small modal volume, the strong-coupling regime occurs15. In this situation new quantum eigenstates of the system are formed as a combination of material and photonic excitations (polaritons) and energy is continuously exchanged between the two ‘fields’ at a rate corresponding to the coupling strength (the so-called vacuum Rabi energy). One question now naturally arises: is it possible to feed perfectly and in full the electromagnetic energy from the outside world into such mixed light–matter polariton states? Or, in other words, is it possible to ‘critically couple’ polaritons without destroying them? The question is intriguing in that the polariton concept intrinsically assumes a system that is nearly ‘closed’ on the timescale of light–matter interaction, and one may intuitively expect an incompatibility of the strong-coupling conditions with those for critical coupling.

A rigorous description of dissipation in a quantum picture would require a master equation approach16,17,18,19,20,21,22 or a Green’s function formalism23. However, under the hypothesis of a small average excitation density, a simpler semiclassical approach can be employed. The matter degrees of freedom and the cavity photons are represented as coupled harmonic oscillators, and a coupled-mode theory—developed in this paper—yields equivalent analytical formulas. This reveals that CPA—in either the weak- or strong-coupling regime—is more deeply understood in terms of matching of damping rates: no additional parameters need to be tailored.

The relevance of strong critical coupling is motivated by the need for efficient optical pumping in the proposal of various intersubband polariton sources24,25. Here, maximizing the absorption into polariton states is of crucial importance, whilst the polariton splitting needs to be precisely tailored to the optical phonon resonance: the concept of CPA indeed enables one to tune the absorption independently of the charge density, the main parameter determining the splitting energy.

Coupled-mode theories (CMT) are commonly applied to deal with different problems involving stationary and propagating modes in optics1,2. In the following, we will employ the notation introduced for photonic crystal resonances (Dirac notation)26. The system under study is sketched in Fig. 1a: it consists of an optical resonator driven from the exterior via a coupling constant d, and the system is assumed to be spatially symmetric. The optical cavity resonance occurs at a pulsation ω0 and coherently exchanges energy with a matter resonator oscillating at the same frequency via the coupling constant Ω. Energy is also re-radiated towards the exterior. The amplitudes of the cavity and matter fields (a and b respectively), the amplitudes of the incoming waves in the two ports |s+〉 = (s1+, s2+), and the corresponding outgoing wave amplitudes |s−〉, are then related by the following equations:

Figure 1: Coupled oscillator model, strong/weak critical coupling, and polaritonic CPA.
figure 1

a, Two-port symmetric photonic resonator coupled to two scattering channels (ports) via the coupling constant d (linked to the radiative damping rate γr), and to a matter resonator depicted as a spring-mass oscillator. Its linear response is given by the scattering matrix S(ω); when its determinant is zero all the incoming energy is absorbed (coherent perfect absorption, CPA). b, Phase diagram of the coupled system. For small enough damping rates (red regions) the absorbance (subplots) exhibits two polaritonic peaks, whereas for large damping rates (orange regions) single-peaked spectra are observed. The dashed line marks the separation between the two regions. In both of these regions the joint absorbance can reach unity (CPA) provided that a critical coupling condition is fulfilled (see text). c, Phase diagram with no cavity–matter coupling (Ω = 0): the ordinary critical coupling condition γr = γnr is recovered.

Full size image

The evolution of the matter and cavity oscillators is damped by the presence of two decay channels, quantified respectively with the decay rates γm and γc. The latter is the cavity total damping rate, which is useful to separate into radiative and non-radiative contributions: γc = γr + γnr; γr represents the radiative losses and γnr accounts for non-radiative, non-resonant cavity losses (for instance, free-carrier absorption and ohmic losses).

In steady-state the system response is given by the frequency-dependent scattering matrix, which connects ingoing to outgoing waves: |s−〉 = S(ω) |s+〉. Straightforward integration of the above equations yields:

The explicit expressions for matrices C and D = |d〉(〈d |)∗ can be found in ref. 26, while the polariton poles are

Consistently with previous reports27, this model predicts reflectance and transmittance lineshapes belonging to a Fano-like manifold; this complexity is lost, however, when dealing with the absorption properties, which are the object of the present work. It turns out then that a single spectral function is involved: B(ω) = (1 − | det S(ω) |2). The explicit expression of the S-matrix determinant following from (1) is given in the Supplementary Information.

In a two-port system the relevant quantity is the joint absorbance Ajoint, defined as the ratio between absorbed and input energies when the two coherent beams excite the system’s ports with equal intensity. By sweeping the input beam dephasing φ = arg(s2+/s1+), the joint absorbance sweeps from a minimum Ajoint, min to a maximum Ajoint, max, which in the CMT model are given by

Indeed, if det S(ω) = 0 one has Ajoint, max(ω) = 1—that is, a φ can be found producing CPA. In addition, Ajoint, min(ω) = 0 means that there always exists another φ that gives coherent perfect transparency (CPT). In essence, a device implementing the two-oscillator CMT with a S-matrix satisfying det S = 0 will behave as an ideal absorption-based interferometer.

If, in contrast, a single beam excites the system either from port 1 or 2, the usual single-beam absorbances are observed. From CMT it follows that in this case A1(ω) = A2(ω) = B(ω)/2; this is consistent with the general theory of coherent absorption, which states that the average between single-beam absorbances coincides with the average between minimum and maximum joint absorbances (Supplementary Information). This means, on one hand, that a sample whose single-beam absorption peaks at 1/2 is expected to show CPA; on the other hand, single-beam absorption never exceeds 1/2 in a symmetric resonator supporting one resonant electromagnetic mode, as predicted by previous CMT calculations28.

The function B(ω) can exhibit either one or two peaks, depending on the region of the parameter space involved, as shown in Fig. 1b; this transition can be regarded as a crossover between weak- and strong-coupling regimes. In both weak- and strong-coupling regions a curve in the parameter space exists corresponding to det S(ω) = 0, hence CPA (Supplementary Information). For small enough matter damping rate (γm < Ω), one observes CPA when the damping rate matching

is fulfilled; notice the contribution of non-radiative losses, which can ‘help’ a ‘good’ matter resonator enter strong critical coupling29. On the other hand, the same system supports a second kind of critical coupling, which occurs when the following is satisfied:

In both weak and strong critical coupling all the incoming energy can be perfectly absorbed by the system, although it is obviously redistributed between the non-radiative cavity losses and the matter oscillator. A special case is found when the resonator–oscillator coupling Ω is set to zero: strong critical coupling no longer exists. Instead, the model shows that weak critical coupling reduces to the conventional CPA. This result is non-trivial, and it is also aesthetically gratifying: CPA is nothing else than critical coupling in a two-port system, and it obeys the simple, usual critical coupling condition γr = γnr. This situation is shown in Fig. 1c, where the absorption lineshapes given by B(ω) become purely Lorentzian.

To experimentally demonstrate strong critical coupling and full interferometric control of absorption, we performed an optical measurement on a polaritonic sample that mostly satisfies the radiative decay rate matching of equation (3). The CPA set-up is sketched in Fig. 2a and the sample consists of a semiconductor membrane structured as a photonic crystal slab resonator (Fig. 2b), embedding a multi-quantum well (MQW) heterostructure whose single intersubband transition is resonant with the photonic crystal mode, giving rise to intersubband polariton states30.

Figure 2: Experimental set-up, sample details and single-beam spectra.
figure 2

a, Interferometric arrangement for double-beam probing of the photonic crystal sample. b, Main features of the sample. A thin semiconductor membrane is patterned with gold stripes implementing a metallo-dielectric photonic crystal resonator. In the membrane a multi-quantum well heterostructure acts as a collection of harmonic oscillators with resonance frequency ω12. c,d, Large dots: experimental single-beam absorbance, reflectance and transmittance obtained by blocking one of the two interferometer input beams. Solid lines represent the coupled-mode theory traces (CMT), whereas dashed lines are obtained via rigorous coupled-wave analysis (RCWA). The mismatch in reflectance and transmittance between CMT and experiment is possibly due to a second photonic resonance located at about 150 meV. This is also responsible for the difference between reflectances at ports 1 and 2. The transmittance was also measured with a broadband light source (small grey dots in d) to fully reveal the double-peak polaritonic structure; the perfect matching with the theoretical RCWA spectrum is here apparent.

Full size image

The single-beam absorbance is plotted in Fig. 2c and shows that the first polaritonic peak (the only one accessible within the tuning range of the laser source) is in good agreement with the theoretical curves obtained for the parameter setω0 = 124.5 meV, γr = 3 meV, γnr = 0, γm = 5 meV and Ω = 8 meV. The single-beam transmission was also probed with a broadband light source and Fourier transform interferometry (Fig. 2d, grey dots), to cover a wider spectral range revealing the characteristic polariton splitting and the perfect matching with theoretical modelling for both polariton peaks. The parameter values were also confirmed by independent rigorous coupled-wave analysis (RCWA) calculations and by absorption measurements on the unpatterned heterostructure, as detailed in the Supplementary Information. The proximity of the single-beam absorption peaks to the 50% value is very promising for the observation of CPA; as explained above, in fact, in the framework of CMT this would automatically imply det S(ω) = 0 at those frequencies. The experimental points plotted in Fig. 2c are the average between the two single-beam absorbances, which differ slightly from each other, in agreement with the differences in reflectance shown in Fig. 2d. This is attributed to the existence of a second resonant photonic mode, located at about 150 meV, which is not included in the CMT model. This further resonance, however, clearly appears in the RCWA transmission (Supplementary Information). This ab initio description, starting from the geometrical parameters and the dielectric response, then correctly reproduces the spectra of Fig. 2d (dashed lines); its drawback is that it does not provide any insight into the critical coupling in terms of damping rate matching.

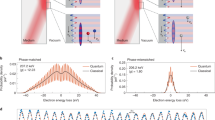
The results of the double-beam experiment are reported in Fig. 3a–c,where we plot the output intensities at ports 1 and 2 on a sweep of the input beam phase difference φ = arg(s2+/s1+), for three different excitation wavelengths. In all three cases the total output intensity |s1−|2 + |s2−|2 reaches 2, giving CPT (units are chosen such that input intensities |s1+|2 = |s2+|2 = 1); at the wavelength corresponding to (b) the φ-phase sweep also enables one to reach |s1−|2 + |s2−|2 ≍ 0, giving CPA. The corresponding joint absorbance values are reported in Fig. 3d as a function of the wavelength for the three phases φ corresponding to minimum, average and maximum output. The CMT and RCWA theoretical traces are also shown for comparison. It is worth noticing that the average joint absorbance, measured via the double-beam experiment, closely follows the average single-beam absorbances (Fig. 2c). The wavelength tuning of the laser covers the whole lower peak of the polariton doublet up to the resonance energy, unambiguously proving the polaritonic nature of the CPA and the existence of strong critical coupling. The occurrence of strong critical coupling in our sample naturally follows from the very fact that for intersubband polaritons the cavity and matter damping rates are easily close to each other. Indeed, the modulation depth of the double-peaked absorption, and hence the strong critical coupling condition, is rather forgiving with respect to the relative damping rate mismatch. In our case, despite having (γm − γr)/(γm + γr) ∼ 25%, we observed Ajoint, max − Ajoint, min ≍ 90%. Careful tailoring of γr is anyway possible by tuning the grating parameters, for instance by a controlled etching of the slits in the underlying semiconductor31. Confirmation that the observed coherent absorption modulation is not an artefact due to other components in the set-up is given by the analysis of the output beam dephasing Δψ. As detailed in the Supplementary Information, Δψ is connected to the phases of the scattering-matrix elements, and hence represents a key sample feature. In Fig. 3e we report the measured Δψ, and compare it with the CMT and RCWA calculations. Excellent agreement with the latter is observed, while the difference in the case of the CMT can again be attributed to the presence of the second photonic mode at higher energy.

Figure 3: Modulation of output intensity on double-beam excitation and polariton CPA.
figure 3

a–c, When the sample is excited from both ports 1 and 2 with unit-amplitude beams phase-shifted by φ, the output intensity recorded at ports 1 and 2 oscillates with a phase shift Δψ; the experimental traces (dots) are fitted by a sinusoid. d, Maximum, average and minimum total output intensities are plotted in terms of joint absorbance, showing very good agreement with the two-peak polaritonic CPA theoretical traces (solid lines, coupled-mode theory; dashed lines, rigorous coupled wave analysis). e, Further confirmation of the phenomenon is gained by analysing the S-matrix determinant and the output beam dephasing. a–c correspond to the energies labelled A–C, respectively, in d,e. The right y axis corresponds to the dark purple data and the left y axis corresponds to the light purple data, as indicated by the arrows.

Full size image

We conclude by providing an experimental estimate of the S-matrix determinant. This estimate does not rely on the link between det S and the absorbance (equation (2))—which is valid only in this CMT model—but rather on the general relation

Employing the single-beam R and T, and the dephasing Δψ extracted from the double-beam experiment, we get the curve reported in Fig. 3e, which shows excellent agreement with the theory.

We have observed complete interferometric control of absorption by dressed light–matter states; further studies will aim at exploring the true quantum regime, in which pairs of individual photons are used to drive a strongly coupled cavity—single-quantum-emitter system. A generalization of the Hong–Ou–Mandel dip phenomenology has been predicted in the case of coherent perfect absorbers32, but this physics is still completely unexplored for polaritonic states.

Methods

The experimental set-up employed is sketched in Fig. 2a: the light source employed is a commercial external-cavity tunable quantum-cascade (QC) laser (Daylight Solutions) operating in the wavelength range 9.9 μm–10.7 μm; the phase-delay stage is composed of a loudspeaker membrane driven by a function generator, and the detectors are liquid-nitrogen-cooled mercury cadmium telluride devices.

The sample consists of a stack of 50 Al0.33Ga0.67As/GaAs QWs, grown by molecular beam epitaxy, with barrier and well thicknesses of 30 nm and 8.3 nm, respectively, and a nominal sheet doping n = 5 × 1011 cm−2 in the well material. The resulting 2-μm-thick membrane was patterned with metal stripes, featuring a period of 4 μm and a duty cycle of 80%. As explained in the Supplementary Information, this parameter choice follows from the need to tune the photonic resonance to the same energy of the intersubband transition and to satisfy the above-mentioned condition (3).