Abstract
When charge carriers are spatially confined to one dimension, conventional Fermi-liquid theory breaks down. In such Tomonaga–Luttinger liquids, quasiparticles are replaced by distinct collective excitations of spin and charge that propagate independently with different velocities. Although evidence for spin–charge separation exists, no bulk low-energy probe has yet been able to distinguish successfully between Tomonaga–Luttinger and Fermi-liquid physics. Here we show experimentally that the ratio of the thermal and electrical Hall conductivities in the metallic phase of quasi-one-dimensional Li0.9Mo6O17 diverges with decreasing temperature, reaching a value five orders of magnitude larger than that found in conventional metals. Both the temperature dependence and magnitude of this ratio are consistent with Tomonaga–Luttinger liquid theory. Such a dramatic manifestation of spin–charge separation in a bulk three-dimensional solid offers a unique opportunity to explore how the fermionic quasiparticle picture recovers, and over what time scale, when coupling to a second or third dimension is restored.
Similar content being viewed by others
Introduction
The success of Fermi-liquid (FL) theory in describing the properties of most ordinary three-dimensional metals makes it one of the triumphs of twentieth-century theoretical physics. Its wide-ranging applicability is testament to the validity of describing a system of interacting electrons by mapping its low-lying quasiparticle excitations onto a Fermi gas of non-interacting electrons. Perhaps the most striking realization of this one-to-one correspondence is the validity of the Wiedemann–Franz (WF) law in almost all known theoretical1,2,3,4 and experimental5,6,7 cases. The WF law states that the ratio of the electronic thermal conductivity κe to the electrical conductivity σ at a given temperature T is equal to a constant called the Lorenz number or Lorenz ratio, L0=κe/σT=(π2/3)(kB/e)2 and reflects the fact that thermal and electrical currents are carried by the same fermionic quasiparticles. Although the WF law is most applicable in the zero temperature (impurity scattering) limit, it is found to hold equally well at room temperature once all inelastic scattering processes become active8.
A marked deviation from the WF law is theoretically predicted when electrons are spatially confined to a single dimension. In systems that are strictly one-dimensional (1D), even weak interactions destroy the single particle FL picture in favour of an exotic Tomonaga–Luttinger liquid (TLL) state in which the fundamental excitations are independent collective modes of spin and charge, referred to, respectively, as spinons and holons. As heat is transported by entropy (spin and charge) and electric current by charge alone, spin–charge separation is a viable mechanism for the violation of the WF law9,10,11,12. Physically, repulsive interactions in a disordered 1D chain can inhibit the propagation of holons relative to that of spinons, leading to a strongly renormalized Lorenz number9.
Experimental signatures of TLL physics have been seen in the spectral response of a number of 1D structures13,14,15 and bulk crystalline solids16,17,18,19,20. Although the ratio κe/σT can in principle provide a direct means of distinguishing between FL and TLL states at low energies, there have been no confirmed reports to date of WF law violation in any 1D conductor. Identifying such systems, particularly bulk systems, is important as it might then allow one to tune, chemically or otherwise, the effective interchain coupling and thereby drive the system from one electronic state to the other. This would then open up the possibility of exploring the TLL-to-FL crossover and the nature of the excitations in the crossover regime.
Here we report a study of the electrical and thermal conductivity tensors of the purple bronze Li0.9Mo6O17, a quasi-1D conductor whose (surface-derived) photoemission lineshapes19, and density of states profiles20 contain features consistent with TLL theory.
Results
Electrical resistivity of Li0.9Mo6O17
As shown in Figure 1a, Li0.9Mo6O17 possesses a set of weakly coupled zigzag chains of MoO6 octahedra with a hole-concentration, believed to be close to half-filling21, running parallel to the crystallographic b axis. The T-dependence of the b axis resistivity, plotted in Figure 1B, varies linearly with temperature above 100 K, then as T is lowered, ρb(T) becomes superlinear. Below around 20 K, Li0.9Mo6O17 undergoes a crossover from metallic to insulating-like behaviour, ascribed to the formation of a putative charge density wave22,23. Also plotted in Figure 1b is the interchain resistivity ρa(T). The anisotropy in the electrical resistivity, ρa∼100ρb (< ρc) agrees well with optical conductivity measurements24 and highlights the extreme one-dimensionality of the electronic system. Note that although the T-dependence of the resistivity is similar along all three crystallographic axes, the corresponding interchain mean free paths are estimated to be less than the spacing between adjacent zigzag chains, implying incoherent interchain transport, at all finite temperatures.
(a) Three-dimensional crystal structure showing isolated, conducting, zigzag chains of MoO6 octahedra along the b axis in dark purple and non-conducting octahedra and MoO4 tetrahedra in light pink. Li ions are shown as green spheres. (b) Intra-chain (ρb) and inter-chain (ρa) resistivities of Li0.9Mo6O17 as a function of temperature. Note that ρa has been scaled by a factor of 1/100. The error bars in ρa and ρb (±7% and 12%, respectively) represent the uncertainty in the determination of the sample dimensions and the standard deviation of the room temperature resistivity of the subset of curves 1–5 shown with solid lines in Supplementary Figure S1a, respectively. For details of how ρb was determined, please refer to the section on isolating the intrinsic in-chain resistivity in the Supplementary information.
Thermal and electrical Hall conductivities of Li0.9Mo6O17
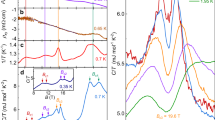
In. most solids, the thermal conductivity κ can be described as the sum of two independent contributions; κ=κe+κph, where κph is the phonon thermal conductivity. In metals with short mean-free-paths, these two terms are comparable in magnitude, making it difficult to accurately determine the Lorenz ratio. As shown in the Methods section however, the transverse Hall conductivity κxy is purely electronic in origin (the phonon current is strictly unaffected by a magnetic field) and thus measurements of the thermal Hall effect (the thermal analogue of the electrical Hall effect) provide a means of isolating the electronic component. Moreover, the ratio of the thermal and electrical Hall conductivities κxy/σxyT, known as the Hall Lorenz number Lxy, is also expected to be equal to L0 for a Fermi liquid. In our thermal Hall apparatus (inset to Fig. 2a and described in more detail in the Methods section), a temperature gradient is applied along the conducting chain direction (b axis, taken here to be the x axis) and a magnetic field H//c (H//z) generates a Lorentz force that produces a transverse thermal gradient along a (y). The main panel in Figure 2a shows the transverse temperature difference ΔTy(H), normalized by the applied power and multiplied by the sample thickness, at a number of selected temperatures. As expected, ΔTy is linear and odd in field. Figure 2b shows the electrical Hall resistivity at comparable temperatures.
(a) Transverse temperature difference ΔTy per unit power (multiplied by the sample thickness) as a function of applied magnetic field at various temperatures. Inset shows a schematic diagram of experimental setup used to measure the thermal Hall effect. Note that the thermocouples were placed either directly opposite to one another or (as shown) displaced longitudinally to allow both κxx and κxy to be measured simultaneously. Both set-ups gave the same response. ΔTy is dominated by the H-linear, odd-component κxy. The field-independent component of ΔTy due to κxx has been subtracted from the data. (b) Hall resistivity as a function of applied magnetic field at various temperatures in the same geometrical arrangement.
To determine κxy and σxy at each temperature, it is also necessary to evaluate the longitudinal terms κxx (=κb), κyy (=κa), σxx (=1/ρb) and σyy (=1/ρa) (see the Methods section for the derivation of κxy). As shown in Figure 3a, κa and κb show marked anisotropy. Due to the extreme resistivity anisotropy, κa is presumed to be purely phononic in origin and the ab anisotropy in κ(T) can be attributed either entirely to the electronic contribution within the chains or to a combination of κe and additional anisotropy in the phonon spectrum and/or scattering rate.
(a) Intra-chain (κb) and inter-chain (κa) thermal conductivities as a function of temperature. The error bars in κ (±15%) represent the uncertainty in the determination of the sample dimensions and the effective distance between the junctions of the differential thermocouple on the sample. (b) Electrical Hall (σxy) and thermal Hall (κxy) conductivities per unit field as a function of temperature. The error bars in σxy (κxy) are estimated from the standard deviation of multiple measurements on different samples. (c) Hall Lorenz ratio (Lxy/L0) for samples no. 1 and no. 2 and the longitudinal Lorenz ratio (Lxx/L0) and its square for no. 1. The error bars in Lxy/L0 and Lxx/L0 represent compound errors obtained from the various sources described above. The dotted line is guide to the eye. The horizontal dashed line represents the expectation from Fermi-liquid theory.
Figure 3b shows the resultant thermal and electrical Hall conductivities as obtained from the data presented in Figures 1b, 2a, 2b and 3a. According to the WF law, the ratio κxy/σxy should decrease (linearly) with decreasing temperature. In Li0.9Mo6O17, however, the opposite is true; while σxy increases by a factor ∼60 between 300 K and 25 K, κxy increases by more than 3,000. This implies a change in the Hall Lorenz number Lxy (=κxy/σxyT) of more than 500 over the same temperature interval. The thermal Hall angle tanθT=κxy/κe, which provides a measure of the electron mobility, reaches a value ∼0.6 at T=50 K and μ0H=10 Tesla comparable with that observed in elemental Cu (ref. 25). (Here we have assumed that κe=κb–κa). By comparison, the corresponding electronic Hall angle σxy/σxx∼1.25×10−3, illustrating the striking difference in mobilities for entropy and charge transport in Li0.9Mo6O17.
Lorenz ratios in Li0.9Mo6O17
Figure 3c shows Lxy/L0(T) for two samples over the entire temperature range studied. (Note that we have confined our Hall measurements to the metallic regime above the resistivity minimum.) At T=300 K, Lxy/L0∼100 and as T falls, Lxy/L0 follows an inverse power-law∼Tαxy (αxy∼−2.3), reaching a value∼105 at T=25 K. The solid triangles in Figure 3c are the corresponding estimates of Lxx/L0=(κb–κa)/σbT, that is, assuming an isotropic κph. At T=300 K, Lxx/L0∼7.5±1.5, rising to ∼35 at T=25 K. The horizontal dashed line is the expected FL result. Significantly, in both conventional metals like Cu (ref. 25) and Ni (ref. 26), and also in correlated metals like YBa2Cu3O6.95 (ref. 25) and URu2Si2 (ref. 27) (whose longitudinal thermal conductivity is dominated by phonons), neither Lxx/L0 nor Lxy/L0 is ever larger than unity. (As shown in Supplementary Figure S1, we have also verified this result for Ni using our own thermal Hall apparatus). Moreover, according to standard Boltzmann transport theory26, Lxx/L0∼<λs>/<λe> whereas Lxy/L0∼<λs>2/<λe>2, where <λs(e)> is the Fermi-surface averaged mean free path for entropy (charge) transport, respectively. Hence, in ordinary metals, Lxy/L0 is expected to vary as (Lxx/L0)2, as found experimentally25. In Li0.9Mo6O17, however, (Lxx/L0)2 does not scale with Lxy/L0 and cannot be made to scale with Lxy/L0 for any reasonable estimate for the phonon contribution to κxx (κb). This, together with the unprecedented enhancement of the WF ratio by several orders of magnitude, provides compelling evidence for the breakdown of the conventional FL picture in this quasi-1D conductor.
Discussion
Before discussing the violation of the WF law in Li0. 9Mo6O17 in terms of 1D correlation physics, we first consider alternative scenarios based on localization effects. In non-interacting systems, it has been shown theoretically that the WF law is robust to impurity scattering of arbitrary strength up to the Anderson transition1,2,3,4. In strongly correlated electron systems, however, the opening of a Mott gap can lead to a strong reduction of the electrical conductivity whereas the transport of heat, through spin fluctuations, can remain high10. Localization corrections associated with electron–electron interactions are also believed to induce corrections to κe that do not scale with the WF ratio, leading to an enhancement in L/L0 (ref. 28). Such interaction corrections only appear in the diffusive limit, however, below a characteristic energy scale kBTd=ћ/2πτ determined by the impurity scattering rate 1/τ. Estimates for 1/τ in Li0.9Mo6O17 from in-chain resistivity or magnetoresistance measurements give Td values of order several tens of Kelvin. Whereas this estimate for the diffusion limit is consistent with the temperature (Tmin∼20 K) below which the resistivity starts to increase with decreasing T, the behaviour of the magnetoresistance below Tmin is found to be more consistent with density wave formation than localization corrections23. In addition, the strong violation of the WF law is observed in the metallic regime between Tmin and room temperature, and more significantly, above 100 K where the resistivity itself is strictly T-linear. Collectively, these observations appear to rule out localization as the origin of the WF law violation in Li0.9Mo6O17.
Turning now to the issue of dimensionality, the form of the enhancement of the WF ratio in Li0.9Mo6O17 is at least qualitatively consistent with the original theoretical prediction for a spinless TLL9. An enhancement in Lxx/L0 originates from the fact that while heat can be transmitted through a non-magnetic impurity (via spinons), the latter acts as a near-perfect reflector (back-scatterer) of charge (holons). According to this picture, Lxx is predicted to be of order L0/K at high T, where K is the dimensionless conductance or Luttinger parameter, and as temperature is lowered, Lxx/L0 varies as a power-law, Lxx/L0∼T4−2/K which diverges for K<0.5, corresponding to repulsive, long-range interactions9. Although the original model considered a single impurity embedded in an interacting spinless 1D chain, the theory has been shown to apply equally to the case of multiple impurities and the inclusion of spin degrees of freedom with only minor modifications9,11. Concerning the magnitude of the violation, a recent theoretical treatment of a weakly disordered TLL in the regime of large Umklapp scattering found an enhancement of Lxx/L0 of several orders of magnitude close to commensurate filling, owing to the fact that the spinon contribution to the thermal current cannot be degraded by Umklapp scattering processes10. To the best of our knowledge, no other 'gapless' model can account for such a gross violation of the WF law in the metallic regime.
Although there is currently no specific theoretical framework for the thermal Hall response in a quasi-1D conductor, it has been shown theoretically that a system of weakly coupled TL chains can exhibit an electrical Hall response that shows a power-law correction to the free Fermi (band) value in the presence of Umklapp scattering29. Moreover, the divergence of Lxy/L0 with decreasing temperature (Fig. 3c) is qualitatively, if not quantitatively, similar to that found in Lxx/L0. This divergence would seem to imply that electronic interactions in Li0.9Mo6O17 are indeed repulsive and long range, in agreement with conclusions drawn from angle-resolved photoemission spectroscopy19 and scanning tunnelling microscopy20 where K, as obtained from the anomalous exponent α, is found to lie between 0.2 and 0.25. The fact that Lxy/L0 does not scale with (Lxx/L0)2, as expected for a FL, might also be an intrinsic property of the TLL. Power-law behaviour is also predicted and indeed found in the T-dependence of the dc resistivity. Specifically, ρb(T)∼T between 100 K and 300 K (Fig. 1b). The value of K extracted from the power-law exponent in ρb(T) depends on the degree of commensurability. An exponent close to unity is consistent with K=0.25 for a system at or near quarter-filling30. According to band-structure calculations21 however, Li0.9Mo6O17 is believed to be closer to half-filling, for which a T-linear resistivity corresponds to g∼1 (ref. 29), that is, to the non-interacting case. The origin of this inconsistency is not understood at present.
Since the TLL state is predicted to occur only in a strictly 1D interacting electron system, the inevitable coupling that exists between the chains in Li0.9Mo6O17 (to generate the Hall response) and parameterized by the interchain hopping integral t⊥, ought to inhibit the observation of TLL physics in the zero-frequency limit31,32. (For simplicity, we assume here that t⊥ is the same in both orthogonal directions). For kBT<t⊥, charge should hop coherently in all three dimensions, albeit with anisotropic velocities, and the system show characteristics of a Fermi-liquid. Once thermal broadening is comparable with the warping of the Fermi sheets, however, hopping between chains will become incoherent, leading to a putative 3D–1D dimensional crossover. Notably, in the presence of strong interactions, the value of t⊥ can be significantly renormalized30,33 and as stated above, both band structure calculations21 and photoemission spectroscopy19 indicate that Li0.9Mo6O17 lies close to half-filling. Thus, provided nearest neighbour interactions are dominant, intra-chain correlation effects in Li0.9Mo6O17 may be strong enough that its physical response is indistinguishable from that of a TLL33, at least at an energy scale kBT∼20 K∼2 meV. Below this scale, the FL ground state should recover, though whether or not such a crossover to FL physics can ever be realized in Li0.9Mo6O17, given its propensity to superconducting22 and density-wave23 order, remains to be seen.
Finally, we turn to consider how one might controllably affect the interaction strength or effective dimensionality in Li0.9Mo6O17 so that the spin and charge are recombined. One obvious route to try is to vary the band filling, for example, through substitution of Mg for Li. On the basis of the diagonal principle, the ionic radius of Li+ ions is comparable with that of Mg2+. This suggests that such substitution could proceed without adversely affecting the 1D nature of the system, allowing the role of correlations in the TLL-to-FL crossover to be explored in a controlled manner. The results reported in this manuscript suggest that an accompanying study of the variation of Lxy with doping would provide a clear litmus test of the recovery of the FL state.
Methods
Sample growth and characterization
Single crystals of Li0. 9Mo6O17 were grown using a temperature gradient flux method22 and cleaved within the a–b plane. The resulting samples were face-indexed using a single-crystal X-ray diffractometer to determine the a- and b-axes. Thereafter bar-shaped crystals (approximate dimensions 700×100×20 μm3) were cut from the face-indexed sample using a wire-saw.
Isolating the intrinsic in-chain resistivity
To test the validity of the WF law, accurate measurements of both the electrical resistivity and thermal conductivity are essential. In a quasi-1D conductor, it is especially problematic to measure the smallest of the resistivity tensor components, because even a small admixture of either of the two larger orthogonal components can give rise to erroneous values and distort the intrinsic temperature dependence of the in-chain resistivity. In Li0.9Mo6O17, reported room-temperature values for the in-chain (b axis) resistivity range from 400 μΩ cm23 to more than 10 mΩ cm34,35. Moreover, in instances where large (that is, >1 mΩ cm) ρb values have been reported, ρb (T) tends to show a sub-linear T-dependence below 300 K.
To isolate the in-chain resistivity extreme care is needed to electrically short out the sample in the two directions perpendicular to the chain and thus ensure that current flow between the voltage contacts is uniaxial. In our experiments, this is achieved either by coating conductive paint or evaporating gold strips across the entire width of the sample in the two orthogonal current directions. The mounting configuration is shown as an inset in Supplementary Figure S2. The zero field measurements were carried out for 4.2 K <T<300 K in a 4He dipper cryostat. In total, we measured ρb(T) of over 30 single crystals to allow us to better identify the intrinsic T-dependence of the chains. For further details of how we determined the in-chain electrical resistivity, please refer to the corresponding section in the Supplementary information.
Electrical Hall effect
The electrical Hall effect was measured using the standard four-point method. Thin long crystals were mounted freestanding using Dupont 4929 silver epoxy. Two pairs of transverse voltage contacts were used, to check for reproducibility, and the whole process was repeated on three different samples. Owing to slight misalignment of the contacts, the measured signal contained both a symmetric (that is, magnetoresistive) and an antisymmetric part (the Hall signal). Using the relation VH=½(V(B)−V(−B)), we were able to isolate the smaller antisymmetric Hall voltage VH, which, when normalized by B, yields the Hall coefficient RH. The uncertainty here reflects the scatter of the data from different measurements using different voltage contact pairs. To determine the Hall Lorenz number Lxy (=κxy/σxyT), we extract σxy from our Hall data using the following expression:

where t is the crystal thickness and I is the applied current.
Thermal conductivity measurements
For the thermal conductivity measurements, we used a zero-field set-up housed in a 4He flow cryostat that covers the temperature range 10 K < T < 300 K. We employed a modified steady-state method36, shown schematically in Supplementary Figure S3, in which a temperature gradient, measured using a differential thermocouple, is set up across the sample through a pair of calibrated heat-links attached to each end. The heat-links are also differential thermocouples. The sample is suspended by the free ends of the heat-links between two platforms that are weakly coupled to the heat-bath. Each platform houses a heater that enables a temperature gradient to be set up across the sample in both directions at a fixed heat-bath temperature. The thermal conductivity κ is related to the measured quantities through the relationship,

where P is the power through the cross-sectional area A and l, the separation of contacts between which the temperature difference ΔTx is measured.
From the temperature drop across the heat-links, we can estimate the power entering and leaving the crystal. This is a distinct advantage of the heat-link method over other thermal conductivity experimental setups, as it ensures that any power loss due to radiative losses and heat conduction through the thermocouple wires to the heat-bath is known. Although power losses due to radiation are significant (of order 20%) at high temperature, the total power loss across the sample falls to below 2% at ∼200 K. Provided the difference between the power entering the sample and leaving the sample remains below 20%, the power through the sample can be taken as the average of the input and output power.
Regarding possible extrinsic contributions to ΔTx, thermocouple readings are always taken with and without heat input (in either current direction), and the direction of the heat current is reversed to remove any effect due to stray thermal gradients. Finally, data are always taken in the regime where the extracted value for the thermal conductivity (or thermal Hall conductivity) is independent of the strength of the heat current, thus eliminating nonlinear effects.
The largest errors associated with our absolute measurement of the thermal conductivity are geometrical errors associated with the finite width of the thermocouple contacts relative to their separation, as well as with the uncertainty in determining the overall dimensions of the samples. Depending on the size of the crystal to be studied, a scanning electron, focused ion beam or high-power optical microscope was used to measure its thickness. The corresponding errors are ±1 μm, ±1 μm and ±5 μm, respectively. The separation between contacts and the width of the sample was determined using a high-power optical microscope with an error of ∼7%. To measure the separation between contacts, we adopted the convention to measure the separation between the mid-point of the contacts for both the thermal and electrical measurements37. From these considerations, we associate an upper bound for the error in the final values of thermal conductivity of ±15% for the samples. The reproducibility in our measurements of κa and κb is shown in the Supplementary Figures S2A and S2B respectively.
Thermal Hall measurements
By definition, the thermal Hall effect (also known as the Righi–Leduc effect) is the development of a transverse thermal gradient (ΛTy) in the presence of a longitudinal thermal gradient (ΛTx) and an orthogonal magnetic field (Bz). Crucially, ΛTx is generated by a thermal heat current along x; Jh,x=−κxx ΛTx where κxx is the total longitudinal thermal conductivity, including the phonon component. The transverse thermal current (κxy ΛTx), due to the magnetic field deflection of the electronic charge carriers, is balanced by a heat current due to the 'total' thermal conductivity in the opposite direction. This is required by the condition that there is no net heat current flow in the transverse direction once steady state has been established. Again, inclusion of the relevant elements of the total thermal conductivity tensor leads to the following expression:

giving,

Hence, the thermal Hall conductivity was calculated as,

where t is the thickness of the sample.
To measure the thermal Hall effect, the same set-up on which the longitudinal (zero-field) thermal conductivity measurements were performed was used, although in this case, the differential thermocouple was positioned on opposite edges of the crystal. The sample was always positioned so that the heat flow in the longitudinal direction was along the b axis of the sample. The experiment was placed in an evacuated chamber immersed in liquid helium within the coil of a superconducting magnet. Heating power was provided by a resistive element thermally connected to the experimental platform and was controlled by a Lakeshore temperature controller. During a measurement of the thermal Hall effect, the temperature was first stabilized, then a fixed field applied and finally heat current passed through the sample. The modified steady state method was then employed as before. The power loss was found to be ∼20% at room temperature, reducing to ∼10% below 200 K. The experiment is then repeated at multiple field values. To isolate the thermal Hall response, both positive and negative polarities of the magnetic field were used. As with the longitudinal thermal conductivity measurements, the heat direction was then reversed and the measurements repeated. Finally, possible extrinsic contributions to the thermal Hall conductivity, for example due to anisotropy in the thermopower, are discussed in detail in the section on possible internal heating effects in the Supplementary Information.
Additional information
How to cite this article: Wakeham, N. et al. Gross violation of the Wiedemann–Franz law in a quasi-one-dimensional conductor. Nat. Commun. 2:396 doi: 10.1038/ncomms1406 (2011).
References
Chester, G. V. & Thellung, A. Law of Wiedemann and Franz. Proc. Phys. Soc. London 77, 1005–1013 (1961).
Strinati, G. & Castellani, C. Energy diffusion in disordered electronic systems near the Anderson transition. Phys. Rev. B 38, 2270–2276 (1987).
Castellani, C., DiCastro, C., Kotliar, G., Lee, P. A. & Strinati, G. Thermal conductivity in disordered interacting-electron systems. Phys. Rev. Lett. 59, 477–480 (1987).
Kearney, M. J. & Butcher, P. N. Thermal transport in disordered systems. J. Phys. C: Solid State Phys. 21, L265–L270 (1988).
Ott, H. R., Marti, O. & Hulliger, F. Low temperature thermal conductivity of CeAl3 . Solid State Commun. 49, 1129–1131 (1984).
Bayot, V., Piraux, L., Michenaud, J. P. & Issi, J. P. Evidence for weak localization in the thermal conductivity of a quasi-two-dimensional electron system. Phys. Rev. Lett. 65, 2579–2582 (1990).
Ronning, F. et al. Thermal conductivity in the vicinity of the quantum critical end point in Sr3Ru2O7 . Phys. Rev. Lett. 97, 067005 (2006).
Ashcroft, N. W. & Mermin, N. D. Solid State Physics 21 (Saunders College, Philadelphia, 1976).
Kane, C. L. & Fisher, M. P. A. Thermal transport in a Luttinger liquid. Phys. Rev. Lett. 76, 3192–3195 (1996).
Garg, A., Rasch, D., Shimshoni, E. & Rosch, A. Large violation of the Wiedemann-Franz law in Luttinger liquids. Phys. Rev. Lett. 103, 096402 (2009).
Li, M.- R. & Orignac, E. Heat conduction and Wiedemann-Franz law in disordered Luttinger liquids. Europhys. Lett. 60, 432–438 (2002).
Dora, B. Wiedemann-Franz law in the SU(N) Wolff model. Phys. Rev. B 74, 161101(R) (2006).
Chang, A. M., Pfeiffer, L. N. & West, K. W. Observation of chiral Luttinger behavior in electron tunneling into fractional quantum Hall edges. Phys. Rev. Lett. 77, 2538–2541 (1996).
Bockrath, M. et al. Luttinger-liquid behavior in carbon nanotubes. Nature 397, 598–601 (1999).
Segovia, P., Purdie, D., Hensberger, M. & Baer, Y. Observation of spin and charge collective modes in one-dimensional metallic chains. Nature 402, 504–507 (1999).
Jompol, Y. et al. Probing spin-charge separation in a Tomonaga-Luttinger liquid. Science 325, 597–601 (2009).
Dardel, B. et al. Possible observation of a Luttinger-liquid behaviour from photoemission spectroscopy of one-dimensional organic conductors. Europhys. Lett. 24, 687–692 (1993).
Kim, C. et al. Observation of spin-charge separation in one-dimensional SrCuO2 . Phys. Rev. Lett. 77, 4054–4057 (1996).
Wang, F. et al. New Luttinger-liquid physics from photoemission on Li0.9Mo6O17 . Phys. Rev. Lett. 96, 196403 (2006).
Hager, S. et al. Non-Fermi-liquid behavior in quasi-one-dimensional Li0.9Mo6O17 . Phys. Rev. Lett. 95, 186402 (2005).
Popovic, S. J. & Satpathy, S. Density-functional study of the Luttinger liquid behavior of the lithium molybdenum purple bronze Li0.9Mo6O17 . Phys. Rev. B 74, 045117 (2006).
Greenblatt, M. et al. Quasi-two-dimensional electronic properties of the lithuim molydenum bronze Li0:9Mo6O17 . Solid State Comm. 51, 671–674 (1984).
Xu, X. et al. Directional field-induced metallization of quasi-one-dimensional Li0:9Mo6O17 . Phys Rev. Lett. 102, 206602 (2009).
Choi, J. et al. Probing localization effects in Li0.9Mo6O17 purple bronze: An optical-properties investigation. Phys. Rev. B 69, 085120 (2004).
Zhang, Y. et al. Determining the Wiedemann-Franz ratio from the thermal Hall conductivity: application to Cu and YBa2Cu3O6.95 . Phys. Rev. Lett. 84, 2219–2222 (2000).
Onose, Y., Shiomi, Y. & Tokura, Y. Lorenz number determination of the dissipationless nature of the anomalous Hall effect in itinerant ferromagnets. Phys. Rev. Lett. 100, 016601 (2008).
Behnia, K. et al. Thermal transport in the hidden-order state of URu2Si2 . Phys. Rev. Lett. 94, 156405 (2005).
Niven, D. R. & Smith, R. A. Electron-electron interaction corrections to the thermal conductivity in disordered conductors. Phys. Rev. B 71, 035106 (2005).
Leon, G., Berthod, C. & Giamarchi, T. Hall effect in strongly correlated low-dimensional systems. Phys. Rev. B 75, 195123 (2007).
Giamarchi, T. Theoretical framework for quasi-one-dimensional systems. Chem. Rev. 104, 5037–5055 (2004).
Castellani, C., Di Castro, C. & Metzner, W. Dimensional crossover from Fermi to Luttinger liquid. Phys. Rev. Lett. 72, 316–319 (1994).
Kopietz, P., Meden, V. & Schonhammer, K. Anomalous scaling and spin-charge separation in coupled chains. Phys. Rev. Lett. 74, 2997–3000 (1995).
Arrigoni, E. Crossover from Luttinger- to Fermi-liquid behavior in strongly anisotropic systems in large dimensions. Phys. Rev. Lett. 83, 128–131 (1999).
da Luz, M. S. et al. Anisotropic electrical resistivity of quasi-one-dimensional Li0.9Mo6O17 determined by the Montgomery method. Phys. Rev. B 76, 233105 (2007).
Chen, H. et al. Magnetotransport properties in purple bronze Li0.9Mo6O17 single crystal. Europhys. Lett. 89, 67010 (2010).
Allen, P. B. et al. Thermal conductivity of insulating Bi2Sr2YCu2O8 and superconducting Bi2Sr2CaCu2O8: Failure of the phonon-gas picture. Phys. Rev. B 49, 9073 (1994).
Narduzzo, A. et al. Fragile three-dimensionality in the quasi-one-dimensional cuprate PrBa2Cu4O8 . New J. Phys. 8, 172 (2006).
Acknowledgements
We acknowledge technical and scientific assistance from A. Carrington, P.J. Heard, R.H. McKenzie, N.P. Ong and N. Shannon and collaborative support from J. He, D. Mandrus and R. Jin (ORNL). This work was supported by EPSRC (UK). N.E.H. acknowledges a Royal Society Wolfson Research Merit Award.
Author information
Authors and Affiliations
Contributions
N.W., A.B., X.X., J-F.M. and N.E.H. designed and performed the experiments and co-wrote the paper. M.G. supplied the single-crystal samples and commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures S1–S3, Supplementary Methods and Supplementary References (PDF 304 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-No Derivative Works 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Wakeham, N., Bangura, A., Xu, X. et al. Gross violation of the Wiedemann–Franz law in a quasi-one-dimensional conductor. Nat Commun 2, 396 (2011). https://doi.org/10.1038/ncomms1406
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms1406
This article is cited by
-
Heat conductance of the quantum Hall bulk
Nature (2024)
-
Anisotropic transport in a possible quasi-one-dimensional topological candidate: TaNi2Te3
Tungsten (2023)
-
Electronic thermal transport measurement in low-dimensional materials with graphene non-local noise thermometry
Nature Nanotechnology (2022)
-
Heat transport through atomic contacts
Nature Nanotechnology (2017)
-
Nonlinear spectra of spinons and holons in short GaAs quantum wires
Nature Communications (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.