Abstract
Experimental band structure analyses of single-walled carbon nanotubes have not yet been reported, to the best of our knowledge, except for a limited number of reports using scanning tunnelling spectroscopy. Here we demonstrate the experimental determination of the excitonic band structures of single-chirality single-walled carbon nanotubes using their circular dichroism spectra. In this analysis, we use gel column chromatography combining overloading selective adsorption with stepwise elution to separate 12 different single-chirality enantiomers. Our samples show higher circular dichroism intensities than the highest values reported in previous works, indicating their high enantiomeric purity. Excitonic band structure analysis is performed by assigning all observed Eii and Eij optical transitions in the circular dichroism spectra. The results reproduce the asymmetric structures of the valence and conduction bands predicted by density functional theory. Finally, we demonstrate that an extended empirical formula can estimate Eij optical transition energies for any (n,m) species.
Similar content being viewed by others
Introduction
For more than 20 years since the discovery of single-walled carbon nanotubes (SWCNTs), we have lacked accurate knowledge of their unique optical and physical properties due to variations in the allowed structures (n,m), which have been defined using chiral indices1. It is known that Eii optical transitions are allowed for the polarization of the electric field of light in parallel to the nanotube axis, whereas Eij (iv→jc) transitions are allowed for cross polarization2,3,4,5. Usually, only the Eii transitions can be observed from optical absorption and photoluminescence spectra because a strong local field induced by the applied field obscures the cross-polarized optical transitions3,4,5. Limited information about the Eii energies alone is insufficient for constructing valence and conduction band structures that require Eij values. Although Miyauchi et al3,4. succeeded in measuring the cross-polarized optical transitions using aligned SWCNTs, the results were limited. Previously, the detailed band structures of specific SWCNTs could only be obtained by density functional theory (DFT) calculations as predictions6 except in the case of experimental studies utilizing scanning tunnelling spectroscopy7,8. On the other hand, the DFT calculations suggest that all optically allowed transitions Eii and Eij are observable in circular dichroism (CD) spectra, even for randomly aligned chiral SWCNTs9,10,11 due to the comparable signal intensities of both transitions. Although SWCNTs have one-dimensional electronic systems, an interaction between right- or left-handed SWCNTs and circularly polarized light should exist. The values of all Eii and Eij transitions allow us to analyse the detailed band structures of the SWCNTs with more precision than can be implemented by other optical measurements.
A mixed chirality sample cannot be used for the band structure analysis because numerous peaks are expected in the CD spectra. Furthermore, this analysis requires the preparation of not only high-purity single-chirality but also highly selected enantiomers because the CD intensity is proportional to the differential ratios between left- and right-handed SWCNTs. Peng et al.12 reported the first enantiomer separation using a specially designed chiral dispersant molecule with different affinities for the left- and right-handed enantiomers13, and Ghosh et al.10 used a nonlinear density-gradient ultracentrifugation (DGU) to achieve enantiomer separation using a common chiral dispersant. However, the purities of these samples were not high enough for the band structure analysis because the observed CD peaks were difficult to assign to a specific chirality. Gel column chromatography with the overloading technique has also been used for the enantiomer separation, but the enantiomer purity was not high enough14. For the detailed analysis of the band structure, even very weak peaks must be recognized. Higher enantiomer purity is required for obtaining a high signal/noise ratio in a CD spectrum.
To improve both single-chirality purity and enantiomer purity, we developed a separation method that combines selective adsorption with the overloading technique and selective desorption15 with a stepwise elution gel chromatography. Using a dextran-based gel for the column medium and a mixed surfactant for the eluent, this method can simultaneously separate single-chirality SWCNTs and enantiomers based on the effects of the optically active dextran. Using this technique, here we successfully separate 12 distinct (n,m) single-chirality species of semiconducting SWCNTs and measure their CD spectra. The CD intensity, which is normalized by its optical absorbance, is higher than that of previous reports to the best of our knowledge, indicating that the highest enantiomer purity is obtained10,13,14. Excitonic band structure analysis is also performed by assigning all the CD peaks to allowed optical transitions. Our results are in excellent agreement with the DFT calculations, which include asymmetries of the valence and conduction bands6. Interestingly, a plot of the allowed Eij transitions against the SWCNT diameters shows a typical ‘family behaviour’, which suggest that our results are quite reasonable. Our challenge of excitonic band structure analysis is based on a simple analysis of the CD spectrum, but it originates from an interaction between a circular polarized photon and the chiral structure of the carbon network. The results presented here could be an important reference for further studies on the physical properties of SWCNTs. Moreover, the new separation method developed in this work may be important for possible biochemical and medical applications because the high-purity SWCNT enantiomers could be used for chiral separation and the synthesis of chiral molecules16.
Results
Single-chirality enantiomer separation and evaluation
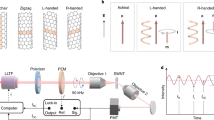
In this work, higher-purity separation was achieved by combining the overloading technique for the C–C bond curvature-selective adsorption of semiconducting SWCNTs17 with diameter-selective desorption by stepwise elution chromatography15. In the first separation step, 80 ml of a SWCNT dispersion in 3% SDS solution was injected onto a multicolumn filled with 5.6 ml of the dextran-based gel to adsorb semiconducting SWCNTs with very narrow C–C bond curvature distributions. After sufficiently flushing the column, 1% sodium cholate (SC) solution was injected for elution. From the first separation step, we obtained a mixture of several species of SWCNTs in a 1% SC solution (Supplementary Fig. 1). Before the second separation step, the same amount of 1% SDS solution was added to the SWCNTs solution to create a 0.5% SC+0.5% SDS mixed solution. This SWCNT solution was injected onto the gel column, and then stepwise elution chromatography was performed using an aqueous solution of 0.5% SC+0.5% SDS+x% sodium deoxycholate (DOC). For the diameter-selective elution, the DOC concentration x was increased stepwise from 0.01 to 0.07%. In this process, single-chirality species with smaller diameters were eluted with lower DOC concentrations. The relationship between the separation order of (n,m) nanotubes and DOC concentration is consistent with our previous report of diameter-selective desorption15,18 (Supplementary Fig 2–4). Importantly, each chirality eluted at two different DOC concentrations, x1 and x2 (for example, (6,5) SWCNTs were eluted at 0.030 and 0.035% DOC, Supplementary Fig. 2d), which corresponded to two enantiomers with the same band structure but different affinities to the gel. Finally, we measured their CD spectra and confirmed enantiomer separation ((+)- or (−)-(n,m), described in detail below). This separation method of stepwise elution chromatography is effective not only for single-chirality separation but also simultaneous enantiomer separation. Compared with our previous work14, a higher resolution of single-chirality enantiomeric separation was achieved in this study, which is mainly contributed by the introduced mixed-surfactant system and the stepwise elution procedure15.
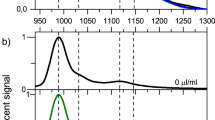
Figure 1a shows the optical absorption spectra of the 12 single-chirality enantiomers of semiconducting SWCNTs obtained in this work. The spectra of either (+)- or (−)-(n,m) enantiomers with higher purities are shown here. Each spectrum exhibits a series of sharp absorption peaks corresponding to the E11, E22, E33 and E44 transitions with very low baseline absorption, which is known as a typical feature of chirality-sorted SWCNTs. These species were identified as (6,4), (9,1), (8,3), (6,5) (7,3), (7,5), (10,2), (9,4), (8,4), (7,6), (10,3) and (11,1) from their E11 and E22 peak positions19,20. Notably, the baseline absorption of each sample was very low, indicating that impurities such as nanotube aggregates, amorphous carbon, and catalyst particles, were successfully removed in the separation processes21,22. The purity of each (n,m) species was basically calculated as an integrated intensity ratio of the absorption peak of the target chirality to the sum of all other peaks using PeakFit software (Supplementary Fig. 5). Since the absorption cross section of each (n,m) species is different23,24, we have corrected the above purity using a theoretical formula of chirality-dependent oscillator strengths reported in ref. 23. The final purity of each species is indicated in Fig. 1a. Most of the samples were more than 90% pure except for species (8,4). Because the band structure analysis requires high-purity, we selected only high-purity species to maintain the reliability of the analysis. The purities of all species except (8,4) were the same or higher than those of previous reports, including studies using DGU10, DNA wrapping25 and gel chromatography17,26 (Supplementary Table 1). Figure 1b shows the photoluminescence (PL) excitation-emission mapping of 12 sorted species corresponding to Fig. 1a. In general, because the E22 excitation - E11 emission peak is dominant in the PL maps, each map had only one bright peak. In addition, the phonon sideband peak is well known to be observed in the excitation spectrum for the E11 emission. In the cases of (10,3) and (11,1), the E11 emission by E33 excitation (∼420 nm) was also observed. Furthermore, we sometimes observe a PL peak from oxide states that were unexpectedly produced in the ultrasonic dispersion process27,28,29. Because the PL intensity of the oxide state was much higher than the original peak, this peak was noticeably bright. Natural oxidation is diameter-dependent and is more frequently observed in small diameter SWCNTs with highly curved side walls, such as (6,4) at 1,050 nm. In general, most of the peaks on the PL map could be assigned to the original E11 transitions, phonon side bands, and oxide states, indicating that high-purity single-chirality SWCNTs were present. In the PL map of (11,1), however, four additional peaks from (10,2), (10,3), (9,4) and (8,4) were observed, while very weak peaks were also observed in the absorption spectra. This suggested that the virtual PL efficiency of (11,1) was lower than that of the impurities, which was probably due to a self-absorption. After obtaining a high-purity single-chirality sample, we could estimate the PL efficiency by measuring the PL intensity, but this was not performed in this work. We assumed that the purity should not be determined by PL intensity, but instead by optical absorption.
Figure 2 shows the CD spectra and optical absorption spectra for the 12 different (n,m) enantiomers. In the CD spectra, the SWCNTs that exhibited a positive E22 CD peak were denoted as (−), whereas the SWCNTs that exhibited a negative E22 CD peak were denoted as (+)10,30. Here, (+) and (−) refer to enantiomers that showed plus and minus E11 CD peaks, respectively. Both (+)- and (−)-(n,m) were obtained for all types except (9,4) and (10,3). The missing (9,4) and (10,3) enantiomers were mixed with the other chiralities and could not be recovered as a single chirality. By comparing the CD spectra with the optical absorptions, the CD peak positions of E22, E33 and E44 were determined and were used for the assignments. A photograph of the separated single-chirality SWCNT enantiomers is shown in Supplementary Fig. 6, in which different colours for each chirality indicate different electronic structures; (+)- and (−)-enantiomers are shown in the same colour when the concentrations are same. For example, the same concentrations of (+)- and (−)-(6,5) enantiomers are shown in exactly the same colour (Supplementary Fig. 7).
The relative enantiomeric purity of sorted enantiomers can be evaluated by a normalized CD intensity (CDnorm)13,14, instead of commonly used anisotropic factor that cannot be defined for SWCNT. Table 1 summarizes the CDnorm values of individual (n,m) enantiomers obtained in this work and in previous reports. All CDnorm values obtained in this study were higher than those obtained using the repeated overloading method14, temperature controlled gel chromatography14, DGU10 and molecular recognition13, indicating that the highest enantiomeric purity was obtained in the present study. The conventional enantiomeric purity of (6,5) enantiomers was roughly estimated to be higher than 90% for both (+)- and (−)-enantiomers. A detailed analysis should be discussed elsewhere.
Alternative behaviour of CD between Type 1 and Type 2
The order of the affinity between the SWCNT enantiomers and the dextran-based gel was scaled by the corresponding DOC concentrations of the stepwise elutions. Figure 3 shows the results of the stepwise elution for the 12 different single-chirality SWCNT enantiomers as a function of nanotube diameter. A clear relationship between the diameter and the DOC concentration can be seen; namely, the required DOC concentration was higher for SWCNTs with larger diameters. Interestingly, for the separation of Type 1 enantiomers (|n−m|=3a+1, where ‘a’ is an integer19,20,31; (7,3), (6,5) (7,6) and (8,4)), higher DOC concentrations were required for the (−)-enantiomers than that for the (+)-enantiomers, whereas lower DOC concentrations were required for the (−)-enantiomers than for the (+)-enantiomers for Type 2 (|n−m|=3a+2; (6,4), (9,1), (8,3) and (7,5)). A similar relationship was obtained in the separation of the (10,2), (11,1) and (10,3) enantiomers, which are large diameter enantiomers requiring the use of 0.5% SC+1% SDS as a solvent instead of 0.5% SC+0.5% SDS (Fig. 3, inset). The enantiomer separation was probably achieved due to the interaction between the optically active SWCNT and the optically active dextran-based gel. If this assumption is correct, the separation order of handedness should be the same for all single-chirality SWCNTs. However, our results showed that the separation order of (+)- and (−)-enantiomers depended on the type of SWCNT index. A possible explanation is that the CD signals of Type 1 and Type 2 SWCNTs with a specific handedness have opposite signs. This statement is supported by theoretical calculation of CD spectra of SWCNTs described below.
The SWCNTs eluted at higher DOC concentrations have higher affinity toward the dextran-based gel. Inset: the relationships for (10,2), (11,1) and (10,3) SWCNTs separated in the solvent containing 0.5% SC and 1% SDS (see Supplementary Methods and Supplementary Fig. 4). Blue and red triangles denote (+)- and (–)-SWCNTs, respectively. Type 1 and Type 2 chirality (n,m) are denoted as blue and pink letters, respectively.
In Fig. 4a, we show the calculated CD signal ΔW as a function of the wavelength of the incident circular polarized lights in the direction perpendicular to the nanotube axis, for (6,5) (red line) and (11,−5) (blue line) SWCNTs in which (n,m) and (n+m,−m) SWCNTs are enantiomers to each other. In the numerical calculation, ΔW is defined by the difference of optical absorption probability of (6,5) (or (11,−5)) SWCNT for the left- and right-handed circular polarized lights within tight-binding method for optical transition of SWCNTs32. It is important to note that the optical absorption probability near the K point for the right-handed circular polarized light is identical to that near the K′ point for the left-handed circular polarized light because of the time reversal symmetry between the K and K′ points, if we adopt an approximation of the vertical optical transition in the k space. It means that we would get ΔW=0 if we adopted this approximation. Thus it is essential in the calculation of ΔW to consider the phase difference of the light for different carbon atom positions that is usually neglected in the calculation of the absolute values of the optical absorption. The detail of the calculation will be reported elsewhere.
(a,b) Calculated CD signal ΔW of enantiomers for (a) (6,5) (red) and (11,−5) (blue) and (b) (7,5) (red) and (12,−5) (blue), as a function of wavelength of incident light. Shaded lines correspond to Eii and Eij van Hove singularity of joint density of states. (c) Reciprocal space of the graphene and cutting lines corresponding to Type 1 (left of panel) and Type 2 (right of panel) SWCNTs.
The calculated results reproduce the experimental results in many aspects: (1) ΔW of (6,5) SWCNT changes the sign at E22, E33, and E44 and (2) ΔW of (11,−5) SWCNTs gives the opposite sign to that of (6,5) for all the wavelength of the light. Further, when we change (n,m) from (6,5) (Type 1 SWCNT) to (7,5) (Type 2 SWCNT) as shown in Fig. 4b, we get the opposite sign of ΔW to that for (6,5) for each Eii energy. This phenomenon can be explained by the difference in the reciprocal space of the graphene and cutting lines between Type 1 and Type 2 SWCNTs as shown in Fig. 4c. The optical absorption for Eii van Hove singularity of Type 1 SWCNT occurs at the opposite k points measured from the K point compared with that of Type 2 SWCNT, whose transition optical dipole moment around the K point gives the opposite sign33. The opposite behaviour between Type 1 and 2 SWCNTs in the calculation is also consistent with the experimental expectation based on their type-dependent affinities with gel. Thus, alternative behaviour of ΔW as a function of the wavelength comes from the change of the wavefunctions on one-dimensional cutting line near the K point34,35.
It should be mentioned that we measure CD of SWCNTs with random orientation in the experiment. For incident circular polarized light, there are two inequivalent geometries of SWCNTs: The propagating directions of the light are (1) perpendicular to the nanotube axis (the case of Fig. 4a,b) and (2) parallel to the nanotube axis (not shown). Even though we should integrate the CD for possible direction of the light, we did not show this for simplicity. We can imagine that the case of (2) gives a minor contribution after integration of azimuth angle of spherical coordinate. Further, we did not consider the effect of the exciton in this calculation in the first approximation. Since the wavefunction of an exciton is given by linear combination of the Bloch functions along one-dimensional Brillouin zone (or cutting line)36,37, we can say that the behaviours of CD do not change even after we consider the exciton effect. Thus the present calculated results are reasonable to simulate the experimental results.
Asymmetric band structure analysis
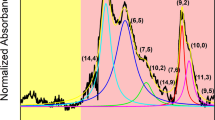
For the analysis of the CD peaks, we needed to know the selection rules for the CD signal and the related optical transitions for an individual SWCNT38. The energy bands and the allowed optical transitions of a semiconducting SWCNT are shown in Supplementary Fig. 8. Optical transitions from the valence band (denoted as nv) to the conduction band (denoted as nc) in a semiconducting SWCNT are characterized by Δn, where Δn=nc−nv. When the electric field polarization of incident light is parallel to the SWCNT axis, optical transitions with Δn=0 (E11, E22, E33…) are allowed, and when the polarization is perpendicular to the axis, optical transitions with Δn=±1 (E12/E21, E13/E31, E24/E42…) are allowed5,38. Usually, only Eii transitions can be clearly observed in optical absorption spectra for randomly aligned SWCNTs because the intensity of the Eii transitions is much higher than the intensity of the Eij transitions. However, it is known that both Eii and Eij can be observed comparably in the CD spectra. Furthermore, based on this alternating behaviour of Eii CD signals of the (+)- and (−)-enantiomers, the E11∼E55 signals of (+)-enantiomers exhibit a (+,−,+,−,+) progression, whereas the signals of the (−)-enantiomers exhibit the inverted (−,+,−,+,−) progression. This rule helped us to assign the deep Eii transitions, in which the trigonal warping effects tended to modify the Eii energy orders9,10,39. Actually, it has been reported that (6,4) has a higher E33 value compared with its E44 value9,39. Optical absorption cannot detect this crossover, but the sign of the CD signal can. Similarly, in this work, three Eii transition peaks were observed in the absorption spectrum of (8,3) SWCNTs, where the corresponding CD sign of the (–)-enantiomer exhibited a (+,+,–) progression from long to short wavelengths, as shown in Fig. 2. On the basis of the signs of the CD signals, the first peak at 668 nm could be assigned to the E22 transition, and the following two peaks at 357 and 307 nm could be assigned to the E44 and E33 transitions, respectively. This crossover is consistent with the reported family pattern of higher order transitions39.
Because a CD spectrum is equally sensitive to optical transitions of parallel and perpendicular polarizations, we could deeply analyse the band structure of SWCNTs using CD spectra. Figure 5a illustrates a symmetric band structure, in which E21=E12, and Fig. 5b shows a more realistic asymmetric band structure model. For both band structures, the values of E11 and E22 were the same, but the 2v and 2c bands were shifted relatively deeper than the Δ value for the asymmetric band (Fig. 5b). Using this simple asymmetric band structure model, we analysed an asymmetric SWCNT band structure for which E21−E12=2Δ. For both the symmetric and asymmetric band structures, the same relationship of (E11+E22)/2=(E12+E21)/2 was satisfied, meaning that the centre position of the E11 and E22 peaks were the same as the centre of the E12 and E21 peaks. This result is shown in a schematic CD spectrum in Fig. 5c. In this spectrum, the E12 and E21 transition peaks are located at the lower (left of panel) and higher (right of panel) energy sides of the centre of E11 and E22 by a distance of Δ. Using this model, we found E12 and E21 peaks between the E11 and E22 peaks that were the same distance from the centre of the E11 and E22 peaks and had opposite signs9. Similarly, we found E13 and E31 between E11 and E33, E24 and E42 between E22 and E44, and so on. Here we did not consider the exciton binding energy difference in these optical transitions.
(a) Schematic diagrams of a symmetric band structure. (b) Schematic diagrams of an asymmetric band structure with a shift of Δ for 2c and 2v bands compared with a. (c) Schematic CD spectrum of a (−)-enantiomer with the asymmetric band structure shown in b. (d) CD spectra (upper panel) and absorption spectra (lower panel) of the sorted (−)-(6,5) SWCNTs. Four vertical dashed lines indicate the center positions of E12/E21, E13/E31, E24/E42, and E35/E53. The Eii and Eij transitions are depicted as purple and green strips, respectively. Individual single Lorenzian peaks were plotted using the energy values of all assigned transitions. The calculated CD spectrum (black dashed curve) is represented as the sum of all plotted peaks for comparing the experimental spectrum (red solid curve). Two unassigned peaks are labelled by green arrows.
Figure 5d shows the CD spectra (upper panel) and absorption spectra (lower panel) of the (−)-(6,5) SWCNTs separated in this work. Highly symmetric CD spectra of (6,5) enantiomers (shown in Fig. 2) indicated that our sample purity is high enough and we did not need to consider any impurities that might have affected the CD spectrum. All CD peaks could be assigned to (6,5) SWCNTs. First, we assigned Eii transitions by comparing the CD spectra with the absorption spectra, which are depicted as purple strips. After the determination of the Eii transition, the centre positions of Eij transition pairs (E12/E21, E13/E31, E24/E42 and E35/E53) were determined and depicted as vertical dashed lines. Then, we looked for Eij transitions on both sides of the centrelines at the same distance and found an appropriate set of Eij transitions, which are depicted as green strips in Fig. 5d. Because the sensitivity of the detector in the low energy region (∼1.7 eV) was not high enough to see the detail of the spectrum structure, we could not find the E12 peak. Thus, the assigned E21 peak did not have a partner E12 peak. Although the transitions higher than E44 can be observed in high energy region, it is difficult to accurately assign them due to the complicated CD peaks. Using all assigned peak energies, the CD spectrum was reproduced by Lorentzian oscillator fitting (black solid curves). The calculated CD spectrum (black dashed curve) was highly consistent with the experimental spectrum (red solid curve), except for two unassigned CD peaks at 2.54 eV, 3.14 eV. These peaks were probably contributed by phonon-assisted excitonic recombination, which was resolved in the PL measurement40. Under the same analysis rules, the CD peaks of the other 11 (n,m) species were assigned (Supplementary Fig. 9).
Using all the Eii and Eij transition energies, the valence and conduction band energy levels (nv and nc) were determined for the 12 different sorted (n,m) species. The experimental results based on CD spectra were compared with the electronic density of states (DOS) calculated by DFT using local density approximation (LDA)6 (see Supplementary Fig. 10). Generally, GW approximation gives more precise band structure including bandgap41. However, GW calculations were limited for very small diameter SWCNTs to date due to required huge resources. On the other hand, Saito et al. have already published DFT band structures for most of SWCNTs using LDA6. They also compared LDA and GW calculations for (7,0) SWCNT and found that well known bandgap underestimation in LDA can be corrected by simple bandgap enlargement42. Therefore, here we corrected DFT results by shifting nc and nv away from the Fermi level for +0.15 and −0.15 eV, respectively. On first observation, all SWCNTs appear to have asymmetric valence and conduction bands, which is roughly consistent with the DFT calculation. Since we modified LDA bandgap to fit the excitonic band gap, it is trivial that 1v and 1c levels show good agreement for most of species. Especially, the species (6,4), (8,3), and (10,2) showed good agreement in the second conduction and valence bands (2c and 2v). However, (6,5), (7,5), (9,4), (8,4), (7,6), (10,3) and (11,1) showed redshift of both 2c and 2v bands keeping good agreement for E22. Since E22 and E21 CD peaks were used to estimate asymmetric 2v and 2c levels, the redshift in 2v and 2c levels from LDA band is probably caused by the difference in exciton binding energy between E21 and E22 transitions. On the other hand, the species (9,1), and (7,3) disagreed with E22 value from DFT calculation. This suggests that the exciton binding energies of E11 and E22 are different in these species. Most of species showed rather large deviations in the higher order energy bands (nc, nv≥3) probably due to more complicated excitonic and environmental effects. As we mentioned above, we did not consider the exciton effects in our analysis. This means that the band structures obtained in our analysis included the excitonic effects because all optical transitions in carbon nanotubes are modified by the one-dimensional exciton effect. By contrast, the LDA calculations did not include the excitonic effects, and only bare band structures were obtained by the LDA calculations. Even if both band structures were perfectly correct, the deviation could be caused by excitonic effects. Another possible explanation is the band gap correction that we employed in the comparison. We shifted the LDA band by ±0.15 eV to correct for the underestimation of the bandgap, though this bandgap correction seems overly simple. In the future, the underestimation of the bandgap in LDA could be corrected by a heavier but more precise GW approximation. Precise calculations would provide a better comparison between the experimental band analysis and theoretical calculations. Furthermore, we must account for environment effects43,44. In our experiments, the SWCNTs were in water containing surfactants, while the SWCNTs in the DFT calculations were in a vacuum. Furthermore, the optical transition energies of SWCNT are highly modified by environmental effects, which were not considered in the DFT calculation or in our CD analysis. Although we must note the potential causes of these deviations, the band structures obtained by our CD analysis were far from those of the tight binding model and generally showed good agreement with the DFT bands. Though the pure experimental band analysis is the first challenge, the crossover of band energy observed in this study is helpful for understanding the DFT calculations because the calculated DOS does not explain the band index in the high energy region. We believe our simple analysis method may provide a tool for the experimental analysis of the unclear band structure of SWCNTs.
Discussion
Because the band structure of a SWCNT is basically determined by a projection from the two dimensional graphene band to the one-dimensional SWCNT band, the band structure of a SWCNT has a systematic trend depending on its chiral structure. Usually, only the family behaviour of Eii transitions is discussed because the usual optical measurements can only give information regarding Eii. However, the CD analysis allows for a discussion of the family behaviour of Eij transitions. The experimental Eii and Eij transition energies of the 12 (n,m) species obtained in this work are plotted as a function of the diameter ( ; Supplementary Fig. 11). In agreement with the previous report38, the transition energy crossover of Eii (E33>E44) was observed in some of Type 2 species such as (6,4), (9,1), (8,3), (10,2) and (9,4). Interestingly, further crossover of the E31 and E42 (E31>E42) was observed in a few Type 2 species, (9,1), (8,3) and (10,2) for the first time. These crossovers are known to be caused by a trigonal warping effect9,10,39. In the previous works, a simple scaling behaviour for the Eii optical transitions have been studied using an empirical formula shown in the following45,46,47,
; Supplementary Fig. 11). In agreement with the previous report38, the transition energy crossover of Eii (E33>E44) was observed in some of Type 2 species such as (6,4), (9,1), (8,3), (10,2) and (9,4). Interestingly, further crossover of the E31 and E42 (E31>E42) was observed in a few Type 2 species, (9,1), (8,3) and (10,2) for the first time. These crossovers are known to be caused by a trigonal warping effect9,10,39. In the previous works, a simple scaling behaviour for the Eii optical transitions have been studied using an empirical formula shown in the following45,46,47,

where θ indicates a chiral angle, pii indicates the cutting line index for Eii transition; pii=1, 2, 4 and 5 for E11, E22, E33 and E44, respectively. To examine our assigned Eii and Eij transitions, the similar analysis was performed. First, we confirmed the same nonlinear scaling behaviour of Eii transitions obtained in this work (Supplementary Fig. 12a). Because resonance energies of Raman scattering was used for the fitting in the previous work, Eii values are limited in the range of excitation laser. The Eii values obtained in this work are in the different diameter range from them but the fitting parameters are almost same and all data are on the same curve. For the analysis of Eij transitions, we tried to extend Eq. 1 as follows.

Here, the cutting line index pij for Eij transition is 1.33, 1.67, 2, 3, 3 and 4 for E12, E21 E13, E31, E24 and E42, respectively. After careful optimization, we found that Eij transitions also exhibit a similar scaling behaviour with Eii transitions although the higher transitions have rather large deviations (Supplementary Fig. 12b). This means that the empirical formula is also available for Eij transitions.
Figure 6a–c shows the Eii and Eij transition energies estimated from the CD analysis as a function of 1/dt (denoted as solid circles and solid triangles). The transition energies calculated from Eq. 1 and Eq. 2 are also shown for comparison (denoted as open circles and open triangles). The empirical calculation well reproduced all experimental values including their family behaviours. For example, E21 is always larger than E12 due to large electron-hole asymmetry. Interestingly, chiral angle dependence of E12 is very small compared with the other transitions. Type dependences are also observed not only in Eii but also in Eij. Even for higher transitions, we can expect the family behaviour. However, rather large deviations were observed especially for small diameter species. The largest error was 0.36 eV for E24 transition of (7,3), which is probably due to the modified band structure by a large curvature effect. Because of the good agreement between the experimental and calculated values, Eij values can be estimated for other species that are not measured. Although the exciton effects are not well known especially for higher lying transitions, our findings firstly reveal that the diameter, chiral angle, type play an important role in the electron-hole asymmetry of SWCNTs, which is very useful for deeper understanding of the physical properties of SWCNT.
In conclusion, we developed an advanced method for separating single-chirality SWCNT enantiomers by column chromatography in combination with overloading selective adsorption and stepwise elution using a mixed surfactant. This separation afforded the highest purity of both single-chirality samples and enantiomeric SWCNTs obtained thus far. The high-purity single-chirality SWCNTs enantiomers enabled us to analyse their complicated CD spectra. We could assign Eii and Eij optical transitions to the CD peaks by considering the selection rules of optical transitions, the alternating CD signs for Eii transitions, the crossovers of Eii transitions, the relationships between Eii and Eij (for example, (E11+E22)/2=(E12+E21)/2), and other factors. Using the obtained Eii and Eij energies, the asymmetric excitonic band structures of the 12 different (n,m) SWCNTs were successfully determined. This is the first experimental determination of asymmetric band structures of an extensive set of (n,m) SWCNTs. Furthermore, based on the present experimental results and empirical formula, we demonstrated Eij for many (n,m) species and revealed (n,m) dependent electron-hole asymmetry.
Methods
Preparation of SWCNT dispersion
SWCNTs produced by high-pressure catalytic CO decomposition (HiPco, Raw, 0.8∼1.2 nm in diameter, NanoIntegris, Skokie, Illinois, USA) were used as a starting material. A net weight of 100 mg of SWCNT powder was dispersed in 100 ml of 3% SDS (ultra-pure ≥99.0%, Sigma-Aldrich) aqueous solution in a glass bottle by an ultrasonic homogenizer (output 30%, Sonifier 250D, Branson) for 20 h (all surfactant concentrations were weight percentage). The bottle was immersed in a water bath at 20 °C. After ultrasonication, the solution was ultracentrifuged for 2 h to sediment bundles and impurities (S50A rotor, 210,000 × g, 25 °C, CS150GX, Hitachi Koki, Tokyo, Japan). The upper 80% of the supernatant was collected as the isolated SWCNT dispersion and was used for the following separation.
Chirality and enantiomer separation
The first separation utilized the overloading selective adsorption method. Five open columns filled with 5.6 ml of gel (Sephacryl S-200, GE Healthcare) were vertically connected. After equilibration with 3% SDS solution, 80 ml of the SWCNT dispersion was loaded into the top of the multicolumn. Because the amount of SWCNTs was much larger than the capacity of the gel, excess SWCNTs flowed through the bottom column (the unadsorbed fraction). The excess SWCNTs were recovered for the next round of overloading selective adsorption. After a wash with 3% SDS solution, the multicolumn was separated into its individual columns. The adsorbed SWCNTs were eluted with 1% SC (ultra-pure ≥99.0%, Sigma-Aldrich) solution, producing fractions from Col.1 to Col.5. Six rounds of the overloading process using the unadsorbed fraction were repeated, and fractions from Col.1 to Col.30 were obtained (Supplementary Fig. 1). Then, the second separation utilizing a stepwise elution with a mixed surfactant was conducted. The same amount of 1% SDS solution was added to the fractions (Col.1, 6, 11, 16 or 26). The resulting SWCNTs in 0.5% SC+0.5% SDS solution were injected into a column filled with 5.6 ml of the gel equilibrated with 0.5% SC+0.5% SDS solution, followed by washing with the same solution. The SWCNTs adsorbed onto the gel were eluted by a stepwise increase in the concentration of DOC (purity ≥96.0%, Wako Pure Chemical Industries, Osaka, Japan) in the 0.5% SC+0.5% SDS solution; the concentration of DOC was successively increased from 0.01 to 0.07% with 0.01 or 0.005% steps (Supplementary Fig. 2). Separation processes were performed at room temperature (23±0.5 °C). The detailed methods and results of the separation under different SDS concentrations in the first separation and of the separation of larger diameter enantiomers are given in the Supplementary Methods, Figs 3 and 4.
Optical measurements
Optical absorption spectra were measured from 1,400 to 200 nm in 2 nm increments using an ultraviolet–visible near-infrared spectrophotometer (UV-3600, Shimadzu, Kyoto, Japan). Photoluminescence spectra were measured using a spectrofluorometer (Nanolog, HORIBA, Kyoto, Japan) equipped with a liquid nitrogen-cooled InGaAs near-infrared array detector. The excitation wavelength was varied from 400 to 800 nm in 5 nm steps, and the emission wavelength was varied from 791 to 1304, nm in 1 nm increments. The spectral slit widths were 7 nm for both the excitations and emissions. All raw intensities were corrected with the intensities of the lamp spectrum. The CD spectra of the sorted single-chirality enantiomers were measured from 900 to 200 nm in 1 nm increments using a CD spectropolarimeter (J-820, JASCO, Tokyo, Japan).
Date availability
The data that support the findings of this study are available from the corresponding author on request.
Additional Information
How to cite this article: Wei, X. et al. Experimental determination of excitonic band structures of single-walled carbon nanotubes using circular dichroism spectra. Nat. Commun. 7, 12899 doi: 10.1038/ncomms12899 (2016).
References
Jorio, A., Dresselhaus, G. & Dresselhaus, M. S. Carbon Nanotubes: Advanced Topics in the Synthesis, Structure, Properties, and Applications Springer (2008).
Uryu, S. & Ando, T. Exciton absorption of perpendicularly polarized light in carbon nanotubes. Phys. Rev. B 74, 155411 (2006).
Miyauchi, Y., Oba, M. & Maruyama, S. Cross-polarized optical absorption of single-walled nanotubes by polarized photoluminescence excitation spectroscopy. Phys. Rev. B 74, 205440 (2006).
Miyauchi, Y., Ajiki, H. & Maruyama, S. Electron-hole asymmetry in single-walled carbon nanotubes probed by direct observation of transverse quasidark excitons. Phys. Rev. B 81, 121415 (R) (2010).
Takase, M. et al. Selection-rule breakdown in plasmon-induced electronic excitation of an isolated single-walled carbon nanotube. Nat. Photon. 7, 550–554 (2013).
Kato, K., Koretsune, T. & Saito, S. Energetics and electronic properties of twisted single-walled carbon nanotubes. Phys. Rev. B 85, 115448 (2012).
Venema, L. C. et al. Spatially resolved scanning tunneling spectroscopy on single-walled carbon nanotubes. Phys. Rev. B 62, 5238–5244 (2000).
Lin, H. et al. Many-body effects in electronic bandgaps of carbon nanotubes measured by scanning tunnelling spectroscopy. Nat. Mater. 9, 235–238 (2010).
Green, A. A., Duch, M. C. & Hersam, M. C. Isolation of single-walled carbon nanotube enantiomers by density differentiation. Nano Res. 2, 69–77 (2009).
Ghosh, S., Bachilo, S. M. & Weisman, R. B. Advanced sorting of single-walled carbon nanotubes by nonlinear density-gradient ultracentrifugation. Nat. Nanotech. 5, 443–450 (2010).
Sánchez-Castillo, A. & Noguez, C. Understanding optical activity in single-walled carbon nanotubes from first-principles studies. J. Phys. Chem. C 114, 9640–9644 (2010).
Peng, X. et al. Optically active single-walled carbon nanotubes. Nat. Nanotech. 2, 361–365 (2007).
Wang, F. et al. Simultaneous discrimination of handedness and diameter of single-walled carbon nanotubes (SWNTs) with chiral diporphyrin nanotweezers leading to enrichment of a single enantiomer of (6,5)-SWNTs. J. Am. Chem. Soc. 132, 10876–10881 (2010).
Liu, H., Tanaka, T. & Kataura, H. Optical isomer separation of single-chirality carbon nanotubes using gel column chromatography. Nano Lett. 14, 6237–6243 (2014).
Yomogida, Y. et al. Industrial-scale separation of high-purity single-chirality single-wall carbon nanotubes for biological imaging. Nat. Commun. 7, 12056 (2016).
Power, T. D., Skoulidas, A. I. & Sholl, D. S. Can chiral single walled carbon nanotubes be used as enantiospecific adsorbents? J. Am. Chem. Soc. 124, 1858–1859 (2002).
Liu, H., Nishide, D., Tanaka, T. & Kataura, H. Large-scale single-chirality separation of single-wall carbon nanotubes by simple gel chromatography. Nat. Commun. 2, 309 (2011).
Liu, H., Feng, Y., Tanaka, T., Urabe, Y. & Kataura, H. Diameter-selective metal/semiconductor separation of single-wall carbon nanotubes by agarose gel. J. Phys. Chem. C 114, 9270–9276 (2010).
Bachilo, S. M. et al. Structure-assigned optical spectra of single-walled carbon nanotubes. Science 298, 2361–2366 (2002).
Weisman, R. B. & Bachilo, S. M. Dependence of optical transition energies on structure for single-walled carbon nanotubes in aqueous suspension: an empirical Kataura plot. Nano Lett. 3, 1235–1238 (2003).
Naumov, A. V., Ghosh, S., Tsyboulski, D. A., Bachilo, S. M. & Weisman, R. B. Analyzing absorption backgrounds in single-walled carbon nanotube spectra. ACS Nano 5, 1639–1648 (2011).
Ghosh, S., Bachilo, S. M. & Weisman, R. B. Removing aggregates from single-walled carbon nanotube samples by magnetic purification. J. Phys. Chem. C 118, 4489–4494 (2014).
Choi, S., Deslippe, J., Capaz, R. B. & Louie, S. G. An explicit formula for optical oscillator strength of excitons in semiconducting single-walled carbon nanotubes: family behavior. Nano Lett. 13, 54–58 (2013).
Streit, J. K., Bachilo, S. M., Ghost, S., Lin, C. & Weisman, R. B. Directly measured optical absorption cross sections for structure-selected single-walled carbon nanotubes. Nano Lett. 14, 1530–1536 (2014).
Tu, X., Manohar, S., Jagota, A. & Zheng, M. DNA sequence motifs for structure-specific recognition and separation of carbon nanotubes. Nature 460, 250–253 (2009).
Liu, H., Tanaka, T., Urabe, Y. & Kataura, H. High-efficiency single-chirality separation of carbon nanotubes using temperature-controlled gel chromatography. Nano Lett. 13, 1996–2003 (2013).
Ghosh, S., Bachilo, S. M., Simonette, R. A., Beckingham, K. M. & Weisman, R. B. Oxygen doping modifies near-infrared band gaps in fluorescent single-walled carbon nanotubes. Science 330, 1656–1659 (2010).
Miyauchi, Y. et al. Brightening of excitons in carbon nanotubes on dimensionality modification. Nat. Photon. 7, 715–719 (2013).
Ma, X. et al. Electronic structure and chemical nature of oxygen dopant states in carbon nanotubes. ACS Nano 8, 10782–10789 (2014).
Magg, M., Kadria-Vili, Y., Oulevey, P., Weisman, R. B. & Bürgi, T. Resonance Raman optical activity spectra of single-walled carbon nanotube enantiomers. J. Phys. Chem. Lett. 7, 221–225 (2016).
Kataura, H. et al. Optical properties of single-wall carbon nanotubes. Synth. Met 103, 2555–2558 (1999).
Grüneis, A. et al. Inhomogeneous optical absorption around the K point in graphite and carbon nanotubes. Phys. Rev. B 67, 165402 (2003).
Saito, R., Dresselhaus, G. & Dresselhaus, M. S. Trigonal warping effect of carbon nanotubes. Phys. Rev. B 61, 2981–2990 (2000).
Samsonidze, G. G. et al. The concept of cutting lines in carbon nanotube science. J. Nanosci. Nanotechnol. 3, 431–458 (2003).
Jiang, J., Saito, R., Grüneis, A., Dresselhaus, G. & Dresselhaus, M. S. Optical absorption matrix elements in single-wall carbon nanotubes. Carbon. 42, 3169–3176 (2004).
Jiang, J. et al. Chirality dependence of exciton effects in single-wall carbon nanotubes: Tight-binding model. Phys. Rev. B 75, 035407 (2007).
Jiang, J. et al. Exciton-photon, exciton-phonon matrix elements, and resonant Raman intensity of single-wall carbon nanotubes. Phys. Rev. B 75, 035405 (2007).
Ajiki, H. & Ando, T. Electronic states of carbon nanotubes. J. Phys. Soc. Jpn 62, 1255–1266 (1993).
Haroz, E. H., Bachilo, S. M., Weisman, R. B. & Doorn, S. K. Curvature effects on the E33 and E44 exciton transitions in semiconducting single-walled carbon nanotubes. Phys. Rev. B 77, 125405 (2008).
Chou, S. G. et al. Phonon-assisted excitonic recombination channels observed in DNA-wrapped carbon nanotubes using photoluminescence spectroscopy. Phys. Rev. Lett. 94, 127402 (2005).
Spataru, C. D., Ismail-Beigi, S., Benedict, L. X. & Louie, S. G. Excitonic effects and optical spectra of single-walled carbon nanotubes. Phys. Rev. Lett. 92, 077402 (2004).
Miyake, T. & Saito, S. Quasiparticle band structure of carbon nanotubes. Phys. Rev. B 68, 155424 (2003).
Ohno, Y. et al. Chirality-dependent environmental effects in photoluminescence of single-walled carbon nanotubes. Phys. Rev. B 73, 235427 (2006).
Hirana, Y., Tanaka, Y., Niidome, Y. & Nakashima, N. Strong micro-dielectric environment effect on the band gaps of (n,m) single-walled carbon nanotubes. J. Am. Chem. Soc. 132, 13072–13077 (2010).
Kane, C. L. & Mele, E. J. Electron interactions and scaling relations for optical excitations in carbon nanotubes. Phys. Rev. Lett. 93, 197402 (2004).
Araujo, P. T. et al. Third and fourth optical transitions in semiconducting carbon nanotubes. Phys. Rev. Lett. 98, 067401 (2007).
Araujo, P. T. et al. Resonance Raman spectroscopy of the radial breathing modes in carbon nanotubes. Phys. E 42, 1251–1261 (2010).
Acknowledgements
We thank Stephen K. Doorn (Los Alamos National Laboratory), Shigeo Maruyama (The University of Tokyo) and Yuhei Miyauchi (Kyoto University) for helpful discussions on the band structure analysis of SWCNTs. R.S. acknowledges MEXT Grant (Nos. 25286005, 25107005). This work was supported by JSPS KAKENHI, grant no. 25220602.
Author information
Authors and Affiliations
Contributions
X.W. performed all the experiments and data analysis. X.W., T.T., Y.Y. and H.K. contributed to the separation and the discussion of the results. N.S. and R.S. contributed to the theoretical calculation of the CD spectra. X.W., T.T. and H.K. contributed to the discussion of the band structure and family behaviour. X.W. wrote the paper. T.T. and H.K. reviewed and corrected the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-12, Supplementary Table 1, Supplementary Methods and Supplementary References (PDF 2308 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Wei, X., Tanaka, T., Yomogida, Y. et al. Experimental determination of excitonic band structures of single-walled carbon nanotubes using circular dichroism spectra. Nat Commun 7, 12899 (2016). https://doi.org/10.1038/ncomms12899
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms12899
This article is cited by
-
Preparing high-concentration individualized carbon nanotubes for industrial separation of multiple single-chirality species
Nature Communications (2023)
-
Chirality-dependent concentration boundaries of single-wall carbon nanotubes for photoluminescence characterization and applications
Nano Research (2023)
-
Comparative study of the extraction selectivity of PFO-BPy and PCz for small to large diameter single-walled carbon nanotubes
Nano Research (2022)
-
Complete structural characterization of single carbon nanotubes by Rayleigh scattering circular dichroism
Nature Nanotechnology (2021)
-
2N+4-rule and an atlas of bulk optical resonances of zigzag graphene nanoribbons
Nature Communications (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.