Abstract
Mapping the strong interaction between Rydberg atoms onto single photons via electromagnetically induced transparency enables manipulation of light at the single-photon level and few-photon devices such as all-optical switches and transistors operated by individual photons. Here we demonstrate experimentally that Stark-tuned Förster resonances can substantially increase this effective interaction between individual photons. This technique boosts the gain of a single-photon transistor to over 100, enhances the non-destructive detection of single Rydberg atoms to a fidelity beyond 0.8, and enables high-precision spectroscopy on Rydberg pair states. On top, we achieve a gain larger than 2 with gate photon read-out after the transistor operation. Theory models for Rydberg polariton propagation on Förster resonance and for the projection of the stored spin-wave yield excellent agreement to our data and successfully identify the main decoherence mechanism of the Rydberg transistor, paving the way towards photonic quantum gates.
Similar content being viewed by others
Introduction
Rydberg excitations of ultracold atoms1 are currently attracting tremendous attention because of possible applications in quantum computing2,3,4,5 and simulation6,7,8,9,10. One particular aspect is the realization of few-photon nonlinearities mediated by Rydberg interaction11,12,13,14, enabling novel schemes for highly efficient single-photon generation15,16, entanglement creation between light and atomic excitations17, single-photon all-optical switches18 and transistors19,20, single-photon absorbers21 and interaction-induced photon phase shifts22,23. Interacting Rydberg polaritons also enable attractive forces between single photons24, crystallization of photons25 and photonic scattering resonances26. The above experiments and proposals make use of the long-range electric dipole–dipole interaction between Rydberg atoms27,28,29,30,31. A highly useful tool for controlling the interaction are Stark-tuned Förster resonances, where two dipole-coupled pair states are shifted into resonance by a dc32 or microwave33,34 electric field. Förster resonances have been studied by observation of dipole blockade35, line shape analysis36, double-resonance spectroscopy37, excitation statistics38 and Ramsey spectroscopy39,40. Recently, resonant four-body interaction41 and the anisotropic blockade on Förster resonance42 and quasi-forbidden Förster resonances43 have been observed, and Förster resonances between different atomic species have been predicted44. For Rydberg-mediated single-photon transistors, the near-resonance in zero field for specific pair states has been used to enhance the transistor gain20, while in experiments on Rydberg atom imaging45,46 an increase in Rydberg excitation hopping has been observed on resonance47.
In this work, we use Stark-tuned Förster resonances to greatly increase the interaction between individual photons inside a Rydberg medium. We achieve this by tuning pair states |S(g),S(s)〉 containing two different Rydberg S-states into resonance with |P(g),P(s)〉 pair states by an electric field. We show that for gate and source Rydberg states |50S1/2,48S1/2〉, we can boost the performance of a Rydberg single-photon transistor. When operated classically, we achieve  , enabling high-fidelity detection of single Rydberg atoms. This improved transistor can be operated such that the gate photon is read out with finite efficiency, reaching a gain
, enabling high-fidelity detection of single Rydberg atoms. This improved transistor can be operated such that the gate photon is read out with finite efficiency, reaching a gain  . We develop theoretical models for the dynamics of Rydberg polaritons in the presence of Förster resonances and the loss of coherence due to photon scattering. Excellent agreement with our experimental data is found. Finally, our all-optical probe represents a novel approach for the high-resolution study of the substructure of Förster resonances caused by fine structure and Stark/Zeeman splitting of the |P(g),P(s)〉 pair states. We demonstrate this technique by resolving the multi-resonance structure of the |66S1/2,64S1/2〉 pair state.
. We develop theoretical models for the dynamics of Rydberg polaritons in the presence of Förster resonances and the loss of coherence due to photon scattering. Excellent agreement with our experimental data is found. Finally, our all-optical probe represents a novel approach for the high-resolution study of the substructure of Förster resonances caused by fine structure and Stark/Zeeman splitting of the |P(g),P(s)〉 pair states. We demonstrate this technique by resolving the multi-resonance structure of the |66S1/2,64S1/2〉 pair state.
Results
Experimental set-up
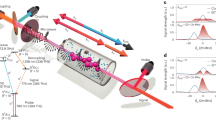
Our experimental scheme13,19,20,45 is shown in Fig. 1a,b: by coupling the excited state |e〉 and the Rydberg state |S(g)〉 with a strong light field Ωg with detuning δg, a gate photon  is converted into a Rydberg excitation inside a cloud of ultracold 87Rb atoms. We then probe the presence of this gate excitation by monitoring the transmission of source photons
is converted into a Rydberg excitation inside a cloud of ultracold 87Rb atoms. We then probe the presence of this gate excitation by monitoring the transmission of source photons  coupled via electromagnetically induced transparency (EIT) to the source Rydberg state S(s). Specifically, we use (δg=40 MHz) for efficient Raman absorption of the gate photon in the experiments without retrieval, while we use EIT-based slow light techniques (δg=0) for photon storage in experiments with gate photon retrieval. At zero electric field, the interaction between the |S(g),S(s)〉 pair is of van der Waals type. The difference in electric polarizability between S- and P-states enables the shift of the initial pair state into degeneracy with specific |P(g),P(s)〉 pairs, resulting in resonant dipole–dipole interaction. We shift the Rydberg levels by applying a homogeneous electric field along the direction of beam propagation. Active cancellation of stray electric fields is done with eight electric field plates in Löw configuration48, while the homogeneous field results from additional voltages V+,V− to four electrodes (Fig. 1a).
coupled via electromagnetically induced transparency (EIT) to the source Rydberg state S(s). Specifically, we use (δg=40 MHz) for efficient Raman absorption of the gate photon in the experiments without retrieval, while we use EIT-based slow light techniques (δg=0) for photon storage in experiments with gate photon retrieval. At zero electric field, the interaction between the |S(g),S(s)〉 pair is of van der Waals type. The difference in electric polarizability between S- and P-states enables the shift of the initial pair state into degeneracy with specific |P(g),P(s)〉 pairs, resulting in resonant dipole–dipole interaction. We shift the Rydberg levels by applying a homogeneous electric field along the direction of beam propagation. Active cancellation of stray electric fields is done with eight electric field plates in Löw configuration48, while the homogeneous field results from additional voltages V+,V− to four electrodes (Fig. 1a).
(a) Tightly focussed source and gate beams (w0=6.2 μm) are overlapped with an optically trapped cloud of 2 × 104 87Rb atoms at 3 μK (cylindrical 1/e dimensions L=40 μm, R=10 μm). For each transistor operation the optical trap is shut off for 200 μs. We perform 23 individual experiments in a single cloud, recapturing the atoms in-between with minimal loss and heating. In-vacuum electrodes are used to apply the electric field. (b) Level scheme for gate and source photons coupled to different Rydberg states, where 2Ω is the Rabi frequency of the control field and 2γ is the decay rate of |e〉. (c,d) At certain electric fields (vertical dashed lines), the |S(g),S(s)〉 pair state is resonant to pair states of type |P(g),P(s)〉. The enhancement of interaction between |S(g)〉 and |S(s)〉 manifests in peaking of the transistor gain (blue dots). In c, the fine structure of the involved P-states and the mJ-dependence of the Stark-shift result in the observed multi-resonance structure. The blue solid line is a theoretical analysis of the full-polariton propagation in the presence of the gate excitation. The error bars are the s.e.m.
Stark-tuned optical nonlinearities
We first study the pair state |S(g),S(s)〉=|66S1/2,64S1/2〉. Due to the fine structure splitting of the Rydberg P-states, this pair is near resonant with two P-state pairs |65P1/2,64P3/2〉 and |65P3/2,64P1/2〉20. Both |P(g),P(s)〉 pairs can be tuned into resonance at electric fields  . The full pair state Stark map in the presence of a magnetic field B=1 G (Fig. 1c, gray lines) reveals a large number of closely spaced resonances arising from the non-degenerate
. The full pair state Stark map in the presence of a magnetic field B=1 G (Fig. 1c, gray lines) reveals a large number of closely spaced resonances arising from the non-degenerate  combinations. The strength of individual resonances depends on the angle θ between the interatomic axis and the quantization axis defined by the external fields, resulting in a non-spherical blockade volume29. We explore these resonances by measuring the optical gain
combinations. The strength of individual resonances depends on the angle θ between the interatomic axis and the quantization axis defined by the external fields, resulting in a non-spherical blockade volume29. We explore these resonances by measuring the optical gain

that is, the mean number of source photons scattered by a single incident gate photon20, as a function of applied electric field (Fig. 1c). Our high-resolution spectroscopy indeed reveals four resonances, matching with the calculated crossings of different pair state groups. In between resonances, the coupling of |S(g),S(s)〉 to multiple |P(g),P(s)〉 pair states with positive and negative Förster defects results in smaller blockade than in the zero-field case. This interplay between different resonances actually decreases the measured gain with respect to the field-free value. This situation does not occur for the Förster resonance |50S1/2,48S1/2〉↔|49P1/2,48P1/2〉 at  (Fig. 1d). For this state combination there is one isolated resonance, resulting in the single peak in the optical gain.
(Fig. 1d). For this state combination there is one isolated resonance, resulting in the single peak in the optical gain.
Rydberg polaritons near Förster resonance
To quantitatively describe the observed resonances, we include in the microscopic description of polariton propagation13,14,26 the special character of the interaction close to Förster resonance, see Supplementary Note 1. For illustration, we consider the |50S1/2,48S1/2〉 pair and angle θ=0, which results in the selection rule  for the magnetic quantum numbers of the involved states. We then need to include four pair states: {|50S1/2,48S1/2〉, |49P1/2,48P1/2〉, |48P1/2,49P1/2〉, |48S1/2,50S1/2〉} with
for the magnetic quantum numbers of the involved states. We then need to include four pair states: {|50S1/2,48S1/2〉, |49P1/2,48P1/2〉, |48P1/2,49P1/2〉, |48S1/2,50S1/2〉} with  . In this basis, the interaction Hamiltonian reduces to
. In this basis, the interaction Hamiltonian reduces to

with two dipolar coupling parameters C3, C3′. Since the interaction is dominated by the Förster resonance, we neglect any residual van der Waals interactions. In general, the Hamiltonian (2) gives rise to flip-flop (hopping) processes of type |50S1/2,48S1/2〉→{|49P1/2,48P1/2〉, |48P1/2,49P1/2〉}→|48S1/2,50S1/2〉. However, for this choice of Rydberg states the dipolar coupling parameters satisfy C3≫C3′, and therefore provide a strong suppression of hopping49. This behaviour is in contrast to the results in ref. 47, where hopping processes strongly influenced the interaction-mediated imaging of Rydberg excitations. In the experimentally relevant regime with ω, γs, γp<<Ω, γ, where ω is the source photon detuning, while γs and γp describe the decoherence rates of |S(s)〉 and |P(s)〉 excitations, the equation describing a single polariton  and its interaction with the gate Rydberg excitation |S(g)〉 at position rj simplifies to
and its interaction with the gate Rydberg excitation |S(g)〉 at position rj simplifies to

as derived in our Supplementary Note 1. Here  is the collective coupling strength with g0 being the single-atom–photon coupling strength and nat is the atomic density. The effective interaction
is the collective coupling strength with g0 being the single-atom–photon coupling strength and nat is the atomic density. The effective interaction  simplifies to
simplifies to

where ΔD is the Förster defect. It is remarkable that, regardless of ΔD, our microscopic derivation provides an effective interaction always based on van der Waals type interaction.
For comparison with experiment, we generalize our calculation to nonzero angles θ between the quantization and interatomic axis, as well as to the larger number of states involved for the |66S1/2, 64S1/2〉 pair. We then integrate equation (3) over the cloud shape and average over the stored spin-wave. We also take into account the Poissonian statistics of the gate and source photons, the storage efficiency, the fact that the blockade radius is comparable to the beam waist and the finite experimental resolution in electric field  , see Supplementary Note 1. The comparison, without any free parameters, with experimental results for the gain is shown in Fig. 1. We find very good agreement for all electric fields except very close to the resonances. One reason for the discrepancy is the following: Close to the Förster resonance and for distances on the order of rb between gate and source, the atomic part of the polariton-excitation pair initially in |50S1/2,48S1/2〉 is converted into the superposition of |49P1/2,48P1/2〉 and |50S1/2,48S1/2〉. This results in additional slowing down of the polariton, and, consequently, an accumulation of polaritons close to rb. Then, the assumption to study the propagation of individual polaritons breaks down as the interaction between the polaritons has to be included.
, see Supplementary Note 1. The comparison, without any free parameters, with experimental results for the gain is shown in Fig. 1. We find very good agreement for all electric fields except very close to the resonances. One reason for the discrepancy is the following: Close to the Förster resonance and for distances on the order of rb between gate and source, the atomic part of the polariton-excitation pair initially in |50S1/2,48S1/2〉 is converted into the superposition of |49P1/2,48P1/2〉 and |50S1/2,48S1/2〉. This results in additional slowing down of the polariton, and, consequently, an accumulation of polaritons close to rb. Then, the assumption to study the propagation of individual polaritons breaks down as the interaction between the polaritons has to be included.
Resonant single-photon transistor
Next, we investigate to what extent these Förster resonances can be used to improve the Rydberg single-photon transistor19,20. We find that for this application, the |50S1/2, 48S1/2〉 resonance is ideal. It enables large-source photon input rates, because of the relatively weak van der Waals interaction between two source photons. On the other hand, the Förster resonance provides sufficient gate–source interaction to observe high transistor gain. For source photon rate Rin=35 μs−1, we reach a maximal gain of  . At such high source rates, we observe small temporal changes in transmission, which we attribute to an accumulation of stationary Rydberg excitations in the medium caused by dephasing of single-source polaritons. This effect has been previously observed for Rydberg S-states14 and differs from the interaction-induced dephasing of D-state polariton pairs50. This accumulation sets an upper limit on the source photon rate for the non-destructive imaging of single Rydberg excitations45, since the creation of additional Rydberg atoms also ‘destroys’ the original system. We thus restrict our analysis in Fig. 2 to non-destructive source input rates for which the maximum temporal change in source transmission remains <10%. In this regime, we observe a linear increase of the optical gain with Rin both at zero electric field and on the Förster resonance (Fig. 2a). Exploiting the Förster resonance, we can improve the optical gain by a factor >2 on resonance (blue dots) compared with the zero-field case (blue squares). The large number of source photons scattered from a single-gate excitation enables the single-shot detection of a stored gate photon with high fidelity18,19,51, see Methods. In Fig. 2, we show this fidelity as a function of the applied electric field for two source photon rates. The Förster resonance enables a substantial increase of the fidelity to a maximal value of
. At such high source rates, we observe small temporal changes in transmission, which we attribute to an accumulation of stationary Rydberg excitations in the medium caused by dephasing of single-source polaritons. This effect has been previously observed for Rydberg S-states14 and differs from the interaction-induced dephasing of D-state polariton pairs50. This accumulation sets an upper limit on the source photon rate for the non-destructive imaging of single Rydberg excitations45, since the creation of additional Rydberg atoms also ‘destroys’ the original system. We thus restrict our analysis in Fig. 2 to non-destructive source input rates for which the maximum temporal change in source transmission remains <10%. In this regime, we observe a linear increase of the optical gain with Rin both at zero electric field and on the Förster resonance (Fig. 2a). Exploiting the Förster resonance, we can improve the optical gain by a factor >2 on resonance (blue dots) compared with the zero-field case (blue squares). The large number of source photons scattered from a single-gate excitation enables the single-shot detection of a stored gate photon with high fidelity18,19,51, see Methods. In Fig. 2, we show this fidelity as a function of the applied electric field for two source photon rates. The Förster resonance enables a substantial increase of the fidelity to a maximal value of  . This number is mainly limited by the fact that our beam waist w0 is slightly larger than the gate–source blockade distance. For spatially resolved Rydberg detection45,46, even higher fidelities are possible using imaging systems with better optical resolution than our beam size w0=6.2 μm.
. This number is mainly limited by the fact that our beam waist w0 is slightly larger than the gate–source blockade distance. For spatially resolved Rydberg detection45,46, even higher fidelities are possible using imaging systems with better optical resolution than our beam size w0=6.2 μm.
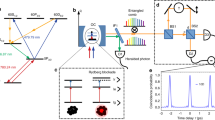
Performance of the single-photon transistor on the |50S1/2,48S1/2〉↔|49P1/2,48P1/2〉 resonance. (a) Gain and single Rydberg detection fidelity increase linearly with the rate of incident source photons Rin in the non-destructive range, where the creation of stationary excitations from source photons is negligible. Both the optical gain (a) and the single Rydberg detection fidelity (a,b) are highly amplified on the Förster resonance at  . The solid curves are linear or Lorentzian fits to guide the eye. The error bars are the s.e.m.
. The solid curves are linear or Lorentzian fits to guide the eye. The error bars are the s.e.m.
Single-photon transistor with gate photon read-out
The improved gate–source interaction on Förster resonance enables us for the first time to operate our transistor with retrieval of the stored gate photon after the transistor operation51. To store the gate photon, we stop the polariton inside the medium by ramping down the control field Ωg to zero for δg=0. Conversely, to read out the gate photon, Ωg is turned on again. Without any source photon input between the storage and the read-out, we measure a lifetime of 3.6 μs for the atomic coherence of the stored gate spin-wave, mainly limited by the finite temperature of our atomic sample. Next, we apply a source pulse containing a mean number of photons  and pulse length T=3.2 μs during a storage time of 4.2 μs. On Förster resonance, we achieve a mean number of scattered source photons within this time of up to 2.7 photons for a single stored gate photon (Fig. 3a). This is the first demonstration of a transistor with gain
and pulse length T=3.2 μs during a storage time of 4.2 μs. On Förster resonance, we achieve a mean number of scattered source photons within this time of up to 2.7 photons for a single stored gate photon (Fig. 3a). This is the first demonstration of a transistor with gain  and read-out, a fundamental step towards quantum circuits employing feedback and gain or the non-destructive detection of the gate photon52.
and read-out, a fundamental step towards quantum circuits employing feedback and gain or the non-destructive detection of the gate photon52.
(a) Efficiency of storing and reading out one single gate photon versus the number of scattered source photons during the storage time of 4.2 μs. When plotted as function of scattered photons, the observed retrieval efficiencies on Förster resonance (red dots) and in zero field (blue squares) are identical. (b) Calculated fidelity, that is, the overlap between the initial gate spin-wave state and the final state after the propagation of a source photon through a one-dimensional Gaussian atomic cloud. The fidelity is the sum of contributions from scattered (short dashes) and transmitted (long dashes) source polaritons. The lines in a show the predicted decay of retrieval efficiency using the full propagation model (solid blue line), as well as different limiting cases (see main text for details).
The overall fidelity of the transistor is limited by projection and dephasing of the gate spin-wave due to scattered and transmitted source photons51,53. In Fig. 3a, we show the absolute retrieval efficiency versus incident and scattered source photons at a mean number of  incident gate photons on and off the Förster resonance. Interestingly, both cases collapse onto one exponential decay if plotted versus the number of scattered source photons. The black curve in Fig. 3a assumes zero retrieval fidelity for one or more scattered source photons. The dotted line and the dashed line, on the other hand, investigate the other hypothetic cases that the coherence of the gate spin-wave is destroyed by one photon of
incident gate photons on and off the Förster resonance. Interestingly, both cases collapse onto one exponential decay if plotted versus the number of scattered source photons. The black curve in Fig. 3a assumes zero retrieval fidelity for one or more scattered source photons. The dotted line and the dashed line, on the other hand, investigate the other hypothetic cases that the coherence of the gate spin-wave is destroyed by one photon of  incident mean photons (dashed) and by one photon of
incident mean photons (dashed) and by one photon of  mean photons incident on the blockade sphere (dotted), respectively. By applying established theory to our data in the next section, we will show that both transmitted photons and scattered photons contribute to the coherence and thus to the retrieval efficiency of the stored spin-wave.
mean photons incident on the blockade sphere (dotted), respectively. By applying established theory to our data in the next section, we will show that both transmitted photons and scattered photons contribute to the coherence and thus to the retrieval efficiency of the stored spin-wave.
Theory on coherent spin-waves
For more quantitative analysis we follow ref. 53, considering a one-dimensional (1D) model of the zero-field case for a single-source photon passing through the atomic cloud with Gaussian density profile. The gate photon is stored in the initial spin-wave state  and interacts with source photons via the potential from equation (4). After the source photon has left the atomic cloud, the state of the atomic ensemble is
and interacts with source photons via the potential from equation (4). After the source photon has left the atomic cloud, the state of the atomic ensemble is  , and the quantum mechanical fidelity between the initial and final state is given by
, and the quantum mechanical fidelity between the initial and final state is given by  (ref. 54). Here, Fp accounts for transmitted and Fs for scattered source polaritons. Both contributions are shown in Fig. 3b as a function of the blockade radius rb=(γC6/Ω2)1/6 for our experimental parameters. For large blockade radii, Fp becomes negligible because source photons are rarely transmitted through the blockaded region. To describe the experimental 3D situation, we average the fidelities from Fig. 3b over the spatial transversal distribution of gate and source photons. With this approach, we obtain the blue solid line in Fig. 3a, which is in very good agreement with our data, despite the simplifications of our model. We consider this as evidence for the assumed mechanisms for the spin-wave decoherence to be correct. By identifying the decoherence mechanisms, we can isolate the required improvements for a high-fidelity coherent Rydberg transistor: the blockade volume of a single-gate excitation must be larger than the stored gate spin-wave to avoid the projection, while the optical depth ODB inside the blockaded region must be large to prevent the dephasing due to transmitted photons. Meeting both requirements simultaneously is challenging due to limits on the atomic density because of Rydberg-ground state interaction18,55.
(ref. 54). Here, Fp accounts for transmitted and Fs for scattered source polaritons. Both contributions are shown in Fig. 3b as a function of the blockade radius rb=(γC6/Ω2)1/6 for our experimental parameters. For large blockade radii, Fp becomes negligible because source photons are rarely transmitted through the blockaded region. To describe the experimental 3D situation, we average the fidelities from Fig. 3b over the spatial transversal distribution of gate and source photons. With this approach, we obtain the blue solid line in Fig. 3a, which is in very good agreement with our data, despite the simplifications of our model. We consider this as evidence for the assumed mechanisms for the spin-wave decoherence to be correct. By identifying the decoherence mechanisms, we can isolate the required improvements for a high-fidelity coherent Rydberg transistor: the blockade volume of a single-gate excitation must be larger than the stored gate spin-wave to avoid the projection, while the optical depth ODB inside the blockaded region must be large to prevent the dephasing due to transmitted photons. Meeting both requirements simultaneously is challenging due to limits on the atomic density because of Rydberg-ground state interaction18,55.
Discussion
Rydberg-mediated single-photon nonlinearities can be greatly enhanced by electrically tuning adjacent pair states to Förster resonance. By carefully choosing the employed Förster resonance, we have simultaneously improved the Rydberg transistor gain and the fidelity of single Rydberg atom detection. We identify the |50S1/2,48S1/2〉↔|49P1/2,48P1/2〉 resonance in 87Rb as ideal both for the Rydberg single-photon transistor and non-destructive imaging of Rydberg atoms45,46. Exploiting this resonance, we have demonstrated the first operation of the Rydberg transistor with read-out of the gate photon. Our quantitative analysis of the reduction of retrieval efficiency caused by source photons points the way towards high-fidelity Rydberg-based photonic gates and transistors. Our polariton propagation theory correctly accounts for the enhanced source–gate interaction and is in excellent agreement with the experiment. It also reveals unexpected and rich properties close to Förster resonances. This regime enables study of the transition from two- to many-body interaction and propagation with excitation hopping47,56. The complexity of the resonances due to the Rydberg-level structure provides a wide range of tuning options. The gate–source interaction can be reduced or even switched off between individual resonances. Similarly, by addressing different Zeeman pair state resonances with the external field the angular dependence of the interaction can be greatly varied. This provides a rich set of new tools for tailoring the interaction of photons coupled to different Rydberg states inside the medium.
Methods
Preparation of the ultracold atomic sample
We load 87Rb from a constant Rubidium background pressure of 10−9 mbar atoms into a magneto-optical trap (MOT). Simultaneously, a crossed optical dipole trap (ODT) from a fibre laser at a wavelength of 1,070 nm superimposes the MOT and attracts atoms of both 52S1/2 hyperfine ground states (F=1,2). After 1 s of loading, the MOT is compressed by ramping up the quadrupole magnetic field by a factor of 8 during 40 ms followed by an optical molasses phase of 5 ms, to maximize the number of atoms loaded into the ODT. The intensity of the ODT laser is ramped down within 200 ms to perform forced evaporation yielding 2 × 104 atoms with a temperature 3 μK in a cigar shaped trapping potential with a 1/e half length of L=40 μm and a radius of R=10 μm. Finally, by shining in two pumping lasers, we transfer atoms from the F=1 state to the F=2 state and optically pump the population to the stretched state mF=2.
Probing the optical nonlinearity
The gate excitation and the source EIT are realized with four independent laser systems, with the lower transition gate and source photons (near-)resonant to the MOT transition to achieve a maximum optical depth and thus highest efficiency of single-photon absorption. The upper transition is at 480 nm. All four laser beams are overlapped on one axis with polarization optics and dichroic mirrors. Achromatic lenses are used from both sides to focus and collimate the laser beams. The transmitted source and gate photons are coupled through single-mode fibres and detected on commercial avalanche photodiodes. Taking loss at optics and fibre coupling into account, photons in the experiment are detected with an efficiency of 30%.
Data acquisition
To reduce the statistical error, we average over multiple experiments. For instance, the data points in Fig. 1c are gathered during 23 transistor measurements per MOT cycle. We measure at 1 electric field during 20 MOT cycles. The same procedure is repeated for the reference measurement which contains no gate photons. The fields are scanned in a triangular electric field scan which was repeated 15 times. That way, systematic errors are suppressed. In addition, by monitoring the source transmission we make sure that electric field drifts are negligible during the measurement. A similar procedure was done to measure the data in Fig. 2, but with yet another scan dimension, the source photon rate.
Single Rydberg detection
The attenuation of many source photons due to one gate photon (gain) is used to predict the single-shot existence of a gate Rydberg excitation via the number of detected source photons. If a low number of source photons is detected, probably a gate excitation was present which attenuated the source. Likewise, if a high number of source photons is detected, probably the gate excitation was absent. To quantify the minimum probability of the correct prediction (detection fidelity), we take two histograms of detected source photons, with and without incident gate photons, respectively. With the knowledge of the storage efficiency (60%) and the Poissonian statistics of the coherent gate photons (mean value  ), it is possible to separate the histogram with this mean gate photon input into two histograms, one corresponding to the events with no gate excitations present and one with gate excitations. With a discrimination line, we set a threshold value for the decision whether or not the excitation was present. Any overlap of both histograms through this line results in a fidelity
), it is possible to separate the histogram with this mean gate photon input into two histograms, one corresponding to the events with no gate excitations present and one with gate excitations. With a discrimination line, we set a threshold value for the decision whether or not the excitation was present. Any overlap of both histograms through this line results in a fidelity  .
.
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
Additional information
How to cite this article: Gorniaczyk, H. et al. Enhancement of Rydberg-mediated single-photon nonlinearities by electrically tuned Förster resonances. Nat. Commun. 7:12480 doi: 10.1038/ncomms12480 (2016).
References
Saffman, M., Walker, T. G. & Mølmer, K. Quantum information with Rydberg atoms. Rev. Mod. Phys. 82, 2313 (2010).
Wilk, T. et al. Entanglement of two individual neutral atoms using Rydberg blockade. Phys. Rev. Lett. 104, 010502 (2010).
Isenhower, L. et al. Demonstration of a neutral atom controlled-NOT quantum gate. Phys. Rev. Lett. 104, 010503 (2010).
Weimer, H., Müller, M., Lesanovsky, I., Zoller, P. & Büchler, H. P. A Rydberg quantum simulator. Nat. Phys. 6, 382–388 (2010).
Jau, Y.-Y., Hankin, A. M., Keating, T., Deutsch, I. H. & Biedermann, G. W. Entangling atomic spins with a Rydberg-dressed spin-flip blockade. Nat. Phys. 12, 71–74 (2015).
Schauß, P. et al. Observation of spatially ordered structures in a two-dimensional Rydberg gas. Nature 491, 87–91 (2012).
Schauß, P. et al. Crystallization in Ising quantum magnets. Science 347, 1455–1458 (2015).
Weber, T. M. et al. Mesoscopic Rydberg-blockaded ensembles in the superatom regime and beyond. Nat. Phys. 11, 157–161 (2015).
Glaetzle, A. W. et al. Designing frustrated quantum magnets with laser-dressed Rydberg atoms. Phys. Rev. Lett. 114, 173002 (2015).
van Bijnen, R. M. W. & Pohl, T. Quantum magnetism and topological ordering via Rydberg dressing near Förster resonances. Phys. Rev. Lett. 114, 243002 (2015).
Friedler, I., Petrosyan, D., Fleischhauer, M. & Kurizki, G. Long-range interactions and entanglement of slow single-photon pulses. Phys. Rev. A 72, 043803 (2005).
Pritchard, J. D. et al. Cooperative atom-light interaction in a blockaded Rydberg ensemble. Phys. Rev. Lett. 105, 193603 (2010).
Gorshkov, A. V., Otterbach, J., Fleischhauer, M., Pohl, T. & Lukin, M. D. Photon-photon interactions via Rydberg blockade. Phys. Rev. Lett. 107, 133602 (2011).
Peyronel, T. et al. Quantum nonlinear optics with single photons enabled by strongly interacting atoms. Nature 488, 57–60 (2012).
Dudin, Y. O. & Kuzmich, A. Strongly interacting Rydberg excitations of a cold atomic gas. Science 336, 887–889 (2012).
Maxwell, D. et al. Storage and control of optical photons using Rydberg polaritons. Phys. Rev. Lett. 110, 103001 (2013).
Li, L., Dudin, Y. O. & Kuzmich, A. Entanglement between light and an optical atomic excitation. Nature 498, 466–469 (2013).
Baur, S., Tiarks, D., Rempe, G. & Dürr, S. Single-photon switch based on Rydberg blockade. Phys. Rev. Lett. 112, 073901 (2014).
Gorniaczyk, H., Tresp, C., Schmidt, J., Fedder, H. & Hofferberth, S. Single-photon transistor mediated by interstate Rydberg interactions. Phys. Rev. Lett. 113, 053601 (2014).
Tiarks, D., Baur, S., Schneider, K., Dürr, S. & Rempe, G. Single-photon transistor using a Förster resonance. Phys. Rev. Lett. 113, 053602 (2014).
Tresp, C. et al. Single-photon absorber based on strongly interacting Rydberg atoms. Preprint at http://arxiv.org/abs/1605.04456 (2016).
Parigi, V. et al. Observation and measurement of interaction-induced dispersive optical nonlinearities in an ensemble of cold Rydberg atoms. Phys. Rev. Lett. 109, 233602 (2012).
Tiarks, D., Schmidt, S., Rempe, G. & Dürr, S. Optical π phase shift created with a single-photon pulse. Sci. Adv. 2, e1600036 (2016).
Firstenberg, O. et al. Attractive photons in a quantum nonlinear medium. Nature 502, 71–75 (2013).
Otterbach, J., Moos, M., Muth, D. & Fleischhauer, M. Wigner crystallization of single photons in cold Rydberg ensembles. Phys. Rev. Lett. 111, 113001 (2013).
Bienias, P. et al. Scattering resonances and bound states for strongly interacting Rydberg polaritons. Phys. Rev. A 90, 053804 (2014).
Singer, K., Stanojevic, J., Weidemüller, M. & Côté, R. Long-range interactions between alkali Rydberg atom pairs correlated to the n s-n s, n p-n p and n d-n d asymptotes. J. Phys. B 38, S295–S307 (2005).
Schwettmann, A., Crawford, J., Overstreet, K. R. & Shaffer, J. P. Cold cs Rydberg-gas interactions. Phys. Rev. A 74, 020701 (2006).
Walker, T. G. & Saffman, M. Consequences of Zeeman degeneracy for the van der Waals blockade between Rydberg atoms. Phys. Rev. A 77, 032723 (2008).
Gallagher, T. F. & Pillet, P. In Advances in Atomic, Molecular, and Optical Physics, Vol. 56 161–218Academic Press (2008).
Comparat, D. & Pillet, P. Dipole blockade in a cold Rydberg atomic sample. J. Opt. Soc. Am. B 27, A208–A232 (2010).
Lukin, M. D. et al. Dipole blockade and quantum information processing in mesoscopic atomic ensembles. Phys. Rev. Lett. 87, 037901 (2001).
Afrousheh, K. et al. Spectroscopic observation of resonant electric dipole–dipole interactions between cold Rydberg atoms. Phys. Rev. Lett. 93, 233001 (2004).
Bohlouli-Zanjani, P., Petrus, J. A. & Martin, J. D. D. Enhancement of Rydberg atom interactions using ac stark shifts. Phys. Rev. Lett. 98, 203005 (2007).
Vogt, T. et al. Dipole blockade at Förster resonances in high resolution laser excitation of Rydberg states of cesium atoms. Phys. Rev. Lett. 97, 083003 (2006).
Ryabtsev, I. I., Tretyakov, D. B., Beterov, I. I. & Entin, V. M. Observation of the stark-tuned förster resonance between two Rydberg atoms. Phys. Rev. Lett. 104, 073003 (2010).
Reinhard, A. et al. Double-resonance spectroscopy of interacting Rydberg-atom systems. Phys. Rev. Lett. 100, 233201 (2008).
Reinhard, A., Younge, K. C. & Raithel, G. Effect of Förster resonances on the excitation statistics of many-body Rydberg systems. Phys. Rev. A 78, 060702 (2008).
Nipper, J. et al. Highly resolved measurements of stark-tuned Förster resonances between Rydberg atoms. Phys. Rev. Lett. 108, 113001 (2012).
Nipper, J. et al. Atomic pair-state interferometer: controlling and measuring an interaction-induced phase shift in Rydberg-atom pairs. Phys. Rev. X 2, 031011 (2012).
Gurian, J. H. et al. Observation of a resonant four-body interaction in cold cesium Rydberg atoms. Phys. Rev. Lett. 108, 023005 (2012).
Ravets, S., Labuhn, H., Barredo, D., Lahaye, T. & Browaeys, A. Measurement of the angular dependence of the dipole–dipole interaction between two individual Rydberg atoms at a Förster resonance. Phys. Rev. A 92, 020701 (2015).
Pelle, B. et al. Quasiforbidden two-body Förster resonances in a cold Cs Rydberg gas. Phys. Rev. A 93, 023417 (2016).
Beterov, I. I. & Saffman, M. Rydberg blockade, Förster resonances, and quantum state measurements with different atomic species. Phys. Rev. A 92, 042710 (2015).
Günter, G. et al. Interaction enhanced imaging of individual Rydberg atoms in dense gases. Phys. Rev. Lett. 108, 013002 (2012).
Olmos, B., Li, W., Hofferberth, S. & Lesanovsky, I. Amplifying single impurities immersed in a gas of ultracold atoms. Phys. Rev. A 84, 041607 (2011).
Günter, G. et al. Observing the dynamics of dipole-mediated energy transport by interaction-enhanced imaging. Science 342, 954–956 (2013).
Löw, R. et al. An experimental and theoretical guide to strongly interacting Rydberg gases. J. Phys. B 45, 113001 (2012).
Paris-Mandoki, A., Gorniaczyk, H., Tresp, C., Mirgorodskiy, I. & Hofferberth, S. Tailoring Rydberg interactions via Förster resonances: state combinations, hopping and angular dependence. J. Phys. B 49, 164001 (2016).
Tresp, C. et al. Dipolar dephasing of Rydberg D-state polaritons. Phys. Rev. Lett. 115, 083602 (2015).
Chen, W. et al. All-optical switch and transistor gated by one stored photon. Science 341, 768–770 (2013).
Reiserer, A., Ritter, S. & Rempe, G. Nondestructive detection of an optical photon. Science 342, 1349–1351 (2013).
Li, W. & Lesanovsky, I. Coherence in a cold-atom photon switch. Phys. Rev. A 92, 043828 (2015).
Uhlmann, A. The ‘transition probability’ in the state space of a *-algebra. Rep. Math. Phys. 9, 273–279 (1976).
Gaj, A. et al. From molecular spectra to a density shift in dense Rydberg gases. Nat. Commun. 5, 4546 (2014).
Li, W., Viscor, D., Hofferberth, S. & Lesanovsky, I. Electromagnetically induced transparency in an entangled medium. Phys. Rev. Lett. 112, 243601 (2014).
Acknowledgements
We thank Johannes Schmidt for construction of the electric field control; Sebastian Weber for calculation of Rydberg potentials; and Christian Zimmer for contribution to the experiment. This work is funded by the German Research Foundation through Emmy-Noether-grant HO 4787/1-1 and within the SFB/TRR21. H.G. acknowledges support from the Carl-Zeiss Foundation. I.L. acknowledges funding from the European Research Council under the European Union’s Seventh Framework Programme (FP/2007–2013)/ERC Grant Agreement No. 335266 (ESCQUMA), the EU-FET Grant No. 512862 (HAIRS), the H2020-FETPROACT-2014 Grant No. 640378 (RYSQ) and EPSRC Grant No. EP/M014266/1. W.L. is supported through the Nottingham Research Fellowship by the University of Nottingham and acknowledges access to the University of Nottingham HPC Facility.
Author information
Authors and Affiliations
Contributions
The experiment was conceived by H.G., C.T. and S.H. and carried out by H.G., C.T., A.P.-M., and I.M.; data analysis was done by H.G., A.P.-M. and C.T.; theory models and calculations were contributed by P.B., W.L., H.P.B., and I.L.; H.G. and S.H. wrote the manuscript with contributions from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Note 1 and Supplementary References (PDF 167 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Gorniaczyk, H., Tresp, C., Bienias, P. et al. Enhancement of Rydberg-mediated single-photon nonlinearities by electrically tuned Förster resonances. Nat Commun 7, 12480 (2016). https://doi.org/10.1038/ncomms12480
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms12480
This article is cited by
-
Three-dimensional solitons in Rydberg-dressed cold atomic gases with spin–orbit coupling
Scientific Reports (2023)
-
Quantum Correlations and Entanglement in Electromagnetically Induced Transparency System
International Journal of Theoretical Physics (2023)
-
Optimized nonadiabatic holonomic quantum computation based on Förster resonance in Rydberg atoms
Frontiers of Physics (2022)
-
Single-photon transistor based on cavity electromagnetically induced transparency with Rydberg atomic ensemble
Scientific Reports (2019)
-
Solitary waves in strongly non-local media with a harmonic potential
Pramana (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.