Abstract
Two-dimensional (2D) spectroscopy is used to study the interactions between energy levels in both the field of optics and nuclear magnetic resonance (NMR). Conventionally, the strength of interaction between two levels is inferred from the value of their common off-diagonal peak in the 2D spectrum, which is termed the cross peak. However, stronger diagonal peaks often have long tails that extend into the locations of the cross peaks and alter their values. Here, we introduce a method for retrieving the true interaction strengths by using sparse signal recovery techniques and apply our method in 2D Raman spectroscopy experiments.
Similar content being viewed by others
Introduction
Quantifying the coupling between energy levels is key to retrieving information about the structure of a molecule and its interaction with the environment. The coupling can be studied using two-dimensional (2D) spectroscopy, where the system is excited via one energy level and probed via another, thus giving information about the energy transfer between them. As excitation and probing directly in the frequency domain would require multiple sources that are both in the correct frequency range to excite these transitions and have some spectral tunability, this approach is technically challenging. Alternatively, the excitation and probing can be done in the time domain by using short pulses. The data may then be Fourier-transformed to retrieve the spectral response. Information about the coupling between two energy levels, ωα and ωβ, is extracted from the magnitude of their cross peak in the 2D spectral response at coordinates (ωα, ωβ)1. This technique, termed two-dimensional Fourier-Transform (2D-FT) spectroscopy, is widely used and applied in two-dimensional optical spectroscopies (2D-Vis, 2D-IR and 2D Raman)1, 2, 3, 4, 5, 6, 7, 8, 9 and two-dimensional nuclear magnetic resonance spectroscopy (2D-NMR)10, 11, 12.
Although the discrete Fourier transform, which is often realized by the fast Fourier transform (FFT) algorithm, is a powerful tool for spectral analysis, it can be limiting in cases in which the time-domain signal is composed of several independent components. In the spectra of such signals, the value at a particular frequency is the coherent sum of the spectral responses of all time-domain signal components at that frequency. As the majority of signals are composed of spectral components that are not infinitely narrow, the tails of the stronger signal components may spill into or even cover other weaker features. This effect is particularly problematic when examining cross peaks in a 2D spectrum, which are inherently weaker than their corresponding diagonal peaks.
Here, we present a signal analysis method based on sparse signal recovery that eliminates such ambiguities by identifying each component of the time-domain signal and finding its individual spectral response. Our method applies the block orthogonal matching pursuit (BOMP) algorithm by Eldar et al. 13 directly to the 2D time-domain data. Using BOMP, the stronger signal components that cause diagonal peaks are first identified and removed, and thereafter the weaker cross peak signal is analyzed.
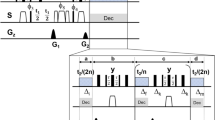
To demonstrate the difficulties that arise in cross peak analysis using FFT and their possible resolution, we discuss an example from 2D Raman spectroscopy8. A typical pulse sequence used for impulsive excitation in 2D Raman spectroscopy is shown in the inset of Figure 1a. The two time delays, t(1) and t(2), are scanned, and the signal is measured for each delay pair (the analysis of time-resolved 2D spectra is discussed at the end of the following section). Figure 1a shows the results of a simulation of 2D Raman spectroscopy performed on CCl4 molecules in which the coupling between energy levels was turned off (see Supplementary Information 2 for details). The corresponding 2D spectrum, which was computed by applying FFT to the data in Figure 1a, is shown in Figure 1b. The reflected second quadrant is presented for clarity due to artifacts on the diagonal of the first quadrant. The peaks on the diagonal (dashed black line) correspond to the three Raman lines of CCl4, namely, 217, 313 and 459 cm−1. Although no cross peaks should be present, the long tail from the diagonal 313 cm−1 peak combines with the tail from the diagonal 459 cm−1 peak to form a false peak at (313 cm−1, 459 cm−1) (marked by a red arrow). Such long tails can be caused by two mechanisms: physical broadening of the vibrational level and artifacts due to the discrete nature of FFT. The former mechanism, homogenous broadening, creates long decaying tails due to the Lorentzian function in the molecular lineshape. The latter mechanism is known as spectral leakage and is a result of the convolution of the true spectral response with a sinc function due to the finite temporal window of the measurement. A partial solution for spectral leakage is provided by apodization, but it comes at the expense of a loss in both resolution and sensitivity14, 15.
Simulation: an example of difficulties in interpreting 2D-FT spectra. (a) The simulated 2D Raman spectroscopy time-domain data of molecules in which the coupling between vibrational levels was turned off. Inset: A typical three-pulse sequence used in 2D Raman spectroscopy measurements. (b) The corresponding 2D spectrum, computed with FFT. The arrows mark false features that appear as cross peaks, although no cross peaks should be present. The plot is presented in log scale.
In addition to the problems caused by the long tails, off-diagonal peaks between each molecular frequency and its overtones add additional strong features to the 2D spectrum that may interfere with reading the cross peak values. These overtone peaks can be caused by both the impulsive excitation of a single level and multiple excitations and are observed when using all Fourier-transform 2D spectroscopy methods (see below). An example of this difficulty is also observed in Figure 1b. An off-diagonal peak at (217 cm−1, 434 cm−1), between the 217 cm−1 line and its first overtone, covers the location of another potential cross peak, at (217 cm−1, 459 cm−1) (marked by a brown arrow).
In this work, the BOMP algorithm is used to separate the spectral responses of the various signal components by using prior knowledge about the signal form. Indeed, compressed sensing (CS)16, 17, which also uses sparse signal recovery techniques, was introduced in recent years as a way to accelerate 2D-FT experiments by reducing the number of measurements needed or, equivalently, super-resolving the acquired data in the spectral domain18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29. However, the aims of our BOMP analysis and CS are fundamentally different. Whereas BOMP analysis is used here to fit the signal to a model, CS is typically used to approximately reconstruct the 2D spectrum that would be obtained using FFT but with a shorter acquisition time. Therefore, CS cannot separate signal components that inherently overlap in the frequency domain, even given unlimited spectral resolution (for example, due to homogenous broadening).
Materials and methods
BOMP is an efficient method for recovering block-sparse signals. A signal is considered sparse if it can be represented in some basis where most of the coefficients of the basis vectors are zero, and a signal is considered block-sparse when these nonzero coefficients represent groups of vectors30. For example, a 1D spectrum is sparse if the number of principle molecular frequencies that it contains is small relative to the spectral window, and it is block-sparse if each such principle frequency predicts the appearance of several related frequencies in the spectrum, such as its overtones. 2D spectroscopy data are a natural candidate for reconstruction with BOMP since their spectral response is highly clustered. To understand why, let us consider the form of the acquired data. In a 2D spectroscopy experiment, the delays t(1) and t(2) in the three-pulse sequence become discrete vectors of equally spaced measurement points,  and
and  . Therefore, the measured data forms a 2D matrix, as in Figure 1a. For a sample with a single energy level ω, a typical matrix element of the experimental data set will have the following form:
. Therefore, the measured data forms a 2D matrix, as in Figure 1a. For a sample with a single energy level ω, a typical matrix element of the experimental data set will have the following form:

where i and j are the matrix indices; D(ω, φ, σ, γ, t) is a decaying oscillatory function of frequency ω that includes homogenous broadening of width γ and inhomogeneous broadening of width σ; φ is the phase of the oscillations with respect to the decaying envelope; n, m, k and l represent the nth, mth, kth and lth overtones, respectively; Anm, Bkl and Ckl are proportionality constants; and the sum is performed up to N, which is the highest overtone with a significant contribution to the signal. The second term of Equation (1) appears as a pulse sequence with two time delays, t(1) and t(2), necessarily also contains their difference (see inset of Figure 1a) and therefore also a signal component that oscillates as a function of that difference. The overtones of each frequency of the sample appear whenever the time-domain signal oscillation is more impulsive than a pure cosine and when transitions due to multiple excitations are present31 (a variable anharmonicity can be added when relevant; see Supplementary Information 1 step 1). The 0th overtone represents a DC component, that is, a vector with decay only; hence, Si0 and S0j appear as axial peaks in the 2D spectrum. For a sample with multiple energy levels, excluding interactions between the levels, the total sample response is  .
.
As seen from Equation (1), the existence of a certain molecular frequency ωα in the sample predicts the appearance of a distinct group of terms in the signal, encompassing the diagonal (n=m), axial (n=0 or m=0), overtone (n≠m and n, m≠0) and time-difference terms of ωα. This group serves as the basic block used by BOMP analysis as follows: a large database of blocks is created (a dictionary), where each block represents a frequency of an energy level that could be present in the sample, and it contains all of the terms described by Equation (1). The algorithm searches iteratively for the block with the maximal sum of inner products between the block members and the data. Each iteration retrieves one molecular frequency and the magnitude of all associated terms, removes these terms from the data and orthogonalizes the residual32. The halting condition may be a bound on the error or the number of molecular frequencies, if known. Prior knowledge of the lineshape parameters or any unknown parameter in the model is not required as BOMP can be used to recover their values in addition to the molecular frequencies (see Supplementary Information 1, step 1). Once BOMP has removed all of the signal components associated with the stronger peaks, represented in Equation (1), the residual data are fitted to a matrix that describes coupling between modes, with entries of the following form:

according to the retrieved molecular frequencies. Here, ωα and ωβ represent two different energy levels of the sample, and A0, B0 and C0 are constants. This step recovers the cross peak values and concludes the analysis.
Since BOMP fits the signal to a model, it is related to spectral analysis methods such as parametric linear prediction techniques, the filter diagonalization method, maximum likelihood, Bayesian analysis, multi-dimensional decomposition, and implementations of nonlinear least-squares fitting33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44. However, for sparse signals such as 2D spectroscopy data, sparse signal recovery methods have been shown to fit the signal robustly in the presence of noise and have provable recovery guarantees16, 45. Moreover, the addition of the block-form constraint serves to reduce the parameter space of the problem. These two properties of BOMP allow the recovery of the correct signal representation in larger solution spaces and higher noise levels than would otherwise be possible. In fact, the BOMP algorithm has been shown to come close to the Cramer-Rao bound46 and could retrieve cross peak values that were an order of magnitude weaker than the noise level in a simulation we performed (Supplementary Information 2.2). Successful recovery with BOMP generally relies on two main criteria in the user input: a sufficient number of measured data points and the quality of the block dictionary. For an in-depth discussion of these criteria and other aspects of the performance of BOMP, see Supplementary Information 2.
When analyzing time-resolved 2D spectra, the 2D spectrum for each waiting time can generally be analyzed with BOMP as currently implemented. Since BOMP extracts the magnitudes of all peaks in an analyzed spectrum, the variations in their magnitudes as functions of the waiting time are directly obtained from the results. As BOMP can be used to extract the values of other parameters, such as lineshape parameters, it also can be used to follow their variations as functions of the waiting time. Models that include population and coherence transfer47, 48, 49 can be accommodated by adding both cross peaks and diagonal peaks shifted by diagonal anharmonicity. The D (ω, φ, σ, γ, t) function used here already includes bimodal decay, but adding a third decay rate might be necessary in some cases of population and coherence transfer. BOMP can be extended to analyze three-dimensional spectra, as discussed in more detail in Supplementary Information 1.
Results and discussion
Numerical results
To test the performance of BOMP analysis, we prepared two sets of simulated 2D Raman spectroscopy data. The first set simulates a sample of CCl4 without any coupling between vibrational levels, and the second simulates a sample of CCl4 with coupling. The sampling rate and window size were set to match those of a typical 2D Raman experiment (see Supplementary Information 3 for simulation details).To start, both data sets were analyzed using FFT, producing the results in Figure 2. We can observe only minor differences between the simulation without coupling (Figure 2a) and that with coupling (Figure 2b) since the tails from the diagonal peaks at 217 cm−1 and 459 cm−1 and the overtone peak at (217 cm−1, 434 cm−1) covered the cross peak locations almost entirely (marked with black Xs).
Analyzing simulations with and without coupling using FFT. (a) The 2D FFT of simulated 2D Raman spectroscopy data from CCl4 molecules without coupling. (b) The 2D FFT of simulated CCl4 data with coupling. Both spectra are normalized. Because of the overtone peaks and the long tails of the diagonal peaks, only minor differences between the simulations are discernible, and the true values of the cross peaks in b are difficult to distinguish (locations marked with black Xs).
In contrast, the analysis of the same two data sets using BOMP clearly shows the differences between the sets with and without coupling. The cross peak values retrieved using BOMP analysis (represented by A0 in Equation (2)) on both sets are presented in Figure 3. We observe that whereas BOMP finds significant energy in the (217 cm−1, 459 cm−1) and (313 cm−1, 459 cm−1) cross peaks in the simulation with coupling (orange), it finds noise-level energy for the same cross peaks in the simulation without coupling (purple). Furthermore, to verify that the retrieved values of the cross peaks are correct, we prepared a third simulated data set that contains only those terms that cause cross peaks and no terms that cause diagonal, axial, or overtone peaks (Supplementary Information 3). In this data set, the cross peak values remain the same, but all of the tails from the diagonal and overtone peaks are absent, so FFT yields the true cross peak values. The results from analyzing this set with FFT, as shown in Figure 3 in blue, agree well with the results of running BOMP on the full simulation with coupling (orange). From both tests, we may conclude that BOMP analysis retrieves the true, background-free, cross peak values. For a comparison with the results from simulated data with additive white Gaussian noise, see Supplementary Information 2.2.
Analyzing the simulations presented in Figure 2 and experimental data with BOMP. The cross peak values retrieved by BOMP from the simulation without coupling (purple), the simulation with coupling (orange) and the experimental data (green). The cross peak values of a simulation with coupling only, and therefore without any tails, as calculated using FFT, are presented for comparison (blue). The cross peak values from the three data sets with coupling agree well.
Experimental results
We now analyze the experimental results from a 2D Raman spectroscopy measurement on liquid CCl4 (Ref. 8) with BOMP. The cross peak values retrieved from the experimental data are shown in green in Figure 3. The error bar values were computed by propagating the error caused by experimental noise in the time-domain measurement (SNR of ~10:1). These results can also be used to create a clean, high-resolution 2D spectral plot of the cross peak signal only. The advantage of plotting the cross peak component of the signal on its own is demonstrated in Figure 4, which compares several methods for analyzing the experimental data. The results from conventional FFT analysis, as shown in Figure 4a, display long tails extending from the diagonal peaks as well as strong overtone peaks and additional artifacts. The plot clearly contains features covering the cross peak locations (marked by black Xs) and lacks the resolution necessary for discerning the cross peak values. Figure 4b shows the full 2D spectral response, including all time-domain signal components, retrieved by BOMP from the same data. The artifact on the diagonal (see Supplementary Information 1, Equation (4)) and features due to noise were not reconstructed for clarity. Since this plot is constructed directly in the spectral domain, it is equivalent to the spectral response that would be retrieved using FFT from a measurement with an infinitely large temporal window. Although the plot is free from spectral leakage and has significantly higher resolution, the physical properties of the signal still prevent proper cross peak analysis. The tails caused by homogenous broadening still cover the location of the (217 cm−1, 313 cm−1) cross peak, and alter the shape of the (313 cm−1, 459 cm−1) cross peak, likely modifying its value. Moreover, the (217 cm−1, 434 cm−1) overtone peak interferes with the (217 cm−1, 459 cm−1) cross peak. Therefore, eliminating spectral leakage alone by adding more data points or with conventional compressed sensing techniques24, 25, 27, 29 would not have provided an adequate solution. We note that simply removing the real part of the lineshape (dispersive), as is done by using phase-cycling50 or computing the sum of the rephasing and non-rephasing spectra51, would have not been sufficient either, as the imaginary part of the homogenously broadened lineshape (absorptive) still creates significant tails. Finally, Figure 4c shows the 2D spectral response corresponding to the cross peak signal only, as retrieved by BOMP. This spectrum is free from any additional components or artifacts that may distort the cross peaks and provides a high-resolution, accurate representation of a relatively weak signal component that would be otherwise difficult to study.
Experimental results: 2D Raman spectra of CCl4, computed with FFT and BOMP. (a) The 2D spectrum computed with FFT from the measured 2D time-domain data. The cross peak locations, which are completely covered by tails of strong features, are marked with black Xs. (b) The full 2D spectrum, including all signal components, retrieved with BOMP from the same data. This spectrum is equivalent to the spectrum that FFT would retrieve from an ideal measurement, with an infinitely large temporal window. The cross peak locations are still partially covered. (c) The 2D spectrum of the coupling component only, retrieved with BOMP from the same data. All spectra are normalized.
Conclusions
In this work, Block Orthogonal Matching Pursuit was used to analyze data from a 2D Raman spectroscopy experiment. The analysis was performed by identifying and removing the stronger signal components from the data before analyzing the coupling signal, thereby eliminating the ambiguities in cross peak analysis that are associated with the use of FFT. Since BOMP provides an approximate analytical representation of the 2D spectral response, the analysis method presented here can be used to explore properties of the signal other than the cross peaks, such as the lineshape, phase, and magnitude of each peak in the spectrum. For highly complex spectra with non-standard features, BOMP can be used in conjunction with FFT and other tools that can assist in building a proper dictionary. Furthermore, BOMP can be combined with dictionary learning algorithms52 so that the optimal dictionary can be learned from the data.
BOMP analysis could be applicable to a wide range of Fourier-transform spectroscopies and may allow the successful recovery of the parametric form of acquired data where non-sparsity-based techniques fail. Although much work has been done in the field of multidimensional NMR with non-Fourier analysis methods for spectral analysis, there are fewer such works in multidimensional optical spectroscopy. We therefore believe that BOMP analysis may enable the study of aspects of spectral responses that would not be possible to study with optical spectroscopy otherwise.
Author contributions
HF, TB, YCE and YS conceived the idea, developed and performed BOMP analysis. HF and YS wrote the manuscript.
References
Jonas DM . Two-dimensional femtosecond spectroscopy. Annu Rev Phys Chem 2003; 54: 425–463.
Tanimura Y, Mukamel S . Two-dimensional femtosecond vibrational spectroscopy of liquids. J Chem Phys 1993; 99: 9496–9511.
Tian PF, Keusters D, Suzaki Y, Warren WS . Femtosecond phase-coherent two-dimensional spectroscopy. Science 2003; 300: 1553–1555.
Brixner T, Stenger J, Vaswani HM, Cho M, Blankenship RE et al. Two-dimensional spectroscopy of electronic couplings in photosynthesis. Nature 2005; 434: 625–628.
Tokmakoff A, Lang MJ, Larsen DS, Fleming GR, Chernyak V et al. Two-dimensional Raman spectroscopy of vibrational interactions in liquids. Phys Rev Lett 1997; 79: 2702–2705.
Asplund MC, Zanni MT, Hochstrasser RM . Two-dimensional infrared spectroscopy of peptides by phase-controlled femtosecond vibrational photon echoes. Proc Natl Acad Sci USA 2000; 97: 8219–8224.
Fayer MD . Fast protein dynamics probed with infrared vibrational echo experiments. Annu Rev Phys Chem 2001; 52: 315–356.
Frostig H, Bayer T, Dudovich N, Eldar YC, Silberberg Y . Single-beam spectrally controlled two-dimensional Raman spectroscopy. Nat Photonics 2015; 9: 339–343.
Dudovich N, Oron D, Silberberg Y . Single-pulse coherently controlled nonlinear Raman spectroscopy and microscopy. Nature 2002; 418: 512–514.
Jeener J, Meier BH, Bachmann P, Ernst RR . Investigation of exchange processes by two-dimensional NMR spectroscopy. J Chem Phys 1979; 71: 4546–4553.
Englander SW, Mayne L . Protein folding studied using hydrogen-exchange labeling and two-dimensional NMR. Annu Rev Biophys Biomol Struct 1992; 21: 243–265.
Frydman L, Blazina D . Ultrafast two-dimensional nuclear magnetic resonance spectroscopy of hyperpolarized solutions. Nat Phys 2007; 3: 415–419.
Eldar YC, Kuppinger P, Bolcskei H . Block-sparse signals: uncertainty relations and efficient recovery. IEEE Trans Signal Proc 2010; 58: 3042–3054.
Naylor DA, Tahic MK . Apodizing functions for Fourier transform spectroscopy. J Opt Soc Am A 2007; 24: 3644–3648.
Parker SF, Patel V, Tooke PB, Williams KPJ . The effect of apodization and finite resolution on Fourier transform Raman spectra. Spectrochim Acta A Mol Spectr 1991; 47: 1171–1178.
Duarte MF, Eldar YC . Structured compressed sensing: from theory to applications. IEEE Trans Signal Proc 2011; 59: 4053–4085.
Kutyniok G, Eldar YC . Compressed Sensing: Theory and Application. Cambridge: Cambridge University Press; 2012. p414–503.
Jaravine V, Ibraghimov I, Orekhov VY . Removal of a time barrier for high-resolution multidimensional NMR spectroscopy. Nat Methods 2006; 3: 605–607.
Lustig M, Donoho D, Pauly JM . Sparse MRI: the application of compressed sensing for rapid MR imaging. Magn Reson Med 2007; 58: 1182–1195.
Rovnyak D, Frueh DP, Sastry M, Sun ZYJ, Stern AS et al. Accelerated acquisition of high resolution triple-resonance spectra using non-uniform sampling and maximum entropy reconstruction. J Magn Reson 2004; 170: 15–21.
Coggins BE, Venters RA, Zhou P . Radial sampling for fast NMR: concepts and practices over three decades. Prog Nuclear Magn Reson Spectr 2010; 57: 381–419.
Holland DJ, Bostock MJ, Gladden LF, Nietlispach D . Fast multidimensional NMR spectroscopy using compressed sensing. Angew Chem Int Ed 2011; 50: 6548–6551.
Kazimierczuk K, Orekhov V . Non-uniform sampling: post-Fourier era of NMR data collection and processing. Magn Reson Chem 2015; 53: 921–926.
Katz O, Levitt JM, Silberberg Y . Frontiers in Optics 2010/Laser Science XXVI; 24–28 October 2010; Rochester, New York, USA. Optical Society of America: Washington, DC, USA. 2010.
Sanders JN, Saikin SK, Mostame S, Andrade X, Widom JR et al. Compressed sensing for multidimensional spectroscopy experiments. J Phys Chem Lett 2012; 3: 2697–2702.
Mobli M, Maciejewski MW, Schuyler AD, Stern AS, Hoch JC . Sparse sampling methods in multidimensional NMR. Phys Chem Chem Phys 2012; 14: 10835–10843.
Almeida J, Prior J, Plenio MB . Computation of two-dimensional spectra assisted by compressed sampling. J Phys Chem Lett 2012; 3: 2692–2696.
Andrade X, Sanders JN, Aspuru-Guzik A . Application of compressed sensing to the simulation of atomic systems. Proc Natl Acad Sci USA 2012; 109: 13928–13933.
Dunbar JA, Osborne DG, Anna JM, Kubarych KJ . Accelerated 2D-IR using compressed sensing. J Phys Chem Lett 2013; 4: 2489–2492.
Eldar YC, Mishali M . Robust recovery of signals from a structured union of subspaces. IEEE Trans Inform Theory 2009; 55: 5302–5316.
Bax A, de Jong PG, Mehlkopf AF, Smidt J . Separation of the different orders of NMR multiple-quantum transitions by the use of pulsed field gradients. Chem Phys Lett 1980; 69: 567–570.
Pati YC, Rezaiifar R, Krishnaprasad PS . Orthogonal matching pursuit: recursive function approximation with applications to wavelet decomposition. Proceedings of the 27th Asilomar Conference on Signals, Systems and Computers; Pacific Grove, CA, USA, IEEE, 1993, pp40–44.
Schussheim AE, Cowbur D . Deconvolution of high-resolution two-dimensional NMR signals by digital signal processing with linear predictive singular value decomposition. J Magn Reson 1987; 71: 371–378.
Wise F, Rosker M, Millhauser G, Tang C . Application of linear prediction least-squares fitting to time-resolved optical spectroscopy. IEEE J Quantum Electron 1987; 23: 1116–1121.
Zeng Y, Tang J, Bush CA, Norris JR . Enhanced spectral resolution in 2D NMR signal analysis using linear prediction extrapolation and apodization. J Magn Reson 1989; 83: 473–483.
Bretthorst GL . Bayesian analysis. I. Parameter estimation using quadrature NMR models. J Magn Reson 1990; 88: 533–551.
de Beer R, van Ormondt D . Analysis of NMR data using time domain fitting procedures spectrum analysis. In: Rudin Meditor. In-Vivo Magnetic Resonance Spectroscopy I: Probeheads and Radiofrequency Pulses Spectrum Analysis. Berlin Heidelberg: Springer; 1992. pp201–248.
Chylla RA, Markley JL . Theory and application of the maximum likelihood principle to NMR parameter estimation of multidimensional NMR data. J Biomol NMR 1995; 5: 245–258.
Mandelshtam V, Taylor H, Shaka AJ . Application of the filter diagonalization method to one- and two-dimensional NMR spectra. J Magn Reson 1998; 133: 304–312.
Massiot D, Fayon F, Capron M, King I, Le Calvé S et al. Modelling one- and two-dimensional solid-state NMR spectra. Magn Reson Chem 2002; 40: 70–76.
Orekhov VY, Jaravine VA . Analysis of non-uniformly sampled spectra with multi-dimensional decomposition. Progr Nuclear Magn Reson Spectr 2011; 59: 271–292.
Khalil M, Demirdöven N, Tokmakoff A . Coherent 2D IR spectroscopy: molecular structure and dynamics in solution. J Phys Chem A 2003; 107: 5258–5279.
van Stokkum IHM, Larsen DS, van Grondelle R . Global and target analysis of time-resolved spectra. Biochim Biophys Acta 2004; 1657: 82–104.
Duan HG, Stevens AL, Nalbach P, Thorwart M, Prokhorenko VI et al. Two-dimensional electronic spectroscopy of light-harvesting complex ii at ambient temperature: a joint experimental and theoretical study. J Phys Chem A 2015; 119: 12017–12027.
Donoho DL, Elad M, Temlyakov VN . Stable recovery of sparse overcomplete representations in the presence of noise. IEEE Trans Inform Theory 2006; 52: 6–18.
Ben-Haim Z, Eldar YC . Near-oracle performance of greedy block-sparse estimation techniques from noisy measurements. IEEE J Sel Topics Signal Proc 2011; 5: 1032–1047.
Piryatinski A, Chernyak V, Mukamel S . Vibrational-exciton relaxation probed by three-pulse echoes in polypeptides. Chem Phys 2001; 266: 285–294.
Khalil M, Demirdöven N, Tokmakoff A . Vibrational coherence transfer characterized with Fourier-transform 2D IR spectroscopy. J Chem Phys 2004; 121: 362.
Nee MJ, Baiz CR, Anna JM, McCanne R, Kubarych KJ . Multilevel vibrational coherence transfer and wavepacket dynamics probed with multidimensional IR spectroscopy. J Chem Phys 2008; 129: 084503.
Bax A, Mehlkopf AF, Smidt J . Absorption spectra from phase-modulated spin echoes. J Magn Reson 1979; 35: 373–377.
Khalil M, Demirdöven N, Tokmakoff A . Obtaining absorptive line shapes in two-dimensional infrared vibrational correlation spectra. Phys Rev Lett 2003; 90: 047401.
Zelnik-Manor L, Rosenblum K, Eldar YC . Dictionary optimization for block-sparse representations. IEEE Trans Signal Proc 2012; 60: 2386–2395.
Acknowledgements
We would like to thank JC Hoch, N Dudovich and L Chuntonov for helpful discussions. This work was supported by Icore (Israeli centres of research excellence of the ISF), and the Crown Photonics Center.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Additional information
Note: Supplementary Information for this article can be found on the Light: Science & Applications’ website.
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Frostig, H., Bayer, T., Eldar, Y. et al. Revealing true coupling strengths in two-dimensional spectroscopy with sparsity-based signal recovery. Light Sci Appl 6, e17115 (2017). https://doi.org/10.1038/lsa.2017.115
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/lsa.2017.115