Abstract
Squeezed states of light are a set of nonclassical states in which the quantum fluctuations of one quadrature component are reduced below the standard quantum limit. With less noise than the best stabilised laser sources, squeezed light is a key resource in the field of quantum technologies and has already improved sensing capabilities in areas ranging from gravitational wave detection to biomedical applications. In this work we propose a novel technique for generating squeezed states of a confined light field strongly coupled to a two-level system, or qubit, in the dispersive regime. Utilising the dispersive energy shift caused by the interaction, control of the qubit state produces a time-dependent change in the frequency of the light field. An appropriately timed sequence of sudden frequency changes reduces the quantum noise fluctuations in one quadrature of the field well below the standard quantum limit. The degree of squeezing and the time of generation are directly controlled by the number of frequency shifts applied. Even in the presence of realistic noise and imperfections, our protocol promises to be capable of generating a useful degree of squeezing with present experimental capabilities.
Similar content being viewed by others
Introduction
One of the remarkable features of quantum theory that makes its predictions different from those of classical physics is the concept of vacuum fluctuations or zero-point motion. An electromagnetic field, even at absolute zero, has a non-zero energy in the vacuum state. This zero-point energy is associated with fluctuations in the quadratures of the field, such as the electric or magnetic fields or the vector potential. These vacuum fluctuations manifest as quantum noise in experiments, placing a fundamental limit on the precision with which pairs of non-commuting observables can be measured simultaneously, as required by the Heisenberg uncertainty principle1.
However, for some types of measurements the effect of quantum noise can be reduced by utilising a special class of quantum states known as squeezed states. In order to understand the properties of squeezed light, it is useful to consider complex phasors ( and
and  ) for the representation of a single light mode with creation and destruction operators denoted by
) for the representation of a single light mode with creation and destruction operators denoted by  and
and  . The operators
. The operators  and
and  correspond to the dimensionless position and momentum quadratures of the field and the associated variances satisfy the Heisenberg uncertainty relation
correspond to the dimensionless position and momentum quadratures of the field and the associated variances satisfy the Heisenberg uncertainty relation  . The vacuum state of the field mode satisfies the minimum uncertainty relation with
. The vacuum state of the field mode satisfies the minimum uncertainty relation with  , which defines the so-called standard quantum limit (SQL)1. Squeezed states, on the other hand, may have a variance lower than the SQL in one quadrature, reflecting reduced quantum noise in that quadrature component. This necessarily comes at the expense of increased fluctuations in the orthogonal quadrature, such that the minimum uncertainty relation is still satisfied in a squeezed state.
, which defines the so-called standard quantum limit (SQL)1. Squeezed states, on the other hand, may have a variance lower than the SQL in one quadrature, reflecting reduced quantum noise in that quadrature component. This necessarily comes at the expense of increased fluctuations in the orthogonal quadrature, such that the minimum uncertainty relation is still satisfied in a squeezed state.
Over the years, the generation of squeezed light has attracted much attention for various practical applications, including high-precision quantum measurements2,3, quantum communication4, and enhanced sensitivity in gravitational wave detectors5. In the quantum optical domain, squeezed light has been more commonly generated using nonlinear optical processes, including degenerate parametric amplification and degenerate four-wave mixing1,6,7,8,9. These nonlinear processes require large optical nonlinearities, low intracavity and detection losses, and low phase noise10,11,12. Over the years, experimental progress has made it possible to generate squeezed states of light in a variety of different experimental setups12, including optical parametric oscillators13, superconducting cavities14, and optomechanical and microwave cavities15,16,17,18.
In this work we present an alternative technique for generating intracavity squeezed states of a field mode dispersively coupled to a two-level system19. This protocol does not require higher order nonlinearities or strong pump power and can tolerate moderate levels of photon losses and imperfections. Much of the motivation for this work comes from the drive toward scalable quantum technology based on hybrid quantum systems, which incorporate qubit-based architectures for storing quantum information, photons for quantum communication, and nanomechanical devices for applications in quantum sensing20. In this direction, light-matter coupled quantum systems have received particular attention in the bid to engineer scalable quantum platforms20,21,22. In these hybrid systems a two-level system (qubit) is coupled to a bosonic (light) field. Theoretically, the basic building block for describing such light-matter systems is the quantum Rabi model, which takes the following form under the dipole approximation23,24,

Here,  and
and  are the annihilation and creation operators for the bosonic field of frequency ω,
are the annihilation and creation operators for the bosonic field of frequency ω,  with
with  the Pauli matrices for the two-level system, Ω is the energy level splitting between the two levels, and g denotes the coupling strength between the bosonic mode and the two-level system (assumed to be positive).
the Pauli matrices for the two-level system, Ω is the energy level splitting between the two levels, and g denotes the coupling strength between the bosonic mode and the two-level system (assumed to be positive).
In conventional cavity QED settings the light-matter coupling strength g is several orders of magnitude smaller than the transition frequencies ω, Ω. In addition, if the system is near resonance, such that ω ~ Ω, the full quantum Rabi model can be simplified by applying the rotating wave approximation (RWA). Under this approximation the so-called “counter-rotating” terms in Eq. (1) can be neglected, leading to the much simpler and readily solvable Jaynes-Cummings (JC) model25

However, the validity of the quantum Rabi model is not only restricted to cavity QED setups. The original quantum Rabi model is a ubiquitous physical model capable of describing a wide variety of other physical systems, including trapped ions26,27, qubit-coupled nanomechanical resonators28,29, and circuit QED systems30,31,32,33,34,35. Circuit QED architectures are particularly interesting because it is possible to reach physical regimes where the light-matter coupling strength g becomes a sizeable fraction of the transition frequency of the boson field and/or the two-level system, meaning that the RWA is no longer a valid approximation. The influence of non-RWA terms has been studied theoretically for some time28,36,37,38,39,40,41,42. However, with recent experimental advances in reaching “ultra-strong” and “deep strong” coupling regimes of light and matter43,44,45, investigations of the full quantum Rabi model are attracting increasing attention27,32,46,47,48,49,50,51,52,53. It has been clearly shown that in these strongly coupled quantum systems the simplified JC model no longer applies and it becomes necessary to consider the full quantum Rabi model to capture the relevant physics. The significance of non-RWA terms has also been elucidated in many-body extensions of the full quantum Rabi model, both in the equilibrium54 and non-equilibrium55,56 settings.
Another regime of significant practical interest in which the quantum Rabi model can be substantially simplified is the so-called “dispersive regime”30. In the dispersive limit, the qubit and the boson field are far detuned compared to the light-matter coupling strength g, i.e.  . This regime is widely considered in experiments, particularly in circuit QED, as it allows a non-demolition type measurement of the qubit to be made by probing the resonator31. Although the dispersive approximation is often applied together with the RWA31, in this work we consider the dispersive limit without making the RWA19,28 and show that it can be used to create squeezed states of the field mode.
. This regime is widely considered in experiments, particularly in circuit QED, as it allows a non-demolition type measurement of the qubit to be made by probing the resonator31. Although the dispersive approximation is often applied together with the RWA31, in this work we consider the dispersive limit without making the RWA19,28 and show that it can be used to create squeezed states of the field mode.
In the dispersive regime beyond the RWA, the ground state of the quantum Rabi model exhibits one-mode squeezing of the boson field19, but the degree of squeezing is very small. We present a protocol which can significantly enhance the degree of squeezing present under this dispersive interaction, making use of a long-known result that any nonadiabatic change in the frequency of a harmonic oscillator (boson field) results in squeezing of the state of the oscillator57,58,59. The degree of squeezing is particularly pronounced if the frequency change is sudden60. Moreover, it is possible to use periodic sudden jumps between two frequencies to produce arbitrarily large squeezing of the field mode61,62,63. We show that this strategy can be used within the dispersive quantum Rabi model to generate significant squeezing of the field mode, taking advantage of the high degree of controllability that exists for qubits. Comparing analytical predictions using the dispersive approximation with numerical simulations of the same protocol using the full Rabi Hamiltonian, we find that, remarkably, an even larger degree of squeezing arises in the latter case. An analysis of the effects of noise and imperfections suggests that considerable squeezing could be achieved with existing experimental capabilities in circuit QED. It is worth pointing out that periodic sudden frequency jumps is, of course, an idealisation to any actual physical realisation. However, as long as the periodic frequency flips are nonadiabatic and the frequency flips are timely controlled it should still be possible to generate squeezed states of the boson field. We will briefly comment on this point towards the end of the paper.
Results
Dispersive regime: beyond the RWA
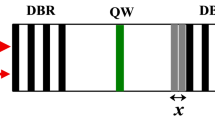
The physical setting we consider is a strongly coupled light-matter system modeled by the Rabi Hamiltonian of Eq. (1). Throughout this paper we focus on the dispersive regime in which the detuning Δ ≡ Ω − ω between the qubit and the cavity is large compared to their coupling, |Δ| ≫ g. As the qubit and cavity are far from resonance, we do not invoke the RWA to simplify the light-matter interaction; this also allows us to work with values of g/ω ranging up to ≈0.1. Although the theory presented here may describe many different types of experimental systems, the dispersive limit is particularly applicable to experiments in circuit QED19,30,31,64,65 and qubit-coupled nanomechanics29, which we touch on near the end of the paper.
An effective Hamiltonian in the dispersive limit may be derived19 using the unitary transformation  , where ζ ≡ g/Δ,
, where ζ ≡ g/Δ,  , and h.c. denotes the Hermitian conjugate. Applying this transformation to the Rabi Hamiltonian and keeping terms up to second order in g, the dispersive Hamiltonian Hdisp is given by
, and h.c. denotes the Hermitian conjugate. Applying this transformation to the Rabi Hamiltonian and keeping terms up to second order in g, the dispersive Hamiltonian Hdisp is given by

The eigenspectra of the dispersive Hamiltonian (3) and the full quantum Rabi model (1) are compared in Fig. 1. The lowest lying energy levels of each model are plotted as a function of the detuning parameter Δ for two different values of the light-matter coupling strength g. As is clear from Fig. 1, the dispersive theory is a valid approximation to the full quantum Rabi model in the large detuning regime but breaks down as expected near Δ = 0. The mismatch between the two becomes more pronounced for larger values of g as Δ → 0.
Comparison between a numerical solution of the lowest energy levels of the full quantum Rabi model [Eq. (1)] (points) and the analytical solutions of the dispersive Hamiltonian [Eq.(4)] (solid) for (a) g/ω = 0.1 and (b) g/ω = 0.2. Note that Ω/ω = 1 + Δ/ω. Our choice to intentionally leave out the point Δ = 0 is based on the fact that the dispersive approximation breaks down at Δ = 0. It is, therefore, only meaningful to compare the predictions of the full quantum Rabi model and the dispersive theory away from Δ = 0.
An alternative form of Eq. (3) makes the physics of the dispersive interaction more transparent. Defining the parameter 2ϕ = g2/Δ + g2/(2Ω − Δ), the dispersive Hamiltonian may be re-expressed as

In this form it is evident that the first term contains a shift in the frequency of the cavity mode that depends on the state of the qubit through  . This is the basis for the commonly used dispersive readout technique for superconducting qubits30,31: the frequency shift of the cavity, which is readily measured, is correlated with the qubit state. As pointed out in ref. 19, a remarkable feature of the above Hamiltonian is that a dispersive readout of the qubit is still possible even when the cavity field and the two-level system are coupled strongly enough that the RWA cannot be made. The final term of the dispersive Hamiltonian is also of interest. It takes the form of a one-mode squeezing interaction, the sign of which again depends on the state of the qubit through
. This is the basis for the commonly used dispersive readout technique for superconducting qubits30,31: the frequency shift of the cavity, which is readily measured, is correlated with the qubit state. As pointed out in ref. 19, a remarkable feature of the above Hamiltonian is that a dispersive readout of the qubit is still possible even when the cavity field and the two-level system are coupled strongly enough that the RWA cannot be made. The final term of the dispersive Hamiltonian is also of interest. It takes the form of a one-mode squeezing interaction, the sign of which again depends on the state of the qubit through  19. This suggests that the dispersive Hamiltonian may be used to generate non-classical states of the field mode, which is the main focus of the present work.
19. This suggests that the dispersive Hamiltonian may be used to generate non-classical states of the field mode, which is the main focus of the present work.
To begin with, we consider the degree of squeezing intrinsic to the ground state of the dispersive Hamiltonian and, from there, the corresponding approximate ground state of the Rabi Hamiltonian40,66,67,68,69. Noting that  is a constant of motion of the dispersive Hamiltonian, the ground state of Eq. (4) can be readily obtained by diagonalizing it in the subspace of the qubit states |↑〉, |↓〉 which denote, respectively, the + and − eigenstates of
is a constant of motion of the dispersive Hamiltonian, the ground state of Eq. (4) can be readily obtained by diagonalizing it in the subspace of the qubit states |↑〉, |↓〉 which denote, respectively, the + and − eigenstates of  :
:

where

To diagonalize the Hamiltonians  we define a unitary transformation
we define a unitary transformation

where  is a unitary squeezing operator1. Under the action of this unitary transformation the annihilation and creation operators
is a unitary squeezing operator1. Under the action of this unitary transformation the annihilation and creation operators  transform as
transform as


where the squeezing parameter is defined as

After the transformation  is applied, the Hamiltonian of Eq. (5) takes the diagonal form
is applied, the Hamiltonian of Eq. (5) takes the diagonal form

where

The resulting Hamiltonian is that of a harmonic oscillator whose frequency shift is correlated with the qubit state |↑〉 or |↓〉. In order for the shifted oscillator frequency to remain real, it is necessary to have ω ≥ |4ϕ| or, equivalently,  . This places a further restriction on the magnitude of the coupling strength g, which is in addition to the requirement that g ≪ |Δ| in order for the truncation at
. This places a further restriction on the magnitude of the coupling strength g, which is in addition to the requirement that g ≪ |Δ| in order for the truncation at  used in deriving Eq. (3) to be valid. The above condition follows simply from requiring the expression under the square root in Eq. (12) to be positive. Violation of the condition effectively signals the breakdown of the dispersive approximation, which is based on second-order non-degenerate perturbation theory in the interaction term, i.e. g is assumed to be small. This treatment is valid for both Ω ≫ ω and Ω ≪ ω but diverges near resonance. We would like to emphasise that this condition is not directly related to the existence of a ‘critical point’ in the ultrastrong coupling regime of the quantum Rabi model68,69. It is only to do with the validity of the dispersive approximation.
used in deriving Eq. (3) to be valid. The above condition follows simply from requiring the expression under the square root in Eq. (12) to be positive. Violation of the condition effectively signals the breakdown of the dispersive approximation, which is based on second-order non-degenerate perturbation theory in the interaction term, i.e. g is assumed to be small. This treatment is valid for both Ω ≫ ω and Ω ≪ ω but diverges near resonance. We would like to emphasise that this condition is not directly related to the existence of a ‘critical point’ in the ultrastrong coupling regime of the quantum Rabi model68,69. It is only to do with the validity of the dispersive approximation.
The eigenstates of  are simply given by
are simply given by  and
and  . The dispersive Hamiltonian (5) consequently has the corresponding eigenstates
. The dispersive Hamiltonian (5) consequently has the corresponding eigenstates

Hence the ground states of the dispersive Hamiltonians  take a separable form with the cavity field in a squeezed vacuum state.
take a separable form with the cavity field in a squeezed vacuum state.
Since a unitary transformation leaves eigenvalues unchanged, the eigenvalues of the dispersive Hamiltonian may be taken as a direct approximation to the eigenvalues of the full quantum Rabi model. However, the same is not true of the eigenstates70. The dispersive Hamiltonian is related to the full quantum Rabi Hamiltonian by two successive unitary transformations. The eigenstates of the original quantum Rabi model (1) are related to the eigenstates of the dispersive Hamiltonian (5) through the unitary transformations  and
and  :
:

To maintain consistency with the dispersive Hamiltonian (5), which is valid to second order in g, we expand the operator  to first order in
to first order in  (which are proportional to g):
(which are proportional to g):

For  , the corresponding approximate eigenstates of the quantum Rabi model are
, the corresponding approximate eigenstates of the quantum Rabi model are


For Δ > 0 the state  is an approximation to the ground state of the Rabi Hamiltonian; we have numerically confirmed this for the parameter values used throughout the work. The state
is an approximation to the ground state of the Rabi Hamiltonian; we have numerically confirmed this for the parameter values used throughout the work. The state  is a little more intriguing as it corresponds to one of the higher excited states of the quantum Rabi model; which excited state depends on the value of Δ. We have numerically confirmed that for values of g/ω ≤ 0.2,
is a little more intriguing as it corresponds to one of the higher excited states of the quantum Rabi model; which excited state depends on the value of Δ. We have numerically confirmed that for values of g/ω ≤ 0.2,  is an approximation to the nth excited state when n = 4 (Δ = 2), n = 7 (Δ = 5) and n = 12 (Δ = 10).
is an approximation to the nth excited state when n = 4 (Δ = 2), n = 7 (Δ = 5) and n = 12 (Δ = 10).
These states are not separable as the dispersive eigenstates are; rather, they represent entangled states of the qubit and the cavity field. What is more, only the first term in each superposition, albeit the dominant one, contains a squeezed vacuum in the field. The second term is a squeezed number or Fock state, which is an even more highly nonclassical state than the squeezed vacuum. Nevertheless, a squeezed vacuum state of the field may be recovered by making a projective measurement onto the appropriate qubit state. The differences between the dispersive eigenstates and the approximate Rabi eigenstates have important consequences for the generation of squeezed states of the field, as we shall see later on.
In order to quantify the degree of squeezing of the cavity field present in the the dispersive and Rabi ground states, we introduce dimensionless position and momentum quadratures for the mode  :
:

First we consider the ground state in each qubit subspace of the dispersive Hamiltonian,  , for which the variances in the position and momentum quadratures are
, for which the variances in the position and momentum quadratures are


Alternatively, in terms of the squeezing parameter given by Eq. (10) the variances may be written as


It is clear that, for ϕ > 0, i.e. Δ > 0, the squeezing parameter r− (which corresponds to the ground state of Equation (11)) results in noise reduction beyond the standard quantum limit in the momentum quadrature and enhanced fluctuations in the position quadrature. The reverse is true for squeezing parameter r+. Hence the quadrature of squeezing depends on the sign of  .
.
In experiments the degree of squeezing  is commonly expressed in decibels (dB), calculated as
is commonly expressed in decibels (dB), calculated as  . The degree of squeezing present in the ground states of both qubit subspaces of the dispersive Hamiltonian
. The degree of squeezing present in the ground states of both qubit subspaces of the dispersive Hamiltonian  and in the approximate ground state of the Rabi Hamiltonian
and in the approximate ground state of the Rabi Hamiltonian  is plotted in Fig. 2 as a function of the light-matter coupling g for three different values of the detuning Δ. Here and in what follows we concentrate on the case Δ > 0, which gives both a larger degree of squeezing and a larger frequency shift of the cavity field for a given value of |Δ|. Figure 2 shows that the degree of squeezing in the ground state of the dispersive Hamiltonian increases with the coupling g. This is expected since the parameter ϕ which controls the degree of squeezing scales as g2. Similarly, the squeezing is reduced as the detuning Δ increases. Hence there is a tradeoff between the validity of the dispersive approximation, which requires |Δ| ≫ g, and the amount of squeezing that is present in the ground state. In any event, the degree of squeezing of the ground state of the dispersive Hamiltonian (5) is not large,
is plotted in Fig. 2 as a function of the light-matter coupling g for three different values of the detuning Δ. Here and in what follows we concentrate on the case Δ > 0, which gives both a larger degree of squeezing and a larger frequency shift of the cavity field for a given value of |Δ|. Figure 2 shows that the degree of squeezing in the ground state of the dispersive Hamiltonian increases with the coupling g. This is expected since the parameter ϕ which controls the degree of squeezing scales as g2. Similarly, the squeezing is reduced as the detuning Δ increases. Hence there is a tradeoff between the validity of the dispersive approximation, which requires |Δ| ≫ g, and the amount of squeezing that is present in the ground state. In any event, the degree of squeezing of the ground state of the dispersive Hamiltonian (5) is not large,  dB. It can be easily verified that the squeezing parameter |r−| ≥ |r+|, which is why the degree of squeezing of
dB. It can be easily verified that the squeezing parameter |r−| ≥ |r+|, which is why the degree of squeezing of  is marginally higher than the degree of squeezing of
is marginally higher than the degree of squeezing of  .
.
Degree of squeezing  as a function of the light-matter coupling strength g for the dispersive eigenstates
as a function of the light-matter coupling strength g for the dispersive eigenstates  (thin solid, blue)and
(thin solid, blue)and  (thick solid, red), the approximate ground state of the quantum Rabi model
(thick solid, red), the approximate ground state of the quantum Rabi model  (crosses, pink), and the numerically determined ground state of the quantum Rabi model
(crosses, pink), and the numerically determined ground state of the quantum Rabi model  (filled-dots, black) for (a) Δ/ω = 2, (b) Δ/ω = 5, and (c) Δ/ω = 10.
(filled-dots, black) for (a) Δ/ω = 2, (b) Δ/ω = 5, and (c) Δ/ω = 10.
For the sake of comparison the degree of squeezing in the exact ground state of the full quantum Rabi model (1), calculated numerically, is also shown in Fig. 2. From the figure it is evident that as the parameter ϕ decreases both the dispersive ground state  and the approximate Rabi ground state
and the approximate Rabi ground state  better approximate the exact ground state of the quantum Rabi model in terms of capturing the degree of squeezing
better approximate the exact ground state of the quantum Rabi model in terms of capturing the degree of squeezing  . The degree of squeezing in the approximate and the exact ground states of the quantum Rabi model is smaller than the degree of squeezing present in the dispersive states
. The degree of squeezing in the approximate and the exact ground states of the quantum Rabi model is smaller than the degree of squeezing present in the dispersive states  . This can be understood by examining the form of Eq. (16), which is a superposition of a squeezed vacuum state
. This can be understood by examining the form of Eq. (16), which is a superposition of a squeezed vacuum state  and a squeezed n = 1 Fock state
and a squeezed n = 1 Fock state  . For n > 0, the Fock states |n〉 are not states of minimum uncertainty; their variances are given by
. For n > 0, the Fock states |n〉 are not states of minimum uncertainty; their variances are given by  . Therefore the state
. Therefore the state  has variances
has variances  and
and  . Since the n = 0 and n = 1 states are associated with orthogonal qubit components, there is no coherence between them and the overall variances are equal to the sums of the variances of the two squeezed Fock states. As a consequence, both quadrature variances are increased over those of the squeezed vacuum and hence the degree of squeezing of the overall state is reduced.
. Since the n = 0 and n = 1 states are associated with orthogonal qubit components, there is no coherence between them and the overall variances are equal to the sums of the variances of the two squeezed Fock states. As a consequence, both quadrature variances are increased over those of the squeezed vacuum and hence the degree of squeezing of the overall state is reduced.
Squeezing generation through sudden qubit flips
In the previous section we evaluated the degree of squeezing in the respective ground states of the dispersive Hamiltonian and the full quantum Rabi model. Unfortunately, the degree of squeezing  is relatively low even for the largest values of the light-matter coupling strength g for which the dispersive approximation holds. In this section we outline a strategy to significantly improve the amount of squeezing of the oscillator mode. The basis of our protocol is a scheme detailed in ref. 61, which uses sudden changes in the frequency of a harmonic oscillator to generate arbitrarily strong squeezing of the oscillator state. We show that this scheme can be directly realised within the dispersive Hamiltonian, using the interaction of the qubit with the field mode to create the required frequency shifts. The use of a dispersively coupled qubit distinguishes our proposal from that of ref. 63, in which the repeated frequency shift protocol of ref. 61 was shown to produce squeezed states in a nonlinear superconducting oscillator.
is relatively low even for the largest values of the light-matter coupling strength g for which the dispersive approximation holds. In this section we outline a strategy to significantly improve the amount of squeezing of the oscillator mode. The basis of our protocol is a scheme detailed in ref. 61, which uses sudden changes in the frequency of a harmonic oscillator to generate arbitrarily strong squeezing of the oscillator state. We show that this scheme can be directly realised within the dispersive Hamiltonian, using the interaction of the qubit with the field mode to create the required frequency shifts. The use of a dispersively coupled qubit distinguishes our proposal from that of ref. 63, in which the repeated frequency shift protocol of ref. 61 was shown to produce squeezed states in a nonlinear superconducting oscillator.
To begin with we re-express the Hamiltonian (5) in terms of position and momentum coordinates for mode  :
:


so that the dispersive Hamiltonian of Eq. (5) can be written as

Within each qubit subspace the Hamiltonian of the field takes the form of a harmonic oscillator of unit mass and shifted oscillation frequency  . The lowering and raising operators associated with the frequency-shifted potentials are defined as
. The lowering and raising operators associated with the frequency-shifted potentials are defined as


Note that the modes defined by  are not independent: both sets of operators depend on the same underlying position and momentum coordinates, so that
are not independent: both sets of operators depend on the same underlying position and momentum coordinates, so that  . Rather, the frequency-shifted mode operators are related to the original oscillator mode by
. Rather, the frequency-shifted mode operators are related to the original oscillator mode by  .
.
Now we imagine a scenario in which the system is initialized in the ground state of the dispersive Hamiltonian  . At time t = 0 the state of the qubit |ψq〉 is flipped suddenly:
. At time t = 0 the state of the qubit |ψq〉 is flipped suddenly:


The orthogonality of the qubit states |↓〉 and |↑〉 implies that prior to t = 0 the effective Hamiltonian of the field mode is  , whereas for t ≥ 0 the mode evolves under the effective Hamiltonian
, whereas for t ≥ 0 the mode evolves under the effective Hamiltonian  . In other words, since the qubit state determines the frequency shift of the mode, flipping the qubit results in a sudden change in the frequency of the harmonic oscillator.
. In other words, since the qubit state determines the frequency shift of the mode, flipping the qubit results in a sudden change in the frequency of the harmonic oscillator.
It has been shown that a suitably timed sequence of sudden frequency changes is capable of generating arbitrarily large squeezing of a field mode61. In our coupled light-matter system, the dispersive interaction together with qubit flips provides the mechanism for changing the frequency of the field mode. For the sake of completeness we briefly summarize the main steps of the protocol developed in ref. 61 within the context of our system.
We assume that for t < 0 the system is prepared in the ground state of the dispersive Hamiltonian
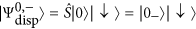 , where |0−〉 is defined as the ground state of the frequency-shifted oscillator potential
, where |0−〉 is defined as the ground state of the frequency-shifted oscillator potential  .
.At t = 0 the qubit is suddenly flipped to its excited state |↑〉. Immediately following the qubit flip, although the expectation values of
 and
and  for the field remain unchanged, the field state is squeezed relative to the new potential
for the field remain unchanged, the field state is squeezed relative to the new potential  .
.The joint state evolves under the Hamiltonian
 for a time duration δT+.
for a time duration δT+.After the time delay δT+, the qubit is suddenly flipped back to its ground state |↓〉. This creates a second sudden frequency jump from ω+ → ω−, following which the state of the field is squeezed with respect to the potential
 .
.The first cycle of the protocol finishes with allowing the joint state to evolve under the Hamiltonian
 for a duration δT−.
for a duration δT−.By carefully choosing δT± and repeating the above steps N times very strong squeezing of the field mode
 can be generated.
can be generated.
These steps are illustrated in Fig. 3. As long as we are working within the dispersive Hamiltonian, the above protocol is directly analogous to the harmonic oscillator with time-dependent frequency envisioned by Janszky and Adam61. Following their Heisenberg-picture analysis, we arrive at the following expressions for the time-evolved operators  after one cycle of the protocol:
after one cycle of the protocol:


The operators for the ω− potential immediately following the second qubit flip are given by


where  are the initial creation and destruction operators before the start of the protocol and
are the initial creation and destruction operators before the start of the protocol and  . The time evolved operators
. The time evolved operators  depend crucially on the choice of δT+. If
depend crucially on the choice of δT+. If  no squeezing is generated by the protocol. Maximal squeezing is obtained when δT+ = (2m + 1)π/2ω+. Likewise, if the protocol is to be further repeated it is critical to choose δT− = (2m + 1)π/2ω−. From now on we therefore fix δT± = π/2ω±. The time evolved position and momentum quadratures defined with respect to the mode with frequency ω− then become
no squeezing is generated by the protocol. Maximal squeezing is obtained when δT+ = (2m + 1)π/2ω+. Likewise, if the protocol is to be further repeated it is critical to choose δT− = (2m + 1)π/2ω−. From now on we therefore fix δT± = π/2ω±. The time evolved position and momentum quadratures defined with respect to the mode with frequency ω− then become


The corresponding variances of the quadrature operators are given by


which clearly illustrates that the protocol decreases quantum noise beyond the standard quantum limit in the momentum quadrature at the expense of increased fluctuations in the position quadrature of the field mode. This protocol can be repeated to produce even greater squeezing: after N cycles the variances are given by  and
and  .
.
Unlike the proposal in ref. 61, the time-dependent frequency changes in our system are achieved via an effective interaction with a qubit. It makes sense, therefore, to consider the squeezing relative to the bare cavity mode with frequency ω and lowering and raising operators  . Following one cycle of the protocol, the time-evolved quadrature operators for the bare cavity mode
. Following one cycle of the protocol, the time-evolved quadrature operators for the bare cavity mode  are related to the operators for the
are related to the operators for the  mode by
mode by


After N cycles of the protocol the variances in the position and momentum quadratures of the bare cavity mode are given by  and
and  , respectively. In the calculations that follow the degree of squeezing
, respectively. In the calculations that follow the degree of squeezing  is always computed with respect to the bare cavity mode.
is always computed with respect to the bare cavity mode.
Figure 4 compares the degree of squeezing present in the ground state  with that obtained after one cycle of the protocol, as a function of the coupling strength g/ω. It can be clearly seen that the protocol using sudden frequency flips can significantly increase the degree of squeezing of the field mode over that naturally present in the ground state.
with that obtained after one cycle of the protocol, as a function of the coupling strength g/ω. It can be clearly seen that the protocol using sudden frequency flips can significantly increase the degree of squeezing of the field mode over that naturally present in the ground state.
The foregoing discussion has been based on the dispersive Hamiltonian and its eigenstates. However, in our system the dispersive Hamiltonian arises as an approximation to the full Rabi Hamiltonian. As the squeezing protocol involves manipulating the state of the system, working with the Rabi Hamiltonian itself will give different results than working with the dispersive Hamiltonian. In order to analyze the outcome of the protocol using the Rabi Hamiltonian, it is useful to work in the Schrödinger picture rather than the Heisenberg picture used previously.
In the Schrödinger picture, one cycle of the protocol based on the dispersive Hamiltonian as described above results in the state

The protocol may be carried out similarly using the Rabi Hamiltonian. For simplicity, we assume that the initial state for the Rabi protocol is the ground state of the Rabi Hamiltonian. As is evident from the approximate solution in Eq. (16), this state is not an eigenstate of the qubit operator  ; rather than being a separable state of qubit and field with the qubit in |↓〉, the Rabi ground state has a component along |↑〉. However, provided that the parameter regime is chosen such that the dispersive approximation holds, the |↑〉 component is small.
; rather than being a separable state of qubit and field with the qubit in |↓〉, the Rabi ground state has a component along |↑〉. However, provided that the parameter regime is chosen such that the dispersive approximation holds, the |↑〉 component is small.
As in the dispersive case, the first step of the protocol is to flip the state of the qubit by applying the  operator. Of course, this does not result in a state that is purely along |↑〉, but again the error induced is small. The flipped state is now allowed to evolve under the full Rabi Hamiltonian for a time δT+. Following this evolution, the qubit is flipped again and the state evolves, again under the full Rabi Hamiltonian, for a time δT−. The evolution time intervals δT± remain the same as in the dispersive case, to a good approximation. This is because the evolution time is related to the differences in energy eigenvalues, which are effectively the same in the dispersive and Rabi cases provided that the parameters are chosen suitably. The resultant state after one cycle of the protocol is then given by
operator. Of course, this does not result in a state that is purely along |↑〉, but again the error induced is small. The flipped state is now allowed to evolve under the full Rabi Hamiltonian for a time δT+. Following this evolution, the qubit is flipped again and the state evolves, again under the full Rabi Hamiltonian, for a time δT−. The evolution time intervals δT± remain the same as in the dispersive case, to a good approximation. This is because the evolution time is related to the differences in energy eigenvalues, which are effectively the same in the dispersive and Rabi cases provided that the parameters are chosen suitably. The resultant state after one cycle of the protocol is then given by

Of course, the protocol may then be repeated multiple times in a similar fashion. Figure 5 shows the results of numerical calculations of the degree of squeezing  that is produced as a function of the number of cycles N for both the dispersive and Rabi cases. It is clear that in both cases the degree of squeezing increases linearly with the number of cycles. The field state produced after 15 cycles of the Rabi protocol is illustrated in Fig. 6, which shows Wigner function plots of the renormalised field components associated with the |↓〉 (a) and |↑〉 (b) qubit states. We define the Wigner function for the field mode to take the following form
that is produced as a function of the number of cycles N for both the dispersive and Rabi cases. It is clear that in both cases the degree of squeezing increases linearly with the number of cycles. The field state produced after 15 cycles of the Rabi protocol is illustrated in Fig. 6, which shows Wigner function plots of the renormalised field components associated with the |↓〉 (a) and |↑〉 (b) qubit states. We define the Wigner function for the field mode to take the following form
 for the dispersive (red, triangles) and Rabi (black, circles) versions of the squeezing protocol, as a function of the number of cycles N.
for the dispersive (red, triangles) and Rabi (black, circles) versions of the squeezing protocol, as a function of the number of cycles N.
where  is the displacement operator, ρRabi is the density matrix corresponding to the cavity field and α = αr + iαm is a complex parameter71. The |↓〉 component of the field closely resembles a squeezed vacuum state, similar to that resulting from the dispersive protocol. More interesting is the |↑〉 component, which is a complicated and strongly nonclassical state that displays multiple peaks and several negative regions in its Wigner function. It should be noted, however, that the amplitude of this component of the overall state is quite small, so while it could in principle be probabilistically selected by a projective measurement on the |↑〉 qubit state, the likelihood of obtaining this state is small. For instance, after 15 cycles of the Rabi protocol the probability associated with the |↓〉 component of the field is close to unity (≈0.993), while the probability for the |↑〉 component of the field to be populated is almost negligible (≈0.007).
is the displacement operator, ρRabi is the density matrix corresponding to the cavity field and α = αr + iαm is a complex parameter71. The |↓〉 component of the field closely resembles a squeezed vacuum state, similar to that resulting from the dispersive protocol. More interesting is the |↑〉 component, which is a complicated and strongly nonclassical state that displays multiple peaks and several negative regions in its Wigner function. It should be noted, however, that the amplitude of this component of the overall state is quite small, so while it could in principle be probabilistically selected by a projective measurement on the |↑〉 qubit state, the likelihood of obtaining this state is small. For instance, after 15 cycles of the Rabi protocol the probability associated with the |↓〉 component of the field is close to unity (≈0.993), while the probability for the |↑〉 component of the field to be populated is almost negligible (≈0.007).
Remarkably, Fig. 5 shows that the protocol using the Rabi Hamiltonian produces considerably more squeezing per cycle (approximately twice as much, for these parameters) than the “ideal” dispersive case. This is particularly surprising since the ground state of the quantum Rabi model shows less squeezing than the dispersive ground state, which can be attributed to the higher variance of the mode state associated with the |↑〉 state of the qubit as discussed previously. Calculations show that the |↓〉 component of the state is squeezed much more strongly after one cycle of the Rabi protocol than predictions based on the dispersive analysis would suggest. The variance in  of the |↑〉 state is also reduced by the squeezing protocol, albeit not below the standard quantum limit of
of the |↑〉 state is also reduced by the squeezing protocol, albeit not below the standard quantum limit of  . However, the overall increase in squeezing in the Rabi case can be attributed to the very large degree of squeezing of the |↓〉 component. Clearly, although the dispersive theory gives good predictions for the energies and the degree of squeezing in the ground state in the quantum Rabi model, it is not particularly good at predicting the results from the Rabi squeezing protocol. The origin of this discrepancy can be traced back to the perturbative nature of the dispersive approximation: the energies are corrected to a higher order in g than the eigenstates. This counterintuitive result highlights the need to be cautious when applying the dispersive approximation in situations where the state of the system is being manipulated70.
. However, the overall increase in squeezing in the Rabi case can be attributed to the very large degree of squeezing of the |↓〉 component. Clearly, although the dispersive theory gives good predictions for the energies and the degree of squeezing in the ground state in the quantum Rabi model, it is not particularly good at predicting the results from the Rabi squeezing protocol. The origin of this discrepancy can be traced back to the perturbative nature of the dispersive approximation: the energies are corrected to a higher order in g than the eigenstates. This counterintuitive result highlights the need to be cautious when applying the dispersive approximation in situations where the state of the system is being manipulated70.
Imperfections in the protocol
In a realistic setting the protocol presented in the previous section will suffer from losses and imperfections. Qubit dephasing and relaxation, cavity losses, timing jitter, and the inability to instantaneously flip the state of the qubit will all affect the outcome of the protocol. We briefly discuss each of these sources of error with an eye toward circuit QED experiments, but their relative contributions will depend on the particular experimental implementation.
In the dispersive version of the protocol, the qubit is always in one of its eigenstates, meaning that the protocol is unaffected by dephasing and only the energy relaxation time T1 needs to be considered. The Rabi case is a little more complicated and qubit dephasing may contribute to noise. However, it is important to note that the qubit need only remain coherent over the evolution time interval δT± rather than throughout the full N cycles of the protocol. To take some numbers relevant to superconducting circuit QED experiments, choosing a cavity frequency ω ~ 1 GHz and a coupling strength g = 0.1ω gives δT± on the order of nanoseconds. Given that superconducting qubits are now routinely achieving relaxation and dephasing times of several tens of microseconds32,33,34,35, it is clear that qubit losses are not expected to be a limiting factor for the protocol or the degree of squeezing that can be achieved.
The loss of photons from the cavity has a more severe effect because the state of the field is built up over successive cycles and therefore must retain coherence over the full N cycles of the protocol. To incorporate photon losses in the squeezing protocol we use a standard master equation approach1, assuming that during the time intervals δT± the field mode couples to a zero temperature reservoir with damping rate Γ. Figure 7 shows the results of a master equation simulation with Γ = 0.01/δT+. In the presence of photon loss the degree of squeezing is no longer linear in the number of cycles N; the additional squeezing generated by another round of the protocol begins to saturate as N increases. However, a substantial increase in squeezing over that present in the initial state can still be obtained. It is worth noting that this value of Γ corresponds to a cavity Q of about 150, which is two orders of magnitude less than Q-factors routinely achieved for microwave resonators in circuit QED29,32,33 and similar to the value recently measured for a qubit-coupled nanomechanical resonator29.
 produced by N cycles of the Rabi protocol.
produced by N cycles of the Rabi protocol.The three lower curves show the effect of photon loss together with three different degrees of timing imperfections: photon loss alone with no timing error (brown, triangles), photon loss plus random timing errors chosen from a Gaussian distribution of width δσ/δΓ± = 0.01 (yellow, crosses), and photon loss plus random timing errors with distribution width δσ/δΓ± = 0.1 (cyan, open circles). For comparison, the ideal case is also shown (black, filled dots). The photon loss rate is Γ = 0.01/δT+; other physical parameters are given by Δ/ω = 2, g/ω = 0.1, Ω/ω = 1 + Δ/ω.
The protocol also requires carefully designed time delays to ensure maximum squeezing of the field mode. In order to model the effect of inaccuracies in timing, we add a random offset ε, chosen from a normal distribution with zero mean and standard deviation δσ, to each time delay δT±. The average degree of squeezing of the field mode  is evaluated by taking an ensemble average over multiple runs of the N-cycle protocol. Figure 7 shows the average degree of squeezing
is evaluated by taking an ensemble average over multiple runs of the N-cycle protocol. Figure 7 shows the average degree of squeezing  when photon losses and random time delay are incorporated in our protocol. When the error in timing is on the order of 1%, the timing jitter has little effect on the degree of squeezing. However, larger timing errors (on the order of 10%) dramatically reduce the degree of squeezing produced. Hence the ability to control the timing of qubit flips to a reasonably precise degree will be important for experimental implementations of our protocol.
when photon losses and random time delay are incorporated in our protocol. When the error in timing is on the order of 1%, the timing jitter has little effect on the degree of squeezing. However, larger timing errors (on the order of 10%) dramatically reduce the degree of squeezing produced. Hence the ability to control the timing of qubit flips to a reasonably precise degree will be important for experimental implementations of our protocol.
The foregoing calculations have relied on the assumption of instantaneous flips of the qubit state, which produce sudden changes in the frequency of the oscillator. A sudden frequency change is of course an idealization for a finite but small switching time  . As long as
. As long as  , a sudden frequency change from ω+ → ω− is a good approximation61. It should be pointed out that
, a sudden frequency change from ω+ → ω− is a good approximation61. It should be pointed out that  ; therefore the requirement for very small values of
; therefore the requirement for very small values of  can be relaxed by decreasing the light-matter coupling g and increasing the number of cycles N to achieve a similar degree of squeezing of the cavity field. Moreover, modifications to the sudden frequency shift scheme of ref. 61 have been discussed in the literature. The case of a sinusoidal frequency modulation was studied in ref. 72, and a Fourier-modified Janszky-Adam scheme for improved nonadiabatic generation of squeezed photons was proposed in ref. 73. While these schemes are not as efficient as the original sudden jump protocol, they are less demanding from an experimental standpoint and still produce significant squeezing of the cavity field.
can be relaxed by decreasing the light-matter coupling g and increasing the number of cycles N to achieve a similar degree of squeezing of the cavity field. Moreover, modifications to the sudden frequency shift scheme of ref. 61 have been discussed in the literature. The case of a sinusoidal frequency modulation was studied in ref. 72, and a Fourier-modified Janszky-Adam scheme for improved nonadiabatic generation of squeezed photons was proposed in ref. 73. While these schemes are not as efficient as the original sudden jump protocol, they are less demanding from an experimental standpoint and still produce significant squeezing of the cavity field.
Discussion
Squeezed light was historically generated through nonlinear optical interactions, but over the years the field has expanded and different physical systems are currently pursued in this direction, including superconducting, microwave and optomechanical cavities. To put things in perspective, impressive experimental advancements have achieved strong squeezing in optical parametric oscillators (12.7 dB)13 and microwave fields (10 dB)14. In this work, we have proposed a new scheme of generating squeezing of a boson field interacting with a qubit under the strong dispersive regime of the quantum Rabi model. Under this interaction, the dispersive frequency shift allows the frequency of the cavity mode to be changed by flipping the state of the qubit. A protocol based on a series of suitably timed sudden frequency jumps can be used to produce an arbitrarily large degree of squeezing in the absence of noise. Even in the presence of a realistic level of noise and experimental imperfections, the degree of squeezing produced under this protocol is comparable to the level of squeezing reported in refs 3 and 15 and, thus, our method of squeezed state generation may find applications in ultra-precise sensing and measurements. We would like to point out that there is no fundamental limit on the maximum degree of squeezing achievable through our protocol, and it will be decided by the limitations of an actual physical implementation. One possible advantage of our method of squeezing generation compared to the use of a parametric amplifier and/or other nonlinearity based methods is that under our protocol the degree of squeezing and the time of generation are directly controlled by the number of frequency shifts applied.
Additional Information
How to cite this article: Joshi, C. et al. Qubit-flip-induced cavity mode squeezing in the strong dispersive regime of the quantum Rabi model. Sci. Rep. 7, 45587; doi: 10.1038/srep45587 (2017).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Walls, D. F. & Milburn, G. J. Quantum Optics (Springer, Berlin, 2007).
Caves, C. M. Quantum-mechanical noise in an interferometer. Phys. Rev. D 23, 1693–1708 (1981).
Taylor, M. A. et al. Biological measurement beyond the quantum limit. Nat Photon 7, 229–233 (2013).
Braunstein, S. L. & van Loock, P. Quantum information with continuous variables. Rev. Mod. Phys. 77, 513–577 (2005).
Aasi, J. et al. Enhanced sensitivity of the LIGO gravitational wave detector by using squeezed states of light. Nat Photon 7, 613–619 (2013).
Yuen, H. P. & Shapiro, J. H. Optical Communication with Two-Photon Coherent States? Part I: Quantum-State Propagation and Quantum-Noise Reduction. IEEE Transactions on Information Theory 24, 657–668 (1978).
Slusher, R. E., Hollberg, L. W., Yurke, B., Mertz, J. C. & Valley, J. F. Observation of Squeezed States Generated by Four-Wave Mixing in an Optical Cavity. Phys. Rev. Lett. 55, 2409–2412 (1985).
Shelby, R. M., Levenson, M. D., Perlmutter, S. H., DeVoe, R. G. & Walls, D. F. Broad-Band Parametric Deamplification of Quantum Noise in an Optical Fiber. Phys. Rev. Lett. 57, 691–694 (1986).
Wu, L.-A., Kimble, H. J., Hall, J. L. & Wu, H. Generation of Squeezed States by Parametric Down Conversion. Phys. Rev. Lett. 57, 2520–2523 (1986).
Loudon, R. & Knight, P. L. Squeezed Light. Journal of Modern Optics 34, 709–759 (1987).
Andersen, U. L., Gehring, T., Marquardt, C. & Leuchs, G. 30 years of squeezed light generation. Physica Scripta 91, 53001 (2016).
Garcés, R. & de Valcárcel, G. J. Strong vacuum squeezing from bichromatically driven Kerrlike cavities: from optomechanics to superconducting circuits. Scientific Reports 6, 21964 (2016).
Eberle, T. et al. Quantum Enhancement of the Zero-Area Sagnac Interferometer Topology for Gravitational Wave Detection. Phys. Rev. Lett. 104, 251102 (2010).
Castellanos-Beltran, M. A., Irwin, K. D., Hilton, G. C., Vale, L. R. & Lehnert, K. W. Amplification and squeezing of quantum noise with a tunable Josephson metamaterial. Nat Phys 4, 929–931 (2008).
Purdy, T. P., Yu, P.-L., Peterson, R. W., Kampel, N. S. & Regal, C. A. Strong Optomechanical Squeezing of Light. Phys. Rev. X 3, 31012 (2013).
Pirkkalainen, J.-M., Damskägg, E., Brandt, M., Massel, F. & Sillanpää, M. A. Squeezing of quantum noise of motion in a micromechanical resonator. Phys. Rev. Lett. 115, 243601 (2015).
Lecocq, F., Clark, J. B., Simmonds, R. W., Aumentado, J. & Teufel, J. D. Quantum nondemolition measurement of a nonclassical state of a massive object. Phys. Rev. X 5, 041037 (2015).
Wollman, E. E. et al. Quantum squeezing of motion in a mechanical resonator. Science 349, 952–955 (2015).
Zueco, D., Reuther, G. M., Kohler, S. & Hänggi, P. Qubit-oscillator dynamics in the dispersive regime: Analytical theory beyond the rotating-wave approximation. Phys. Rev. A 80, 33846 (2009).
Kurizki, G. et al. Quantum technologies with hybrid systems. Proceedings of the National Academy of Sciences of the United States of America 112, 3866–73 (2015).
Xiang, Z.-L., Ashhab, S., You, J. Q. & Nori, F. Hybrid quantum circuits: Superconducting circuits interacting with other quantum systems. Rev. Mod. Phys. 85, 623–653 (2013).
Devoret, M. H. & Schoelkopf, R. J. Superconducting Circuits for Quantum Information: An Outlook. Science 339, 1169–1174 (2013).
Rabi, I. I. On the Process of Space Quantization. Phys. Rev. 49, 324–328 (1936).
Rabi, I. I. Space Quantization in a Gyrating Magnetic Field. Phys. Rev. 51, 652–654 (1937).
Jaynes, E. T. & Cummings, F. W. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proceedings of the IEEE 51, 89–109 (1963).
Blatt, R. & Roos, C. F. Quantum simulations with trapped ions. Nat Phys 8, 277–284 (2012).
Pedernales, J. S. et al. Quantum Rabi Model with Trapped Ions. Scientific Reports 5, 15472 (2015).
Irish, E. K. & Schwab, K. Quantum measurement of a coupled nanomechanical resonator\char21{}Cooper-pair box system. Phys. Rev. B 68, 155311 (2003).
Rouxinol, F. et al. Measurements of nanoresonator-qubit interactions in a hybrid quantum electromechanical system. Nanotechnology 27, 364003 (2016).
Blais, A., Huang, R.-S., Wallraff, A., Girvin, S. M. & Schoelkopf, R. J. Cavity quantum electrodynamics for superconducting electrical circuits: An architecture for quantum computation. Phys. Rev. A 69, 62320 (2004).
Wallraff, A. et al. Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics. Nature 431, 162–167 (2004).
Rigetti, C. et al. Superconducting qubit in a waveguide cavity with a coherence time approaching 0.1 ms. Phys. Rev. B 86, 100506 (2012).
Barends, R. et al. Coherent Josephson Qubit Suitable for Scalable Quantum Integrated Circuits. Phys. Rev. Lett. 111, 80502 (2013).
Braumüller, J. et al. Concentric transmon qubit featuring fast tunability and an anisotropic magnetic dipole moment. Applied Physics Letters 108 (2016).
Yan, F. et al. The Flux Qubit Revisited. arXiv 1508.06299.
Neu, P. & Silbey, R. J. Tunneling in a cavity. Phys. Rev. A 54, 5323–5326 (1996).
Bishop, R. F. & Emary, C. Time evolution of the Rabi Hamiltonian from the unexcited vacuum. Journal of Physics A: Mathematical and General 34, 5635 (2001).
Irish, E. K., Gea-Banacloche, J., Martin, I. & Schwab, K. C. Dynamics of a two-level system strongly coupled to a high-frequency quantum oscillator. Phys. Rev. B 72, 195410 (2005).
Johansson, G., Tornberg, L. & Wilson, C. M. Fast quantum limited readout of a superconducting qubit using a slow oscillator. Phys. Rev. B 74, 100504 (2006).
Larson, J. Dynamics of the Jaynes? Cummings and Rabi models: old wine in new bottles. Physica Scripta 76, 146 (2007).
Irish, E. K. Generalized Rotating-Wave Approximation for Arbitrarily Large Coupling. Phys. Rev. Lett. 99, 173601 (2007).
Hausinger, J. & Grifoni, M. Dissipative dynamics of a biased qubit coupled to a harmonic oscillator: analytical results beyond the rotating wave approximation. New Journal of Physics 10, 115015 (2008).
Forn-Díaz, P. et al. Ultrastrong coupling of a single artificial atom to an electromagnetic continuum. arXiv 1602.00416.
Yoshihara, F. et al. Superconducting qubit-oscillator circuit beyond the ultrastrong-coupling regime. arXiv 1602.00415.
Yoshihara, F. et al. Characteristic spectra of circuit quantum electrodynamics systems from the ultrastrong to the deep strong coupling regime. arXiv 1612.00121.
Niemczyk, T. et al. Circuit quantum electrodynamics in the ultrastrong-coupling regime. Nat Phys 6, 772–776 (2010).
Solano, E. The dialogue between quantum light and matter. Physics 4, 68 (2011).
Casanova, J., Romero, G., Lizuain, I., Garca-Ripoll, J. J. & Solano, E. Deep Strong Coupling Regime of the Jaynes-Cummings Model. Phys. Rev. Lett. 105, 263603 (2010).
Peropadre, B., Forn-Díaz, P., Solano, E. & Garca-Ripoll, J. J. Switchable Ultrastrong Coupling in Circuit QED. Phys. Rev. Lett. 105, 023601 (2010).
Braak, D. Integrability of the Rabi Model. Phys. Rev. Lett. 107, 100401 (2011).
You, J. Q. & Nori, F. Atomic physics and quantum optics using superconducting circuits. Nature 474, 589–597 (2011).
Nataf, P. & Ciuti, C. Protected Quantum Computation with Multiple Resonators in Ultrastrong Coupling Circuit QED. Phys. Rev. Lett. 107, 190402 (2011).
Ballester, D., Romero, G., Garca-Ripoll, J. J., Deppe, F. & Solano, E. Quantum Simulation of the Ultrastrong-Coupling Dynamics in Circuit Quantum Electrodynamics. Phys. Rev. X 2, 21007 (2012).
Schiró, M., Bordyuh, M., Öztop, B. & Türeci, H. E. Phase Transition of Light in Cavity QED Lattices. Phys. Rev. Lett. 109, 53601 (2012).
Schiró, M. et al. Exotic Attractors of the Nonequilibrium Rabi-Hubbard Model. Phys. Rev. Lett. 116, 143603 (2016).
Joshi, C., Larson, J. & Spiller, T. P. Quantum state engineering in hybrid open quantum systems. Phys. Rev. A 93, 43818 (2016).
Lo, C. F. Squeezing by tuning the oscillator frequency. Journal of Physics A: Mathematical and General 23, 1155–1165 (1990).
Agarwal, G. S. & Kumar, S. A. Exact quantum-statistical dynamics of an oscillator with time-dependent frequency and generation of nonclassical states. Phys. Rev. Lett. 67, 3665–3668 (1991).
Rashid, M. et al. Experimental Realisation of a Thermal Squeezed State of Levitated Optomechanics 10, 1–6 (2016).
Janszky, J. & Yushin, Y. Y. Squeezing via frequency jump. Opt. Commun. 59, 30–33 (1986).
Janszky, J. & Adam, P. Strong squeezing by repeated frequency jumps. Phys. Rev. A 46, 6091–6092 (1992).
Dodonov, V. V., Man’ko, O. V. & Man’ko, V. I. Time-dependent oscillator with Kronig-Penney excitation. Physics Letters A 175, 1–4 (1993).
Zagoskin, A. M., Il’ichev, E., McCutcheon, M. W., Young, J. F. & Nori, F. Controlled Generation of Squeezed States of Microwave Radiation in a Superconducting Resonant Circuit. Phys. Rev. Lett. 101, 253602 (2008).
Didier, N., Qassemi, F. & Blais, A. Perfect squeezing by damping modulation in circuit quantum electrodynamics. Phys. Rev. A 89, 13820 (2014).
Elliott, M. & Ginossar, E. Enhancement and state tomography of a squeezed vacuum with circuit quantum electrodynamics. Phys. Rev. A 92, 13826 (2015).
Chen, H., Zhang, Y.-M. & Wu, X. Variational ground state of the model of a two-state system coupled with phonons. Phys. Rev. B 40, 11326–11327 (1989).
Sandu, T., Chihaia, V. & Kirk, W. P. Dynamic squeezing in a single-mode boson field interacting with two-level system. Journal of Luminescence 101, 101–104 (2003).
Ashhab, S. & Nori, F. Qubit-oscillator systems in the ultrastrong-coupling regime and their potential for preparing nonclassical states. Phys. Rev. A 81, 42311 (2010).
Ashhab, S. Superradiance transition in a system with a single qubit and a single oscillator. Phys. Rev. A 87, 13826 (2013).
Govia, L. C. G. & Wilhelm, F. K. Entanglement generated by the dispersive interaction: The dressed coherent state. Phys. Rev. A 93, 12316 (2016).
Barnett, S. M. & Radmore, P. M. Methods in Theoretical Quantum Optics (Oxford University Press, Oxford, 1997).
Wilson, C. M. et al. Observation of the dynamical Casimir effect in a superconducting circuit. Nature 479, 376–379 (2011).
Matsuo, S., Fujii, T. & Hatakenaka, N. Nonadiabatic squeezed-photon generation by a Fourier-modified Janszky-Adam scheme. Physica B: Condensed Matter 468–469, 57–60 (2015).
Acknowledgements
C.J. is supported by a York Centre for Quantum Technologies (YCQT) Fellowship. We would like to acknowledge useful discussions with Borja Peropadre, Frank Deppe, Eran Ginossar, Matthew Elliott, and Matt LaHaye. TPS acknowledges support from EPSRC grant EP/I038683/1.
Author information
Authors and Affiliations
Contributions
C.J. and E.K.I. conceived the idea and carried out the calculations. T.P.S. supervised the work. All the authors discussed the results and contributed to the preparation of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Joshi, C., Irish, E. & Spiller, T. Qubit-flip-induced cavity mode squeezing in the strong dispersive regime of the quantum Rabi model. Sci Rep 7, 45587 (2017). https://doi.org/10.1038/srep45587
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep45587
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.



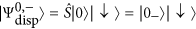 , where |0−〉 is defined as the ground state of the frequency-shifted oscillator potential
, where |0−〉 is defined as the ground state of the frequency-shifted oscillator potential  .
. and
and  for the field remain unchanged, the field state is squeezed relative to the new potential
for the field remain unchanged, the field state is squeezed relative to the new potential  .
. for a time duration δT+.
for a time duration δT+. .
. for a duration δT−.
for a duration δT−. can be generated.
can be generated.

 is also shown (solid). Other physical parameters include: Δ/ω = 2, Ω/ω = 1 + Δ/ω.
is also shown (solid). Other physical parameters include: Δ/ω = 2, Ω/ω = 1 + Δ/ω.

