Abstract
We present a class of gauge-invariant models of quantum electrodynamics with nonlocal interaction. The models have translation, Lorentz and gauge invariance and reduce to the conventional local quantum electrodynamics under the appropriate limit conditions, both the equations of motion of the charged particle and electromagnetic field obtained by the action principle lead to the normal form of current conservation. Quantization of the models is realized by taking advantage of the formalism based on the Yang-Feldman equations and the Lehmann-Symanzik-Zimmermann reduction formulas. Finally, we employ a special choice of the models to calculate the vacuum polarization as an example to demonstrate the possibility of establishing a theory of quantum electrodynamics without divergence.
Similar content being viewed by others
Introduction
There is a large literature on nonlocal field theory (for a review and references, see refs 1, 2). One of the motivations for investigating nonlocal field theory is to establish a theory without divergence; since the renormalized theory of local gauge fields leads to finite predictions and to an unprecedented agreement between theory and experiment, if divergences still appear in the corresponding nonlocal theory and must still be eliminated by a renormalization procedure, then such a nonlocal field theory is not interesting.
Of course, according to the contemporary point of view, any field theory must be renormalized; if a nonlocal field theory involves finite renormalization constants, then such a theory accords with the contemporary point of view and standard mathematical theory at the same time, since standard mathematical theory allows ignoring small or finite quantities (but ignoring an infinitely large quantity does not accord with standard mathematical theory)3.
Some models of quantum electrodynamics (QED) with nonlocal interaction have been proposed4,5,6. In this paper, we present a class of models of QED with nonlocal interaction.
After looking back on some known nonlocal models of QED, we present the action of a class of models and the equations of motion of a charged particle and electromagnetic field obtained by the action principle. Translation, Lorentz and gauge invariance of the models are proved, and we prove that both the equations of motion of a charged particle and electromagnetic field lead to the normal form of current conservation. The models are reduced to the conventional local QED under the appropriate limit condition.
Similar to some known nonlocal modes of QED, for guaranteeing the gauge invariance of the theory, the form of the models presented in this paper is far from that of conventional field theory.
Next, based on the fact that a free charged particle and free electromagnetic field still obey the local Dirac equation and the local Maxwell equation of free fields, respectively, quantization of the model is realized by taking advantage of the formalism based on the Yang-Feldman equations and the Lehmann-Symanzik-Zimmermann reduction formulas. Some properties, e.g., Lorentz and gauge invariance, unitarity and causality of the elements of the S-matrix, are discussed.
The models presented in this paper provide a wide range of choices; we employ a special choice of the models to calculate the vacuum polarization as an example to show the possibility of establishing a theory of QED without divergence.
All symbols and conventions of this paper follow ref. 7, for example, gαβ = gαβ = diag (+1, −1, −1, −1) and A · B = AλBλ = A0B0 − A · B .
Looking back on models of quantum electrodynamics with nonlocal interaction
As is well known, the action of the conventional local QED is

where



In (3),  . The theory is invariant under the gauge transformation
. The theory is invariant under the gauge transformation

where θ(x) is an arbitrary scalar function. The relation between the two functions χ(x) and θ(x) in (4) reads

and both the equations of motion of the charged particle and electromagnetic field obtained by the action principle lead to the current-conservation equation

Since  given by (3) can be written in the form
given by (3) can be written in the form  , by replacing δ4(x − y) by a scalar function f(x − y), which is independent of ψ(x) and Aμ(x),
, by replacing δ4(x − y) by a scalar function f(x − y), which is independent of ψ(x) and Aμ(x),  becomes
becomes

Thus, H. McManus in ref. 4 establishes a model of QED with nonlocal interaction, of which the action is  , where SEM, Se and
, where SEM, Se and  are given by (1), (2) and (7), respectively. H. McManus in ref. 4 proves that the theory is invariant under the gauge transformation (4), but now, the relation between the two functions χ(x) and θ(x) in (4) reads
are given by (1), (2) and (7), respectively. H. McManus in ref. 4 proves that the theory is invariant under the gauge transformation (4), but now, the relation between the two functions χ(x) and θ(x) in (4) reads

Specifically, by choosing  , where r0 is a constant, a theory of classical electrodynamics without singularities is obtained in ref. 4. However, M. Chretien and R. E. Peierls in ref. 5 point out that this theory is incapable of removing the divergence of the vacuum polarization in the corresponding quantum theory.
, where r0 is a constant, a theory of classical electrodynamics without singularities is obtained in ref. 4. However, M. Chretien and R. E. Peierls in ref. 5 point out that this theory is incapable of removing the divergence of the vacuum polarization in the corresponding quantum theory.
On the other hand,  , in which Se and
, in which Se and  are given by (2) and (3), respectively, can be written in the form 8
are given by (2) and (3), respectively, can be written in the form 8

where the integral  is taken over the straight line in space-time joining xρ and yρ. By replacing δ4(x − y) in (9) by a scalar function f(x − y), which is independent of ψ(x) and Aμ(x), M. Chretien and R. E. Peierls in ref. 5 establish a different model of nonlocal QED, of which the action is
is taken over the straight line in space-time joining xρ and yρ. By replacing δ4(x − y) in (9) by a scalar function f(x − y), which is independent of ψ(x) and Aμ(x), M. Chretien and R. E. Peierls in ref. 5 establish a different model of nonlocal QED, of which the action is  , where SEM is still given by (1), and
, where SEM is still given by (1), and

Although the form of this theory is far from that of conventional field theory, the theory is still invariant under the gauge transformation (4) and (5). For this theory, current conservation is no longer the normal form (6), and there still exist divergences in the theory5.
K. Scharnhorst in ref. 6 investigates a generalization of the above theory, of which the action is  , where SEM is still given by (1), and
, where SEM is still given by (1), and

Class of models of quantum electrodynamics with nonlocal interaction
A generalization of (7) is to replace xλ and yλ in the function f(xλ − yλ) in (7) by two four-vector functions Uλ(x) and Vλ(y), respectively,  thus becomes
thus becomes

However, we can prove that the theory whose action is  , where SEM, Se and
, where SEM, Se and  are given by (1), (2) and (12), respectively, breaks gauge invariance, no matter how the relation between the two functions χ(x) and θ(x) in (4) is chosen.
are given by (1), (2) and (12), respectively, breaks gauge invariance, no matter how the relation between the two functions χ(x) and θ(x) in (4) is chosen.
In order to restore gauge invariance, for the two functions Uμ(x) and Vμ(y), we introduce

If we regard  and
and  as two 4 × 4 matrices, then we ask that both the corresponding determinants U(x) and V(y) do not vanish:
as two 4 × 4 matrices, then we ask that both the corresponding determinants U(x) and V(y) do not vanish:

Hence, the corresponding inverse matrices  and
and  exist and satisfy
exist and satisfy

Taking advantage of the functions  , V(y) and
, V(y) and  corresponding to Uμ(x) and Vμ(y), respectively, we construct an interaction action
corresponding to Uμ(x) and Vμ(y), respectively, we construct an interaction action

We ask that f(z) be independent of ψ(x) and Aμ(x); Uμ(x) and Vμ(y) can be dependent on ψ(x) and Aμ(x), but both of them are invariant under the transformation (4). Under these conditions, we now prove that the action SEM + Se + SI, where SEM, Se and SI are given by (1), (2) and (16), respectively, is invariant under the gauge transformation (4), but now, the relation between the two functions χ(x) and θ(x) in (4) reads

At first, it is easy to obtain that under the transformation (4), the sum of  and
and  , in which the field quantities are
, in which the field quantities are  and ψ′(x), becomes
and ψ′(x), becomes

On the other hand, under the transformation (4), j′α(x) = jα(x) and  are invariant, because f(z) is independent of ψ(x) and Aμ(x), and both Uμ(x) and Vμ(y) are invariant; therefore, under the transformation (4),
are invariant, because f(z) is independent of ψ(x) and Aμ(x), and both Uμ(x) and Vμ(y) are invariant; therefore, under the transformation (4),  , in which the field quantities are
, in which the field quantities are  and ψ′(x), becomes
and ψ′(x), becomes

where SI is expressed by (16), and

In the last section of this paper, we shall prove

Thus, the last term in (20) vanishes; by an integration by parts with respect to yλ, ΔSI becomes

In the last section of this paper, we shall prove

Substituting (23) into (22) and using some of the formulas in (15), ΔSI becomes

Combining (18) with (19), and using (24), we obtain

thus, if the function χ(x) is as introduced by (17), then we obtain  ; this means that the action SEM + Se + SI is invariant under the gauge transformation (4) and (17).
; this means that the action SEM + Se + SI is invariant under the gauge transformation (4) and (17).
It is obvious that the action SEM + Se + SI has Lorentz invariance; therefore, SEM + Se + SI is Lorentz and gauge invariant. However, if both Uμ(x) and Vμ(y) are independent of ψ(x) and Aμ(x), then it is difficult to find two functions Uμ(x) and Vμ(y) such that SEM + Se + SI has translation invariance. Contrarily, if Uμ(x) and Vμ(y) are dependent on ψ(x) or Aμ(x), then it is easy to choose Uμ(x) and Vμ(y) such that SEM + Se + SI has translation invariance.
For example, if we take

where a′, a and bk are all constants (some constants can be zero), and  and Wk(y − y′) are independent of ψ(x) and Aμ(x), then it is obvious that uλ(x) and vλ(y), as well as Uμ(x) and Vμ(y), are invariant under the transformation (4), and both Uμ(x) and Vμ(y) satisfy (14). Besides these properties, according to translation invariance of the field quantities ψ(x) and Aμ(x), and using
and Wk(y − y′) are independent of ψ(x) and Aμ(x), then it is obvious that uλ(x) and vλ(y), as well as Uμ(x) and Vμ(y), are invariant under the transformation (4), and both Uμ(x) and Vμ(y) satisfy (14). Besides these properties, according to translation invariance of the field quantities ψ(x) and Aμ(x), and using

we can prove that SEM + Se + SI has translation invariance.
Of course, besides (25), there are many choices for Uμ(x) and Vμ(y) such that SEM + Se + SI has translation invariance.
On the other hand, in the appropriate limit, SEM + Se + SI should reduce to the conventional local QED. This condition can be realized very easily; for example,  in the limit a′ → 0, a → 0 in (25) and f(z) → δ4(z).
in the limit a′ → 0, a → 0 in (25) and f(z) → δ4(z).
Although the function f(z) in (7), (10) and (16) seems to be arbitrary, it must satisfy f(z) → δ4(z); hence, all different forms of f(z) have the same feature. On the other hand, the characteristics of SEM + Se + SI vary with the forms of the two functions Uμ(x) and Vμ(y) in (16); therefore, SEM + Se + SI represents a class of models rather than a single model.
We now take

in (25) and f(z) = δ4(z) as an example to show some properties of the corresponding equations of motion of a charged particle and electromagnetic field. For this choice, (16) becomes

where Vλ(y) is given by (25) and (26), i.e.,

V(y) and  are given by (58) and (59), respectively, in the last section of this paper, and vλ(y) in (58) and (59) is given by (26).
are given by (58) and (59), respectively, in the last section of this paper, and vλ(y) in (58) and (59) is given by (26).
From the action SEM + Se + SI(1) and the action principle, we obtain the equations of motion of the electromagnetic field and charged particle:



It is obvious that (28) is invariant under the transformation given in (4) and (17). By the same method as in the proof that the action SEM + Se + SI is invariant under the gauge transformation (4) and (17), we can prove that (29) has the same gauge invariance.
It is easy to prove that the equation of motion (29) of a charged particle leads to the current conservation (6); on the other hand, as is well known, a very important and basic property of the equation of motion of the electromagnetic field  of the conventional local QED is that which leads to the current conservation (6) by the approach
of the conventional local QED is that which leads to the current conservation (6) by the approach  . We prove that (28) has the same property.
. We prove that (28) has the same property.
From (28), we have

according to (21), the first term in the last expression of (31) vanishes; according to (23), we have  . Thus (31) becomes
. Thus (31) becomes

where we have used some of the formulas in (15) and performed integration by parts with respect to xλ. From the above result, we obtain the current conservation (6).
In the above discussions, Uμ(x) and Vμ(y) are mainly dependent on ψ and  ; on the other hand, Uμ(x) and Vμ(y) can be dependent on Aλ alone. For example, if we take uλ(x) = 0 and
; on the other hand, Uμ(x) and Vμ(y) can be dependent on Aλ alone. For example, if we take uλ(x) = 0 and  in (25) and f(z) = δ4(z), where
in (25) and f(z) = δ4(z), where  is the transverse four-vector corresponding to electromagnetic four-potential Aμ, whose formal definition can be found in ref. 9,10, then (16) becomes
is the transverse four-vector corresponding to electromagnetic four-potential Aμ, whose formal definition can be found in ref. 9,10, then (16) becomes

where V(y) and  are still given by (58) and (59), respectively, in the last section of this paper, but now in (58) and (59),
are still given by (58) and (59), respectively, in the last section of this paper, but now in (58) and (59),  .
.
For this case, from the action SEM + Se + SI(2), we obtain the equations of motion of the charged particle and electromagnetic field:


where Jμ(y) is given by (28),  is the transverse four-vector corresponding to Kμ(y), and
is the transverse four-vector corresponding to Kμ(y), and

The action SEM + Se + SI(2) and two equations of motion (32) and (33) are invariant under the gauge transformation (4) and (17), since the transverse four-vector  is invariant under the gauge transformation (4); besides, it is easy to prove that the equation of motion (32) of the charged particle leads to the current conservation (6), and, using the above method that proves that (28) leads to (6), we can prove that the equation of motion of the electromagnetic field (33) leads to (6).
is invariant under the gauge transformation (4); besides, it is easy to prove that the equation of motion (32) of the charged particle leads to the current conservation (6), and, using the above method that proves that (28) leads to (6), we can prove that the equation of motion of the electromagnetic field (33) leads to (6).
Similar to (9), it is easy to prove that Se + SI can be written in the form

hence, similar to (10), by replacing δ4(x − y) in the above formula by a scalar function g(x − y) that is independent of ψ(x) and Aμ(x), we can establish a class of models of nonlocal QED, of which the action is SEM + Se−I, where SEM is still given by (1), and

We can further extend the above action in terms of (11).
Quantization of the models
From (28) and (29), or (32) and (33), we see that the free charged particle and free electromagnetic field still obey the local Dirac equation and the local Maxwell equation of free fields, respectively. The models thus belong to the so-called “theory with nonlocal interaction”. For this theory, so far, the unique method of quantization is to employ the formalism based on the Yang-Feldman equations11,12. Here, we list only the main steps of quantization of the models as follows. In the last step, we include brief discussions, since we shall employ the Lehmann-Symanzik-Zimmermann reduction formulas instead of the S-matrix.
The method of quantization works in the Heisenberg Picture; for simplicity, we employ the Coulomb gauge ∇ · A = 0 for electromagnetic four-potential Aμ.
I “in” and “out” fields and the Fock space.
The field operators ψin(out)(x),  and
and  of the “in” and “out” fields satisfy the equations
of the “in” and “out” fields satisfy the equations  ,
,  , and ∇ · Ain(out)(y) = 0, respectively, for which the concrete expressions are given by (13.50) and (14.33) in ref. 7. All states of the corresponding Fock space are generated by repeatedly acting with the creation operators
, and ∇ · Ain(out)(y) = 0, respectively, for which the concrete expressions are given by (13.50) and (14.33) in ref. 7. All states of the corresponding Fock space are generated by repeatedly acting with the creation operators  ,
,  and
and  in the expressions of ψin(out)(x),
in the expressions of ψin(out)(x),  and
and  on the vacuum state
on the vacuum state  .
.
II The asymptotic conditions and the Yang-Feldman equations.
Using the idea of “weak convergence”7,13,14, the asymptotic conditions for the field operators ψ(x),  and A (y) read:
and A (y) read:

And, furthermore, considering the asymptotic conditions (35), from the equations of motion (30) and (28) we obtain the Yang-Feldman equations7:



In (38), Jtr(y) is the transverse three-vector corresponding to Jμ(y) introduced by (28). If the equations of motion of the charged particle and electromagnetic field are (32) and (33), respectively, then it is easy to write out the corresponding Yang-Feldman equations, similar to (36)~(38); besides, under the Coulomb gauge and the asymptotic conditions (35), the transverse four-vector  corresponding to Aμ reads
corresponding to Aμ reads

III The Lehmann-Symanzik-Zimmermann (LSZ) reduction formulas
The last step of the method of quantization employing the formalism based on the Yang-Feldman equations is to introduce the S-matrix by

some examples of calculating the S-matrix in terms of (39) can be found in refs 15, 16.
However, generally speaking, for infinite-dimensional matrices ψin(out)(x),  and Ain(out)(y), perhaps such a matrix S does not exist7,13; even if it exists, it may not be unitary11.
and Ain(out)(y), perhaps such a matrix S does not exist7,13; even if it exists, it may not be unitary11.
Conversely, for the theory with nonlocal interaction, we can prove that the LSZ reduction formulas7,13,14 still hold. Hence, we employ the LSZ reduction formulas instead of the S-matrix to calculate the transition amplitude. For example, for the case that the initial and final states are an electron, the corresponding transition amplitude is

Substituting the field operators ψ(x) and  obtained from (36)~(38) by an iterative method into (40), we can calculate the transition amplitude 〈( p ′, r′)out|( p , r)in〉.
obtained from (36)~(38) by an iterative method into (40), we can calculate the transition amplitude 〈( p ′, r′)out|( p , r)in〉.
A question naturally arises from the above discussions: now that the transition amplitude is only an element of the S-matrix, if the S-matrix defined by (39) does not exist, or exists but is not unitary, then is the transition amplitude determined by the LSZ reduction formula correct?
Here, we only address this question briefly. Notice that there are in fact two types of S-matrices: one is defined based on operators, e.g., introduced by (39); the other is defined based on a state vector7,13,14 whose element, i.e., transition amplitude, can be determined by the LSZ reduction formula. The differences between the two types of S-matrices are subtle. For example, the asymptotic conditions (35) based on operators are in fact incorrect; the correct forms of the asymptotic conditions are based on the state vector7,13,14:

(The exact expressions of the asymptotic conditions can be found in ref. 14, e.g., the formulas 7(106a) and 7(106b) in ref. 14). And, thus, instead of (36)~(38), the correct forms of the Yang-Feldman equations should be14

etc. Hence, regardless of whether the S-matrix based on operators exists, we can introduce the type of S-matrix based on the state vector, and, in addition, take advantage of the LSZ reduction formula to determine the element of this type of S-matrix, i.e., the transition amplitude.
We therefore obtain a complete quantum theory of the models of QED with nonlocal interaction, as presented in the above section.
However, although we employ the LSZ reduction formulas instead of the S-matrix, basic principles such as Lorentz and gauge invariance, unitarity and causality of the S-matrix must be satisfied, of course. We now ask that the elements of S-matrix, i.e., transition amplitude, satisfy these principles. And, furthermore, according to the LSZ reduction formulas, the question of whether the elements of the S-matrix satisfy these principles is reduced to investigating the properties of such Green functions as  .
.
For example, it is obvious that if such Green functions as  are Lorentz and gauge invariant, then the elements of the S-matrix are as well. And, the condition of unitarity corresponding to that of the S-matrix is now
are Lorentz and gauge invariant, then the elements of the S-matrix are as well. And, the condition of unitarity corresponding to that of the S-matrix is now  , which also leads to the investigation of the properties of such Green functions as
, which also leads to the investigation of the properties of such Green functions as  .
.
As for the condition of causality of the S-matrix, following N. N. Bogoliubov and D. V. Shirkov17, we write the interaction action (16) in the form

where 0 ≤ g(x) ≤ 1. When g(x) = 0, the interaction does not exist; when 0 < g(x) < 1, the interaction is joined partly; when g(x) = 1, the interaction is joined fully. Because the function g(x) appears in SI, it will appear in the equations of motion of the charged particle and electromagnetic field, and, additionally, in such Green functions as  and the elements of the S-matrix 〈β|S(g)|α〉. Therefore, determining whether the elements of the S-matrix satisfy the condition of causality
and the elements of the S-matrix 〈β|S(g)|α〉. Therefore, determining whether the elements of the S-matrix satisfy the condition of causality

which corresponds to the condition of causality of the S-matrix given by ref. 17 (see the formula (17.30) in ref. 17), is still reduced to investigating the properties of such Green functions as  .
.
On the other hand, experiences with some known theories show that the properties mentioned above of Green functions can be investigated only after the theories are researched deeply. For example, if we employ the Coulomb gauge in the conventional local QED, then Lorentz and gauge invariance of the elements of the S-matrix can be proved only after the rules of the Feynman diagrams of the theory are obtained (see ref. 7, Chapter 17). A different example is unitarity of the S-matrix of the theory of the non-Abelian gauge field: although as early as 1963, R. P. Feynman pointed out that one must add some additive terms in the theory of the non-Abelian gauge field to guarantee unitarity of the S-matrix under Feynman gauge18, and even though a general approach of adding additive terms was given by L. Fadeev and V. N. Popov19, the unitarity of the S-matrix of the theory of the non-Abelian gauge field can be proved only after Slavnov-Taylor identities are established.
What should we do when the models presented in this paper do not satisfy unitarity or (and) causality? A revelation from the theory of the non-Abelian gauge field is that, if the elements of the S-matrix of the models presented in this paper do not satisfy unitarity or (and) causality, then maybe we can add some appropriate additive terms to restore unitarity and causality, similarly to the addition of ghost fields to restore the unitarity of the S-matrix in the theory of the non-Abelian gauge field. These questions will be studied further.
Calculation result of the vacuum polarization
Concrete calculation of the transition amplitude based on the LSZ reduction formula is lengthy and complex even for the conventional local QED. For example, for the conventional local QED, (correspondingly, Φα = Aα and Jμ = jμ in (36)~(38)), in order to obtain the self energy of the electron and the vacuum polarization in terms of (40), we must calculate the field operators ψ(x) and  in terms of (36)~(38) by an iterative method up to second-order and third-order approximations, respectively. Of course, the vacuum polarization can be obtained from the self energy of the photon, but for this, we still must calculate the field operator A (x) in terms of (36)~(38) by an iterative method up to second-order approximation. On the other hand, G. Källén in ref. 20 presents an approach to obtain the vacuum polarization for the conventional local QED: the approach is to calculate the linear response of the vacuum expectation value of current to an external electromagnetic field without using the LSZ reduction formula; one only needs to calculate the field operators ψ(x) and
in terms of (36)~(38) by an iterative method up to second-order and third-order approximations, respectively. Of course, the vacuum polarization can be obtained from the self energy of the photon, but for this, we still must calculate the field operator A (x) in terms of (36)~(38) by an iterative method up to second-order approximation. On the other hand, G. Källén in ref. 20 presents an approach to obtain the vacuum polarization for the conventional local QED: the approach is to calculate the linear response of the vacuum expectation value of current to an external electromagnetic field without using the LSZ reduction formula; one only needs to calculate the field operators ψ(x) and  in terms of (36) and (37) by an iterative method up to first-order approximation. Here we follow this approach to calculate the vacuum polarization; of course, in (36) and (37), Φα(x) is now given by (30).
in terms of (36) and (37) by an iterative method up to first-order approximation. Here we follow this approach to calculate the vacuum polarization; of course, in (36) and (37), Φα(x) is now given by (30).
The concrete calculation process is lengthy and complex; here we only present the main steps and results.
According to (36) and (37), up to first-order approximation, we have

In (41), Φα(in)(x) is given by (30), in which all field quantities are zero-order approximations, namely,

where  is an external electromagnetic field.
is an external electromagnetic field.
If we use

to deal with the factor δ4(xλ − Vλ(y)) in (30), then we should in principle calculate all terms in (43); in other words, we should calculate all orders of the parameter a in (43).
Based on (43), we obtain

where we have used the expressions (58) and (59) of V(y) and  in the last section of this paper, respectively, and ignored all derivative terms of
in the last section of this paper, respectively, and ignored all derivative terms of  , since what we calculate is the linear response of the vacuum expectation value of the current to
, since what we calculate is the linear response of the vacuum expectation value of the current to  .
.
Since the function W(x − y) in (26) is a (real) function but not a matrix, we can choose

or by taking advantage of20

where J1(z) is a Bessel function, we choose

where all bn and Mn are real constants.
Substituting (44) into (41), a problem of operator ordering of ψin and  arises; we can prove that all operator orderings of ψin and
arises; we can prove that all operator orderings of ψin and  in (41) can be determined by the current conservation (6).
in (41) can be determined by the current conservation (6).
Based on the above discussions, we obtain

where all  and
and  (n ≥ 2) are constants arising from (43) and (47),
(n ≥ 2) are constants arising from (43) and (47),


and  (n ≥ 3) in (48) are additional terms that cannot be written in the form of the second term in (48). Notice that no term is proportional to a1(=a) in (48), since the traces of the γ-matrices in this term vanish; this result is obtained by the software FeynCalc.
(n ≥ 3) in (48) are additional terms that cannot be written in the form of the second term in (48). Notice that no term is proportional to a1(=a) in (48), since the traces of the γ-matrices in this term vanish; this result is obtained by the software FeynCalc.
We can prove that the first term in (48) is exactly the same as the results (2.18) and (2.20) in ref. 21. J. Schwinger in ref. 21 writes  , given by (49), in the form
, given by (49), in the form



J. Schwinger in ref. 21 proves that if no real pair creation has occurred, then  introduced by (52) vanishes; this conclusion is proved in the Interaction Picture in ref. 21, but here we work in the Heisenberg Picture, and, thus, have to use a different method to deal with
introduced by (52) vanishes; this conclusion is proved in the Interaction Picture in ref. 21, but here we work in the Heisenberg Picture, and, thus, have to use a different method to deal with  .
.
The method we use is to calculate  straightforwardly. This method can not only prove J. Schwinger’s conclusion in ref. 21, but also obtain a concrete result for
straightforwardly. This method can not only prove J. Schwinger’s conclusion in ref. 21, but also obtain a concrete result for  for the case that real pair creation has occurred.
for the case that real pair creation has occurred.
The calculation result of  given by J. Schwinger in ref. 22 is
given by J. Schwinger in ref. 22 is

where

is logarithmically divergent.
We follow the above approach to deal with  given by (50); for the case that no real pair creation has occurred, we finally obtain
given by (50); for the case that no real pair creation has occurred, we finally obtain

where K is given by (54),  , and the third term including Λ is a new divergent term arising from the new theory.
, and the third term including Λ is a new divergent term arising from the new theory.
From (55), we see that
-
1
By choosing constants
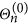 and
and 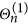 satisfying
satisfying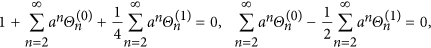
the first (divergent) term in (55) is eliminated and the second term in (55) presents the lowest nontrivial order of the vacuum polarization given by the formula (A.39) in ref. 21.
-
2
The third term (new divergent term) in (55) arising from the new theory can be eliminated by imposing Lorenz gauge
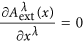 on external electromagnetic field
on external electromagnetic field 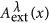 .
. -
3
We have not dealt with
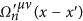 (n ≥ 3) in the last term in (55). It is possible that some terms arising from
(n ≥ 3) in the last term in (55). It is possible that some terms arising from 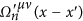 are similar to the first three terms in (55), and, thus, contribute to the first three terms in (55).
are similar to the first three terms in (55), and, thus, contribute to the first three terms in (55). -
4
Generally speaking, since the new theory brings many new terms, it can be predicted that new divergent terms in the new theory presented in this paper will appear. Just as the method of higher covariant derivative regularization of gauge theories23,24,25 removes divergences in the original theory while at the same time bringing many new divergent terms, of course, all divergences are removed finally. We predict that the divergences brought by new terms arising from the new equations of motion (28) and (30) can be removed finally. For example, even if we don’t impose the Lorenz gauge on the external electromagnetic field, the third term (new divergent term) in (55) cannot be eliminated; however, it is possible that it can be eliminated by some terms arising from the last term in (55).
-
5
Our purpose is to establish a theory of QED without divergence, but there are still two divergent constants K and Λ in (55). For this result we emphasize that (I) both K and Λ arise from the calculation approach from (43) to (48); and (II) it is because of the structure and properties of the theory, but not renormalization procedure, that both K and Λ are eliminated. As for the calculation approach from (43) to (48), which not only leads to a complex computation process, but also causes some divergent integrals, e.g., (49) and (50), strictly speaking, the divergent integrals bring uncertainty, especially for the case of changing variables in the integral. Hence, seeking a different calculation approach for the models presented in this paper, especially for the treatment method of the δ - function given by (43), is necessary. Can we find a calculation approach such that there is no divergence in the calculation result? This question will be studied further.
Finally, we emphasize that the theory we employ in this section to calculate the vacuum polarization is only a special choice of the models presented in the section “A class of models of quantum electrodynamics with nonlocal interaction” of this paper. Concretely, the theory employed in this section is the result of defining the two functions Uμ(x) and Vμ(y) in (16) by (25) and (26), and, also of defining the function W(y − y′) in (26) by (45) or (47). On the other hand, the models presented in the section “A class of models of quantum electrodynamics with nonlocal interaction” of this paper provide a wide range of choices. Hence, maybe it is possible to establish a theory of QED without divergence by choosing appropriate functions f(z), Uμ(x) and Vμ(y) in the action (16).
Proofs of (21) and (23)
Both (21) and (23) play important roles in the proofs of the gauge invariance of the model and the conclusion that the equation of motion of the electromagnetic field (28) leads to the current conservation (6). Eqs (21) and (23) can be proved by a basic function algorithm. Here we prove them by straightforward calculation. Some expressions obtained in the proof process are also used in the calculation of the vacuum polarization.
In order to prove (21), without loss generality, we assume

since the arbitrary vector function Vμ(y) can always be written in such a form. According to (13),

By a straight forward calculation, we obtain the determinant V(y) and the inverse matrix  of
of  as follows.
as follows.




where V(1)(y), V(2)(y) and V(3)(y) are introduced by (58).
Therefore,  , and according to the above expressions of
, and according to the above expressions of  , we can verify that
, we can verify that  . Thus, (21) is proved.
. Thus, (21) is proved.
In order to prove (23), based on the Fourier transform  of f(x), we have
of f(x), we have

similarly,

From the above two expressions and using some of the formulas in (15), we obtain

According to (60), each of  and
and  can be transformed to the other; for example, from (60) we have
can be transformed to the other; for example, from (60) we have

which is just (23).
When we use a basic function algorithm to prove (60), we do not need to take advantage of the form of the Fourier transform of f(x).
Additional Information
How to cite this article: Mei, T. Class of gauge-invariant models of quantum electrodynamics with nonlocal interaction. Sci. Rep. 7, 45386; doi: 10.1038/srep45386 (2017).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Efimov, G. Nonlocal interactions of quantum field. Nauka, Moscow (1977).
Efimov, G. Problems of quantum theory of nonlocal interactions. Nauka, Moscow (1985).
Dirac, P. Directions in Physics. John Wiley & Sons Inc, New York (1978).
McManus, H. Classical electrodynamics without singularities. Proc. Roy. Soc. (London) A 195, 323 (1948).
Chretien, M. & Peierls, R. A study of gauge-invariant non-local interactions. Proc. Roy. Soc. (London) A 223, 468 (1954).
Scharnhorst, K. Non-local quantum electrodynamics admits a finitely induced gauge field Action. Proc. Roy. Soc. (London) A 451, 571 (1995).
Bjorken, J. & Drell, S. Relativistic quantum fields. McGraw-Hill, New York (1965).
Bloch, C. On field theories with non-localized interactions. Dan. Mat. Fys. Medd. 27(8), 2 (1952).
Gribov, V. Quantization of non-Abelian gauge theories. Nucl. Phys. B 139, 1 (1978).
Young, B.-L. Introduction to quantum field theories. Science Press, Beijing (1987).
Marnelius, R. Can the S matrix be defined in relativistic quantum field theories with nonlocal interaction? Phys. Rev. D 10(10), 3411 (1974).
Yang, C. & Feldman, D. The S-Matrix in the Heisenberg representation. Phys. Rev. 79, 972 (1950).
Itzykson, C. & Zuber, J.-B. Quantum field theory. McGraw-Hill, New York (1980).
Lurie, D. Particles and fields. Interscience, New York (1968).
Källén, G. Formal integration of the equations of quantum theory in the Heisenberg representation. Arkiv för Fysik. 2(37), 371 (1950).
Vancura, A. On formal solutions in field theories with non-localized interaction. CERN Report No. CERN-TH 1212 (1970) http://cds.cern.ch/record/944370/files/?ln=zh_CN.
Bogoliubov, N. & Shirkov, D. Introduction to the theory of quantized fields (Third edition). John Wiley & Sons Inc, New York (1980).
Feynman, R. Quantum theory of gravitation. Acta Phys. Polonica 24, 697 (1963).
Faddeev, L. & Popov, V. Feynman diagrams for the Yang-Mills field. Phys. Lett. B 25, 29 (1967).
Källén, G. Higher approximation in the external field for the problem of vacuum polarization. Helv. Phys. Acta. 22, 637 (1949).
Schwinger, J. Quantum electrodynamics. II. Vacuum polarization and self-Energy. Phy. Rev. 75(4), 651 (1949).
Schwinger, J. Quantum electrodynamics. III. The electromagnetic properties of the electron—radiative corrections to scattering. Phy. Rev. 76(6), 790 (1949).
Slavnov, A. Invariant regularization of gauge theories. Theor. and Math. Phys. 13, 1064 (1972).
Lee, B. & Zinn-Justin, J. Spontaneously broken gauge symmetries. II. Perturbation theory and renormalization. Phys. Rev. D 5, 3137 (1972).
Faddeev, L. & Slavnov, A. Gauge fields: an introduction to quantum theory (Second Edition). Westview Press, New York (1991).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The author declares no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Mei, T. Class of gauge-invariant models of quantum electrodynamics with nonlocal interaction. Sci Rep 7, 45386 (2017). https://doi.org/10.1038/srep45386
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep45386
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

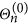 and
and 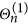 satisfying
satisfying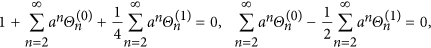
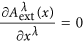 on external electromagnetic field
on external electromagnetic field 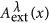 .
.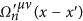 (n ≥ 3) in the last term in (55). It is possible that some terms arising from
(n ≥ 3) in the last term in (55). It is possible that some terms arising from 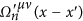 are similar to the first three terms in (55), and, thus, contribute to the first three terms in (55).
are similar to the first three terms in (55), and, thus, contribute to the first three terms in (55).