Exact research on the theory of the blackbody thermal radiation

Abstract

After studying the normalized Planck equation in depth, a brand-new type of spectrum curves of blackbody thermal radiation is given. Two important parameters of the new type curves, namely relative width RW_η and symmetric factor RSF_η, are defined. The paper points out that the experimental verification of the parameters has three significant applications: (1) Giving a method to measure temperature by detecting the radiation wavelength. (2) Determining the blackbody grade. (3) The temperature obtained from the law of the blackbody thermal radiation can be used as a criterion.

Introduction

It is well known that, over the past hundred years, the theoretical basis of the blackbody thermal radiation is expressed in the form of Planck’s law, given by^1,2,3,4

where C₁ = 3.7415 × 10⁻⁴ W·μm², C₂ = 1.4388 × 10⁻⁴ μm²·K. e_b(λ, T) is the monochromatic radiant emittance of the blackbody at the temperature T(K) and radiation wavelength λ(μm). For a given temperature, the e_b(λ, T) and wavelength λ are related by the traditional spectrum curve of the blackbody thermal radiation⁵, as shown in Fig. 1. When the first derivative of function e_b(λ, T) with respect to λ is equal to 0, the relationship of the temperature with the peak wavelength λ_m of the curves in Fig. 1 results, which is the famous Wien displacement law⁶

Figure 1

The traditional spectrum curve of the blackbody radiation.

Under the development of the remote sensing⁷, night vision⁸, and thermal radiation thermometry technology⁹, many further studies on the blackbody thermal radiation have been carried out. For examples, by studying the inflection point feature along the both sides of the curves in Fig. 1, the lightwave equation of the inflection point was obtained as

then the relationship of the wavelength at the left inflection point λ_li and right inflection point λ_ri with temperature T was derived from (3)¹⁰

In order to find the wavelength domain of Eq. (1), ref. 11 proposed a normalized Planck’s equation

where the normalization coefficient η is defined by the following equation

Obviously, η ranges from 0 to 1, inclusive. And the value of x in Eq. (6) is given by

When η trends to zero, the variation of x or λ in Eq. (8) with temperature T was studied in reference 11. For η equal to 10⁻⁶, the conclusion of the reference is that the domain of the wavelength λ is between 88 and 1051(μm), when temperature between 200 and 6000(K).

Based on these studies above, the relationships between λ and η are investigated in this paper. And from the obtained relationships in this paper, a brand-new type of spectrum curves of the blackbody thermal radiation results, which is much clearer than that was. Then the relative width and symmetric factor of the spectrum curves are defined. Finally, a wavelength thermometry is presented, and the significant applications of the results obtained in this paper are shown as well.

Results

Normalized spectrum curve of the blackbody thermal radiation

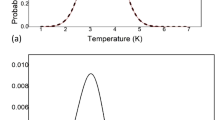
For different values of η, Eq. (6) is a series of transcendental equations without analytical solutions, thus a brand-new normalized spectrum curve of the blackbody thermal radiation can be obtained from their numerical solutions. In order to numerically solve (6), it is necessary to determine its roots distribution. Programming to find out the roots of Eq. (6), Fig. 2 shows that, for a given η, the curve has two intersection points with the x-axis, which indicates that the transcendental Eq. (6) has two roots, denoted as x_ηs and x_ηl (x_ηl < x_ηs). In accordance with Eq. (8), the two roots of x_ηs and x_ηl can lead to the wavelengths of λ_ηs and λ_ηl, respectively, which locate on the left and right side of the spectrum curve with the corresponding value of η.

Figure 2

The curve of the left side of Eq. (6), when η = 0.8, 0.85, and 0.9.

Programming to numerically solve (6), the relationship of η with its corresponding x_ηs and x_ηl results, as shown in Table 1. If necessary, any magnitude of x_ηs or x_ηl can be obtained by solving (6) based on the different value of η. RW_ηt and RSF_ηt in Table 1 are the theoretical results of the relative width and symmetric factor of the spectrum curves obtained from Eqs (14) and (15).

Table 1 Values of x_ηl and x_ηs obtained from Eq. (6) with different η.

For η = 1, the values of x_ηl are equal to x_ηs, which are both recorded as x_m. Substituting x_ηs, x_ηl and x_m of each η and the previous value of C₂ into Eq. (8) can produce the following equations

Then, Table 1 can lead to a brand-new type of spectrum curves of the blackbody thermal radiation, as shown in Fig. 3.

Figure 3

The brand-new type of normalized spectrum curve of the blackbody thermal radiation, where λ_mi represents the peak wavelength of each spectrum curve numbered i, i = 1, 2, …, and 8.

For a given Kelvin temperature T and under the condition of η equal to 1 in Table 1, the substitution of the x_m into (11) can lead to the same peak wavelength λ_m of Eq. (2). The short wave edge λ_ηs and long wave edge λ_ηl, sitting on the both sides of the curve’s peak, can be obtained from Eqs. (9) and (10), then the relationship at this temperature of η with λ results. For example, when T = 1000 K, substituting any values of x_ηs and x_ηl, which correspond to a certain value of η in Table 1, into Eqs (9) and (10) can obtain the values of λ_ηs and λ_ηl in Table 2. Then, using Table 2 can yield the η-λ curve 4 in Fig. 3(a). Similarly, other η-λ curves in Fig. 3 at different temperature can be obtained as well, which are the normalized spectrum curve of the blackbody thermal radiation presented in this paper. It should be noted that it will spend considerable software resources and time to solve Eq. (6), using the unknown of η in Table 1 to get a curve. Therefore, the data in Table 1 is already enough to be used in general conditions, and may also be used as a manual text to plot the other spectrum curves. In addition, the monochromatic radiant emittance of λ_ηs and λ_ηl at any temperature can be obtained from the right side of Eq. (7), when necessary.

Table 2 Data of the normalization coefficient η with wavelength λ when T=1000 K.

Feature description and application analysis on the spectrum curve

In order to accurately describe the characteristics of the normalized spectrum curve of the blackbody thermal radiation, the actually measured wavelength λ_ηs, λ_m and λ_ηl can give a definition for the curve of the relative width RW_η and symmetric factor RSF_η as

On the other hand, substituting the wavelength of Eqs (9) to (11), into (12) and (13) respectively, RW_η and RSF_η can be theoretically defined as follows

The RW_ηt and RSF_ηt of Table 1 are the theoretical results produced from (14) and (15), with the corresponding x_ηs, x_ηl, and x_m. Obviously, RW_ηe and RSF_ηe are closely associated with η. But it is usually more concerned with RW_0.5e and RSF_0.5e, i.e., η = 0.5.

For any of the RW_η or RSF_η, the Eqs (12) and (13) are the experimental results, and Eqs (14) and (15) are the theoretical. Thus, if the experiment systems are reliable and the experimental results are consistent with the theoretical values, it will prove that the object tested in the experiment is a blackbody. In addition, the following equations can be derived from Eqs (9) to (11),

The Eqs (16) to (18), show that the true temperature of the tested object can be detected by measuring the wavelength of _ηs, _ηl, and λ_m, namely, which provides a thermometry based on the measurement of the radiation wavelength.

Discussion

Only the local spectrum characteristics of the blackbody thermal radiation have been studied in refs 6, 10, and 11 based on the traditional spectrum curve. In this paper, its global characteristics are studied based on the brand-new type of spectrum curves of blackbody thermal radiation as shown in Fig. 3. The results obtained in this paper have three important significances.

First, it provides a novel method to verify blackbody and its grade. From the Eqs (12) to (15), given by the experimental and theoretical results, two errors of a and b can be defined as follows

Then, using a and b can give an exact definition to the blackbody. When a and b are both equal to 1, it represents an ideal blackbody. When a and b are very close to 1, such as 0.9, 0.99, 0.999 and so on, it can define different grades of the actual blackbody.

Second, using an actual high-level blackbody as the experimental subject and applying a high-precision spectrometer to detect the radiation wavelength, it can be seen from Eqs (16) to (18), that, at a constant temperature, the actual temperature of a blackbody can be determined by measuring three wavelength values: the peak wavelength and two wavelengths corresponding to a suitable η. Therefore, the temperatures calculated from the three wavelengths have a cross-calibration function, which can fully verify the credibility of the measured temperature. As long as the errors between them are small enough, the temperature obtained from Eqs (16) to (18), can be used as a criterion.

Table 1, Fig. 3 and these two points above are the most important conclusions of this paper, which are enlightening and helpful for further researches on the blackbody thermal radiation. Unfortunately, there are no equipments for authors to do relevant experiments. So we can only provide the theoretical results here to share with readers.

Finally, based on the researches available on the blackbody thermal radiation, it must be noted for the earth’s thermal radiation that the microwave, which has been detected by the passive microwave remote sensing technology¹², cannot be predicted by Planck’s law in Eq. (1), even at the nearly lowest temperature of the Earth’s surface¹¹. To solve this problem for describing the characteristics of the gray body thermal radiation, authors believe, it maybe go one step further and deeply study Kirchhoff’s law¹³, and that will be our next research topic.