Abstract
Blackbody radiation inversion is a mathematical process for the determination of probability distribution of temperature from measured radiated power spectrum. In this paper a simple and stable blackbody radiation inversion is achieved by using an analytical function with three determinable parameters for temperature distribution. This inversion technique is used to invert the blackbody radiation field of the cosmic microwave background, the remnant radiation of the hot big bang, to infer the temperature distribution of the generating medium. The salient features of this distribution are investigated and analysis of this distribution predicts the presence of distortion in the cosmic microwave background spectrum.
Similar content being viewed by others
Introduction
A blackbody is an ideal object which can absorb all of the incident radiation of all frequency. The total power radiated per unit frequency per unit solid angle by a unit area of a blackbody emitter can be expressed by Planck’s law1,2
where ν is frequency, T is the absolute temperature, h is Planck’s constant, k is Boltzmann’s constant and c is the speed of light. Usually telescopes are used to measure this power spectrum of any celestial object. But due to its finite field of view a telescope can observe a small portion of the sky at any time. These small portions consist of different blackbody radiators with different temperature T and each of them are in thermal equilibrium. When a collection of blackbodies with probability distribution \({\upalpha }\left( {\text{T}} \right)\) and temperature T is considered, the total radiated power per unit area is given by the integration over the distribution as3
where W(ν) is the radiated power per unit frequency per unit area and per unit solid angle and \({\upalpha }\)(T) is the probability distribution of temperature of the blackbody. The dimension of \({\upalpha }\)(T) is \(\frac{1}{{\text{K}}}\).
The blackbody radiation inversion problem aims to find the probability distribution of temperature from the radiated power spectrum.
In practice, a set of discrete values of W(ν) are available experimentally. By using this set of data, \({\upalpha }\)(T) can be calculated by blackbody inversion method.
For mathematical convenience, a dimensionless parameter G(ν) = \(\frac{{c^{2} }}{{2h{\upnu }^{3} }}\) W(ν) is used.
Equation (3) is the first kind of Fredholm integral equation and is an ill-posed problem. Bojarski was the first to propose a solution to this problem using Laplace transform with an iterative process4. Since then various other methods have been proposed for solving this problem like Tikonov regularization method5, universal function set method6, Mellin transform method7, modified Mobius inverse formula8, variational expectation maximization method9, maximum entropy method10, regularised GMRES method11. There are also several other methods available in literature as solutions to this problem12,13,14,15.
However, the required number of input data is large in the existing method. The number of data points required for successful inversion is 50 in6, 50 in11 and 32 in15. In this paper, a simple and robust method for blackbody radiation inversion is developed which uses 3 input data. The size of programming is also small in comparison to the previous methods. The present method for blackbody radiation inversion reduces the complexity of the overall program significantly.
This method is applied to obtain the probability distribution of temperature of the universe using cosmic microwave background radiation (CMB) from COBE, FIRAS data16. “Method and validation” section describes the method and its validation and “Cosmic microwave background radiation” section describes the application of this method in CMB radiation.
Method and validation
Equation (3) takes all possible values of temperature into consideration; hence the limit runs from zero to infinity. Here it is assumed that the temperature of black body radiators in a collection of blackbodies vary from T1 to T2 and they have a finite frequency range of ν. Therefore, Eq. (3) can be written as
Using change of variable T = T1 + (T2 – T1)t, Eq. (4) becomes15
And a(t) = \({\upalpha }\)(T1 + (T2 – T1) t).
The required interval of a(t) is [0,1].
Equation (6) informs that the problem of solving \({\upalpha }\)(T) is equivalent to solving a(t).
In the present article, an analytical function represented by Eq. (8) is proposed as a(t).
Equation (8) can be expanded as
In this method we are trying to obtain the probability distribution of temperature. The nature of the probability distribution is expected to be close to gaussian. So, Eq. (8) is chosen in such a way that for large vales of k3, the \({\text{e}}^{{ - {\text{k}}_{3}^{2} {\text{t}}}}\) part in the sine hyperbolic function is very small. When k2 \(\approx\) \({\text{k}}_{3}^{2}\), Eq. (8) represents a gaussian distribution provided the value of k1 is small.
The lower and upper limits of temperatures (T1, T2) are taken as 1 K and 6 K respectively. The motive behind this choice is that we will use this method to analyse the CMB spectrum and it closely resembles a blackbody radiation at a temperature range similar to T1 and T2. Then, t = \(\frac{{{\text{T}} - 1}}{5}\) or,
where k1, k2 and k3 are three determinable parameters such that the interval of \({\upalpha }\left( {\text{t}} \right)\) is [0,1] and T is absolute temperature.
The data have been simulated by using model function Eq. (11),
Equation (11) is used in Eq. (4) in place of \({\upalpha }\left( {\text{T}} \right)\) and the values of G(ν) are calculated. This process is repeated with different frequencies \(\nu\). These simulated data are put in the left-hand side of Eq. (6). Three of such equations for three different values of frequency \(\nu\) are obtained. These three equations with three unknowns k1, k2 and k3 are then solved. Thus, the function \({\upalpha }\left( {\text{T}} \right)\) is obtained with these three parameters.
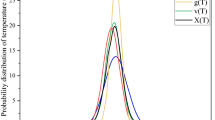
Taking b(T) = \({\text{e}}^{{ - { }\frac{{\left( {{\text{T}} - 3.5} \right)^{2} }}{1}}}\), we calculate \({\upalpha }\left( {\text{T}} \right)\) for three different frequencies of 5 \(\times\) 1011 Hz, 6 \(\times\) 1011 Hz and 7 \(\times\) 1011 Hz. Since we will be using this method in the CMB spectrum, the range of frequency is chosen such a way that it resembles the frequencies in the data we have16. It is observed in Fig. 1a that we have reconstructed the temperature distribution that resembles the model temperature distribution. The difference between b(T) and \({\upalpha }\left( {\text{T}} \right)\) is expressed as d1(T) = b(T) − \({\upalpha }\left( {\text{T}} \right)\) and it is plotted in Fig. 1b against absolute temperature.
(a) Model function b(T) and reconstructed function \({\upalpha }\)(T) are plotted against absolute temperature. Here b(T) = \({\text{e}}^{{ - { }\frac{{\left( {{\text{T}} - 3.5} \right)^{2} }}{1}}}\) and three frequencies of 5 \(\times\) 1011 Hz, 6 \(\times\) 1011 Hz and 7 \(\times\) 1011 Hz are used to calculate \({\upalpha }\)(T). (b) The difference between b(T) and \({\upalpha }\left( {\text{T}} \right)\), d1(T) = b(T) − \({\upalpha }\left( {\text{T}} \right)\) is plotted against absolute temperature.
The \(\frac{{\Delta {\text{I}}}}{{\text{I}}}\) value obtained from Fig. 1b is 0.0119 for T = 3 K. Here I is the value of b(T) and \(\Delta {\text{I}}\) is the value of d1(T) for a specific temperature T. The method is sensitive to the chosen frequency. To quantify this sensitivity, we choose sets of frequencies as i, where i includes three frequencies with \({\upnu }_{1}\) = i \(\times\) 1011 Hz, \({\upnu }_{2}\) = (i + 1)\(\times\) 1011 Hz and \({\upnu }_{3}\) = (i + 2)\(\times\) 1011 Hz. This set is then used in Eq. (5) to calculate \({\upalpha }\)(T). The standard deviation from the model function is calculated by Eq. (12)
where N is the number of data used for the calculation of standard deviation and we have taken N = 51.
It is inferred from Fig. 2 that the standard deviation is less for the sets of i = 1, 2, 5 and 6. Therefore, it is expected to use either of these set of frequencies. All the values of k1, k2 and k3 that are calculated during the validation, are listed in Table 1.
The standard deviation is plotted against the chosen set of frequencies. We have used different profiles of b(T) by varying \({\updelta }\) and \(\gamma\) in Eq. (10). For (a) \({\updelta }\) = 3, (b) \({\updelta }\) = 3.5 and (c) \({\updelta }\) = 4. For different \(\gamma\) values, the standard deviation differs slightly.
Cosmic microwave background radiation
Cosmic microwave background radiation is the afterglow as predicted by the hot big bang model. The presence of such radiation in the universe was first suggested in the late 1940s17. It was only in 1965 when a signal was first detected which was reported to be coming from every direction of the observed sky18. This was the first detection of the radiation which later became to be known as cosmic microwave background radiation. The study of CMB can unravel the mysteries of the initial stage of the universe and its evolution for the last 13.7 billion years. Right after its first detection a lot of work has been done on CMB19,20,21,22,23,24,25.
The first detection showed the radiation to be isotropic, i.e. similar in every direction. But subsequent studies showed that the radiation is in fact anisotropic in nature26,27. More recent studies focus on the different types of distortions in the CMB spectrum28,29,30,31,32. It suggests that the radiation is not of a blackbody with single temperature, rather it is a superposition of different blackbodies that are at different temperatures. When several blackbodies of different temperatures are mixed together it creates y and \({\upmu }\) type distortions32,33. In this paper we have calculated the distortions present in the CMB spectrum.
The blackbody radiation inversion (BRI), as discussed in “Method and validation” section, is applied to the cosmic microwave background radiation for obtaining the temperature of the universe and the probability distribution of temperature. We have used the data of COBE FIRAS to calculate intensity16. For the input of the BRI, the spectral irradiance I(λ) is transformed to the power spectrum W(ν) according to the relation
where λ (= \(\frac{c}{{\upnu }}\)) is the wavelength. For each value of W(ν) corresponding to a particular frequency ν, we have an integral equation in Eq. (6). Three of such equations are taken to calculate k1, k2 and k3 of Eq. (10). Table 2 shows the values of k1, k2 and k3 that we have calculated.
We have taken the average of these probability distribution functions as M(T),
Since M(T) is a probability distribution, it should be normalised for the temperature range T1 = 1 K to T2 = 6 K. We normalise M(T) with normalisation constant 0.982 (\(\frac{1}{{\mathop \smallint \nolimits_{1}^{6} {\text{M}}\left( {\text{T}} \right){\text{dT}}}}\) = 0.982). \({\upalpha }\)(T) is the normalised probability distribution of temperature.
The moments of different order of \({\upalpha }\)(T) are calculated by using Eq. (16)
where n is the order of the moment and µ is the mean value.
First order moment or mean value is calculated as
The mean temperature is 2.69 K, which is close to the average value 2.725 K23.
Second order moment or variance is calculated as
So, standard deviation
σ indicates the uncertainty in temperature which is 0.195 K23.
Third order standardised moment or Skewness is calculated as
An ideal normal distribution has a skewness of 0. We get a positive skewness which describes its deviation from ideal behaviour. A positive skewness suggests that the tail of the distribution right to the mean is more extended than the left-hand side tail34,35.
Fourth order standardised moment about mean
Kurtosis represents the peakedness and tailedness of a distribution. An ideal normal distribution has a kurtosis of 3, so 3 is subtracted from β2 to measure the deviation from ideal normal behaviour. In our calculation \({\upgamma }_{2}\) (= β2 − 3) yields 0.0563, a positive number. A distribution with positive kurtosis is called Leptokurtic. A positive kurtosis means that the peak of the curve is slightly higher than the normal distribution while the tail and shoulder portion is slightly pushed towards the mean value34,35.
From the standard deviation \({\upsigma }\) and mean value µ, a Gaussian function (\(\frac{1}{{{\upsigma }\sqrt {2{\uppi }} }}{\text{e}}^{{ - \frac{{\left( {{\text{x}} - {\upmu }} \right)^{2} }}{{2{{\upsigma }}^{2} }}}} { }\)) is constructed in Eq. (24).
\({\upalpha }\)(T) and s(T) are plotted against absolute temperature in Fig. 3a. And the difference between α(T) and s(T), expressed as d2(T) = \({\upalpha }\)(T) – s(T) is plotted against absolute temperature in Fig. 3b.
A deviation from the ideal gaussian behaviour is observed. The \(\frac{{\Delta {\text{I}}}}{{\text{I}}}\) value obtained from Fig. 3b is 0.0194 for T = 2.5 K. Here I is the value of s(T) and \(\Delta {\text{I}}\) is the value of d2(T) for a specific temperature T. The deviation in Fig. 3b (0.0194) is larger than the deviation in Fig. 1b (0.0119). So, this deviation in Fig. 3b is not due to the error in the inversion method we have used. A small deviation from ideal Gaussian behaviour is also predicted when non-extensive case is considered36. The temperature distribution of CMB is found to be primarily between 2 and 3.5 K.
To verify the accuracy of our method to obtain probability distribution of temperature, we reconstructed the intensity of the radiation by using the calculated \({\upalpha }\)(T) in Eq. (2) for different frequencies ν. W(\(\nu\)) is then converted to I(λ) by using Eq. (13). Figure 4 displays the overlay of reconstructed data on the original data of COBE FIRAS.
The small error bars are not visible in Fig. 4. Hence the values of the intensity and the error are given in Table 3 for the original and reconstructed data. The order of the error in the reconstructed spectrum (~ 10−13 W/m2 × μm × sr) is larger than the error in the original spectrum (~ 10−14 W/m2 × μm × sr). It is evident from Fig. 4 that the present method can faithfully reconstruct the original data.
In this paper, the original data of COBE/FIRAS are used as the input in the blackbody radiation inversion problem. These data are thus mathematically processed to obtain the distortion of the CMB spectrum. The standard deviation between the original and reconstructed data is 0.142 \(\times\) 10−10 W/m2 × μm × sr or 5.209 \(\times\) 10−20 W/m2 \(\times \;{\text{Hz}} \times\) sr for the wavelength of 1049 μm. The deviation is the distortion present in the CMB spectrum. The spread in the probability distribution of the temperature (Fig. 3a) suggests that there are multiple blackbodies with different temperatures (\(\Delta {\text{T}} = {\upsigma }\)). Due to this mixing of blackbodies, the original spectrum becomes distorted. So, the calculated deviation is interpreted as the distortion of the CMB spectrum.
The COBE data shows a spectrum similar to a perfect blackbody21. But the possible distortions are limited by the maximum sensitivity of the instrument. It has y distortion of |y|< 1.5 \(\times\) 10−5 and \({\upmu }\) distortion of |\({\upmu }\)|< 9.0 \(\times\) 10−521. In our calculation we have obtained the temperature as Tnew = T [1 + \(\left( {\frac{{\Delta {\text{T}}}}{{\text{T}}}} \right)^{2}\)] = 2.704 K for T = 2.69 K and \(\Delta {\text{T}} = { }\) 0.195 K. The y and \({\upmu }\) distortions are calculated as y = \(\frac{1}{2}\left( {\frac{{\Delta {\text{T}}}}{{\text{T}}}} \right)^{2}\) \(\approx\) 10−3 and \({\upmu }\) = \(2.8 \times \left( {\frac{{\Delta {\text{T}}}}{{\text{T}}}} \right)^{2}\) \(\approx\) 10−230.
The present set of data, collected by the COBE/FIRAS satellite is not sensitive enough to detect the distortions beyond the 10−5 order. More precise datasets are required to study these distortions. The TRIS, used between 1996 to 2000, had the limit of \({\upmu } <\) 6.0 \(\times\) 10−537. A balloon borne instrument ARCADE (Absolute Radiometer for Cosmology, Astrophysics, and Diffuse Emission) used in 2006, had the upper limit of \({\upmu } <\) 6.0 \(\times\) 10−438. Two new projects, PIXIE39 and PRISM40 aim to find the distortions with 103–104 times better sensitivity than COBE/FIRAS. PIXIE has \(\Delta\)I = 5 \(\times\) 10−26 W/m2srHz and detection of |y|= 1 \(\times\) 10−8 and |\({\upmu }\)|= 5.0 \(\times\) 10−8 is possible. PRISM is better than PIXIE with \(\Delta\)I = 6 \(\times\) 10−27 W/m2srHz and sensitive to y and \({\upmu }\) distortion of ~ 10−9.
The distortions obtained in our calculation are limited by the sensitivity of available measured data. The experiments planned in the future39,40 are expected to provide data with better precision that will help in carrying out more precise calculations and lead to a better understanding of CMB.
Discussion
A novel method of blackbody radiation inversion is studied. This technique is then applied to study cosmic microwave background radiation and some of its most important features. We have described the deviation of the temperature probability distribution from ideal gaussian distribution. The distortion in the spectrum, caused due to mixing of blackbodies are mathematically described as well. Our approach is much simpler than the existing techniques and the computational bulkiness is significantly reduced. While we can obtain the probability distribution of the temperature effectively, the present method is not completely general in nature. The frequency range needs to be selected to minimise the error in the calculation.
References
Beiser, A. Concepts of Modern Physics, Tata McGraw-Hill Edition, Twentieth reprint, 313 (2008).
Choudhury, S. L. & Paul, R. K. A new approach to the generalization of Planck’s law of black-body radiation. Ann. Phys. 395, 317–325 (2018).
Sun, X. & Jaggard, D. L. The inverse blackbody radiation problem: A regularization solution. J. Appl. Phys. 62, 4382 (1987).
Bojarski, N. Inverse black body radiation. IEEE Trans. Antennas Propag 30, 778–780 (1982).
Tikhonov, A. N. & Arsenin, V. Y. Solutions of Ill-Posed Problems (Wiley, New York, 1977).
Ye, J. P. et al. The black-body radiation inversion problem, its instability and a new universal function set method. Phys. Lett. A 348, 141–146 (2006).
Lakhtakia, M. N. & Lakhtakia, A. On some relations for the inverse blackbody radiation problem. Appl. Phys. B 39, 191–193 (1986).
Chen, N.-X. Modified Möbius inverse formula and its applications in physics. Phys. Rev. Lett. 64, 3203 (1990).
Brito-Loeza, C. & Ke, C. A variational expectation-maximization method for the inverse black body radiation problem. J. Comput. Math. 26(6), 876–890 (2008).
Dou, L. & Hodgson, R. J. W. Maximum entropy method in inverse black body radiation problem. J. Appl. Phys. 71(7), 3159–3163 (1992).
Jieer, Wu. & Ma, Z. A regularized GMRES method for inverse blackbody radiation problem. Therm. Sci. 17(3), 847–852 (2013).
Kirsch, A. An Introduction to the Mathematical Theory of Inverse Problems (Springer, New York, 2011).
Li, H.-Y. Solution of inverse blackbody radiation problem with conjugate gradient method. IEEE Trans. Antennas Propag. 53(5), 1840–1842 (2005).
Chen, N. & Li, G. Theoretical investigation on the inverse black body radiation problem. IEEE Trans. Antennas. Propag. 38, 1287–1290 (1990).
Jieer Wua, Yu., Zhoua, X. H. & Chengb, S. The blackbody radiation inversion problem: A numerical perspective utilizing Bernstein polynomials. Int. Commun. Heat Mass Transfer 107, 114–120 (2019).
COBE/FIRAS CMB monopole spectrum, May 2005, http://lambda.gsfc.nasa.gov/product/cobe/firas_monopole_get.cfm.
Alpher, R. A., Bethe, H. & Gamov, G. The origin of chemical elements. Phys. Rev. 73, 803 (1948).
Penzias, A. A. & Wilson, R. W. A measurement of excess antenna temperature at 4080 Mc/s. Astrophys. J. 142, 421 (1965).
Thaddeus, P. The short wavelength spectrum of the 2037 microwave background. Annu. Rev. Astron. Astrophys. 10, 305–334 (1972).
Weiss, R. Measurements of the cosmic background radiation. Annu. Rev. Astron. Astrophys. 18, 489–535 (1980).
Fixen, D. J. et al. The cosmic microwave background spectrum from the full COBE FIRAS data set. Astrophys. J. 473, 576–587 (1996).
Fixen, D. J. et al. The temperature of the cosmic microwave background at 10 GHz. Astrophys. J. 612, 86–95 (2004).
Fixsen, D. J. The temperature of the cosmic microwave background. Astrophys. J. 707, 916–920 (2009).
Hinshaw, G. et al. Nine-yearwilkinson microwave anisotropy probe (WMAP) observations: Cosmological parameter results. Astrophys. J. Suppl. Ser. 208, 19 (2013).
Aghanim, N. et al. Planck 2018 results. I. Overview and the cosmological legacy of Planck, A&A 641, A1 (2020).
Hanany, S., Jaffe, A. H. & Scannapieco, E. The effect of the detector response time on bolometric cosmic microwave background anisotropy experiments. Monthly Notices R. Astron. Soc. 299(3), 653–656 (1998).
Hu, W. & White, M. CMB anisotropies: Total angular momentum method. Phys. Rev. D. 56(2), 596 (1997).
Burigana, C., de Zotti, G. & Danese, L. Constraints on the thermal history of the universe from the cosmic microwave background spectrum. Astrophys. J. 379(Part 1), 1–5 (1991).
Burigana, C., Danese, L. & de Zotti, G. Formation and evolution of early distortions of the microwave background spectrum—A numerical study. Astron. Astrophys. 246, 49 (1991).
Chluba, J. & Sunyaev, R. A. The evolution of CMB spectral distortions in the early Universe. Monthly Notices R. Astron. Soc. 419, 1294–1314 (2012).
Chluba, J., Khatri, R. & Sunyaev, R. A. CMB at 2 × 2 order: The dissipation of primordial acoustic wavesand the observable part of the associated energy release. Monthly Notices R. Astron. Soc. 425, 1129–1169 (2012).
Chluba, J., Khatri, R. & Sunyaev, R. A. Mixing of blackbodies: Entropy production and dissipation of sound waves in the early universe. Astron. Astrophys. 543, A136 (2012).
Tashiro, H. CMB spectral distortions and energy release in the early universe. Prog. Theor. Exp. Phys. (6), 06B107 (2014).
Groeneveld, R. A. & Meeden, G. Measuring skewness and kurtosis. J. R. Stat. Soc. Ser. D. 33(4), 391–399 (1984).
DeCarlo, L. On the meaning and use of Kurtosis. Psychol. Methods 2(3), 292–307 (1997).
Bernui, A., Tsallis, C. & Villela, T. Temperature fluctuations of the cosmic microwave background radiation: A case of nonextensivity? Phys. Lett. A 356(6), 426–430 (2006).
Gervasi, M., Zannoni, M., Tartari, A., Boella, G. & Sironi, G. TRIS. II. Search for CMB spectral distortions at 0.60, 0.82, and 2.5 GHz. Astrophys. J. 688, 24–31 (2008).
Seiffert, M. et al. Interpretation of the ARCADE 2 absolute sky brightness measurement. Astrophys. J. 734, 6 (2011).
Kogut, A. et al. The Primordial Inflation Explorer (PIXIE): A nulling polarimeter for cosmic microwave background observations. J. Cosmol. Astropart. Phys. 2011, 25 (2011).
Andre, P. et al. PRISM (Polarized Radiation Imaging and Spectroscopy Mission): A White Paper on the Ultimate Polarimetric Spectro-Imaging of the Microwave and Far-Infrared Sky, arXiv:1306.2259, (2013).
Acknowledgements
We are thankful to the Department of Physics of Birla Institute of Technology, Mesra, Ranchi for facilitating a wonderful environment during the research work. We would also like to acknowledge the help and support of B. Pathak, R. Kumar, M. K. Sinha (Department of Physics, BIT Mesra, Ranchi) and Soumen Karmakar (BIT Deoghar).
Author information
Authors and Affiliations
Contributions
K.K. has performed the analysis and wrote the main manuscript text with figure. K.B. has performed computational work. R.K.P. conceived the idea and execute the mathematical model. R.K.P. has also performed computational work and wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Konar, K., Bose, K. & Paul, R.K. Revisiting cosmic microwave background radiation using blackbody radiation inversion. Sci Rep 11, 1008 (2021). https://doi.org/10.1038/s41598-020-80195-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-020-80195-3
This article is cited by
-
Investigation on CMB monopole and dipole using blackbody radiation inversion
Scientific Reports (2023)
-
Calculation of Cosmic microwave background radiation parameters using COBE/FIRAS dataset
Experimental Astronomy (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.