Optimal Universal Uncertainty Relations

Abstract

We study universal uncertainty relations and present a method called joint probability distribution diagram to improve the majorization bounds constructed independently in [Phys. Rev. Lett. 111, 230401 (2013)] and [J. Phys. A. 46, 272002 (2013)]. The results give rise to state independent uncertainty relations satisfied by any nonnegative Schur-concave functions. On the other hand, a remarkable recent result of entropic uncertainty relation is the direct-sum majorization relation. In this paper, we illustrate our bounds by showing how they provide a complement to that in [Phys. Rev. A. 89, 052115 (2014)].

Introduction

Uncertainty relations¹ are of profound significance in quantum mechanics and quantum information theory. Various important applications of uncertainty relations have been discovered such as entanglement detection², steering inequalities³ and quantum cryptography^4,5,6. The well-known form of the Heisenberg’s uncertainty relations, given by Robertson⁷, says that the standard deviations of the observables ΔA and ΔB satisfy the following inequality,

As a consequence of the uncertainty relations, it is impossible to determine the exact values of the two incompatible observables simultaneously. However, the lower bound in the above uncertainty inequality may become trivial if the measured state |ψ〉 belongs to the nullspace of the commutator [A, B].

In fact, the uncertainty relations provide a limitation on how much information one can obtain by measuring a physical system, and can be characterized in terms of the probability distributions of the measurement outcomes. In order to overcome the drawback in the product form of variance base uncertainty relations, Deutsch⁸ introduced the entropic uncertainty relations, which were later improved by Maassen and Uffink⁹: H(A) + H(B) ≥ −2 log c(A, B), where H is the Shannon entropy, is maximum overlap between the basis elements {|a_m〉} and {|b_n〉} of the eigenbases of A and B, respectively. Recently, the Maassen-Uffink bound has been surprisingly improved by Coles and Piani¹⁰, Rudnicki, Puchaa and yczkowski¹¹, for a review on entopic uncertainty relations see refs 12 and 13.

Friedland, Gheorghiu and Gour¹⁴ proposed a new concept called “universal uncertainty relations” which are not limited to considering only the well-known entropic functions such as Shannon entropy, Renyi entropy and Tsallis entropy, but also any nonnegative Schur-concave functions. On the other hand, Puchaa, Rudnicki and yczkowski¹⁵ independently used majorization technique to establish entropic uncertainty relations similar to “universal uncertainty relations”. Let  and be orthonormal bases of a d-dimensional Hilbert space H. Denote by p_m(ρ) = 〈a_m|ρ|a_m〉 and q_n(ρ) = 〈b_n|ρ|b_n〉 the probability distributions obtained by measuring the state ρ with respect to these bases, which constitute two probability vectors p(ρ) = (p₁, p₂, …, p_d) and q(ρ) = (q₁, q₂, …, q_d), respectively. It has been shown that the tensor product of the two probability vectors p(ρ) and q(ρ) is majored by a vector ω independent from the state ρ,

where “” stands for “majorization”: in R^d if for all 1 ≤ k ≤ d − 1 and . The down-arrow vector x^↓ denotes that the components of x are rearranged in descending order, . The d²-dimensional vector ω is given by

where

with I_k ⊂ [d] × [d] being a subset of k distinct pairs of indices (m, n) and [d] is the set of the natural numbers from 1 to d. The outer maximum is over all subsets I_k with cardinality k and the inner maximum runs over all density matrices.

Equation (2) is called a universal uncertainty relation, as for any uncertainty measure Φ, a nonnegative Schur-concave function, one has that

The universal uncertainty relation (UUR) (2) generates infinitely many uncertainty relations, for each Φ, in which the right hand side provides a single lower bound.

In relation (2), the state independent vector ω decided by Ω_k in Eq. (4) is too hard to evaluate explicitly in general, as it is involved with a highly nontrivial optimization problem. For this reason, only an approximation of Ω_k has been presented^14,15 to construct a weaker majorization vector . Naturally, how to find a stronger approximation than previous works becomes an interesting open question.

Results

We first introduce a scheme called “joint probability distribution diagram” (JPDD) to consider the optimization problem involved in calculating Ω_k. Next, we present a stronger approximation by proposing an analytical formula for Ω_k. To facilitate presentation, we denote our stronger approximation as Ω_k without ambiguity. All uncertainty relations considered in the paper will be in the absence of quantum side information.

To construct the joint probability distribution diagram, we associate each summand p_i(ρ)q_j(ρ) in Ω_k to a box located at the position (i, j). Then the summation in Ω_k corresponds to certain region of boxes (or rather lattice points) in the first quadrant. We configure the region in a combinatorial way. Suppose that p₁ ≥ p₂ ≥ ··· ≥ p_d, q₁ ≥ q₂ ≥ ··· ≥ q_d. Consider the following d × d-matrix

where the entries descend along the rows and columns by assumption. Now, we use a box □ to represent an entry of the matrix. A shadow or grey box in the JPDD means the corresponding entry in the matrix. For example, the top left shadow of the block box specifies the entry p₁q₁, see Fig. 1. Thus the region corresponding to the summation in will be a special region of the rectangular matrix.

Figure 1

The left-top shadow of the block box specifies the entry p₁q₁.

Our scheme, JPDD, provides a combinatorial method to compute the special region with respect to the Ω_k. First, it is easy to see that the top upper left box in JPDD is the maximal element, i.e. Ω₁, since p₁q₁ − p_iq_j ≥ p_iq₁ − p_iq_j = p_i(q₁ − q_j) ≥ 0. The main idea is that each exact solution of Ω_k corresponds to a particular region in this matrix.

Suppose that the k-th region is found, i.e. Ω_k is obtained, then the next (k + 1)-th region is obtained from the k-th region by adding a special box, which must be “connected” with certain boundary of the k-th region. This iterative procedure enables us to compute all Ω_k. Before proving the statement rigorously, we first introduce some terminologies.

[Definition 1] (Different boxes) Two boxes (matrix elements) p_iq_j and p_kq_l are said to be different if they occupy different positions in JPDD, namely, i ≠ k or j ≠ l. The Fig. 2 shows three examples of different boxes. Note that it may happen that even if the numerical values of p_iq_j and p_kq_l are the same, but graphically they are treated as different boxes. “different” and “same” do not imply their quantitative relation. For example, p₁q₁ may equal to p₁q₃ in general.

Figure 2

Different boxes.

[Definition 2] (Connectedness). Two boxes p_iq_j and p_kq_l in JPDD are connected if there does not exist any box p_mq_n, different from both p_iq_j and p_kq_l, such that min{p_iq_j, p_kq_l} < p_mq_n < max{p_iq_j, p_kq_l}. For example, different boxes p_iq_j and p_kq_l are connected if p_iq_j = p_kq_l. For d = 4, if p₁ > p₂ > p₃ > p₄, q₁ > q₂ > q₃ > q₄, p_iq_j ≠ p_kq_l, p_mq_n ≠ p_iq_j, p_mq_n ≠ p_kq_l, for any i, j, k, l ∈ {1, 2, 3, 4}, then p₂q₂ and p₃q₃ are not connected while p₂q₃ and p₂q₂ are connected, see Fig. 3.

Figure 3

Connectedness.

[Definition 3] (Connected region). A set of different boxes is called a region, denoted by . A region is connected if , then either or , where is the maximal value of all the elements in . Note that the region of boxes corresponding to a Ω_k must contain the top-left element p₁q₁ in JPDD as its largest element.

For any probability vector p(ρ) on a d-dimensional Hilbert space with p_i = 〈a_i|ρ|a_i〉, let , ,  ··· , . Similarly, are defined similarly for another probability vector q(ρ) on the same Hilbert space. For any sequence k₁,  ··· , k_n, 1 ≤ n ≤ d, we define In particular, if p₁ ≥ ··· ≥ p_d, q₁ ≥ ··· ≥ q_d, then , which can be configured by the Fig. 4. In a JPDD when the first k boxes are chosen, the next (maximal) (k + 1)-th box must appear at the top left corner in the unoccupied region, we give this as follow lemma:

Figure 4

related joint probability distribution diagram.

[Lemma]: The maximal k boxes for Ω_k in the JPDD can be selected to form a connected region. ■

Lemma gives a way to get Ω_k+1 from Ω_k in a JPDD. As an example, we show how to get Ω₃ from Ω₂. Set , , . If c₂₁ ≥ c₂₂, then . If c₂₁ ≤ c₂₂, then . That is, if , then . If , then . Namely, . Thus Ω₃ is determined by Ω₂.

In general, , subjecting to . By Lemma it follows that

which gives an iterative formula of Ω_k in terms of ’s.

We list in Figs 5 and 6 all the possible Ω_k for k = 1, 2 ,..., 4. The above example to get Ω₃ from Ω₂ corresponds to move from the second row to the third. Now we are ready to show the main result.

Figure 5

The (k + 1)-th box is fixed by Ω_k.

The arrows show the position of the (k + 1)-th box.

Figure 6

The tree diagrams to get the JPDDs in the k-th row by adding one shadow box to the JPDDs in the k − 1 row.

[Theorem] The quantities Ω_k are given by

The solution given in Eq. (8) can be explained as follows. First, for k = 1, 2, they are solved simply as

where , , the maximum is taken over all indices m ≠ m′, n ≠ n′, and over all n = n′,m ≠ m′. Then, for k = 3 in JPDD, Furthermore, and . Since , we get and We have shown how to calculate Ω₁, Ω₂ and Ω₃. For the cases k ≥ 4, interested readers can calculate Ω_k using a similar method and we sketch the details in the Methods.

The above theory enables us to formulate a series of Ω_k, based on all quantities we obtain a tighter majorization vector ω. Note that our method is valid when all the maximums are taken over the same quantum state, otherwise our bounds will fail to hold. Even so, our results can outperform B_Maj2¹¹ to some extent.

Our results enable us to strengthen the bounds on the sum of two Shannon entropies by B_JPDD = H(ω), where ω is given by the improved Ω_k in Eq. (8) and H is the Shannon entropy. To see this phenomenon, let us first consider a 4-dimensional system with incompatible observables

and the unitary transformation U (U_mn = 〈a_m|b_n〉) between them

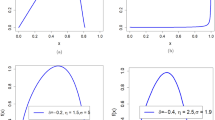
In Fig. 7, we plot the difference between B_JPDD and B_Maj2¹¹, i.e. B_JPDD − B_Maj2 (the red line). Clearly, our bound B_JPDD is tighter than B_Maj2 to some extent. Note that, the entropies are defined with base 2 in general. But in our figures, in order to make them more readable, we take the natural logarithm instead.

Figure 7

Difference between B_JPDD and B_Maj2.

To appreciate the stronger vector ω in the improved UUR, we can consider Shannon entropy in the uncertainty relations to obtain a tighter bound than the previous work¹⁶. Namely if we Φ in Eq. (5) as the Shannon entropy H, then we have

where c^* ≈ 0.834, the bound H₁(c) is the same as the one given in Vincente and Ruiz’s work¹⁶, and G(c) = H(ω) with ω given by our formula Eq. (3). The bound G(c) outperforms the Vincente and Ruiz’s bound F(c)¹⁶ in the interval [c^*, 1]. For further details, see Fig. 8.

Figure 8

The vertical coordinate is G(c) − F(c).

The horizontal coordinate is for random runs. It can be seen that our bound outperforms the bound¹⁶ 100% of the time, while a bound given by Friedland¹⁴ outperforms the bound¹⁶ around 90% of the time.

Conclusion

In conclusion, we have presented a method called joint probability distribution diagram to strengthen the bounds for the universal uncertainty relations. As an example, we consider the bounds on the sum of the Shannon entropies. As the universal uncertainty relations capture the essence of uncertainty in quantum theory, it is unnecessary to quantify them by particular measures of uncertainty such as Shannon or Renyi entropies. Our results give a way to resolve some important cases in this direction, and is shown to offer a better bound for any uncertainty relations given by the nonnegative Schur-concave functions. Furthermore, how to extend this method to the case of multiple measurements are interesting, which requires further studies.

Methods

Proof of the Lamma

The case of k = 1 is obvious since the maximal element is p₁q₁. Assume that the statement holds for the case of k − 1: is connected with k₁ > … > k_n > 0. Suppose on the contrary that the next maximum Ω_k = Ω_{k − 1} + p_iq_j is not connected. Then there are two possibilities: (i) i > n or j > k₁, thus we can replace p₁q_j by p_iq₁ or p₁q_j and move further to p_n+1q₁ or to get a possible bigger value for Ω_k. (ii) i ≤ n and j > k_i, in this case we can also replace the box p_iq_j by a connected box p_i′q_j′ to the region of Ω_{k − 1} by sliding it leftward or upward. Hence the statement is true by induction. ■

Proof of the Theorem

To calculate , k₁ ≥ … ≥ k_n and k₁ + ··· + k_n = k, we note that

where R and S are subsets of distinct indices from [d], |R| is the cardinality of R, and ||·||_∞ is the infinity operator norm which coincides with the maximum eigenvalue of the positive operator. For a given k, there exist sets of k₁ ≥ … ≥ k_n such that for some n. For any such given k₁ ≥ … ≥ k_n, the quantity in [.] in Eq. (8) can be calculated. The outer max picks up the largest quantity for all such possible k₁, …, k_n. Then and . Continuing in this way we have

which gives the improved values of , where max is taken over with k₁ ≥ … ≥ k_n, and hence ω = (Ω₁, Ω₂ − Ω₁, …, Ω_d − Ω_d−1, 0, …, 0) for any ρ. ■