Abstract
We study N-dimensional measurement-device-independent quantum-key-distribution protocol where one checking state is used. Only assuming that the checking state is a superposition of other N sources, we show that the protocol is secure in zero quantum-bit-error-rate case, suggesting possibility of the protocol. The method may be applied in other quantum information processing.
Similar content being viewed by others
Introduction
Quantum key distribution (QKD)1,2 enables two remote users, normally called Alice and Bob, to generate key (private random sequence), which is not a possible task classically. QKD is not only a practically important field but also a theoretically appealing one.
After security of QKD for ideal devices was shown1,3,4, problems due to imperfect devices protruded. Although a main problem due to imperfect source was resolved5, problem due to imperfect detectors still had remained6,7. Then no-signaling QKD was discovered8,9. Remarkably, the no-signaling QKD’s were found to be immune against the imperfect device problems, because security analysis of the protocol is based only on outcomes of detectors. Soon device-independent (DI) QKD’s were found10. DI QKD has ideal security but not yet feasible. Measurement-device-independent (MDI) QKD was proposed11 and demonstrated12,13,14,15 in the background. MDI QKD is secure provided that source is ideal, that is, source is exactly in prescribed quantum states. Later protocols16,17 with more relaxed condition adapt un-characterized source. The only assumption is that the sources are within 2-dimensional subspace.
It can be expected that MDI QKD can be generalized to N-dimensional case. However, security of MDI QKD with un-characterized source relies16,17 on Shor-Preskill proof4. Thus it is not yet clear that N-dimensional MDI QKD with un-characterized source works. In this paper, we consider the N-dimensional MDI QKD with un-characterized source. The only assumption for security is that the sources are within N-dimensional subspace. In the protocol, a single quantum state is enough for checking eavesdropper, normally called Eve. (It is known that a single checking state is enough18). We show that the protocol is secure in zero quantum-bit-error-rate (QBER) case. This suggests possibility of N-dimensional MDI QKD with un-characterized source.
Results
For the protocol, each user prepares N encoding states. Let the states prepared by Alice and Bob denoted by |φm〉 and  , respectively, where m = 0, 1, 2, …, N − 1. Here nothing is assumed for the encoding states so they are completely un-characterized. Each user also prepares a checking state which is assumed to be a superposition of the encoding states. Alice’s and Bob’s checking states are, respectively,
, respectively, where m = 0, 1, 2, …, N − 1. Here nothing is assumed for the encoding states so they are completely un-characterized. Each user also prepares a checking state which is assumed to be a superposition of the encoding states. Alice’s and Bob’s checking states are, respectively,

Here cm and  are real numbers with constraints
are real numbers with constraints  and
and  , respectively, and θm and
, respectively, and θm and  are real. The protocol is as follows.
are real. The protocol is as follows.
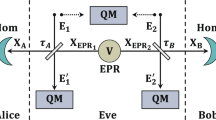
(1) Alice generates a random number i where i = 0, 1, 2, …, N. She sends a state |φi〉 to Charlie. Here Charlie can be anyone. So Charlie can be either Eve or users themselves. (2) Bob independently generates a random number j where j = 0, 1, 2, …, N. He sends a state  to Charlie. (3) Charlie performs a measurement on set of the states |φi〉 and
to Charlie. (3) Charlie performs a measurement on set of the states |φi〉 and  . The measurement can be any one which finally gives two outcomes 0 and 1. Charlie announces the outcome. (4) When the outcome is 0, users discard the data. Otherwise, they keep the data. By sacrificing some of the data for public discussion, users estimate, p(1|ij) ≡ pij, conditional probability to get outcome 1 for each i, j. (5) For each measurement, if both i and j are less than N, the i and j become raw key. Otherwise, the data are used only for checking purposes. Then users do post-processing to get final key.
. The measurement can be any one which finally gives two outcomes 0 and 1. Charlie announces the outcome. (4) When the outcome is 0, users discard the data. Otherwise, they keep the data. By sacrificing some of the data for public discussion, users estimate, p(1|ij) ≡ pij, conditional probability to get outcome 1 for each i, j. (5) For each measurement, if both i and j are less than N, the i and j become raw key. Otherwise, the data are used only for checking purposes. Then users do post-processing to get final key.
Now let us consider Eve’s (Charlie’s) measurement on the states |φi〉 and  . In the most general collective attack, Eve attaches an ancilla |e〉 to the states and then applies a unitary operation to them17
. In the most general collective attack, Eve attaches an ancilla |e〉 to the states and then applies a unitary operation to them17

Eve gets the outcome by measuring the quantum state indexed by M in basis of |0〉 and |1〉. Now let us consider the attack from Eve’s viewpoint. Clearly she can get no information about key from the data with outcome 0 which are not used by the users. Thus she analyze the states for outcome 1, |Γij1〉’s. For convenience, let us omit 1, |Γij1〉 ≡ |Γij〉. We can see that Eqs (1) and (2) give constraints

where n = 0, 1, …, N − 1 and  . Then Eve’s goal is to maximize IEA her information about Alice’s or IEB her information about Bob’s. Eve is constrained only by Eq. (3) and the conditional probabilities pij’s. Let us consider the case when Eve maximizes IEA. In this case she should discriminate mixed states
. Then Eve’s goal is to maximize IEA her information about Alice’s or IEB her information about Bob’s. Eve is constrained only by Eq. (3) and the conditional probabilities pij’s. Let us consider the case when Eve maximizes IEA. In this case she should discriminate mixed states  So the IEA is bounded by1
So the IEA is bounded by1

where  and
and  . Analogously we also get a bound
. Analogously we also get a bound

where  and
and  . The bounds can be used to obtain key rate1.
. The bounds can be used to obtain key rate1.
Now let us consider zero QBER case when pmn = δmn(1/N), pmN = pNn = 1/N2, and pNN = 1/N. Here δmn is Kronecker delta. This conditional probabilities can be obtained by choosing that |φm〉 = |m〉,  ,
,  , and Eve’s measurement is a one composed of
, and Eve’s measurement is a one composed of  and
and  with outcome 1 and 0, respectively. Here |m〉’s are mutually orthonormal states and a generalized Bell state
with outcome 1 and 0, respectively. Here |m〉’s are mutually orthonormal states and a generalized Bell state  . However, here we assume nothing about the states and measurements. Conversely, we show that if the conditional probabilities were obtained anyhow, we can get security and the states should be such. By inserting the conditional probabilities to the first and second of Eq. (3), we get
. However, here we assume nothing about the states and measurements. Conversely, we show that if the conditional probabilities were obtained anyhow, we can get security and the states should be such. By inserting the conditional probabilities to the first and second of Eq. (3), we get  . Combining this with the third of Eq. (3), we obtain
. Combining this with the third of Eq. (3), we obtain  . Now by normalization condition (|ΓNN〉, |ΓNN〉) = 1, we get
. Now by normalization condition (|ΓNN〉, |ΓNN〉) = 1, we get

Eq. (6) means that all |Γmm〉’s are essentially identical and that righthandside terms in Eqs (4) and (5) are zero, implying the security. Moreover, combining  , Eq. (1), and normalization condition, we obtain that all |φm〉’s are orthogonal with one another and the same property holds for
, Eq. (1), and normalization condition, we obtain that all |φm〉’s are orthogonal with one another and the same property holds for  ’s. We can also see that the states |φN〉 and
’s. We can also see that the states |φN〉 and  are expected ones.
are expected ones.
Let us consider another set of conditional probabilites pmn = δmn and piN = pNj = pNN = 1/N. This corresponds to a case when Eve performs measurement in the encoding bases on each quantum states received, and announces 1 (0) when the same (different) outcomes are obtained. Analogously we get  . Then we obtain
. Then we obtain  . Combined by normalization condition, we get that all |Γmm〉’s are orthogonal each other. The righthandside terms in Eqs (4) and (5) are N and there is no security clearly.
. Combined by normalization condition, we get that all |Γmm〉’s are orthogonal each other. The righthandside terms in Eqs (4) and (5) are N and there is no security clearly.
Discussion and Conclusion
In principle, the method is applicable to other set of conditional probabilities physically realizable. Within Eq. (3) with given conditional probabilities, optimize the bounds in Eqs (4) and (5). However, it does not seem to be feasible because of its complexity. Robustness of the method can be shown by the fact that functions involved here are all continuous. If the set of conditional probabilities are arbitrarily close to the ones discussed above, the bounds are also arbitrarily close to the given ones. Only with the assumption about dimensionality, security was obtained. It seems to be worthwhile to search for application of the method in other tasks in quantum information processing.
Good candidates for real implementation of the N-dimensional states seems to be time-bins of single photons which are adapted in the phase-reference-free MDI QKD15,19 and round-robin-differential-phase-shift QKD20,21,22. Here the checking state can be made by opening optical switches such that all time-bins have non-zero possibility to contain a photon. Also spatial-bins may be a good candidate23.
In conclusion, we studied N-dimensional MDI QKD where one checking state is used. With the assumption about dimensionality, Eq. (1), we showed that the protocol is secure in zero QBER case. In the case when Eve’s does full measurement attack, the method also works. This suggests possibility of the protocol.
Additional Information
How to cite this article: Hwang, W.-Y. et al. N-dimensional measurement-device-independent quantum key distribution with N+1 un-characterized sources: zero quantum-bit-error-rate case. Sci. Rep. 6, 30036; doi: 10.1038/srep30036 (2016).
References
Scarani, V., Helle, B.-P., Cerf, N. J., Dusek, M., Lütkenhaus, N. & Peev, M. The security of practical quantum key distribution. Rev. Mod. Phys. 81, 1301 (2009).
Nielsen, M. A. & Chuang, I. L. Quantum computation and quantum information (Cambridge universtiy press, Cambridge, UK, 2000).
Mayers, D. Unconditional security in quantum cryptography. J. ACM 48, 351 (2001).
Shor, P. W. & Preskill, J. Simple proof of security of the BB84 quantum key distribution protocol. Phys. Rev. Lett. 85, 441 (2000).
Hwang, W.-Y. Quantum key distribution with high loss: toward global secure communication. Phys. Rev. Lett. 91, 057901 (2003).
Gottesman, D., Lo, H.-K., Lütkenhaus, N. & Preskill, J. Security of quantum key distribution with imperfect devices. Quant. Inf. Comput. 5, 325 (2004).
Makarov, V., Anisimov, A. & Skaar, J. Effects of detector efficiency mismatch on security of quantum cryptosystems. Phys. Rev. A 74, 022313 (2006).
Barrett, J., Hardy, L. & Kent, A. No signaling and quantum key distribution. Phys. Rev. Lett. 95, 010503 (2005).
Acín, A., Gisin, N. & Masanes, L. From Bell’s theorm to secure quantum key distribution. Phys. Rev. Lett. 97, 010503 (2006).
Acín, A. et al. Device-independent security of quantum cryptography against collective attacks. Phys. Rev. Lett. 98, 230501 (2007).
Lo, H.-K., Curty, M. & Qi, B. Measurement-device-independent quantum key distribution. Phys. Rev. Lett. 108, 130503 (2012).
Rubenok, A., Slater, J. A., Chan, P., Lucio-Martinez, I. & Tittel, W. Real-world two-photon interference and proof-of-principle quantum key distribution immune to detector attacks. Phys. Rev. Lett. 111, 130501 (2013).
Liu, Y. et al. Experimental measurement-device-independent quantum key distribution. Phys. Rev. Lett. 111, 130502 (2013).
Tang, Z. et al. Experimental deomonstration of polarization encoding measurement-device-independent quantum key distribution. Phys. Rev. Lett. 112, 190503 (2014).
Wang, C. et al. Phase-reference-free experiement of measurement-device-independent quantum key distribution. Phys. Rev. Lett. 115, 160502 (2015).
Yin, Z.-Q. et al. Measurement-device-independent quantum key distribution with uncharacterized qubit sources. Phys. Rev. A 88, 062322 (2013).
Yin, Z.-Q. et al. Mismatched-basis statistics enable quantum key distribution with uncharacterized qubit sources. Phys. Rev. A 90, 052319 (2014).
Tamaki, K., Curty, M., Kato, G., Lo, H.-K. & Azuma, K. Loss-tolerant quantum cryptography with imperfect sources. Phys. Rev. A 90, 052314 (2014).
Yin, Z.-Q. et al. Reference-free-independent quantum key distribution immune to detector side channel attacks. Quantum Inf. Process. 13, 1237 (2014).
Sasaki, T., Yamamoto, Y. & Koashi, M. Practical quantum key distribution protocol without monitoring signal disturbance. Nature 509, 475 (2014).
Takesue, H., Sasaki, T., Tamaki, K. & Koashi, M. Experimental quantum key distribution without monitoring signal disturbance. Nature Photon. 9, 827 (2015).
Wang, S. et al. Experimental demonstration of a quantum key distribution without signal disturbance monitoring. Nature Photon. 9, 832 (2015).
Etcheverry, S. et al. Quantum key distribution session with 16-dimensional photonic states. Sci. Rep. 3, 2316 (2013).
Acknowledgements
This study was supported by Institute for Information and Communications Technology Promotion (IITP) grant funded by the Korea Government (MSIP) (No. R0190-16-2028, Practical and Secure Quantum Key Distribution).
Author information
Authors and Affiliations
Contributions
W.-Y.H. applied the method to analyse the protocol. H.-Y.S. and J.B. contributed to the analysis. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Hwang, WY., Su, HY. & Bae, J. N-dimensional measurement-device-independent quantum key distribution with N + 1 un-characterized sources: zero quantum-bit-error-rate case. Sci Rep 6, 30036 (2016). https://doi.org/10.1038/srep30036
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep30036
This article is cited by
-
High-dimensional quantum key distribution implemented with biphotons
Scientific Reports (2023)
-
Enhanced Bell state measurement for efficient measurement-device-independent quantum key distribution using 3-dimensional quantum states
Scientific Reports (2019)
-
Plug-and-play round-robin differential phase-shift quantum key distribution
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.