Abstract
The realization of reliable quantum channels, able to transfer a quantum state with high fidelity, is a fundamental step in the construction of scalable quantum devices. In this paper we describe a transmission scheme based on the genuinely quantum effect known as Bloch oscillations. The proposed protocol makes it possible to carry a quantum state over different distances with a minimal engineering of the transmission medium and can be implemented and verified on current quantum technology hardware.
Similar content being viewed by others
Introduction
The possibility of transferring, or sharing, a quantum state between different parties of a quantum network is of fundamental importance in quantum computation and communications systems. In solid-state implementations of quantum devices, for example, several small units need to be connected in order to share information among them, much the same way current (classical) computers components are. The realization of reliable channels, able to the transfer of quantum information with high fidelity, is therefore a fundamental step in the construction of a scalable quantum computer1. The latter, in turn, hold the promise of speeding up the solution of certain problems perceived as difficult on a classical computer2 and of enabling controlled simulations of the behavior of complex quantum systems3,4. Different quantum state transfer (QST) schemes have been proposed in the last decade. The range of systems that can be engineered for the task is quite large5,6. However, on ground of physical implementability and scalability, protocols that: i) avoid interactions with the system except at initialization and read-out; ii) are time-independent Hamiltonian, are to be preferred6. A periodical switching of a control field can be also of interest in view of an almost dispersionless transport over long distances2,7. Recently, an experimental verification on waveguide lattices8 of the perfect-state transfer protocols proposed in9,10,11 and12,13 has been reported in14,15 and16.
Here we propose a protocol to exploit Bloch oscillations17 in order to achieve nearly optimal state transfer. We use the probability of transfer of an information carrier between two different regions of a transmission line as a figure of merit and study the trade-off between the amount of resources used to prepare the initial state of the carrier and the transfer probability.
Our protocol requires a minimal engineering of the channel, consisting in the introduction of an externally tunable temperature18 gradient, or an electric field19. It offers the remarkable possibility of changing the transmission distance without modifying the geometry of the device. This feature represents a major innovation compared to previous QST protocols. The existing QST schemes are static: a given device, or channel, is able to transfer information only between two fixed endpoints. Our proposal, though based on a time-independent Hamiltonian, opens instead the possibility of dynamically reconfiguring the “routing” of the transmitted quantum information, a fundamental requirement in any quantum information processing device. This innovative scheme can be implemented and verified on current photonic lattices technology18,19,20,21 and can lead to the realization of the first reconfigurable QST device for photonic qubits. Moreover, it can find applications in all-optical switching of light in communication systems22.
Results
The model
The system we deal with is a 1D lattice. We indicate each site of the lattice by |n〉,  . The system Hamiltonian is given by (we set
. The system Hamiltonian is given by (we set  = 1):
= 1):

where Δ is the coupling between next neighbor sites. The same Hamiltonian also governs the dynamics of the Tight Binding Model (TBM)23 and of waveguide-array systems8. The corresponding Schrödinger equation is easily solved once we consider the representation in Bloch waves24,25, namely:

where d is the distance between each site composing the chain, with the (quasi-)momentum κ confined to the Brillouin zone −π/d ≤ κ ≤ +π/d. These states are eigenstates for the Hamiltonian (1) with eigenvalues

Equation (3) expresses the well-known momentum/energy dispersion relation in lattices.
The evolution of a generic state  is obtained by the propagator U(t) = exp(−iH0t). In this simple setting we have
is obtained by the propagator U(t) = exp(−iH0t). In this simple setting we have  , where Jn(x) is the n-th Bessel-J function of the first kind. In Fig. 1 we show the evolution of two different initial conditions: a (sharp) localized condition (upper left frame) and a Gaussian wavepacket (upper right frame), both centered in the site labelled by 0, namely:
, where Jn(x) is the n-th Bessel-J function of the first kind. In Fig. 1 we show the evolution of two different initial conditions: a (sharp) localized condition (upper left frame) and a Gaussian wavepacket (upper right frame), both centered in the site labelled by 0, namely:
Evolution of the probability distribution |〈n|ψ(t)〉|2 (density plot) for Δ = 1, F = −1/40, β = 0.01 and for different initial conditions and system Hamiltonians.
(Top left): Sharp initial condition  (4), H = H0 (1); (top right): Gaussian distribution
(4), H = H0 (1); (top right): Gaussian distribution  (5), H = H0; (bottom left): Sharp condition
(5), H = H0; (bottom left): Sharp condition  , H = HB (6); (bottom right): Gaussian wavepacket .., H = HB.
, H = HB (6); (bottom right): Gaussian wavepacket .., H = HB.


If our task is to transfer the excitation/electron/photon from the initial position nI = 0 to a final position, or target site, p (p = 40 in the examples shown in the figures), this simple setup is completely uneffective. When starting from the sharp initial condition (4) the probability of reaching the target site decreases polynomially with the distance |p|. Starting from (5) leads to a diffusive behavior, since the initial momentum has mean 0 and variance 2β24.
Bloch oscillations
We now add a linear potential to the Hamiltonian (1), mimicking the action of a “force” trying to pull the excitation in the desired direction. This could induce inter-band transitions26,27; however, since we are going to consider initial states with negligible transverse moment and small values of the force parameter, transitions to higher bands can be safely neglected28. We can therefore introduce the following single-band Hamiltonian:

The eigenvalues of HB are  and the corresponding eigenstates are the Wannier-Stark states
and the corresponding eigenstates are the Wannier-Stark states  , m = 0, ±1, …, where
, m = 0, ±1, …, where

and γ = Δ/(2dF)24. The propagator, in the Bloch basis (2), is

The quasi-momentum κ is changed by the force as κ(t) = κ(0) − Ft. On the other side, the group velocity vg(κ) of the wave, is defined through the dispersion relation (3) by

it changes sign every time the quasi-momentum κ reaches the boundaries of the first Brillouin zone, leading to Bloch oscillations17. The evolution of the initial states (4) and (5) in the presence of a potential is illustrated in Fig. 1. The appearance of the breathing modes (see lower left panel) is a consequence of the flat momentum spectrum corresponding to the sharp initial condition (4). The components having absolute initial momentum |κ| ≈ 0(±π) travel the furthest along the chain, reaching a distance Δ/F. Their speed, initially close to dΔ/2 sin(0(±π)) = 0, increases in module until it reaches the maximum value dΔ/2 at t = π/2dF. Then the velocity decreases in modulus until t = π/dF when it changes sign (Bragg reflection). The initially fastest components of the wave packet, corresponding to |κ| ≈ π/2, get Bragg reflected sooner and are confined in a region (−Δ/2F, Δ/2F). The presence evenly distributed initial positive and negative momenta, leads moreover to an even spreading of the wavepacket over both the positive and negative axes; this leads to a further halving of the probability of reaching a target site p.
On the other side, if we take a Gaussian initial condition of the form (5), with  , the distribution of the momentum can be peaked around κ = 0. The wavepacket will now travel in a definite direction, set by the sign of F and the shape of the starting Gaussian is preserved during the evolution. In fact, besides a phase factor
, the distribution of the momentum can be peaked around κ = 0. The wavepacket will now travel in a definite direction, set by the sign of F and the shape of the starting Gaussian is preserved during the evolution. In fact, besides a phase factor  24 the coefficients distribution is the same as in (5) with the substitution:
24 the coefficients distribution is the same as in (5) with the substitution:  , where
, where  is the mean of the position observable
is the mean of the position observable  . The second relevant point is that the center
. The second relevant point is that the center  of this Gaussian shape performs an oscillation with period TB = 2π/(Fd) within the coordinate space. So, as long as the initial shape is weakly localized in the coordinate space, we expect that the whole Gaussian shape - representing the probability distribution for each site - performs an oscillation with amplitude 2|γ|. We point out, moreover, that after a half period the coefficients cn(t) take the form:
of this Gaussian shape performs an oscillation with period TB = 2π/(Fd) within the coordinate space. So, as long as the initial shape is weakly localized in the coordinate space, we expect that the whole Gaussian shape - representing the probability distribution for each site - performs an oscillation with amplitude 2|γ|. We point out, moreover, that after a half period the coefficients cn(t) take the form:

i.e. the wavefunction is the same as the initial one but shifted of −2γ and with alternate phase factors. Then, in this toy model, we are able to transfer the excitation from a site to another arbitrarily just varying the force acting on the system.
Constraining the resources
We now want to understand under which conditions the dynamics on a finite chain approximates properly the one discussed so far. This issue is quite relevant since in any realistic setting the number of lattice sites or waveguides would be limited. Let p once more indicate the target site and suppose that the excitation is initially localized in a neighborhood of the site labelled by 0. We suppose to attach η1 sites before the site labelled by 0 and η2 after the one labelled by p, as shown in Fig. 2.
The total number of sites composing the chain is therefore c = (p + 1) + η1 + η2. In order so simplify the notation we introduce the quantities: l ≡ −η1 and r ≡ p + η2. Dealing with the finite case the Hamiltonian governing the system will be:

Of course, the Gaussian superposition in (5) cannot be extended to an infinite number of sites, but at most to the ones composing the chain. Moreover the state |p〉 must not appear in the Gaussian superposition: if it were the case, we would have a non-vanishing initial probability of finding the spin-excitation in the target site. It is clear then the necessity of taking the Gaussian superposition truncated in certain interval on the chain, so that it involves only a restricted number of sites. In particular we considered a Gaussian superposition symmetrically truncated with respect to its center. Chosen a truncation parameter δ < η1 we set the initial state to be:

where A is a normalization factor and investigate how the truncation affects the transport property. As a figure of merit we employ the probability of finding the excitation in a neighborhood of the final site p. Upon denoting by

the probability of finding the spin excitation in the n-th site, we define the success probability as:

Our main aim is to maximize such probability. The parameters we can control are the force intensity F, the truncation parameter δ and the Gaussian superposition width β. The value F is automatically set once we decide how far the excitation has to travel. Notice that, if δ is taken too close to 1 the Gaussian superposition becomes very similar to the sharp condition, leading to the unproductive breathing modes shown in the lower left panel of Fig. 1. As already discussed above, moreover, we need  in order to have a momentum distribution peaked at 0. In our numerical simulations we set η1 = η2 = 2δ to avoid dangerous edge effects on the evolution of the truncated Gaussian superposition. As an example we plotted the values of success probability for Δ/F = −60 in Fig. 3 at the optimal time t = TB/2 (which does not depend on β or δ).
in order to have a momentum distribution peaked at 0. In our numerical simulations we set η1 = η2 = 2δ to avoid dangerous edge effects on the evolution of the truncated Gaussian superposition. As an example we plotted the values of success probability for Δ/F = −60 in Fig. 3 at the optimal time t = TB/2 (which does not depend on β or δ).
We notice that the mutual dependence of β and δ is clearly visible in all the region plotted. The behavior of the success probability at the vary of δ is clearly expected. In fact, as δ increases the region on which we collect the squared amplitudes cn(TB/2) covers an always wider part of the whole lattice. Obviously in the extreme case in which the region covered is the whole lattice the success probability is exactly 1. It is clear that exists a value for β for which the success probability is almost independent on δ and very close to 1. The value we find is about β = 0.01. For δ = 5 the success probability is already around 0.9 and reaches the value 1 for δ = 16. As we deal with a finite chain, it makes sense to take the lowest value of δ that makes the success probability larger than an assigned threshold value.
Discussion
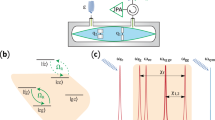
Now that we know in good approximation the dynamics of an excitation on a finite chain we can use the results obtained to perform an information transfer. The Hamiltonian (1), with n = 1, 2, …, N is equivalent to the one governing the propagation of the light in an array of N evanescently coupled optical waveguides8. The introduction of a linear potential will lead to solutions of the form (7), i.e. the Wannier-Stark states19,24. The external force acting on the lattice would be implemented by a linear gradient in the effective refractive index of the waveguides. This could be realized statically, but also dynamically, e.g. imposing a temperature gradient in the substrate and exploiting the thermo-optic effect18. In Fig. 4(a) we show the scheme of a possible implementation and the simulation of the propagating signals. We plot in Fig. 4(b) the mean position of the wavepackets simulated in (a) during the propagation through the waveguide array together with the intensity profiles P(n, L), defined as in (13), at the output: it is evident that the output states are well distinguishable and only slightly deformed with respect to the input [the grey profile in Fig. 4(b)]. In both figures the time parameter t has been replaced by the length L of the waveguide array.
(a) A possible scheme of the experimental implementation with a simulation of the propagating signals from left to right. We set the coupling constant J = 1 and the initial condition is a truncated Gaussian with β = 0.01, δ = 10 centered at n = 0. The colors correspond to different values of F, determined by the temperature gradient between T1 and T2: F = 1/80 (blue), F = 1/60 (red), F = 1/50 (magenta) and F = 1/40 (green). (b) The left plot shows the mean position of the wavepackets simulated in the scheme (a) as a function of the distance from the input point; n refers to the number of the waveguide. On the right we show the intensity profiles P(n, L) of the wavepackets at the output of the waveguide array, as obtained through numerical simulations. The grey profile in the left plot refers to the the intensity profile of input truncated Gaussian where we used the same scale as for P(n, L) (not shown for the sake of clarity).
In this setting, we have also an additional degree of freedom, namely the polarization of the light propagating in the array. This additional two-level degree of freedom does not interfere with the motion of the light in the lattice, as long as the coupling between the guides is polarization independent. We can then suppose that the light propagating through the lattice preserves its polarization. Light is thus carrying a qubit of information, encoded in its polarization state, from an initial region of the lattice to the target one. By modulating the external force the qubit could be displaced and dynamically redirected in different regions of the lattice.
The polarization state is analogous to a spin-1/2 state, characterized by the eigenstates |↓p〉 and |↑p〉, with respect to the Pauli operator  . The necessary Hilbert space for such a degree of freedom is
. The necessary Hilbert space for such a degree of freedom is  . The overall Hilbert space needed for the complete description of the system is:
. The overall Hilbert space needed for the complete description of the system is:  . As the initial wavefuction we use
. As the initial wavefuction we use  defined above with the addition of the polarization state, i.e.
defined above with the addition of the polarization state, i.e.

where  is the polarization state. Since in non-birefringent media the polarization of the light is not affected during the propagation, the Hamiltonian governing the motion of the electron through the lattice is
is the polarization state. Since in non-birefringent media the polarization of the light is not affected during the propagation, the Hamiltonian governing the motion of the electron through the lattice is  , where
, where  is the identity operator on the Hilbert space
is the identity operator on the Hilbert space  . Under the influence of this Hamiltonian the light particle can carry quantum information under the form of its polarization from a site to another following the dynamics discussed above.
. Under the influence of this Hamiltonian the light particle can carry quantum information under the form of its polarization from a site to another following the dynamics discussed above.
Waveguide arrays supporting such a dynamics could be fabricated by femtosecond laser writing29. This technique allows to directly inscribe high quality waveguides in glass substrates, exploiting the non-linear absorption of ultrashort laser pulses. This technology has widely proved its capabilities in producing complex three-dimensional waveguide arrays, able to reliably implement or simulate diverse quantum dynamics30,31 and, in particular, the Bloch oscillations of light32,33,34. Furthermore, it has been recently shown that femtosecond laser written circuits are specially suitable for the manipulation of polarization-encoded qubits, thanks to the relatively low birefringence that characterizes the waveguides fabricated with this technique20 and the possibility of fabricating polarization insensitive devices35.
Glass substrates are insensitive to external dc-generated fields19. To establish the required linear potential a stationary temperature gradient can be applied. In this case, the thermal gradient should stabilize before the state transfer begins. The response time is in the order of seconds, depending on the temperature gradient to be established and it limits the switching rate that can be achieved. Finding a substrate that allows a much shorter reconfiguration time represents a technological challenge issued by the proposed protocol: it should have negligible birefringence and be sensitive to dc (or ac) fields at the same time.
A truncated Gaussian input state can be experimentally implemented in free space by using hard apertures together with a cylindrical telescope and a microscope objective to launch light in the array36. Although this method may be extremely effective to characterize the device and to demonstrate the quantum transfer effect, it may not be the best choice when this device will be used in an integrated environment, e.g. inside a quantum computer. In that case, it would be more appropriate to exploit engineered photonic lattices to transform the single mode of an incoming waveguide into a truncated Gaussian state that will constitute the input state of the quantum transfer device. In particular, the engineered photonic lattice could consist in a linear array of waveguides implementing a discrete fractional Fourier transform, as recently demonstrated by femtosecond laser waveguide writing in glass37. In such waveguide array, single waveguide excitation can produce a Gaussian output distribution. By connecting only a truncated set of such waveguides to the quantum transfer chip one would achieve the desired input state. The collection of the output state after the quantum transfer chip can be performed in two ways. The first one considers the case where just detection of the photons is required; in this case an array of multimode fibers, connected to the detectors, can be butt-coupled to the chip, where the core of each multimode fiber is large enough and of sufficiently high numerical aperture to collect the whole Gaussian distribution, as represented in Fig. 4(a). The second collection scheme considers instead the case when further processing of the signal is foreseen; in this case a coherent reduction of the Gaussian wavepacket to a single waveguide should be achieved. This task could be accomplished by using again a waveguide array that implements the discrete fractional Fourier transform and by taking into account the phases acquired in the transfer process. As described in (10), alternating phases will be present in the different output modes; such phases are however constant and fully predictable and can therefore be statically compensated by a suitable geometrical deformation of the waveguides38 before applying the Fourier transform module.
While Bloch oscillations are well known since the early stages of quantum mechanics, here we propose a way to take advantage of them for the task of quantum state transmission. We showed that the constraints imposed by the finiteness of the resources available for the preparation of the initial state induce a minor lowering of the protocol efficiency. The minimal amount of engineering required to implement the system Hamiltonian and to prepare the initial state, make the realization of the protocol feasible with current quantum technology. Our results pave the way for further investigations concerning the system, such as the effects of noise39,40 and imperfections41 on the transmission probability.
Additional Information
How to cite this article: Tamascelli, D. et al. Quantum state transfer via Bloch oscillations. Sci. Rep. 6, 26054; doi: 10.1038/srep26054 (2016).
References
Di Vincenzo, D. The physical implementation of quantum computation. Fortschr. Phys. 48, 771–783 (2000).
Childs, A. M. & van Dam, W. Quantum algorithms for algebraic problems. Rev. Mod. Phys. 82, 1 (2010).
Feynman, R. Simulating physics with computers. Int. J. Theor. Phys. 21, 467–488 (1982).
Georgescu, I. M., Ashhab, S. & Nori, F. Quantum simulation. Rev. Mod. Phys. 86, 153 (2014).
Bose, S. Quantum communication through spin chain dynamics: an introductory overview. Cont. Phys. 48, 13–30 (2007).
Kay, A. Perfect, efficient, state transfer and its application as a constructive tool. Int. J. Quant. Inf. 08, 641–676 (2010).
Breid, B. M., Witthaut, D. & Korsch, H. J. Manipulation of matter waves using Bloch and Bloch–Zener oscillations. New J. Phys. 9, 62 (2007).
Christodoulides, D. N., Lederer, F. & Silberberg, Y. Discretizing light behaviour in linear and nonlinear waveguide lattices. Nature 424, 817–823 (2003).
Peres, A. Reversible logic and quantum computers. Phys. Rev. A 32, 3266–3276 (1985).
Christandl, M. et al. Perfect transfer of arbitrary states in quantum spin networks. Phys. Rev. A 71, 032312 (2005).
Nikolopoulos, G. M., Petrosyan, D. & Lambropoulos, P. Coherent electron wavepacket propagation and entanglement in array of coupled quantum dots. Europhys. Lett. 65, 297 (2004).
Gordon, R. Harmonic oscillation in a spatially finite array waveguide. Opt. Lett. 29, 2752–2754 (2004).
Kay, A. Interfacing with Hamiltonian dynamics. Phys. Rev. A 79, 042330 (2009).
Nikolopoulos, G. M., Petrosyan, D. & Lambropoulos, P. Electron wavepacket propagation in a chain of coupled quantum dots. J. Phys.: Cond. Mat. 16, 4991 (2004).
Perez-Leija, A. et al. Coherent quantum transport in photonic lattices. Phys. Rev. A 87, 012309 (2013).
Weimann, S., Kay, A., Keil, R., Nolte, S. & Szameit, A. Photonic coherent state transfer with hamiltonian dynamics. Opt. Lett. 39, 123–126 (2014).
Bloch, F. Über die Quantenmechanik der Elektronen in Kristallgittern. Z. Phys. 52, 555–600 (1929).
Pertsch, T., Dannberg, P., Elflein, W., Bräuer, A. & Lederer, F. Optical bloch oscillations in temperature tuned waveguide arrays. Phys. Rev. Lett. 83, 4752–4755 (1999).
Peschel, U., Pertsch, T. & Lederer, F. Optical Bloch oscillations in waveguide arrays. Opt. Lett. 23, 1701–1703 (1998).
Sansoni, L. et al. Polarization entangled state measurement on a chip. Phys. Rev. Lett. 105, 200503 (2010).
Corrielli, G. et al. Rotated waveplates in integrated waveguide optics. Nat. Comm. 5, 2549 (2014).
Dawes, A. M. C., Illing, L., Clark, S. M. & Gauthier, D. J. All-optical switching in rubidium vapor. Science 308, 672–674 (2005).
Harrison, W. A. Electronic structure and the properties of solids (Dover Publications, Inc., 1989).
Hartmann, T., Keck, F., Korsch, H. J. & Mossmann, S. Dynamics of Bloch oscillations. New J. Phys. 6, 2 (2004).
Holthaus, M. & Hone, Q. W. Localization effects in ac-driven tight-binding lattices. Phil. Mag. B 74, 105 (1996).
Glück, M., Kolovsky, A. R. & Korsch, H. J. Wannier–Stark resonances in optical and semiconductor superlattices. Phys. Rep. 366, 103–182 (2002).
Mandelik, D., Eisenberg, H. S., Silberberg, Y., Morandotti, R. & Aitchison, J. S. Band-gap structure of waveguide arrays and excitation of Floquet-Bloch solitons. Phys. Rev. Lett. 90, 053902 (2003).
Longhi, S. et al. Semiclassical motion of a multiband Bloch particle in a time-dependent field: Optical visualization. Phys. Rev. B. 74, 155116 (2006).
Della Valle, G., Osellame, R. & Laporta, P. Micromachining of photonic devices by femtosecond laser pulses. J. Opt. A: Pure Appl. Opt. 11, 013001 (2009).
Longhi, S. Quantum-optical analogies using photonic structures. Laser & Phot. Rev. 3, 243–261 (2009).
Szameit, A. & Nolte, S. Discrete optics in femtosecond-laser-written photonic structures. J. Phys. B: Atom. Molec. Opt. Phys. 43, 163001 (2010).
Chiodo, N. et al. Imaging of Bloch oscillations in erbium-doped curved waveguide arrays. Opt. Lett. 31, 1651–1653 (2006).
Dreisow, F. et al. Observation of anharmonic Bloch oscillations. Opt. Lett. 36, 3963–3965 (2011).
Corrielli, G., Crespi, A., Della Valle, G., Longhi, S. & Osellame, R. Fractional Bloch oscillations in photonic lattices. Nat. Comm. 4, 1555 (2013).
Sansoni, L. et al. Two-particle bosonic-fermionic quantum walk via integrated photonics. Phys. Rev. Lett. 108, 010502 (2012).
Pertsch, T., Zentgraf, T., Peschel, U., Bräuer, A. & Lederer, F. Anomalous refraction and diffraction in discrete optical systems. Phys. Rev. Lett. 88, 093901 (2002).
Weimann, S. et al. Implementation of quantum and classical discrete fractional Fourier transforms. arXiv:1508.00033 [quant-ph] (2015).
Crespi, A. et al. Anderson localization of entangled photons in an integrated quantum walk. Nat. Photon. 7, 322–328 (2013).
Benedetti, C., Buscemi, F., Bordone, P. & Paris, M. G. A. Dynamics of quantum correlations in colored-noise environments. Phys. Rev. A 87, 052328 (2013).
Rossi, M. A. C., Benedetti, C. & Paris, M. G. A. Engineering decoherence for two-qubit systems interacting with a classical environment. Int. J. Quant. Inf. 12, 1560003 (2014).
de Falco, D. & Tamascelli, D. Noise-assisted quantum transport and computation. J. Phys. A: Math. Theor. 46, 225301 (2013).
Acknowledgements
D.T., S.O., S.R. and M.G.A.P. acknowledge financial support by EU through the Collaborative Project QuProCS (Grant Agreement 641277) and by UniMI through the H2020 Transition Grant 14-6-3008000-625 and the grant Sviluppo UniMi 2015. R.O. acknowledges financial support by EU through the Collaborative Project QWAD (Grant Agreement 600838).
Author information
Authors and Affiliations
Contributions
D.T. and S.O. conceived the protocol. D.T., S.R. and S.O. performed the numerical and analytical analysis. D.T., S.O., R.O. and M.G.A.P. studied the feasibility of the protocol with current waveguide technology. All authors contributed to the preparation of the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Tamascelli, D., Olivares, S., Rossotti, S. et al. Quantum state transfer via Bloch oscillations. Sci Rep 6, 26054 (2016). https://doi.org/10.1038/srep26054
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep26054
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

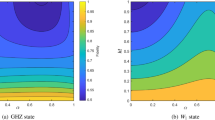



 as a function of β and δ for Δ/F = −60.
as a function of β and δ for Δ/F = −60.