Introduction

Universal quantum gate is the key element for quantum computation1,2,3,4,5,6,7,8,9. Two-qubit universal controlled-phase (c-phase) gate, the equivalent of two-qubit controlled-not (CNOT) gate (or the hyper-parallel two-photon CNOT gates on photon systems with two degrees of freedom7,8,9), can form universal quantum computing assisted by single-qubit operations and it has attracted much attention in recent years. To realize the deterministic quantum entangling gates, nonlinear interactions on qubits are required. Cavity quantum electrodynamics (QED)10 provides a promising platform to realize the nonlinear interaction between an atom and a field and it can achieve indirect nonlinear interaction among atoms or fields. To simulate cavity QED, atom11,12,13, spin14,15,16,17,18,19,20,21,22,23,24,25, or superconducting qubits26,27,28,29,30,31,32,33,34,35,36 coupled to optical cavities37,38,39,40,41, superconducting resonators42,43,44,45, or nanomechanical resonators46,47 have been studied a lot for quantum information processing both in experiment and in theory48.

Circuit QED, composed of a superconducting qubit coupled to a superconducting resonator42,43, gives a powerful candidate platform for quantum computation49 because of large-scale integration of superconducting qubits and all-electrical control using standard microwave and radio-frequency engineering techniques. It can work from the dispersive weak regime to the resonant strong regime50 and even the ultra-strong regime51. In microprocessors based on circuit QED, there are some interesting types of integration of superconducting qubits or resonators for quantum information processing, including several qubits coupled to a resonator52,53,54, several resonators coupled to a qubit or several qubits55,56,57,58,59,60,61,62,63,64, or some circuit QED systems coupled to each other by using qubits, superconducting transmission lines, or capacitance65,66,67,68,69. The basic tasks of quantum computation in circuit QED have been demonstrated in experiment, such as the c-phase gate52,70,71,72 and the controlled-controlled-phase gate53,54 on transmon qubits in the processor by integrating several superconducting qubits coupled to a 1D superconducting resonator, the generation of the entangled states on transmon qubits73 or two resonator qudits60 and the measurement on superconducting qubits69,74 or the microwave photons in a superconducting resonator75,76,77,78.

To avoid the indirect interaction among qubits in the processor by integrating more superconducting qubits coupled to a 1D superconducting resonator for complex quantum computation, one should take much smaller coupling strength between a qubit and the resonator or tunable coupling qubits. To integrate more resonators coupled to a qubit, smaller or tunable coupling between the qubit and each resonator is required as well. Small coupling strength leads to a slow quantum operation which limits the performance of the quantum computation due to the coherence time of qubits and decay rate of resonators. Tunable coupling between a qubit and multiple resonators increases the difficulty to design the superconducting circuits. As another candidate for integration of large-scale quantum computation, superconducting qubits hosted in different resonators interconnected by a qubit has been studied in experimental and theoretic works67,71. Up to now, there are no schemes to construct the multi-qubit universal gates on the distant transmon qubits in the similar systems.

In this paper, we propose a scheme to complete the c-phase gate on two distant transmon qutrits (DTQs) hosted in different resonators interconnected by a connection transmon qutrit (CTQ). Different with the schemes for entanglement generation and information transfer in the similar device67, our c-phase gate on two DTQs is achieved with one step by taking the same frequencies of qutrits and resonators and small coupling strengths of DTQs. Finally, we discuss the feasibility about its possible experiment implementation with the similar systems in previous works70,71 and construct a conventional two-dimensional surface code (SC) layout79,80 as an interesting possible application of our c-phase gate. Although our layout needs extra CTQs than the one in the previous work70, there is almost no demand on the life time of the CTQ as the information does not be populated in it during the gate operation and the interactions between nearest DTQs are reduced into four-step coupling. On one hand, the small coupling strength of DTQs can reduce the interactions between a qutrit and the nearest resonators. On the other hand, four-step coupling between nearest DTQs can be turned on and off easily by CTQs. These characters make our layout suitable to be integrated with a large scale.

Results

C-phase gate on distant transmon qutrits

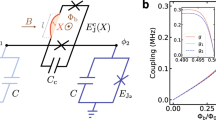
Let us consider a system composed of two DTQs coupled to different superconducting resonators interconnected by a CTQ, shown in Fig. 1. The Hamiltonian of the system in the interaction picture is (ħ = 1)

Figure 1
figure 1

(a) The setup for the construction of our c-phase gate on the distant transmon qutrits q1 and q2. q1 (q2) is coupled to the high-quality resonator ra (rb). The two resonators are interconnected by a connection transmon qutrit q3. (b–d) are the illustrations of interactions between q1 and ra, q3 and ra (rb) and q2 and rb, respectively.

Full size image

Here, a and b are the annihilation operators of the resonators ra and rb, respectively. and are the creation operators of the transitions and of qI(J), respectively. and are the coupling strengths between the two transitions of qI(J) and ra(b), respectively. and . is the transition frequency between the states and and of the qutrit qI(J). ωa(b) is the frequency of the resonator ra(b). |g〉 is the ground state of a transmon qutrit and |e〉 and |f 〉 are the first and the second excited states, respectively.

In order to obtain the effective Hamiltonian of the system composed of the two resonators (ra and rb) and three superconducting qutrits (q1, q2 and q3) to construct our c-phase gate, we take small values of , , and with and to make the transitions of q1 and of q2 to detune largely with ra and rb, respectively, which indicates the dispersive coupling between the transition and ra and that between and rb can be ignored. Besides, only the transition of the CTQ q3 should be considered as the coupling is the dispersive one and there is just one microwave photon can be generated in the resonators (just the transitions of q1 and of q2 are used in our scheme), respectively. Here, the Hamiltonian can be reduced from Eq. (1) to

To our purpose, we then take the transformations , and with the condition and 81,82,83. The transformations give us three new normal modes and only one of them (that is, c) resonates with the qutrits, so we can ignore the other two detuning modes and the system is reduced to a two-qubit one resonantly coupled to a single mode of the resonant field (further details can be found in the method). Eq. (2) becomes

Here, the frequencies of c mode and c± mode are ωa(b) and , respectively and the modes of c± are highly suppressed, which indicates the information cannot be populated in the state of q3. Here c, c− and c+ are three normal composite-particle operators.

If we take the initial states of the system with the Hamiltonian are , , and , respectively, the evolutions of the system can be expressed as

Here . By using these evolutions, we can construct the c-phase gate on q1 and q2. Its principle can be described as follows.

Suppose that the initial state of the system shown in Fig. 1 with the Hamiltonian is

Here . By evolving the system with and (k, m = 1, 2, 3, . . .), one can keep the states and unchanged from Eqs. (4) and (5), respectively. Meanwhile, the state undergoes an odd number of periods and generates a minus phase from Eq. (6) and the state goes through an even number of periods and maintains unchanged from Eq. (7). That is, the system evolves from Eq. (8) into

Here, α1 = cos θ1cos θ2, α2 = cos θ1sin θ2, α3 = sin θ1cos θ2 and α4 = sin θ1sin θ2. This is just the result of a c-phase gate on q1 and q2, whose matrix reads

in the basis .

Possible experimental implementation and the SC layout

The performance of our c-phase gate

To show the fidelity of our c-phase gate on the two distant qutrits q1 and q2, we numerically simulate the fidelity of our c-phase gate with the Hamiltonian Hcp of the whole system which contains the following dispersive couplings:

The dynamics of the system is determined by the master equation

Here, κa,b is the decay rate of the resonator ra,b. γj;g,e (γj;e,f) and are the energy relaxation and the dephase rates of the transition of qj, respectively. and . D[L]ρ = (2LρL+ − L+Lρ − ρL+L)/2.

Let us define the fidelity of our c-phase gate as17,58,81

Here is the final state of a system by using an ideal c-phase gate operation on its initial state with the effective Hamiltonian . ρ(t) is the realistic density operator after our c-phase gate operation on the initial state with the realistic Hamiltonian Hcp in which the coherence time of qubits, decay rates of resonators and the unwanted influence on qutrits from the unresonant parts should be taken into account. By taking the feasible experimental parameters as  GHz,  GHz,  GHz,  GHz84, ωa/(2π) = ωb/(2π) = 7.0 GHz,  μs85,   MHz,  MHz,  MHz71 and κa = κb  κ = 50 μs44, we numerically simulate the fidelity of our c-phase gate, which can reach 99.5% within 86.3 ns. Here the coupling strengths of q1 and q2 are the optimized ones with k = m = 1.

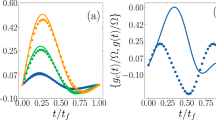
To show the possible influences from the realistic condition, we give the relation between the fidelity of our c-phase gate and one of the parameters γ1,2,3;g,e, κ, and , shown in Fig. 2. In Fig. 2(a), the probability of the information populated in the excited state of the CTQ is almost zero, which indicates the assumption that we take q3 as a two-energy-level qubit for obtaining Eq. (2) is reasonable. This agrees with the relation between the fidelity and the energy relaxation rate γ3;g,e of q3, shown in Fig. 2(b). Figure 2(c–f) show that the fidelity of the c-phase gate can be enhanced by a longer life time, small coupling strengths and large anharmonicities δ of q1 and q2. In Fig. 2(e), the fidelity of the gate is enhanced when  MHz (the operation time of the gate is about 86.3 ns), compared with the one when  MHz (the time is about 140.5 ns). In Fig. 2(f), the fidelity of our c-phase gate is reduced largely when the anharmonicity of the CTQs is δ = 0.37 GHz as the transition of q2 is resonant with the mode c+ at this time, which leads to the influence that its excitation cannot be suppressed. In detail, the difference between the effective Hamiltonian and the realistic Hamiltonian Hcp becomes a large one. The overlape between the final states and ρ(t) obtained by the evolutions with and Hcp, respectively from the same initial state is reduced largely.

Figure 2
figure 2

(a) The probability of the information populated in the state of q3 during the c-phase gate operation on the maximally entangled state of q1 and q2 with in Eq. (8). (b–f) The fidelity of the c-phase gate on the DTQs q1 and q2 varies with , κ, and the anharmonicity of the two transitions of q1 and q2 .

Full size image

Application of our c-phase gate in surface code layout

Operations on superconducting qubit cannot perform sufficiently well to let the qubit act as a computational qubit directly with recent techniques and several works are focused on the realization of the surface code on superconducting qubits for fault-tolerant quantum computing. The tolerance of the SC layout to errors allows as high as about 1% error rate of per operation, which is much bigger than 2 × 10−5 error rate of the per operation required in quantum correction code80. Qubits in SC code are divided into three types: data qubits, measure-z qubits and measure-x qubits. Away from the boundaries, each data (measure) qubits interact with four measure (data) qubits. As an application of our c-phase gate on two distant transmon qutrits, we construct a SC layout with a conventional square lattice70,80 for fault-tolerant quantum computing on the DTQs in an effective way.

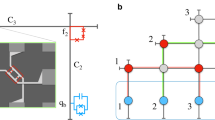
Our setup for the SC layout is shown in Fig. 3(a) in which each blue square represents a transmon qutrit with the 6.2 MHz coupling strength, each red circle is a transmon qutrit with the 5 MHz coupling strength and each gray triangle means a CTQ. The small strengths are used to avoid the interactions between the idle resonators and DTQs. To discuss the performance of our c-phase gate on nearest DTQs in the layout, we consider a cell of the layout shown in Fig. 3(b). Here, q1, ra, q3, rb and q2 are the same as those in our c-phase gate shown in Fig. 1. The couplings between q1 and rc, rd and re are considered when the interactions between q1 and the nearest DTQs are tuned off except for q2. The Hamiltonian of the cell is

Figure 3
figure 3

An application of our c-phase gate on two distant transmon qutrits for fault-tolerant quantum computing.

(a) The setup for the surface code layout. (b) A cell of the layout.

Full size image

Here, the frequencies of rc, rd and re are taken as 7.5 GHz, 8.0 GHz and 8.5 GHz, respectively. Except for the coupling strengths which are chosen here as

 MHz and  MHz, the other parameters are the same as the ones in the construction of our c-phase gate. For simplification, we calculate the fidelity of a cell or our c-phase gate on an initial maximally entangled state as

Here

The fidelities of both a cell and our c-phase gate on the given initial states change with the time t, shown in Fig. 4 in which we do not consider the decay and the energy relaxation rates of the resonators and the qutrits. One can see that the fidelity of a cell composed of our gate and three additional resonators on the given initial state decreases just a little, compared to that of our c-phase gate. Besides, small coupling strengths of DTQs, a tunable range of 2.5 GHz of a transmon qubit86 and a tunable range of 500 MHz within 1 ns87 of 1D superconducting resonator allow us to maintain the states of the idle qutrits. That is, our c-phase gate works effectively in the construction of the SC layout for fault-tolerant quantum computing.

Figure 4
figure 4

The fidelity of a cell in the surface code layout with our c-phase gate on an initial maximally entangled state of the system composed of q1 and q2, , shown with the blue dash-dotted line.

For comparison, the fidelity of our c-phase gate on the same initial state is given with the red solid line.

Full size image

In the SC layout for fault-tolerant quantum computing70,80, only the c-phase gate on nearest DTQs are required. Our scheme for the SC layout has some interesting advantages. First, small coupling strengths of DTQs allow us to complete the c-phase gates on nearest DTQs effectively. It can avoid the unwanted interactions from the other transmon qutrits and resonators by choosing proper frequency anharmonicity between a DTQ and its four nearest resonators. Second, CTQs makes the coupling between a pair of DTQs as a four-step one and it can be turned on and off easily. Third, CTQ cannot be excited during the operation of the c-phase gate and the energy relaxation time of the CTQ has little influence on the fidelity of the gate, which means the tunable-coupling phase qubit with the energy relaxation time of about 130 ns88 can also be used here (100 MHz ≫ {6.2, 5.0} MHz). A tunable regime from 0 MHz to 100 MHz88 gives us another way to turn on and off the unwanted interactions from the other DTQs in the layout robustly. All these features make the integration of the layout with a large scale easier.

Conclusion

In conclusion, we have proposed a scheme to construct the c-phase gate on two distant transmon qutrits (q1 and q2) which are coupled to different high-quality 1D superconducting resonators (ra and rb) intercoupled by a CTQ (q3) in the resonant regime of . The gate on distant transmon qutrits has not been studied before. Maybe our scheme can support the solid-state quantum computation based on this device. With our c-phase gate, we have proposed a SC layout for fault-tolerant quantum computing on transmon qutrits, which has attracted much attention70,72 as the error rate of quantum gate is hard to be reduced to 10−5 with recent techniques. The layout can be devided effectively into some cells by tuning the frequency of CTQs to detune with two nearest resonators largly. It can avoid the interactions from the other parts of the layout and provides a probability for the large scale integration of a SC layout for fault-tolerant quantum computing with circuit QED.

Methods

Hamiltonian and canonical transformations

In the Schrödinger picture, Eq. (2) can be rewritten as

Taking the canonical transformations , and with the conditions and , the Hamiltonian in Eq. (23) can be expressed as

The frequencies of modes c± are . When we take , the excitations of modes c± are highly suppressed as it detunes with the resonance modes (c, q1 and q2 with the frequency of ω) largely and the Hamiltonian in Eq. (24) can be reduced into

which can be written as

in the interaction picture.

Additional Information

How to cite this article: Hua, M. et al. One-step resonant controlled-phase gate on distant transmon qutrits in different 1D superconducting resonators. Sci. Rep. 5, 14541; doi: 10.1038/srep14541 (2015).