Scalable quantum computer with superconducting circuits in the ultrastrong coupling regime

Abstract

So far, superconducting quantum computers have certain constraints on qubit connectivity, such as nearest-neighbor couplings. To overcome this limitation, we propose a scalable architecture to simultaneously connect several pairs of distant qubits via a dispersively coupled quantum bus. The building block of the bus is composed of orthogonal coplanar waveguide resonators connected through ancillary flux qubits working in the ultrastrong coupling regime. This regime activates virtual processes that boost the effective qubit–qubit interaction, which results in quantum gates on the nanosecond timescale. The interaction is switchable and preserves the coherence of the qubits.

Introduction

Superconducting circuits are a very promising hardware platform for quantum computers with capabilities beyond the ones of classical computers (see, e.g., refs. ^1,2,3,4,5 and references therein). A basic requirement to perform quantum logic gates is to have controllable interactions among qubits (e.g., refs. ^6,7,8,9). Obviously, quantum computers benefit from higher and better connectivity among qubits, and this becomes more challenging to achieve as the system is scaled up. Unfortunately, so far, superconducting quantum computers have certain constraints on qubit connectivity, such as nearest-neighbor couplings¹⁰. Although the distant interaction between two or more qubits, mediated by a cavity bus, has been demonstrated (e.g., refs. ^11,12,13), this scheme is not convenient to connect many pairs of distant qubits simultaneously in a superconducting quantum computer. Indeed, in this case, the qubit–qubit interaction is activated by tuning qubit frequencies, leading to possible unwanted couplings and to a reduction of the coherence time of the qubits.

In addition to applications to quantum computing, superconducting circuits are a very versatile platform to investigate new quantum phenomena and to engineer quantum devices (e.g., refs. ^{14,15,16,17,18,19,20,21}). Note that the coupling between a superconducting artificial atom (e.g., refs. ^22,23,24,25) and a resonator can be a significant fraction of the bare atom and cavity energies (e.g., refs. ^{26,27,28,29,30,31}). In this ultrastrong coupling regime, the usual Jaynes–Cummings approximation breaks down and the counter-rotating terms must be taken into account^32,33.

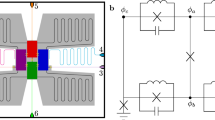
Here, we theoretically propose a scalable architecture to simultaneously couple pairs of distant superconducting qubits. The building block of this architecture is composed of three waveguides. Two of them (C₁ and C₂), see Fig. 1a, are directly connected to the qubits (q_a and q_b) that form the computational basis, while a third (C₃) is connected to the first two in a Π-shape form. At the intersection point, the interaction is mediated by ancillary flux qubits (f₁ and f₂) in the ultrastrong coupling regime. All components of the Π-connector are on resonance with each other. However, the two qubits, q_a and q_b, are detuned with respect to the eigenenergies of the bus. The last condition guarantees that the coupling between qubits is mediated by virtual excitations, thereby not affecting their coherence. Moreover, the bus takes advantage of the counter-rotating terms activated by the ultrastrong coupling, enhancing the coupling between the qubits. This allows to perform fast two-qubit gates on nanosecond timescales. To achieve scalability, these building blocks can be arranged in an array, see Fig. 1b, so that every qubit is connected with each other. Couplings between qubits can be switched on and off by tuning the ancillary flux qubit frequencies on and off resonance with the waveguides. Importantly, this allows the qubits q_a and q_b to remain in their optimal working point, preserving their coherence times.

Fig. 1: Π-connector and scalable architecture.

a Sketch of the Π-connector. Dark gray lines represent the coplanar waveguide resonators, C₁, C₂, and C₃. Red lines represent the flux qubits, f₁ and f₂, connecting the waveguides. Blue lines represent the data qubits (transmon here, but could also be other types), q_a and q_b. The inset inside the green dashed square represents the connection between the flux qubit (red box) and the constriction of the center conductor of the two orthogonal waveguides (light gray). b An array of data qubits (blue disks) at the bottom part are connected through a net of waveguides. At each node, a flux qubit tuned with the waveguides (red disk) mediates the interaction between data qubits. The gray disks (connector is “OFF”) denote detuned flux qubits.

Results

The Hamiltonian describing the Π-connector in Fig. 1a is $\hat{H}={\hat{H}}_{{{q}}}+{\hat{H}}_{\Pi }+{\hat{H}}_{{\rm{int}}}$, where ${\hat{H}}_{{{q}}}=\frac{1}{2}{\sum }_{i = {{a}},{{b}}}{\omega }_{{{{q}}}_{i}}\ {\hat{\sigma }}_{z}^{(i)}$ represents both qubit q_a and q_b (${\hslash}$ = 1),

$${\hat{H}}_{\Pi }=\frac{1}{2}\mathop{\sum }\limits_{i = 1}^{2}{\omega }_{{{\rm{f}}}_{i}}{\hat{\sigma }}_{z}^{(i)}+\mathop{\sum }\limits_{i = 1}^{3}{\omega }_{{\rm{c}}}{\hat{a}}_{(i)}^{\dagger }{\hat{a}}_{(i)}^{}+\mathop{\sum }\limits_{i = 1}^{2}{\lambda }_{{\rm{s}}}\ {\hat{\sigma }}_{x}^{(i)}\left({\hat{X}}_{i}+{\hat{X}}_{3}\right)$$

(1)

is the Hamiltonian of the ultrastrongly coupled quantum bus, and ${\hat{H}}_{{\rm{int}}}=\lambda \left(\ {\hat{\sigma }}_{x}^{({{a}})}{\hat{X}}_{1}+{\hat{\sigma }}_{x}^{({{b}})}{\hat{X}}_{2}\right)$ represents the interaction between the qubits and the quantum bus. Here, ${\hat{\sigma }}_{z}^{(i)}$ and ${\hat{\sigma }}_{x}^{(i)}$ are Pauli operators for the qubits q_a and q_b (i = a, b) and for the flux qubits (i = 1, 2), with transition energies ${\omega }_{{{{q}}}_{i}}={\omega }_{{{q}}}$ and ${\omega }_{{{{f}}}_{i}}={\omega }_{{{c}}}$, respectively. We set the fundamental frequency of all resonators C_k to be ω_c = 3ω_q, and we denote the annihilation, creation, and quadrature operators by ${\hat{a}}_{(k)}^{}$, ${\hat{a}}_{(k)}^{\dagger }$, and ${\hat{X}}_{k}={\hat{a}}_{(k)}^{}+{\hat{a}}_{(k)}^{\dagger }$ (k = 1, 2, 3). Flux qubit f₁ (f₂) is ultrastrongly coupled to cavity C₁ (C₂) and C₃, with coupling strength λ_s > 0.1ω_c. Instead, the coupling strength between qubit q_a (q_b) and resonator C₁ (C₂) is set to λ = 0.05ω_q. The latter interaction, operating in the dispersive regime, causes a shift in the qubit frequency,

$${\tilde{\omega }}_{{{{q}}}_{i}}={\omega }_{{{{q}}}_{i}}-{\lambda }^{2}/({\omega }_{{{c}}}+{\omega }_{{{{q}}}_{i}})\ ,$$

(2)

and a dressing in the qubit states^34,35. These qubit dressed states $\{\left|0\right\rangle ,\left|1\right\rangle \}$ are the ones forming our computational basis. We call “data qubits” the dressed qubits, which are generating the computational basis.

The quantum bus provides an effective XX interaction between data qubits mediated by virtual excitations, as it is guaranteed by the detuning condition ω_c − ω_q = 2ω_q. This interaction causes a two-qubit oscillation between states with one excitation: $\left|1,0\right\rangle$ and $\left|0,1\right\rangle$. The inset of Fig. 2a shows the swap from the state $\left|1,0\right\rangle$ to the state $\left|0,1\right\rangle$ in a time t = π/ω_R, where ω_R = 2λ_eff, and λ_eff is the effective coupling strength between data qubits. At t = π/2ω_R, as indicated by the arrow, a maximally entangled Bell state is generated, and a universal $\sqrt{i{\rm{SWAP}}}$ gate is obtained. Figure 2a shows the average gate fidelity^36,37

$${\mathcal{F}}=\int\,{\mathrm{d}}\Psi \left\langle \Psi \right|{\hat{U}}_{\sqrt{i{\rm{SWAP}}}}^{\dagger }\ {\hat{\rho }}_{\left|\Psi \right\rangle }{\hat{U}}_{\sqrt{i{\rm{SWAP}}}}\left|\Psi \right\rangle$$

(3)

generated by the quantum bus as a function of the ultrastrong coupling λ_s (blue circles), taking into consideration decoherence channels originating from the components of the bus. Here, ${\hat{\rho }}_{\left|\Psi \right\rangle }$ is the resulting density matrix after evolving the system for a time ${t}_{\sqrt{i{\rm{SWAP}}}}=\pi /2{\omega }_{{\rm{R}}}$, under the action of the full Hamiltonian in Eq. (1). The integral in Eq. (3) uses the unitarily invariant measure dΨ on the state space, normalized such that ∫dΨ = 1, the operator ${\hat{U}}_{\sqrt{i{\rm{SWAP}}}}$ is the ideal $\sqrt{i{\rm{SWAP}}}$ gate, and $\left|\Psi \right\rangle$ is the input state. For the data qubits, we choose T₁ = 70 μs and pure dephasing time T_φ = 92 μs (data are taken from ref. ³⁵, which fulfill our parameter conditions).

Fig. 2: Fidelity and effective coupling.

a Average gate fidelity of the $\sqrt{i{\rm{SWAP}}}$ gate generated by the quantum bus (blue circles) and by a direct qubit–qubit coupling (red solid curve) with coupling strength λ_eff. The chosen frequency transitions of the data qubits is ω_q = 4 GHz, the relaxation time is 70 μs and the pure dephasing time is 92 μs. Flux qubits have a relaxation time of 20 μs and pure dephasing time of 10 μs; resonators have a Q-factor of 5 × 10⁵. The inset shows the fidelity of the $\left|1,0\right\rangle$ (blue solid curve) and $\left|0,1\right\rangle$ states (green dotted curve). Here, the evolution is numerically calculated using the quantum bus, no dissipation is considered. b Effective coupling calculated numerically using the full Hamiltonian $\hat{H}$ (solid blue curve), dropping the counter-rotating terms (dashed black curve) and calculated using the semi-analytical expression in Eq. (4) (red dots).

When the interaction is activated, the ultrastrong coupling induces a small energy shift of the data qubit, resulting in a z-axis single-qubit rotation. This can be compensated using standard procedures³⁸. In our simulations, it is compensated by a rotation in the opposite direction. Figure 2a also shows the average fidelity of the $\sqrt{i{\rm{SWAP}}}$ gate (red solid curve) when the data qubits are directly coupled through the ideal interaction Hamiltonian ${\lambda }_{{\rm{eff}}}\ {\hat{\sigma }}_{x}^{(a)}{\hat{\sigma }}_{x}^{(b)}$. A comparison between the two curves proves that the bus does not affect the coherence of the data qubits, and shows that the only limitation to performance is the intrinsic decoherence of the data qubits. Considering data qubits with transition frequency of 4 GHz³⁵, for λ_s = 0.32ω_c, the fidelity is 99.87% and the gate time is 11.7 ns. Beyond this coupling point, the gate performance degrades due to the hybridization between the computational and bus states. All the dynamics are calculated using the master equation developed in ref. ²⁰, for T = 0.

Every type of superconducting qubit can be used as data qubit in our protocol. Currently, due to their long coherence time³⁵, transmon qubits are commonly used. However, the low anharmonicity of these artificial atoms could lead to non-negligible detrimental effects on the gate performance. To estimate these effects, we calculated the average gate fidelity using as data qubit the two lowest states of a three-level system with low anharmonicity. We set the transition frequency between the first and second excited states to 0.8ω_q, where ω_q is now the transition frequency between the ground and the first excited state. All other parameters are as above. In this setting, the average gate fidelity is 99.72% for λ_s/ω_c = 0.3 (instead of 99.75% calculated using the two-level system). Moreover, in the absence of decoherence channels, the fidelity is 99.99%. These results indicate that the low anharmonicity has a negligible impact on the performance of the gate.

Effective coupling

As explained in the “Methods” section, to calculate the effective qubit–qubit coupling we perform a projection of the full Hamiltonian $\hat{H}$ into the ground state of the bus Hamiltonian ${\hat{H}}_{\Pi }$. Considering the dispersive regime between data qubits and the bus, neglecting the dressing, the effective coupling becomes

$${\lambda }_{{\rm{eff}}}={\mathop {\sum}\limits_k}\frac{{g}_{k}^{(1)}{g}_{k}^{(2)}}{{\omega }_{{{q}}}-\Delta {E}_{k}}\ ,$$

(4)

where E_k and $|\tilde{k}\rangle$ are the eigenenergies and eigenstates of H_Π, and where ${g}_{k}^{(i)}=\lambda \ \langle \tilde{k}|{\hat{X}}_{i}|\tilde{0}\rangle$(i = 1, 2), and ΔE_k = E_k − E₀³⁹. In Fig. 2b, we numerically computed the effective coupling as a function of λ_s using the full Hamiltonian $\hat{H}$, and compared it with Eq. (4). The agreement is very good in the coupling range under investigation. According to perturbation theory to sixth order^40,41,42, the virtual processes that provide the main contribution to the qubit–qubit effective interaction, neglecting the dressing, are the ones that connect the state $\left|1,0\right\rangle {\left|0\right\rangle }_{{{b}}}$ to $\left|0,1\right\rangle {\left|0\right\rangle }_{{{b}}}$ (where ${\left|0\right\rangle }_{{{b}}}=\left|g,g,0,0,0\right\rangle$) through states with the lowest-energy differences with the initial state, $\left|1,0\right\rangle {\left|0\right\rangle }_{{{b}}}$. It appears clear now that the main process, Fig. 3 (red solid arrows), is the one that transfers one excitation through all the elements that compose the bus. In the same diagram, it is also shown a virtual process (red dashed arrows) involving the simultaneous excitation of the flux qubit f₁ and the resonator C₃, which is activated by the counter-rotating terms in the interacting part of the bus Hamiltonian ${\hat{H}}_{\Pi }$.

Fig. 3: Virtual states connecting q_a and q_b.

The main path (solid arrows) connecting the states $\left|1,0\right\rangle$ and $\left|0,1\right\rangle$ (blue states) through the virtual bus states (black states). The order of the labels in the black kets is $\left|{{{f}}}_{1},{{{f}}}_{2},{{{C}}}_{1},{{{C}}}_{2},{{{C}}}_{3}\right\rangle$. The dashed arrows indicate a path due to the counter-rotating terms.

In the ultrastrong coupling regime, the counter-rotating terms become relevant and activate virtual processes that strongly boost the effective coupling. To prove this, we have numerically calculated the effective coupling after dropping the counter-rotating terms in $\hat{H}$ (see Fig. 2b, dashed curve). Comparing this with the results from the full Hamiltonian (blue solid curve), we notice that λ_eff(λ_s), calculated with the counter-rotating terms, increases much faster compared to the one calculated without it, as a function of the coupling λ_s. It is standard procedure in perturbation theory to use virtual excitations to derive an effective interaction. These are the virtual photons we are referring to, not the ones in the ultrastrong coupling of cavity QED.

Switch-on and switch-off of the effective interaction

To realize a properly scalable system, it is important to be able to switch-on and switch-off the interaction between arbitrary data qubits. We achieve this by tuning (switch-on) and detuning (switch-off) to the bus the transition frequency of the ancillary flux qubit by varying the external flux Φ_ext = fΦ₀ threading it²¹. We set the switch-on condition at the optimal bias point, f → f_on = 0.5, where the flux qubit has a symmetric potential energy and maximum dipole moment M_on⁴³. To switch-off the interaction, we move the flux qubit away from its optimal point, by changing the external flux, f → f_off.

If we detune f₁ and f₂ from the Π-connector in Fig. 1a, using f_off = 0.522, the flux qubit transition frequency becomes $\approx 14\ {\omega }_{{{{f}}}_{1}}$, and the dipole moment becomes M_off = 6 × 10⁻²M_on (other parameters are provided in “Methods”). For λ_s = 0.3ω_c, the residual interaction is ${\lambda }_{{\rm{eff}}}^{({\rm{off}})}\approx 2\times \ 1{0}^{-11}{\omega }_{{\rm{q}}}$ and the on/off coupling ratio between data qubits is ≈6 × 10⁷, which is almost independent of λ_s. When the flux qubit f₂ is detuned and f₁ is tuned, the on/off coupling ratio is ≈9 × 10³. In this case, if the system consists of only two data qubits, no interaction occurs. This happens as the ultrastrong coupling shifts the frequency of data qubit q_a by a quantity larger than the residual effective coupling. For instance, if f₂ is detuned and λ_s = 0.3ω_c, the qubit q_b interacts with qubit q_a at ${\omega }_{{{{q}}}_{{{b}}}}={\omega }_{{{q}}}-9.3\times 1{0}^{-4}\ {\omega }_{{{q}}}$, with a residual effective coupling of ${\tilde{\lambda }}_{{\rm{eff}}}^{({\rm{off}})}=1.5\times 1{0}^{-7}{\omega }_{{{q}}}$. Note that when the flux qubits are not in the optimal bias point, a charge interaction with the second quadrature of the resonators is activated, but its contribution is negligible²⁶.

Scalable architecture

Figure 1b shows a possible scalable architecture for quantum computation using the Π-connector. In the bottom part of Fig. 1b, we represent an array of data qubits (blue disks). In the upper part we present the quantum bus. At each node, ancillary flux qubits can either couple (red disks) or decouple (gray disks) to the waveguides, depending on their frequency. In this way, it is possible to control the connectivity among arbitrary pairs of data qubits. For example, in Fig. 1b qubit 1 is connected to qubit 3, and qubit 2 is connected to qubit N. It is also possible to connect more than two qubits simultaneously. If the fundamental mode of the superconducting coplanar resonator is 12 GHz³⁵, and if the distance between two consecutive flux qubits in the resonator is 0.1 mm (which could be even shorter), it could be possible to connect about 100 data qubits. The effective interaction among N data qubits in the scalable architecture is described by

$${\hat{H}}_{{\rm{I}}}=\mathop{\sum }\limits_{k = 1}^{N-1}\mathop{\sum }\limits_{l = \ k+1}^{N}k{\lambda }_{{\rm{eff}}}^{kl}\ {\hat{\sigma }}_{x}^{(l)}{\hat{\sigma }}_{x}^{(k)}\ .$$

(5)

This considers that qubit 1 is connected (on or off) with all the other qubits using one path, qubit 2 is connected with the rest of the qubits using two paths for each qubit, qubit 3 is connected with the remaining qubits using three paths, and so on.

To evaluate cross-talk, we calculate the interaction of qubit N, the one with more connections, with all the other data qubits in the off coupling condition, ${\lambda }_{{\rm{eff}}}^{kl}={\lambda }_{{\rm{eff}}}^{({\rm{off}})}$. From Eq. (5), we find

$${\hat{H}}_{{\rm{I}}}^{(N)}={\hat{\sigma }}_{x}^{(N)}\left[\left(N-1\right){\lambda }_{{\rm{eff}}}^{({\rm{off}})}{\hat{\sigma }}_{x}^{(N-1)}+\left(N-2\right){\lambda }_{{\rm{eff}}}^{({\rm{off}})}{\hat{\sigma }}_{x}^{(N-2)}+\cdots +{\lambda }_{{\rm{eff}}}^{({\rm{off}})}{\hat{\sigma }}_{x}^{(1)}\right]\ .$$

(6)

Considering the (N − 1) data qubits as a single effective qubit, which is interacting with qubit N, ${\hat{\sigma }}_{x}^{(k)}\to {\hat{\sigma }}_{x}$ for all k ≠ N, we obtain

$${\hat{H}}_{{\rm{I}}}^{(N)}=\frac{N(N-1)}{2}{\lambda }_{{\rm{eff}}}^{({\rm{off}})}{\hat{\sigma }}_{x}^{(N)}{\hat{\sigma }}_{x}\ .$$

(7)

Now,

$${\Lambda }_{{\rm{eff}}}^{({\rm{off}})}={\lambda }_{{\rm{eff}}}^{({\rm{off}})}N(N-1)/2$$

(8)

is the residual interaction that affects qubit N in the off coupling condition. For λ_s = 0.3ω_c, using N = 100 data qubits, the coupler has a numerically measured on/off ratio of ≈12,000.

In this architecture, when each pair of data qubits is interacting, all the data qubits have the same frequency shift and the residual coupling ${\tilde{\lambda }}_{{\rm{eff}}}^{({\rm{off}})}$ is active. It is possible to cancel out this small interaction by detuning every pair of interacting data qubits from all other pairs by a quantity larger than the residual interaction. This can be achieved by changing the flux qubit frequency, which in turn changes the data qubit dressing.

Discussion

By taking advantage of the large coupling between flux qubits and the modes of waveguides or LC resonators, we proposed a scalable architecture that allows to control the coupling between many distant qubits. We numerically showed that the effective coupling is boosted by the counter-rotating terms of the Rabi Hamiltonian, whose contribution become more relevant in the ultrastrong coupling regime. The switch-on and switch-off of the interaction between data qubits is controlled by the magnetic fluxes threading the flux qubits, which tune their transition frequencies to the bus. Note that the resonant condition among the waveguides and flux qubits in the bus does not have to be perfect, because there is considerable tolerance. In fact, the strength of the effective coupling does not depend on this condition, but it depends on the detuning between each element of the bus and the data qubits, and on the couplings between elements of the bus. However, the resonant condition between data qubits must be satisfied. Unfortunately, current fabrication tolerances do not allow to set the frequency of the qubits precisely, and SQUID loops must be used to tune the data qubit frequencies. However, near-future improvements in the fabrication quality of qubits will eventually allow to take full advantage of this proposal. We believe that this architecture might lead to a new generation of quantum computer architectures controlled by elements largely detuned from the data ones, allowing to increase the complexity of the system without affecting the coherence times. A natural evolution could be the connection of a matrix of data qubits through waveguides in a 3D circuit¹⁹.

Methods

Effective coupling

In this section, we derive an effective model to describe the dynamics of two data qubits in contact with a quantum bus. We do this by projecting the full dynamics (which takes place in the total Hilbert space ${\mathcal{H}}$ of both data qubits and bus) into the subspace ${{\mathcal{H}}}_{\text{eff}}=P{\mathcal{H}}$, where the bus is in the ground state. Here, $\hat{P}={\hat{{\mathbb{I}}}}_{{q}}\otimes \left|\tilde{0}\right\rangle \left\langle \tilde{0}\right|$ denotes the projector into the ground state $\left|\tilde{0}\right\rangle$ of the bus (${\hat{{\mathbb{I}}}}_{{q}}$ being the identity operator on the data qubits).

As a first step, we decompose the total Hamiltonian $\hat{H}$ into a “diagonal” contribution ${\hat{H}}_{0}$ (which preserves ${{\mathcal{H}}}_{\text{eff}}$, i.e., $[{\hat{H}}_{0},\hat{P}]=0$) and an “off-diagonal” contribution $\hat{V}$ (for which $[\hat{V},\hat{P}]\, \ne \,0$). By defining a complementary projector $\hat{Q}$, such that $\hat{P}+\hat{Q}=\hat{{\mathbb{I}}}$, we can write

$$\begin{array}{lll}\hat{H}=(\hat{P}+\hat{Q})\hat{H}(\hat{P}+\hat{Q})\\ ={\hat{H}}_{0}+\hat{V},\end{array}$$

(9)

where ${\hat{H}}_{0}=\hat{P}\hat{H}\hat{P}+\hat{Q}\hat{H}\hat{Q}$ and $\hat{V}=\hat{P}{\hat{H}}_{\text{int}}\hat{Q}+\hat{Q}{\hat{H}}_{\text{int}}\hat{P}$. The potential $\hat{V}$ can be explicitly written as

$$\begin{array}{lll}\hat{V}={\mathop {\sum}\limits_k}\left[{g}_{k}^{(1)}{\hat{\sigma }}_{x}^{(a)}\left(\left|\tilde{k}\rangle\langle \tilde{0}\right|+\left|\tilde{0}\rangle\langle \tilde{k}\right|\right)+{g}_{k}^{(2)}{\hat{\sigma }}_{x}^{(b)}\left(\left|\tilde{k}\rangle\langle \tilde{0}\right|+\left|\tilde{0}\rangle\langle \tilde{k}\right|\right)\right]\\ \simeq {\mathop {\sum}\limits_k}\left[{g}_{k}^{(1)}{\hat{\sigma }}_{-}^{(a)}\left|\tilde{k}\rangle\langle \tilde{0}\right|+{g}_{k}^{(2)}{\hat{\sigma }}_{-}^{(b)}\left|\tilde{k}\rangle\langle \tilde{0}\right|\right]+{\rm{H}}.{\rm{c}}.,\ \end{array}$$

(10)

where we made a rotating-wave approximation under the assumption that $| {g}_{k}^{(1)}| ,| {g}_{k}^{(2)}| \ll {\omega }_{{q}},\Delta {E}_{k}$. We further assume to be in a dispersive regime, where the detuning between the splitting of the data qubits ω_q and the transition energies of the bus ΔE_k are much larger than the couplings ${g}_{k}^{(1)}$ and ${g}_{k}^{(2)}$ (i.e., $| {\omega }_{q}-\Delta {E}_{k}| \gg | {g}_{k}^{(1)}| ,| {g}_{k}^{(2)}|$). In this limit, it is possible to perturbatively define a rotating frame where the dynamics is effectively constrained in ${{\mathcal{H}}}_{\text{eff}}$ (Schrieffer–Wolff transformation). Specifically, a change of frame $\exp [\hat{S}]$ (for an anti-Hermitian operator $\hat{S}$, such that $[{\hat{H}}_{0},\hat{S}]=\hat{V}$) allows to define the effective Hamiltonian

$${\hat{H}}_{\text{eff}}=\hat{P}{e}^{\hat{S}}\hat{H}{e}^{-\hat{S}}\hat{P}\simeq \hat{P}\hat{{H}_{0}}\hat{P}+\frac{1}{2}\hat{P}[\hat{S},\hat{V}]\hat{P}\ ,$$

(11)

at the lowest nontrivial order in $\hat{S}$. Specifically, by choosing

$$\hat{S}=\mathop {\sum}\limits_{k \,{>}\,0}\left(\frac{{g}_{k}^{(1)}}{{\omega}_{q}-\Delta {E}_{k}}{\hat{\sigma }}_{+}^{(a)}+\frac{{g}_{k}^{(2)}}{{\omega}_{q}-\Delta {E}_{k}}{\hat{\sigma}}_{+}^{(b)}\right)\left|\tilde{0}\rangle\langle\tilde{k}\right|-\,\text{H.c.},$$

(12)

and computing the commutator $[\hat{S},\hat{V}]$ in Eq. (11), we obtain the effective coupling between the data qubits described in the main text.

Flux qubit resonator

The energies and electric dipole moments were calculated considering a flux qubit composed of three Josephson junctions with energies E_J1 = E_J2 = E_J, and E_J3 = αE_J. The Hamiltonian of the flux qubit is⁴³

$${H}_{{\rm{F}}}={E}_{{\rm{C}}}\ {P}_{+}+\frac{{E}_{{\rm{C}}}}{1+2\alpha }\ {P}_{-}+U({\varphi }_{+},{\varphi }_{-})\ ,$$

(13)

with $U({\varphi }_{+},{\varphi }_{-})=-{E}_{{\rm{J}}}[2\cos\,{\varphi }_{+}\cos\,{\varphi }_{-}+\alpha \cos\,(2\pi f+2{\varphi }_{+})]$, having defined φ₊ = (φ₁ + φ₂)/2 and φ₋ = (φ₁ − φ₂)/2, where φ₁ and φ₂ are the phase drops across the larger junctions. P₊ and P₋ are the conjugate momenta of φ₊ and φ₋. Choosing E_J = 35E_C, E_C = 27.1 GHz, and α = 0.8, the dipole moment was determined by the matrix element $\left\langle g\right|\sin (2\pi f+2{\varphi }_{+})\left|e\right\rangle$.

Interaction between a flux qubit and two orthogonal coplanar waveguides

The derivation of the flux qubit-resonator Hamiltonian ${\hat{H}}_{\Pi }$ is standard²⁶, but here the voltage condition for the flux qubit (red loop in Fig. 4) is $\mathop{\sum }\nolimits_{i = 1}^{3}{\varphi }_{i}+\Delta {\psi }_{{{{C}}}_{1}}+\Delta {\psi }_{{{{C}}}_{2}}={\Phi }_{{\rm{ext}}}$, where $\Delta {\psi }_{{{{C}}}_{1}}={\psi }_{{{{C}}}_{1}}({x}_{2})-{\psi }_{{{{C}}}_{1}}({x}_{1})$ and $\Delta {\psi }_{{{{C}}}_{2}}={\psi }_{{{{C}}}_{2}}({y}_{1})-{\psi }_{{{{C}}}_{2}}({y}_{2})$.

Fig. 4: Equivalent circuit diagram.

Coplanar waveguides (black lines) connected to the flux qubit (red lines).

The ultrastrong coupling between a flux qubit and two superconducting coplanar stripline resonators has been experimentally realized⁴⁴. However, our scheme further requires the waveguides to cross and the resonator modes not to be significantly modified by the coupling with the flux qubit. The inset in Fig. 1a represents a sketch of the connection between the orthogonal waveguides mediated by the ancillary flux qubit. The latter is directly connected to both the center conductor of the coplanar waveguide transmission-line resonators, see also Fig. 4. At the insertion point, the width of the center conductor is narrower and the local inductance is larger, to enhance the coupling between the flux qubit and the resonator²⁶. The three Josephson junctions forming the flux qubits must be inserted in the two tiny flux qubit arms that connect the center conductors of both waveguides. In this way, the current in the resonator flows predominantly through the center conductor constrictions of the waveguides and the resonator modes are not significantly modified. Since the distribution of the electromagnetic field is not uniform in the resonator, we suggest to fabricate waveguides with progressively narrower constrictions, in order to maintain a uniform coupling for all qubits. Alternatively, one can increase the coupling strength by inserting several Josephson junctions in the constrictions with a progressively increasing inductance along the waveguide²⁶.