Abstract
We propose a novel method to determine the complex amplitude of each eigenfunction composing a vibrational wavepacket of  /
/ molecular ions evolving with a ~10 fs time scale. We find that the two-dimensional spectrogram of the kinetic energy release (KER) of H+/D+ fragments plotted against the time delay of the probe pulse is equivalent to the spectrogram used in the frequency-resolved optical gating (FROG) technique to retrieve the complex amplitude of an ultrashort optical pulse. By adapting the FROG algorithm to the delay-KER spectrogram of the vibrational wavepacket, we have successfully reconstructed the complex amplitude. The deterioration in retrieval accuracy caused by the bandpass filter required to process actual experimental data is also discussed.
molecular ions evolving with a ~10 fs time scale. We find that the two-dimensional spectrogram of the kinetic energy release (KER) of H+/D+ fragments plotted against the time delay of the probe pulse is equivalent to the spectrogram used in the frequency-resolved optical gating (FROG) technique to retrieve the complex amplitude of an ultrashort optical pulse. By adapting the FROG algorithm to the delay-KER spectrogram of the vibrational wavepacket, we have successfully reconstructed the complex amplitude. The deterioration in retrieval accuracy caused by the bandpass filter required to process actual experimental data is also discussed.
Similar content being viewed by others
Introduction
The coherent ultrafast dynamics of matter is governed by the coherent superposition of multiple quantum states described with wavefunctions, which we call a wavepacket. We can find many studies that deal with the real-time evolution of a wavepacket composed of various quantum states, such as electronic bound states in an atom1,2,3,4, continuum electronic states with the ionization of an atom5 and rotational6 and vibrational7,8 states of a molecule. This is due to the fact that the wavepacket exhibits the fundamental characteristics of quantum mechanics9,10,11 and thus has fascinated many researchers. In addition, the wavepacket is a strong candidate system for manipulating quantum information12.
As a specific target for investigating fundamental physics in a molecule, the vibrational wavepacket of  /
/ 13,14,15,16,17,18 has strongly attracted our interest because
13,14,15,16,17,18 has strongly attracted our interest because  /
/ is the simplest molecular system composed of only two nuclei and one electron. The ultrashort vibrational period with 10 fs order is another feature attractive to the community of ultrafast optical science.
is the simplest molecular system composed of only two nuclei and one electron. The ultrashort vibrational period with 10 fs order is another feature attractive to the community of ultrafast optical science.
The common basic scheme for observing the wavepacket dynamics follows the conventional pump-probe measurement, in which the pump pulse ionizes a neutral H2/D2 molecule to create a vibrational wavepacket and then, after a delay, the probe pulse is irradiated to dissociate a  /
/ molecular ion. The spectrogram of the kinetic energy release (KER) determined from the observed H+/D+ fragment ions with the scanning delay of the probe pulse reveals the vibrational motion of the wavepacket. The most significant and basic requirement for the pump and probe pulses is that both pulse durations should be much shorter than the vibrational period. Ergler et al.14 successfully observed the vibrational motion by using a pair of intense sub-10-fs pulses of a Ti:sapphire laser as the pump and probe pulses. Kelkensberg et al.16 demonstrated that an isolated attosecond pulse generated as a high-harmonic field of an a-few-cycle Ti:sapphire laser pulse is useful for generating the vibrational wavepacket of
molecular ion. The spectrogram of the kinetic energy release (KER) determined from the observed H+/D+ fragment ions with the scanning delay of the probe pulse reveals the vibrational motion of the wavepacket. The most significant and basic requirement for the pump and probe pulses is that both pulse durations should be much shorter than the vibrational period. Ergler et al.14 successfully observed the vibrational motion by using a pair of intense sub-10-fs pulses of a Ti:sapphire laser as the pump and probe pulses. Kelkensberg et al.16 demonstrated that an isolated attosecond pulse generated as a high-harmonic field of an a-few-cycle Ti:sapphire laser pulse is useful for generating the vibrational wavepacket of  , the time evolution of which was revealed with another a-few-cycle Ti:sapphire laser pulse. We have also shown18 that an attosecond pulse train (APT), which was generated from a 14 fs terawatt pulse of a Ti:sapphire laser, can decompose the time evolution of vibrational states into the KER region thanks to the multiple color components in deep/vacuum ultraviolet (DUV/VUV) regions included in the sub-10-fs probe pulse.
, the time evolution of which was revealed with another a-few-cycle Ti:sapphire laser pulse. We have also shown18 that an attosecond pulse train (APT), which was generated from a 14 fs terawatt pulse of a Ti:sapphire laser, can decompose the time evolution of vibrational states into the KER region thanks to the multiple color components in deep/vacuum ultraviolet (DUV/VUV) regions included in the sub-10-fs probe pulse.
The physical model for specifying the vibrational wavepacket of  /
/ is also common in these studies13,19,20,21,22. The probability amplitude for finding the wavepacket at the internuclear distance R at time t is described as a coherent superposition of the vibrational states with the time-evolving phase factor:
is also common in these studies13,19,20,21,22. The probability amplitude for finding the wavepacket at the internuclear distance R at time t is described as a coherent superposition of the vibrational states with the time-evolving phase factor:

where  and
and  are the νth vibrational eigenfunction and its eigenenergy, respectively. We denote Planck’s constant divided by π as ħ. The amplitude of each eigenfunction, aν, which determines the wavepacket function at the initial time, should be found by considering all the quantum degrees of freedom in the pumping (ionization) process. Nevertheless, the overlap integral between
are the νth vibrational eigenfunction and its eigenenergy, respectively. We denote Planck’s constant divided by π as ħ. The amplitude of each eigenfunction, aν, which determines the wavepacket function at the initial time, should be found by considering all the quantum degrees of freedom in the pumping (ionization) process. Nevertheless, the overlap integral between  and
and  is often substituted for this amplitude by assuming the Franck-Condon principle via ionization, where
is often substituted for this amplitude by assuming the Franck-Condon principle via ionization, where  is the ground vibrational function of the H2/D2 molecule. The phase of the complex amplitude aν, arg{aν}, is fixed under this approximated condition (Franck-Condon approximation, FCA). Urbain et al. found that the magnitude of aν significantly deviated from that obtained under the FCA via tunneling ionization23. Jiang and coworkers17,24 pointed out that aν should generally be a complex number and that the non-FC model accompanying the transition of the electronic state with a continuum electron was essential for reproducing their experimental data. They still did not, however, observe arg{aν}.
is the ground vibrational function of the H2/D2 molecule. The phase of the complex amplitude aν, arg{aν}, is fixed under this approximated condition (Franck-Condon approximation, FCA). Urbain et al. found that the magnitude of aν significantly deviated from that obtained under the FCA via tunneling ionization23. Jiang and coworkers17,24 pointed out that aν should generally be a complex number and that the non-FC model accompanying the transition of the electronic state with a continuum electron was essential for reproducing their experimental data. They still did not, however, observe arg{aν}.
The aim of our research reported in this paper is to determine the complex amplitude, aν, from experimental data so as to completely reconstruct the vibrational wavepacket of  /
/ . This is very similar to the determination of the Fourier amplitude of an ultrashort optical pulse at the (angular) frequency ω,
. This is very similar to the determination of the Fourier amplitude of an ultrashort optical pulse at the (angular) frequency ω,  , because the complex amplitude of the optical electric field, ε(z;t), is described as
, because the complex amplitude of the optical electric field, ε(z;t), is described as

when we can approximate the optical electric field as a plane wave propagating along the z-axis. The plane-wave function, eik(ω)z, alters with ω through the dispersion relation of the wavenumber, k(ω), against ω and gives us the functional basis set used to expand ε(z;t), as the vibrational wavefunction,  , in Eq.(1) forms the functional basis for φg(R;t).
, in Eq.(1) forms the functional basis for φg(R;t).
Therefore, it is reasonable to consider that a technique used to retrieve the amplitude of an optical pulse may also be useful for reconstructing a vibrational wavepacket. We have developed this simple idea and found that the experimental scheme in our previous study18 is desirable for applying the frequency-resolved optical gating (FROG) technique25,26, which is nowadays considered a conventional technique for characterizing an ultrashort optical pulse in the range from ps27 to as28. In the following section, we briefly review our previous study in which we observed the real-time motion of the vibrational wavepacket of  and then we show that the physical model of the probing process for the vibrational wavepacket is very similar to that for describing the FROG spectrogram. After describing the development of the FROG algorithm for the vibrational wavepacket, which we call ‘Matter-Wave FROG (MW-FROG)’, we report on the implementation of MW-FROG for a modeled vibrational wavepacket and discuss the accuracy of the retrieved data.
and then we show that the physical model of the probing process for the vibrational wavepacket is very similar to that for describing the FROG spectrogram. After describing the development of the FROG algorithm for the vibrational wavepacket, which we call ‘Matter-Wave FROG (MW-FROG)’, we report on the implementation of MW-FROG for a modeled vibrational wavepacket and discuss the accuracy of the retrieved data.
Experimental scheme
The experimental setup for the measurement of the vibrational wavepacket of  reported in ref. 18 was similar to that adopted for the measurement of the interferometric autocorrelation (IAC) signal of an APT29,31, as shown in Fig. 1. The high-order harmonic fields of a Ti:sapphire laser with a duration of 14 fs32 were generated from a Xe gas target in a 10-cm-long static gas cell and spatially split into two beams with a pair of silicon harmonic separator mirrors. Each harmonic separator mirror strongly attenuated the fundamental laser pulse, while the 11th- or higher-order harmonic fields, the photon energy of which exceeded the ionization energy of the H2 molecule, were efficiently reflected by the harmonic separator mirrors. The weak residual fundamental, 3rd- and 5th-order harmonic components were also contained in the reflected pulse.
reported in ref. 18 was similar to that adopted for the measurement of the interferometric autocorrelation (IAC) signal of an APT29,31, as shown in Fig. 1. The high-order harmonic fields of a Ti:sapphire laser with a duration of 14 fs32 were generated from a Xe gas target in a 10-cm-long static gas cell and spatially split into two beams with a pair of silicon harmonic separator mirrors. Each harmonic separator mirror strongly attenuated the fundamental laser pulse, while the 11th- or higher-order harmonic fields, the photon energy of which exceeded the ionization energy of the H2 molecule, were efficiently reflected by the harmonic separator mirrors. The weak residual fundamental, 3rd- and 5th-order harmonic components were also contained in the reflected pulse.
The twin harmonic pulses reflected from the silicon mirror pair were focused into a molecular beam of D2 injected through a skimmer to partition the chamber from a differential pumping section that contained a pulsed gas valve. The generated ion fragments of D+ were analyzed using a velocity-map-imaging (VMI) spectrometer to resolve the angular distribution and kinetic energy (KE) of the fragments. We obtained the KER spectrum for the dissociation of D+ + D by angularly integrating the recorded VMI with double the KE.
We had already specified in preceding studies18,29 that the dissociation process was accompanied by the excitation of the  molecule from the ground bound electronic state (1sσg) to the repulsive electronic state (2pσu) by the one-photon absorption of the fundamental, 3rd-order and 5th-order harmonic components. We could discriminate which order harmonic component contributed to the dissociation by resolving the KER spectrum, because the excitation is likely to occur at the nuclear distance where the energy difference between the two states is similar to the photon energy. The energy diagram of the relevant adiabatic potentials is shown in Fig. 2.
molecule from the ground bound electronic state (1sσg) to the repulsive electronic state (2pσu) by the one-photon absorption of the fundamental, 3rd-order and 5th-order harmonic components. We could discriminate which order harmonic component contributed to the dissociation by resolving the KER spectrum, because the excitation is likely to occur at the nuclear distance where the energy difference between the two states is similar to the photon energy. The energy diagram of the relevant adiabatic potentials is shown in Fig. 2.
Energy diagram of the D2 molecular system relevant to the pump-probe measurement in our experimental scheme.
The vibrational wavepacket on the adiabatic potential of the  state is created by one-photon ionization by the irradiation of harmonic components in the APT, the orders of which are 11th and higher. The vibrational state is probed by excitation to the
state is created by one-photon ionization by the irradiation of harmonic components in the APT, the orders of which are 11th and higher. The vibrational state is probed by excitation to the  state with the one-photon absorption of the fundamental, 3rd- and 5th-order components in the APT.
state with the one-photon absorption of the fundamental, 3rd- and 5th-order components in the APT.
We scanned the delay between the twin harmonic pulses by translating one of the silicon harmonic separator mirrors and found that the KER spectrum is periodically modulated in accordance with the delay, as shown in Fig. 3 in ref. 18, as clear evidence of the vibrational wavepacket motion with a period of ~22 fs. This is due to the short pulse duration of the ionizing pulse, which was expected to be ~5 fs or less from the results of the IAC measurement utilizing the two-photon ionization of the N2 molecule33,34 and that of the probe pulse with a duration expected to be ~7 fs. We adopt a well-known theoretical model for the two-level system of the electronic state to describe the probing process used in the experiment in the next subsection.
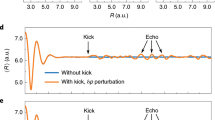
(a) Delay-KER spectrogram calculated from |T(ωu;τ)|2 in Eq.(16) by assuming that aν coincides with the overlap integral and that the gate pulse is the Fourier-limited pulse obtained from the measured spectra of the 3rd- and 5th-order harmonic fields. (b) Magnitude square of the Fourier transform of the delay-KER spectrogram depicted in Fig. 3(a). The color scale used to plot the intensity is logarithmic. The bandpass filter applied to the test target image depicted in the first panel in the last figure of this paper is also shown as contour plots.
Theoretical model for the probe process
We assume that the initial vibrational wavepacket instantaneously appears in the ground electronic state of  (1sσg), instead of
(1sσg), instead of  , for simplicity, at t = 0 and then the probe optical pulse, which is composed of the coherent superposition of the 3rd- and 5th-order harmonic pulses of a Ti:sapphire laser pulse, is irradiated at a delay of τ, resulting in the excitation of
, for simplicity, at t = 0 and then the probe optical pulse, which is composed of the coherent superposition of the 3rd- and 5th-order harmonic pulses of a Ti:sapphire laser pulse, is irradiated at a delay of τ, resulting in the excitation of  from the 1sσg state to the 2pσu state. The essential features of the vibrational states of
from the 1sσg state to the 2pσu state. The essential features of the vibrational states of  and
and  are the same. We neglect the contribution of the fundamental laser pulse because of the low signal-to-noise ratio of the beat frequency observed in the experiment18.
are the same. We neglect the contribution of the fundamental laser pulse because of the low signal-to-noise ratio of the beat frequency observed in the experiment18.
It is well known13,19,20,21,22 that the physical model of this system can be described with the Hamiltonian

and with the electronic state

satisfying the Schrödinger equation

Here, R is the relative nuclear distance coordinate and the vectors |u〉 and |g〉 are the eigenvectors of the electronic excited and ground states, expressed as |u〉 ≡ T(1,0) and |g〉 ≡ T(0,1), respectively. The Hamiltonian Hu/g(R) describes the nuclear motion in the 2pσu and 1sσg states and is defined as Hu/g(R) ≡ −(2M)−1ħ2∂2/∂R2 + Vu/g(R) for the reduced hydrogen mass M and adiabatic potential Vu/g(R). The delayed probe laser pulse at time t is expressed as E(t − τ) and this laser pulse interacts with the electronic states via the dipole moment μ(R), which generally depends on the relative nuclear distance. Thus, D(R,t) in the off-diagonal elements in the Hamiltonian matrix on the right-hand side of Eq.(3) is expressed as D(R,t) ≡ μ(R) E(t − τ). The wave functions ψu(R,t) and ψg(R,t) give us the probability amplitudes of the nuclear motion in the 2pσu and 1sσg states, respectively.
When we already know the eigenstates of Hu/g(R), we can regard  as the unperturbed Hamiltonian and the total Hamiltonian,
as the unperturbed Hamiltonian and the total Hamiltonian,  , should be divided into two parts,
, should be divided into two parts,  , where we define the perturbing Hamiltonian as
, where we define the perturbing Hamiltonian as  . In these equations, we define the projection operator to the 2pσu (1sσg) state as
. In these equations, we define the projection operator to the 2pσu (1sσg) state as  (
( ) and the raising (lowering) operator from the 1sσg (2pσu) state to the 2pσu (1sσg) state as
) and the raising (lowering) operator from the 1sσg (2pσu) state to the 2pσu (1sσg) state as  (
( ).
).
Thus, we apply the standard recipe of time-dependent perturbation theory to Eq.(5) with the initial condition that the wavefunction, |ψ(R, t = 0)〉, is equal to ψ0g(R)|g〉, where ψ0g(R) should be the initial vibrational wavepacket,

by considering the amplitude of the 2pσu state to be 0 at t = 0. The νth vibrational wavefunction,  , satisfies the eigenequation
, satisfies the eigenequation  and this functional basis set satisfies the orthogonal relation
and this functional basis set satisfies the orthogonal relation  .
.
The general solution up to the first order of the perturbation should be in the form

where  is the 0th-order expansion term describing the free propagator in each electronic state and is expressed as
is the 0th-order expansion term describing the free propagator in each electronic state and is expressed as

The first-order term of the propagator,  , expresses the one-photon transition between the two electronic states, that is,
, expresses the one-photon transition between the two electronic states, that is,

We observe, in the actual experiment, the KE spectrum of H+ (D+) from the dissociation, which should be equivalent to the KER spectrum of the dissociative H + H+ (D + D+) in the 2pσu state. Thus, we impose the final state,  , as an eigenstate of Hu(R) in the 2pσu state, which is given by
, as an eigenstate of Hu(R) in the 2pσu state, which is given by

where χu(ωu; R) satisfies the eigenequation Hu(R)χu(ωu; R) = ħωuχu(ωu; R). The phase factor of  describing the time evolution of the wavefunction appears in Eq.(10) because the time interval from τ to t is t − τ. We can obtain the transition amplitude by the first-order approximation,
describing the time evolution of the wavefunction appears in Eq.(10) because the time interval from τ to t is t − τ. We can obtain the transition amplitude by the first-order approximation,

Putting the initial and final states in this equation and using the eigenequations for  and χu(ωu; R), ρ(1)(ωu; τ; t) should be given by
and χu(ωu; R), ρ(1)(ωu; τ; t) should be given by

with the dipole matrix elements

It is reasonable to assume that time t at the detection of H+ (D+) is infinitely large compared with the delay τ; thus, the upper limit of the time integral in Eq.(12) can be infinity.
We apply another approximation to Eq.(12). The magnitude of the probe pulse, |E(t)|, should be negligibly small in the time regions t ≲ – τp and τp ≲ t, where τp is the pulse (train envelope) width of |E(t)|. Therefore, we can approximate the time integration as

under the condition τ ≳ τp With this approximation, we obtain

where  and
and  are the positive- and negative-frequency parts of the complex Fourier amplitude
are the positive- and negative-frequency parts of the complex Fourier amplitude  , respectively.
, respectively.
We neglect the negative-frequency part in Eq.(15) (rotating wave approximation) because (i) the relation  holds for the real optical field of E(t), (ii) the magnitude of
holds for the real optical field of E(t), (ii) the magnitude of  should be finite only in the frequency region around Ω~ω3 > 0 and Ω~ω5 > 0 and 0 otherwise and (iii) the argument of the Fourier amplitude
should be finite only in the frequency region around Ω~ω3 > 0 and Ω~ω5 > 0 and 0 otherwise and (iii) the argument of the Fourier amplitude  is a positive number for all eigenenergies of ħωu and
is a positive number for all eigenenergies of ħωu and  .
.
By removing the overall constant factor from the right-hand side in Eq.(15) and replacing  with
with  , which is equivalent to the Fourier amplitude of the complex optical field of the probe (gate) pulse, we obtain the transition amplitude, T(ωu;τ), as
, which is equivalent to the Fourier amplitude of the complex optical field of the probe (gate) pulse, we obtain the transition amplitude, T(ωu;τ), as

We can easily recognize the similarity between the transition amplitude, T(ωu;τ), in Eq.(16) and the FROG amplitude obtained by the equation

where |S(Ω;τ)|2 gives us the frequency-delay spectrogram of the correlation signal of an optical field of ε(t) and the gate field G(t − τ), by considering the correspondence between  , ∑ν ↔ ∫dω,
, ∑ν ↔ ∫dω,  and ωu ↔ Ω. Although we find the difference of T(ωu;τ) from S(Ω;τ) by
and ωu ↔ Ω. Although we find the difference of T(ωu;τ) from S(Ω;τ) by  , we can obtain this matrix element with a modeled theoretical calculation based on the spectroscopic data. Thus, we conclude that the FROG algorithm can be applied to T(ωu; τ) provided that we give the theoretical result of
, we can obtain this matrix element with a modeled theoretical calculation based on the spectroscopic data. Thus, we conclude that the FROG algorithm can be applied to T(ωu; τ) provided that we give the theoretical result of  to the algorithm.
to the algorithm.
We show the delay-KER spectrogram calculated from |T( ωu;τ)|2 in Fig. 3(a). We substitute  for aν, where
for aν, where  is the conventional overlap integral under the FCA condition in this calculation. We put the square root of the measured profile of the spectrum of the probe pulse, which is obtained by the superposition of the measured spectra of the 3rd- and 5th-order harmonic fields, into the magnitude profile of the gate field,
is the conventional overlap integral under the FCA condition in this calculation. We put the square root of the measured profile of the spectrum of the probe pulse, which is obtained by the superposition of the measured spectra of the 3rd- and 5th-order harmonic fields, into the magnitude profile of the gate field,  . We also assume a flat spectral phase of
. We also assume a flat spectral phase of  . The vibrational structure lies in two separate KER regions, one of which is around ~3 eV and the other is around ~5.6 eV. The 3rd- and 5th-harmonic components in the gate field contribute to the formation of the structure in the former and latter KER regions, respectively.
. The vibrational structure lies in two separate KER regions, one of which is around ~3 eV and the other is around ~5.6 eV. The 3rd- and 5th-harmonic components in the gate field contribute to the formation of the structure in the former and latter KER regions, respectively.
Note that we cannot distinguish an arbitrary delay of the gate field from an advance of the wavepacket by observing |T(ωu;τ)|2. When the gate field includes an additional delay, τG, the transition amplitude, T(ωu;τ), is modified to TG(ωu;τ) such that

We find that  is the wavepacket amplitude that has already evolved with time τG. This group delay (GD) may also be an unintentional offset of the delay origin; thus, we can eliminate an arbitrary phase proportional to the binding energy from the retrieved phase of aν to find a nontrivial phase modulation.
is the wavepacket amplitude that has already evolved with time τG. This group delay (GD) may also be an unintentional offset of the delay origin; thus, we can eliminate an arbitrary phase proportional to the binding energy from the retrieved phase of aν to find a nontrivial phase modulation.
The magnitude square of the Fourier transform of |T(ωu;τ)|2 shown in Fig. 3(b) exhibits the beat frequency components  and
and  , which are spectrally resolved along the KER direction. This is due to the fact that the gate field,
, which are spectrally resolved along the KER direction. This is due to the fact that the gate field,  , actually performs a ‘gate’ action by bandpass filtering for ωu so as to satisfy the condition
, actually performs a ‘gate’ action by bandpass filtering for ωu so as to satisfy the condition  (n = 3, 5), where ωn and Δωn are the peak frequency and bandwidth of the nth harmonic component, respectively. The highest vibrational number that appears as a beat frequency is 9 or 10. Thus, we do not expect the reconstruction of the wavepacket amplitudes of these vibrational states and higher states from the delay-KER spectrogram. Although the gate action restricts the range of beat frequency components that can be observed, it is essential to retrieve the amplitude of the wavepacket by using the FROG algorithm. We show the numerical values of beat frequencies that appear in Fig. 3(b) in Table 1. These values do not exhibit significant differences from the beat frequencies calculated from the vibrational energies given in ref. 35 and hence we conclude that our MW-FROG software code can correctly reproduce the vibrational period in the frequency-KER spectrogram. The frequency-KER spectrogram in Fig. 3(b) can be used to calibrate the delay and KER of the experimental data and to generate the bandpass filter mentioned in the following subsections.
(n = 3, 5), where ωn and Δωn are the peak frequency and bandwidth of the nth harmonic component, respectively. The highest vibrational number that appears as a beat frequency is 9 or 10. Thus, we do not expect the reconstruction of the wavepacket amplitudes of these vibrational states and higher states from the delay-KER spectrogram. Although the gate action restricts the range of beat frequency components that can be observed, it is essential to retrieve the amplitude of the wavepacket by using the FROG algorithm. We show the numerical values of beat frequencies that appear in Fig. 3(b) in Table 1. These values do not exhibit significant differences from the beat frequencies calculated from the vibrational energies given in ref. 35 and hence we conclude that our MW-FROG software code can correctly reproduce the vibrational period in the frequency-KER spectrogram. The frequency-KER spectrogram in Fig. 3(b) can be used to calibrate the delay and KER of the experimental data and to generate the bandpass filter mentioned in the following subsections.
MW-FROG algorithm
We define Iex(ωu;τ) as the experimental data of a delay-KER spectrogram and  as
as

to simplify the expressions. The amplitude of the delay-KER spectrogram described in Eq.(16) is expressed as

with this notation. The retrieval algorithm that we have adopted is the same as the conventional FROG algorithm using a generalized projection method to optimize the wavepacket (aν) and gate-field amplitudes ( ) in the frequency domain, as shown schematically in Fig. 4. The initial guesses for
) in the frequency domain, as shown schematically in Fig. 4. The initial guesses for  and aν generate the frequency-KER amplitude,
and aν generate the frequency-KER amplitude,  , by multiplying the projection matrix
, by multiplying the projection matrix  by the product of these two quantities in operation (i) in this figure. The frequency-KER amplitude is converted to a delay-KER amplitude, T(ωu;τ), by accumulating
by the product of these two quantities in operation (i) in this figure. The frequency-KER amplitude is converted to a delay-KER amplitude, T(ωu;τ), by accumulating  in terms of ν with the phase factor
in terms of ν with the phase factor  ((ii)). We obtained the experimental delay-KER amplitude, Tex(ωu;τ), by substituting (Iex(ωu;τ))1/2 for |T(ωu;τ)|, such that
((ii)). We obtained the experimental delay-KER amplitude, Tex(ωu;τ), by substituting (Iex(ωu;τ))1/2 for |T(ωu;τ)|, such that

in operation (iii). We apply a Fourier transform to Tex(ωu;τ) and choose the frequency components at  to obtain
to obtain  ((iv)). The next guesses for aν and
((iv)). The next guesses for aν and  for the second loop of iterations are determined by minimizing the functional distance Z between
for the second loop of iterations are determined by minimizing the functional distance Z between  and
and  ((v)) defined as
((v)) defined as

where  is the weight function used to ensure the appropriate convergence in iterations. Note that we do not perform the singular value decomposition of
is the weight function used to ensure the appropriate convergence in iterations. Note that we do not perform the singular value decomposition of  to determine aν and
to determine aν and  as principal components25 because the number of ν (vibrational states) is much smaller than the number of discretized ωu and the
as principal components25 because the number of ν (vibrational states) is much smaller than the number of discretized ωu and the  are unequally spaced in the frequency axis. We instead sequentially determine aν and
are unequally spaced in the frequency axis. We instead sequentially determine aν and  such that the functional derivative of Z with respect to aν or
such that the functional derivative of Z with respect to aν or  should be 0. We can also limit the parameters to be optimized in the functional space; for example, |aν| can be optimized with a fixed arg{aν}. The convergence of the iterative loop is monitored by the normalized functional difference defined as Δrms ≡ (Z/Zex)1/2, where Zex is the area of
should be 0. We can also limit the parameters to be optimized in the functional space; for example, |aν| can be optimized with a fixed arg{aν}. The convergence of the iterative loop is monitored by the normalized functional difference defined as Δrms ≡ (Z/Zex)1/2, where Zex is the area of  weighted with
weighted with  .
.
In the actual optimization of aν and  , we implement the following procedures to make the unintentional GD in aν, which is complementary to the advance of
, we implement the following procedures to make the unintentional GD in aν, which is complementary to the advance of  as stated in the explanation for Eq.(18), as small as possible. First, we substitute
as stated in the explanation for Eq.(18), as small as possible. First, we substitute  into aν and then optimize the heights of the two peaks in the gate field while the magnitude profiles are fixed to the measured spectral magnitudes of the 3rd- and 5th-order harmonic fields. The spectral phase of the gate field is also fixed to 0 in this process. Second, we optimize |aν| under the condition of the fixed gate and the 0-phase of aν. Third, the gate field is optimized under the initial condition of the noise field. An unintentional GD should be mainly imposed on the GD of the gate field in this process because the phase of aν is fixed to 0. After the third process, we repeat the optimization of aν and
into aν and then optimize the heights of the two peaks in the gate field while the magnitude profiles are fixed to the measured spectral magnitudes of the 3rd- and 5th-order harmonic fields. The spectral phase of the gate field is also fixed to 0 in this process. Second, we optimize |aν| under the condition of the fixed gate and the 0-phase of aν. Third, the gate field is optimized under the initial condition of the noise field. An unintentional GD should be mainly imposed on the GD of the gate field in this process because the phase of aν is fixed to 0. After the third process, we repeat the optimization of aν and  sequentially and finally, we optimize the polynomial coefficients describing the phase of aν. The reason for performing the last process will be given later.
sequentially and finally, we optimize the polynomial coefficients describing the phase of aν. The reason for performing the last process will be given later.
In order to determine whether our software code implementing the MW-FROG algorithm can accurately reproduce a known target spectrogram, we generate a target spectrogram, as shown in Fig. 5(a), in accordance with a model wavepacket amplitude and gate field, the magnitude and phase of which are depicted in Fig. 5(c,d), respectively. In this model calculation, the magnitude of aν is similar to that obtained in a theoretical model of ionization with the one-photon absorption of an APT. The phase of aν is modulated with the 5th-order polynomial with respect to the binding energy. The modulation depth is approximately 0.2 rad. The target amplitude of aν for all ν is determined in this manner, while we set aν to zero for ν > 8 in the retrieved result because of the missing beat frequencies for this range of vibrational numbers in the spectrogram. The magnitude of the gate field coincides with the magnitude profile composed of the measured 3rd- and 5th-order harmonic components. The group delays of the 3rd- and 5th-order harmonic components are set to 0.9 rad/eV (illustration 592 as) and 0.5 rad/eV ( 263 as), respectively.
(a) Delay-KER spectrogram used as a target for retrieval in MW-FROG algorithm. This spectrogram is generated from the modeled wavepacket amplitude and gate field, the magnitudes of which are depicted as crosses with bars in the bottom panel of Fig. 5(c) and as a shaded area in the bottom panel of Fig. 5(d), respectively. The phases for these quantities are also shown as crosses with connecting lines in the top panel of Fig. 5(c) and as a dashed curve in the top panel of Fig. 5(d). (b) Delay-KER spectrogram retrieved from that in Fig.5(a). (c) Magnitude and phase of the wavepacket amplitude, aν. The magnitude and phase retrieved from the delay-KER spectrogram are shown as solid squares with bars (magnitude) and connecting lines (phase) in the bottom and top panels, respectively. The phases depicted as hollow squares are obtained by optimization of aν, while those depicted by solid squares are obtained by optimization of the polynomial expansion coefficients of the phases. (d) Magnitude and phase of the gate field  . Solid curves in the bottom and top panels are the retrieved magnitude and phase, respectively.
. Solid curves in the bottom and top panels are the retrieved magnitude and phase, respectively.

By setting the target delay-KER spectrogram to that obtained by the exact calculation of |T(ωu;τ)|2, we retrieve the delay-KER spectrogram shown in Fig. 5(b). The retrieved magnitude and phase of aν are shown as squares with bars and squares with connecting lines in the bottom and top panels in Fig. 5(c), respectively. The deviation (root mean square of differences) of the magnitude of the retrieved aν from that of the target aν is estimated to be only 6.5 × 10−3 on the arbitrary unit scale of |aν| depicted in the bottom panel of Fig. 5(c). This result ensures the reliability of our MW-FROG algorithm. Nevertheless, it should be noted that the wavepacket magnitude should always include the deviation from the actual magnitude obtained from experimental data because we use an approximated formula (Eq.(13)) to obtain  in Eq.(16).
in Eq.(16).
The phase of aν, labeled ‘retrieved 1’ in the top panel in Fig. 5(c), is derived by optimization of aν. We corrected the GD so as to minimize the deviation from the target phase. The resultant phase shows scattering from the target phase with an r.m.s. error of 56 mrad. This is due to the processes in the MW-FROG algorithm labeled (ii) and (iv) in Fig. 4. The operation of  in process (ii) is not exactly the same as the inverse Fourier transform of
in process (ii) is not exactly the same as the inverse Fourier transform of  because of the unharmonicity of the vibrational frequencies,
because of the unharmonicity of the vibrational frequencies,  . Nevertheless, we execute the Fourier transform of Tex(ωu;τ) in process (iv) as the inverse operation in process (ii), then obtain the Fourier amplitude of
. Nevertheless, we execute the Fourier transform of Tex(ωu;τ) in process (iv) as the inverse operation in process (ii), then obtain the Fourier amplitude of  by assuming that ωg is a continuos variable. In the actual calculation in this process, the variables τ and ωg are discretized with equal steps of Δωg and Δτ, respectively, where these two quantities satisfy the equation Δωg = 2π/(NΔτ), where N is the number of points. We replace ωg by
by assuming that ωg is a continuos variable. In the actual calculation in this process, the variables τ and ωg are discretized with equal steps of Δωg and Δτ, respectively, where these two quantities satisfy the equation Δωg = 2π/(NΔτ), where N is the number of points. We replace ωg by  (n = 0,1,…,N − 1) and τ by τm ≡ τoffset + mΔτ (m = 0,1,…,N − 1). The Fourier amplitude is expressed as
(n = 0,1,…,N − 1) and τ by τm ≡ τoffset + mΔτ (m = 0,1,…,N − 1). The Fourier amplitude is expressed as  . Therefore, we have to always choose the nearest-neighbor frequency,
. Therefore, we have to always choose the nearest-neighbor frequency,  , as the approximated
, as the approximated  and regard
and regard  as
as  . This situation is graphically explained in FIG. S-1 of the supplementary information. The deviation of
. This situation is graphically explained in FIG. S-1 of the supplementary information. The deviation of  from
from  in the algorithm is the source of the scatter in the retrieved phase of aν.
in the algorithm is the source of the scatter in the retrieved phase of aν.
We have confirmed that the scatter is significantly reduced by zero padding to increase the number of points, N, before the Fourier transform because of the reduced frequency step, Δωg. The results are presented in FIG. S-2 of the supplementary information. Currently, the maximum available N is 216, which is limited by the 4 GB memory size in the 32-bit architecture of our personal computer software, resulting in the phase error of 56 mrad mentioned above. The functional error, Δrms, is 3.1%. In FIG. S-5 of the supplementary information, we also show another test of the performance of the MW-FROG algorithm using a different target aν and  , resulting in a phase error of 73 mrad.
, resulting in a phase error of 73 mrad.
Although this accuracy is sufficient to detect a phase modulation with a magnitude of 0.2 rad, even a small amount of scattering can cause deviation in the differentiation of the phase with respect to the frequency, which is regarded as a GD modulation possibly contained in the measured spectrogram. Thus, we expand the phase into a polynomial in terms of  to smoothly connect the adjacent phases and optimize the coefficients in the MW-FROG algorithm. The resultant phase using the optimized polynomial coefficients is shown as ‘retrieved 2’ in the top panel of Fig. 5(c). Although Δrms somewhat increases to 3.2%, the phase deviation is reduced to 47 mrad.
to smoothly connect the adjacent phases and optimize the coefficients in the MW-FROG algorithm. The resultant phase using the optimized polynomial coefficients is shown as ‘retrieved 2’ in the top panel of Fig. 5(c). Although Δrms somewhat increases to 3.2%, the phase deviation is reduced to 47 mrad.
We note that the phase of the wavepacket amplitude should be accurately obtained from the experimental data even though we use the approximated formula of  in the MW-FROG algorithm. This is because the phase information is only contained in the phases at the beat frequency components in the Fourier domain, which should not be affected by the deviation of a real function of
in the MW-FROG algorithm. This is because the phase information is only contained in the phases at the beat frequency components in the Fourier domain, which should not be affected by the deviation of a real function of  . Hence, there may be another possible analytical method to extract the phase of the wavepacket from the relative phases in the beat frequencies if we can determine the characteristic of the gate field by a separate measurement. The robustness for phase retrieval under worse situations that mimic experiments is shown in the next section and the supplementary information.
. Hence, there may be another possible analytical method to extract the phase of the wavepacket from the relative phases in the beat frequencies if we can determine the characteristic of the gate field by a separate measurement. The robustness for phase retrieval under worse situations that mimic experiments is shown in the next section and the supplementary information.
The retrieved gate field is depicted in Fig. 5(d). The magnitude of the retrieved gate field coincides with that of the target field. The retrieved phase is also similar to that of the target except for the GD offset. Although the GD difference between the 3rd- and 5th-order harmonic components is estimated to be 0.26 rad/eV (171 as) larger than that of the target (0.4 rad/eV = (0.9 −0.5) rad/eV), the resultant GD difference does not significantly change the temporal profile of the gate field.
Toward application to experimental data
To apply the MW-FROG algorithm to the experimental data, we have to resolve some issues. One is the short scanning range of the delay. The beat frequency components among the vibrational states must be clearly distinguished from each other by the Fourier transform of the delay-KER spectrogram against the delay axis so as to execute the MW-FROG algorithm correctly. The frequency resolution required is approximately 3 THz and thus, the scanning range of the delay should be much longer than 300 fs, while the scanning range of our experimental data in the previous study18 is only ~140 fs. We can, however, easily extend the scanning range by replacing the translation stage used to adjust the position of the silicon harmonic separator mirror and we expect a delay range of more than 500 fs with this modification.
Another issue may arise from the noise inherent in the experiment. This is common in conventional FROG measurements of ultrashort optical pulses, which can be resolved using a method similar to that adopted in the FROG measurement. High-frequency noise far from the relevant frequency range of the measured optical pulse is rejected using a low-pass filter before implementing the FROG algorithm25. We will also need a filter to eliminate the frequency components unnecessary for determining the wavepacket amplitude from the target spectrogram in our MW-FROG measurement. For this purpose, it is appropriate to apply a bandpass filter to the target delay-KER spectrogram obtained with the experimental data because the discrete frequency peaks of the Fourier transform of the spectrogram should be fixed to the beat frequencies of the vibration, unlike the continuum frequency spectrum of the Fourier transform of the FROG spectrogram for an isolated ultrashort optical pulse, as shown in Fig. 3(b).
In order to examine the performance of the MW-FROG algorithm with a filtered target spectrogram, we determined the transmission band of the bandpass filter, shown as contours in Fig. 3(b), by extracting the KER profile at each beat frequency in Fig. 3(b). The beat notes whose number difference is greater than 2 are omitted. The positions of KER peaks in the bandpass filter are adjusted to coincide with those in Fig. 3(b). The KER width of the filter, which is fit to a Gaussian profile, is set to twice that in Fig. 3(b). The window function for the frequency is the δ-function with a finite number of points, N, that is, sin((N + 1)(ω − ωpeak)Δτ/2)/sin((ω − ωpeak)Δτ/2), where Δτ is the time step for the delay increment. N is set to twice the number of points used for delay scanning to reduce the endpoint effects.
Before Fourier transforming the spectrogram to apply the bandpass filter, we remove the DC component from the spectrogram to eliminate the background tail (ringing) of the high-DC component in the beat frequency range. After applying the bandpass filter, we add a DC component as the delta function with the average KER profile such that the intensity of the spectrogram after the inverse Fourier transform is greater than or equal to zero. Unintentional negative parts in the spectrogram are truncated.
We obtained the target delay-KER spectrogram by applying the bandpass filter, as shown in Fig. 6(a), then checked the accuracy of the retrieved aν and  . The resultant delay-KER spectrogram is shown in Fig.6(b) and the magnitude and phase of aν are depicted as diamonds with bars and diamonds with connecting lines in the bottom and top panels of Fig. 6(c), respectively. The retrieved magnitude is scattered from the target magnitude with a deviation of 0.15 on the arbitrary unit scale of |aν| depicted in the bottom panel of Fig. 6(c), which is sufficiently large to disturb the observation of the change in magnitude of the target aν. This is due to the fact that the bandpass filter accompanied by DC compensation disturbs the intensity profile of the target spectrogram. The functional error is increased to 18.3% (with the optimization of aν) or 18.7% (with the optimization of the polynomial coefficients expressing the phase of aν).
. The resultant delay-KER spectrogram is shown in Fig.6(b) and the magnitude and phase of aν are depicted as diamonds with bars and diamonds with connecting lines in the bottom and top panels of Fig. 6(c), respectively. The retrieved magnitude is scattered from the target magnitude with a deviation of 0.15 on the arbitrary unit scale of |aν| depicted in the bottom panel of Fig. 6(c), which is sufficiently large to disturb the observation of the change in magnitude of the target aν. This is due to the fact that the bandpass filter accompanied by DC compensation disturbs the intensity profile of the target spectrogram. The functional error is increased to 18.3% (with the optimization of aν) or 18.7% (with the optimization of the polynomial coefficients expressing the phase of aν).
(a) Target delay-KER spectrogram after passing through the bandpass filter, which is depicted as contour plots in Fig.3. The modeled wavepacket amplitudes and gate field are the same as those used to generate the delay-KER spectrogram in Fig. 5(a). (b) Delay-KER spectrogram retrieved from that in Fig. 6(a). (c) Magnitude and phase of the wavepacket amplitude, aν. The magnitude and phase retrieved from the delay-KER spectrogram are shown as solid diamonds with bars (magnitude) and connecting lines (phase) in the bottom and top panels, respectively. The phases depicted as hollow diamonds are obtained by optimization of aν, while those depicted by solid diamonds are obtained by optimization of the polynomial expansion coefficients of the phases. (d) Magnitude and phase of the gate field  . Solid curves in the bottom and top panels are the retrieved magnitude and phase, respectively.
. Solid curves in the bottom and top panels are the retrieved magnitude and phase, respectively.
In spite of the visible deviation of the retrieved magnitude, the retrieved phase is not significantly affected by the bandpass filter, as shown in the top panel of Fig. 6(c). The phase of aν does not depend on the magnitudes of beat frequencies nor that of the DC component. To retrieve the phase of aν, we only require the phase at each beat frequency. This is the reason why we can successfully retrieve the phase of aν. The r.m.s. error between the target and retrieved phases is sufficiently small and is estimated to be 79 mrad. (with the optimization of aν) or 51 mrad. (with the optimization of the polynomial coefficients expressing the phase of aν).
The retrieved gate field, depicted in Fig. 6(d), exhibits somewhat degraded profiles in both the magnitude and phase compared with the target gate field, whereas the discrepancy is negligibly small. The GD difference between the 3rd- and 5th-order harmonic components in the retrieved gate field deviates by only 0.11 rad/eV (74 as) from that in the target gate field.
In order to simulate an experimental situation, we further examined the retrieval of the wavepacket amplitude from target delay-KER spectrograms, which were intentionally deteriorated under the following conditions. (i) The KER resolution of our VMI spectrometer is 0.18 eV around the KER value of 5.6 eV. We thus generated a target delay-KER spectrogram by convolving a Gaussian KER response function with a width of 0.2 eV in full width at half maximum with the exact target spectrogram shown in Fig. 5(a). A noise was then added. (ii) We generated a delay-KER spectrogram by using a wavepacket showing non-polynomial phase modulation, which is different from the phase shown in Fig. 5(c). The gate field is the same as that shown in Fig. 5(d). We processed the generated delay-KER spectrogram in the same manner as that described for (i). (iii) We changed the spectral magnitude profile of the gate field to have double peaks in the photon energy regions of both the third and fifth harmonic components. We also applied a group-delay dispersion to the spectral phase in both the photon energy regions and added a constant phase offset in the photon energy region of the fifth harmonic component. Then, we generated a delay-KER spectrogram using this gate field and the same wavepacket as that used to generate the spectrogram in (ii). The exact spectrogram without applying the simulated experimental condition was used as the target spectrogram in the MW-FROG algorithm. (iv) We applied the same simulated experimental condition as that implemented for (i) to the exact spectrogram used in (iii) in order to generate the target spectrogram.
The retrieved spectrograms, wavepacket amplitudes and gate fields are depicted in FIGS S-3, S-4, S-5 and S-6 in the supplementary information. We show how the phase offset in (iii) changes the temporal profile of the gate field in FIG. S-7 in the supplementary information. We confirmed that the convergence criterion of the spectrogram, R < 2, defined in refs. 36,37 was satisfied under our simulated experimental conditions (i), (ii) and (iv). Even though the r.m.s. errors of the retrieved phase in aν were increased under the simulated experimental conditions, they were still less than 120 mrad with the aν-optimization and less than 100 mrad with the optimization of the polynomial coefficients expressing the aν-phase.
As a result, we conclude that the MW-FROG algorithm is sufficiently reliable to resolve the aν-phase modulation with a depth larger than ~120 mrad even when the delay-KER spectrogram is degraded to have a finite KER resolution and noise. This is due to the extraction of the relevant phase information contained in the beat frequency peaks by the bandpass filter.
Summary and prospects
We have proposed the MW-FROG method to retrieve the vibrational wavepacket amplitude of aν generated in the ground electronic state of a  /
/ molecule based on the theoretical model of photoexcitation from the bound ground state to the repulsive excited state. The similarity of the transition amplitude in Eq.(16) to the optical FROG amplitude in Eq.(17) is due to the fact that the excitation is induced by a simple one-photon absorption process without considering the distortion of adiabatic potentials usually caused by an intense near-infrared laser pulse15.
molecule based on the theoretical model of photoexcitation from the bound ground state to the repulsive excited state. The similarity of the transition amplitude in Eq.(16) to the optical FROG amplitude in Eq.(17) is due to the fact that the excitation is induced by a simple one-photon absorption process without considering the distortion of adiabatic potentials usually caused by an intense near-infrared laser pulse15.
We have successfully retrieved the amplitude of the vibrational wavepacket by applying the MW-FROG algorithm to the modeled target spectrogram. Although a bandpass filter, which reduce s the noise of the spectrogram obtained in an actual experiment, degraded the accuracy of the magnitude of the vibrational wavepacket, we can still accurately find a phase modulation with a modulation depth larger than ~120 mrad.
The MW-FROG method requires a priori knowledge of the nuclear wavefunctions of the system consisting of vibrational and dissociative electronic states. The scanning range of the delay should be sufficiently long to resolve each beat frequency between the vibrational states. Therefore, we may apply this method to diatomic molecules other than  provided we obtain accurate adiabatic potential curves relevant to the system through the use of theoretical calculation and spectroscopic data. The delay-KER spectrogram originating from the vibrational motion of
provided we obtain accurate adiabatic potential curves relevant to the system through the use of theoretical calculation and spectroscopic data. The delay-KER spectrogram originating from the vibrational motion of  demonstrated in ref. 38 may be suitable for the application of MW-FROG if the delay range can be extended to much longer than 1.1 ps (revival time) to resolve the beat frequencies.
demonstrated in ref. 38 may be suitable for the application of MW-FROG if the delay range can be extended to much longer than 1.1 ps (revival time) to resolve the beat frequencies.
We have already carried out an experimental study of MW-FROG measurement for both  and
and  molecules by extending the scanning delay range to ~700 fs. The resultant amplitudes of the vibrational wavepackets for
molecules by extending the scanning delay range to ~700 fs. The resultant amplitudes of the vibrational wavepackets for  and
and  exhibit nontrivial phase modulations. Details of this study will be reported elsewhere.
exhibit nontrivial phase modulations. Details of this study will be reported elsewhere.
Additional Information
How to cite this article: Nabekawa, Y. et al. Frequency-resolved optical gating technique for retrieving the amplitude of a vibrational wavepacket. Sci. Rep. 5, 11366; doi: 10.1038/srep11366 (2015).
References
Goulielmakis, E. et al. Real-time observation of valence electron motion. Nature 466, 739–744 (2010).
Xie, X. et al. Attosecond Probe of Valence-Electron Wave Packets by Subcycle Sculpted Laser Fields. Phys. Rev. Lett. 108, 193004-1-5 (2012).
Beck, A. R. et al. Attosecond transient absorption probing of electronic superpositions of bound states in neon: detection of quantum beats. New J. Phys. 16, 113016-1-12 (2014).
Wang X. et al. Subcycle laser control and quantum interferences in attosecond photoabsorption of neon. Phys. Rev. A 87, 063413-1-4 (2013).
Wollenhaupt, M. et al. Interferences of Ultrashort Free Electron Wave Packets. Phys. Rev. Lett. 89, 173001-1-4 (2002).
Hasegawa, H. & Ohshima, Y. Quantum State Reconstruction of a Rotational Wave Packet Created by a Nonresonant Intense Femtosecond Laser Field. Phys. Rev. Lett. 101, 053002-1-4 (2008).
Dantus, M., Bowman, R. M. & Zewail, A. H. Femtosecond laser observations of molecular vibration and rotation. Nature 343, 737–739 (1990).
Gruebele, M. & Zewail, A. H. Femtosecond wave packet spectroscopy: Coherences, the potential and structural determination. J. Chem. Phys. 98, 883–902 (1993).
Scherer N. F. et al. Fluorescence detected wave packet interferometry: Time resolved molecular spectroscopy with sequences of femtosecond phaselocked pulses. J. Chem. Phys. 95, 1487–1511 (1995).
Katsuki, H., Chiba, H., Girard, B., Meier, C. & Ohmori, K. Visualizing Picometric Quantum Ripples of Ultrafast Wave-Packet Interference. Science 311, 1589–1592 (2008).
Katsuki, H., Chiba, H., Meier, C., Girard, B. & Ohmori, K. Actively Tailored Spatiotemporal Images of Quantum Interference on the Picometer and Femtosecond Scales. Phys. Rev. Lett. 102, 103602-1-4 (2009).
Hosaka, K. et al. Ultrafast Fourier Transform with a Femtosecond-Laser-Driven Molecule. Phys. Rev. Lett. 104, 180501-1-4 (2010).
Calvert, C. R., Bryan, W. A., Newell, W. & Williams, I. D. Time-resolved studies of ultrafast wavepacket dynamics in hydrogen molecules. Phys. Rep. 491, 1–28 (2010).
Ergler, T. et al. Spatiotemporal Imaging of Ultrafast Molecular Motion: Collapse and Revival of the
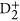 Nuclear Wave Packet. Phys. Rev. Lett. 97, 193001-1-4 (2006).
Nuclear Wave Packet. Phys. Rev. Lett. 97, 193001-1-4 (2006).Feuerstein, B. et al. Complete Characterization of Molecular Dynamics in Ultrashort Laser Fields. Phys. Rev. Lett. 99, 153002-1-4 (2007).
Kelkensberg, F. et al. Molecular Dissociative Ionization and Wave-Packet Dynamics Studied Using Two-Color XUV and IR Pump-Probe Spectroscopy. Phys. Rev. Lett. 103, 123005-1-4 (2009).
Jiang, Y. H. et al. Investigating two-photon double ionization of D2 by XUV-pump-XUV-probe experiments. Phys. Rev. A 81, 051402(R)-1-4 (2010).
Furukawa Y. et al. Resolving vibrational wave-packet dynamics of using multicolor probe pulses. Opt. Lett. 37, 2922–2924 (2012).
Tannor, D. J., Kosloff, R. & Rice, S. A. Coherent pulse sequence induced control of selectivity of reactions: Exact quantum mechanical calculations. J. Chem. Phys. 85, 5805–5820 (1986).
Alnaser, A. S. et al. Simultaneous real-time tracking of wave packets evolving on two different potential curves in
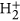 and . Phys. Rev. A 72, 030702(R)-1-4 (2005).
and . Phys. Rev. A 72, 030702(R)-1-4 (2005).Thumm, U., Niederhausen, T. & Feuerstein, B. Time-series analysis of vibrational nuclear wave-packet dynamics in . Phys. Rev. A 77, 063401-1-12 (2008).
He, F. & Thumm, U. Dissociative ionization of H2 in an attosecond pulse train and delayed laser pulse. Phys. Rev. A 81, 053413-1-9 (2010).
Urbain, X. et al. Intense-Laser-Field Ionization of Molecular Hydrogen in the Tunneling Regime and Its Effect on the Vibrational Excitation of . Phys. Rev. Lett. 92, 163004-1-4 (2004).
Jiang, Y. H. et al. Tracing direct and sequential two-photon double ionization of D2 in femtosecond extreme-ultraviolet laser pulses . Phys. Rev. A 81, 021401(R)-1-4 (2010).
Kane, D. J., Rodriguez, G., Taylor, A. J. & Clement, T. S. Simultaneous measurement of two ultrashort laser pulses from a single spectrogram in a single shot. J. Opt. Soc. Am. B 14, 935–943 (1997).
Trebino, R. et al. Measuring ultrashort laser pulses in the time-frequency domain using frequency- resolved optical gating. Rev. Sci. Instrum. 68, 3277–3295 (1997).
Lacourt, P. A. et al. Milliwatt-peak-power pulse characterization at 1.55 μm by wavelength-conversion frequency-resolved optical gating. Opt. Lett. 27, 863–865 (2002).
Mairesse, Y. & Quéré, F. Frequency-resolved optical gating for complete reconstruction of attosecond bursts. Phys. Rev. A 71, 011401(R)-1-4 (2005).
Furukawa, Y. et al. Nonlinear Fourier-transform spectroscopy of D2 using high-order harmonic radiation. Phys. Rev. A 82, 013421-1-5 (2010).
Okino, T. et al. Attosecond nonlinear Fourier transformation spectroscopy of CO2 in extreme ultraviolet wavelength region. J. Chem. Phys. 129, 161103-1-4 (2008).
Nabekawa, Y. et al. Interferometric Autocorrelation of an Attosecond Pulse Train in the Single-Cycle Regime. Phys. Rev. Lett. 97, 153904-1-4 (2006).
Nabekawa, Y. et al. Multi-terawatt laser system generating 12-fs pulses at 100 Hz repetition rate. Appl. Phys. B 101, 523–534 (2010).
Okino, T. et al. Dissociative Ionization Dynamics of Nitrogen Molecule with Interferometric Autocorrelation of a-few-pulse Attosecond Pulse Train. In: OSA Technical Digest, CLEO: QELS Fundamental Science (CLEO_QELS), OSA, 10.1364/CLEO_QELS.2013.QF2C.6 (2013).
Okino, T. et al. Attosecond Frequency Resolved Momentum Imaging of Two-photon Dissociative Ionization Dynamics of Nitrogen Molecule. In: OSA Technical Digest, International Conference on Ultrafast Phenomena (UP), OSA, 10.1364/UP.2014.09.Wed.P3.4 (2014).
Karr, J. P. & Hilico, L. High accuracy results for the energy levels of the molecular ions and HD+, up to J=2. J. Phys. B 39, 2095–2105 (2006).
Fittinghoff, D. N., DeLong, K. W., Trebino, R. & Ladera, C. L. Noise sensitivity in frequency-resolved optical-gating measurements of ultrashort pulses. J. Opt. Soc. Am. B 12, 1955–1967 (1995).
Wang, H. et al. Practical issues of retrieving isolated attosecond pulses. J. Phys. B 42, 134007 (2009).
Okino, T. et al. Simultaneous Observation of Vibrational Wavepackets of Nitrogen Molecule in Neutral and Singly-charged Manifolds. In: OSA Technical Digest, International Conference on Ultrafast Phenomena (UP), OSA, 10.1364/UP.2014.07.Mon.P1.6 (2014).
Acknowledgements
This work was part of the Advanced Photon Science Alliance Project commissioned by the Ministry of Education, Culture, Sports, Science and Technology (MEXT) of Japan and also part of the Extreme Photonics Research Project of RIKEN. Y.N., T.O., E.J.T. and K.M. gratefully acknowledge the financial support from Grants-in-Aid for Scientific Research Nos. 26247068, 26600123, 25286074, 26600122 and 26220606.
Author information
Authors and Affiliations
Contributions
Y.N. proposed and developed the MW-FROG technique. Y.F. and T.O. supported the theoretical and experimental background of molecular physics. A.A.E. and E.J.T. joined in the preliminary experiment on implementing the MW-FROG technique. K.Y. proposed the application of an APT to investigate molecular dynamics. K.M. directed the entire research.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Nabekawa, Y., Furukawa, Y., Okino, T. et al. Frequency-resolved optical gating technique for retrieving the amplitude of a vibrational wavepacket. Sci Rep 5, 11366 (2015). https://doi.org/10.1038/srep11366
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep11366
This article is cited by
-
Sub-10-fs control of dissociation pathways in the hydrogen molecular ion with a few-pulse attosecond pulse train
Nature Communications (2016)
-
Settling time of a vibrational wavepacket in ionization
Nature Communications (2015)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.



 ) pulses.
) pulses.




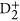 Nuclear Wave Packet. Phys. Rev. Lett. 97, 193001-1-4 (2006).
Nuclear Wave Packet. Phys. Rev. Lett. 97, 193001-1-4 (2006).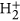 and . Phys. Rev. A 72, 030702(R)-1-4 (2005).
and . Phys. Rev. A 72, 030702(R)-1-4 (2005).