Abstract
We propose a method to construct universal order parameters for quantum phase transitions in many-body lattice systems. The method exploits the H-orthogonality of a few near-degenerate lowest states of the Hamiltonian describing a given finite-size system, which makes it possible to perform finite-size scaling and take full advantage of currently available numerical algorithms. An explicit connection is established between the fidelity per site between two H-orthogonal states and the energy gap between the ground state and low-lying excited states in the finite-size system. The physical information encoded in this gap arising from finite-size fluctuations clarifies the origin of the universal order parameter. We demonstrate the procedure for the one-dimensional quantum formulation of the q-state Potts model, for q = 2, 3, 4 and 5, as prototypical examples, using finite-size data obtained from the density matrix renormalization group algorithm.
Similar content being viewed by others
Introduction
Order parameters are pivotal to the Landau-Ginzburg-Wilson description of phase transitions for a wide range of critical phenomena, both classical and quantum, in many-body systems arising from spontaneous symmetry breaking (SSB)1,2. Despite their importance, relatively few systematic methods for determining order parameters have been proposed. One method proposed for quantum many-body lattice systems utilizes reduced density matrices3. This approach takes advantage of the degenerate ground states which appear when a symmetry of the Hamiltonian is broken spontaneously in the thermodynamic limit. An order parameter can be identified with an operator that distinguishes the degenerate ground states. The idea of the method is to search for such an operator by comparing the reduced density matrices of the degenerate ground states for various subareas of the system. This method was demonstrated in models that are considered to exhibit dimer, scalar chiral and topological orders3.
Another approach makes use of the ground-state fidelity of a quantum many-body system4,5,6,7,8,9. For a quantum phase transition arising from SSB, a bifurcation appears in the ground-state fidelity per lattice site, with a critical point identified as a bifurcation point10,11,12. This in turn results in the concept of the universal order parameter (UOP)13, in terms of the fidelity per site between a ground state and its symmetry-transformed counterpart. The advantage of the UOP over local order parameters in characterizing quantum phase transitions is that the UOP is model independent and thus universal, in sharp contrast with local order parameters, which are usually determined in an ad hoc fashion.
UOPs have been calculated with algorithms for systems with translational invariance. For Hamiltonians possessing symmetry group G with g the element of G, UOPs for translational invariant infinite-size systems are defined based on the orthogonal degenerate ground states corresponding to SSB, as a measure of distinguishability between ground state |ψ〉 and quantum state g|ψ〉, which can be interpreted in terms of the fidelity F as a measure of the similarity between two states14.
Such UOPs satisfy the basic definition of an order parameter: namely in the SSB phase, with |ψ〉 and g|ψ〉 two of the degenerate ground states, the corresponding UOP is nonzero, whilst in the symmetric phase, with g|ψ〉 ≡ |ψ〉, the UOP is zero. It has been demonstrated that such UOPs can successfully describe the symmetry broken phases in both one-dimensional and two-dimensional quantum systems13,15.
Since SSB occurs only in the thermodynamic limit, this construction of UOPs only makes sense in infinite-size quantum many-body systems. It is clearly desirable however, to construct UOPs directly from finite-size systems. This will not only make it possible to perform finite-size scaling, but also make it possible to take full advantage of currently available numerical algorithms, such as quantum Monte Carlo16, finite-size density matrix renormalization group (DMRG)17,18,19 and finite-size tensor network algorithms20,21,22,23. Here we propose and test a specific scheme to do this in the finite-size context for systems with SSB.
Results
Construction of UOPs from H-orthogonal states
First, we recall the notion of fidelity per lattice site. The fidelity F(|φ1〉, |φ2〉) = |〈φ1|φ2〉| between two states |φ1〉 and |φ2〉 scales as F(|φ1〉, |φ 2〉) ~ d(|φ1〉, |φ2〉)L, with L the number of lattice sites. The fidelity per lattice site4,5,6,7 d is the scaling parameter

which is well defined in the thermodynamic limit. With |φ1〉 and |φ2〉 ground states for different values of the control parameter, the fidelity per lattice site is nothing but the partition function per site in the classical statistical lattice model24.
We consider a hamiltonian H of a quantum system possessing symmetry group G with g a unitary representation of G, i.e., UgHUg† = H, with Ug = g × g × g … an infinite string of copies of matrix g. With the SSB, the UOP is defined in terms of the fidelity per lattice site d∞ for an infinite-size system by

where d∞ = |〈ψ|g|ψ〉|1/L with L → ∞ the fidelity per lattice site between the ground state |ψ〉 and the quantum state g|ψ〉13,15. Note that there are other possible definitions of the UOP. E.g., one could define  or
or  , which also vanish in the symmetric phase.
, which also vanish in the symmetric phase.
To study UOPs in the finite-size context, it is natural to think of using the fidelity per lattice site dL for systems of finite size L to construct d∞ = limL→ ∞ dL. However, applying the same definition of dL with the ground states of a finite-size system fails because d∞ ≡ 0 in all the range for |〈ψ|g|ψ〉|1/L = 0 in both phases, as SSB occurs only in an infinite-size system. There is however, a way to overcome this obstacle for finite-size systems.
To outline the general idea, consider a system whose hamiltonian has Zq,  symmetry. At zero temperature, for the symmetry broken phase, we have q degenerate ground states in the thermodynamic limit and we do expect that the symmetry is spontaneously broken. First we calculate q low-lying states of this system with finite size L, denoting the ith eigenstate and corresponding eigenvalue by |φi〉 and Ei, satisfying H|φi〉 = Ei|φi〉. The Zq symmetry can be understood as rotations among the variables pointing in the corresponding field directions. Thus the Hilbert space associated with Zq can be separated into disjoint sectors labeled by the phases ωm = exp (2πi(m − 1)/q) with m = 1, 2, …, q. For our purpose, we construct q H-orthogonal states |ψm〉 from the q low-lying states |φm〉 by
symmetry. At zero temperature, for the symmetry broken phase, we have q degenerate ground states in the thermodynamic limit and we do expect that the symmetry is spontaneously broken. First we calculate q low-lying states of this system with finite size L, denoting the ith eigenstate and corresponding eigenvalue by |φi〉 and Ei, satisfying H|φi〉 = Ei|φi〉. The Zq symmetry can be understood as rotations among the variables pointing in the corresponding field directions. Thus the Hilbert space associated with Zq can be separated into disjoint sectors labeled by the phases ωm = exp (2πi(m − 1)/q) with m = 1, 2, …, q. For our purpose, we construct q H-orthogonal states |ψm〉 from the q low-lying states |φm〉 by

in terms of the above defined phases ωm.
Here, each pair of the q states are set to be orthogonal with respect to H, i.e.,

with m ≠ t, so called H-orthogonality. The general notion of H-orthogonality appears in many guises in various matrix problems, e.g., as conjugacy or A-orthogonality in the Lanczos algorithm25,26.
The q coefficients cj in (3) are fixed by the H-orthogonality and normalization conditions. The fidelity per lattice site of two H-orthogonal states |ψt〉 and |ψm〉 takes the form

The final step in the scheme is to extrapolate the fidelity per lattice site dL between two H-orthogonal states, d∞ = limL→ ∞ dL, with the UOP following from the definition in Eq. (2). This explains how degenerate ground states in the thermodynamic limit, responsible for symmetry breaking order, emerge from near degenerate low-lying states in the finite-size system.
Application: the q-state Potts model
The quantum formulation of the q-state Potts model has hamiltonian27

where i are the lattice sites and λ denotes the external field along the z direction. The operators are written in matrix form:

with Mα = (M1)α for α = 1, …, q − 1, where Iq is the q × q identity matrix. The hamiltonian has Zq symmetry. For λ < 1 the system is in the Zq symmetry broken ferromagnetic phase and a symmetric paramagnetic phase when λ > 1. It is well known that a continuous (discontinuous) quantum phase transition occurs for q ≤ 4 (q > 4) at λ = 1 where the model is exactly solved28,29.
Consider first the case q = 2, the quantum transverse Ising model, where matrices M1 and Mz are the Pauli matrices σx and σz. Here the continuous quantum phase transition at λ = 1 is between the Z2 symmetry broken ferromagnetic phase and the symmetric paramagnetic phase. We compute the ground state wave function |φgs〉 and the first excited state wave function |φex1〉 for a system with finite size L, with corresponding ground state energy Egs and first excited state energy Eex1. Substituting ω1 = 1 and ω2 = −1 into Eq. (3) gives the two H-orthogonal states


which satisfy the H-orthogonality and normalization conditions 〈ψ1|H|ψ2〉 = 0 and 〈ψ1|ψ1〉 = 〈ψ2|ψ2〉 = 1. Thus, equivalently, we get


with solution |c1|2 = Eex1/(Egs + Eex1) and |c2|2 = Egs/(Egs + Eex1). The fidelity per lattice site between the two H-orthogonal states is thus

with energy gap δL = Eex1 − Egs.
In a similar fashion we have constructed the UOPs from the q low-lying states of the q = 3, 4 and 5-state quantum Potts model. The q − 1 excited states share the same energy Eex above the ground state Egs. Proceeding as for the q = 2 case, the coefficients cj in Eq. (3) ensuring the H-orthogonality (Eq. (4)) and normalization conditions are obtained, with the expression for the fidelity per lattice site now

where δL(λ) = Eex(λ) − Egs(λ). As such we have established an explicit connection between the fidelity per site between two H-orthogonal states and the energy gap between the ground state and low-lying excited states, which in turn renders clear physical implication for the UOP. We emphasize that each pair of H-orthogonal states shares the same value of dL for given λ. We note also that the relevant physics is accommodated in the numerator of equation (13), i.e., in the energy gap δL(λ). This will be seen below in the discussion on scaling.
For values of the transverse field in the range 0.7 ≤ λ ≤ 1.3, we calculated the fidelity per lattice site dL(λ) between the H-orthogonal states for finite-size systems L ranging from 10 to 500 using the DMRG algorithm. We obtained d∞(λ) and thus the UOP for each value of λ by simple extrapolation with dL(λ) = d∞(λ) + αL−β.
Fig. 1 shows the UOPs obtained for q = 3, 4 and 5 for values of the transverse field in the range 0.7 ≤ λ ≤ 1.3 from finite-size systems L ranging from 10 to 500 using the DMRG algorithm. Also shown for comparison are the results obtained for infinite-size translation-invariant systems with the infinite time-evolving block decimation (iTEBD) algorithm30. The UOPs obtained from the finite-size approach outlined here and the infinite-size approach match with a relative difference of less than 2.5 percent, which indicates the success of our scheme. In general, as also shown in Fig. 1, the UOP is seen to be capable of characterizing the nature of the quantum phase transition. For q = 2, 3 and 4 there is a continuous phase transitions at λ = 1, whilst for q = 5 the phase transition is first-order (discontinuous) at λ = 1. Here we remark that the fidelity per site has been demonstrated to be capable of detecting the discontinuous phase transitions in this model through the so-called multiple bifurcation points31.
Scaling
For the q-state Potts model, the q low-lying eigenstates are the single ground state and q − 1 degenerate first excited states. The energy gap δL for a system of finite size L obeys the relation  as Eq. (13) indicates. In the SSB phase with λ < 1 away from the phase transition point, the eigenspectrum is gapful and the energy gap δL is related to the correlation length ξL by δL ~ exp (−L/2ξL). Taking L → ∞, the fidelity per lattice site d∞ and correlation length ξ∞ are expected to be related by
as Eq. (13) indicates. In the SSB phase with λ < 1 away from the phase transition point, the eigenspectrum is gapful and the energy gap δL is related to the correlation length ξL by δL ~ exp (−L/2ξL). Taking L → ∞, the fidelity per lattice site d∞ and correlation length ξ∞ are expected to be related by

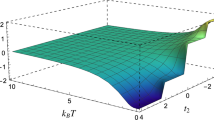
Fig. 2 shows this expected relation between d∞(λ) and ξ∞(λ) for different values of λ. Here, the data are mainly obtained using the iTEBD algorithm for infinite-size systems. The results are consistent with the relation (14) holding throughout the SSB phase λ < 1. At the critical point λ = 1, the correlation length ξ and energy gap δL scale as ξ ~ 1/δL. With scale invariance at criticality, ξ ~ L and thus δL ~ 1/L. Then with  the expected relation between the fidelity per site of the H-orthogonality states and finite size L at criticality is ln dL ~ − ln L/L. The results presented in Fig. 3 indicate that this relation is more precisely
the expected relation between the fidelity per site of the H-orthogonality states and finite size L at criticality is ln dL ~ − ln L/L. The results presented in Fig. 3 indicate that this relation is more precisely
The effective relation between the correlation length ξ∞ and the UOP.
In each case we calculate the correlation length ξ∞(λ) and UOP  for control parameter λ < 1 then fit ξ∞(λ) and ln d∞(λ) to the relation ξ∞ = −a/ln d∞, with
for control parameter λ < 1 then fit ξ∞(λ) and ln d∞(λ) to the relation ξ∞ = −a/ln d∞, with  . A simple linear fit gives the values (a) a = −0.503, (b) a = −0.490, (c) a = −0.491 and (d) a = −0.506.
. A simple linear fit gives the values (a) a = −0.503, (b) a = −0.490, (c) a = −0.491 and (d) a = −0.506.

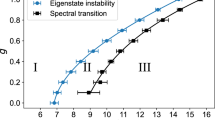
At the same time, keeping enough states with the DMRG algorithm, we have accurately obtained the gap Δ between the ground state and the (q + 1)-th lowest state at criticality. Here it is known that Δξ = constant, which can be seen in the results of Fig. 4. The case q = 5 is particularly challenging because the mass gap is small, with the exact value Δ = 0.0020544 …29,32,33,34. We note that in principle one could perform calculations on the equivalent staggered XXZ Heisenberg chain, using the known mapping between the two models29. However, it is not clear how this mapping applies to the wave functions.
Physical gap Δ vs correlation length ξ for the q-state quantum Potts model at criticality.
For systems size L ranging from 40 to 300 and a maximum number of 240 states kept during simulations with the DMRG algorithm, we fit the data to Δξ = constant. For q = 5 a finite gap is obtained by extrapolating with finite truncation dimensions from the iTEBD algorithm. In each case convergence is expected towards the origin. However, at q = 5 the mass gap terminates at the exact value Δ = 0.0020544 ….
Discussion
We have introduced a scheme for constructing UOPs to investigate quantum phase transitions using a set of H-orthogonal states in finite-size systems. We have established an explicit connection between the fidelity per site between two H-orthogonal states and the energy gap between the ground state and low-lying excited states in the finite-size system, which clarifies the physical meaning of the UOP. This makes it possible to perform finite-size scaling and take full advantage of currently available numerical algorithms. The scheme has been tested for the q–state quantum Potts model with q = 2, 3, 4 and 5 using the finite-size DMRG algorithm. We have demonstrated that the UOPs obtained in the finite-size context agree with the UOPs obtained directly from the infinite-size context (Fig. 1). Our results suggest that, in the range where SSB occurs, the H-orthogonal states defined and obtained in finite-size systems correspond to the q degenerate ground states for the infinite system when system size L → ∞. This clarifies how degenerate ground states emerge in the thermodynamic limit from low-lying near-degenerate states through H-orthogonality. The UOPs we have thus defined are a further application of the fidelity per site in the characterisation of quantum phase transitions.
Furthermore, the general relation (14) between the correlation lengths and the fidelity is seen to hold in the SSB phase. At criticality we have established the result (15) for the scaling of the fidelity per site. Although we have considered UOPs from the point of view of finite-size systems with Zq symmetry breaking, it is anticipated that the scheme outlined here can also be extended and applied to any system undergoing a phase transition characterized in terms of SSB. For example, it can be applied to systems in which the symmetry is broken with a continuous symmetry group.
References
Landau, L. D., Lifshitz, E. M. & Pitaevskii, E. M. Statistical physics (Butterworth-Heinemann, New York, 1999).
Anderson, P. W. Basic notions of condensed matter physics (Westview Press, Boulder, 1997).
Furukawa, S., Misguich, G. & Oshikawa, M. Systematic derivation of order parameters through reduced density matrices. Phys. Rev. Lett. 96, 047211 (2006).
Zhou, H.-Q. & Barjaktarevič, J. P. Fidelity and quantum phase transitions. J. Phys. A 41, 412001 (2008).
Zhou, H.-Q., Zhao, J.-H. & Li, B. Fidelity approach to quantum phase transitions: finite size scaling for quantum Ising model in a transverse field. J. Phys. A 41, 492002 (2008).
Zhao, J.-H., Wang, H.-L., Li, B. & Zhou, H.-Q. Spontaneous symmetry breaking and bifurcations in ground state fidelity for quantum lattice systems. Phys. Rev. E 82, 061127 (2009).
Li, B., Li, S.-H. & Zhou, H.-Q. Quantum phase transitions in a two-dimensional quantum XYX model: ground-state fidelity and entanglement. Phys. Rev. E 79, 060101R (2009).
Zhao, J.-H. & Zhou, H.-Q. Singularities in ground state fidelity and quantum phase transitions for the Kitaev model. Phys. Rev. B 80, 014403 (2009).
Li, S.-H. et al. Tensor network states and ground-state fidelity for quantum spin ladders. Phys. Rev. B 86, 064401 (2012).
Wang, H.-L., Zhao, J.-H., Li, B. & Zhou, H.-Q. Kosterlitz-Thouless phase transition and ground state fidelity: a novel perspective from matrix product states. J. Stat. Mech. L10001; 10.1088/1742-5468/2011/10/L10001 (2011).
Wang, H.-L., Dai, Y.-W., Hu, B.-Q. & Zhou, H.-Q. Bifurcation in ground-state fidelity for a one-dimensional spin model with competing two-spin and three-spin interactions. Phys. Lett. A 375, 4045 (2011).
Wang, H-L., Chen, A-M., Li, B. & Zhou, H-Q. Ground-state fidelity and Kosterlitz-Thouless phase transition for spin 1/2 heisenberg chain with next-to-the-nearest-neighbor interaction. J. Phys. A 45, 015306 (2012).
Liu, J.-H., Shi, Q.-Q., Wang, H.-L., Links, J. & Zhou, H.-Q. Universal construction of order parameters for translation-invariant quantum lattice systems with symmetry-breaking order. Phys. Rev. E 86, 020102(R) (2012).
Nielsen, M. A. & Chuang, I. L. Quantum computation and quantum information (Cambridge University Press, Cambridge, 2000).
Li, S.-H., Wang, H.-L., Shi, Q.-Q. & Zhou, H.-Q. Bifurcation in ground-state fidelity and universal order parameter for two-dimensional quantum transverse Ising model. e-print arXiv:1105.3008[cond-mat.str-el] (2011).
Ceperley, D. M. & Alder, B. J. Ground state of the electron gas by a stochastic method. Phys. Rev. Lett. 45, 566 (1980).
White, S. R. Density matrix formulation for quantum renormalization groups. Phys. Rev. Lett. 69, 2863 (1992).
White, S. R. Density-matrix algorithms for quantum renormalization groups. Phys. Rev. B 48, 10345 (1993).
Schollwoeck, U. The density-matrix renormalization group. Rev. Mod. Phys. 77, 259 (2005).
Vidal, G. Efficient classical simulation of slightly entangled quantum computations. Phys. Rev. Lett. 91, 147902 (2003).
Vidal, G. Efficient simulation of one-dimensional quantum many-body systems. Phys. Rev. Lett. 93, 040502 (2004).
Verstraete, F., Porras, D. & Cirac, J. I. Density matrix renormalization group and periodic boundary conditions: a quantum information perspectiv. Phys. Rev. Lett. 93, 227205 (2004).
Cirac, J. I. & Verstraete, F. Renormalization and tensor product states in spin chains and lattices. J. Phys. A 42, 504004 (2009).
Zhou, H.-Q., Orús, R. & Vidal, G. Ground state fidelity from tensor network representations. Phys. Rev. Lett. 100, 080602 (2008).
Hestenes, M. R. & Stiefel, E. Methods of conjugate gradients for solving linear systems. J. Res. Natl. Inst. Stan. 49, 6 (1952).
Golub, G. H. & Van Loan, C. F. Matrix computations (Johns Hopkins University Press, Baltimore, 2013).
Solyom, J. & Pfeuty, P. Renormalization-group study of the Hamiltonian version of the Potts model. Phys. Rev. B 24, 218 (1981).
Baxter, R. J. Potts model at the critical temperature. J. Phys. C 6, L445 (1973).
Hamer, C. J. Q-state Potts models in Hamiltonian field theory for Q ≥ 4 in (1 + 1) dimensions. J. Phys. A 14, 2981 (1981).
Vidal, G. Classical simulation of infinite-size quantum lattice systems in one spatial dimension. Phys. Rev. Lett. 98, 070201 (2007).
Su, Y.-H., Hu, B.-Q., Li, S.-H. & Cho, S.-Y. Quantum fidelity for degenerate ground states in quantum phase transitions. Phys. Rev. E 88, 032110 (2013).
Klümper, A., Schadschneider, A. & Zittartz, J. Inversion relations, phase transitions and transfer matrix excitations for special spin models in two dimensions. Z. Phys. B 76, 247 (1989).
Klümper, A. Investigation of excitation spectra of exactly solvable models using inversion relations. Int. J. Mod. Phys. 04, 871 (1990).
Buffenoir, E. & Wallon, S. The correlation length of the Potts model at the first order transition point. J. Phys. A 26, 3045 (1993).
Acknowledgements
This work is supported in part by the National Natural Science Foundation of China (Grant Nos. 11174375 and 11374379) and by Chongqing University Postgraduates' Science and Innovation Fund (Project No. 200911C1A0060322). M.T.B. acknowledges support from the 1000 Talents Program of China.
Author information
Authors and Affiliations
Contributions
H.Q.Z. defined the project. Q.Q.S. performed the numerical computations. Q.Q.S., H.Q.Z. and M.T.B. contributed to the analysis, the interpretation and the preparation of the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Shi, QQ., Zhou, HQ. & Batchelor, M. Universal Order Parameters and Quantum Phase Transitions: A Finite-Size Approach. Sci Rep 5, 7673 (2015). https://doi.org/10.1038/srep07673
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep07673
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

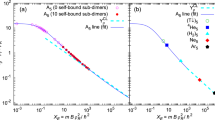

 for the q-state quantum Potts model for q = 2; 3; 4 and 5 shown in (a), (b), (c) and (d), respectively.
for the q-state quantum Potts model for q = 2; 3; 4 and 5 shown in (a), (b), (c) and (d), respectively.

