Introduction

The spin-orbit coupling (SOC) describes an intrinsic interaction between the spin and orbital degrees of freedom of a particle. In condensed-matter physics, the SOC of electron not only generates some important quantum phenomena such as the spin and anomalous Hall effects1,2 and the topological insulators and topological superconductors3, but also plays a key role in realizing the spintronics4 and the topological quantum computing5. However, the observations of SOC physics in naturally-occurring solid-state systems are often hindered by the unavoidable disorder and impurity effects. In this context, the neutral atom gases provide an ideal platform for exploring novel SOC physics and device applications6, owing to their unprecedented level of control and precision in experiments. Recently, a synthetic SOC, with equal Rashba and Dresselhaus strengths, has been created in a trapped Bose-Einstein condensate (BEC) by a pair of Raman lasers7. Moreover, its strength is far larger than that in the typical solid-state materials. Under the strong SOC strength, rich superfluid phenomena have been revealed8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36. Here we present that this novel SOC technique has important applications in quantum metrology, such as spin squeezing.

Spin squeezing is a quantum correlation with reduced fluctuations in one of the collective spin components37. It not only has possible applications in atom interferometers and high-precision atom clocks38, but also is closely related to and implies quantum entanglement39. Nonlinear spin-spin interactions are the heart for producing spin squeezing40. In experiments, the multi-component BEC is a powerful system to achieve spin squeezing41,42,43,44,45,46,47,48,49, since the required spin-spin interactions can be induced by the intrinsic atom-atom collision interactions. Although these atom-atom collision interactions can, in principle, be tuned widely by varying the scattering lengths via Feshbach resonances50, the experimental achievements are still difficult and thus the maximal squeezing factors measured experimentally are higher than −15 dB51. Moreover, the atom-atom collision interactions usually induce atom decoherence and dissipations, which limits the achievable squeezing factor52,53.

In this report, we show that the important spin-spin interaction can be induced by controlling the orbital degree of freedom (i.e., the momentum) of the ultracold atoms in the trapped BEC, with the equal Rashba and Dresselhaus SOCs. Since the generated interaction by the orbit is an indirect spin-spin interaction, it has advantages of no dissipation, high tunability and strong coupling, compared with previous schemes41,42,43,44,45,46,47,48,49. Then, we obtain an analytical spin squeezing factor by means of the frozen-spin approximation. Interestingly, the maximal squeezing factor can reach a large negative value (lower than −30 dB) by tuning the Raman lasers in current experimental setup of NIST. This giant squeezing factor is far larger than previous ones51. Finally, we find numerically that the phase factor of the prepared initial state affects dramatically on spin squeezing.

Results

Model and hamiltonian

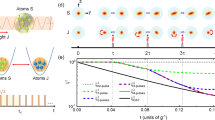
Figure 1(a) shows the experimental setup of NIST for realizing the equal Rashba and Dresselhaus SOCs in the trapped BEC, with 87Rb atoms7. In their experiment, all ultracold atoms are prepared in the xy plane, using a strong confinement along the z direction. Moreover, two hyperfine ground states, |F = 1, mF = −1〉 and |F = 1, mF = 0〉, act respectively as effective spin-↑ and spin-↓ components in a large detuning Δ from the excited state, as shown in Fig. 1(b). When these components are coupled by a pair of Raman lasers incident at a π/4 angle from the x axis, as shown in Fig. 1(a), the equal Rashba and Dresselhaus SOCs can be created in a dressed-state basis and , where k1 and k2 are the wave vectors of the Raman lasers). The corresponding dynamics is governed by the following Gross-Pitaevskii (GP) equation7

where Φ = (Φ↑, Φ↓)T is the normalization wave function in the dress-state representation. The harmonic trap potential , where m is the mass of the ultracold atom and ωx and ωy are the trap frequencies in the x and y directions. The Hamiltonian for the equal Rashba and Dresselhaus SOCs is written as HSOC = γpxσz + ℏΩσx/2, where is the strength of SOC, λ is the wavelength of the Raman lasers, is an effective Rabi frequency, Ω1 and Ω2 are the Rabi frequencies of the Raman lasers and σz and σx are the Pauli matrices. The mean-field atom-atom collision interactions HINT = diag(g↑↑|Φ↑|2 + g↑↓|Φ↓|2, g↑↓|Φ↑|2 + g↓↓|Φ↓|2), where g↑↑ = g↑↓ = 4πℏ2N(c0 + c2)/(maz) and g↓↓ = 4πℏ2Nc0/(maz) reflect the inter- and intra- spin collision interactions, respectively, c0 and c2 are the s-wave scattering lengths and with trap frequency ωz in the z direction.

Figure 1
figure 1

Illustration about how to achieve spin squeezing, using the experimental setup of NIST.

(a) The specified experimental setup for realizing the equal Rashba and Dresselhaus SOCs in the trapped BEC. (b) The energy levels, labeled respectively by |F = 1, mF = −1〉, |F = 1, mF = 0〉 and |F = 1, mF = +1〉, are coupled by a pair of Raman lasers. (c) A schematic diagram about how to use SOC to create spin correlation between the ultracold atoms. Under the strong atom-atom collision interactions, all ultracold atoms are forced to occupy the same many-body quantum state. As a result, the momentum for each atom has the same term. This identical momentum acts as a bus, generating an effective spin-spin interaction.

Full size image

Since the s-wave scattering lengths have been measured experimentally as c0 = 100.86 aB and c2 = −0.46 aB7, where aB is the Bohr radius, we can find immediately that . This means that the trapped BEC exhibits strong atom-atom collision interactions, which can force all ultracold atoms to occupy the same many-body quantum state. As a result, we can introduce two boson operators, and , to map the Hamiltonian for the GP equation (1) into a generalized Dicke model 21, where and are the collective spin operators, with the field operators ψ↑ and ψ↓ for the different spin components and v = (g↑↑ + g↓↓ − 2g↑↓)/4 is an effective spin-spin interaction induced by the direct atom-atom collision interactions. Due to the fact , this effective spin-spin interaction disappears (v = 0), but the strong atom-atom collision interactions have still remained. On the other hand, the boson mode in the y direction does not interact with the ultracold atoms. Thus, the system's properties of the spin-orbit coupled BEC in Fig. 1(a) is governed by the standard Dicke model54

We emphasize that the Hamiltonian (2) is valid for current experimental conditions of NIST. For a sufficiently strong repulsive interaction between the different spin components, i.e., g↑↓ > 0 and , the trapped BEC undergoes an imaginary excitation and is thus unstable20,55. In such a case, the mapping of the Dicke model is invalid. On the other hand, for the opposite limit that the trapped BEC has no interactions, including both the same and different spin components, all ultracold atoms occupy both in the momentum space with an artificial ratio21 and there is no correlation between the ultracold atoms. This means that the resulting spatial distribution of the trapped BEC is artificial and the above single spatial mode approximation in the Hamiltonian (2) cannot be applied.

Orbit-induced spin-spin interaction

For the Hamiltonian (2), it seems that no spin-spin interaction can be found, i.e., spin squeezing cannot be achieved. In fact, we can demonstrate, as shown in Fig. 1(c), that the spin-spin interaction can be induced by the momentum, i.e., ~ i(a† − a), which reflects the orbital degree of freedom of the ultracold atoms. To prove this argument clearly, we employ a unitary transformation, U = exp[iG(a† + a)Sz] with , to rewrite the Hamiltonian (2) as , where q = 4mγ2/(ℏN) = 8EL/(ℏN) and EL is the recoil energy. In experiment of NIST, the trap frequency ωx and the Rabi frequency Ω are of the orders of 10 Hz and kHz, respectively. For a large atom number, we have and thus 〈a†a〉 ~ 0, since 〈a†a〉 is inversely proportional to ωxN21. This means that the term ℏΩSy sin [G(a† + a)] can be omitted safely and . Finally, we obtain an effective Hamiltonian

 Before proceeding, we check the validity of the Hamiltonian (3) by investigating the ground-state properties, as well as the time-dependent spin dynamics, under current experimental parameters of NIST7. As shown in the Methods section, the atom population for the Hamiltonian (3) is derived by |〈Sz〉| = 0 for and for γ2 > ℏΩ/(4m). This analytical result agrees well with the direct numerical simulation of the GP equation (1), as shown in Fig. 2(a), as well as the experimental observation31. In addition, the spin dynamics for the Hamiltonian (3) is also similar to that of the GP equation (1), as shown in Fig. 2(b). Based on the above demonstrations, we can argue that the spin properties for the trapped BEC, with the equal Rashba and Dresselhaus SOCs, can be described by the generalized one-axis twisting model (3).

Figure 2
figure 2

The ground-state properties and the time-dependent spin dynamics for both the Hamiltonian (3) and the GP equation (1).

(a) The atom population 2|〈Sz〉|/N as a function of the strength of SOC, when N = 1.8 × 105. The critical point is evaluated as γc ≈ 0.003 m/s. The black line denotes the analytical result (AR) (see the Methods section), whereas the red open symbol reflects the direct numerical simulation (NS) of the GP equation (1). (b) The time-dependent spin dynamics 2 〈Sz(t)〉/N for both the Hamiltonian (3) and the GP equation (1), when N = 2 × 103. Initially, all ultracold atoms are prepared as the spin-↑ component. Here the black line and the red open symbol denote the numerical results for the Hamiltonian (3) and the GP equation (1), respectively. In (a) and (b), the other parameters are chosen as the experimental parameters, i.e., m = 1.44 × 10−25 kg, λ = 804.1 nm, ωx = 2π × 50 Hz and Ω = 2π × 17.8 kHz.

Full size image

The Hamiltonian (3) is a key result of this report. It shows clearly that the effective spin-spin interaction is generated by controlling the orbital degree of freedom (i.e., the momentum) of the ultracold atoms. If the realized SOC disappears (γ = 0), the Hamiltonian (3) reduces to the form H′ = ℏΩSx, in which no spin-spin interaction can be found. In fact, the spin-spin interaction can also be realized by controlling the direct atom-atom collision interactions via Feshbach resonance. However, its strength v( = (g↑↑ + g↓↓ − 2g↑↓)/4) is still very weak in current experimental setups. For example, in the experiment of producing spin squeezing46, the spin-spin interaction strength v = 2π × 0.063 Hz, when N = 2300. Moreover, this direct spin-spin interaction usually induces atom decoherence and dissipations, which limit the achievable squeezing factor52,53. In addition, in atom-cavity interacting systems, the virtual photon can also generate a weak spin-spin interaction56,57. Compared with the previous results, our proposal in this report has two advantages. The first is that the generated interaction induced by the orbit is an indirect spin-spin interaction, which does not lead to the atom decoherence and dissipations. The other is that the corresponding spin-spin interaction strength can reach a large value. For instance, when we choose N = 2300 in the experimental setup of NIST, q = 2π × 6.175 Hz, which has 2 orders larger than v. This strong spin-spin interaction will generate a giant spin squeezing factor.

Spin squeezing

In the absence of the Rabi frequency (Ω = 0), the Hamiltonian (3) reduces to the form , in which the squeezing factor was demonstrated analytically to scale as N−2/3 37. However, in our proposal, the Rabi frequency Ω cannot be considered to be zero. In fact, it ranges from 10−2 kHz to MHz and thus satisfies the condition of in current experimental setup7. In such a case, the squeezing factor can be derived from the frozen-spin approximation40.

We first consider the following initial coherent spin state , with the mean spin 〈Sx(0)〉 = N/2 and 〈Sy(0)〉 = 〈Sz(0)〉 = 0. For a weak spin-spin interaction q (or strong Rabi frequency Ω) in the Hamiltonian (3), all ultracold atoms are almost uncorrected in the framework of this prepared coherent spin state. As a result, the quantum noise is evenly distributed in the yz components of spin, namely, , which is governed by the standard Heisenberg uncertainty relation ΔSy(0)ΔSz(0) = |〈Sx(0)〉|/2, where ΔA2 = 〈A2〉 − 〈A〉2 is the standard deviation. This quantum noise leads to the standard quantum limit, if the coherent spin state is used in a Ramsey interferometer, such as an atom clock38. In order to reduce variance of one spin quadrature in the yz plane (the variance of the orthogonal one increases), quantum correlation between the ultracold atoms is very important and results in a spin-squeezing state37. For the given initial coherent spin state in the Hamiltonian (3), quantum correlation can be created by increasing the nonlinear spin-spin interaction (or decreasing the Rabi frequency). Moreover, the corresponding squeezing factor is defined as40

where . Since 〈Sz(t)〉 stands for the atom population, Eq. (4) is also called the atom squeezing factor. If , all ultracold atoms are squeezed and vice versa.

We now obtain the explicit solution of Eq. (4) by applying the Heisenberg equation of motion, with respect to the collective spin operators Sy and Sz in the Hamiltonian (3), namely, and . In general, these differential equations cannot be solved analytically. However, when remains approximately unchanged under the initial state |ψ0〉. This implies that we can make an approximation by replacing Sx by N/2, which leads to the following harmonic solutions: and , where . Based on these solutions, we have and . Since ω > Ω, the reduced spin fluctuations occurs in the z direction. Moreover, when t = (2n + 1)π/(2ω) with , the maximal squeezing factor is obtained by

In Fig. 3, we compare the analytical result in Eq. (5) with the direct numerical simulation. When , the analytical result agrees well with the numerical calculation. It implies that the orbit-induced spin squeezing can be well described by the formula (5) in the case of . Based on Eq. (5), we find that if we choose current experimental parameters, especially with Ω = 50q and N = 1.8 × 105 7, the maximal squeezing factor can reach . This giant squeezing factor is far larger than previous ones51. In Fig. 4, we numerically plot the maximal squeezing factor as a function of the phase φ of the initial state, defined as . This figure shows that the maximal squeezing factor depends strongly on the phase φ. It means that if we choose a proper phase φ in preparing the initial state, the maximal squeezing factor can also be largely enhanced.

Figure 3
figure 3

The maximal squeezing factor as a function of the Rabi frequency Ω.

The black solid line stands for the analytical result (AR) in Eq. (5), whereas the red open symbol reflects the direct numerical simulation (NS). The atom number is chosen as N = 2 × 103.

Full size image
Figure 4
figure 4

The maximal squeezing factor as a function of the phase φ of the prepared initial state.

This initial state is defined as , with the atom number N = 200. The Rabi frequency is chosen as (a) Ω = 30q and (b) Ω = 50q, respectively.

Full size image

Discussion

In summary, we have proposed a new way to generate the spin-spin interaction by controlling the orbital degree of freedom (i.e., the momentum) of the ultracold atoms in the trapped BEC, with the equal Rashba and Dresselhaus SOCs. More importantly, a giant spin squeezing factor (lower than −30 dB) has been achieved by manipulating a pair of Raman lasers. We have also found that the maximal squeezing factor can be largely enhanced by tuning the phase of the prepared initial state. We hope that our predictions could be observed in future experiments, since spin squeezing has an important concept in quantum information and moreover, are closely related to design the best atomic clocks.

Methods

Ground-state properties under a mean-field method

Here we employ the Holstein-Primakoff transformation and boson expansion method to discuss the ground-state properties of the Hamiltonian (3)58. By means of the Holstein-Primakoff transformation, which is defined as , and Sz = c†c − N/2, with [c, c†] = 1, the Hamiltonian (3) is rewritten as

We now introduce a shifting boson operator , where β is a auxiliary parameter to be determined, to describe the collective excitation of the ultracold atoms. Substituting this shifting boson operator d† into the Hamiltonian (6) and then using the boson expansion method, we have .

In terms of the expanded Hamiltonian, the scaled ground-state energy is obtained by58

The corresponding auxiliary parameter β can be derived from the equilibrium condition ∂E(β)/∂β = 0. The result is given by

where and . Equation (8) has two solutions, including η = 0 and η2 = (4mγ2 − ℏΩ)/(4mγ2 + ℏΩ). Finally, with the help of the stability condition ∂2E(β)/∂β2 > 0, we obtain η = 0 for and for γ2 > ℏΩ/(4m). This implies that the Hamiltonian (3) exhibits a quantum phase transition from a zero-momentum phase (η = 0) to a separate phase () at the critical point 21,24,31. In addition, by means of Eq. (8), the atom population is obtained by