Abstract
How the surface state (SS) develops and how the spin transport in a curved cylindrical topological insulator nanowire have attracted theoretical attention recently. However, experimental confirmation for the SS in such a real modeling system still remains insufficient. Here we carried out a systematic comparative study on the cylindrical single-crystal Bi2Te3 nanowires of various diameters and report unambiguously dual evidence for the Dirac SS. Both the predicted anomalous Aharonov-Bohm (AB) quantum oscillations with a period of h/e in H// and the 1/2-shifted Shubnikov-de Haas (SdH) oscillations (i.e., γ = −1/2) in H⊥ were indentified below 1.4 K. In addition, Altshuler-Aronov-Spivak (AAS)-like oscillations with a period of h/2e and ordinary SdH oscillations with γ = 0 were also resolved. These data provide clear evidence of coexistence of the nontrivial topological Dirac state and trivial electron state on the surface of topological insulator nanowire.
Similar content being viewed by others
Introduction
Topological insulator (TI) is a rapidly growing field of research in condensed matter physics1,2,3. It is characterized by a full insulating gap in the bulk and gapless spin-resolved surface states (SS) in which the spin of the electrons is locked perpendicular to its momentum by strong spin-orbit interaction. These spin helical properties of the Dirac fermions in SS have made them relevant for applications on improved spintronic devices and potentially useful for quantum computing4,5,6,7. While the topologically nontrivial surface state has been unambiguously indentified by angle-resolved photoemission spectroscopy (ARPES) in Bi2X3 (X = Te or Se) compounds8,9,10,11,12,13, direct probing the topological nature by electrical transport is still a major challenge14,15,16,17,18,19,20,21. This is because the electrical transport measurement is a bulk sensitive experiment, even small imperfections in the as-grown near-stoichiometric crystals will result in a metallic behavior in bulk and thus overwhelm or mask the surface contribution20,21. In order to overcome the material's obstacles and enhance the surface contribution, a number of efforts have been made recently by growing bulk single-crystals with compositional gradient15, chemical doping16,22,23 or gate-voltage tuning of the chemical potential in ultrathin films24,25,26. Recognition of the 2D surface state in 3D crystal was mostly based on the observation of angular dependent Shubnikov-de Haas (SdH) quantum oscillations or quantum Hall (QH) effect in high magnetic fields15,16.
Topological insulator nanowire with perfectly insulating bulk and curved two-dimensional metallic surface realizes an ideal hollow cylinder and thus exhibits more advantages for detection of the SS using transport measurement17,18,19,27. A key or probably clear-cut transport signature closely related to the nontrivial surface Dirac electrons or the surface curvature induced Berry's phase in a TI nanowire is the anomalous Aharonov-Bohm (A–B) effect with a period of φ0 = h/e flux quantum (i.e., twice the conventional period for an ordinary metallic hollow cylinder) when applying a magnetic field (H//) along the length of the cylinder and meanwhile, the oscillations at zero flux φ0 = 0 have a minimum (0-AB) or maximum (π-AB) depending on the doping level28,29,30. In the case of weak antilocalization and strong disorder-induced diffusive motion from topological trivial surface electrons away from the Dirac point, an ordinary Altshuler-Aronov-Spivak (AAS) effect with a period of h/2e and a minimum in MR at zero flux φ0 = 0 will appear31. While the anomalous AB or AAS-like oscillations were reported in both Bi2Se3 and Bi2Te3 nanoribbons previously17,18,27, no evidence of topological SS was reported in a curved cylindrical TI nanowire of different diameters. It is still not clear how the SS develops and how the spin transports in such a real curved quasi-1D wire.
It was well known that, in a 2D metal, the SdH oscillations are due to the successive emptying of the Landau levels (LLs) as the magnetic field (H) is increased, where the LL index n is related to the extremal cross-section, SF, of the Fermi surface by  16. For the quadratic Schrodinger spectrum, there are n-filled LLs below the Fermi energy, EF, when the applied fields equal to Hn. By contrast, in the Dirac case, there have n + 1/2 filled LLs between, EF and the Dirac point at E = 0, wherein the conduction band and the valence band each contribute half of the state in the n = 0 LL and thus result in an important 1/2-shift of the spectrum at ultra quantum limit. In other words, the plot of 1/Hn vs. LL index number n intercepts the n-axis at the value of γ = −1/2, whereas the interception γ = 0 in the Schrodinger case. Therefore, the observation of the 1/2-shifted SdH oscillations is considered to be another criterion for the topological nature of the surface Dirac states in TI32,33. Unfortunately, such a 1/2-shifted SdH spectrum has not been identified in a curved ultrathin TI wire yet.
16. For the quadratic Schrodinger spectrum, there are n-filled LLs below the Fermi energy, EF, when the applied fields equal to Hn. By contrast, in the Dirac case, there have n + 1/2 filled LLs between, EF and the Dirac point at E = 0, wherein the conduction band and the valence band each contribute half of the state in the n = 0 LL and thus result in an important 1/2-shift of the spectrum at ultra quantum limit. In other words, the plot of 1/Hn vs. LL index number n intercepts the n-axis at the value of γ = −1/2, whereas the interception γ = 0 in the Schrodinger case. Therefore, the observation of the 1/2-shifted SdH oscillations is considered to be another criterion for the topological nature of the surface Dirac states in TI32,33. Unfortunately, such a 1/2-shifted SdH spectrum has not been identified in a curved ultrathin TI wire yet.
Here we carried out a systematic comparative study on cylindrical single-crystal Bi2Te3 nanowires of various diameters (40 nm, 100 nm and 320 nm) fabricated by template-assisted electrodeposition, and, for the first time, we report unambiguously dual evidence for the Dirac SS in the wires. Both the predicted anomalous AB oscillations with a period of h/e in H// and the 1/2-shifted SdH oscillations (i.e., γ = −1/2) in H⊥ were indeed observed clearly below 1.4 K. In addition, AAS-like quantum interference oscillations with a period of h/2e and ordinary SdH oscillations with γ = 0 were also resolved. These data provide clear evidence of coexistence of the nontrivial topological Dirac states and trivial electron states on the surface of TI nanowires. Interestingly, when the wire diameter increases, both AB and SdH quantum oscillations were considerably suppressed and finally unresolved in 320 nm wires and instead, the universal conduction fluctuation (UCF)-like behavior was seen though the similar positive MR behavior remains. These results demonstrated that the topological surface states in ultrathin wires are extreme robust regardless of the surface oxidation of the wire and the data also led to the unique situation for detection of the coexistence of the nontrivial topological and trivial metallic surface states in the ultrathin wire due to the enhanced surface contribution. We anticipated that our experimental data will inspire more sophistical theoretical and experimental considerations on one-dimensional (1D) ultrathin TI nanowires, which have not been well explored, such as the possible helical Luttinger liquid30 that was ever described as the edge mode of the 2D quantum spin hall (QSH) topological insulator.
Results
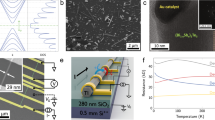
All of Bi2Te3 nanowires used in this work were synthesized by electrochemical deposition via customer-made porous anodic aluminum oxide (AAO) membrane. The wire diameter was exactly controlled by the pore size of the template so that we are able to carry out a systematic comparative study on wires of various diameters by selecting the templates with proper pore size. While the diameter of each wire along its length is uniform, it shows variations from wire to wire within an uncertainty of ~20%, verified by both scanning electron microscopy (SEM) and transmission electron microscopy (TEM). Fig. 1 (a) and the inset show, respectively, the low magnification SEM and TEM images from the smallest diameter wires we studied. The majority of the nanowires displays a length of 8–15 μm and a diameter of 40–50 nm. High-resolution TEM and the selected area electron diffraction pattern on a randomly selected nanowire revealed single-crystal morphology (Fig. 1b and the inset). An oxidation layer of approximately ~5.0 nm as indicated in Fig. 1(b), which was probably formed after the nanowires were released from the membrane, is visible on the surface. Therefore, the actual diameter of the nanowires inside the oxidation shell is about 30–40 nm. All of the samples fabricated under the same controlled conditions showed very similar structure, verified by XRD measurement on the nanowire arrays (see Supplementary Fig. S1), where the (110) diffraction is always the dominant peak in the spectra.
Panel (a) and the inset, respectively, show the low magnification SEM and TEM images of the Bi2Te3 nanowires.
The majority of nanowires display a length of 8–15 μm and a diameter of 40–50 nm. High-resolution TEM and the selected area electron diffraction pattern on a randomly selected nanowire, as shown in panel (b) and the inset, revealed single-crystal morphology. An oxidation layer of approximately ~5.0 nm is visible on the surface.
Standard 4-probe transport measurements on an individual nanowire were carried out with a physical property measurement system (PPMS, Quantum Design Inc.) cryostat equipped with a dilution refrigerator insert and a 16 T superconducting magnet. Four Pt-electrodes were patterned on an individual wire using focused-ion beam (FIB) technique (see Fig. S2 in supplementary materials). There is always a possibility of Ga or Pt implantation on the wire during the process, the ion beam imaging was therefore suspended during the process and the deposition current was set below 30 pA (prior to the Pt deposition, the contact areas were milled for 5 second with a beam current of 10–30 pA in order to remove the surface oxidation, then the four Pt electrodes were deposited subsequently with the same beam current; the extended leads were made by a relative large current beam based on the stripe areas). It was found that the maximum spreading or diffusion distance of the actual Pt along the wire is less than 300 nm under the mentioned deposition parameters verified through a profile analysis of the TEM energy dispersive X-ray spectroscopy (EDS) studies34. The Ga+ implantation or the damage-induced defects on the wire were expected to be near the contact areas within ~300 nm. The wire far away from the contacts is supposed to be less effected due to the natural protection of the 5 nm surface oxidation. Especially, the distance (L) between the inner edges of the two voltage electrodes were kept much larger than the spreading distance of Pt or Ga, they are, respectively, 5.4, 4.0, 4.2 μm for 40 nm, 100 nm and 320 nm wires used in this work, respectively.
Figs. 2(a) shows resistance (R) versus temperature (T) of three diameter wires measured at a zero magnetic field. Fig. 2 (b) is the variation, ΔR/R0, of the MR versus H⊥ for 100 nm, 320 nm wires at 2 K and 40 nm wire at 2.5 K. The R-T curves of 100 nm and 320 nm wires show very similar behavior, i.e., a resistance hump near 220 K in high-T range and an upturn below 14 K. In contrast, the 40 nm wire displays a nonmetallic transport behavior with a weak T-dependence over the temperature range of 14–300 K and then turns up below about 14 K. The hump around 220 K and the shallow minimum in R vs. T curves were usually found in TI – bulk crystals when the carrier density decreases, such as n < 1017 cm−3 15,20. When n > 1017 cm−3, a good metallic behavior was attributed to the contribution of the bulk conductivity. The broad hump of the resistance in large diameter wires was considered to be the competition of the conductivity between the surface state and the bulk. When the temperature decreases, the contribution of the insulating bulk conductivity decreases sharply and thus the surface conductivity will be dominant in low-T range. The absence of the resistance hump in this 40 nm wire likely provides an indication that the surface contribution of the 40 nm wire dominates over the entire T-range due to the enhanced surface to volume ratio. The upturn feature of the resistance below 14 K in all three samples is probably from the electron-electron interactions35,36 due to the enhanced disordering in one- or two-dimensional metals. The positive MR with a sharp valley (or a cusp in conductivity) in low-H region, as shown in Fig. 2 (b) can be understood in terms of the weak antilocalization (WAL) model and such a positive MR behavior is a common feature in TI system due to the strong spin-orbit coupling or the e-e interaction35,36. The most remarkable data we focused here are that the MR fluctuations or quantum oscillations were found to be enhanced with the decrease of the wire diameter, as shown in Fig. 2 (c) by subtraction of a fitted smooth background. The amplitude of the MR fluctuations or oscillations in 40 nm wire at 2.5 K was found to be 8 and 40 times larger than those in 100 nm and 320 nm wires obtained at 2 K, respectively (we have no the 2.5 K data for comparison). To understand the nature of these MR oscillations intensified in ultrathin nanowire, we focus our attention on the data of 40 nm wire.
(a) R vs. T curves of 320 nm, 100 nm and 40 nm diameter wires measured at a zero magnetic field. While the R-T curves in high T-range display variations from wire to wire, the low-T behavior exhibits a common feature with an upturn of the resistance below 14 K. (b) ΔR/R0-H⊥ curves at 2.0 K for 320 nm and 100 nm wires, 2.5 K for 40 nm wire; all of the wires show similar positive MR behavior in low-H regime except for the oscillations of the MR in high-H regime in 40 nm wire. (c) MR variations, ΔR, vs. H⊥ curves by subtraction of a smooth background. The amplitude of the fluctuations or quantum oscillations increases with the decrease of wire diameter.
Figs. 3 (a) and 3 (b), respectively, show the R vs. H// and R vs. H⊥ curves of 40 nm ultrathin wire at different T. Both curves display remarkable MR oscillations at temperatures below 4.0 K. Compared with the well recognized oscillation spectra in H⊥ orientation, the quantum oscillations in parallel H// direction become relatively weak but definitely resolvable and all tiny features are reproducible when scanning the field from 16 T to −16 T or vice versa.
Panels (a) and (b), respectively, show the R vs. H// and R vs. H⊥ curves of 40 nm wire measured at different temperatures (The curves in each plot were shifted by adding a certain constant value for clarity).
The quantum oscillations in both H-orientations were well-recognized and reproducible when scanning the field from 16 T to −16 T or vice versa.
Discussion
Fig. 4 (a) shows the variations of the resistance, ΔR, vs. H// measured at different T after subtraction of a background by fitting the original data with a polynomial function (each curve was shifted up by adding a certain constant value for clarity; the fitted background curves were shown in Fig. S3). The big bump near 6 T is probably from the MR effect of the bulk contribution in parallel H and thus was omitted by the subtraction. It is noticed that the significant minima of the MR oscillations indicated by the vertical lines are equal gaped. In other words, the MR-oscillation spectra are periodic with H// and have a period of about ΔH// = 4.45 T. Such a period corresponds to the AB oscillations from a 35 nm diameter metallic hollow cylinder evaluated from the formula of ΔH//(πd2)/4 = Φ0, with d the wire diameter and Φ0 = h/e the magnetic flux quanta. As described above, the estimated value, d~35 nm, for a cylinder is indeed, as expectedly, on the order of the actual wire diameter of 30–40 nm without the oxidation layer verified by TEM study. A fact that the minima in resistance exactly fall on the multiple integer of Φ0 provides an unambiguous evidence that the observed quantum oscillations in parallel H// are the consequence of the ordinary 0-AB effect due to the metallic surface states of the cylindrical wire. As expected theoretically28,29 that the 0-AB effect with a period of Φ0 can be realized at doping large enough that the resistance is less than the quantum resistance h/e2. In our case, there is no reason to expect that the Fermi energy coincides exactly with the Dirac point in surface state.
Panel (a) shows the variations, ΔR, of the resistance vs. H// measured at different T after subtraction of a background by fitting the original data with a polynomial function (the fitted background curves were shown in Fig. S3).
The significant minima indicated by the solid lines are located nicely at integer multiples of flux quanta Φ0 = h/e. Tiny dips superimposed on the most of the broad peaks were seen and located approximately at the odd multiples of Φ0/2 within an uncertainty of 10%. Bottom panel (b) shows the variations, ΔR, of the resistance vs. H⊥ after subtraction of a background measured at different T. The oscillation spectra do not show simple periodic behavior with H⊥. At 0.2 K, some additional fine structures, such as tiny peaks or kinks, appear.
Besides the 0-AB effect, we also noticed a double-peak feature in the oscillation spectra, where tiny dips were found to superimpose on the most of the broad peaks of the 0-AB oscillations. Although the dips at the odd multiples of Φ0/2 are relatively weak and smeared out with the increase of temperatures, the double-peak feature is at least well resolved below 1.4 K and reproducible with H-scan from -16 T to 16 T. There are two possibilities for these tiny dips. (1) They are the consequence of the weak π–AB oscillations with a period of Φ0 but the minima at each odd multiple of Φ0/2 due to the massless Dirac carriers on the SS of the TI-wire induced by the topological Berry's phase, as predicted by the theories28,29. (2) They are the normal AAS effect of the weak topological trivial electrons with a period of Φ0/2, where the dips at even multiples of Φ0/2 are exactly at the same positions with the 0-AB effect and thus cannot be recognized. It is difficult to verify either scenario suggested above being more adequate from the present data. However, our observation, at least, clearly demonstrated that the topological surface state is not destroyed by the surface oxidation of the wire and, in contrast, it becomes more robust with the decrease of the wire diameter. We have to mention that the AB oscillations well-recognized in 40 nm diameter wire were not resolved clearly in 100 nm and 320 nm larger diameter wires although the SdH oscillations or universal conductance fluctuations (UCF) were definitely observable in perpendicular field as shown in Fig. 2 (c). This is because the quantum oscillations were enhanced with the decrease of wire diameter and their amplitude in perpendicular field is much larger than that in parallel field.
Fig. 4 (b) shows the variation of the resistance, ΔR, as a function of H⊥ at different T after the subtraction of a fitted smooth background (each curve was shifted up for clarity by adding a constant value). Compared with the R-oscillations in H//, the amplitude of the oscillation spectra in H⊥ become more significant and, especially, some resolvable fine structures, such as the tiny kinks, are visible at 0.2 K. The influences of the AB oscillations in H⊥ orientation can be completely excluded because the AB spectrum is expected only in parallel field. It was seen that the oscillation spectra in H⊥ do not display periodic behavior with H⊥. However, when we plot the variations of the resistance, ΔR, as a function of 1/H⊥ at different T as shown in Fig. 5 (a), the spectra do display a periodic behavior with 1/H⊥ in the high field regime if defining each minima, together with the tiny kinks resolved at 0.2 K as marked specifically by the dashed lines. The periodicity of the oscillations is about Δ(1/H⊥) = 0.036T−1. Such periodic feature of the conduction spectra as a function of 1/H⊥ is generally considered to be a direct signature of the SdH oscillations.
Panel (a) show the variations of the resistance, ΔR, vs. 1/H⊥ after the subtraction of a fitted smooth background at different T.
If defining the minima, together with the tiny kinks resolved at 0.2 K, as marked specifically by the dashed lines, the R-oscillations display a periodic behavior with 1/ H⊥ in high field regime, an indicative of the SdH oscillations. Another set of SdH oscillations with a large periodicity was indicated by the thin solid lines. In panel (b), curve (A) plots the integer LL index, n (open squares) vs. 1/ H⊥ at the minima or kinks of the SdH spectrum. The data defined from the maxima are also shown additionally in the plot as the solid squares (shifted by 1/2 in LL index). The best-fit straight line intercepts the n-axis at the value of γ = −0.41 ± 0.1, almost at the ideal value of γ = −1/2 for Dirac spectrum. Curve (B) plots the integer LL index, n (open squares) vs. 1/ H⊥ for another set of SdH spectrum in low-H regime. Clearly, the best-fit straight line passes exactly through the zero point of the n-axis with the ideal value γ = 0.
To verify these quantum oscillations in H⊥ is truly from the SdH effect, Fig. 5 (b) plots the integer LL index, n (open squares) vs. 1/H⊥ at the minima or kinks of the SdH spectrum and the data defined from the maxima are also shown additionally in the plot as the solid squares (shifted by 1/2 in LL index). It was clearly seen that the curve (A) nicely falls on a straight line. While both two dimensional electron gas (2DEG) in conventional semiconductors and in 2D Dirac electron system have a linear n vs. 1/H⊥ dependence, the different Berry's phase would make the intercept zero for regular 2DEG and nonzero for Dirac system at ultra quantum limit. Clearly, the best-fit straight line intercepts the n-axis at the value of γ = −0.41± 0.1, almost close to the ideal value of γ = −1/2 than 0 or 1. Such a 1/2-shifted SdH effect in high H⊥ regime provides unambiguously transport evidence for the surface Dirac spectrum in TI due to the nontrivial Berry's phase.
From Fig. 5 (b), the best fit of the straight line gives a Fermi cross-section areas, SF, of 30.7 T (i.e., 3.1 × 1017 m−2). The Fermi wave vector,  and the 2D carrier density,
and the 2D carrier density,  , can be, therefore, estimated to be respectively, 0.055Å−1 and 4.9 × 1012 cm−2. All of these values estimated from 40 nm Bi2Te3 nanowire are well on the same order of those obtained in the surface states of Bi2Te3 crystals16,18,32,33 and Bi2Se3 nanoribon19.
, can be, therefore, estimated to be respectively, 0.055Å−1 and 4.9 × 1012 cm−2. All of these values estimated from 40 nm Bi2Te3 nanowire are well on the same order of those obtained in the surface states of Bi2Te3 crystals16,18,32,33 and Bi2Se3 nanoribon19.
In order to fully understand the surface SdH oscillations, it might be useful to directly compare the MR data with the theoretical expression for the SdH oscillations of a 2DEG system, where the general formula is described as19,

HF is the frequency of the SdH oscillations in 1/H⊥ and A, μ and β × 2π are respectively the temperature dependent amplitude, carriers mobility and the Berry's phase. Using the HF extracted from the slope of the curve (A) in Fig. 5 (b), the best fit, as shown by the solid red curve in Fig. 6 (a), results in β = 0.49 ± 0.01, A = 39.01 ± 6.81 Ω and μ = 0.33 ± 0.07 m2/Vs, respectively. For 2D Dirac electrons, the Berry's phase of π should be β = 0.5, the fitted value of β = 0.49 from eq.(1) is in good agreement with the expectation for surface Dirac electrons. Since the mobility,  and kF = 0.055 Å−1, the electron mean free path,
and kF = 0.055 Å−1, the electron mean free path,  , in the surface Dirac states is estimated to be 119.6 nm. Hence, the metallicity parameter,
, in the surface Dirac states is estimated to be 119.6 nm. Hence, the metallicity parameter,  , is then estimated to be ~66, which is also in excellent agreement with those obtained from the SS of high quality Bi2Te3 bulk crystals16.
, is then estimated to be ~66, which is also in excellent agreement with those obtained from the SS of high quality Bi2Te3 bulk crystals16.
(a), (b) and (c) respectively, show the ΔR vs. H⊥ curves at 0.2 K by subtraction of a smooth background.
The blue curve is the experimental data and the red and green ones are respectively the theoretical fitting for the data in high and low field (H⊥) regimes in terms of the theoretical model. The data defined from the minima of the fitted curves are also displayed in Fig. 5 (b) as the solid and open triangles, respectively. The magenta solid curve in (c) is the sum of the two set of the SdH oscillations, which almost manifasts the main feature of the experimental data.
However, one may notice that the amplitude of the SdH spectrum was poorly described by eq.(1) in low field regime, such as the initial three big peaks cannot be described and the predicted minima at n = 5 and 6 shrink to tiny kinks. A probable origin is that there also exists an additional set of SdH oscillations superimposed on the surface Dirac spectrum. Indeed, the three broad peaks in 1/H⊥ spectrum in low field regime, as indicated by the solid lines in Fig. 5 (a), are equal gaped, indicating a nature of another set of SdH oscillations. The LL index, n vs. 1/H⊥ dependence (shifted by 1/2) by defining the maxima of three broad peaks is shown in Fig. 5 (b) as the solid circles in curve (B) (the data defined from the minima are also additionally shown in the curve as the open circles). The best-fit straight line of the curve (B) passes exactly through the zero point of n-axis with the ideal value γ = 0. The best fit of the straight line gives a Fermi cross-section area, SF, of 8.0 T (i.e., 0.77 × 1017 m−2). The Fermi wave vector, kF and surface carrier density n2D are, therefore, evaluated to be respectively, 0.016 Å−1 and 2.56 × 1012 cm−2. Similarly, the initial three SdH peaks in low field regime at T = 0.2 K can be well described with three fitting parameters of β = 0.9 ± 0.01, A = 37.99 ± 9.23 Ω and μ = 0.61 ± 0.13 m2/Vs, as shown by the solid green curve in Fig. 6 (b). Hence, the conventional electron mean-free path,  and the metallicity parameter,
and the metallicity parameter,  , are then respectively ~64.1 nm and 10. For conventional 2DEG, the Berry's phase of 2π should be β = 1.0, the fitted value of β is ~0.9, again in agreement with our expectation for a massive fermions. These data clearly indicated that this set of the SdH oscillations with a relative large period of Δ(1/H2) = 0.128 T−1 is less dependent on the topological nontrivial surface Dirac carriers, but probably has a nature of the trivial carriers in the surface states away from the Dirac point. The magenta solid curve in Fig. 6 (c) is the sum of the two set of the SdH oscillations, which almost manifasts the main feature of the experimental data. Back to the previous data in parallel H//, the tiny dips superimposed on the broad peaks of the 0-AB spectra might have the same origin due to the trivial electrons in the SS, instead of the π-AB effect. All of the data support the coexistence of the nontrivial topological Dirac state and trivial electron state on the surface of TI wires37.
, are then respectively ~64.1 nm and 10. For conventional 2DEG, the Berry's phase of 2π should be β = 1.0, the fitted value of β is ~0.9, again in agreement with our expectation for a massive fermions. These data clearly indicated that this set of the SdH oscillations with a relative large period of Δ(1/H2) = 0.128 T−1 is less dependent on the topological nontrivial surface Dirac carriers, but probably has a nature of the trivial carriers in the surface states away from the Dirac point. The magenta solid curve in Fig. 6 (c) is the sum of the two set of the SdH oscillations, which almost manifasts the main feature of the experimental data. Back to the previous data in parallel H//, the tiny dips superimposed on the broad peaks of the 0-AB spectra might have the same origin due to the trivial electrons in the SS, instead of the π-AB effect. All of the data support the coexistence of the nontrivial topological Dirac state and trivial electron state on the surface of TI wires37.
One may comment on why the SdH oscillations were not detected in H//. To account for this issue, let's estimate the magnetic lengths,  at n = 1. From Fig. 5 (b), the 1/H1 of both SdH spectra are respectively 0.05 T−1 and 0.116 T−1 and thus we get
at n = 1. From Fig. 5 (b), the 1/H1 of both SdH spectra are respectively 0.05 T−1 and 0.116 T−1 and thus we get  ~5.7 and 8.7 nm, respectively. Both values are larger than the thickness of the topological surface states which were considered to be on the order of ~2 nm or less. In other words, all of the radii of the electron cyclotron orbits at LLs with n ≥ 1 exceed the thickness of the surface states and therefore omits the possible SdH oscillations of the SS in H//.
~5.7 and 8.7 nm, respectively. Both values are larger than the thickness of the topological surface states which were considered to be on the order of ~2 nm or less. In other words, all of the radii of the electron cyclotron orbits at LLs with n ≥ 1 exceed the thickness of the surface states and therefore omits the possible SdH oscillations of the SS in H//.
Finally, we have to emphasize that the positive MR behavior with a steep valley in low H regime is a common feature for all of the TI-wires while their R-T curves might display variations from wire to wire. In our three diameter nanowire samples, we observed the hump and the upturn or the shallow minimum in R-T curves, but the estimated 2D density n2D ~4.9 × 1012 cm−2, is almost 4 times larger than the density measured in other Bi2Te3 nanoribbons18 and Bi2Te3 bulk16 having a metallic behavior. Actually, we have not very satisfied explanation on why our nanowires with a relative high carrier density display the hump, upturn and the non-metallic behavior. However, a possible understanding is the inhomogeneity of defects or impurities along the wire created by the process of nanofabrication for the electrodes, especially near the contact area, where the e-e interactions might be dominant due to the strong disordering. This means that the MR behavior actually echoes the intrinsic surface property of the TI-wires and are directly related to the metallic surface state, while the resistivity is a consequence of the combinations of all band charge carriers interacted with their environment. Secondly, the 0-AB and the SdH oscillations are always visible in all of 40 nm wires we investigated, in contrast, only UCF can be seen in large diameter wires (see Fig. 2c). Thirdly, the topological TI surface state in 40 nm wire was found to be robust and still survive regardless of the surface oxidation. This data is also consistent with the previous observations by Peng et al.38 that the Dirac cone of the surface states can be clearly seen in months-old samples exposing to air for a few days and in samples with controlled surface contaminations of CO and O2 gas molecules by Liu et al.39. A fact that the quantum oscillation phenomena were enhanced considerably with the decrease of wire diameter indicates that the Dirac point which usually closes to the valence band in Bi2Te3 bulk samples was fortunately lifted up to the midgap region due to the surface oxidation-induced disorder in ultrathin wires39. In other words, the small diameter Bi2Te3 wires with a natural surface oxidation might be a nice candidate for the detection of TI surface states and the potential application for electronic devices. A very interesting scenario for checking the theoretical model in 1D TI wire as suggested by Bardarson et al.28 is that, by varying the chemical potential of the surface states of the TI, the minimum of the resistance should shift back and forth between Φ = 0 and Φ = π or, alternatively, change the period of the resistance oscillations from Φ0 to Φ0/2 by increasing the surface disorder. It might be possible to realize the switching behavior between 0- and π–AB oscillations by reducing the wire diameter continuously by considering the surface band-banding and the size confinement effect.
In summary, we provide unambiguously dual transport evidence of topological surface Dirac states in 40 nm Bi2Te3 single-crystal nanowire by measurement of both AB oscillations with a period of Φ0 in H// and the 1/2-shifted SdH oscillations in H⊥. Both types of the quantum oscillations are expected only from the Dirac spectrum of the topological surface states. In addition, our data also showed that the AAS effect with a period of Φ0/2 and the ordinary SdH quantum oscillations coexisted with the anomalous 0-AB and 1/2-shifted SdH oscillations in the surface states of the wire. The nature of these ordinary quantum oscillations might be the consequence of the conventional electrons confined to the same region of space or due to the inhomogeneity of defects or disordering alone the wire, which are probably tunable for application on future electronics.
Methods
Synthesis
Bi2Te3 nanowires used in this work were synthesized by AAO template-assisted electrodeposition. The solution was prepared by dissolving 10 mM Te (powder: 99.9998% purity) and 7.5 mM Bi (shots: 99.999% purity) elements into concentrated nitric acid (69.1%) and the solution was then diluted to 1 M final concentration with distilled water. The synthesis of nanowires was carried out using a three-electrode system at a constant potential of −62 mV, relative to an Ag/AgCl reference electrode at room temperature. A pure Pt-wire was used as the counter electrode and Au film evaporated on one side of the AAO membrane prior to the electrodeposition was used as the working electrode. Freestanding nanowires were obtained by dissolving the membrane with 2 M aqueous NaOH solution, followed by several cycles of cleaning process via centrifugation.
Device fabrication and characterization
To make standard four-probe devices on an individual Bi2Te3 Nanowire for transport measurement, we dispersed the nanowires onto a silicon substrate with a 1 μm thick Si3N4 insulating layer. Then, the sample was transferred into FEI SEM/FIB dual beam system for the deposition of Pt-electrodes. The size of the four Pt-stripe electrodes has a nominal width of 100 nm and a thickness of 150 nm deposited from a precursor gas of (methylcyclopentadienyl)trimethyl platimum (CH3)3CH3C5H4Pt. Usually, the film by FIB-induced Pt deposition is amorphous consisting of Pt, C, Ga or O depending on the deposition condition. The resistivity of the FIB-deposited Pt stripes varies from 70 to 700 μΩ.cm, almost 1-2 orders higher than that for a Pt bulk, but the contact resistance between the Pt electrode and TI wire is almost transparent with a resistance less than 10 Ω. While the maximum spreading or diffusion distance of the actual Pt along the wire is on the order of 300 nm, the distance (L) between the inner edges of the two voltage electrodes for all of the studied samples was kept larger than 4 μm, which is much longer than the spreading distance.
References
Fu, L., Kane, C. L. & Mele, E. J. Topological insulators in three dimensions. Phys. Rev. Lett. 98, 106803 (2007).
Qi, X. L. & Zhang, S. C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011) and the references therein.
Hasan, M. Z. & Kane, C. L. Colloquium: Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010) and the references therein.
Fu, L. & Kane, C. L. Topological insulators with inversion symmetry. Phys. Rev. B 76, 045302 (2007).
Qi, X. L., Hughes, T. L. & Zhang, S. C. Topological field theory of time-reversal invariant insulators. Phys. Rev. B 78, 195424 (2008).
Seradjeh, B., Moore, J. E. & Franz, M. Exciton condensation and charge fractionalization in a topological insulator film. Phys. Rev. Lett. 103, 066402 (2009).
Bernevig, B. A., Hughes, T. & Zhang, S. C. Quantum spin Hall effect and topological phase transition in HgTe quantum well. Science 314, 1757–1761 (2006).
Xia, Y. et al. Observation of a large-gap topological insulator class with a single Dirac cone on the surface. Nat. Phys. 5, 398–402 (2009).
Zhang, Y. et al. Crossover of the three-dimensional topological insulator Bi2Se3 to the two-dimensional limit. Nat. Phys. 6, 584–588 (2010).
Hsieh, D. et al. A tunable topological insulator in the spin helical Dirac transport regime. Nature 460, 1101–1105 (2009).
Chen, Y. L. et al. Experimental realization of a three-dimensional topological insulator Bi2Te3 . Science 325, 178–181 (2009).
Zhang, T. et al. Experimental demonstration of topological surface states protected by time-reversal symmetry. Phys. Rev. Lett. 103, 266803 (2009).
Zhang, H. J. et al. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with single-Dirac cone on the surface. Nat. Phys. 5, 438–442 (2009).
Checkelsky, J. G. et al. Quantum interference in macroscopic crystals of nonmetallic Bi2Se3 . Phys. Rev. Lett. 103, 246601 (2009).
Analytis, J. G. et al. Two-dimensional surface state in the quantum limit of a topological insulator. Nat. Phys. 6, 960–964 (2010).
Qu, D. X. et al. Quantum oscillations and Hall anomaly of surface states in the topological insulator Bi2Te3 . Science 329, 821–824 (2010).
Peng, H. et al. Aharonov-Bohm interference in topologcial insulator nanoribbons. Nat. Mater. 9, 225–229 (2010).
Xiu, F. et al. Manipulating surface states in topological insulator nanoribbons. Nat. Nanotech. 6, 216–212 (2011).
Tang, H., Liang, D., Qiu, R. L. J. & Gao, X. P. A. Two-dimensional transport-induced linear magnetoresistance in topological insulator Bi2Te3 nanoribbons. ACS Nano 5, 7510–7516 (2011).
Butch, N. P. et al. Strong surface scattering in ultrahigh-mobility Bi2Se3 topological insulator crystals. Phys. Rev. B 81, 241301 (2010).
Eto, K. et al. Angular-dependent oscillations of the magnetoresistance in Bi2Se3 due to the three-dimensional bulk Fermi surface. Phys. Rev. B 81, 195309 (2010).
Ren, Z. et al. Large bulk resistivity and surface quantum oscillations in the topological insulator Bi2Te2Se. Phys. Rev. B 82, 241306 (2010).
Wang, Z. et al. Tuning carrier type and density in Bi2Se3 by Ca-doping. Appl. Phys. Lett. 97, 042112 (2009).
Checkelsky, J. G., Hor, Y. S., Cava, R. J. & Ong, N. P. Bulk band gap and surface state conduction observed in voltage-tuned crystals of the topological insulator Bi2Se3 . Phys. Rev. Lett. 106, 196801 (2011).
Chen, J. et al. Gate-voltage control of chemical potential and weak antilocalization in Bi2Se3 . Phys. Rev. Lett. 105, 176602 (2010).
Steinberg, H., Gardner, D. R., Lee, Y. S. & Jarillo-Herrero, P. Surface state transport and ambipolar electric field effect in Bi2Se3 nanodevices. Nano Lett. 10, 5032–5036 (2010).
Ihn, T. Topological insulators: oscillations in the ribbons. Nat. Mater. 9, 187–188 (2010).
Bardarson, J. H., Brouwer, P. W. & Moore, J. E. Aharonov-Bohm oscillations in disordered topological insulator nanowires. Phys. Rev. Lett. 105, 156803 (2010).
Zhang, Y. & Vishwanath, A. Anomalous Aharonov-Bohm conductance oscillations from topological insulator surface states. Phys. Rev. Lett. 105, 206601 (2010).
Egger, R., Zazunov, A. & Yeyati, A. L. Helical Luttinger liquid in topological insulator nanowires. Phys. Rev. Lett. 105, 136043 (2010).
Aharonov, Y. & Bohm, D. Significance of electromagnetic potentials in the quantum theory. Phys. Rev. 115, 485–491 (1959).
Xiong, J. et al. Quantum oscillations in a topological insulator Bi2Te2Se with large bulk resistivity (6 Ω.cm). ArXiv: 1101.1315v1, 6 Jan 2011.
Xiong, J. et al. Evidence for a Dirac spectrum in the topological insulator Bi3Te2Se from high-magnetic field Shubnikov-de Haas oscillationjs. ArXiv: 1111.6031v1, 25 Nov. 2011.
Wang, J. et al. Interplay between superconductivity and ferromagnetism in crystalline nanowires. Nat. Phys. 6, 389–394 (2010).
He, H. T. et al. Impurity effect on weak antilocalization in the topological insulator Bi2Te3 . Phys. Rev. Lett. 106, 166805 (2011).
Wang, J. et al. Evidence for electron-electron interaction in topological insulator thin films. Phys. Rev. B 83, 245438 (2011).
Bianchi, M. et al. Coexistence of the topological state and a two-dimensional electron gas on the surface of Bi2Se3 . Nat. Commun. 1, 128 (2010).
Peng, H. et al. Topological insulator nanostructures for near-infrared transparent flexible electrodes. Nat. Chem. 4, 281–286 (2012).
Liu, Z. K. et al. Robust topological surface state against direct surface contamination. Physica E 44, 891–894 (2012).
Acknowledgements
We acknowledge fruitful discussions with Prof. H. W. M. Chan, Zhong Fang, Lin He, Jianxin Li, Ying Liu and Yi Zhou. This work was supported by the National Key Basic Research of China, under Grant Nos. 2011CBA00111 and 2010CB923403; the National Nature Science Foundation of China, Grant Nos. 11174292, No. 11104281 and No. 11104280; Dr Tian also thanks the support of the Hundred Talents Program of the Chinese Academy of Science and the Center for Nanoscale Science (Penn State MRSEC) funded by NSF under Grant No. DMR-0820404, USA.
Author information
Authors and Affiliations
Contributions
M.T. supervised the research and contributed to the analysis. M.T., W.N., H.D. and J.W. synthesized the Bi2Te3 nanowires and fabricated the devices. W.N., Z.Q. and H.D. carried out the transport measurement in high magnetic field and performed structural analysis. M.T. and W.N wrote the paper, together with help of all other co-authors.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplimentary materials
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareALike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Tian, M., Ning, W., Qu, Z. et al. Dual evidence of surface Dirac states in thin cylindrical topological insulator Bi2Te3 nanowires. Sci Rep 3, 1212 (2013). https://doi.org/10.1038/srep01212
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep01212
This article is cited by
-
Electromagnetic response of the surface states of a topological insulator nanowire embedded within a resonator
Communications Physics (2023)
-
Quantum confinement of the Dirac surface states in topological-insulator nanowires
Nature Communications (2021)
-
Spin-dependent scattering induced negative magnetoresistance in topological insulator Bi2Te3 nanowires
Scientific Reports (2019)
-
Evidence of robust 2D transport and Efros-Shklovskii variable range hopping in disordered topological insulator (Bi2Se3) nanowires
Scientific Reports (2017)
-
Spiral Modes and the Observation of Quantized Conductance in the Surface Bands of Bismuth Nanowires
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.