Abstract
Both computational and biological systems have to make decisions about switching from one state to another. The ‘Approximate Majority’ computational algorithm provides the asymptotically fastest way to reach a common decision by all members of a population between two possible outcomes, where the decision approximately matches the initial relative majority. The network that regulates the mitotic entry of the cell-cycle in eukaryotes also makes a decision before it induces early mitotic processes. Here we show that the switch from inactive to active forms of the mitosis promoting Cyclin Dependent Kinases is driven by a system that is related to both the structure and the dynamics of the Approximate Majority computation. We investigate the behavior of these two switches by deterministic, stochastic and probabilistic methods and show that the steady states and temporal dynamics of the two systems are similar and they are exchangeable as components of oscillatory networks.
Similar content being viewed by others
Introduction
At the core of the biochemical networks that regulates the cell cycle there is a switch that triggers an irreversible transition from one critical stage to the next1. To understand the general properties of this switch across different species one may simplify the molecular interactions found in real organisms and abstract over the molecular species that are used by different organisms for the same functions2,3. In that abstract sense, the cell cycle transition to M phase has been shown to employ a universal switching mechanisms in all eukaryotes4,5. The mitotic entry regulator Cyclin Dependent Kinase (Cdk) activates its own activator Cdc25 and inhibits its inhibitor Wee1 and with these two positive feedback loops the system can abruptly switch from low to high Cdk activity state. The structure and properties of this molecular switch have been widely studied6,7,8 and successful mathematical models of the switch and its functional context (the cell cycle oscillator) have been built9,10. There is evidence that related networks are used in other cell cycle transitions11,12.
From the point of view of dynamical systems, the basic features of the cell cycle switch are essentially understood: non-linear kinetics and positive feedbacks induce bistability (needed for switching) and result in hysteresis (needed to resist switch-back)13,14,15. Such kinetic behavior, however, could be achieved by many different networks, while in nature we find a specific universal structure of the network. For example, the required positive feedbacks are produced by double-negative and double-positive loops together16,17. What is special about this structure of the universal network, apart from its required function? How does the system handle noise and how does it relate to other non-biological switches?
To answer these questions we shift our perspective from dynamical systems to computing systems. We ask: what does the cell cycle switch compute and how does it compute it? We find that a fundamental algorithm from distributed computing18,19, the Approximate Majority (AM) algorithm20 matches both the networks structure and the kinetics of the cell cycle (CC) switch; therefore, as we shall describe, the network structure derives from the algorithm, subject to biological constraints. The AM algorithm computes the majority of two finite populations by converting the minority population into the majority population, so that a single population results; it uses a third ‘undecided’ state of the population, from where autocatalysis can drive the individuals into either of the final states. The algorithm has been studied in the context of Population Protocols21: a model of computation and related algorithms for resource-limited interacting agents (such as networks of environmental sensors). It not only switches a majority into a totality, but it does so in a particular way that is (1) fast: with high probability only O(N log N) binary interactions (consult the Methods section for asymptotic notation) are required for a population of size N (20 Theorem 1), (2) reliable: above a certain threshold the true initial majority wins with high probability (20 Theorem 2) and (3) robust: the algorithms still functions correctly in presence of a subpopulation of the order of sqrt(N) that behaves incorrectly or even ‘deviously’ (20 Theorem 4). Moreover, the algorithm is asymptotically optimal in the number of reactions required to switch a majority into a totality, because at least order of N log N interactions are required for each element of the population to interact, directly or indirectly, with every other member. An interesting question is how close nature can come to this optimum.
The AM algorithm can be described chemically in terms of just 4 catalytic and autocatalytic reactions (equation 1). The comparison between AM and CC, however, is not straightforward. To carry it out we need to extend our understanding of both systems: in the computing literature it is not common to consider AM in terms of dynamical systems, which are usually continuous and in the biological literature is not common to consider CC in terms of computational systems, which are usually discrete. The AM network structure is different from (simpler than) the CC structure, but we argue that the differences are dictated by biological constraints and that both the computational and the dynamical properties of AM are preserved by the transformations required to turn it into CC so that the constraints are satisfied. In particular, we show that (1) the structure of AM well implements an input-driven switching function (in addition to the known majority function), (2) the structure of CC well implements a input-less majority function (in addition to the known switching function), (3) the structures of AM and CC are related and an intermediate network shares the properties of both, (4) the behaviors of AM and CC in isolation are related, (5) the behaviors of AM and CC in oscillator contexts are related, (6) a refinement of the core CC network, known to occur in nature, improves switching performance and brings it in line with AM performance.
Results
We investigate and compare four networks that perform switching between a population x and a population y. In all our systems (Fig. 1) x and y are converted to each other by reactions that are directly or indirectly driven by x and y, in such a way that each system contains two positive feedback loops that may also act through intermediaries or by double inhibition.
Switch kinetics in absence of external control.
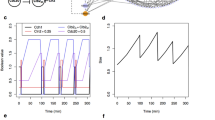
We study the convergence time (time to reach a stable state) of switching networks; in each column, one of two stable states can be reached from the initial conditions. All the reaction rates are set equal and all the species start at equal quantities (details are provided in Supplementary Materials). Columns A-D concern the DC, AM, SC, CC switches respectively. Row 1 gives a depiction of the networks from which one can precisely recover the chemical reaction networks according to our notation. A catalytic reaction is represented by a circle on top of an arrow; for example, the top right of (F) contains the reaction b+z→z+y with catalyst z. A reaction like x+y→y+y is said to be autocatalytic. The full diagram (F) depicts two catalysts, z and r, acting on species x and y through a shared intermediary b, representing the 4 reactions x+z→z+b, b+z→z+y, y+r→r+b and b+r→r+x. We use a more compact pinched-arrow graphical notation (E) to represent the same network as (F), hiding the intermediary species b that is assumed not to enter any other reaction. Note that if multiple catalysts act on the same pinched arrow (as in Fig. 2), they all act on the hidden intermediary in the same way. Row 2 contains deterministic simulations for the mass action ODEs of the respective systems for four values of the initial discrepancy between x and y, from 10% to 0.01% (not meaningful for DC as the system would rest at its initial setting), (Y-axis scale on the right). Row 3 shows sample stochastic simulations consisting of individual traces (black lines) of the Gillespie algorithm. The background heat maps, shown in logarithmic scale, give the probability Pr(xi|tj) that a system will have xi molecules of x at time tj. The horizontal axis is time and the vertical axis is concentration (row 2) or number of molecules (row 3). Subscripts ‘s’ are for stochastic variables and ‘p’ for probabilistic variables.
We consider first a system derived from AM by removing the intermediate species b, leading to two coupled positive feedbacks that works by Direct Competition (DC) between x and y. This network is depicted in figure 1A.1 and corresponds to the two autocatalytic reactions x + y → y + y and y + x → x + x. (A black ball over a reaction arrow represents presence of a catalyst.) The AM (Approximate Majority) network is depicted by an abbreviated graphical notation in figure 1B.1, which is explained in figure 1E,F. Namely, a pair of ‘pinched arrows’ between a pair of species such as x,y represents four reactions with a common intermediate species b (specific to the pair x,y): the intermediate species is omitted. The AM network therefore consists of 4 reactions (of mass action kinetics):

for some intermediate b. The pinched-arrow motif is suggestive of multi-site modification (e.g.: phosphorylation/dephosphorylation)22,23.
In nature it is not common to find direct autocatalytic reactions and especially mutually autocatalytic reactions like in AM. We can however replace them with mutually catalytic reactions that are not directly autocatalytic. We introduce intermediate catalysts r, activated by x (from a reservoir p) and activating x and z, activated by y (from a reservoir w) and activating y. This transformation results in the network SC (Simply Catalytic) of figure 1C.1, where we use pinched-arrow transitions for the new species too (other choices might be suitable). Here we need to introduce additional catalysts t,s to give a threshold for the self-activation reactions of x and y respectively.
Natural systems that switch a molecule between two states will normally have that molecule being active in one state and inactive in the other. However in AM and still in SC, both states x and y are active and catalyze different reactions. Bifunctional enzymes exists in various organisms24,25, but in the case of the cell cycle switch there is no evidence that Cdk would have separate type of activities in its different forms. To move closer to CC we further transform SC in figure 1D.1: we remove the catalytic activity from y and we are therefore left with z activating y, which is inactive. To deactivate y we must therefore deactivate z; this function is taken over by x, which on one hand activates itself through r and on the other hand deactivates y through z (note that the role of s also has reverted compared to its role in SC). This final transformation of the network is certainly non-obvious, but the network so obtained turns out to be the characteristic network of the cell cycle (CC) switch4,8, with x and y corresponding to active and inactive forms of cyclin dependent kinases and z and r resembling active forms of Wee1 and Cdc25 respectively (see Supplementary Materials for the exact correspondence).
AM and CC as isolated systems
We now compare the performance of these four switches by deterministic26, stochastic27 and probabilistic analysis28. We first examine the convergence time of the switches: the time to switch from an unstable initial state to one of two stable states. In our analysis, all the rates are set to 1.0 and the populations start at similar levels. The second row of Figure 1 contains simulations of the deterministic ODEs of the systems, for different initial small, but non-zero, differences between x and y. The black traces in the third row of Figure 1 are individual stochastic simulations for systems with molecular counts of the order of thousands of molecules, starting with all species at the same level including x = y. The deterministic system would not show the break of the symmetry from a totally balanced initial condition, while stochastic noise is enough to move the systems out of this unstable steady state. The heat maps in the third row of Figure 1 are probability distributions for systems with low molecular counts, of the order of tens of molecules, again starting with all species at the same level. The three analysis techniques address different aspects and constraints. Deterministic simulation gives a characterization of the mean behavior of a system, but does not address noise characteristics. Noise can be readily observed in the stochastic simulations, but at very low counts and high noise individual traces give little information. The probability distributions, on the other hand, give a precise picture of a system at low count, but become computationally unfeasible at higher count.
Timing of transitions
The analysis of AM, SC and CC indicates rapid switching and convergence to a stable state after an initial hesitation due to breaking of the symmetry of the initial conditions. If the initial conditions are not so symmetrical, the switching happens more quickly: we essentially investigate the worst-case scenarios. We now discuss the performance of the individual switches.
The Direct Competition switch (DC) (Fig. 1A.3) can rest in two different states, if all the molecules are ever found in state x or state y then the system remains in that state, because at least a single molecule from the other species is needed to catalyze reactions that move the system away from these states. However, the path to reach such a steady state from arbitrary starting conditions is a random walk, taking expected O(N2) molecular interactions to achieve, with each interaction moving the system randomly one way or the other. Moreover, any small perturbation of such a steady state has a chance to move the system to the other state, again by a random walk: the steady states are not robust to noise, thus the system is not bistable from a dynamical point of view. The deterministic ODE model of this system has all the right hand sides of the equations equal to zero, thus the deterministic system remains at its initial condition (not shown).
The Approximate Majority switch (AM) is bistable (Fig. 1B.2–3) and the expected time to reach a stable state from any starting condition is with high probability less than O(N log N) molecular interactions and O(log N) time steps and in fact approximately 3 log N in the worst case of equal starting conditions x = y20. The stable states are completely stable: once reached, no further reactions can happen. Moreover, if the initial state has a majority of either x or y exceeding ω(sqrt(N) · log N) (a low percentage at high molecule numbers), then with high probability the system will settle in the state that has the initial majority20. This implies that the vicinity of the two stable states, where either x or y have a wide or total majority, is resistant to perturbations.
The Simply Catalytic switch (SC) exhibits the same convergence behavior as AM modulo a small time factor (Fig. 1C.2–3). Note however that SC no longer stabilizes at the maximal level completely. The stable states are overwhelmingly but not completely stable because of the continued bias of the reverse reaction catalysts (s and t) which work against x.
The Cell Cycle switch (CC) preserves much of the AM-like behavior, such as fast decision (Fig. 1D.2–3). In addition to the lack of complete stability, as in (SC), the switch is no longer fully symmetrical: when y is in majority x approaches zero and y (not shown) reaches maximum, but when x is in majority it is counteracted by the fixed bias s that keeps some z active and constantly drives some x to y, thus x settles well below the maximum level. SC and CC have a bit slower transition time as well (approximately double the time, compared to AM), which might be caused by the same effect. These discrepancies between AM and CC are resolved in biological systems: in Discussion we examine extra feedbacks that appear in cell cycle systems29 and maximize x levels. Possibly such feedbacks evolved exactly to allow a full activation of x, making CC dynamics even closer to that of the efficient system of AM.
Effect of noise on switches
The stochastic and probabilistic analyses, both ultimately based on the chemical master equations of the systems30, can be compared directly in the third row of Figure 1, showing that the stochastic traces at a certain system size are compatible with the probability distributions at a smaller system size (the relative time scaling is based on the computational complexity of the algorithms and is described in Supplementary Materials). This comparison shows close similarity between AM and SC and good similarity between those two and CC apart for the fact that CC does not switch fully to x due to the bias provided by s. Noticeably, even though a system starts in neutral initial conditions (x = b = y), it randomly but rapidly converges to x or y dominance in AM, SC and CC. DC is however quite different from the others, with two steep hills representing the stable states and a wide flat region in between where stochastic trajectories may wander.
The deterministic analysis in the second row or Figure 1, based on the mass action ODEs, is not directly comparable with the other two. For example, in the extreme case of initial conditions x = y the stochastic system still converges with high probability according to the O(N log N) theoretical bound, but the ODEs describe the system as remaining in the unstable steady state x = y forever. Therefore, in the deterministic case we analyze various non-zero initial discrepancies between x and y, which still show similarities between AM and CC: a logarithmic decrease in disparity leads to linear increase in timing. (The deterministic version of DC, omitted, is degenerate: its stochastic version is a pure bounded random walk.)
Both the deterministic and stochastic/probabilistic analyses indicate that CC is only about twice as slow as the ‘optimal’ AM algorithm and has the same speed as SC. Hence there is not a great penalty for the more complex CC network. Further speed optimizations of CC are examined in Discussion.
External control of the AM and CC systems
We now compare the steady state response of the four switches to external stimuli. The switches of figure 1 are augmented in Figure 2 with external inputs sx (switch-to-x) and sy (switch-to-y) acting on both internal steps of the pinched arrows in panels B-D. The plots in the second row of figure 2 integrate three types of steady-state analysis: deterministic, stochastic and probabilistic, for different system sizes. In each case we vary the input value sx and we observe the steady state output value of x, with sy remaining fixed; all rates are 1.0 and all species start at equal level, except for the varying sx and the fixed sy.
Switch equilibrium in presence of external control.
We study the steady state response of our switching networks. Row 1 shows the four systems of figure 1 extended with external controls sx (switch-to-x) and sy (switch-to-y) in gray. On row 2, the horizontal axis represents the value of the sx input and the vertical axis the value of the resulting x output at steady state. The value of sy remains fixed throughout; as in figure 1 all other initial values and rates are set equal. In each plot, the black line is the bifurcation diagram for the mass action ODEs of the systems (solid = stable, dashed = unstable steady states), showing that each system except the first one exhibits hysteresis; the axes represent concentrations with values that match the ovelayed plots (arbitrary units). The heat map in the background details the discrete probability distribution (in log scale) of a system composed of 5 molecules of each species, except for sy = 3 and with sx varying in 0..15. A point (sxi, xj, zk) in the heat map, for 0 ≤ zk ≤ 1, means that at equilibrium (after a sufficiently long time) the discrete probability of the system being found with xj molecules of species x on an input of sxi molecules of species sx is equal to zk. The noisy red line is a single run of a steady-state stochastic simulation with maximum x = 150 and with sy = 30; sx is increased slowly to obtain the lower trajectory and the jump up and is then decreased slowly to obtain the upper trajectory and the jump down.
DC shows a hyperbolic response, with no ultrasensitivity, bistability, or hysteresis (Fig. 2A.2). AM and SC show very similar hysteresis responses (Fig. 2B,C.2): starting at the origin with increasing sx the system stays on the lower trajectory until the jump point indicated by the stochastic trace and continues on the upper trajectory. With decreasing sx, the system jumps from high to low at a different jump point. CC shows a similar hysteresis response, again somewhat depressed in its maxima as in figure 1. The presence of a clear hysteresis cycle in AM, SC and CC confirms the ability of these systems to act as good switches, unlike DC. Although the hysteresis parameters are tunable in the different systems and AM has fewer species and parameters, there is good agreement between their dynamical behavior. There is also uniform agreement about the response of each network at different systems sizes, with the deterministic, stochastic and probabilistic analysis largely overlapping. Still, the stochastic and probabilistic analysis show that noise can induce the transitions slightly before the deterministic bifurcation point is reached, thus noise can advance the transitions between the two states31.
All the models of figure 1 contain two positive feedback loops. In general, it is known that to establish bistability and hysteresis one positive feedback (and the presence of nonlinearity) is enough14,32. Models of the cell-cycle switch have been investigated in face of the removal of one of the two positive feedback loops and it has been shown that the removal of one of the two loops decreases the efficiency and the robustness of the CC switch6,7,12. In the Supplementary Materials we repeat this analysis for the AM and CC models and show that the removal of either loops leads to a reduced parameter regime for bistability in both models. Thus, also in this respect the AM and CC models behave qualitatively similarly, but it is worth noting that the CC module is more sensitive (works in a smaller parameter range and does not provide full conversion to both states), suggesting that AM is indeed the minimal model that can provide robust and complete switching dynamics.
AM and CC switches in the context of oscillators
Having established that AM and CC have similar characteristics as stand-alone computational systems and dynamical systems, we investigate whether AM switches can drive oscillations with characteristics similar to those of the cell cycle. There is a large literature on various models of cell cycle oscillators9,10,33. In many of these a CC switch is coupled with another switch in a negative feedback loop34. Negative feedback loops can induce oscillations even without the presence of positive feedbacks, but the positive loops make the oscillations more robust as the system periodically switches between two states (relaxation oscillations)35,36,37. Connectivity between these switches may vary, but all such switches show nonlinearity38.
We consider first an oscillator network structure inspired by a mechanical oscillator (the Trammel of Archimedes39), where each stable state of a switch produces a transition in the other switch, in a repeating pattern (Fig 3A.1 and Supplementary Materials). Two AM switches coupled in such way produce a robust limit-cycle oscillator (2AM Full) with a self-stabilizing amplitude and frequency (Fig. 3A.2). Oscillations are found when ratio between the internal AM rates (ri) and the external rates connecting the switches (re) is approximately between 0.2 and 1.0. The detailed response to these parameters is investigated in a bifurcation diagram (Fig. 3A.3) and on a heat map of the full probability distribution (Fig. 3A.4). We observe that even at the trivial parameter combination of all internal AM rates equal to 1, the system shows oscillations that are robust in a wide regime of external coupling rates that control the strength of the negative feedback loops between the two switches. The oscillations are born with high amplitude at a SNIC/SNIPER bifurcation (Fig. 3A.3), as it has been shown for detailed cell cycle models11.
Switches in the context of oscillators.
We study the three oscillators depicted in column 1: (A) one consisting of two fully connected AM switches; (B) one where two of the connections are replaced by fixed biases; (C) one where we further replace an AM switch with a CC switch. Column 2 (stochastic high-molecular-count simulations) shows oscillations over time for chosen values of re/ri, where re is the common rate for the connections between switches (gray lines), while ri is the common rate for all the reactions within a switch (black lines). Column 3 explores deterministic parameter variation in phase space (x1 vs. x2) and bifurcations (re/ri or sx vs. x1). Column 4 combines a deterministic plot (black line) and a probabilistic low-molecular-count heat map in phase space (x1 vs. x2) for a single value of re/ri, from column 2. The values of sx and sy are fixed to 1/3 of the max value of the switching species and their reactions have rate re.
The model of Figure 3A contains several feedback loops connecting the switches, while the majority of cell cycle models contain a single negative feedback loop. To better reflect those models, two connections have been cut in Figure 3B (2AM Inner) and replaced by fixed inputs resembling the effects of cyclin production (sx) and a threshold on Cdc20/APC activation (sy)40. This network is still able to produce robust oscillations, although in a slightly reduced range of the parameters of the negative feedback loop (Fig. 3B.3). Some of the parameter regimes produce the profiles of relaxation oscillators (Fig. 3B.2, top and Fig. 3B.4), typically shown by complex cell-cycle models15,40.
Finally, in Figure 3C we replace one of the AM switches with a CC switch, so that the resulting oscillator (CC-AM Inner) as a whole more clearly resembles a cell-cycle oscillator. This also shows that even in the context of a wider network the AM and CC switches are comparable and interchangeable. The choice of the re/ri ratio now becomes more critical and large oscillation amplitude is more difficult to obtain, but the system still show oscillations similar to those of the similarly wired 2AM Inner system and to those of earlier cell cycle models15,40. The bifurcation diagrams of these two systems also look similar to each other and to classical published analysis11,15: in figure 3B.3 and 3C.3 we plot the steady states and amplitudes of oscillations depending on the input parameter sx.
The external inputs to the oscillators are analogous to cyclin production for sx and to cyclin degradation for sy. In natural networks these inputs feed into the oscillator in more complex configurations than in our models9,10,33 (Supplementary Materials). Still, we have demonstrated that switches with the general characteristics of AM easily lead to robust oscillators if wired in an appropriate configuration.
Discussion
The boundary between dynamical systems and computational systems is not clear-cut: when does an ‘analog’ continuous system give rise to ‘digital’ information processing and when does a collection of ODEs become a digital circuit? Still, there are precise characterizations of computational power, both qualitative (e.g., whether a computational system is Turing-powerful or not) and quantitative (e.g., whether an algorithm runs in O(log N) or not). One can discuss whether a dynamical system falls in one of those classes and what kind of algorithm it implements when seen as a computational system. There is increasing interest in understanding what kind of physical and biological systems can compute in that sense41 and it has been proposed that a computational outlook can help in our understanding of biological systems42,43,44,45,46,47.
Here we have investigated a classical cell cycle network in terms of the algorithm it implements and we claim we have gained new insights in its structure, function and performance. We have illustrated how the computationally effective AM network and the biologically relevant CC network are two ways of achieving ‘majority switching’, yielding two distinct algorithmic implementations of essentially the same behavior with the same asymptotic properties. Moreover, we have shown that their behavior is sufficiently similar that they can be readily exchanged for one another in an oscillator context. We now discuss some general characteristics of switching networks in the context of AM.
The effectiveness of both AM and CC comes from the fact that they both employ two non-linear positive feedback loops. The non-linearity in our systems comes from (a purely catalytic version of) multi-step modifications23. In the context of cell cycle regulation, both transcriptional and post-translational modifications have been associated with nonlinearity38. In relation to the mitotic-switch regulating post-translational feedback the role of multisite phosphorylation has been carefully investigated48,49. It has been established that for nonlinear response the phosphate groups have to be added and removed independently (distributive multisite phosphorylation), while if enzymes can add or remove all groups sequentially during a single binding event (processive multisite phosphorylation) then the nonlinearity is lost23,50. AM works like a distributive system (Fig. 4A): the common intermediate can be modified independently in both directions. (Adding more than one intermediate step for the conversion between x and y does not change the fundamental dynamics of AM.) If instead we use separate intermediates (Fig. 4B), then the system works processively: the separate intermediates can be further modified in only one direction during the transitions between x and y, and the system no longer exhibits an irreversible convergence to stable states.
Nonlinearity in switching systems.
We compare the nonlinear dynamics of the AM switch with some alternatives, via sample individual traces obtained form stochastic simulations. We have uniformly chosen rate 1.0 for unimolecular reactions (in (C) and (D)) and 0.001 for bimolecular reactions, with x = y initial conditions (all other species set at zero) and with 15000 max molecule counts as in figure 1. Panel (A) shows the same AM circuit as in figure 1B. Panel (B) shows a variation with two separate intermediates that are processively modified; the upper trajectories converge with a mixture of x and b, hence we plot x+b. Panel (C) shows mutual competition between x and y via dimerization; the upper trajectories converge with a mixture of x and b (the x-dimer), hence we plot x+2b, the total amount of x. Panel (D) shows direct mutual competition between x and y regarded as two enzymes regulated by Michaelis-Menten reactions; we plot x+c, the sum of the enzyme x plus the complex c with its substrate y. Note that x+c is not constant and similarly for y+b and hence the system does not operate as a pair of normal enzymatic reactions where those sums are preserved.
Another way to build nonlinearity into biological systems is to let the regulators oligomerize, with only the complex having a catalytic activity38. Similar changes can be made in AM: we can allow dimerization of x and y and have these dimers drive transitions between the two stable states (Fig. 4C). Models incorporating these changes allow AM-like switching between all-x and all-y states, but in the stable states we find a mixture of monomers and dimers of the winning species. Thus, such protocol would not work efficiently from a computational point of view.
Another option is to consider a direct competition network like DC but where the catalytic reactions are Michaelis-Menten enzymatic reactions: these are intrinsically nonlinear reactions and could potentially replace the nonlinear multisite modification mechanism of AM. Note however that again here we have two separate (substrate-enzyme complex) intermediaries (Fig. 4D). When enzymatic reactions work in saturation we have zero-order ultrasensitivity or Goldbeter-Koshland switching51: these mechanisms are often used in biological network models to capture the dynamics of fast switches52. The AM-like positive feedback network incorporating enzymatic reactions, however, does not switch properly as some x and y always accumulate in one of the two intermediates53,54. On long time scales, the primary species and to a lesser degree the complexes oscillate randomly, revealing again that the common ‘undecided’ intermediate of the transition between x and y is an important feature of AM.
Therefore, other plausible mechanisms for achieving nonlinearity in chemical systems do not appear to lead to improvements or alternatives to the AM switching algorithm. This suggests that distributive multisite modification is the simplest, most effective way of introducing nonlinearity in the system.
Previous literature has shown AM to be an efficient and robust decision algorithm20 and CC to be a robust biological switch7,12. We used deterministic, stochastic and probabilistic methods to characterize the kinetic and dynamic behaviors of the two systems and those that stand in the way of transforming one into the other. Cells do not use AM in its original form, since multifunctional enzymes that change their activity through modification are rare55. AM is robust to parameter changes, but due to its small size it is fragile to removal of its components and thus evolutionary it cannot be stable56,57. Probably CC is the closest similar system that evolution has found to deal with important cellular decisions.
Similar network structures may have evolved to deal with other biological decisions. The cell cycle switch is probably the most well characterized biological switch and it is highly conserved among eukaryotes. There are many other biological switches that are less well characterized13,58, but the existence of two positive feedbacks in their structure has been proposed. Such systems include the membrane transport regulatory switch, were Rab5 helps its activation by activating Rabex5 and by inhibiting Rab759,60. Another example is the apoptotic switch, where the caspase CASP3 cleaves and by this, activates its activator caspases CASP8 and CASP9 while also inhibiting its own inhibitor, XIAP61. Various models of the cell polarity establishment regulatory Cdc42 activation also incorporate double positive feedbacks in the system62,63,64. There could be many other biological switches that work with similar, Approximate Majority-type switching dynamics and our other findings on the AM behavior may apply to these systems as well.
The main difference between the behavior of AM and CC is that CC cannot fully turn on because external biases (s and t on Fig. 1D) keep inactivating the system. This leads to a reduced maximum in the steady state of the CDK-analog species x (Fig. 2D); thus CC is not as effective at switching as AM. But nature has solved this problem: CDK, through the Greatwall kinase65, also inhibits the phosphatase PP2A, which has the catalytic role of both s and t in our CC model. With this extra feedback loop, once CDK is active it suppresses the activity of the external inhibitors and allows its own full activation.
The incorporation of this additional feedback into the CC model does in fact enable the full activation of x. The extended circuit (GW) is shown in Figure 5A, where s and t have been merged into s (analogous to PP2A), with x now inhibiting s. When x is not present, s can self-activate (PP2A inactivates its inhibitor, the Greatwall kinase29) from an inactive form m, with the help of a fixed bias v. Even though v is still continuously counteracting x, its effect is much weaker than the direct effect of s in CC and as a result x can achieve full activation. The resulting kinetics is shown in figure 5B for the deterministic system (cf. Fig. 2D.2) and in figure 5C for the stochastic and probabilistic systems (cf. Fig. 2D.3).
Cell cycle switch with Greatwall loop.
We study the GW network: a version of CC from Figure 1D.1 enriched with a feedback loop where x modulates the s and t biases (now unified into the s species). Panel (B) is analogous to Fig 1D.2 and panel (C) is analogous to Fig 1D.4, both showing an improved activation of x. Panel (D) is a comparison between the switching speeds of AM, GW and CC, showing GW performing better than CC and about as well as AM.
Full activation is now achieved, but even more remarkably, the switching speed improves in the GW circuit, making it almost as fast as AM. This is shown in figure 5D via sample stochastic traces, with GW traces coming very close in performance to AM traces as opposed to CC traces. The additional circuitry has therefore two beneficial effects: improving the activation level of x and also improving the activation speed of x by about a factor of 2, making it about as fast as the best known circuit. One could suspect that the original decrease in switching speed in SC and CC with respect to AM (Fig. 1) is due to the introduction of the intermediate catalysts and therefore that the increased speed in GW is somehow due to the direct self-activation of s. However, introducing an intermediate species in the s loop still leads to the same speedup (Supplementary Materials).
In conclusion, we have shown that the AM algorithm is the simplest expression of the task that is performed by the CC network. Although the AM algorithm has features that may be biologically unrealistic, it can guide the understanding of the properties of more complex biological networks. One may also speculate about whether related networks, such as SC might exist in nature and whether other complex biological networks may have simple algorithmic explanations.
Methods
Asymptotic notation
“f(x) is O(g(x))”, or “f is bounded by g asymptotically” is defined as: A function over the reals f(x) belongs to the set O(g(x)) iff there exist real numbers k > 0 and x0 such that f(x) ≤ k · g(x) for all x > x0. Further, “f (x) is ω(g(x))”, or “f dominates g asymptotically” is defined as: A function over the reals f(x) belongs to the set ω(g(x)) iff for all real numbers k > 0 there exists a real number x0 such that k · g(x) ≤ f(x) for all x > x0. Note that in, e.g., O(log x) the basis of the logarithm is not important because of the multiplicative constant k and the fact that logarithms in different bases differ only by a constant factor.
Ordinary differential equation models
Implementation of deterministic models were done as .ODE models, executable by the XPPAUT (http://www.math.pitt.edu/~bard/xpp/xpp.html)26 or Oscill8 (http://sourceforge.net/projects/oscill8) software packages. The model files and used parameter sets are provided in Supplementary Materials.
Stochastic models
The various chemical networks were modeled in SPiM Player v1.13 http://research.microsoft.com/en-us/projects/spim27. SPiM can represent a variety of reactive systems in its modeling language, including chemical reaction networks and can then provide numerical simulations with a Gillespie-style solver: the models are included in Supplementary Materials. SPiM's modeling language is a general computational language and it allows us for example to program the slow sweeping of sx values in figure 1 within the model and in a single run. In SPiM we can study stochastic systems of the order of hundreds of thousands of molecules and obtain an indication of the noise in the systems. For figure 1 row 3 we produced a sample of individual Gillespie trajectories: since we used a high molecular count, the stochastic noise is quite limited on the individual trajectories (for AM, SC, CC), but still the trajectories differ considerably. For figure 2 row 2 we run a Gillespie simulation at steady-state for each value of sx, except that all these simulations were done in a single run, slowly incrementing sx from 0 to max value and then slowly decrementing it back to 0. The decreasing trajectory was then reflected and superimposed on the increasing trajectory, obtaining an image of the hysteresis cycle. We used low molecular counts to emphasize the noise. For figure 3 column 2 we run stochastic simulations at high molecular count; these are therefore comparable to deterministic simulations, but show that even stochastically we can obtain regular oscillations.
Probabilistic models
The various chemical reaction networks were modeled in PRISM v4.0.3 http://www.prismmodelchecker.org28. PRISM can encode a variety of stochastic and probabilistic systems in its modeling language, including stochastic chemical networks: the models are included in Supplementary Materials. When PRISM is given such a model with initial conditions (initial number of molecules and stochastic rates), it generates a continuous-time Markov chain for the system as a sparse matrix, where a state of the Markov chain is the vector of number of molecules of each species and a transition in the Markov chain is the propensity of moving from the source state to the target state. We can then use the PRISM modelchecking language to ask questions about the (possibly very large) Markov chain, such as computing the probability of reaching a state from another state. We ask three basic questions and display the answers as heat maps. For figure 1 row 3, what is the probability that at time T there will be i molecule of species x (“P = ? [F[T,T]x = i]”); for figure 2 row 2, what is the probability that at steady state there will be i molecules of species x (“S = ? [x = i]”) for each value of sx; and for figure 3 column 4, what is the probability that at steady state there will be i molecules of species x1 and j molecules of species x2 (“S = ? [ x1 = i & x2 = j ]”). The results we can obtain are limited by the size of the generated Markov chain; for example, the analysis of the CC circuit in figure 2 (with 15 molecules of x+b+y, etc.) generates ~2.5 million states and ~25 million transitions. That Markov chain is built in a few seconds, but uses nearly all the memory we have available; the computation of the probabilities then takes about 48 hours on a standard laptop. In contrast, the AM circuit takes only a few minutes to analyze completely for the same size. The heat maps were generated in SigmaPlot www.sigmaplot.com from the PRISM data.
References
Novak, B. et al. Irreversible cell-cycle transitions are due to systems-level feedback. Nat Cell Biol 9, 724 (2007).
Brandman, O. et al. Interlinked fast and slow positive feedback loops drive reliable cell decisions. Science 310, 496 (2005).
Chang, D. E. et al. Building biological memory by linking positive feedback loops. Proc Natl Acad Sci U S A 107, 175 (2010).
Lindqvist, A. et al. The decision to enter mitosis: feedback and redundancy in the mitotic entry network. J Cell Biol 185, 193 (2009).
Nurse, P. Universal control mechanism regulating onset of M-phase. Nature 344, 503 (1990).
Domingo-Sananes, M. R. & Novak, B. Different effects of redundant feedback loops on a bistable switch. Chaos 20, 045120 (2010).
Ferrell, J. E. Jr. Feedback regulation of opposing enzymes generates robust, all-or-none bistable responses. Curr Biol 18, R244 (2008).
O'Farrell, P. H. Triggering the all-or-nothing switch into mitosis. Trends Cell Biol 11, 512 (2001).
Csikasz-Nagy, A. Computational systems biology of the cell cycle. Brief Bioinform 10, 424 (2009).
Ferrell, J. E. et al. Modeling the Cell Cycle: Why Do Certain Circuits Oscillate? Cell 144, 874 (2011).
Csikasz-Nagy, A. et al. Analysis of a generic model of eukaryotic cell-cycle regulation. Biophys J 90, 4361 (2006).
Romanel, A. et al. Transcriptional Regulation Is a Major Controller of Cell Cycle Transition Dynamics. PloS one 7, e29716 (2012).
Angeli, D. et al. Detection of multistability, bifurcations and hysteresis in a large class of biological positive-feedback systems. Proc Natl Acad Sci U S A 101, 1822 (2004).
Griffith, J. S. Mathematics of cellular control processes: II. Positive feedback to one gene. J. Theor. Biol. 20, 209 (1968).
Tyson, J. J. et al. Sniffers, buzzers, toggles and blinkers: dynamics of regulatory and signaling pathways in the cell. Curr Opin Cell Biol 15, 221 (2003).
Ferrell, J. E. Jr. Self-perpetuating states in signal transduction: positive feedback, double-negative feedback and bistability. Curr Opin Cell Biol 14, 140 (2002).
Tyson, J. J. & Novák, B. Functional motifs in biochemical reaction networks. Annual review of physical chemistry 61, 219 (2010).
Kshemkalyani, A. D. & Singhal, M. Distributed computing: principles, algorithms and systems. (Cambridge Univ Press, 2008).
Lynch, N. A. Distributed algorithms. (Morgan Kaufmann, 1996).
Angluin, D. et al. A simple population protocol for fast robust approximate majority. Distributed Computing 21, 87 (2008).
Aspnes, J. & Ruppert, E. An introduction to population protocols. Middleware for Network Eccentric and Mobile Applications 1, 97 (2009).
Barik, D. et al. A model of yeast cell-cycle regulation based on multisite phosphorylation. Mol Syst Biol 6, 405 (2010).
Salazar, C. & Höfer, T. Multisite protein phosphorylation–from molecular mechanisms to kinetic models. Febs Journal 276, 3177 (2009).
Bazan, J. F. et al. Evolution of a bifunctional enzyme: 6-phosphofructo-2-kinase/fructose-2, 6-bisphosphatase. Proceedings of the National Academy of Sciences 86, 9642 (1989).
Fülöp, V. et al. The anatomy of a bifunctional enzyme: Structural basis for reduction of oxygen to water and synthesis of nitric oxide by cytochrome cd1. Cell 81, 369 (1995).
Ermentrout, B. Simulating, Analyzing and Animating Dynamical Systems: A Guide to XPPAUT for Researchers and Students. (SIAM, 2002).
Phillips, A. & Cardelli, L. Efficient, correct simulation of biological processes in stochastic pi calculus. in CMSB2007 Vol. 4695 (eds Calder M., & Gilmore S.) 184 (Springer-Verlag, 2007).
Kwiatkowska, M. et al. PRISM: Probabilistic symbolic model checker. Computer Performance Evaluation: Modelling Techniques and Tools, 113 (2002).
Mochida, S. & Hunt, T. Protein phosphatases and their regulation in the control of mitosis. EMBO reports 13, 197 (2012).
Gillespie, D. T. Exact stochastic simulation of coupled chemical reactions. J Phys Chem 81, 2340 (1977).
Steuer, R. Effects of stochasticity in models of the cell cycle: from quantized cycle times to noise-induced oscillations. Journal of theoretical biology 228, 293 (2004).
Thomas, R. & Kaufman, M. Multistationarity, the basis of cell differentiation and memory. I. Structural conditions of multistationarity and other nontrivial behavior. Chaos 11, 170 (2001).
Tyson, J. J. & Novak, B. Temporal organization of the cell cycle. Curr Biol 18, R759 (2008).
Tsai, T. Y. et al. Robust, tunable biological oscillations from interlinked positive and negative feedback loops. Science 321, 126 (2008).
Griffith, J. S. Mathematics of cellular control processes. I. Negative feedback to one gene. J. Theor. Biol. 20, 202 (1968).
Novak, B. & Tyson, J. J. Numerical analysis of a comprehensive model of M-phase control in Xenopus oocyte extracts and intact embryos. J Cell Sci 106 (Pt 4), 1153 (1993).
Pomerening, J. R. et al. Building a cell cycle oscillator: hysteresis and bistability in the activation of Cdc2. Nat Cell Biol 5, 346 (2003).
Novák, B. & Tyson, J. J. Design principles of biochemical oscillators. Nature Reviews Molecular Cell Biology 9, 981 (2008).
Sangwin, C. The wonky trammel of Archimedes. Teaching Mathematics and its Applications 28, 48 (2009).
Tyson, J. J. et al. The dynamics of cell cycle regulation. Bioessays 24, 1095 (2002).
Vinson, V. et al. Does It Compute? Science 336, 171 (2012).
Fisher, J. & Henzinger, T. A. Executable cell biology. Nature biotechnology 25, 1239 (2007).
Kwiatkowska, M. Z. & Heath, J. K. Biological pathways as communicating computer systems. Journal of Cell Science 122, 2793 (2009).
Navlakha, S. & Bar-Joseph, Z. Algorithms in nature: the convergence of systems biology and computational thinking. Molecular Systems Biology 7, 546 (2011).
Nurse, P. Life, logic and information. Nature 454, 424 (2008).
Priami, C. Algorithmic systems biology. Commun. ACM 52, 80 (2009).
Regev, A. & Shapiro, E. Cellular abstractions: Cells as computation. Nature 419, 343 (2002).
Kim, S. Y. & Ferrell, J. E. Substrate competition as a source of ultrasensitivity in the inactivation of Wee1. Cell 128, 1133 (2007).
Nash, P. et al. Multisite phosphorylation of a CDK inhibitor sets a threshold for the onset of DNA replication. Nature 414, 514 (2001).
Gunawardena, J. Distributivity and processivity in multisite phosphorylation can be distinguished through steady-state invariants. Biophysical journal 93, 3828 (2007).
Goldbeter, A. & Koshland, D. E. An amplified sensitivity arising from covalent modification in biological systems. Proceedings of the National Academy of Sciences 78, 6840 (1981).
Goldbeter, A. Zero-order switches and developmental thresholds. Mol Syst Biol 1 (2005).
Blüthgen, N. et al. Effects of sequestration on signal transduction cascades. Febs Journal 273, 895 (2006).
Ciliberto, A. et al. Modeling networks of coupled enzymatic reactions using the total quasi-steady state approximation. PLoS Comput Biol 3, e45 (2007).
Kirschner, K. & Bisswanger, H. Multifunctional Proteins. Annual Review of Biochemistry 45, 143 (1976).
Kitano, H. Biological robustness. Nature Reviews Genetics 5, 826 (2004).
Kitano, H. Towards a theory of biological robustness. Mol Syst Biol 3 (2007).
Blüthgen, N. & Herzel, H. How robust are switches in intracellular signaling cascades? Journal of theoretical biology 225, 293 (2003).
Del Conte-Zerial, P. et al. Membrane identity and GTPase cascades regulated by toggle and cut-out switches. Mol Syst Biol 4, 206 (2008).
Grosshans, B. L. et al. Rabs and their effectors: achieving specificity in membrane traffic. Proceedings of the National Academy of Sciences 103, 11821 (2006).
Legewie, S. et al. Mathematical modeling identifies inhibitors of apoptosis as mediators of positive feedback and bistability. PLoS Comput Biol 2, e120 (2006).
Jilkine, A. & Edelstein-Keshet, L. A comparison of mathematical models for polarization of single eukaryotic cells in response to guided cues. PLoS computational biology 7, e1001121 (2011).
Maree, A. F. et al. Polarization and movement of keratocytes: a multiscale modelling approach. Bull Math Biol 68, 1169 (2006).
Wedlich-Soldner, R. & Li, R. Yeast and fungal morphogenesis from an evolutionary perspective. Semin Cell Dev Biol 19, 224 (2008).
Glover, D. M. The overlooked greatwall: a new perspective on mitotic control. Open Biology 2, 120023 (2012).
Author information
Authors and Affiliations
Contributions
Both authors conceived and performed the research and together they wrote the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary info
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareALike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Cardelli, L., Csikász-Nagy, A. The Cell Cycle Switch Computes Approximate Majority. Sci Rep 2, 656 (2012). https://doi.org/10.1038/srep00656
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep00656
This article is cited by
-
A kinetic approach to investigate the collective dynamics of multi-agent systems
International Journal on Software Tools for Technology Transfer (2023)
-
Iteratively reweighted least squares and slime mold dynamics: connection and convergence
Mathematical Programming (2022)
-
Phase transition of a nonlinear opinion dynamics with noisy interactions
Swarm Intelligence (2022)
-
Population-induced phase transitions and the verification of chemical reaction networks
Natural Computing (2021)
-
Approximate majority analyses using tri-molecular chemical reaction networks
Natural Computing (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.