Abstract
The metabolism of organisms can be studied with comprehensive stoichiometric models of their metabolic networks. Flux balance analysis (FBA) calculates optimal metabolic performance of stoichiometric models. However, detailed biological interpretation of FBA is limited because, in general, a huge number of flux patterns give rise to the same optimal performance. The complete description of the resulting optimal solution spaces was thus far a computationally intractable problem. Here we present CoPE-FBA: Comprehensive Polyhedra Enumeration Flux Balance Analysis, a computational method that solves this problem. CoPE-FBA indicates that the thousands to millions of optimal flux patterns result from a combinatorial explosion of flux patterns in just a few metabolic sub-networks. The entire optimal solution space can now be compactly described in terms of the topology of these sub-networks. CoPE-FBA simplifies the biological interpretation of stoichiometric models of metabolism and provides a profound understanding of metabolic flexibility in optimal states.
Similar content being viewed by others
Introduction
A comprehensive view of the metabolic capacities of organisms can be obtained with genome-scale stoichiometric models of their metabolic networks21,26. The development of these models has been greatly facilitated by the availability of annotated genome sequences and semi-automated computational pipelines for reconstruction13,14,21. Models currently exist for various unicellular organisms, including various pathogens, industrially relevant microorganisms and man21 and their number continues to grow. They typically incorporate hundreds to thousands of reactions and metabolites.
In the last decade, a large number of computational methods have been developed for studying the systemic properties of genome-scale metabolic networks for applications in biotechnology and medicine21,42,26. Flux balance analysis (FBA)24,8,30 is arguably the most frequently used method for analysis of stoichiometric models. FBA predicts maximal yields of metabolic products (e.g. biomass) and the associated optimal flux distributions of genome-scale stoichiometric models and, therefore, FBA sets bounds for metabolic engineering studies24,26. The predictions of FBA often come close to the outcome of laboratory evolution studies15,43 and can be used to identify metabolic constraints and objectives at the level of the entire metabolic network36. Generally, the constraints defined by the stoichiometric model are insufficient in number to guarantee a unique optimal flux route through the metabolic network. A whole solution space of flux distributions is then consistent with the prediction of the maximal yield. The set of all optimal flux distribution solutions of a FBA problem defines a so-called polyhedron35.
In this work, we report a computational method, Comprehensive Polyhedra Enumeration Flux Balance Analysis (CoPE-FBA), that gives directly a network-topological understanding of the solution spaces resulting from FBA, including flux ranges (in the literature also referred to as flux spans) and flux coupling20,7, in terms of a compact set of subnetworks that display alternative flux distributions in the optimal state calculated by FBA. The software for the computations of CoPE-FBA is described in the Methods section.
Methods proposed in the past for the full characterization of polyhedra of metabolic networks47,19,44,45,46,37,40, e.g. elementary flux modes (EFMs) and extreme pathways (ExPas), have their limitations for two reasons: excessive running times and output (millions of flux vectors) that is too large for any sensible analytical biological inspection. Here we present how those limitations can be overcome for FBA polyhedra, which are smaller than those associated with EFMs and ExPas. However, they are still considered intractable. Previous studies have obtained various partial characterizations of FBA polyhedra. Mixedinteger linear programming has been used to partially characterize the optimal flux space28. Flux variability analysis was introduced to quantify the range of flux values that a single reaction can take in a polyhedron20. Flux coupling analysis allows for the identification of reaction pairs with a fixed flux ratio or flux direction across all optimal solutions within the polyhedron7. Monte Carlo sampling of optimal solutions has also been used to probe the geometric properties of a polyhedron48,27,33,6. However, these studies do not give any insight into how the topology of the entire metabolic network gives rise to a polyhedron of a specific FBA problem.
CoPE-FBA of various genome-scale metabolic networks shows that a few relatively small subnetworks (involving typically about 5–10% of all the reactions) shape the geometry of the polyhedron of optimal FBA solutions. We tested whether our results apply to genome-scale stoichiometric models in general. We compared eight such models and nine different growth conditions and found in all cases that the solution space could be understood in terms of the topology of a few small subnetworks. The computational pipeline that we have developed for the calculation of polyhedra of FBA problems is described in the Methods section. We start by explaining the compact mathematical representation of the optimal flux space using a toy metabolic network. Subsequently, we present the results we obtained by applying CoPE-FBA to real-life genome scale metabolic networks. The main body of the paper ends with a discussion. The paper is completed by a section on methodology with information on the design and implementation of the associated computational pipeline.
Results
Network topological interpretation of optimal solution spaces
Any FBA polyhedron can be described in two ways. One by linear equalities and inequalities, which is given by the specification of the FBA problem as a linear program (see Methods). The other, which is more relevant for biological investigations, involves the geometric description of a polyhedron in terms of its extremities35, which are expressed as flux vectors19,44,45,46,37,40. All these flux vectors have a topological interpretation in terms of cycles and paths in metabolic networks. However, existing methodologies have so far been incapable of determining these polyhedral properties of genome-scale stoichiometric models, even when restricted to optimal FBA spaces.
We start with analyzing a toy metabolic network (figure 1A) to introduce the mathematical description of optimal solution spaces (polyhedra) that arise in FBA. The network consists of 26 reactions and contains reversible as well as irreversible reactions. To facilitate the exposition we assume that each reaction, apart from R25, transforms one molecule of substrate into one molecule of product. We consider the network at steady state, i.e. for every intermediate metabolite the net production and synthesis rates balance. The FBA objective will be to maximize flux through reaction R26 under a restriction on the network input flux, i.e. R1 = 1. Formulating this problem as a linear programming (LP) problem and solving by any LP-solver (or in this case by inspection of figure 1A) it can be verified that the solution value to this FBA program is a maximal flux of reaction R26 equal to 1. For additional introductory expositions of flux balance analysis we refer the reader to three papers24,8,30.
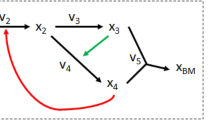
Topological characterization of the optimal solution space of an artificial metabolic network in terms of vertices, rays and linealities.
A. A metabolic network with 23 metabolites and 26 reactions. The source and sink metabolites, X, Y, T and U, are underlined to indicate that their concentrations are considered fixed in order to ensure a steady state, which we assume to be stable. Reversible reactions are depicted by two-way arrows, irreversible reactions by one-way arrows. A reaction carries a positive flux when running from lower alphabetic to higher alphabetic order (e.g for R19 and R21 production of O and L correspond to positive fluxes). FBA was applied to maximize the flux through reaction R26 under the constraint that the flux of reaction R1 is smaller than or equal to 1. B. Overview of the linealities (green subnetworks) and the single ray (blue) that exist for this FBA program. The linealities correspond to reversible cycles whereas rays resemble irreversible cycles. These cycles are elementally balanced, such that no net conversions take place. Irreversible cycles (rays) are thermodynamically infeasible. The reactions in these cycles that are dashed in the figure show a choice of reactions included in vertices. C. The four vertices of this FBA solution space are displayed. They each represent a route from source to sink metabolites that have the same maximal yield. Reaction R25 is not used among the optimal vertices because it would give rise a lower yield than any of the other vertices. Any optimal flux distributions can be reconstructed from the vertex, rays and linealities.
Clearly any route in the toy network from X to Y that avoids R25 corresponds to an optimal flux vector. Each route has value 1 for each of the reactions on the route and 0 otherwise. Inspection of the network indicates that multiple such routes exist. One such a route is composed out of the reactions, {R1, R2, R5, R6, R7, R8, R12, R13, R14, R15, R22, R23, R26}. Let us denote the corresponding flux vector by f1. Another one is obtained by replacing reactions R6, R7 and R8 by reactions R9, R10 and R11. Let f2 be the corresponding flux vector. Any convex combination of these two fluxes, i.e., for any positive λ < 1, sending a flux of λ over the first route and 1 − λ over the second, constitutes an optimal flux vector f = λf1 + (1 − λ)f2. In addition, various cycles exist in the network that, when run at different rates, do not influence the yield of Y on X. For instance, reaction R2, R3 and R4 can run at any rate as long as metabolites A, B and C are at steady state and this will not enhance nor reduce the yield of Y on X. This analysis indicates that alternative optimal flux distributions exist in the network and that each of those agrees with the FBA optimum.
These alternative optimal flux distributions are each related to three topological features of the solution space: vertices, rays and linealities. Vertices represent paths in the metabolic network (figure 1) and they correspond to corner points of (a suitably chosen projection) of the polyhedron describing the solution space. A ray is generally an irreversible cycle in the network (figure 1). In linear algebraic terms, a ray is a direction (flux vector) v such that given any point v′ in the polyhedron the point v′ + υv is also in the polyhedron, for all values of υ ≥ 0. These directions together form a cone. Linealities are reversible cycles in the network (figure 1). In linear algebraic terms, they are defined as directions (flux vectors) v such that given any point v′ in the polyhedron the point v′ + µv is also in the polyhedron, for all values of µ. The latter directions together span a linear subspace, the lineality space, which can be fully characterized by a relatively small number of basis vectors, which we call linealities in this paper. We emphasize that the rays and the linealities do not belong to the optimal solution space themselves; they do not contribute to optimization of the metabolic objective. They merely give directions in which the solution space is unbounded. Every flux vector in the optimal FBA polyhedron can be expressed in terms of these three sets of vectors. For a precise mathematical explanation of these concepts we refer to the Supplementary Information. In figure 1B,C we display the vertices, rays and linealities for the toy network.
Rays and linealities correspond to, respectively, irreversible and reversible cycles, in which no net conversion takes place, see Figure 1B. For instance, the conversion by the lineality composed of R2, R3 and R4 involves no net conversion, only the recycling of B. The same holds for the single ray solution and the other linealities. We notice that rays correspond to thermodynamically infeasible loops (see Discussion). Four vertices exist for this FBA problem (Figure 1C). They differ in the routes taken through the reactions R6 to R11 and R13 to R18. They each give rise to the maximal yield of 1 unit of Y per 1 unit of X. For incompletely defined networks, rays and linealities can in principle also occur as paths rather than cycles.
Several computational pipelines have been proposed to compute these extremities of polyhedra. We refer especially to Polco41 developed for determining EFMs in metabolic networks. The size of the problems usually prevents these methods to find a complete enumeration of the extremities. We emphasize here two aspects of our method that allows us to overcome these problems. Firstly, we correct the common practice in FBA to model fluxes without bounds by bounds with artificially high numbers. Such bounds are entirely superfluous and cause the disappearance of the rays and the linealities at the expense of an explosion of the number of vertices. Secondly, we perform a preprocessing step. We noticed that in optimal FBA solution space, usually many fluxes have a fixed value throughout the space. We detect these fixed fluxes first by flux variability analysis. Fixing them at these values reduces the search space so much that e.g. Polco can be used for enumeration. Moreover, fixing these fluxes shows that the variability in the optimal solution space is captured by relatively small subnetworks constituted by reactions with variable fluxes. We find these subnetworks by performing a correlation analysis on the vertices found. This allows for a compact and insightful description of the optimal solution space in terms of subnetworks that can be studied independently by visual inspection. We illustrate this at the hand of the toy model. All details of the method are described in the Methods section.
In the toy model flux variability analysis finds that in every optimal solution R5, R12 and R22 have value 1. After fixing these fluxes, we can now see that the number of vertices of a FBA problem arises through a combinatorial phenomenon. The 22 vertices, corresponding to 22 paths from R1 to R26, that are obtained by firstly choosing between {R6, R7, R8} and {R9, R10, R11} (which together form the first subnetwork) and then choosing between {R13, R14, R15} and {R16, R17, R18}, which form the second subnetwork. Notice that because R23 and R24 together form a cycle (corresponding to a ray) they are not regarded as a third subnetwork. In each vertex we must choose the flux in R23 equal to 1 and in R24 to 0. The same flux vectors with flux 0 on R23 and 1 on R24 is not another vertex: it can be expressed as a convex combination of two other solutions: 1/2 times the vector with flux in R23 equal to 1 and in R24 to 0 plus 1/2 times the vector with flux in R23 equal to −1 and in R24 to 2.
Flux path variability in such subnetworks is the crux of the combinatorial explosion of vertices, which we will report in the next sections for genome-scale models. This combinatorial explosion can arise because subnetworks may exist in metabolism with alternative internal flux distributions that can be independently chosen without compromising the optimality requirement. These subnetworks have a fixed net input-output stoichiometry, i.e. D → I and J → Q in Figure 1, regardless of their internal flux distribution. If there were k such subnetworks each having 2 alternative routes, then there would have been (at least) 2k vertices, emphasizing that the total number of vertices can in general be much larger than the number of reactions in the system.
CoPE-FBA for Escherichia coli on glucose
Using CoPE-FBA, we characterized the optimal solution space for an FBA program where a genome-scale model of Escherichia coli version iJR90429 was optimized for growth in mineral medium on glucose. The uptake glucose flux was set such that a maximal growth rate of 1 was obtained. Through subsequent enumeration we found 17280 vertices, 8 rays and 1 lineality (i.e. the lineality space has dimension 1). Across all vertices, out of the 1066 reactions in the model: 733 carried no flux, 274 had a single value and 59 were variable. Thus, 59 variable reactions gave rise to the 17280 vertex solutions; below we explain how. The software pipeline for CoPE-FBA and the scripts for obtaining the results described in this section can be found in the Methods section.
Of these 59 variable reactions, 44 reactions had 2 different flux values, 3 reactions had 16 values, 2 reactions had 4 values and 10 reactions had 3 values across all 17280 vertices. The identity and ranges of all variable reactions were independently verified using flux variability analysis. We found a total of 79 fluxes variable in the flux variability analysis: as already mentioned above, 59 of them are variable across all vertices, 19 are variable and occur in reactions making up the rays and 3 reactions occur in the lineality space. Out of those lineality space reactions, 2 also occurred as variable fluxes across the vertices (figure 2C).
Topological characterization of the optimal solution space with CoPE-FBA of Escherichia coli iJR904 growing on mineral medium supplemented with glucose as carbon source.
A. The flux variability analysis of the 59 reactions that display variable fluxes across all the vertices. The color coding refers to the five different subnetworks. The symmetric matrix with Pearson correlation coefficients is always displayed and indicates the five subnetworks that vary independently in flux value across all 17280 vertices. B. Depiction of the network topology of the five subnetworks. List_1, list_2, list_3 and list_4 denote the following ordered lists of reactants respectively: {DGMP, GMP, GSN, AMP, DAMP, UDP, DGDP, DUDP, DADP, UMP, DUMP, DUMP, GDP, ADN}, {DGDP, GDP, GMP+H,ADP, DADP, UTP, DGTP, DUTP, DATP, UDP, DUDP, GTP, AMP+H}, {ADP, GDP, UDP, GTP, UTP, ATP}, {DADP, DGDP, DUDP, DGTP, DUTP, DATP}. Subnetwork 1 is composed out of 3 reactions and has 2 different flux distributions across all vertices. Subnetwork 2 contains 9 reactions and has 24 different flux distributions across all vertices. Subnetwork 3 contains 18 reactions and achieves 90 different flux distributions across all vertices. Subnetwork 4 contains 5 reactions and carries 2 different flux distributions. Subnetwork 5 carries 4 reactions and 2 different flux distributions across all vertices. Since all the flux distributions of the subnetwork occur independently the total number of vertices equals 2 × 24 × 90 × 2 × 2 = 17280. C. Two piecharts indicating the numbers of variable fluxes among the vertices, the rays and the linealities.
To determine the origin of the 17280 vertices in terms of the metabolic network topology we determined the Pearson correlation coefficients between the 59 variable reactions across all vertex solutions (figure 2A). The resulting 59 × 59 correlation matrix could be block diagonalized into five blocks, indicating that the fluxes of those 5 sets of reactions vary independently across all vertices. The sets contain 29, 18, 5, 4 and 3 reactions (59 in total). Each of these sets contain reactions that together form a (connected) metabolic subnetwork (figure 2B). For each subnetwork, we determined the number of different flux distributions that specify the vertices. The subnetwork with 29 reactions had 24 such different flux distributions, the set with 18 reactions had 90 and the other three sets each had 2 such flux distributions. Multiplying these numbers yields 17280, the number of vertices. In other words, the 17280 vertices are derived from five subnetworks that each can independently be described by a relatively small number of flux distributions within the FBA optimum (see Supplementary Information for details of the various subnetworks).
Each subnetwork is linked to the core 274 reactions that are fixed in the optimum network state, i.e. across all vertices. This suggests that the overall stoichiometry of the subnetworks should be fixed across all vertices. This is indeed the case, as we verified computationally. Thus, the subnetworks can achieve the same net reaction stoichiometry using different internal flux distributions while the entire flux distribution obeys the same optimal yield. The overall stoichiometries of the five subnetworks can be found in the Supplementary Information. For Escherichia coli iJR904 we found eight rays and a single lineality which matched irreversible and reversible cycles.
Comparison of the optimal solution space topologies across growth conditions and species
In order to address how different nutrients influence the geometry of the optimal solution space, we compared the polyhedra of Escherichia coli iJR904 growing on nine different carbon sources in mineral medium using CoPE-FBA. The number of vertices across these nine cases differ by a factor of about two and the number of subnetworks is always very small. This indicates that the polyhedron can be understood in terms of a small number of subnetworks each involving at most several tens of reactions. As expected, the rays and linealities appeared to be independent of the growth medium.
To test how different network topologies affect the number and size of metabolic subnetworks we repeated our analysis on a number of genome scale reconstructions representing different micro-organisms. Table 1 shows that network size is not the only determinant of the number of vertices of a polyhedron. For instance, Mycobacterium tuberculosis has only half the number of reactions of Escherichia coli iAF1260 and nearly an equal number of vertices. Comparison of the number of vertices of the two Escherichia coli metabolic network reconstructions, iJR904 and iAF1260, does indicate an effect of network size on the number of vertices. The number of subnetworks remained the same. In the Supplementary Information we report the subnetworks of iAF1260 and one of them involves a large segment of central metabolism. The increase in the number of vertices for growth on threonine (over 4000 fold) indicates that iAF1260 has greater flexibility in amino acid metabolism.
In Table 1, we present the polyhedral characterization of eight different microorganisms and find that a small fraction of the total number of reactions end up in the subnetworks that determine the number of vertices, i.e. the major topological feature of the polyhedron. Across all organisms, the number of subnetworks is always very small indicating that the optimal solution space (the polyhedron) can be quickly assessed by studying the individual subnetworks. By doing so this can greatly simplify the results of a FBA and can give direct insight into properties such as flux variability and coupling.
Discussion
Genome-scale stoichiometric models of metabolic networks allow for a comprehensive view of the metabolic capabilities of an organism. FBA is an indispensable tool for such studies. In this work, we presented Comprehensive Polyhedra Enumeration Flux Balance Analysis (CoPE-FBA), an approach to fully characterize the optimal solution space of genome-scale stoichiometric models (a polyhedron) corresponding to FBA. Using our methodology, the outcome of FBA can be quickly assessed in its entirety in terms of a few metabolic subnetworks, even though the models consist of thousands of metabolic reactions and reactants.
Through the development of our enumeration pipeline (CoPE-FBA) we developed several techniques to make the step from determining a single FBA optimum to the enumeration of all optima tractable at genome-scale. This entailed careful pre-processing of the genome-scale stoichiometric models. Redundant reactions, pairs of reactions with matching stoichiometry but that differed only in reversibility, were scanned for and in all cases the irreversible reaction was deleted. Explicitly-encoded infinity constraints i.e. bounds on reactions represented by a large number and reactions that carry a fixed flux at optimality (as determined by rational-arithmetic FVA) were removed. The technical details of these engineering techniques are discussed in the Supplementary Information.
We emphasize that enumerating all the elementary flux modes40,37 or the extreme pathways of a metabolic network5,34,49, is a computationally much more demanding task than determining all the rays and vertices of the FBA polyhedron. The reason is that there are in general a lot less of the latter than of the former; the vertices only consider reaction paths through the network that give rise to the maximization of an objective.
Rays and linealities of a polyhedron generally represent irreversible and reversible cycles that catalyze no net conversions; hence, they only achieve the recycling of components. From a thermodynamic point of view, this means that they are not driven by any Gibbs free energy potential at steady state. As a consequence, linealities represent subnetworks that are only thermodynamically feasible at steady states if all their reactions carry zero flux, i.e. they operate in thermodynamic equilibrium. Rays are thermodynamic inconsistencies in the network. For instance, consider the ray network composed out of the following reactions: A  B, B
B, B  C and A
C and A  C. Clearly, the third reaction should be reversible as the first two reactions together form a reversible path. All the rays we found for the genome-scale stoichiometric models were of this kind. If rays exist then the model contains thermodynamical inconsistencies. CoPE-FBA therefore detects such inconsistencies and can be used as a tool to improve the description of metabolic networks (cf.31,18). For instance, networks with many rays (such as Lactoccocus bulgaricus, Table 1) suffer from a significant number of thermodynamic inconsistencies. Even though mass-conserving reversible cycles (linealities) are not thermodynamically infeasible, a great number of them in a metabolic network does warrant further investigation into their physiological role (e.g. M. tuberculosis and L. lactis in table 1).
C. Clearly, the third reaction should be reversible as the first two reactions together form a reversible path. All the rays we found for the genome-scale stoichiometric models were of this kind. If rays exist then the model contains thermodynamical inconsistencies. CoPE-FBA therefore detects such inconsistencies and can be used as a tool to improve the description of metabolic networks (cf.31,18). For instance, networks with many rays (such as Lactoccocus bulgaricus, Table 1) suffer from a significant number of thermodynamic inconsistencies. Even though mass-conserving reversible cycles (linealities) are not thermodynamically infeasible, a great number of them in a metabolic network does warrant further investigation into their physiological role (e.g. M. tuberculosis and L. lactis in table 1).
From a biological perspective, CoPE-FBA greatly simplifies the communication of FBA simulation results to the experimental biologist as it can be done completely in terms of network structures (figure 2). One can envision a depiction of the metabolic network with different colors for fixed fluxes, vertex subnetworks, rays and linealities. An overlay of experimental flux data would then greatly simplify the assessment of the predictive power of a genome-scale model. In addition, subnetworks communicate other useful information to experimental biologists. E. coli physiologists would immediately observe that subnetwork 3 (figure 2B) involves the respiratory chain of E. coli and that the flux variability partially derives from the usage of alternative electron carriers, i.e. ubiquinone-8, menaquinone-8 and demethylmenaquinone-8. But the levels of these quinones are dependent on the oxygen availability4 and this knowledge further reduces the solution space when the aerobicity of the environment is specified. In addition, consideration of secondary objectives to reduce the optimal solution space (e.g. minimal pathway length or protein costs38,3) is greatly simplified by CoPE-FBA; reduction of the solution space will only concern reactions in the subnetworks (only 10 s of reactions; table 1). Another advantage of CoPE-FBA is that it gives a network topological explanation of flux coupling, flux correlation and flux variability analysis. Only fluxes within the same subnetwork will correlate or be coupled in the optimal solution space (cf. Supplementary Information).
Methods
The stoichiometry of a metabolic network with m metabolites and r reactions is described by a m × r stoichiometry matrix N. The (i, j)-th entry of N, nij, is the stoichiometric coefficient of the i-th metabolite in the j-th reaction, which denotes the amount of metabolite i consumed (nij < 0) or produced (nij > 0) per unit reaction rate. Any reaction rate (flux) vector v vector that satisfies

contains reaction fluxes such that the system is in steady state. Typically, v = 0 is not the only steady state flux vector. In Flux Balance Analysis (FBA) some objective is optimised over the steady state flux vectors24.
In FBA, the steady-state conditions (eq. 1) are augmented with capacity bounds on reaction fluxes. In addition, a linear objective is postulated, by which we obtain a linear programming problem. A typical FBA linear program has the form:

Here c is a vector of objective coefficients and cv is the way we write the inner product of c and v. vmin and vmax are column vectors representing lower and upper bounds (respectively) on each of the r fluxes. Irreversibility constraints on reactions can be expressed by setting vmin or vmax to 0. Reversible reactions without lower (or upper) bound get −∞ (or +∞).
Typically, a few fluxes will be fixed to some experimentally determined value or one of their bounds correspond to a measured value. All predictions are relative to a few fixed fluxes and therefore FBA predicts yields (ratios of flux). FBA typically involves maximizing a growth rate given a fixed uptake rate of a given nutrient. In fact in our computations we have minimized the uptake rate under a fixed growth rate. A little thought should make it clear that this does not effect the space of optimal solutions (it only scales every value involved by the same constant multiplicative factor). Therefore, we keep the presentation of the method as if we maximize growth rate.
Minimization of uptake rate is modeled by choosing the objective coefficient corresponding to the uptake reaction equal to 1 and all other objective coefficients equal to 0. Fixing growth rate is simply a matter of setting the flux rate corresponding to the reaction representing growth to the fixed value (making the upper and lower bound on the variable equal to this value). As is common practice in LP +∞ and −∞ are not regarded as bounds, whence constraints of the type vj > −∞ or vj < ∞ are omitted in the LP. As we will explain later, it is essential not to replace the ∞'s by arbitrarily large enough constants. Although this does not influence the optimal solution value it causes the polyhedral structure to change in a significant and undesirable way.
To facilitate the exposition we express the feasible set in (2) as a set of inequalities only. This is easily obtained by rewriting (2) as

We write then the set of all these constraints shortly as Av ≥ b.
For genome scale model analysis we use PySCeS-CBM (an unpublished but online available extension of the PySCeS software22,23) for reading, editing, translating and writing genome-scale models. However, other constraint based modelling tools e.g. the COBRA Toolkit could also be used32.
In general optimal solutions of FBA programs are hardly ever unique. Suppose that the optimal value of (3) is Z* then we are interested in describing the polyhedron

in terms of its extremities: vertices, rays and linealities (see the Results section and the Supplementary Information).
Mathematical software exists for conversion between the two descriptions. Most popular are methods based on either the Double Description Method or for specific polytopes Reverse Search enumeration10,2 e.g. implemented in the software CDD and LRS9,2. However, a theoretically efficient method for enumerating the vertices of polytopes has yet to be found. Indeed it is a major open question in computational geometry if such a method exists. This, together with the enormous number of vertices that we usually encounter in the high-dimensional polyhedra involved in modelling metabolism, implies that there is no guarantee that existing software will be able to cope with our problems. Indeed, initial attempts to do so in the literature19,44,45,46,40,37 have reported vast numbers of vertices for small, reduced metabolic systems (hundreds of thousands of vertices is not atypical) or intractability. While these studies focussed on enumeration of entire metabolic networks we consider an analogous problem i.e. the enumeration of an optimal FBA space. We do this for complete genome scale metabolic networks by reducing the complexity of the problem, not by finding a better conversion method, but by smart preprocessing.
Our approach can be thought of as working in several steps. We work with rational (i.e. exact) arithmetic.
-
1
Compute the FBA optimum. We formulate the FBA program as the LP (3) described in the main text. We solve the LP using QSOpt_ex version 2.5.01, a rational LP-solver. Let Z* be the optimal FBA value.
-
2
Formulate the optimal FBA set. This is done simply by replacing the objective in the LP by the optimality restriction f(v) ≥ Z*. We write this constraint together with the set Av ≥ b of all constraints, as expressed in (4), shortly as Dv ≥ d.
-
3
Perform Flux Variability Analysis (FVA). For each flux vj, j = 1, …, r we solve, using QSOpt_ex, two linear programs:
 and
and  .
. -
4
Remove fixed fluxes. For each variable vj for which
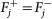 , remove from D the corresponding column Dj and subtract
, remove from D the corresponding column Dj and subtract 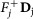 from d. Delete the rows that have now become all-0-rows. Let the new system be D′v′ ≥ d′.
from d. Delete the rows that have now become all-0-rows. Let the new system be D′v′ ≥ d′. -
5
Compute a basis for the lineality space. The lineality space of the polyhedron is given by the null-space of D′, i.e., all solutions to the system D′v′ = 0. Compute a basis for this linear subspace using a linear algebra library (such as JLinAlg17).
-
6
Compute rays and vertices of the system D′v′ ≥ d′. For genomescale systems we use the enumeration program Polco (version 4.2.0) for this41. Note that Polco automatically detects whether the system has a lineality space, but it does not report a basis for it, it only returns rays and vertices.
-
7
Reintroduce the fixed fluxes that were removed earlier. In each of the vertices reintroduce the fluxes that are fixed across all optima and were removed. Note the latter fluxes have value 0 in rays and linealities.
To detect the subnetworks resulting from the vertices found, a complete metabolic subnetwork/module analysis was performed in three steps (details of these steps are found in the Supplementary Information):
-
1
The vertices are translated in an array K, which is scanned for fixed and variable fluxes in order to now generate a sub-matrix K′ by removing the fixed fluxes from K;
-
2
Using K′ the correlation coefficients are calculated, which are then stored as the correlation coefficient matrix, P;
-
3
Define a graph with vertices the row indices of P and an edge between m and n if and only if Pm,n ≠ 0. Each connected component of this graph corresponds to a metabolic module/subnetwork. For each metabolic module/subnetwork a pattern matching algorithm is used to determine the number of unique flux distributions that occur within a particular module, across all vertices.
References
Applegate, D., Cook, W., Dash, S., Espinoza, D. QSopt_ex: Rational LP Solver. http://www2.isye.gatech.edu/~wcook/qsopt/ex/index.html
Avis, D. lrs: A Revised Implementation of the Reverse Search Vertex Enumeration Algorithm. In Kalai, G., Ziegler, G. (eds.) Polytopes - Combinatorics and Computation, Birkhauser-Verlag, 177–198 (2000). LRS software can be downloaded from cgm.cs.mcgill.ca/~avis/C/lrs.html
Beg, Q. K., Vazquez, A., Ernst, J., de Menezes, M. A., Bar-Joseph, Z., Barabasi, A. L. & Oltvai, Z. N. Intracellular crowding defines the mode and sequence of substrate uptake by Escherichia coli and constrains its metabolic activity. Proceedings of the National Academy of Sciences of the United States of America 104, 12663–12668 (2007).
Bekker, M., Alexeeva, S., Laan, W., Sawers, G., Teixeira de Mattos, J. & Hellingwerf, K. The ArcBA two-component system of Escherichia coli is regulated by the redox state of both the ubiquinone and the menaquinone pool. J Bacteriol 192, 746–754 (2010)
Bell, S. L. & Palsson, B. O. Expa: a program for calculating extreme pathways in biochemical reaction networks. Bioinformatics 21, 1739–1740 (2005).
Bordel, S., Agren, R., & Nielsen, J. Sampling the solution space in genome-scale metabolic networks reveals transcriptional regulation in key enzymes. PLoS Comput Biol 6 (2010).
Burgard, A. P., Nikolaev, E. V., Schilling, C. H. & Maranas, C. D. Flux coupling analysis of genome-scale metabolic network reconstructions. Genome Res 14, 301–312 (2004)
Feist, A. M. & Palsson, B. O. The biomass objective function. Curr Opin Microbiol 13, 344–349 (2010).
Fukuda, K. cdd and cddplus homepage. http://www.cs.mcgill.ca/~fukuda/soft/cdd%5Fhome/cdd.html
Fukuda, K. Prodon, A. Double Description Method Revisited. In Combinatorics and Computer Science, Lecture Notes in Computer Science. 1120, 91–111 (1996)
Feist, A. M., Henry, C. S., Reed, J. L., Krummenacker, M., Joyce, A. R., Karp, P. D., et al. A genome-scale metabolic reconstruction for Escherichia coli K-12 MG1655 that accounts for 1260 ORFs and thermodynamic information. Mol Syst Biol 3 (2007).
Feist, A. M., Scholten, J. C. M., Palsson, B., Brockman, F. J. & Ideker, T. Modeling methanogenesis with a genome-scale metabolic reconstruction of Methanosarcina barkeri. Mol Syst Biol 2 (2006).
Francke, C., Siezen, R. J. & Teusink, B. Reconstructing the metabolic network of a bacterium from its genome. Trends Microbiol 13, 550–558 (2005).
Henry, C. S., DeJongh, M., Best, A. A., Frybarger, P. M., Linsay, B. & Stevens, R. L. High-throughput generation, optimization and analysis of genome-scale metabolic models. Nature Biotechnology 28, 977–982 (2010)
Ibarra, R. U., Edwards, J. S. & Palsson, B. O. Escherichia coli K-12 undergoes adaptive evolution to achieve in silico predicted optimal growth. Nature 420, 186189 (2002).
Jamshidi, N. & Palsson, B. Investigating the metabolic capabilities of Mycobacterium tuberculosis H37Rv using the in silico strain iNJ661 and proposing alternative drug targets. BMC Systems Biology 1, 26 (2007).
JLinAlg: An open source and easy-to-use Java library for linear algebra. http://jlinalg.sourceforge.net/
Kummel, A., Panke, S. & Heinemann, M. Systematic assignment of thermodynamic constraints in metabolic network models. BMC Bioinformatics 7, 512–512 (2006)
Larhlimi, A. & Bockmayr, A. A new constraint-based description of the steady-state flux cone of metabolic networks. Discrete Applied Mathematics 157, 2257–2266 (2009).
Mahadevan, R. & Schilling, C. H. The effects of alternate optimal solutions in constraint-based genome-scale metabolic models. Metab Eng 5, 264–276 (2003).
Oberhardt, M. A., Palsson, B. O. & Papin, J. A. Applications of genomescale metabolic reconstructions. Mol Syst Biol 5, 320–320 (2009).
Olivier, B. G. PySCeS-CBM: a toolkit for Constraint Based Modelling in Python. http://pysces.sf.net/cbm (2011)
Olivier, B. G., Rohwer, J. M. & Hofmeyr, J. H. Modelling cellular systems with PySCeS. Bioinformatics 21, 560561 (2005).
Orth, J. D., Thiele, I. & Palsson, B. O. What is flux balance analysis? Nature Biotechnology 28, 245–248 (2010).
Pastink, M. I., Teusink, B., Hols, P., Visser, S., de Vos, W. M. & Hugenholtz, J. Genome-Scale Model of Streptococcus thermophilus LMG18311 for Metabolic Comparison of Lactic Acid Bacteria. Applied and Environmental Microbiology 75, 3627–3633 (2009).
Price, N. D., Reed, J. L. & Palsson, B. O. Genome-scale models of microbial cells: evaluating the consequences of constraints. Nat Rev Microbiol 2, 886–897 (2004).
Price, N. D., Schellenberger, J. & Palsson, B. O. Uniform sampling of steady-state flux spaces: means to design experiments and to interpret enzymopathies. Biophys J 87, 21722186 (2004).
Reed, J. L. & Palsson, B. O. Genome-scale in silico models of E. coli have multiple equivalent phenotypic states: assessment of correlated reaction subsets that comprise network states. Genome Res 14, 1797–1805 (2004).
Reed, J. L., Vo, T. D., Schilling, C. H. & Palsson, B. O. An expanded genome-scale model of Escherichia coli K-12 (iJR904 GSM/GPR). Genome Biology 4 (2003).
Santos, F., Boele, J. & Teusink, B. A practical guide to genome-scale metabolic models and their analysis. Methods Enzymol 500, 509–532 (2011).
Schellenberger, J. & Palsson, B. O. Use of randomized sampling for analysis of metabolic networks. The Journal of Biological Chemistry 284, 5457–5461 (2009).
Schellenberger, J., Lewis, N. E. & Palsson, B. O. Elimination of thermodynamically infeasible loops in steady-state metabolic models. Biophys J 100, 544–553 (2011)
Schellenberger, J., Que, R., Fleming, R. M., Thiele, I., Orth, J. D., Feist, A. M., et al. Quantitative prediction of cellular metabolism with constraintbased models: the COBRA Toolbox v2.0. Nature Protocols 6, 1290–1307 (2011).
Schilling, C. H., Letscher, D. & Palsson, B. O. Theory for the systemic definition of metabolic pathways and their use in interpreting metabolic function from a pathway-oriented perspective. J Theor Biol 203, 229–248 (2000).
Schrijver, A. Theory of Linear and Integer Programming John Wiley & Sons 1988).
Schuetz, R., Zamboni, N., Zampieri, M., Heinemann, M. & Sauer, U. Multidimensional optimality of microbial metabolism. Science 336, 601–604 (2012).
Schuster, S., Fell, D. A. & Dandekar, T. A general definition of metabolic pathways useful for systematic organization and analysis of complex metabolic networks. Nature Biotechnology 18, 326–332 (2000).
Shlomi, T., Benyamini, T., Gottlieb, E., Sharan, R. & Ruppin, E. (2011). Genome-scale metabolic modeling elucidates the role of proliferative adaptation in causing the Warburg effect. PLoS Comput Biol 7(3). 10.1371/journal.pcbi.1002018
Sieuwerts, S. Analysis of Molecular Interactions between Yoghurt Bacteria by an Integrated Genomics Approach (PhD thesis, Wageningen University 2009).
Terzer, M. & Stelling, J. Large-scale computation of elementary flux modes with bit pattern trees. Bioinformatics 24, 2229–2235 (2008).
Terzer, M. Polco: A Java tool to compute extreme rays of polyhedral cones. http://www.csb.ethz.ch/tools/polco (2009).
Teusink, B. & Smid, E. J. Modelling strategies for the industrial exploitation of lactic acid bacteria. Nat Rev Microbiol 4, 46–56 (2006).
Teusink, B., Wiersma, A., Jacobs, L., Notebaart, R. A. & Smid, E. J. Understanding the adaptive growth strategy of Lactobacillus plantarum by in silico optimisation. PLoS Comput Biol 5 (2009).
Urbanczik, R. & Wagner, C. An improved algorithm for stoichiometric network analysis: theory and applications. Bioinformatics 21, 1203–1210 (2005).
Urbanczik, R. Enumerating constrained elementary flux vectors of metabolic networks. IET Systems Biology 1, 274–279 (2007).
Urbanczik, R. & Wagner, C. Functional stoichiometric analysis of metabolic networks. Bioinformatics 21, 4176–4180 (2005).
Vo, T. D., Greenberg, H. J. & Palsson, B. Reconstruction and Functional Characterization of the Human Mitochondrial Metabolic Network Based on Proteomic and Biochemical Data. Journal of Biological Chemistry 279(38), 39532–39540 (2004).
Wiback, S. J., Famili, I., Greenberg, H. J. & Palsson, B. O. Monte Carlo sampling can be used to determine the size and shape of the steady-state flux space. J Theor Biol 228, 437–447 (2004).
Wiback, S. J., Mahadevan, R. & Palsson, B. O. Reconstructing metabolic flux vectors from extreme pathways: defining the alpha-spectrum. J Theor Biol 224, 313324 (2003).
Acknowledgements
SMK and BGO were funded by the NWO Computational Life Science MEMESA project 635-100-021, BGO by the ZonMW Genomics-Zenith program, project 93511039. FJB thanks the Netherlands Institute for Systems Biology (NISB) for funding. LS thanks the Tinbergen Institute for support. The authors thank Prof Dr Bas Teusink (VU University, Amsterdam), Dr Gunnar Klau (CWI, Amsterdam) and Dr. Frank Vallentin (TU Delft, CWI, Amsterdam) for insightful discussions.
Author information
Authors and Affiliations
Contributions
SMK and BGO performed the research. LS and FJB wrote the grant.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplemental material
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareALike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Kelk, S., Olivier, B., Stougie, L. et al. Optimal flux spaces of genome-scale stoichiometric models are determined by a few subnetworks. Sci Rep 2, 580 (2012). https://doi.org/10.1038/srep00580
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep00580
This article is cited by
-
Improvement of Lutein Production in Auxenochlorella protothecoides Using Its Genome-Scale Metabolic Model and a System-Oriented Approach
Applied Biochemistry and Biotechnology (2023)
-
Sampling with poling-based flux balance analysis: optimal versus sub-optimal flux space analysis of Actinobacillus succinogenes
BMC Bioinformatics (2015)
-
Metabolomics integrated elementary flux mode analysis in large metabolic networks
Scientific Reports (2015)
-
Flux modules in metabolic networks
Journal of Mathematical Biology (2014)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.



 and
and  .
. 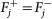 , remove from D the corresponding column Dj and subtract
, remove from D the corresponding column Dj and subtract 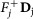 from d. Delete the rows that have now become all-0-rows. Let the new system be D′v′ ≥ d′.
from d. Delete the rows that have now become all-0-rows. Let the new system be D′v′ ≥ d′.