Growth dynamics and the evolution of cooperation in microbial populations

Abstract

Microbes providing public goods are widespread in nature despite running the risk of being exploited by free-riders. However, the precise ecological factors supporting cooperation are still puzzling. Following recent experiments, we consider the role of population growth and the repetitive fragmentation of populations into new colonies mimicking simple microbial life-cycles. Individual-based modeling reveals that demographic fluctuations, which lead to a large variance in the composition of colonies, promote cooperation. Biased by population dynamics these fluctuations result in two qualitatively distinct regimes of robust cooperation under repetitive fragmentation into groups. First, if the level of cooperation exceeds a threshold, cooperators will take over the whole population. Second, cooperators can also emerge from a single mutant leading to a robust coexistence between cooperators and free-riders. We find frequency and size of population bottlenecks and growth dynamics to be the major ecological factors determining the regimes and thereby the evolutionary pathway towards cooperation.

Introduction

One pivotal question in evolutionary biology is the emergence of cooperative traits and their sustainment in the presence of free-riders^1,2,3,4,5,6. By providing a public good, cooperative behavior of every single individual would be optimal for the entire population. However, non-contributing free-riders may take evolutionary advantage by saving the costs for providing the benefit and hence jeopardize the survival of the whole population. In evolutionary theory kin selection^1,7,8,9, multi-level selection^10,11,12,13 and reciprocity¹⁴ have been found to provide conceptual frameworks to resolve the dilemma^4,5,6. For higher developed organisms, stable cooperation is generally traced back to specific mechanisms like repeated interaction^2,14, punishment^15,16 and kin discrimination^1,6,17,18. But how can cooperation emerge in the first place and be maintained without abilities like memory or recognition? Answering this question is especially important within the expanding field of biofilm formation^{19,20,21,22,23,24}. There, a successfully cooperating collective of microbes runs the risk to be undermined by non-producing strains saving the metabolically costly supply of biofilm formation^18,20,23,24. Sophisticated social behavior cannot be presumed to explain the high level of cooperation observed in nature and experiments^{18,19,20,24,25,26,27,28,29,30,31}. Instead, different forms of limited dispersal, such as spatial arrangements, or fragmentation into groups are essential to resolve the dilemma of cooperation among such microbial organisms^1,32,33. Indeed, in nature microbes typically live in colonies and biofilms. Remarkable, although details strongly differ from species to species, most microbial populations follow a life-cycle of colony initiation, maturation, maintenance and dispersal leading to new initiation, see e.g.^{24,34,35,36,37}. Well-studied examples include Pseudomonas aeruginosa³⁸, Escherichia coli³⁹, Bacillus subtilis⁴⁰ and Myxococcus xanthus⁴¹. Even though such a life-cycle is often complexly regulated e.g. by environmental impacts and including collective behavior of colonies, populations bottlenecks alternating with growth phases are essential components of most microbial life-cycles. Employing simplified setups, recent experiments address the role of population bottlenecks and growth by studying structured microbial populations of cooperators and free-riders^{25,26,28,29,31}. In these setups small founder colonies differing in composition were cultivated in separate habitats. For example, Chuang et al.²⁹ used 96-well plates as structured environment with a dilution of synthetically designed E.coli strains where the cooperative strain is producer of a public good provoking antibiotic resistance. A microbial life-cycle was generated in the lab by regularly mixing all colonies after a certain time and inoculating new cultures. Under these conditions, an increase in the overall level of cooperation was observed even though free-riders have a growth advantage within every colony. However, the precise conditions under which cooperation is favored are subtle^{8,9,11,13,31,33,42,43,44,45,46,47,48,49}. A possible theoretical explanation for the observed increase in cooperation is the antagonism between two levels of selection, as widely discussed in the literature¹². Here, these levels, intra- and inter-group evolution, arise as population dynamics alternates between independent evolution in subpopulations (groups) and global competition in a merged well-mixed population. Due to the dilemma of cooperation, free-riders are always better off than cooperators within each group (intra-group evolution). In contrast, on the inter-group level, groups with a higher fraction of cooperators are favored over groups with a lower one.

In this article, we study the interplay between the dynamics at the intra- and inter-group evolution and how it may provoke the maintenance or even the emergence of cooperation. We propose a generic individual-based model which includes three essential elements: a growth disadvantage of cooperators within each group, an advantage of groups incorporating more cooperative individuals and regularly occurring regrouping events; cf. Fig. 1. Well-known from the theories of kin^1,7,9,49 and multi-level selection^12,29,49,50, cooperation can increase in principle: While, within a group i, the fraction of cooperators, ξ_i, decreases, groups also change their size, υ_i, such that the fraction of cooperators in the total population, given by the weighted average, , may still increase. Such an increase is an example of Simpson's paradox²⁹. To occur, a decreasing fraction of cooperators, ξ_i, within groups must be compensated by changing weights, , in the total population of size , i.e. by a sufficiently high positive correlation between a group's size and its fraction of cooperators⁵⁰. Here we want to go beyond stating this mathematical fact and reveal the ecological factors underlying these correlations. To this end the full stochastic dynamics at the intra- and inter-group level will be analyzed. A key element will be the intricate coupling between the dynamics of the composition and the dynamics of the overall size of a group. This applies in particular to microbial populations where the reproduction rate of microbes strongly depends on environmental conditions and thereby also on the composition of the population⁵¹. Therefore, a proper theoretical formulation has to account for a dynamics in the group size^52,53 rather than assuming it to be constant as in most classical approaches^54,55,56. Such a dynamic formulation will allow us to investigate ecological mechanisms for the evolution and maintenance of cooperation.

Figure 1

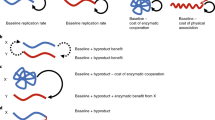
Repetitive cycle of population dynamics.

The time evolution of a population composed of cooperators (blue) and free-riders (red) consists of three cyclically recurring steps. Group formation step: we consider a well-mixed population which is divided into M separate groups (i = 1, …, M) by an unbiased stochastic process such that the initial group size and the fraction of cooperation vary statistically with mean values n₀ and x₀, respectively. Group evolution step: groups grow and evolve separately and independently; while the fraction of cooperators decrease within each group, cooperative groups grow faster and can reach a higher carrying capacity. Group merging step: after a regrouping time, T, all groups are merged together again. With the ensuing new composition of the total population, the cycle starts anew.

Motivated by microbial life-cycles^{24,34,35,36,37} and the aforementioned experiments^{25,26,28,29,31}, we consider a population of cooperators and free-riders and its evolution in a repetitive cycle consisting of three consecutive steps³³, cf. Fig. 1. In the group formation step, the total population with a fraction of cooperators, x₀, is divided into a set of M groups by an unbiased stochastic process such that the group size and the fraction of cooperation vary statistically with mean values n₀ and x₀, respectively. Subsequently, the groups evolve independently (group evolution step). In each group, both the fraction of cooperators and the group size vary dynamically and change over time. Independent of the specific details, the groups' internal dynamics has the following characteristic features: First, because of the costs for providing the benefit, cooperators have a selection disadvantage, s, compared to cheaters in the same group. In particular, cooperators reproduce slower than cheaters and hence the fraction of cooperators decreases within each group (intra-group evolution). Second, considering the benefit of cooperation, groups with more cooperators grow faster and can reach a higher maximum size (carrying capacity) than groups of mainly cheaters (inter-group evolution)^52,53. The benefit of cooperators is implemented by the growth rate of an individual proportional to is the fraction of cooperators in the group the individual belongs to. Resource-limited logistic growth is considered by a death term depending on the group size. For specificity we assume growth conditions comparable to those observed by Chuang et al.²⁹. Details are given in the materials and method section and the supplementary information. After evolving separately for a certain time t = T, all groups are merged (group merging) and the cycle restarts by forming new groups according to the current fraction of cooperators, x, in the whole population. It is the interplay of these three steps, characterized by the initial group size, n₀, the selection strength, s and the regrouping time, T, which determines the long-term evolution of the population.

Results

Fig. 2A shows the time evolution of the overall fraction of cooperators during a group evolution step. We find three distinct scenarios: decrease (red), transient increase (green) and permanent increase of cooperation (blue). Their origin can be ascribed to two ecological mechanisms: more cooperative groups grow faster (group-growth mechanism) and purely cooperative groups can reach a larger carrying capacity (group-fixation mechanism).

Figure 2

Evolution while individuals are arranged in groups (group-evolution step).

(A) Population average of cooperator fraction, x, as a function of time t. Depending on the average initial group size, n₀, three different scenarios arise: decrease of cooperation (red line, n₀ = 30), transient increase of cooperation (green line, n₀ = 6, increase until cooperation time t_c) and permanently enhanced cooperation (blue line, n₀ = 4). These three scenarios arise from the interplay of two mechanisms. While the group-growth mechanism, due to faster growth of more cooperative groups, can cause a maximum in the fraction of cooperators for short times, the group-fixation mechanism, due to a larger maximum size of purely cooperative groups, assures cooperation for large times. Both mechanisms become less efficient with increasing initial group sizes and are not effective in the deterministic limit (dashed black line, solution of Eq. (S7) for N₀ = 6) as the rely on fluctuations. (B) The strength of the group-growth mechanism decreases with an increasing initial fraction of cooperators. This is illustrated by comparing the time evolution for three different initial fractions of cooperators and a fixed initial group size n₀ = 5. After a fixed time, here t = 3.03, the fraction of cooperators is larger than the initial one for x₀ = 0.2, equal to it for x₀ = 0.5 and eventually becomes smaller than the initial value, as shown for x₀ = 0.8. (C) Change of the average group size, n = Σ_iv_i /M. At the beginning the groups grow exponentially, while they later saturate to their maximum group size. As this maximum size depends on the fraction of cooperators, the average group size declines with the loss in the level of cooperation (n₀ = 6, green line). The deterministic solution for the same set of parameters which does not account for fluctuations (dashed black line, solution of Eq. (S7)) describes this behavior qualitatively. s = 0.1, p = 10.

A permanent increase of cooperation can be explained on the basis of the group-fixation mechanism: for asymptotically long times the intra-group evolution reaches a stationary state, where each group consist solely of either cooperators or free-riders. Which state is favored depends on the interplay between selection pressure and stochastic effects. Because cheaters have a relative fitness advantage, they tend to outcompete cooperators in groups with a mixed initial composition. However, there are two stochastic effects leading to purely cooperative groups. First, the stochastic process of group formation results in a distribution of group compositions also containing a fraction of groups which consist of cooperators only. Second, random drift^57,58, which is most pronounced during a population bottleneck where group sizes are small, can cause a group to become fixed in a state with cooperators only. Due to the benefit of cooperators for the whole group, these purely cooperative groups reach a much higher carrying capacity than those left without any cooperator. Hence, although inferior in terms of number of groups, purely cooperative groups through their large group size contribute with a large statistical weight to the total composition of the population and thereby ensure maintenance or even increase of the level of cooperation for long times, cf. Fig. 2A blue curve.

In order for the group-fixation mechanism to become effective the evolutionary dynamics has to act for time scales longer than the selection time, t_s: = 1/s, which measures the time scale on which selection acts. For smaller times, a temporary increase in cooperation level is observed provided the initial group size is small enough, cf. Fig. 2A. The initial rise is caused by the group-growth mechanism during the growth phase of colonies, see Fig. 2C. Given a distribution of initial group compositions, it asymmetrically amplifies the size of those groups which contain more cooperators. This effect becomes stronger with a broader distribution, or, equivalently, a smaller initial group size n₀. Eventually the initial rise has to decline since, due to the internal selection advantage of free-riders, the fraction of cooperators is always decreasing within each mixed group. As a consequence, the overall benefit of cooperators through faster growth of more cooperative groups is only transient. After a certain time, the cooperation time, t_c, the fraction of cooperators, x(t), falls again below its initial value, x₀, unless the group-fixation mechanism is strong enough to ensure a permanent increase. Finally, if group-internal selection is too strong compared with the growth advantage of cooperative groups, the level of cooperation cannot increase even transiently, cf. Fig. 2A, red curve.

Combining all three steps of the cycle we now ask for the evolutionary outcome after many iterations, k, of the cycle. For very small bottlenecks, n₀ ≤ 3, both the groupfixation and the group-growth mechanism result in a a purely cooperative population and cannot be distinguished. This is shown in Fig. 3A for parameters corresponding to the experiments by Chuang et al.²⁹; the experimental results and the results of our stochastic model are in excellent agreement. For larger bottlenecks, n₀ = 5 and depending on the relative magnitude of the regrouping time T, we find two fundamentally distinct scenarios, see Fig. 3B. For large regrouping times, T ≫ t_s, there is a threshold value, , for the initial cooperator fraction, x₀, above which cooperators take over the whole population and below which they go extinct. In contrast, for regrouping times smaller than the selection time, T ≤ t_s, independent of the initial value, x₀, the population reaches a stationary state where cooperators are in stable coexistence with free-riders. As explained next, these two scenarios are closely tied to the group-growth and group-fixation mechanisms; for an illustration see the supplementary videos. The threshold value for maintenance of cooperation at large regrouping times is a consequence of group-fixation and the larger carrying capacity of purely cooperative groups. Since for T ≫ t_s the intra-group dynamics has reached a stationary state, fixation leaves the population with groups consisting of either cooperators or defectors only. The probability of fixation in the respective state and hence the fraction of purely cooperative groups after completing one cycle strongly depends on the initial cooperator fraction. Now, if the initial cooperator fraction becomes too low, the number of cooperative groups will be too rare such that even their larger maximum group size is no longer sufficient for them to gain significant weight in the total population and the overall cooperator fraction in the population will decline. Thus there must be a critical value for the cooperator fraction, , below which, upon iterating the cycle the fraction of cooperators will decline more and more, see Fig. 3B (red line). In contrast, above the critical value purely cooperating groups are becoming more frequent upon regrouping and therefore cooperators will eventually take over the population completely, cf. Fig. 3B (blue line).

Figure 3

Evolution of the overall cooperator fraction under repeated regrouping.

After many iterations, k, of the evolutionary cycle, a stationary level of cooperation is reached. (A) For small population bottlenecks, n₀ ≤ 3, group-growth and group-fixation mechanisms are effective and lead to purely cooperative populations. Growth parameters, bottleneck size and the regrouping time are chosen according to the experiments by Chuang et al.²⁹, see supplementary information. Without any fitting parameters, our simulation results (colored lines) are in good agreement with the experimental data (black points). (B) For larger bottlenecks, n₀ = 5 and depending on the relative efficiency of the group-growth and group-fixation mechanism, two qualitatively different regimes can be distinguished. While the group-growth mechanism leads to stable coexistence of cooperators and free-riders (green lines), the group-fixation mechanism can lead to a pure state of either only cheaters (red line) or only cooperators (blue line). The relative impact of these mechanisms depends strongly on the regrouping time T. For short regrouping times (T_short = 2.5 < t_s, green lines), the group-growth mechanism is effective, while for sufficiently long regrouping times (T_long = 20 > t_s, blue and red lines) the group-fixation mechanism acts more strongly. (C) With parameters equal to (B), the detailed interplay of the group-growth and group-fixation mechanisms is summarized in a bifurcation diagram showing the stationary levels of cooperation as a function of the regrouping time T. Depending of the relative efficiency of both mechanism, four different regimes arise: pure cooperation, coexistence, intermediate and bistability. The times T_short and T_long correspond to the green and red/blue lines shown in (B). Parameters are x₀ = 0.086, T = 3.1, s = 0.05 and p = 6.6 in (A); see also supplementary information. In (B), x₀ = {0.1 (green), x₀ = 0.9 (green)} and x₀ = {0.5 (red), x₀ = 0.6 (blue)} for T_short = 2.5 and T_long = 20, respectively. s = 0.1 and p = 10 in (B/C).

When groups are merged during the phase of transient increase of cooperation, T ≤ t_s, the stationary level of cooperation does not depend on the initial one. This behavior is due to the dependence of the change of the cooperator fraction during one cycle, Δx, on the initial fraction, x₀ as discussed in the following; see also Fig. 2B. As we have already eluded to in the discussion of the group-growth mechanism, stochasticity during group formation and during the initial neutral phase of the group evolution dynamics results in a broad distribution of group compositions. The evolutionary dynamics is acting on this distribution in an antagonistic fashion. While, due to the higher growth rate of more cooperative groups, the distribution develops a positive skew leading to an increase in the average overall cooperation, the group-internal selection pressure is counteracting this effect by reducing the cooperator fraction within each group. The relative strength of the former effect is largest for small initial cooperator fraction since this allows the largest positive skew to develop. Hence, for a given regrouping time, if the change in overall cooperator fraction Δx is positive for small x₀ it must become negative for sufficiently large x₀, as illustrated in Fig. 2B. For a more detailed mathematical discussion of these effects we refer to the supplementary information. As a consequence, in populations with a small initial fraction of defectors, the defectors increase in frequency. At the same time, when the initial fraction of cooperators is low, they also increase in number, finally leading to stable coexistence of cooperators and defectors at some fraction . This stationary fraction of cooperators is independent of the starting fraction and solely determined by the parameters of the evolutionary dynamics.

The interplay of both the group-growth and group-fixation mechanism leads, depending on the regrouping time, to different scenarios for the levels of cooperation. These are summarized in the bifurcation diagram Fig. 3C, where the stable and unstable fixed points of the regrouping dynamics, and , are shown as functions of the regrouping time. The scenarios can be classified according to their stability behavior under regrouping as follows: For large regrouping times, T ≫ t_s, the group-fixation mechanism leads to bistable behavior. With decreasing T, the fixation mechanism loses ground while the group-growth mechanism becomes more prominent. There is a intermediate scenario: the dynamics is bistable with full cooperation as well as coexistence as stable fixed points. For even smaller times, only the group-growth mechanism remains effective and the rare strategy here always outperforms the common one such that each strategy can invade but not overtake the other: coexistence. Finally, for T ≪ t_s, cooperators always take over the population, effectively leading to purely cooperative populations.

Discussion

In this article, we have studied the influence of population dynamics and fluctuations on the evolution and maintenance of cooperation. We specifically account for alternating population bottlenecks and phases of microbial growth. Thereby, our model serves as a null-model for cooperation in rearranging populations^{25,26,28,29,31}, e.g. during microbial and parasitic life-cycles^{24,41,59,60,61} and bacterial biofilm formation^{24,34,35,36,37}. The final outcome of the dynamics depends on the interplay between the time evolution of size and composition of each subpopulation. While a growth advantage of more cooperative groups favors cooperators, it is counteracted by the evolutionary advantage of free-riders within each subpopulation. We have investigated the stochastic population dynamics and the ensuing correlations between these two opposing factors. Depending on whether groups are merged while they are still exponentially growing or already in the stationary phase, two qualitatively different mechanisms are favored, the group-growth and the group-fixation mechanism. Importantly, our analysis identifies demographic noise as one of the main determinants for both mechanisms. First, demographic noise during population bottlenecks creates a broad distribution in the relative abundance of cooperators and free-riders within the set of subpopulations. The growth advantage of more cooperative subpopulations implies an asymmetric amplification of fluctuations and possibly yields to an increase of cooperation in the whole population (group-growth mechanism). Our analysis shows that this can enable a single cooperative mutant to spread in the population which then, mediated by the dynamics, reaches a stationary state with coexisting cooperators and free-riders. Second, if the founder populations contain only very few individuals, demographic fluctuations strongly enhance the fixation probability of each subpopulation which then consists of cooperators or free-riders only. Purely cooperative groups can reach a much higher carrying capacity. However, only if the relative weight of purely cooperative groups is large enough, this effect leads to an increase in the level of cooperation in the whole population (group-fixation mechanism). From our theoretical analysis of the population dynamics we conclude this to be the case only if the initial fraction of cooperators is above some threshold value.

As shown by comparison with experiments by Chuang et al.²⁹ the proposed model is able to describe microbial dynamics quantitatively. Moreover, our model makes predictions how the evolutionary outcome varies depending on population dynamics and bottlenecks and how the discussed mechanisms can provoke cooperation. These predictions can be tested experimentally by new experiments similar to those of Chuang et al. and others^{25,26,28,29,31}: For example, by varying easily accessible parameters like the bottleneck size n₀ or the regrouping time T, the relative influence of both mechanisms can be tuned. Then the resulting level of cooperation and the ensuing bifurcation diagrams can be quantitatively compared with our theoretical predictions.

As we assume the worst case scenario for cooperators, e.g randomly formed groups and no additional assortment, our findings are robust: The discussed pathways towards cooperation based on a growth-advantage of more cooperative groups and restructuring are expected to stay effective when accounting also for other biological factors like positive assortment, spatial arrangements of groups, mutation, or migration¹.

Shown by our analysis, a regular life-cycle favors cooperation. Besides better nutrient exploitation, this advantage for cooperation might be one reason for the evolution of more complex, controlled life-cycles including collective motion of microbes, local lysis and sporulation^{24,34,35,36,37}.

Methods

We used a stochastic, individual-based model where each individual is either a cooperator or a free-rider. In the group formation step groups are formed at random. The initial group size, ν_0,i, is Poisson distributed (with mean n₀). Given this size, the fraction of cooperators ξ_0,i follows by a binomial distributed number of cooperators. During the evolution step, each individual is subject to random birth and death events. The dynamics is given by a time-continuos Markov process where the change of the probability, ∂_tP(ν_i, ξ_i; t), is given by a master equation. In detail, the basal per capita birth rate of each individual depends linearly on the group level of cooperation ξ_i, while the per capita death rate increases linearly with the group size ν_i the individual belong to. In addition, free-riding individuals have a higher birth-rate where the strength of selection s measures the advantage of free-riding individuals. Full details are given in the supplementary information. The time scale is such that a small population of only free-riders initially grows exponentially with the average size ν_i,0 exp t. To investigate the dynamics and both evolutionary mechanisms we performed extensive computer simulations by employing the Gillespie algorithm⁶². Group size is M = 5 · 10³ in Fig. 2 and M = 5 · 10⁴ in Fig. 3.