Abstract
The tumor necrosis factor related apoptosis-inducing ligand (TRAIL) induces apoptosis in malignant cells, while leaving other cells mostly unharmed. However, several carcinomas remain resistant to TRAIL. To investigate the resistance mechanisms in TRAIL-stimulated human fibrosarcoma (HT1080) cells, we developed a computational model to analyze the temporal activation profiles of cell survival (IκB, JNK, p38) and apoptotic (caspase-8 and -3) molecules in wildtype and several (FADD, RIP1, TRAF2 and caspase-8) knock-down conditions. Based on perturbation-response approach utilizing the law of information (signaling flux) conservation, we derived response rules for population-level average cell response. From this approach, i) a FADD-independent pathway to activate p38 and JNK, ii) a crosstalk between RIP1 and p38 and iii) a crosstalk between p62 and JNK are predicted. Notably, subsequent simulations suggest that targeting a novel molecule at p62/sequestosome-1 junction will optimize apoptosis through signaling flux redistribution. This study offers a valuable prospective to sensitive TRAIL-based therapy.
Similar content being viewed by others
Introduction
The search to induce apoptosis, or programmed cell death, in cancer cells has led to the emergence of a new and fast growing field termed cancer immunology1, also referred to as tumor immunology2. Here, the interactions between the immune system with malignant cancers have shown the suppression of disease progression. Among the many immune factors found within the tumor microenvironment, the tumor necrosis factor (TNF) family members are noted for their ability to induce cellular apoptosis3. In particular, the TNF-related apoptosis ligand (TRAIL), also known as Apo-2 ligand and TNFSF10, has received primal attention due to its ability to recognize and induce apoptosis of tumors and metastases while leaving normal cells mostly unaffected4.
The endogenous TRAIL is prevalently found in several types of immune cells (e.g. macrophages, natural killer cells, T-cells) and its expression can be elevated in these cells by infected agents, such as, through the Toll-like receptor and the interferon gamma signaling pathways5. TRAIL is known to bind with TRAIL-R1 (or death receptor (DR) 4), TRAIL-R2 (or DR5), TRAIL-R3 (or decoy receptor (DcR) 1), TRAIL-R4 (or DcR2) and osteoprotegerin. Notably, TRAIL-R1 and -R2 possess intracellular death domains and, subsequently, have the ability to mediate TRAIL-induced apoptosis. The remaining receptors are decoys that compete for TRAIL, thereby, possibly negatively regulate the effects of TRAIL-R1 and -R2 signaling6.
The immune defense role of TRAIL was shown to kill pathogen-infected or malignant cells7. Notably, increased expressions of TRAIL-R1 and -R2 have been found on several kinds of tumor cells' extracellular membrane with corresponding increases in apoptosis compared with normal cells. The deficiency of TRAIL-R1 and -R2 has also led to malignancy8. Further investigations using TRAIL-induced apoptosis for effective control of cancer proliferation have yielded successes at preclinical settings for certain cancer cells. In majority of cases, such as melanoma and neuroblastoma, however, TRAIL stimulation has little or no effect9.
The non-sensitivity of TRAIL-stimulated cancers occurs due to several factors including: very low expression levels of TRAIL-R1 and -R2s, increased levels of DcR1, DcR2, elevated levels of negative regulators of apoptosis9 such as cFLIP, etc. On top of these, the upregulation of cell survival and proliferation pathways, through mitogen-activated protein kinases (MAPK) and nuclear factor-κB (NF-κB) activations, are crucial for the resistance10.
More recently, to overcome resistance, TRAIL has been used in conjunction with other treatment strategies. Several studies have made combination therapies with proteasome inhibitors, histone deacetylase inhibitors, ionizing radiation etc., for enhancing apoptosis11,12. Also, specific intracellular targets, such as tyrosine kinase inhibitors and IκBα suppressors, have been used to show reduced survival of cancer13,14. These works have focused on a single mode of action by either targeting survival or apoptotic pathways. However, as cancers are known to show high activities of both survival and apoptotic pathways15, it remains unclear whether the suppression of survival or the enhancement of apoptosis, independently, will yield optimal results. It is perhaps so that the clinical results so far have only shown partial response in majority of cases and ask for a deeper understanding of the synergistic effect of combinatorial treatments16. Thus, clear mechanistic insights into the conflicting roles of the cell survival and apoptotic pathways triggered by TRAIL are required. For example, when are cell survival and apoptotic pathways activated? Do they regulate each other? Are they induced at different time points? Finding answers to these questions can provide an improved strategy to treat cancers using TRAIL.
So, in spite of numerous studies targeting TRAIL resistance, we are still far from successfully understanding and controlling the mechanisms for the resistance. Another possible reason may lie in the way intracellular data are generated, analyzed and interpreted. For example, many studies use single time point readout of survival or apoptotic molecules to compare treated with untreated cancer cells. Although such data provide qualitative snapshot information of cancer cells response to the treatments, they may not necessarily show the overall effectiveness in time. For example, in lipopolysaccharide-stimulated macrophages, we observed that molecules that are upregulated (based on mRNA expressions) at early time points can become downregulated at later time points17. Thus, it is important to rigorously analyze the temporal data generated by TRAIL-stimulated experiments using multidisciplinary approaches.
Here, to shed light into the resistance mechanisms and to identify an effective intracellular target for TRAIL-resistant human fibrosarcoma (HT1080), we investigated, using a computational model, the activation dynamics of several cell survival (IκB, JNK, p38) and apoptotic (caspase-8, -3) signaling molecules. The model, based on perturbation-response approach, does not require the full knowledge of all signaling species and their reaction kinetics. Rather, it uses linear response rules, derived from the fundamental law of information (signaling flux) conservation, to elucidate novel features of population-level average cell signaling pathways and has been successfully used in Toll-like receptors (TLRs) signaling studies18,19,20,21. Using the approach of comparing experimental data with model simulations, firstly we uncover novel pathway features for TRAIL signaling in HT1080 cells. Secondly, we evaluate the net effect of cancer cell survival and apoptosis under various intracellular mutations by developing a theoretical cell survival metric (CSM). Using the computational model together with CSM, our approach predicts an optimal target for overcoming TRAIL resistance.
Results
Dynamic computational model for TRAIL-stimulated HT1080 cells
A previous experimental work on HT1080 cells has shown that TRAIL stimulation not only activate the apoptotic pathways (caspases), but also display cell survival activities, through NF-κB and MAPKs, resulting in the overt resistance to death22. However, the systemic understanding of the counterbalancing survival and death mechanisms still remains unclear23. For developing effective strategies to control TRAIL resistant cancer cells, a mechanistic understanding of the temporal activations of the cell survival and apoptosis pathways is required.
To investigate the dynamical activations of cell survival (NF-κB, MAPKs) and apoptosis (caspases) in TRAIL-resistant HT1080 cells, we developed a computational model of TRAIL signaling (see text below). The original model was developed using the widely accepted TRAIL signaling topology: upon ligation of TRAIL, TRAIL-R1 (DR4) and TRAIL-R2 (DR5) form receptor clusters facilitated by O-glycosylation and/or palmitoylation. This allows the intracellular death domain of TRAIL-R1 and -R2 to recruit FADD, caspase-8 and cFLIP, collectively called the primary death-inducing signaling complex (DISC). Still attached to the membrane, the DISC becomes enriched in lipid rafts, subsequently allowing caspase-8 to interact with CUL3/RbxI-based E3 ligase complex. Polyubiquitylation of caspase-8 occurs and the ubiquitin-binding protein p62/sequestosome-1 binds with caspase-8 to detach it from the DISC. Consequently, caspase-8 interacts with RIP1, TRAF2 and IKK-γ to form secondary DISC, which activates downstream NF-κB, MAPKs and caspase-3, a member of the cysteinyl-aspartate-specific proteases, through the extrinsic pathways23,24,25 (Figure 1A). The static TRAIL topology was converted into a dynamic computational model (see “Perturbation-Response approach”), where each species is connected to another by first-order response equations and the parameters were chosen from temporal experimental data (see “TRAIL Modeling Strategy” and Figure 1B).
TRAIL signaling pathway and experimental activation profiles of signaling molecules.
(A) Schematic topology of TRAIL signaling pathway. See maintext for details. (B) Experimental activation profiles of p38, IκB, JNK, caspase-8 and -3 in wildtype, RIP1 KD*, FADD KD*, caspase-8 KD* and TRAF2 KD in arbitrary units (a.u.) at t = 0, 10, 30, 60** and 120 min after TRAIL stimulation of HT1080 cells. The original source was obtained from Figure 3A of ref. 22 and was processed through imageJ (see Methods). *data is unavailable for caspase-8 and -3, ** available only for caspase-8 and -3. Note: interpolated dotted lines between experimental data points are inserted as a guide, they might not represent the actual temporal dynamics.
In recent years, there have been calls for understanding biology including spatial and stochastic processes26. This is especially observed for single cell analysis where the heterogeneity of each molecular component can result in distinct response profiles between cells27. However, at population level, many of the differences in single cell response profiles can be averaged out to reveal deterministic patterns for the entire population. For example, the well-coordinated response of cell populations, such as differentiation or growth, demonstrates that the single cell noise or heterogeneity effect could cancel out when ensembles of cells are formed to generate a stable and robust response. Here, the data that is used to develop the TRAIL model represents population level average response (Figure 1B).
Perturbation-Response approach
At cell population level, macroscopic descriptions of complex reaction mechanisms connect a series of reacting species into well-defined “average” pathways. The connectivity of the reaction species, in general, can be anticipated to be governed by non-linear expressions as biology is a complex system. Given a fixed perturbation to one of the species in the connected system will result in propagation of response waves through the connectivity.
In general, for system with n species, the reaction mechanisms are:

where the corresponding vector form of Eq. 1 is  , F is a vector of the unknown non-linear function which includes diffusion and reaction terms and X = (X1 , X2 , .., Xn ) is the species response profiles28,29. For a fixed perturbation, the resultant changes in species profiles can be written by X = X0 + δX , where X0 is the reference steady-state vector and δX is the relative response from steady-states (δXt = 0 = 0).
, F is a vector of the unknown non-linear function which includes diffusion and reaction terms and X = (X1 , X2 , .., Xn ) is the species response profiles28,29. For a fixed perturbation, the resultant changes in species profiles can be written by X = X0 + δX , where X0 is the reference steady-state vector and δX is the relative response from steady-states (δXt = 0 = 0).
When the actual reaction mechanisms are unknown or difficult to solve analytically, Eq. 1 can be expanded into Taylor series:

where F ( X0) = 0 at the steady-state X0 . Eq. 2 shows the presence of first and higher-order terms to the response wave propagation through the connected species. In such a discretized manner, we can investigate which of the individual terms become dominant to a given perturbation. This approach is unlike the conventional “bottom-up” strategy of defining each reaction equation through the stoichiometry of reactions, isolated kinetics and in vitro defined parameters.
In our previous works on TLR signaling18,19,21, the use of first-order response equations was sufficient to reveal experimentally verifiable novel signaling features for the macrophage population response. In Eq. 2, this occurs for small or pulse perturbation around steady-state, when the higher-order terms become negligible, that is,  . That is, from our “top-down” approach, we found that the first-order term is the most dominant in population-level TLR signaling. Such macroscopic first-order terms are not necessarily restricted to reaction terms only, they can also represent the averaging effect of spatial information such as diffusion and transport mechanisms. For example, we showed that the endocytosis of TLR4 involving diffusion and transport30, can be approximated by several first-order terms18.
. That is, from our “top-down” approach, we found that the first-order term is the most dominant in population-level TLR signaling. Such macroscopic first-order terms are not necessarily restricted to reaction terms only, they can also represent the averaging effect of spatial information such as diffusion and transport mechanisms. For example, we showed that the endocytosis of TLR4 involving diffusion and transport30, can be approximated by several first-order terms18.
The amount of fixed perturbation chosen for the model depends on the experimentally stimulated concentration, while the parameter values, or the elements of the Jacobian or linear stability matrix  , are chosen by fitting δX with corresponding experimental profiles along the activation topology. Thus, each species in our model can represent a signaling molecule, different modified state of a molecule (e.g. ubiquitinated state) or a signaling event such as diffusion, endocytosis, etc. That is, each species in our signaling network does not necessarily represent a specific molecular species. For illustration, in a pathway q1→q2→q3→q4→q5, q1 to q5 can each be a different protein or the same protein at different stages in signaling, for example, (q1) being internalized (q2), transported to a different organelle (q3), ubiquitinated (q4) and become part of a protein complex (q5).
, are chosen by fitting δX with corresponding experimental profiles along the activation topology. Thus, each species in our model can represent a signaling molecule, different modified state of a molecule (e.g. ubiquitinated state) or a signaling event such as diffusion, endocytosis, etc. That is, each species in our signaling network does not necessarily represent a specific molecular species. For illustration, in a pathway q1→q2→q3→q4→q5, q1 to q5 can each be a different protein or the same protein at different stages in signaling, for example, (q1) being internalized (q2), transported to a different organelle (q3), ubiquitinated (q4) and become part of a protein complex (q5).
Thus, unlike typical signaling models, which often use kinetic equations to model the dynamics, our perturbation-response approach considers the network as a sequence of events rather than just molecules. As signaling networks are largely not fully understood, this difference is crucial as it prevents rigidly fixing the network topology and allows it to be modified according to experimental data so as to prevent overfitting problems and to identify novel features of signaling networks. In addition, as signaling process involve large number (thousands) of intracellular molecular activations31, it is currently not plausible to model the dynamics of all possible reactions with the generally limited data. To overcome such difficulties, our approach permits the lumping of several molecules into a species and the averaging nature of the response equations does not require detailed kinetics. In this way, our model does not become a comprehensive representation of entire signaling process, however, it allows the identification of overtly missing key features.
Therefore, for TRAIL signaling, it would not be appropriate to develop a hard-wired model based on wildtype data alone. For example, our previous works on TLR signaling have demonstrated that an initial model developed using up-to-date literature topology and fitted with wildtype data would not be sufficient to simulate other mutant conditions, e.g. in MyD88 or TRAF6 knock-outs18,19,21. To overcome this fundamental issue, we create an initial model developed using wildtype data and test it with other available experimental conditions. By reducing wildtype parameter space and allowing the topology to carefully evolve using response rules (see below), from the law of information conservation and first-order response, we are able to successful produce a model that simulates multiple experimental conditions.
TRAIL modeling strategy
To develop and analyze the TRAIL model, we created a computational modeling framework (Figure 2). An initial model is constructed using the known TRAIL topology and the parameters of the first-order response equations are chosen, with the aid of a genetic algorithm32, to fit the semi-quantitative data of each tested molecule's activation profile (e.g. p38, JNK, etc.) in wildtype (Methods). Once the simulation for all tested molecules fit reasonably well in wildtype, we next test their validity in other mutant conditions (RIP1 KD, FADD KD, etc.). If the simulations are not satisfactory in any experimental condition (based on the area between the experimental profiles and simulations curves, see Methods), we modify the current TRAIL topology according to the response rules. For example, in wildtype, if a time delay is observed in the experimental activation onset compared with simulation, then according to response rule 1 (see below and Figure 3), additional intermediary first-order terms are added to provide delay. The process of modifying TRAIL topology and parameter values for each molecule and in each condition is done iteratively until all tested molecules are able to successfully reproduce experimental data in all tested conditions (Figure 2).
Computational modeling framework for TRAIL signaling.
Parameters of the initial model based on the original topology (1) are determined by overall fitting of experimental data using a genetic algorithm (GA, see Methods) for all molecules (i = 1,2,..n) and at all conditions (k = 0,1,…m), here n = 5 and m = 4. (2). If the overall error E = max(ει,κ ) between experimental and simulation profiles is higher than the set tolerance (3) (see Eq. 5) in Methods), the model is not acceptable. As the next step, the n molecules' activation profiles are ranked from the one showing highest (i = 1) to the lowest (i = n) error (4) for individual molecule's (5) best fitting in wildtype (6) and m other experimental conditions (6′). If the simulation of the ith molecule fit reasonably in the kth condition (individual error εi,k ≤ 0.15) (7), we check the next condition (k+1), else we modify the current topology according to response rules (8) (see Figure 3) and restart the procedure from wildtype condition again (6). If all m conditions fit for the ith molecule (9–10) without any changes applied to the topology, we proceed to the next molecule (i+1) (11). If any change is necessary to the topology, the parameters have to be refitted for all molecules from the first molecule (i = 1). The whole procedure is repeated until the resultant model fit all experimental profiles of the n molecules within the error tolerance (12).
Response rules to modify signaling topologies when the first molecule is perturbed.
(A) Analyzing time to activation: Rule 1, Time delay and Rule 2, Rapid bypass, (B) Analyzing peak activation levels: Rule 3, Missing flux, Rule 4, Signaling Flux Redistribution (SFR), Rule 5, Lack of SFR and Rule 6, Dominant and Recessive flux, (C) Analyzing activation patterns: Rule 7, Reversible flux, Rule 8, Superposing flux, Rule 9, Continuous flux, and Rule 10, Oscillations. See maintext for descriptions. Note that rules 1–6 are developed from first-order response and the law of signaling flux conservation in pulse perturbation. Rules 7–10 are introduced to interpret any non-linear response or those that do not obey the law of conservation. These rules are not exhaustive and can possibly be further categorized if detailed experimental data for each molecule is available. The rules serve as guide to modify the overt topology highlighting the key missing features only.
Overall, we utilized 5 experimental conditions (wildtype, RIP1 KD, FADD KD, caspase-8 KD and TRAF2 KD) to generate a single robust model that simulates 5 molecules (IκB, JNK, p38, caspase-8 and -3) over 5 measured time points (0, 10, 30, 60 and 120 min) for TRAIL-stimulated HT1080 cells (Figure 1B). This is in contrast to most computational studies, which only use wildtype data to develop signaling models. Notably, as a result of our approach, we are able to modify the initial literature model to a final one (consisting of 32 species with 39 reactions) indicating several novel features for TRAIL signaling (Table 1).
Response rules
Here we introduce a more formal way to modify the initial signaling topology to infer novel network features by deriving 10 main response rules from the law of signaling flux conservation and first-order average response to pulse perturbation (Figure 3A–C). Analyzing time to activation: Rule 1, Time delay: by comparing the time to reach peak activation, any time delay in target signaling molecule's activation represents ‘missing’ cellular features such as directed transport machinery, protein complex formation and novel molecular interactions. Rule 2, Rapid flux: when the activation of a downstream molecule is noticeably quicker than the experimental activation, a novel rapid bypass pathway is inferred. Analyzing peak activation levels: Rule 3, Missing flux: when the removal of a molecule along a pathway does not completely abolish its downstream intermediates, the presence of a novel bypass is indicated. Rule 4, Signaling Flux Redistribution (SFR): At pathway junctions, the removal of a molecule enhances the entire alternative pathways. Rule 5, Lack of SFR: At pathway junctions, the removal of a molecule does not enhance the alternative pathway, suggesting novel i) intermediate(s) between the removed molecule and the pathway junction or ii) pathway link between the removed molecule and the alternative pathway. Rule 6, Dominant and Recessive flux: quantifies each pathway branch by comparing activation levels between wildtype and mutants data. Analyzing activation patterns: Rule 7, Reversible flux: when a response profile show limiting decay that cannot be modeled by first-order decay, the presence of reversible step is expected to produce limiting decay33. Rule 8, Superposing flux: when a response profile show multiple peaks, the superposition principle indicates the presence of novel i) bypass pathway from the same source or ii) alternative pathway with delayed response. Rule 9, Continuous flux: when a response profile shows a continuous increase of activation not following pulse perturbation response, this indicates additional continuous flux from feedback mechanisms such as posttranslational effect or secondary signaling34. Rule 10, Oscillations: When oscillatory response is observed, i) continuous feedback loop35 is suggested for regular dynamics and ii) non-linear effects such as chaotic biochemical dynamics36 are inferred for irregular dynamics.
Simulations of initial TRAIL signaling model
First, we performed parameter fitting of the initial model (Figure 4A) with the wildtype data (Figure 1B). Several parameter sets were examined so that the simulations could match the experimental profiles. The IκB, JNK, caspase-8 and -3 simulations were able to successfully fit with experimental profiles, however for p38, experiment shows rapid activation compared with the model simulation (Figure 4B, wildtype).
Simulation of initial TRAIL signaling model.
(A) Static topology of the TRAIL signaling pathway used in developing our computational model. Note that we lump the similar effects of DR4/5 as TRAILR1/2 and ignore the response of DcR1/R2/OPG. Also, note that we include molecular conditions such as receptor clustering as additional first-order terms. (B) Comparison of simulations (solid lines) with experimental data (dotted lines) in wildtype, RIP1 KD, FADD KD, caspase-8 KD* and TRAF2 KD in arbitrary units (a.u.). The error  between simulations and experimental data for the ith molecule in the kth condition is calculated based on the area between experimental and simulation curves (see Eq. 5 in Methods). *caspase-8 KD also refers to pro-caspase-8 KD.
between simulations and experimental data for the ith molecule in the kth condition is calculated based on the area between experimental and simulation curves (see Eq. 5 in Methods). *caspase-8 KD also refers to pro-caspase-8 KD.
Next, we compared the model simulations for other mutant conditions (RIP1 KD, FADD KD, caspase-8 KD and TRAF2 KD) and notice that although IκB, caspases-8 and -3 simulations recapitulate experiments in all conditions, the simulations of p38 and JNK activations are not satisfactory (Figure 4B). RIP1 KD shows impaired activation of p38 compared to wildtype, however, in silico RIP1 KD simulation shows similar levels to wildtype at 120 min (Figure 1B and 4B, RIP 1KD). Furthermore, the simulation produces delayed p38 activation, similarly to wildtype simulation, in contrast to experiment.
For FADD, caspase-8 and TRAF2 KDs, in contrast to experimental profiles (Figure 1B), the simulations failed to show any p38 or JNK activations (Figure 4B). Collectively, the TRAIL model developed using the current topology reasonably simulates IκB, caspase-8 and -3 temporal activation profiles in all KD conditions, however, it fails to capture the dynamics of p38 and JNK.
Revealing novel features of TRAIL signaling using response rules
To overcome the shortfall of our model simulations using the current TRAIL topology, we utilized the response rules, so as to modify the network to investigate whether the model simulations could be improved, especially for p38 and JNK profiles.
Analyzing p38 dynamics
In wildtype and RIP1 KD, we notice p38 is experimentally activated within 10 min after TRAIL stimulation, whereas, in model simulations it takes at least 20 min (Figure 4B and 5A, M0). According to response rule 2, this can be achieved through introducing a novel rapid bypass pathway to activate p38 more directly and specifically, perhaps not involving the primary or secondary DISC as these may take longer activation times. Adding the novel bypass from TRAIL-R1 to MKK3/6 produced a good match between simulations not only for wildtype data, but also for FADD and caspase-8 KDs (Figure 5B, M1). Note that the novel bypass is not sensitive whether the origin starts from TRAIL-R1 or the receptor process terms. However, adding a bypass downstream, from FADD onwards, incurs noticeable delay in p38 activation (data not shown). Hence, we call this novel bypass as FADD-independent pathway.
Revealing novel features of TRAIL signaling using modeling strategy and response rules.
Model simulations compared with experiments. For p38, (A) M0, the initial model, (B) M1 with the addition of a rapid bypass and (C) M2 with the addition of a missing link between RIP1 and p38 pathway. For JNK (D) M2, (E) M3 with intermediates to introduce delay in activation, (F) M4 with a missing link for the activation of JNK in FADD and caspase-8 KDs and (G) M5 a missing link between p62 and JNK pathway to show enhancement through SFR in TRAF2 KD.
For RIP1 KD, although the delay activation is succumbed, the late phase peak activation (at 120 min) is enhanced in simulations and for TRAF2 KD, the p38 activation is still under predicted at 120 min (Figure 5B). Response rules 5i and 5ii suggest that RIP1 activates p38 so that its removal will negatively affect p38 activation. The inclusion of this feature alone was sufficient to reasonably match experimental and simulation results for both RIP1 KD and TRAF2 KD (Figure 5C, M2).
Analyzing JNK dynamics
Using the updated model, we next investigated JNK dynamics. This time, the JNK simulation for wildtype and RIP1 KD is quicker than experimental profiles (Figure 5D, M2). Hence, according to response rule 1, we added additional novel intermediates (proteins, complex formation, etc.) specifically to JNK. This improved the JNK simulations, however, for FADD and caspase-8 KDs, the JNK dynamics are still absent (Figure 5E, M3). Utilizing response rule 3, we added a link from the FADD-independent pathway for p38 to also activate JNK. Thus, we introduced a novel molecule Y to branch from TRAIL-R1 to p38 and JNK and specifically inserted the additional novel intermediates between Y and JNK via MKK4/6.
This procedure significantly improved the JNK simulations in wildtype, RIP1 KD, FADD KD and caspase-8 KD, but not in TRAF2 KD (Figure 5F, M4). To achieve specific activation of JNK in TRAF2 KD, we require a bypass from p62 to novel molecule Z (one of the novel intermediate predicted above) on the FADD-independent pathway to activate JNK (response rules 3 and 4). Overall these modifications, based on the response rules, to the initial model remarkably recapitulate IκB, p38, JNK, caspase-8 and -3 activations in all tested experimental conditions (wildtype, RIP1 KD, FADD KD, caspase-8 KD and TRAF2 KD) with a good degree of consistency (Figure 1B, 5G and 6A, M5).
Simulations of the proposed TRAIL signaling topology.
(A) Comparison of M5 simulations (solid lines) with experimental data (black points) in wildtype, RIP1 KD, FADD KD, caspase-8 KD and TRAF2 KD. (B) Static topology of the proposed model for TRAIL signaling pathway. Modifications are indicated by blue arrows.
Next, adopting response rule 6, we evaluated the relative significance of each novel network features. Based on the model simulation levels, the FADD-independent pathway contributes about 17% and 43% of total JNK and p38 activations, respectively, the RIP1 to p38 crosstalk provides about 45% flux for p38 activation. The bypass from p62 to molecule Z provides about 82% flux to JNK, whereas TRAF2 provides about 1% flux to JNK and the TRAF2 to MKK3/6 axis provide about 12% flux to p38. Thus, RIP1 is key for p38 and Z is crucial for JNK activation.
In summary, we propose: i) a FADD-independent pathway to activate p38 and JNK, bypassing the primary and secondary DISC and through novel molecules Y and Z , ii) a crosstalk between RIP1 and p38 via MKK3/6, iii) a crosstalk between p62 and JNK via molecule Z and iv) intermediary step(s) or molecule(s) upstream of JNK (Figure 6B).
Identifying in silico targets for enhancing cell death in HT1080 cells
To identify a promising target for overcoming TRAIL resistance in HT1080 cell populations, we used the updated TRAIL signaling model, which simulates multiple experimental conditions. We next wondered the roles of the novel molecules Y and Z in the survival and apoptosis activities and were interested to check whether any of them could potentially be a crucial target for enhancing cell death.
To investigate this, we examined the population level survival ratios (SRs) for wildtype, FADD KD, TRAF2 KD and RIP1 KDs, which are known to be about 59, 76, 28 and 18%, respectively for TRAIL-stimulated HT1080 cells (see Figure 3C of ref. 22). Since our model simulates signaling molecules' dynamics and does not directly predict SR, to evaluate the SRs for Y and Z KDs, we developed a link between SR and the survival and apoptotic molecules' temporal activation profiles (see Methods).
As area under each apoptosis and survival molecule's activation profile with time indicates an intensity measure of its respective process, we used this to estimate a link with the SR. In order to perform this, we introduce a novel theoretical metric, CSM, which compares the area under curves of survival (IκB, JNK, p38) and apoptotic (caspase-8 and -3) molecules and links it to SR (see Methods). The CSM evaluates the net effect of survival and apoptosis activations. A positive CSM indicates net survival mode and a negative CSM indicates net apoptosis mode.
We next performed in silico KDs of Y and Z molecules, simulated IκB, JNK, p38, caspase-8 and -3 and evaluated their resultant CSMs and SRs (Figure 7A–C). Notably, we observe among all investigated KDs, the X KD results in the most negative CSM and the least SR (with only about 5% surviving cells compared with 18% and 36% for RIP1 and Y KDs, respectively, Figure 7B–C). This is because, through SFR (response rule 4), the Z KD enhances the caspases activations more than the survival molecules (Figure 7A). Thus, Z KD shows the most desirable outcome of maximizing cell death in all tested conditions, making it clearly the best target candidate for TRAIL-resistant HT1080 cells.
Identifying key target for sensitizing TRAIL resistance.
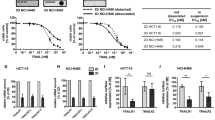
(A) Simulation profiles of p38, JNK, IκB, caspase-8 and -3 in Y and Z KDs. (B) Cell survival metric (CSM) for all KDs. (C) Survival ratio, SR, (experimental versus evaluated, from t = 0 to 120 min) in all conditions. Evaluated data is obtained using experimental data of RIP1 and FADD KDs (see Methods). (D) Wildtype HT1080 and HT29 (control) cells shows 60% and 95% survival, respectively, for 1000 ng/mL of TRAIL stimulation.
To verify our overall result, we performed our own experiments on wildtype TRAIL-stimulated HT1080 cells. Although we are unable to perform experiments on the still uncharacterized Z KD cells, we wanted to check the result of wildtype cells to TRAIL stimulation. Notably, we successfully reproduced approximately 60% SR for 1000 ng/mL of TRAIL stimulation (compare Figure 1A of ref. 22 with Figure 7D). The validation of wildtype data demonstrates that our average response model can be legitimately used to identify an appropriate candidate, through computational simulations, for enhancing TRAIL-based strategy.
Discussion
Over the last decade, there has been great interest leading to numerous studies focusing on the usage of TRAIL, due to its ability to trigger the apoptotic pathways, as a strategy to fight the progression of cancer. Although successful in certain cancer types, TRAIL has not become a general candidate as many types of cancers are able to evade TRAIL's apoptotic property. Although recent works have shed light into the resistance mechanisms in TRAIL-based therapies37, nevertheless, the understanding of counteracting cell survival and apoptotic pathways and finding ways to sensitize TRAIL-based strategy remain poor.
Drugs that upregulate TRAIL receptors (e.g proteasome inhibitors) in resistant cancers may not be effective as they are likely to enhance both cell survival and apoptotic pathways with the net effect not necessarily enhanced cell death. Further studies on using combinatorial treatment of TRAIL with downstream targets that selectively suppress cell survival, such as NF-κB and MAP kinases inhibitors, or enhancing apoptosis by suppressing the suppressors of caspases have recently been investigated12. The reduced cell survival activity or increased apoptosis produced, generally, an increase in the net effect of cell death, providing good prospective for increasing the efficacy of TRAIL-based strategies. However, these strategies have focused on suppressing either the cell survival or apoptosis activity, independently. It remains unclear which strategy among these is optimal for the various TRAIL-resistant cancer types and, hence, we require a strategy that considers dual mode of suppressing the survival and enhancing the apoptosis pathway simultaneously.
Here, we report a systemic strategy that considers both the cell survival and apoptotic dynamics to provide a more mechanistic way to target TRAIL resistance. Our dynamic computational approach, successful to model TLR19 and TNF34 pathways, is used to examine the signaling mechanisms of NF-κB, MAP kinases and caspases activations in TRAIL-stimulated HT1080 cells. Starting from a literature curated generalized TRAIL signaling topology, firstly, using response rules we infer novel features, namely i) a FADD-independent pathway(s) to activate p38 and JNK, bypassing the primary and secondary DISCs and through novel molecules Y and Z , ii) a crosstalk between RIP1 and p38 via MKK3/6, iii) a crosstalk between p62 and the JNK pathway and iv) intermediary step(s) or molecule(s) upstream of JNK (Figure 6B). These inclusions are necessary for the computational model to successfully recapitulate experimental outcome in all investigated conditions (wildtype, RIP1 KD, FADD KD, caspase-8 KD and TRAF2 KD).
Secondly, to determine the best strategy to induce apoptosis in TRAIL-resistant HT1080 cells, we investigated the net effect of NF-κB, MAP kinases and caspases activations by evaluating their cell survival metric, CSM and making a link to the survival ratios (SRs) for various KD conditions. Overall, our simulations suggest that the optimal target is the novel molecule Z , whereby its removal is predicted to produce about 95% HT1080 cell population death (Figure 7C).
Recent studies have indicated the roles of PI3K, Akt and MADD for TRAIL resistance38,39. We believe that these may belong to the novel FADD-independent pathways and one of these could well represent the molecule Y . On the other hand, the novel molecule Z , which is activated by p62 to specifically activate JNK in our model, acts like a connector between the primary and secondary DISC. Performing a search of the protein-protein interaction database40 for p62 interacting partners, we obtain protein kinase C (PKC) family members as likely candidates. Further literature search supports PKC-ζ41 as a possible candidate.
It is important to note that although our average response model may not pinpoint a specific molecular target exactly, nevertheless, it will be worthwhile to investigate molecules that interact with p62 for the search for optimal target for effective cell death in TRAIL-resistant HT1080 cells. Taken as a whole, the approach presented here provides a promising contribution towards systemically analyzing the dynamics of cell survival and apoptotic pathways, for the sensitization strategy for TRAIL-based cancer therapy.
In this paper, we show that novel features of the TRAIL signaling can be revealed through the law of conservation and first order response equations. From this result, we theoretically demonstrate that targeting a molecule at the survival and apoptosis pathway junction can provide an optimal solution to treat TRAIL-resistance. It suppresses JNK and, at the same time, enhances caspases activities.
This result can be viewed surprising as the vast diversity of molecular constituents42, issues of heterogeneity43, spatio-temporal effects44 such as diffusion and crowding within cells, are likely to make the TRAIL signaling response non-linear and difficult to conceptualize computationally. In contrary, our data suggests that cells, as a population, are able to discard individual differences to achieve a global average response that follows simple rules20. This is clearly the underlying success that our final first-order response model is able to simulate multiple experimental conditions.
Although we do recognize that biological complexity such as heterogeneity and fluctuations or noises observed at single cell resolution45 are important, at the same time we do need to accept that biology, like any other complex system, possesses both microscopic (single cell) and macroscopic (population average cell) dynamics20. Thus, it is necessary to treat the two dynamics distinct and investigate their individual merits. For example, stochastic fluctuations are necessary to induce probabilistic differentiation from genetically identical cells, allowing multi-cellular organisms to switch fates and states to yield diversity, such as for development or stress, which, otherwise, may be impossible from a purely deterministic system46,47. On the other hand, the well-coordinated response of cell populations, such as differentiation or growth, demonstrates that the single cell noise could cancel out when ensembles of cells are formed to generate a stable and robust response. For instance, the observation of guided average behavior in the synchronization of neuronal signaling48, persistence mechanisms of bacteria49 and collective decisions in ants50 are all noteworthy.
In the future, as single cell techniques continue to make impressive progress51, it will be interesting to compare the single cell dynamics of HT1080 cells in wildtype and PKC-ζ mutants with the population response presented here. Also, it will be crucial to investigate how the heterogeneous single cells responses43 in TRAIL signaling could be guided to provide a possible 100% cell death, at least in a dish. In this light, large-scale tumor sequencing data52 and the study of single cell noise53 will be critical to enhance our modeling aspects further to generate and investigate single cell response models.
Methods
Experimental data of cell survival and apoptosis molecules
We utilized time-course experimental data22 of IκB, JNK, p38, caspase-8 and -3 in wildtype, RIP1 KD, FADD KD, caspase-8 KD and TRAF2 KD of HT1080 cells with 1000 ng/ml of TRAIL stimulation. The activation levels of IκB, JNK, p38, caspase-8 and -3 (Figure 1B) were quantified from the western blots data using ImageJ (http://rsbweb.nih.gov/ij/) and the normalized experimental value of the ith molecule in the kth condition (wildtype (WT), RIP1 KD, FADD KD, TRAF2 KD) at time t is evaluated as:

where  is the raw experimental value obtained from quantification and
is the raw experimental value obtained from quantification and  indicates the maximum value obtained in wildtype condition. Values lower than 0.05 are likely to possess significant signal-to-noise ratio and, therefore, noted as zero. Simulations values of the ith molecule in the kth condition are also normalized to wildtype data such as:
indicates the maximum value obtained in wildtype condition. Values lower than 0.05 are likely to possess significant signal-to-noise ratio and, therefore, noted as zero. Simulations values of the ith molecule in the kth condition are also normalized to wildtype data such as:

Note texp = 60 min is available only for caspase-8 and -3.
Parameter fitting and fitness of simulations
The fitting of the reactions parameters of a given topology is obtained by minimizing the error between experimental and simulation profiles of all investigated molecules. We used a genetic algorithm where the fitness function f is given by:

and  is the error between the experimental and simulation curves of the ith molecule in the kth condition represented by normalized area between the experimental and simulation curves and
is the error between the experimental and simulation curves of the ith molecule in the kth condition represented by normalized area between the experimental and simulation curves and  . The algorithm evolves the parameter sets from one generation to the next by the operations of selection, crossover and mutations32. The model is considered acceptable when the tolerance is set for
. The algorithm evolves the parameter sets from one generation to the next by the operations of selection, crossover and mutations32. The model is considered acceptable when the tolerance is set for  . To avoid local minima, the algorithm is performed multiple times in multiple conditions.
. To avoid local minima, the algorithm is performed multiple times in multiple conditions.
Flow cytometry analysis
HT1080 cells were cultured in 12 well plates (60000 cells/well) and incubated for 24 hours. HT29 cells (negative control) were incubated in the same manner. Cells were transferred to a culture medium containing TRAIL/Apo2L (0 and 1000 ng/mL) and incubated for 18 hours, then washed using Phosphate buffered saline (PBS) solution, detached from the plate using Trypsin-EDTA and centrifuged. Cell pellets were re-suspended in 200μL 1x Binding buffer, 5μL AnnexinV-FITC and 10μL Propidium Iodide and incubated at room temperature, protected from light for 15 min. Cell suspension was pipetted into Poly Round Tubes through cell-strainer cap, then fluorescence intensity was measured using an EPICS XL flow cytometer. TRAIL stimulation did not induce apoptosis of HT29 cells (negative control). On the other hand, 40% of HT1080 cells underwent apoptosis after 18 hours upon TRAIL stimulation (1000 ng/ml) (Figure 7D).
Cell Survival Metric (CSM) and Survival Ratio (SR)
Evaluating the level of each survival and apoptotic molecule, independently, may not truly reflect the optimal conditions for determining cell death. For example, by just analyzing the levels of caspase-3 without considering IκB does not indicate the survival potential of cells. Hence, we develop a simple metric that quantifies each investigated molecule's activity and evaluates their net effect: the CSM measures the relative difference in the area under curve (AUC) for the relative apoptotic and survival activities with time for the kth condition, i.e.

where the summation of AUCs for the survival (Eq. 7) and apoptotic (Eq. 8) molecules are averaged:


α and β are weight constants determined from the experimental data (see below). Thus, positive and negative CSMk denotes net survival and death, respectively, for the kth condition.
The relative difference in the AUC for the ith molecule's activity compared to wildtype condition is noted:

where  is the normalized simulation values for the ith molecule in the kth condition and
is the normalized simulation values for the ith molecule in the kth condition and  . Note that we used the AUCs of our final model simulations which fit well with all experimental conditions.
. Note that we used the AUCs of our final model simulations which fit well with all experimental conditions.
Next, we make a link between the CSM and SR. We note that  (from Eq. 6–8) and that the SR for each kth condition is obtained from experimental data22:
(from Eq. 6–8) and that the SR for each kth condition is obtained from experimental data22:

Thus, we make an exponential relationship:

where for wildtype,  and λ indicates the basal net survival with
and λ indicates the basal net survival with  . Putting Eq. 11 into equation Eq. 6 and solving them simultaneously produces 3 possible solutions for α and β (since we have 2 parameters for 3 equations). For example, solving α and β using i)
. Putting Eq. 11 into equation Eq. 6 and solving them simultaneously produces 3 possible solutions for α and β (since we have 2 parameters for 3 equations). For example, solving α and β using i)  and
and  , we obtain evaluated (predicted) SR for TRAF2 KD, X KD and Y KD (Figure 7C). We performed α and β using ii)
, we obtain evaluated (predicted) SR for TRAF2 KD, X KD and Y KD (Figure 7C). We performed α and β using ii)  and
and  and iii)
and iii)  and
and  to predict SR for other conditions (Figure S1). Notably, among the 3 solutions, the most conservative survival ratios for the best candidate Z KD is,
to predict SR for other conditions (Figure S1). Notably, among the 3 solutions, the most conservative survival ratios for the best candidate Z KD is,  .
.
TRAIL model limitations
Like any other modeling approach, there are certain limitations. Firstly, the perturbation-response approach discussed does not comprehensively represent the details of each signaling reaction's kinetics. Secondly, the small perturbation assumption leading to the first-order mass-action equations represents an average cell response and this cannot be used to study single cell stochastic behavior or oscillatory dynamics. Thirdly, the model predictions will show relative and not absolute, activation levels. However, the approach is not restricted to the TRAIL pathways and can be applied to model any pathways that experimentally display formation and depletion waves, e.g. the TLRs20, TNF34 and EGF receptor signaling54.
References
Finn, O. J. Cancer immunology. N. Engl. J. Med. 358, 2704–2715 (2008).
Zitvogel, L., Apetoh, L., Ghiringhelli, F. & Kroemer, G. Immunological aspects of cancer chemotherapy. Nat. Rev. Immunol. 8, 59–73 (2008).
Wang, S. The promise of cancer therapeutics targeting the TNF-related apoptosis-inducing ligand and TRAIL receptor pathway. Oncogene 27, 6207–6215 (2008).
Johnstone, R. W., Frew, A. J. & Smyth, M. J. The TRAIL apoptotic pathway in cancer onset, progression and therapy. Nat. Rev. Cancer 8, 782–798 (2008).
Yagita, H., Takeda, K., Hayakawa, Y., Smyth, M. J. & Okumura, K. TRAIL and its receptors as targets for cancer therapy. Cancer Sci. 95, 777–783 (2004).
Sheridan, J. P. et al. Control of TRAIL-induced apoptosis by a family of signaling and decoy receptors. Science 277, 818–821 (1997).
Yang, A., Wilson, N. S. & Ashkenazi, A. Proapoptotic DR4 and DR5 signaling in cancer cells: toward clinical translation. Curr. Opin. Cell Biol. 22, 837–844 (2010).
F., Andres, J. P. K. & El-Deiry, W. S. TRAIL-R deficiency in mice promotes susceptibility to chronic inflammation and tumorigenesis. The Journal of Clinical Investigation 118, 111 (2008).
Zhang, L. & Fang, B. Mechanisms of resistance to TRAIL-induced apoptosis in cancer. Cancer Gene Ther. 12, 228–237 (2005).
Falschlehner, C., Emmerich, C. H., Gerlach, B. & Walczak, H. TRAIL signalling: decisions between life and death. Int. J. Biochem. Cell Biol. 39, 1462–1475 (2007).
Frew, A. J. et al. Combination therapy of established cancer using a histone deacetylase inhibitor and a TRAIL receptor agonist. Proc. Natl. Acad. Sci. U. S. A. 105, 11317–11322 (2008).
Munshi, A., McDonnell, T. J. & Meyn, R. E. Chemotherapeutic agents enhance TRAIL-induced apoptosis in prostate cancer cells. Cancer Chemother. Pharmacol. 50, 46–52 (2002).
Ammann, J. U., Haag, C., Kasperczyk, H., Debatin, K. & Fulda, S. Sensitization of neuroblastoma cells for TRAIL-induced apoptosis by NF-κB inhibition. Int. J. Cancer 124, 1301–1311 (2009).
Jin, C. et al. Genistein enhances TRAIL-induced apoptosis through inhibition of p38 MAPK signaling in human hepatocellular carcinoma Hep3B cells. Chem. Biol. Interact. 180, 143–150 (2009).
Fabregat, I., Roncero, C. & Fernández, M. Survival and apoptosis: a dysregulated balance in liver cancer. Liver Int. 27, 155–162 (2007).
Baxevanis, C. N., Perez, S. A. & Papamichail, M. Combinatorial treatments including vaccines, chemotherapy and monoclonal antibodies for cancer therapy. Cancer Immunol. Immunother. 58, 317–324 (2009).
Tsuchiya, M. et al. Emergent genome-wide control in wildtype and genetically mutated lipopolysaccarides-stimulated macrophages. PLoS ONE 4, e4905 (2009).
Selvarajoo, K. Discovering differential activation machinery of the Toll-like receptor 4 signaling pathways in MyD88 knockouts. FEBS Lett. 580, 1457–1464 (2006).
Helmy, M. et al. Predicting novel features of Toll-like receptor 3 signaling in macrophages. .PLoS ONE 4, e4661 (2009).
Selvarajoo, K. Macroscopic law of conservation revealed in the population dynamics of Toll- like receptor signaling. Cell Commun. Signal. 9, 9 (2011).
Selvarajoo, K. et al. Signaling flux redistribution at toll-like receptor pathway junctions. PLoS ONE 3, e3430 (2008).
Varfolomeev, E. et al. Molecular determinants of kinase pathway activation by Apo2 ligand/tumor necrosis factor-related apoptosis-inducing ligand. J. Biol. Chem. 280, 40599–40608 (2005).
Gonzalvez, F. & Ashkenazi, A. New insights into apoptosis signaling by Apo2L/TRAIL. Oncogene 29, 4752–4765 (2010).
Wagner, K. W. et al. Death-receptor O-glycosylation controls tumor-cell sensitivity to the proapoptotic ligand Apo2L/TRAIL. Nat. Med. 13, 1070–1077 (2007).
Holland, P. M. Targeting Apo2L/TRAIL receptors by soluble Apo2L/TRAIL. Cancer Lett. (2011). 10.1016/j.canlet.2010.11.001
Wilkinson, D. J. Stochastic modelling for quantitative description of heterogeneous biological systems. Nat. Rev. Genet. 10, 122–133 (2009).
Tay, S. et al. Single-cell NF-κB dynamics reveal digital activation and analog information processing in cells. Nature. 466, 267–271 (2010).
Selvarajoo, K., Tomita, M. & Tsuchiya, M. Can complex cellular processes be governed by simple linear rules? J Bioinform. Comput. Biol. 7, 243–268 (2009).
Ross, J. From the determination of complex reaction mechanisms to systems biology. Annu. Rev. Biochem. 77, 479–494 (2008).
Kagan, J. C. et al. TRAM couples endocytosis of Toll-like receptor 4 to the induction of interferon-beta. Nat. Immunol. 9, 361–368 (2008).
Morandell, S., Stasyk, T., Skvortsov, S., Ascher, S. & Huber, L. A. Quantitative proteomics and phosphoproteomics reveal novel insights into complexity and dynamics of the EGFR signaling network. Proteomics 8, 4383–4401 (2008).
Carroll, D. A. Chemical laser modelling with genetic algorithms. AIAA 34, 338–346 (1996).
Selvarajoo, K. & Tsuchiya, M. Systematic Determination of Biological Network Topology: Non-integral Connectivity Method (NICM). In: Introduction to Systems Biology (ed Choi S., ed. ). The Humana Press, New Jersey, 449–471 (2007).
Hayashi, K., Piras, V., Tomita, M., Tsuchiya, M. & Selvarajoo, K. Emergence of macroscopic simplicity from the Tumor Necrosis Factor-alpha signaling dynamics. The International Symposium on Nonlinear Theory and Its Applications, Kobe, Japan. (2011).
Cloutier, M. & Wang, E. Dynamic modeling and analysis of cancer cellular network motifs. Integr. Biol. 3, 724–732 (2011).
Kaneko, K. & Furusawa, C. Origin of complexity in multicellular organisms. Phys. Rev. Lett. 13, 6130–6133 (2000).
Thorburn, A., Behbakht, K. & Ford, H. TRAIL receptor-targeted therapeutics: resistance mechanisms and strategies to avoid them. Drug Resist. Updat. 11, 17–24 (2008).
Xu, J., Zhou, J., Wei, W. & Wu, G. S. Activation of the Akt survival pathway contributes to TRAIL resistance in cancer cells. PLoS ONE 5, e10226 (2010).
Li, P. et al. Akt-phosphorylated mitogen- activated kinase-activating death domain protein (MADD) inhibits TRAIL-induced apoptosis by blocking Fas- associated death domain (FADD) association with death receptor 4. J. Biol. Chem. 285, 22713–22722 (2010).
He, M., Wang, Y. & Li, W. PPI Finder: A mining tool for human protein-protein interactions. PLoS ONE 4, e4554 (2009).
Hirai, T. & Chida, K. Protein kinase Cζ (PKCζ): activation mechanisms and cellular functions. J. Biochem. 133, 1–7 (2003).
Bar-Even, A. et al. Noise in protein expression scales with natural protein abundance. Nat. Genet. 38, 636–643 (2006).
Chang, H. H., Hemberg, M., Barahona, M., Ingber, D. E. & Huang, S. Transcriptome-wide noise controls lineage choice in mammalian progenitor cells. Nature 22, 544–547 (2008).
Kholodenko, B. N., Hancock, J. F. & Kolch, W. Signalling ballet in space and time. Nat. Rev. Mol. Cell. Biol. 11, 414–426 (2010).
Eldar, A. & Elowitz, M. B. Functional roles for noise in genetic circuits. Nature 467, 167–173 (2010).
Losick, R. & Desplan, C. Stochasticity and cell fate. Science 320, 65–68 (2008).
Raj, A., Rifkin, S. A., Andersen, E. & van Oudenaarden, A. Variability in gene expression underlies incomplete penetrance . Nature 463, 913–918 (2010).
Axmacher, N., Mormann, F., Fernández, G., Elger, C. E. & Fell, J. Memory formation by neuronal synchronization. Brain Res Rev 52, 170–182 (2006).
Vázquez-Laslop, N., Lee, H. & Neyfakh, A. A. Increased persistence in Escherichia coli caused by controlled expression of toxins or other unrelated proteins. J. Bacteriol. 188, 3494–3497 (2006).
Stroeymeyt, N., Franks, N. R. & Giurfa, M. Knowledgeable individuals lead collective decisions in ants. J. Exp. Biol. 214, 3046–3054 (2011).
Faley, S. L. et al. Microfluidic single cell arrays to interrogate signaling dynamics of individual, patient-derived hematopoietic stem cells. Lab Chip 9, 2659–2664 (2009).
Cui, Q. et al. A map of human cancer signaling. Mol. Syst. Biol. 3, 152 (2007).
Elowitz, M. B., Levine, A. J., Siggia, E. D. & Swain, P. S. Stochastic gene expression in a single cell. Science 297, 1183–1186 (2002).
Blagoev, B., Ong, S., Kratchmarova, I. & Mann, M. Temporal analysis of phosphotyrosine-dependent signaling networks by quantitative proteomics. Nat. Biotechnol. 22, 1139–1145 (2004).
Acknowledgements
We thank Daiki Yamada and Masa Tsuchiya for initial collaboration and Tomoe Egashita (Takara Biosciences) for experimental support. This work was supported by the research fund of Yamagata Prefecture and Tsuruoka City, Japan Society for the Promotion of Science (JSPS) Grants-in-Aid for Scientific Research F11815 and Japan Student Services Organization (JASSO).
Author information
Authors and Affiliations
Contributions
V.P., K.H. and K.S. designed the response rules and developed, analysed and interpreted the TRAIL model and simulations. V.P., K.H., M.T. and K.S. wrote and reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Figure S1
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-No Derivative Works 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Piras, V., Hayashi, K., Tomita, M. et al. Enhancing apoptosis in TRAIL-resistant cancer cells using fundamental response rules. Sci Rep 1, 144 (2011). https://doi.org/10.1038/srep00144
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep00144
This article is cited by
-
Defining rules for cancer cell proliferation in TRAIL stimulation
npj Systems Biology and Applications (2019)
-
The apoptotic mechanisms of MT-6, a mitotic arrest inducer, in human ovarian cancer cells
Scientific Reports (2017)
-
Systems biology of death receptor networks: live and let die
Cell Death & Disease (2014)
-
A systems biology approach to suppress TNF-induced proinflammatory gene expressions
Cell Communication and Signaling (2013)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.