Introduction

Earthquakes can cause hundreds of thousands of landslides, and in some cases, the losses may exceed those directly associated with the ground shaking1. This hazard chain takes place in just few minutes as the wavefield transits and interacts with the terrain, leading to widespread slope instabilities. Such short-term interactions can have repercussions lasting tens of years2. Therefore, understanding the failure mechanisms within those few minutes is vital to foresee the full chain of events2,3,4.

Physics-based and data-driven solutions2 encompass most of the available coseismic landslide models. Physics-based ones rely on geotechnical data, information hardly accessible for regional scale assessments5. Therefore, the main difference between these two approaches resides in the flexibility of data-driven models to be applied for regional or even global scale analyses. As for the physics-based category, Jibson5 mainly divides them into three alternatives: pseudo-static, stress-deformation, and permanent-deformation5. Permanent-deformation techniques such as the Newmark6 method and its simplifications7 are most commonly used for regional coseismic landslide modeling. This approach identifies critical acceleration thresholds in the ground motion signal, above which a given slope exhibits permanent deformation. This framework assumes that the main factors responsible for higher slope deformation are large amplitude and duration of shaking8. The main limitation in the applicability of the Newmark method is in the sparse density9 of seismic stations. Therefore, spatially continuous records of ground motion data cannot be retrieved even in tectonically active regions, where dense seismic networks are deployed9,10.

Data-driven approaches offer an alternative by using proxies rather than parameters required in physics-based methods11. Statistical methods such as binomial Generalized Linear12 and Additive13 Models reflect most of the literature until recently when they shared the stage with machine learning14 approaches. Overall, data-driven models perform analogous operations, where a set of explanatory variables is used to optimize the numerical distinction between slopes that have failed in response to ground shaking and those that did not. To date, data-driven approaches incorporate several ground motion intensity parameters such as peak ground velocity (PGV), acceleration (PGA), or Arias intensity2. Dahal et al.15 use synthetic waveforms to test 28 ground motion parameters and demonstrate that frequency content, total shaking, and duration can complement the information usually carried by peak proxies. However, even these parameters still convey a scalar representation of the full waveform, and they do not reflect the characteristics of seismic waves (e.g., frequency content and duration) that may play a role in the occurrence of landslides.

The problem of suitably exploiting time series exists across all scientific fields. For instance, a branch of machine learning known as natural language processing has been developed to recognize important characteristics in the continuous signal of written and spoken language. The two most common solutions correspond to long short-term memory16 (known as LSTM) and gated recurrent units17 (known as GRU). However, both have limits in capturing long-range dependencies in time-series data because of their sequential processing nature18,19,20. In other words, their structure sequentially processes the signal, and the influence estimated at each step is a priori constrained to decay over time. Thus, both models tend to forget the contribution coming from portions of the time sequence that are far away from each other. In geoscience, these models have been demonstrated to be convenient in the context of long-term precipitation analysis and associated landslides because they naturally reflect the different contributions coming from early preparatory21 and triggering22 precipitation. However, in the context of earthquake-induced landslides, the energy released by an earthquake propagates on very short timescales, making sequential models unsuited to treat an impulsive signal.

Conversely, a transformer architecture relies on an attention mechanism23 capable of looking at portions of the time series without prior assumptions on how certain information should be forgotten moving away from the start of the sequence24. Due to their flexibility, transformers have become a staple in computer vision25,26, natural language processing27 and constitute the fundamental backbone of the famous ChatGPT model series28.

Therefore, here, we aim to remove any scalar simplification requirement and implement a modeling architecture capable of interpreting the ground motion time series as a whole. For this reason, we designed an experiment where the prediction of coseismic landslides is tasked to a transformer architecture fed with full waveform. We also translated the model results to examine which segments of the synthetic waveforms carry relevant information for landslide hazard assessment. This model is benchmarked against a standard scalar counterpart to test whether the use of full waveforms is useful in the first place.

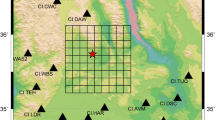
The study area where we run our experiment corresponds to the Nepalese landscape struck by the 7.8 Mw Gorkha Earthquake in 2015, for which ground motion simulations15, landslide inventory29, terrain30, and geological31 data are available. The earthquake occurred along the Main Himalayan Thrust (MHT) fault, and the hypocentre is located in the Northwestern sector (Fig. 1). The unilateral rupture propagated 110° east, lasting for ~50 s32, and the strike and dip of the fault was 293° and 7°, respectively33. Overall, more than 8,800 people were lost, with 23,000 injured34, followed by widespread infrastructural damage. An area of 28,344 km2 was scanned, and a polygonal inventory containing 24,990 coseismic landslides associated with this event was mapped (Fig. 1)29. We defined our experiment over the same region to ensure the validity of landslide presence/absence information and obtained ground motion data from the simulations made by Dahal et al.15. The authors simulated the Gorkha earthquake by using the finite fault model built by Wei et al.35, including the 3D topography through Salvus36,37. The 1D velocity structure is the same as proposed by Mahesh et al.38 with a mesh capable of simulating up to 3.0 Hz, although the waveforms were filtered down to 1.5 Hz due to the limitations in subsurface data and finite fault model.

Fig. 1: Study area, ground motion simulation extent, and observed landslides.
figure 1

a Dashed polygon shows the ground motion simulation domain defined by Dahal et al.15; the black solid polygon represents the study area where Roback et al.29 performed the landslide mapping. The epicenter is symbolized with a star, whereas locations where the landslide was initiated, are plotted with a red dot. The main Himalayan thrust fault system is shown in a yellow soild line. b Location of the study area with respect to administrative boundary of Nepal. Basemap source: Esri, USGS, and the GIS User Community.

Full size image

Using the simulation by Dahal et al.15, full waveforms were extracted at the crown of each landslide reported by Roback et al.29. These locations constituted our landslide presence data. In binary classification, it is also necessary to extract the landslide absence information39. Therefore, we extracted a random and equal number of stable slopes at least steeper than 10° and located 500 m away from a failed slope. The combination of landslide presence and absence will constitute the modeling target of our analyses.

Results

Benchmarking

We recall that our transformer model is equipped with a full waveform time series (Mod1) and that we benchmarked its outputs against a standard model that simplifies the ground motion into its peak velocity (Mod2). The difference between the two is significant, as demonstrated by a 22% increase in performance. To enrich our experiment, we also added terrain and lithological information to the two models above (i.e., Mod3 and Mod4, respectively). As a result, the performance observed in Mod1 (AUC = 0.94) increased to 0.96 in Mod3. As for the jump from Mod2 to Mod4, this translated into a performance of 0.72 and 0.80, respectively. Therefore, even the more complex benchmark still showed an overall improvement of 16% between Mod3 and Mod4 (Fig. 2a).

Fig. 2: Performance evaluation of the models.
figure 2

a Receiver operating characteristic (ROC) curves and b full suite of examined metrics, including the area under the curve (AUC), accuracy score (ACC), intersection over union (IOU) and F1 score.

Full size image

A similar modeling performance among the four models is also maintained when examining accuracy, intersection over union (IOU), and F1 scores (Fig. 2b). Mod2 and Mod4 appear significantly less capable of distinguishing failed slopes compared to Mod1 and Mod3, respectively. Also, the role of terrain and lithological characteristics led to a larger performance increase from Mod2 to Mod4 (i.e., 8%) rather than from Mod1 to Mod3 (i.e., 2%), likely because the latter can already rely on a large amount of information carried by the full waveforms.

Aside from the performance metrics, we also presented the spatial pattern of landslide probabilities for each model (Fig. 3). The output of Mod2 appears spatially smoothed (Fig. 3b). Even when including terrain and lithology, Mod4 still exhibits a smooth spatial pattern (Fig. 3d) represented by smeared values that are in the medium to small range without a clear distinction between landslide and non-landslide locations. Actually, what happens is that coseismic unstable slopes become associated mostly with high relief (Fig. 3e) and only marginally with high shaking (Fig. 3f). As a result, Mod4 largely overestimates slope instabilities in the north-east and north-west sectors, an effect that was not present in the simpler Mod2. Despite the spatial differences, another element of concern in both Mod2 and Mod4 is in their range of probabilities, which is biased toward small and medium values.

Fig. 3: Spatial distribution of the model outputs together with observed landslides, relief, and peak ground velocity.
figure 3

Mod1 to Mod4 output converted in map form (panels a–d). Panel e shows the relief map, whereas panel f reports the PGV overlayed by the landslide inventory. Basemap source: Esri, USGS, and the GIS User Community.

Full size image

The use of full waveforms in Mod1 (Fig. 3a) largely addresses both issues mentioned above. The landslide predictive pattern appears less smooth, and the probability contrast between stable and unstable slopes becomes much more evident (the range now extends from 0 to 1). Another characteristic is that probabilistically unstable slopes cluster at the center of the study area. However, this sector unrealistically appears homogeneously unstable. Only in Mod3 (Fig. 3c), combining terrain and lithology to the full waveforms’ information, do the predictive patterns reach their best expression among all models.

Explainability

In the previous section, we acknowledged that the best performance metrics are obtained for Mod3. In this section, we will explore the reasons behind such a result, comparing Mod3 against its simpler version, Mod4. To do so, we identified failed slopes to which both models assigned landslide occurrence probability equal to or greater than 0.5, or (\(p\left\langle {{{{{\rm{Mod}}}}}}4\right\rangle \ge 0.5\wedge p\left\langle {{{{{\rm{Mod}}}}}}3\right\rangle \ge 0.5{|y}=1\)). These are unstable slopes correctly classified by both Mod3 and Mod4. Similarly, we checked failed slopes that only Mod3 was able to characterize with a probability equal to or greater than 0.5, or (\(p\left\langle {{{{{\rm{Mod}}}}}}4\right\rangle\, < \,0.5\wedge p\left\langle {{{{{\rm{Mod}}}}}}3\right\rangle \ge 0.5{|y}=1\)). These are unstable slopes correctly classified only by Mod3. In Fig. 4, we plot each of the two respective groups (panels a–c and d–f) according to the results obtained for the three main directions: East–West, North–South, and Up–Down. Along the y-axis, we present the 2-dimensional histogram of the explainability score generated by Mod3 for each time step of all waveforms, shown along the abscissa. The explainability score quantifies each time step’s contribution with respect to the final landslide occurrence probability. The x-axis is organized according to the PGV arrival (set at zero and symbolized with the solid purple line).

Fig. 4: Difference in explainability scores and predicted probability between static and full waveform models.
figure 4

Explainability scores for all slopes in the study area were correctly classified by Mod3 and Mod4 (panels a–c), and failed slopes were recognized only by Mod3 (panels d–f). The purple line points at the arrival of the PGV. Panel g and h present the difference in probability between Mod3 and Mod4 (i.e., Mod3–Mod4) for the entire study area as well as a zoomed location, respectively. Basemap source: Esri, USGS, and the GIS User Community.

Full size image

The first observation to be made is that in both cases, the direction where most of the explainability is scored corresponds to East-West, which is also the main direction of the rupture propagation during the Gorkha earthquake. The most important element to be stressed is the comparison between the E–W direction belonging to panels a and d. In the first case, where both Mod3 and Mod4 correctly perform, most of the yellow grids (the frequency of explainability scores) cluster around the PGV arrival. This is actually why the two models agree, as even a scalar representation of the full waveform would point at this approximate portion of the signal without relying on the information coming from the rest of the waveform. However, the situation is very different in panel d, where only Mod3 suitably recognizes landslides. There, the explainability scores shown in panel d do not only cluster around the PGV arrival as shown in panel a. Conversely, the explainability is shown to be densely distributed over most of the time series, even ~120 to ~160 s after the PGV.

This observation requires further investigation into what it potentially implies numerically, geographically, physically, and geomorphologically. Numerically, Mod4 is blind to the occurrence of 5260 landslides (or 21.26% with respect to the total). Conversely, Mod3 only misses 2059 landslides (or 8.32% with respect to the total) and captures 3201 landslides that Mod4 misses. As for what this translates in terms of landslide area, Mod4 captures landslides that failed up to 8.4 km2 as compared to the 11.1 km2 estimated by Mod3. Notably, the observed total failed surface is equal to 11.7 km2. Thus, Mod4 misses ~28% of the failed surface, whereas Mod3 only misses ~5%. Looking more into the extremes of the landslide area distribution, above the 95th percentile, Mod4 identifies landslides with an area of ~3700 m2, whereas the same estimated by Mod3 is ~4300 m2. The observed reference is 4315.99 m2. We also explore frequency area distributions40 in Supplementary Fig. 1, observing a higher capacity of Mod3 to predict the two tails of the distribution as compared to Mod4.

Extending the investigation towards geographic implications, we plot the landslide probability difference (Mod3–Mod4) in Fig. 4g. There, both models agree at locations highlighted in yellow (probability difference ~0) and disagree wherever the map presents blue (Mod4 > Mod3) and red colors (Mod3 > Mod4). Interestingly, the highest positive differences in probability (Mod3 > Mod4) cluster along topographic incisions (valleys) running roughly orthogonal to the Himalayan direction.

As for the physical meaning behind Mod3 and Mod4 differences, we revise the idea behind Fig. 4, leave behind probabilistic considerations, and focus on failed slopes. In Fig. 5, we select two representative slopes correctly classified by both Mod3 and Mod4, and two slopes only failed according to Mod3. In such a way, we graphically present the actual waveforms (gray lines) against their site-specific Mod3 scores, exploring potential physical considerations.

Fig. 5: Evaluation of landslide predictions in relation to ground motion data and geomorphological characterstics.
figure 5

Panels a–d present the Mod3 scores against the synthetic waveforms. The x-axis is centered at zero, which corresponds to the PGV arrival time. Panels a and b correspond to slope examples correctly classified by Mod3 and Mod4; panels c and d only apply to correct classification examples from Mod3. Panel e presents the spatial distribution of the respective landslides. Panels f, g, and h show the difference in terms of slope, PGV, and landforms, respectively. Basemap source: Esri, USGS, and the GIS User Community.

Full size image

Panels a and b show that landslides recognized by both Mod3 and Mod4 exhibit the largest explainability score (green line) close to the PGV (zero along the abscissa). The situation appears very different for landslides only predicted by Mod3. Panel c of Fig. 5 shows two large explainability scores in the early stages of the waveform. The first one is well aligned with the P wave arrival time, an observation that could indicate the ability of our transformer model to capture the influence of waveform phases. Panel d of Fig. 5 depicts another situation where the explainability scores in the early stages of the waveform are relatively low, and a peak score is visible around 150 seconds after the PGV. These results highlight the inadequate capacity of PGV to reflect influences across the full waveform and, in turn, the limited capacity to explain the whole coseismic landslide population. This also means that the Mod3 extracts valuable information from the full waveform, towards which Mod4 is blind.

To conclude the investigation, we explore the geomorphological differences between Mod3 and Mod4 (Fig. 5e). There, we plot landslide locations correctly predicted by both (in green) and those only recognized by Mod3 (in red). Landslides located by Mod3 occur on a gentler topography (Fig. 5f, maximum density at 30°) and with a lower shaking (Fig. 5g, maximum density at 0.2 m/s) compared to landslides predicted by both models (maxima at 40° and 0.4 m/s, respectively). Along the same reasoning, we also classified the Nepalese landforms41 and checked which type is associated with the most misclassifications in Mod4 (Fig. 5h). Open and upper slopes, midslope, and high ridges are also well represented in Mod4. However, Mod4 fails to predict failures at locations close to valleys, stream slopes, and midslope drainages. These are otherwise well recognized as unstable by Mod3.

Overall, these results imply that landslides on less susceptible hillslopes can be more successfully predicted by exploiting the full waveform information. Conversely, landslides triggered on high susceptible hillslopes (i.e., characterized by steep topography and high ground shaking) are already predictable using traditional peak intensity parameters. The realization of such distinction is particularly important because very steep and heavily shaken slopes are already intuitively susceptible. Thus, predicting that location should not require large modeling efforts, and the less susceptible slopes should rather be the target.

Discussion

Traditionally, data-driven coseismic landslide modeling approaches have always focused on ground motion intensity parameters2. These are essentially single scalar representations of the whole seismic sequence42. In turn, this has hindered considerations of the full characteristics of seismic signals. Even though intensity parameters carry important information about the seismic waveforms, they cannot accurately inform about the phase and amplitude and their temporal variations during the earthquake propagation43.

Our findings based on the coseismic landslides triggered by the 2015 Gorkha earthquake showed that the full waveform information translates into a minimum 16% increase across all the examined performance metrics. This occurs because earthquake properties such as amplitude, phase, frequency, and duration are embedded in the seismic waves. When exploring this theme further, what stood out is that Mod3 and Mod4 mostly agree in the northern sector of the earthquake-affected area. As for the slopes below the high mountain range, in particular, the use of PGV is not enough. Mod4 produces very smooth predictive patterns, underestimating the middle section of the Himalayan topographic profile and overestimating failures in safe locations. Notably, also the U.S. Geological Survey (USGS) near-real-time system44 seems to overpredict coseismic landslides45.

To benchmark our full waveform approach, below, we will present a series of additional experiments where our Mod3 is compared to alternatives equipped with scalar ground motion estimates. Looking into what is available at the USGS ShakeMap service46, some parameters constitute the standard for the coseismic landslide community44,47, and they are usually available in multiple versions, one empirically generated right after a major earthquake and few updates as more data becomes available with time48. Here, we opt to benchmark Mod3 against an equivalent that uses PGA and PGV, both in their first (2015) and last (2020) updated versions48. Moreover, we also include two more tests that look back at the original simulations from Dahal et al.15. The first one calculates Arias Intensity49,50, a common scalar proxy for amplitude and duration and widely used for coseismic landslide prediction51. The second one makes use of the full waveforms, like in Mod3, but filters out frequencies above 0.5 Hz. The rationale behind the latter is to include a sensitivity analysis. All the corresponding results are reported in Table 1. There, Mod3 outperforms all the alternatives across all metrics. The two pairs of USGS intensity parameters perform between ~8% and 13% worse than our Mod3. An even greater loss in performance is seen with Arias Intensity, likely because the synthetic waveforms do not contain high frequencies. For the very same reason, we interpret the minimal performance loss over the filtered waveforms. Furthermore, it is also interesting that Mod4 performs worse than the analogous equipped with ShakeMap intensity parameters. This demonstrates that the inclusion of high frequencies adds valuable information in the case of a scalar model. Nevertheless, this performance is still far from what full waveforms can achieve.

Table 1 Model performance compared to multiple benchmark datasets
Full size table

Moving away from performance-oriented considerations, Mod3 assigns its largest scores both close to the time of the peak velocity arrival and far from it. Determining which physical information corresponds to these portions of the ground motion sequence is not straightforward. Mod3 captures the E-W direction as responsible for most instabilities (see Fig. 4, panels a and d). This is reasonable as it aligns well with the Main Himalayan Thrust rupture, oriented at 110°.

Looking at single slopes such as in Fig. 5 (panels c and d), our transformer seems to highlight the importance of specific sections of the full waveform, these being potentially linked to the phase information, the interactions with topography, and surface wave arrival. We recall here that deep learning architectures are highly nonlinear and transform the available information into features from which a clear interpretation becomes challenging52. Therefore, the considerations we present below correspond to our understanding, something usually referred to as attribution in the literature53,54. For instance, Fig. 5 shows explainability scores that mark specific sections of the full waveform. Panel c highlights two explainability peaks very close to each other, one reasonably well aligned with the P phase arrival and one most likely with the S. This could be interpreted as the effect of two very different motion patterns affecting a given hillslope almost simultaneously. However, this could be the result of a number of interpretations. This is also the case for panel d. There, despite the similarity of the waveform with the one mentioned above, a relatively smaller explainability score can be seen in the early stages, followed by a much larger one in the late stages. This could be due to the different terrain and geological characteristics of the two sites, as well as the total shaking duration effect. A quick shaking, as intense as it may be, could still leave a slope unfailed. Conversely, a prolonged yet milder shaking could bring a slope to the brink of failure.

Focusing on the portion of the landscape these slopes occupy, Fig. 5 (panels f and g), a static PGV model identifies coseismic failures in slopes around 40° steep and with peak velocities of around 0.5 m/s (i.e., open and upper slopes, midslope and high ridges). Yet, slightly gentler slopes 30° with peak velocities centered around 0.25 m/s) are only predicted when using full waveforms, highlighting Mod3’s ability to predict failures occurring in the proximity of midslope drainages, valleys, and streams. These landforms, especially if far away from the source, only fail when considering the whole ground motion signal.

Although these are interesting observations, they still do not support near-real-time landslide hazard assessment tools. A number of reasons make this the case. Firstly, ground motion simulations require a relatively long time to generate, even when using high-performance computing facilities. Secondly, a good earthquake rupture model is usually not available right after an earthquake, thus limiting the quality of the synthetic waveforms. In relation to the quality, more could be said because coseismic landslides may also occur due to topographic amplification, a phenomenon that is dependent on the interaction between earthquake and landscape characteristics55. Therefore, to obtain a reliable description of the process, a 3D subsurface velocity structure, as well as the geotechnical characterization of the study area, may be required.

Therefore, in light of near-real-time requirements for disaster rescue operations, our Mod3 is still unsuitable at the current state of technology. This implies that we are and will still likely be largely dependent on peak-intensity models in the future to help mountainous communities that have suffered a large earthquake in a timely manner. However, further development to produce more reliable and fast ground motion simulations would definitely help make our approach operational.

Alternatively, scenarios could also be built prior to an earthquake occurrence. One could simulate several theoretical earthquakes and use the synthetic waveforms to obtain coseismic landslide scenarios that could be stored in an emergency response system56. Then, if and when an earthquake of similar characteristics would take place, the predicted scenario could be used to strategize disaster relief actions. The main limitations would boil down to the requirements for the numerical reproduction of shaking, especially in data-scare regions. In fact, the rupture geometry, energy release, and the subsurface structure are fundamental requirements for a reliable ground motion simulation. There are already challenges for data-rich situations, and they would become less and less reliable in regions with proportionally less information available.

Another fundamental element to be explored in the future lies in the size of coseismic landslides and the dependence on the full waveform characteristics. Frequency content and duration of ground shaking may alter the size of coseismic landslides57. For instance, higher frequencies exit hillslopes to the point of releasing small failures, and low frequencies exit much larger landslide bodies58,59. These arguments are not been tested yet in regional scale assessments exploiting the full waveforms. And yet, our results show that the use of full waveforms could enable a better prediction of landslide sizes and with it, the threat they pose to mountainous communities.

Aside from the long-term potential, the overarching theme related to the use of full waveforms to estimate coseismic landslides is where we believe research should mostly be dedicated to in the coming years. Future steps should involve testing a similar framework for different terrains, earthquake magnitudes, and rupture mechanisms. If analogous conclusions could be reached for different contexts, then the knowledge obtained could definitely be translated into better disaster responses in mountainous regions affected by large earthquakes.

Methods

The model in this study incorporates the entire ground-motion signal with morphometric parameters with a modified transformer neural network to include the terrain and lithological factors. In addition, we developed an explainable AI approach that enables us to understand how the model uses waveform information to predict landslides. This method allows both waveform and other predisposing conditions to be considered simultaneously. We then compared our model with three different models (benchmark models, see Table 2), which included intensity parameters and removed morphometry. The tested benchmark models included ground motion waveform only (Mod1), peak ground velocity only (Mod2), terrain, lithology, and ground motion waveform (Mod3), terrain, lithology, and peak ground velocity (Mod4). Furthermore, we developed an explainable artificial intelligence approach to understand the role of ground motion signals. The following section will further explain the details of each developed method.

Table 2 Input model branches and data for the developed waveform model and benchmark models
Full size table

Model definition and training

The existing transformer models25,60 only work with waveform data and do not include static variables, which are more common in geoscientific problems. In earth surface processes, many parameters are temporally varying (dynamic), whereas some stay the same over human timescale (static). In our case, ground motion is a dynamic variable, whereas the terrain properties are static. To resolve this problem, we modified the vanilla transformer neural network from Vaswani et al.60 to include static covariates.

Landslides (\(L\left(s,t\right)\)) are a spatiotemporal processes that are considered stochastic for modeling purposes61. In this case, let us assume that the landslide is a stochastic spatial process \(\left(L\left(s\right)\right)\) because we do not consider the multiple time frames to model a spatio-temporal process. Being a binary variable, a landslide can be represented by Bernoulli distribution as:

$$L\left(s\right)\sim {{\mbox{Ber}}}\left(p\left(s\right)\right)$$

Where the probability of landslide \(p\left(s\right)\in \left({{{{\mathrm{0,1}}}}}\right)\) is what we try to estimate as a landslide susceptibility. For this, the landslide susceptibility is a function of different terrain and geologic as well as seismic variables. The main distinction between those two variables are that terrain and geologic factors are static and does not change during an earthquake event while the seismic energy is dynamic and changes over the time. Therefore, we can define them as static covariates \({X}_{S}\left(s\right)={x}_{S}\left(s\right)\) and dynamic covariates as \({X}_{D}\left(s,t\right)={x}_{D}\left(s,t\right)\). Now the landslide susceptibility, defined by the probability of occurrence of landslide is given by: \(p\left(s\right)=\Pr \in (0,1):\Pr \{{{{{{\rm{L}}}}}}\left({{{{{\rm{s}}}}}}\right)=1{{{{{\rm{|}}}}}}{{{{{{\rm{X}}}}}}}_{{{{{{\rm{s}}}}}}}\left({{{{{\rm{s}}}}}}\right)={{{{{{\rm{x}}}}}}}_{{{{{{\rm{s}}}}}}},{{{{{{\rm{X}}}}}}}_{{{{{{\rm{D}}}}}}}\left({{{{{\rm{s}}}}}},{{{{{\rm{t}}}}}}\right)={{{{{{\rm{x}}}}}}}_{{{{{{\rm{D}}}}}}}\left({{{{{\rm{s}}}}}},{{{{{\rm{t}}}}}}\right)\}\). To model this we use the deep learning model which will represent the potentially highly non-linear function which estimates \(p\left(s\right)\) given the input variables.

Now, to design the deep learning model, let the encoding part of the transformer model from Vaswani et al.60 be \({\tau }_{\left(s,t\right)}\). The function \({\tau }_{\left(s,t\right)}\) takes the input data \({X}_{D}\left(s,t\right)\) and generates feature space over the spatial domain s as \(f{1}_{\left(s\right)}={\tau }_{\left(s,t\right)\left({X}_{D}\left(s,t\right)\right)}\), where all the processing for dynamic data occurs, such as multi-head attention and positional encoding. Then, let us assume there is a deep neural network \({\delta }_{\left(s\right)}\), which is a function of static covariates \(X\left(s\right)={x}_{s}\) and produces the feature space \(f{2}_{\left(s\right)}={\delta }_{\left(s\right)}\left({X}_{s}\left(s\right)={x}_{s}\right)\). We concatenate both feature spaces into one tensor \(f{3}_{(s)}=f{1}_{(s)}\oplus f{2}_{(s)}\), which is then passed to a decoding block of deep neural networks \({\eta }_{\left(s\right)}\) providing a final output as the probability of landslide occurrence \(p\left(s\right)\). Therefore, the final model \({{{{{{\mathcal{M}}}}}}}_{\left(s\right)}\) looks like \(p(s)={{{{{{\mathcal{M}}}}}}}_{\left(s\right)}=\eta (\tau ({X}_{D}\left(s,t\right))\bigoplus \delta ({X}_{s}\left(s\right)={x}_{s}))|{X}_{s}\left(s\right)={x}_{s},{X}_{D}\left(s,t\right)={x}_{D}\left(s,t\right).\) The parameters in all functions \(\tau (s,t),\delta (s),\eta (s)\) (therefore, \({{{{{\mathcal{M}}}}}}(s)\)) is then estimated through backpropagation using a binary cross entropy loss function62 \(\iota =-\left(L\left(s\right)\log \left(p\left(s\right)\right)+\left(1-L\left(s\right)\right)\log \left(1-p\left(s\right)\right)\right)\). Where, L(s) is the observed landslide over space and \(p\left(s\right)\) is the predicted landslide probability over space.

The function \({\tau }_{\left(s,t\right)}\) consists of three input waveform parameters represented in east–west (E–W), north-south (N–S) and up–down (U–D) directions and has a depth of two transformer blocks. Each transformer block consists of a set of sequential layers where input \({X}_{D}\left(s,t\right)\) goes through layer normalization and multi-head attention followed by a dropout layer creating vector \(v{1}_{\left(s,t\right)}\). The vector \(v{1}_{\left(s,t\right)}\) is then added with \({X}_{D}\left(s,t\right)\) to include the attention mechanism and is normalized through a normalization layer creating the vector \(v{2}_{\left(s,t\right)}\). Subsequently, \(v{2}_{\left(s,t\right)}\) flows through a feed-forward block of convolution, rectified linear unit, dropout, convolution, and rectified linear unit. Finally adding the attention layer from the previous part (\(v{3}_{\left(s,t\right)}=v{1}_{\left(s,t\right)}+v{2}_{\left(s,t\right)}\)) to create an output of transformer encoder making a new input \({X}_{D}{\left(s,t\right)}_{n+1}\), for the next block. This is repeated many times as the number of transformer blocks, and after that, the output vector \(v{3}_{\left(s,t\right)}\) is passed through the global average pooling layer, creating feature space \(f{1}_{s}\). The global average pooling layer therefore squeezes the temporal information into spatial only information allowing us to combine the dynamic variables with static variables.

The part of \({\delta }_{\left(s\right)}\left({X}_{s}\left(s\right)={x}_{s}\right)\) processes the input static data \({X}_{s}\left(s\right)\) sequentially through dense blocks consisting of a series of fully connected, batch normalization, dropout, and rectified linear activation units. In this model, we have eight blocks to process the input \({X}_{s}\left(s\right)\) to obtain \(f{2}_{s}\). With both \({{{{{\rm{f}}}}}}{1}_{{{{{{\rm{s}}}}}}},f{2}_{s}\) available, we further process through a series of blocks consisting of a fully connected network, rectified linear units, and dropout layers. Finally passing it through the sigmoid activation function to generate pseudo-probabilities in terms of \(p(s)\).

We trained the model with Adam optimizer63 and the binary cross entropy loss function. The optimizer started with a learning rate of 1e−3 and exponentially decayed every 10,000 steps by a factor of 0.95 until the model converged (for further details, see parameters in the provided code). The training data was generated by randomly selecting 70% of the receiver locations, and the remaining 30% were kept as the test set. Moreover, the training data was further divided into the subset of 20% for the validation set during the model training process to evaluate the model and stop the training before overfitting. This data selection is kept constant for the entirety of the research, making it consistent over benchmarks.

Since our developed model consisted of a deep neural network and transformer components, we designed it in such a way that both \({\tau }_{\left(s,t\right)}\) and \({\delta }_{\left(s\right)}\) components can be turned off. Multiple benchmark models were created by turning each component off and on with different input variables, while keeping the output variables and ground truth (\(p(s)\) and \(L(s)\)) the same. Table 2 lists the models, their respective components, and used input variables.

Evaluation framework

We evaluated the classification capacity of the model by computing multiple evaluation metrics common to statistics and machine learning39,64. To evaluate the model performance, we used the area under the curve (AUC) of the receiver operating characteristics curve (ROC), which is a well-accepted method to evaluate the model performance and fit65. The ROC curve is generated by evaluating the fit between \(L(s)\) and \(p(s)\) by using a confusion matrix for different probability threshold values in the range of [0,1]. ROC represents the relation between false positive rate (FPR) and true positive rate (TPR), which are calculated as the ratio of false positive with negative instances and true positive with true instances, respectively. Once the ROC curve is identified, the AUC is calculated as \({{{{{\rm{AUC}}}}}}={\int }_{0}^{1}{{{{{\rm{TPR}}}}}}\cdot d\left({{{{{\rm{FPR}}}}}}\right)\).

To evaluate the model performance on the validation set, we used different scoring methods designed for the classification problem: Accuracy score (ACC), F1 score, and intersection over union (IOU) score. The accuracy score is a ratio between the total number of correct predictions and the total number of samples. The F1 score is more robust than the accuracy score and is sensitive to false positives as well as false negatives. It is calculated as twice the ratio of the product of precision and recall over the summation of precision and recall (\(F1=2\cdot \frac{{{{{{\rm{precision}}}}}}\cdot {{{{{\rm{recall}}}}}}}{{{{{{\rm{precision}}}}}}+{{{{{\rm{recall}}}}}}}\)). Precision and recall are the ratios of correctly predicted positive observations to the total predicted positives and the ratio of correctly predicted positive observations to the total actual positives, respectively. IOU score, on the other hand, represents the overlap between the observed and predicted landslides and A higher IOU indicates better alignment between the predicted and ground truth. It is calculated as a ratio of true positives over the union of all instances predicted as positive (both true and false positives) and all instances that are actually positive (both true positives and false negatives).

Explainability

To understand how the waveform component in our input data \({X}_{D}\left(s,t\right)\) influences the model output \({{{{{\rm{p}}}}}}\left({{{{{\rm{s}}}}}}\right)\), we implemented an explainable approach. The explainable artificial intelligence based evaluation in landslide hazard modeling is recent yet meaningful approach to understand the influence of input covariates on model output66. The method is based on the work of Cisneros et al.67 and Shrikumar et al.53, where we calculate the influence scores \(S\) based on the gradient of p(s) with respect to input vector \({X}_{D}\left(s,t\right)\) where it is set to zeros (\({X}_{D0}\left(s,t\right)\)) for baseline gradient \({\nabla }_{b}=\frac{\partial {{{{{{\mathscr{M}}}}}}}_{s}\left({X}_{D0}\left(s,t\right),{X}_{S}\left(s\right)\right)}{\partial {X}_{D0}\left(s,t\right)},\) and actual values for instance gradient \({\nabla }_{i}=\frac{\partial {{{{{{\mathscr{M}}}}}}}_{s}\left({X}_{{Di}}\left(s,t\right),{X}_{S}\left(s\right)\right)}{\partial {X}_{{Di}}\left(s,t\right)}\). This gradient can be assumed as the regression coefficient (\(m\)) in the case of linear regression problem \(y={mx}+c\). Since our model is highly non-linear, a direct comparison of \(m\) cannot be made; thus, we compare their relative change to understand how the variable \(t\) influences the model output. For that, we take a relative ratio of the gradients, also considering the actual change in values as below:

$${{{{{\rm{S}}}}}}=\left({X}_{{Di}}\left(s,t\right)-{X}_{D0}\left(s,t\right)\right)\cdot \frac{{\nabla }_{i}}{{\nabla }_{i}-{\nabla }_{0}}$$

Notably, the score (\(S\)) here is calculated only for the waveform component and not for the constant variables because the influence of other covariates on landslide occurrence is well-known, and our focus is on understanding the role of ground motion waveform on landslide occurrences.