Cooling of hydrothermal fluids rich in carbon dioxide can create large karst cave systems in carbonate rocks

Abstract

Karst systems, comprising interconnected voids and caves, are ubiquitous in carbonate formations and play a pivotal role in the global water supply. Accumulating evidence suggests that a significant portion of the global karst is hypogenic, formed via rock dissolution by groundwater ascending from depth (rather than by infiltration from the surface), yet the exact formation mechanism remains unclear. Here we show that cooling of carbon dioxide-rich geothermal fluids, which turns them into highly corrosive agents due to their retrograde solubility, can dissolve and sculpt large caves on short geological timescales. A conceptual hydro-thermo-geochemical scenario is numerically simulated, showing cave formation by rising hot water discharging into a confined layer. Our models predict field observations characteristic of hypogenic caves, including enigmatic locations of the largest passages and intricate maze-like networks. Finally, we suggest that deep-seated carbon dioxide consumption during karst formation may constitute a link to the global carbon cycle.

Introduction

Karst systems, comprising interconnected voids and caves, both deep and shallow, are widespread in carbonate formations around the world. These cave systems played a crucial role from the dawn of the history of mankind, providing shelter and water supply^1,2. About 25% of the global population currently depends on water supply from karstic origin, and a large part of the global population lives on carbonate karst terrains (comprising >15% of the continental land surface)^2,3. The general mechanism responsible for the formation of karstic cave systems (speleogenesis) is the dissolution of the aquifer’s country rocks by infiltrating groundwater. Rock dissolution occurs either by descending (downward infiltrating) CO₂-rich meteoric waters, which commonly form near-surface caves, called epigenic karst caves^4,5,6, or by groundwaters ascending from deep sources (typically >1 km), that form so-called hypogenic karst cave systems^7,8. While epigenic caves are easily discovered, since they originate from the surface and often discharge via springs, hypogenic cave systems often form at depth and are usually hidden in deep rock formations until their exposure by erosion or tectonics^9,10.

Continuously accumulating evidence shows that hypogene karst forms in continental and oceanic crust at depths ranging down to several kilometers, and suggests that hypogenic karst is the globally dominant karst phenomenon^4,11. Hypogenic karst systems can be voluminous and complex, with cumulative length of passages of up to hundreds of kilometers and shafts reaching hundreds of meters in depth^4,8,11 (particularly, see a comprehensive report in ref. ¹¹, describing numerous extensive case studies and demonstrating the worldwide extent of hypogene karst). Studies indicate that hypogenic karst, which often forms by thermal brines originating deep within the crust, is linked to major geological processes such as: diagenesis, fluid-rock hydrothermal interactions, hydrogeology and global geochemical cycles^7,8,12. Hypogenic karst is also linked to a range of geoengineering applications, including management of water resources^4,10, geothermal energy^13,14, CO₂ geological storage¹⁵, ore exploration^12,16 and mitigation of induced-seismicity^17,18 and geotechnical hazards^8,19. Despite its importance, hypogenic karst remains enigmatic and sparsely studied, with only few quantitative modeling studies exploring its formation process^20,21,22,23. In this manuscript, we suggest a simple general mechanism for the formation of hypogenic karst systems in carbonate rocks. The proposed dynamic hydro-thermo-geochemical mechanism is demonstrated to drive large-scale dissolution and speleogenesis in the country rocks, reproducing the major morphological characteristics of hypogene caves. These results contribute important insights to the current debate regarding the formation mechanism of hypogenic cave systems and provide an explanation for their global abundance^{12,20,24,25,26}.

Previous studies commonly attributed the aggressiveness of groundwater which form hypogenic karst in carbonates, to mixing corrosion (i.e., mixing of CaCO₃ saturated solutions of different compositions to produce an undersaturated solution) and to condensation of undersaturated water on rock walls above the groundwater table, commonly involving corrosive sulfuric vapors (so-called condensation corrosion)^{22,27,28,29,30,31}. Here, we suggest a largely overlooked path to undersaturation: by the Cooling of Hydro-Thermal Fluids (abbreviated here as CHTF), and the increase of carbonate solubility with decreasing temperature (so-called retrograde solubility of carbonate minerals). The cooling of deep-origin hydrothermal fluids turns them into undersaturated solutions with respect to carbonate minerals, triggering rock dissolution. The CHTF mechanism was discussed in earlier studies (e.g., ref. ³²) but was considered negligible and only capable of producing diffuse and dispersed karst, and thus not likely to produce well-developed hypogenic karst and cave systems^10,12,33. In contrast to these earlier estimates, the present study shows that the CHTF mechanism, in particular in fluids that are enriched in CO₂, which enhances the retrograde effect, produces highly aggressive solutions that can drive continuous dissolution and form large hypogene cave systems on geologically short timescales. It is also demonstrated that the CHTF mechanism can produce the observed natural cave morphologies, including the maze-like pattern of the passages characteristic of hypogenic caves.

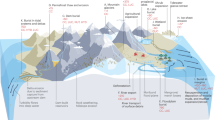
Inspired by a case study of a large group of hypogene caves in a confined carbonate aquifer⁹, we propose a scenario for hypogene karst formation through CHTF, which requires two main ingredients: focused hot incoming CO₂-rich water and a confined and permeable (water saturated) soluble layer. Figure 1a describes this scenario, in which groundwater originates from a deep aquifer (>1 km), where it is heated and considerably enriched with CO₂ (i.e., a few folds compared to surface values)^12,22,34. This hot groundwater ascends in a pipe-like manner through permeable sub-vertical faults and fractures, driven by artesian or tectonic pressures and buoyancy forces^8,35. Such pipe-like water flow arises either at fault or fracture-plane intersections^36,37,38,39 or at flow conduits that naturally occur on the rough surfaces of fractures^14,40,41. The rapidly ascending fluids maintain their heat and temperature until they approach a flow barrier (e.g., an aquiclude layer), which diverts their flow sideways and radially around the conduit within the permeable, water saturated, bedding horizon of the soluble rock layer^42,43. During their radial flow, the fluids cool rapidly by transferring heat to the rock below and above. Given the retrograde solubility of carbonate minerals, the rapidly cooling groundwater becomes undersaturated, significantly increasing the solubility of the aquifer’s rocks, causing intensive rock dissolution.

Fig. 1: Conceptual model for speleogenesis by cooling of hydrothermal fluids.

The formation of hypogene caves depicted by (a) a conceptual model and (b) the field appearance. a Thermal, CO₂-enriched groundwater upwells rapidly through a pipe-like conduit pathway in a fault and/or fractures (red arrows). Due to a confining low-permeability layer, flow is diverted sideways to permeable bedding horizons within a soluble layer (dashed brown line), where radial spreading slows it down. The temperature of the water remains high during the rapid flow through the narrow fault conduit and then drops quickly when the water slows during its radial flow and transfers heat to the rock below and above (color-gradient arrows). The rapid cooling of hydrothermal fluids (CHTF) leads to large undersaturation with respect to calcite, inducing localized dissolution of the rock and cave formation (black ellipses). b Field appearance of hypogene caves in carbonate rocks located near Jerusalem, Israel (photograph by R.R.). A confining low-permeability layer overlays the main karstic layer (bordered by dashed lines).

The components required for the proposed scenario (i.e., elevated temperature and CO₂ concentration at depth, ascending flow through fractures and faults, and confinement of the soluble layer) are ubiquitous and globally widespread. This mechanism likely played a major role in forming cave systems worldwide, including very extensive hypogene karst systems like those in the Black Hills of South Dakota^32,44, the Buda thermal karst cave systems in Hungary⁴⁵, and the cave systems throughout Europe^46,47,48,49, Brazil^50,51, Southern Africa⁵² and in many other locations worldwide¹¹.

This work presents results from four models, that build one on top of the other. The first model is conceptual, providing the basic setup of the investigated reactive geothermal system (Fig. 1a). The second tier is a geochemical model used to evaluate the geochemical driving effect in inducing substantial dissolution during the cooling of geothermal waters. The third tier is numerical model which describes heat transport and dissolution in a confined-bedding horizon, demonstrating the feasibility of localized and continuous dissolution required for forming a cave [the Axisymmetric Horizon Dissolution model (AHD)]. The last tier is a network model, which uses the physics and parameters from the previous models to simulate channelized dissolution and cave-pattern formation (the AHD and network models are described in the Methods section).

Results and discussion

The applicability of the conceptual model to the case study

The conceptual model in Fig. 1a is consistent with the configuration and morphological features of many hypogenic cave systems (e.g., refs. ^{11,32,44,45,46,47,48,49,50,51,52}). In particular, its setting applies to the group of caves in our case study⁹ (Fig. 1b). This group comprises dozens of extended caves located along the fold system adjacent to the Dead Sea Transform in Israel. Large rooted faults at the base of the folds are assumed to facilitate the upwelling of thermal flow in a pipe-like manner^{14,36,37,38,39,40,41}. The caves commonly developed along prominent bedding horizons in limestone formation located at the upper part of a massive limestone and dolostone layers (>400 m thick), which is overlaid by low-permeability layers comprising mainly soft chalk and marl horizons-rich limestone (i.e., an aquiclude flow barrier). The cave systems usually present a maze-like pattern with occasional chamber caves. The maze caves were inferred to have developed via relatively uniform dissolution of a network of conduits, formed by the intersection of the bedding horizon and subvertical fracture network^9,53.

The groundwater that formed this karst probably originated and upwelled from a large, deeper artesian sandstone aquifer (located at a depth of 1 to 2 km below the limestone and dolostone sequence), as suggested by mineral assemblages and the temperature and composition of local recent spring systems⁹. However, a shallower origin and upwelling from the carbonate aquifer, cannot be excluded (<1 km depth)⁹. Tectonic and hydrological events constrain the karst-formation period to within a window of several million years (Oligocene–early Miocene). Karst formation was terminated by the Neogene uplifting and deepening of the Dead Sea Transform, which disconnected the far-field groundwater flow, and caused water-level drop and cave dewatering. A detailed description of the caves and their geological setting is provided by Frumkin et al.⁹ and references therein.

The geochemical drive for dissolution

The potential for karst formation by carbonate rocks interaction with groundwater depends on carbonate solubility, c_s, and the evolving undersaturation in the system. In our system the important parameters controlling carbonate solubility are temperature and partial CO₂ pressure (PCO₂). In order to evaluate carbonate solubility as function of these parameters, we conducted simulations with the PHREEQC (v.3.7.0) software package⁵⁴. We assume that the target carbonate rocks interacted with groundwater rising from deep aquifers in a closed system (no gas exchange). Two types of source aquifers are investigated, representing two common sedimentary rock types: carbonate and sandstone (for calculation details see the Geochemical Calculations section in Methods).

The thermodynamic predictions for PCO₂ in these two aquifer types (lines in Fig. 2a) agree with the range of field data measured in natural sedimentary aquifers comprising carbonate and clastic rocks (brown region in Fig. 2a)^34,55. The CO₂ partial pressure, PCO₂, of porewater in confined aquifers increases with both temperature and pressure (i.e., with depth). Figure 2a shows only PCO₂ versus T, however p and T values used in simulations are correlated, since we assume hydrostatic and geothermal depth-dependence. Elevated PCO₂ of groundwater in deep-seated aquifers is maintained over time by large CO₂ fluxes originating, for example, from deep magmatic bodies and from the decomposition of sedimentary organic matter (presumably leading to the typical much higher PCO₂ in sedimentary compared to crystalline rocks)^22,34,56. Figure 2a also shows that, for T ≳ 30 °C, PCO₂ increases much faster with p and T in sandstone aquifers than in carbonate aquifers (cf. red and blue lines). Next, the saturation concentration of calcium ions in water (solubility), c_s, was calculated as function of temperature, T, and initial levels of PCO₂, assuming a sandstone aquifer, which is the likely source for groundwater that upwelled and formed the caves in our case study section. Figure 2b shows that c_s depends strongly on the initial PCO₂ and temperature (in agreement with previous work, e.g., refs. ^10,33). At high initial PCO₂, c_s increases dramatically with reduction of temperature (due to retrograde solubility), which indicates a highly aggressive dissolution process during cooling.

Fig. 2: Geochemical Calculations.

a Theoretical predictions of PCO₂ as function of temperature for water in equilibrium with clastic sandstone (red line) and carbonate (blue line) confined aquifers. In simulations, each T value was used with its corresponding p value, according to crustal depth-dependence (see Methods section). The brown region depicts the range of field data for sedimentary (carbonate and clastic) aquifers (modified from refs. ^34,55). For pore water at T ≳ 30 °C, PCO₂ progressively increases in sandstone aquifers above that in carbonate aquifers, with PCO₂ reaching over 0.5 MPa for T ≳ 85 °C (see point (i) on dotted lines, corresponding to the most corrosive and extreme conditions of the batch calculation in main text). b Thermodynamic calculations of saturation concentration of calcium ions as a function of temperature, c_s(T), for different initial values of PCO₂. Note that calcite solubility, c_s, depends on initial PCO₂: a greater initial PCO₂ corresponds to a greater c_s and the potential of the fluid to induce aggressive dissolution due to the retrograde solubility of calcite and the increase of c_s with decreasing T. Here, in the numerical calculations we consider upwelling from a sandstone aquifer and inlet fluid temperature of T_in = 60 °C and PCO₂ ≈ 0.03 MPa (point (ii) on dashed lines).

These results can be then used to show, that at reasonable environmental conditions (e.g., water flow, Q, of 1 m³ day⁻¹ and ΔT = 65 °C, where ΔT is the temperature difference between incoming water and that of the host rock, typical of geothermal fluids sourced from depth^35,57,58), it takes less than 300 years for the corrosive groundwater to form a hypothetical 6 m-diameter hemisphere-shaped cave within a limestone rocks sequence. This batch calculation estimates the volume of dissolved solid to be ${V} = {Q} {t} {\Delta} {c}_{s} {m}_{{{\mathrm{{Ca}}}{CO}_{3}}} { \rho_{\rm r}^{-1}}$, where t is the time, Δc_s is the difference between the solubilities under cold and warm conditions, ${m}_{{{\mathrm{{Ca}}}{CO}_{3}}}$ is the molar mass of calcite, and ρ_r is the rock density (ρ_r = 2200 kg m⁻³). The prediction of speleogenesis in 300 years assumes that the groundwater came from a sandstone aquifer with PCO₂ = 0.5 MPa, which corresponds to a temperature ≳ 85 °C and a depth of about 3 km (point (i) on the dotted line in Fig. 2a). Under these most corrosive conditions, the change in solubility, Δc_s as the water cools from 85 to 20 °C, exceeds 12 mmol kg⁻¹ H₂O (point (i) on the dotted line in Fig. 2b shows c_s(T = 85 °C) ≈ 6 mmol kg⁻¹, compared to 18 mmol kg⁻¹ at 20 ^oC). For comparison, under atmospheric pressure and epigenic karst conditions, a typical value of c_s is much smaller: about 2 mmol kg⁻¹ H₂O⁶.

Figure 3a shows the calculated time needed to form a 6-m diameter cave, as function of PCO₂ and T of the incoming water (used to calculate ∆c_s from the results of Fig. 2b). The calculations demonstrate that even for a small temperature difference of ∆T = 5 °C, and with PCO₂ as low as 0.001 MPa, the hypothetical cave can form within several tens of thousands of years. To simulate our case study, we consider upwelling from a sandstone aquifer about 2 km deep and with T = 60 °C and PCO₂ ≈ 0.03 MPa, that discharges into a shallow limestone aquifer and cools to 20 °C (see Table 1). From Fig. 3a we calculate that cave formation in our case study takes a few thousands of years, and generally extensive caves may form within tens of thousands of years or less, which is a very short geological time interval. This finding is in contrast to the prevailing view in literature, which puts this timescale at millions of years^7,24, some two orders of magnitude longer. Thus, it appears that the extensive cave systems observed worldwide in the geological section could have formed using the geochemical driving force of cooling hydrothermal waters under very mild and ubiquitous hydrogeological conditions: a small drop in temperature and a small PCO₂ excess.

Fig. 3: Results of the geochemical and numerical (AHD model) analyses.

a Calculated plots of time for dissolving a 6-m-diameter hemisphere-shaped hypothetical cave in limestone rock, as function of the PCO₂ and temperature of the incoming groundwater. The cave is fed by slowly flowing groundwater (1 m³ day⁻¹), which cool by a different degree: ∆T = 65, 30, and 5 °C (see text). The plots show that a cave can form within 300 yr (dashed brown line) under favorable conditions, or in several tens of thousands of years at very mild conditions. b–d Results from the AHD model for temperature, T, degree of undersaturation, θ, (see text for definition) and cave profile and aperture, h (the vertical distance between the curves) versus the radial distance, r, from the inlet, at different times during cave development (legend in b). b The temperature profile shows rapid cooling of the water, reaching quasi-steady thermal state in about 50 yrs (see text). c θ (which is 0 in the incoming water), increases sharply with distance due to high cooling and advective rates, reaches a maximum, and then decreases downstream because of the dissolution reaction. d The cave aperture (grayscale), h, increases substantially with time and distance from inlet, r. In accordance with θ, h develops a pronounced maximum a few meters from the inlet.

Table 1 Parameter values.

Cave formation by cooling and localized dissolution

The next model in our hierarchy is the Axisymmetric Horizon Dissolution (AHD) model, which solves the heat and reactive flow equations (Eqs. 1–8) as described in the Methods. In this setting a hot fluid flows through a thin horizon, dissolving it via the CHTF mechanism, eventually forming caves. Results of the AHD model show that during the radial flow within the horizon, the geothermal groundwater cools relatively quickly (from 60 °C at the inlet to 25 °C at r ≈ 10 m; Fig. 3b). The rapid cooling is promoted by the radial flow away from a localized low-discharge source, which allows the fluid to reach a quasi-steady thermal state after about 50 yr [see, e.g., the solution for a continuous point source in infinite space given in ref. ¹³ (Eq. 3.24, pg. 114)]. The fluid is hot and saturated with respect to the calcite at the inlet, c = c_s(T_in), where T_in is the inlet temperature, but as the fluid moves away from the inlet, the undersaturation, θ, first increases with r, and then, after several meters, reaches a maximum and decreases thereafter (Fig. 3c; here, θ = [c_s(T(r)) − c(r)]/∆c_s0, where ∆c_s0 = c_s(T₀) − c_s(T_in), and T₀ is the initial temperature of the host rock). Undersaturation along the flow path is controlled by the interplay between three variables: (I) dissolution that reduces undersaturation, (II) progressive cooling that increases undersaturation, and (III) advection that transports reaction products (i.e., calcium ions) outward and helps maintain undersaturation. Note that the advection effects decay with distance as 1/r.

The high advection and cooling rates near the inlet cause a buildup of undersaturation (Fig. 3c). Further downstream, cooling and advection rates are much lower, and undersaturation decreases with r due to the dissolution reaction. Accordingly, the cave profile develops a pronounced maximum several meters from the inlet (Fig. 3d). Over time, the widening cave aperture, h (the vertical distance between the lines, indicated by the gray regions in Fig. 3d) results in a slowdown of diffusion across the aperture. Given that the reaction is transport-limited [see Eq. 5], this reduces the dissolution rate, which in turn leads to the progressive buildup of undersaturation, with the maximum undersaturation shifting downstream (Fig. 3c).

The flow rate, Q, significantly affects karst formation, particularly in terms of the geometry of the dissolution cavity, as demonstrated by the plots of the degree of dissolution focusing, η, versus total fluid volume, V_f, discharged over time t (V_f = Qt; see cave shapes for three different values of Q in Fig. 4). The degree of dissolution focusing, η, is defined as the aspect ratio η = h_p/l_v, which is the ratio of the maximum cave height (h_p) to its length along the flow direction, r, (l_v) for h > 1.01h₀, where h₀ is the size of the initial aperture of the bedding horizon (see Fig. 4). The plots show that η decreases (caves become more elongated) with increasing volumetric flow rates. This is because (I) a higher Q transports heat further downstream, leading to more gradual cooling and undersaturation profiles; and (II) a higher Q accelerates the advection of undersaturated fluid, promoting dissolution farther from the inlet.

Fig. 4: Flow rate effect on the evolving cavity geometry.

Cavity aspect ratio (or degree of dissolution focusing), η = h_p/l_v, versus the integrated fluid discharge volume, V_f, over time interval t (V_f = Qt). The plots are for three different volumetric flow rates Q = 1, 2, and 4 m³ day⁻¹ for t = 1 to 20 kyr. The curves show that lowering Q increases η, indicating increasingly localized dissolution, as depicted by the three-dimensional visualizations of the caves after 20 kyr (the vertical cave dimension, h_p, is exaggerated by a factor of 30 relative to the cave length, l_v).

Timescales for speleogenesis and origin of thermal water

The results indicate that speleogenesis and the formation of human-size passages due to CHTF in limestone rocks occur over timescales ranging from 300 years to several tens of thousands of years (Fig. 3a, d). The timescale for hypogene speleogenesis in dolomite rocks may be similar or somewhat slower, depending on the PCO₂ of the water: dolomite dissolution rate is typically lower by about one order of magnitude than that of limestone⁵⁹, thus under relatively high PCO₂ conditions, dissolution of dolomite will remain transport-limited [see Eq. 5] and the timescale will be comparable to those of limestone. However, for relatively low PCO₂ the timescale will be longer approximately by one order of magnitude compared to speleogenesis in limestone (providing an upper bound timescale).

The predicted timescale range is comparable to (and even shorter than) the typical timescales of epigenic speleogenesis^6,10. The short timescale associated with the CHTF mechanism leads us to suggest a further hypothesis, that will be tested later in this paper: given reasonable time spans of a few tens of thousands of years or less, the CHTF mechanism may form voluminous hypogenic maze-cave systems, as known worldwide, with cumulative passage lengths of hundreds of kilometers (e.g., the Jewel and Wind caves in South Dakota³²). This contrasts with the general dogma, rooted in earlier works, that estimated a much longer timescale of 10⁶ yr for hypogene cave formation by this mechanism^10,12,24. Specifically, early calculations by Palmer (ref. ¹⁰, pg. 18) of dissolution due to rising thermal waters assumed rather low cooling rates and thermal gradients (5 °C 100 m⁻¹). He concluded that “only under the most favorable conditions can dissolution by cooling of thermal water produce caves of traversable size. Even then, times on the order of 10⁵ to 10⁶ yr are required.” For comparison, the relevant thermal gradients in our simulations are the strong radial gradients away from the inlet, which can reach 35 °C 10 m⁻¹ (Fig. 3b).

The geological setting of our case study suggests that the geothermal fluids that formed the caves ascended from a deep sandstone aquifer^9,60, which is hotter and its groundwater has a substantially higher PCO₂ than the overlying carbonate aquifer (see Fig. 2a). Geological constraints suggest the caves in our case study formed within a time window of several million years or less⁹. According to our calculations, this time interval far exceeds the time required for the high PCO₂, high-temperature groundwater ascending from the deep sandstone aquifer to form similar-sized caves in the case study area. The time window of several million years even suffices for lower PCO₂ and temperature groundwater, originating from the shallower carbonate aquifer, to form these caves. In fact, our calculations indicate that these caves may have formed within the geologically constrained timeframe, even by groundwater that was only a few degrees warmer than the country rocks.

Fundamental conditions for the formation of caves by the CHTF mechanism

Localized dissolution and hypogene cave formation require both (I) a substantial physico-geochemical driving force (cooling and high PCO₂) and (II) an appropriately confined hydrogeological setup, as described above (e.g., Fig. 1a). Under these conditions, upwelling pipe-like flow spreads radially within the confined layer and quickly cools, inducing the speleogenesis observed along bedding horizons.

In contrast to our confined setting, previous models of hypogene karst assumed unconfined conditions for which thermal flow upwells through a fault and discharges at the surface as springs. These studies predict diffuse dissolution^33,61 or localized dissolution only near the surface¹⁴. We argue that the confined hydrological conditions, which our conceptual model requires, are ubiquitous: ascending hydrothermal flow often encounters a confining layer on its way upward through a thick heterogeneous sedimentary sequence^11,12. In fact, hypogene cave systems located immediately under or in close proximity to confinement are prevalent worldwide^{32,44,45,46,47,48,49,50,51,52}. Furthermore, one may also ask whether unconfined flow near Earth’s surface, which often cools rapidly (due to proximity to the cooled surface), promotes localized dissolution^14,33? This is unlikely since CO₂ outgassing at shallow depths, close to the surface, is expected to drive supersaturation with respect to calcite and thus promote precipitation instead of dissolution (e.g., speleothems formation), as observed in many caves^6,29.

Cave morphology and pattern formation

This section shows that the characteristic cave shapes predicted by the AHD model are consistent with field observations and briefly analyzes the formation of the patterns of cave passages. Small-scale morphologic features that are characteristic of hypogene processes (e.g., smooth walls, cupolas, and solution pockets) are usually inconclusive indicators^24,62 and thus are not discussed here.

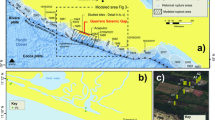
At most cave locations it is impossible to identify cave feeders (water inlets) because they are covered by debris and sediment. However, such cave feeders have been identified and carefully mapped in two hypogene karst systems, the Ashalim and Berenike, which are within the area of our case study^60,63 (Fig. 5). This allows us to compare the results of the numerical model with the morphology of these caves. The Ashalim cave includes feeders and dissolution features along a prominent oblique fracture or fault (dash-dotted red line in Fig. 5a), comprising the backbone of the three-dimensional-maze cave⁶⁰. While feeders and dissolution along the fracture appear clearly in many parts of the cave, the largest chambers and their ceiling peaks (see A.1–A.5 in Fig. 5a) are located away (up to 20 m) from the fracture and feeders. Similarly, the Berenike cave reveals a characteristic convex profile with the most spacious region (see B.1 in Fig. 5b) appearing approximately 10 m from the inlet, with diminishing passage sizes further downstream⁶³. These previously enigmatic findings are consistent with the results of our numerical model, which predicts that the maximum cave height is several meters from the feeder (Fig. 3d).

Fig. 5: Morphology of two hypogenic caves with identified feeders.

a Plan view (normal to the z direction) of the Ashalim cave where feeders are visible at the lower level along a fracture (dash-dotted red line). Note that the largest chambers (denoted A.1–A.5) and their maximum ceiling height (not shown) are located 2 to 20 m from the fracture and feeders. The gray zones mark overlapped lower levels⁶⁰. b Plan view of the upper level of the Berenike cave (top) and its vertical profile a-a′ (bottom). Note that the largest hall (denoted B.1) is located approximately 10 m from the feeder (red region), with the passage size gradually decreasing downstream⁶³.

Finally, we present results from our network model (described in the Methods, Network Model sections), which applies an extended version of our AHD numerical model to a point injection of geothermal fluid (red dot in Fig. 6a) flowing into a network of conduits in a fractured bedding horizon. The network model simulates dissolution of the conduits, considering CHTF as the source of aggressiveness of the solution and uses the fact that the temperature distribution rapidly becomes almost time-invariant (Fig. 3b). The resulting maze pattern of the passages, which emerges in the simulation (Fig. 6a), is a typical morphological characteristic of hypogene karst caves observed worldwide^12,24, as demonstrated, e.g., by the Chariton cave map⁹ (Fig. 6b; we note that a maze pattern appearance by CHTF is also supported by the analysis in ref. ¹⁰, pg. 18).

Fig. 6: Maze cave pattern formation.

a Plan view (normal to the z direction) of simulation results. The simulated maze developed over 43 kyr. Results are from a network model for dissolution by cooling hydrothermal fluids (CHTF) within a fractured bedding horizon (the thin gray lines represent initial model fractures, the red point marks the inlet, and black represents passages ≥1 m wide). Note that the simulation produces a typical maze-like pattern characterized by numerous closed loops. See in Supplementary Fig. 4 the progression of speleogenesis up to the final state shown in panel (a). b A map of Chariton cave showing its typical maze-like pattern (feeders were not identified)⁹. c Schematic presentation of a branched network pattern typical of epigenic caves. These branched-network caves develop from many source points (recharge zones) at the surface, that interact with the carbonate country rocks, forming a drainage-basin-like passages pattern that resembles a river and its tributaries^4,5,6. d Schematic diagrams of the THCO model (see text).

Maze-pattern caves differ notably from other speleological patterns and especially from the characteristic ramified branched-network patterns of epigenic karst, which are not evident in hypogenic karsts^5,10,12 (see Fig. 6c). Several alternative and long-debated mechanisms have been proposed for maze cave formation (summarized in refs. ^10,24). If the cave is hydrologically linked to the surface (i.e., epigenic origin), then mazes may form as a result of intense flooding, leading to the uniform dissolution of a fracture network^64,65. Other mechanisms involve diffuse and distributed recharge to the cave-forming layer^{10,12,23,24,66}, such as the commonly invoked concept of Transverse Hypogenic Cave Origin (THCO)^23,67,68.

According to the THCO model, an ascending fluid forms a hypogene maze within a soluble rock layer sandwiched between permeable but insoluble rock layers (Fig. 6d). This setting sustains an upward-distributed flow within the soluble strata and precludes the channelized flow that can develop due to preferential dissolution^5,7. The vertical and distributed flow discharges via multiple feeders, enlarging all major fractures in the soluble layer at comparable rates. The best-known example described by the THCO model is the giant gypsum caves in Ukraine⁶⁷. However, this mechanism often cannot explain the hypogene-maze-cave formation, such as in aquifers confined by an impermeable caprock layer, or the formation of caves in soluble carbonate rock successions (see, e.g., refs. ^{32,44,45,46,47,48,49,50,51,52}). Furthermore, in many cases, the THCO model is not supported by field observations because multiple ceiling and floor feeders are not observed^9,11,53. Thus, the geological setting of the CHTF mechanism proposed here for the formation of maze caves (i.e., by cooling of CO₂-rich hydrothermal fluids discharging from a feeder within a confined aquifer) is apparently more general and ubiquitous and thus is likely to have formed many of the hypogenic karst systems worldwide.

Guided by the results of Fig. 3, the maze pattern in Fig. 6a was obtained by using a relatively low volumetric flow rate (2 m³ day⁻¹), which is typical of geothermal fluids sourced from depth^35,57,58. For higher flow rates, a more uniform maze structure develops around the inlet, whereas lower flow rates, and diffusion-dominant transport, produce caves dominated by large chambers. The formation of large chambers in the simulation (see bulky black regions in Fig. 6a) results from the merging of adjacent passages and resembles some of the halls observed in natural maze caves⁹ (see, e.g., Fig. 6b). Finally, note that the formation of a maze pattern in the simulations requires only that the initial fractures be hydraulically connected. The spatial distribution of these initial fractures mainly controls the pattern properties (e.g., number of loops) and their statistics. Finally, we note that the maze pattern presented in Fig. 6a was attained after 43 kyr of dissolution without reaching a steady-state. Considering longer times and/or several feeders and higher flow rates, may explain the formation of the giant maze caves known worldwide with cumulative passage lengths of hundreds of kilometers (e.g., the Jewel and Wind caves in South Dakota³²).

Potential interaction of the CHTF mechanism with other speleological mechanisms

One may ask how other hypogenic karst formation mechanisms, in particular mixing corrosion and condensation corrosion, interact with CHTF. With regards to mixing corrosion, it is questionable if it may substantially enhance speleogenesis by CHTF in the setup of Fig. 1a. This is because the two mechanisms are likely to operate at different regions in the aquifer. While mixing corrosion acts at the front of the invading fluid plume (where a mixing fringe develops that will migrate further downstream with time, see, e.g., ref. ²²), dissolution by CHTF mainly takes place near the inlet, where the cooling rate is highest (i.e., front vs gradient mechanisms). Interaction with condensation corrosion is also not expected, since the CHTF mechanism operates at a fully water-saturated medium. However, speleogenesis by CHTF may be further enhanced if the ascending fluids arrive already undersaturated with respect to the cave-forming rock layer (depending, e.g., on lithology, fluid composition and flow conditions)^12,24.

Implications to the carbon cycle

Via groundwater-carbonate rock interactions, induced by CHTF, dissolved CO₂ can be entrapped as carbonate alkalinity in groundwater (e.g., CaCO₃ + CO₂ + H₂O = 2HCO₃⁻+Ca²⁺) and reduce CO₂ outgassing from the continental crust into the atmosphere⁶⁹. Particularly, dissolved CO₂ may interact with the country rocks and cause either dissolution or outgassing which may trigger calcium carbonate precipitation (e.g., speleothems formation). However, the higher the carbonate alkalinity that was produced by the dissolution process, the lower the amount of CO₂ that will escape to the atmosphere (see detailed explanation in ref. ⁷⁰). Since hypogene karst may lead to very large and extensive porosity change in carbonate aquifers^10,12 over timescales of tens of thousands of years (as shown here), this may affect the mid-term global carbon cycle: longer than the fast biogenic pathway but presumably shorter than the glacial-interglacial timescale. Interestingly, while karst formation by the cooling of CO₂-rich thermal flows may act as a net CO₂ sink, karst formation by rock interaction with volcanic strong acid (e.g., sulfuric acid), may act as a net CO₂ source⁶⁹. The opposite effects of these two mechanisms on the net CO₂ flux from the shallow continental crust and its impact on the global carbon cycle, remain subjects for future research and evaluations.

Summary and conclusions

The geological, geochemical, and theoretical evidence provided here suggest a rather simple hydro-thermo-geochemical mechanism for the formation of globally abundant large hypogenic karstic cave systems. According to this mechanism, CO₂-rich geothermal groundwater rapidly ascends from depth in a preferred, high-permeability flow path (such as provided by intersecting faults). If the ascending hot flow reaches a low-permeability layer, which confines a carbonate aquifer, the flow deflects laterally and radially within this aquifer. The slow radial flow within the aquifer promotes rapid cooling of the fluid. Upon cooling, carbonate solubility increases (owing to its retrograde solubility and the CHTF mechanism), so the water induces rock dissolution and cave formation at relatively short geological timescales, e.g., tens of thousands of years, facilitated by the typically high PCO₂ levels of geothermal fluids. Model simulations of this scenario may explain a previously puzzling morphology, whereby the largest openings form at some distance away from the inlet. Model simulations also explain the formation of many enigmatic cases of hypogenic maze caves, e.g., in confined conditions and soluble rock successions. The geological conditions for operating this mechanism are ubiquitous in the global crust, and may be applicable to many large maze-cave systems around the world, such as in the Black Hills of South Dakota³², the Buda thermal karst in Hungary⁴⁵, and many others¹¹.

From a wider viewpoint, the results suggest that Earth’s geothermal heat loss by upper-crust advective circulation of fluids⁵⁷, in conjunction with the fluxes of deep-seated CO₂, may induce dissolution of carbonate strata in upper continental crust, to form extensive karst. In turn, this process may also reduce CO₂ outgassing from the continental crust into the atmosphere and constitute a link to the carbon cycle⁶⁹. Finally, the globally common environmental conditions which may trigger the formation of extensive hypogene speleogenesis, may stimulate a re-evaluation of many other related issues in geoscience, e.g., diagenesis, hydrogeology and geochemical cycles.

Methods

In this section, we describe the methodology and provide details about hierarchical model tiers. We begin by explaining the geochemical calculations and analysis, followed by a comprehensive description of the AHD and network numerical models, including setup, equations, initial and boundary conditions, and numerical scheme or implementation. Table 1 detailing the physical parameter values used in the simulations. Supplementary Table 1 summarizes the notation used in this work.

Geochemical calculations

Geochemical simulations, whose results are presented in Fig. 2, were conducted with the PHREEQC (v.3.7.0) software package⁵⁴ in order to evaluate the potential for karst formation by carbonate rocks interaction with groundwater. Calculations assume a confined aquifer and closed system conditions, at which no degassing occurs (e.g., this requires for PCO₂ = 0.1 MPa the existence of fresh groundwater head higher than 10 m). In order to simulate the appropriate conditions for this study, we made modifications to the PHREEQC script from ref. ⁵⁵, mainly by changing the initial conditions of the solution, rock composition and PCO₂ (see compositions in Supplementary Methods 1). We begin with a surface temperature of T₀ = 20 °C and an atmospheric pressure of p = 0.1 MPa and elevate p and T according to a geothermal gradient of 20 °C·km⁻¹ and hydrostatic pressure of 10 MPa·km⁻¹ (100 bar·km⁻¹). The numerical calculations in Fig. 2a compare upwelling from a sandstone aquifer and a carbonate aquifer (red and blue lines, respectively). Point (ii) marks our case study conditions (inlet fluid temperature of T_in = 60 °C and PCO₂ ≈ 0.03 MPa) for water originating from the sandstone aquifer. Under these conditions, the saturation concentration of calcite can change by ∆c_s ≈ 3 mmol kg⁻¹ H₂O when cooled to 20 °C, approximately twice the ∆c_s of groundwater originating from a carbonate aquifer³³.

For completeness, we also tested the effect of groundwater salinity on the solubility of the aquifer’s carbonate minerals (e.g., calcite), which demonstrated a very small effect. For example, an increase in groundwater salinity by a factor of 10 (reaching a concentration equivalent to 5% of seawater salinity) has only a minimal effect on the calculated solubility of calcite (see Supplementary Note 1).

AHD model: setup

In accordance with the conceptual model of Fig. 1a, we construct the numerical AHD (Axisymmetric Horizon Dissolution) model depicting a simple physical system (Fig. 7): fluid discharges through a central inlet of a radius r₀, representing channelized upwelling. The fluid enters radially into a permeable bedding horizon at a constant temperature T_in and volumetric flow rate Q. In the horizon, we assume axisymmetric flow and dissolution (an analysis of channelized flow and dissolution is made using the network model, described in the Methods, Network Model sections). Furthermore, flow in the rock matrix is neglected because we assume orders-of-magnitude contrast in permeability^5,64. Basal heat flow and the initial background geothermal gradient are assumed negligible compared to the heat input of the ascending fluid. The low-permeability caprock is sufficiently thick to act as a thermal insulator, so heat transfer to the surface is negligible. When this is not the case, the cooling rate increases, and dissolution and speleogenesis will take place closer to the inlet.

Fig. 7: Numerical AHD model setup.

Schematic diagram of AHD model geometry and its settings: (a) fluid discharges from a pipe through an inlet of radius r₀ (red point) with total flow rate Q and temperature T_in. The flow is distributed radially, where it cools by transferring heat to the rock below and above (color-gradient arrow). b Heat transport in the bedding horizon and the rock and its effect on calcite solubility (magnified). Heat transport is governed by conduction in the rock (Eq. 1) and by advection-conduction equation in the fluid (Eq. 2), with a heat exchange term (Θ) accounting for conduction between the rock and fluid (Eq. 3). As the fluid cools, the concentration at saturation (solubility), c_s(T), increases (Eq. 7), inducing carbonate dissolution, which alters the horizon aperture, h (Eq. 8). c The calcite dissolution reaction at the horizon surface. An advection-diffusion-reaction equation (Eq. 4) assumes fully transport-limited dissolution of Ca²⁺ ions that depends on the surface-to-fluid mass-transfer coefficient, k(h).

The model further assumes closed-system conditions and the following: fluid pressure, p, in the aquifer exceeds the CO₂ partial pressure, PCO₂, in the thermal water (p > PCO₂), so no gas phase forms (i.e., bubbles). This is facilitated by the confinement above the cave-forming layer; otherwise, degassing of CO₂ near the water table can lead to calcite supersaturation and precipitation^29,71. The volumetric flow rate from the cave feeder (i.e., fluid inlet) remains constant because the cavities are formed as isolated voids, and the overall permeability of the system is unaffected¹². This last assumption breaks down if speleogenesis occurs near the surface^40,72. However, our case study deals with dissolution under a thick impermeable rock section.

The changes in the aperture, which affect solute distribution, are several orders of magnitude slower compared to solute relaxation time and allow to use a stationary reactive transport equation (i.e., adopting the quasi-steady-state assumption for the concentration field)^{73,74,75,76,77}. Specifically, neglecting the transient term is justified by the large separation of the characteristic timescales between solute transport by advection (t_a) and diffusion across the aperture (t_d) on one hand, and aperture evolution (t_dis) on the other. Since conduction in the confining rocks, which affects solubility and reaction, reaches steady-state after a relatively short time (tens of years, see Fig. 3b), it does not impose transient variations on solute transport after this time. Note that while the transient term in the solute conservation equation is neglected, temporal variations on the scale t_dis do occur due to changes in the aperture and its effect on solute transport and reaction rates.

The characteristic timescales are given by ${t}_{a}={\int }_{0}^{{l}_{c}}\frac{1}{v(r)}{{{\rm{d}}}}{r}$, t_d = h_p/k(h) and t_dis = Δh/γk(h), where l_c is the characteristic length scale of advection (corresponding to the reactive front length), v(r) is the position dependent velocity, h_p is the maximal aperture width, k(h) is the mass-transfer coefficient, which is inversely proportional to h [L T⁻¹] and Δh is a change in aperture due to the dissolution. γ = ∆c_s0/c_solν is the acid capacity number, defined as the ratio between the total change of the saturation concentration due to the thermal variations, ∆c_s0 = |c_s(T₀)-c_s(T_in)|, and the molar concentration of a mineral phase (c_sol), with ${{\nu}}$ equal to the stoichiometry of the reaction^73,78.

Supplementary Note 2 presents a theoretical analysis of dissolution in a uniform horizon due to heat exchange with the rock and fluid cooling, considering the same geometry as the AHD model but with a few simplifying assumptions. The results from this analysis serve to validate the numerical model presented here (see Supplementary Note 3). The theoretical derivation utilizes the so-called Lauwerier thermal solution⁷⁹ to calculate spatial and temporal-dependent solubility in the horizon. The closed-form expression is then substituted into the reactive transport equation, which is solved for solute transport and aperture evolution.

AHD model: main equations

Heat transport through rock confining the horizon above and below is governed by the heat equation (Fig. 7), which in polar coordinates takes the form

$$\frac{\partial T}{\partial t}=\frac{{\alpha }_{{{\rm{r}}}}}{r}\frac{\partial }{\partial r}\left(r\frac{\partial T}{\partial r}\right)+{\alpha }_{{{\rm{r}}}}\frac{{\partial }^{2}T}{\partial {z}^{2}},$$

(1)

where T is the temperature, t is time, and r and z are the radial and vertical coordinates, respectively, with origin at the inlet. The quantity α_r = K_r(ρ_rC_pr)^-1 is the thermal diffusivity, where the subscript r denotes rock, K is the thermal conductivity, ρ is the density, and C_p is the heat capacity¹³.

Assuming that, along the horizon, heat transport in the fluid is governed by advection and conduction and that complete thermal mixing occurs along the horizon aperture, the depth-averaged heat-transport equation can then be written as

$$\frac{\partial \left({hT}\right)}{\partial t}=-\frac{1}{r}\frac{\partial \left({rqT}\right)}{\partial r}+\frac{{\alpha }_{{{\rm{f}}}}}{r}\frac{\partial }{\partial r}\left({hr}\frac{\partial T}{\partial r}\right)-\varTheta \left(r,t\right),$$

(2)

where q is the fluid velocity integrated over the horizon aperture h [L² T⁻¹] and calculated from the total volumetric flow rate Q using q = Q(2πr)⁻¹, and α_f is the thermal diffusivity of the fluid^14,33. The function Θ accounts for the heat exchange between the flow within the horizon and the rock above and below and is calculated using Fourier’s law, assuming continuous temperature at the fluid-solid interface:

$$\varTheta =-\frac{2{{\rm K}}_{{{\rm{r}}}}}{{\rho }_{{{\rm{f}}}}{C}_{{{{\rm{p}}}}_{{{\rm{f}}}}}}\frac{\partial T}{\partial \left|z\right|}$$

(3)

The absolute value accounts for conduction to the rock both above and below the horizon. The complete mixing approximation can be validated a posteriori and is justified because the transverse temperature gradients in the horizon remain relatively small throughout speleogenesis. The depth-averaged solute transport advection-diffusion-reaction equation in the horizon is

$$0=-q\frac{\partial c}{\partial r}+\frac{D}{r}\frac{\partial }{\partial r}\left({hr}\frac{\partial c}{\partial r}\right)+\varOmega \left(r,t\right),$$

(4)

where c is the flow-weighted dissolved-calcite-ion concentration (mixing-cup concentration) [M L^-3], defined as $c=\frac{1}{Q}{\int }_{-h/2}^{h/2}c\left(z\right)v\left(z\right)2\pi {r}{{{\rm{d}}}}{z}$, where v is the value of radial component of the local (r- and z-dependent) fluid velocity within the horizon. D is the molecular diffusion coefficient, and Ω is the reaction term^14,80. The transient term in Eq. 4 is neglected, and the quasi-static approach is justified by the separation of timescales between mineral dissolution and the relaxation of solute concentration (see previous section, AHD Model: setup).

The reaction term Ω is proportional to the difference between c_s (i.e., c at calcite saturation or equilibrium at the given conditions) and c:

$$\varOmega =2k\left(h\right)\varepsilon \left[{c}_{{{\rm{s}}}}\left(T\right)-c\right],$$

(5)

where the factor of two accounts for the upper and lower surfaces and ε is a geometrical correction term, which accounts for the increase of the reactive surface area due to the inclination of the fracture surfaces

$$\varepsilon =\sqrt{1+{\left(\frac{1}{2}\frac{\partial h}{\partial r}\right)}^{2}}$$

(6)

k(h) is the mass-transfer coefficient [L T⁻¹], which is inversely proportional to the aperture h. Here, the initial CO₂ partial pressure, PCO₂, is relatively high and the kinetics are rapid, so the rate-limiting step for the reaction is the diffusion of reaction products away from the mineral surface so that undersaturation is sustained. Consequently, the reaction rate can be calculated from the transport rate alone, regardless of kinetics (so-called equilibrium dissolution model)^33,81. In Supplementary Methods 2, we provide explicit expression for k(h) and the complete derivation of Eq. 5, and the equilibrium model^33,81; its verification for the conditions considered here is given in Supplementary Note 4.

The saturation concentration c_s depends on the temperature and is expressed as a Taylor expansion to account for retrograde solubility:

$${c}_{{{\rm{s}}}}\left(T\right)={c}_{{{\rm{s}}}}\left({T}_{0}\right)-\beta \left(T-{T}_{0}\right),$$

(7)

where the constant β is evaluated from the data presented in Results and Discussion section and Fig. 2b, and T₀ is the reference (ambient) temperature. Finally, the change in the horizon aperture is calculated by using

$$\frac{\partial h}{\partial t}=\frac{\varOmega }{\nu {c}_{{{{\rm{sol}}}}}},$$

(8)

where ${{\nu}}$ is a stoichiometric constant and c_sol is the concentration of the mineral in the rock (inverse of the mineral molar volume)⁷³.

AHD model: initial and boundary conditions

The initial conditions are uniform temperature, T₀ = 20 °C. The boundary conditions at the horizon inlet (r = r₀) are constant volumetric flow rate (Q) of the fluid with a temperature T_in = 60 °C and initially zero undersaturation, θ = 0, where θ = [c_s(T(r)) − c(r)]/∆c_s0 with ∆c_s0 = c_s(T₀) − c_s(T_in). We model conditions of a large domain so that no substantial heat transport occurs near the boundaries (r → ∞ and |z | → ∞). In practice, z and r are limited to 1 km. The upper surface is assigned a constant temperature, T₀. At the horizon outlet (r = 1 km), the temperature and concentration are calculated by using the thermal and solute conservation Eqs. 2 and 4 for a free-flow boundary. The remaining boundaries are assumed to be thermally insulating, so zero conductive heat flux crosses these boundaries.

AHD model: numerical scheme

The equations were implemented in a finite-difference code, with upwind difference for first derivatives and central difference for second derivatives (conduction and diffusion terms). For temporal discretization, an explicit method was adopted^82,83. The use of short time-steps (imposed by the stability criteria of the explicit method⁸³), allows us to decouple the equation solutions and solve the equations at each time-step sequentially: (I) heat transport in the horizon was calculated (Eq. 2), including the heat exchange between the fluid and the rock, which was then used to calculate (II) conduction in the rock (Eq. 1) and (III) the equilibrium concentration, c_s (Eq. 7), and solve reactive transport (Eq. 4). Last, (IV) using Eq. 8 the aperture evolution was calculated and used in the subsequent time-step. The large timescale separation between advection, conduction in the rock and dissolution, also enables to increase efficiency: heat conduction in the rock mass and reactive transport within the horizon are calculated only after several iterations, where short time-steps were used to calculate heat transport in the horizon.

Spatial discretization was refined near the inlet point, and accuracy was verified using a sensitivity test for the different time-step lengths and spatial discretization. Integral balances of heat and solute in the model were verified, and the code was further benchmarked using analytical solutions for heat and reactive transport (as detailed in Supplementary Note 3).

The network model: setup

The network model is the last one in the hierarchy of models. It is used to study cave formation in a more realistic setting, which mimics the natural environment. This model extends the AHD model of dissolution from an initially uniform bedding horizon to dissolution in a heterogeneous fractured horizon and allows study the cave passages pattern formation. Conceptually, the network model comprises an idealized representation of a 2‐D network of permeable conduits formed at the intersection of bedding horizon with the subvertical fracture network, where the maze caves develop^6,9.

Such an analog modelling approach has widely been applied for deciphering subsurface karst evolution and speleogenesis: from karstic aquifers evolution at various settings^6,84,85 to speleogenesis of branchwork systems^6,64,86, floodwater mazes^64,65, and gypsum caves by transverse flow^87,88. Network models are commonly also applied to study porous rocks dissolution on the pore- to core-scale^{89,90,91,92,93,94,95}. Despite their simplicity, regular pore network models were shown to capture well the major characteristics of dissolution conduit evolution (wormholing) observed experimentally, including their structure, advancement rate and medium permeability evolution^{89,91,94,96,97}.

Here, the network model invokes similar settings and assumptions as the AHD model (see Methods, AHD Model: setup section). In accordance, we consider discharge of hot and saturated fluid at the center of the system. The injected fluid flows radially while cooling, thus becoming undersaturated and corrosive. The circular system comprises a 2-D regular network of channels that are divided into two categories: narrow ones with relatively low permeability, representing the rock matrix porosity, and wider ones representing the permeable conduits formed by the intersecting fractures, which are power-law distributed⁹⁸ (Fig. 8).

Fig. 8: Schematic of the network model for dissolution in bedding horizon.

a Saturated hot fluid discharges at flow rate Q and temperature T_in at the center (red point) and flows radially towards the perimeter while cooling and thus becoming reactive. An axisymmetric temperature field is imposed (depicted by color arrow; derived from the AHD model, see text), and used to calculate the saturation concentration, c_s(T) (Eq. 7); system diameter is 150 m. b The system comprises 2-D rectangular network of cylindrical channels and nodes (junctions). Node i is connected to its neighbor j through channel ij, and heterogeneity is introduced via channel radii. Channels are divided into two categories: narrow channels which represent the rock matrix (not shown in (a)), and wider ones, which focus most of the flow, representing the permeable conduits formed by intersecting fractures. These fractures (depicted as thin lines in (a)) obey a power-law distribution. c The channels are of length l and variable radius R, which changes by ΔR following dissolution over a time-step Δt. The reaction is transport-controlled and depends on the rate of diffusive mass transfer of dissolved ions to the bulk fluid and the surface-to-fluid mass-transfer coefficient, k(R).

In the network model, conservation equations for fluid and solute are written for individual channels and nodes (channel junctions). Calculations involve solving the continuity equation for the fluid and Poiseuille’s law for the pressure drop in the channels, from which fluid pressures and fluxes are calculated. Solute conservation equations are used to calculate concentrations and mass of dissolved solid component. Here, though the volumetric flow rate is relatively low, Q, the radial flow velocity is relatively high within the cave-forming zone, around the feeder, and the solute Péclet number is large, Pe = v̅l_c/D >> 1, where v̅ is an average flow velocity in the channel, D is the molecular diffusion coefficient and l_c is characteristic length scale of advection (here l_c = 1 m). Consequently, solute transport in the cylindrical channels is assumed to be controlled by advection in the axial direction (flow direction), and by diffusion in the channels’ perpendicular (radial) direction, with axial diffusion neglected. It is noted, however, that mechanical dispersion is inherently incorporated in network models⁹⁹.

In terms of reaction, the high initial PCO₂ (0.03 MPa) dictates fast kinetics and the dissolution described by the equilibrium model, where the rate-limiting step for the reaction is the diffusion of reaction products away from the mineral surface^33,81,100 (see Supplementary Note 4). As reaction is proportional to the degree of solute undersaturation, the saturation concentration, c_s, which in turn depends on the temperature distribution, must be known. Here, we exploit the fact that temperature distribution in the system approaches the quasi-steady thermal state over short timescales (tens of years) compared to the timescale of speleogenesis (tens of thousands of years), which allows treating the axisymmetric temperature field as stationary [see, e.g., the analysis results in Fig. 3b and solution for continuous point source in infinite space given in ref. ¹³ (Eq. 3.24, pg. 114)]. Under such conditions, c_s(r) is calculated from the known stationary temperature field using Eq. 7, which significantly simplifies the calculations. For the fractured horizon, in which flow and dissolution are focused in permeable conduits, the assumption of an axisymmetric temperature field is valid if (I) the conduits are closely spaced and (II) dissolution takes place in the network relatively uniformly around the feeder. In these conditions, the temperature will equilibrate in the radial direction, and axisymmetric distribution will prevail.

Finally, as discussed in the Methods section, AHD Model: setup, the large separation of timescales between mineral dissolution and flow and solute fields relaxations allows adopting a quasi-static approach^{74,76,77,101,102}. Additionally, as the relaxation time of the flow field is much faster than that of solute, the processes can be solved sequentially at each time-step. Next, the geometrical properties are updated at the end of each time-step to be used in the subsequent step^73,75,91,103.

The network model: equations

For an incompressible fluid, steady-state fluid mass conservation at each node i yields

$${\Sigma }_{{{\rm{j}}}}{u}_{{{{\rm{ij}}}}}=0,$$

(9)

where u_ij is the volumetric flow rate through channel ij (u_ij > 0 indicates flow from node i to j), and the summation is over all neighboring nodes j, linked to node i (see Fig. 8b). The channel flow rates are calculated using Hagen-Poiseuille equation

$${u}_{{{{\rm{ij}}}}}=\frac{\pi {R}_{{{{\rm{ij}}}}}^{4}}{8\mu l}\varDelta {p}_{{{{\rm{ij}}}}},$$

(10)

where R_ij is channel radius, μ is fluid viscosity and Δp_ij = p_i-p_j is the pressure drop between two nodes, which are a distance of l apart (l is assumed to be constant). The system of linear Eqs. 9 and 10 is solved for the pressures at the nodes. In the equations below, indices are dropped due to brevity.

Similar to the AHD model, the reaction is transport-controlled and the equilibrium dissolution model can be applied. Under these conditions the reaction rate, which varies spatially and within each channel, can be calculated using

$$\varOmega =k\left(R\right)\left[{c}_{{{\rm{s}}}}\left(T\right)-c\right],$$

(11)

where k is the mass-transfer coefficient that is inversely proportional to R (see Eq. SM.2.3 in Supplementary Methods 2), c_s is the retrograde saturation concentration calculated using Eq. 7 and c is the flow-weighted average concentration (mixing-cup concentration) [M L⁻³], defined as $c=\frac{1}{u}{\int }_{0}^{R}c({r}_{{{\rm{o}}}})v({r}_{{{\rm{o}}}})2\pi {r}_{{{\rm{o}}}}{{{\rm{d}}}}{r}_{{{\rm{o}}}}$, with v the fluid flux and r_o is the channels’ radial coordinate.

The derivation of the equilibrium dissolution model given for the AHD model in Supplementary Methods 2, applies also for Eq. 11 with the difference that the Sherwood number for parallel plates, Sh₌, is replaced with Sherwood number for cylindrical channel, Sh_o. Also here we approximate Sh_o by a constant value, Sh_o = 4^89,104.

In the network model dissolution within each of the channels is modeled assuming advection-dominant transport along its axial direction, ξ, (Pe >> 1) and radial transport effects are incorporated in the mass-transfer coefficient, k(R), resulting in a 1-D advection-reaction equation

$$u\frac{{{{{\rm{d}}}}c}}{{{{\rm{d}}}}{\xi }}=-2\pi {Rk}\left(R\right)\left[{c}_{{{\rm{s}}}}\left(T\right)-c\right].$$

(12)

For a given solute concentration at the channel inlet, c(ξ = 0) = c_in, Eq. 12 can be solved for the concentration at the channel outlet, c(ξ = l) = c_out

$${c}_{{{{\rm{out}}}}}={c}_{{{\rm{s}}}}\left(T\right)-\left[{c}_{{{\rm{s}}}}\left(T\right)-{c}_{{{{\rm{in}}}}}\right]{e}^{-({{sk}}/{u})},$$

(13)

where s = 2πRl is the channel surface area, and for tractability we assume that c_s(T) is constant along each channel, and equal to its value at channel center. c_s(T) is calculated using Eq. 7, where the stationary temperature field is obtained using the AHD model (i.e., the numerical temperature profile from Fig. 3b). Lastly, the concentration of solute at the nodes is calculated from channel outlet concentrations, c_out, and solute balance, assuming full mixing at the channel intersections^105,106.

Given the reaction rate (Eq. 11), the erosion rate of the channels can be calculated based on the mass conservation

$$\frac{\partial R}{\partial t}=\frac{\Omega }{\nu {c}_{{{{\rm{sol}}}}}}.$$

(14)

Then, the total volume of mineral dissolved from a single channel surface during a time-step Δt, can be calculated using,

$$\Delta {V}_{{{{\rm{dis}}}}}=\frac{2\pi R\Delta {tk}}{\nu {c}_{{{{\rm{sol}}}}}}{\int }_{\!\!\!\!0}^{l}\left[{c}_{{{\rm{s}}}}\left(T\right)-c(\xi )\right]{{{\rm{d}}}}\xi =\Delta {tu}\frac{\left[{c}_{{{\rm{s}}}}\left(T\right)-{c}_{{{{\rm{in}}}}}\right]}{\nu {c}_{{{{\rm{sol}}}}}}\big(1-{e}^{-({{sk}}/{u})}\big).$$

(15)

In order to keep the model tractable, we assume that each cylindrical channel dissolves uniformly along its length. The corresponding change in channel radius is then

$$\varDelta R=\frac{\Delta {V}_{{{{\rm{dis}}}}}}{s}=\frac{\varDelta {tu}}{s}\frac{\left[{c}_{{{\rm{s}}}}\left(T\right)-{c}_{{{{\rm{in}}}}}\right]}{\nu {c}_{{{{\rm{sol}}}}}}\big(1-{e}^{-({{sk}}/{u})}\big).$$

(16)

The model also accounts for a finite amount of soluble solid and if locally between adjacent channels solid is fully dissolved, channel merging is accounted for by the associated hydraulic conductivity increase¹⁰⁷.

The network model: initial and boundary conditions

We consider discharge of hot, T_in, and saturated fluid, c = c_s(T_in), of constant volumetric flow rate, Q, at the center of the system that outflow at the perimeter, and impose the pressure at the boundaries

$$p\left(r=0\right)={p}_{{{{\rm{in}}}}}\, {{{\rm{and}}}} \, \,p\left(r={r}_{{{{\rm{out}}}}}\right)=0.$$

(17)

As permeability increases in the course of dissolution, to maintain the flow rate, Q, fixed, p_in is adjusted at every time-step. Concentration at the outlet nodes is calculated from solute mass conservation (Eq. 13; free-flow boundary).

The network model: implementation

We consider a circular system and regular network of channels with 300 nodes along the diameter (7.07·10⁴ nodes in total; see Fig. 8). The network is composed of narrow channels with average radius, R_M, (representing the matrix porosity) and wider channels with an average radius, R_F, (representing fracture conduits) with a permeability ratio of ~300. The fracture center position is distributed uniformly with their lengths sampled from a truncated power-law, L_fr = L_min[1-n + n(L_min/L_max)^m]^−1/m, where n is a random number sampled uniformly from the unit interval, L_min and L_max are min and max fracture length and m is an exponent. Here, a characteristic value of m = 2 was used^98,108 (see Table 1 for parameter values). A fracture of length L_fr comprises a few channels in a row, each with length l. Fracture apertures are linearly proportional to fracture length, L_fr, and are maximal at the center (twice larger than their average value) and linearly decay towards their edges^109,110. The heterogeneity of the void-space was accounted by further imposing variability in small and large channel radii, sampled from a lognormal distribution with a relative standard deviation of 0.25.

Each time-step begins with the calculation of the flow field by solving the system of Eqs. 9 and 10. Next, using the channel flow rates, u, the solute concentration at the nodes is calculated by solving the system of Eq. 13 and solute balance at the nodes. Lastly, the change in channel radii is calculated using Eq. 16. The time-step is kept small enough so that the changes in channel radii will constitute a small fraction of the original radius. Additionally, a sensitivity test of the effect of time-step was performed: simulations were run with decreasing time-step until the volume of reactive fluid (V_f) needed to achieve 100-fold permeability increase of the model computational domain stabilized.

A flow rate of Q = 2 m³/day is considered, characteristic of relatively low volumetric flow rate of the deep origin thermal flows^35,57,58, and the appropriate temperature field is calculated using the AHD model (see Fig. 3b). The average solute Péclet number is large, corresponding to the assumption of the dominance of advective transport. The average Pe at the outlet is 1000, and is even much larger in channels which represent fractures, where most of the flow and dissolution are focused.