Element-specific Curie temperatures and Heisenberg criticality in ferrimagnetic Gd₆(Mn_1−xFe_x)₂₃ via Kouvel-Fisher analysis

Abstract

Many large unit-cell rare-earth transition metal ternary alloys of the type R_a(M_1−xM’_x)_b exhibit non-monotonic ferrimagnetic Curie temperatures (T_C) coupled to monotonic composition-controlled magnetization. Its origin remains an important long-standing puzzle in the absence of studies probing their temperature-dependent element-specific magnetism. Here, in order to resolve this issue and identify design principles for new R-M-M’ permanent magnets, we carry out x-ray magnetic circular dichroism (XMCD) for the series Gd₆(Mn_1−xFe_x)₂₃, x = 0.0 − 0.75. The results show that the net Mn-moment reduces and switches from parallel to antiparallel for x ≥ 0.2, while the Fe-moment is always antiparallel to the Gd-moment. Kouvel-Fisher analyses of XMCD data reveals distinct sublattice T_C’s and 3D Heisenberg criticality. Band structure calculations show magnetic moments and density of states consistent with experiments. The magnetic phase diagram shows three regions characterized by (i) Mn-sublattice bulk-T_C > Gd-sublattice T_C, (ii) a reduced common-T_C for all sublattices, and (iii) Fe-sublattice bulk-T_C > Gd-sublattice T_C. The Mn-moment switching and gradual increase of Fe-moment combine to cause non-monotonic T_C’s with monotonic magnetization. The study indicates the importance of element-specific T_C’s for tuning magnetic properties.

Introduction

Binary and ternary intermetallics containing rare-earths(R) and transition metals(M) play an important role in the fields of heavy-fermions^1,2,3, Non-Fermi-liquids⁴, magnetic metals^2,3,4,5,6, magnetocaloric materials⁷, etc. In addition to applications as strong permanent magnets, magnetocalorics, thermoelectrics, fracture toughness, ductility, etc., R-M based materials are now also used in phosphors, lasers, energy storage batteries, catalysts, etc. ⁸

The variety of their applications stem from distinct properties of the R f-electrons and M d-electrons. Typically, f-electrons are localized with large magnetic moments µ and strong spin-orbit coupling (SOC), negligible bandwidths (W) and weak intersite exchange (J’) interactions^5,6. In comparison, delocalized M d-electrons in intermetallics show a smaller µ and weaker SOC, but larger W and J’ which results in M d-electrons determining the bulk T_C’s. Several intermetallic series R_a(M_1−xM’_x)_b, such as R(M_1−xM’_x)₂, R₂(M_1−xM’_x)₁₇, R₆(M_1−xM’_x)₂₃ with R = Gd-Tm and M, M’ = Mn, Fe, Co show non-monotonic variation of T_C’s with a monotonic variation of the total bulk magnetization ${M}_{{Tot}}^{B}$(x) at low-T, or vice-versa^{5,6,9,10,11,12,13}. In the absence of element specific T_C’s, this behavior remains an open question and it is generally considered that three types of exchange interactions are important in R-M-M’ alloys: R-R indirect exchange proceeding via 4f - conduction electrons - 4f states, M-M/M-M’ direct exchange between 3d states, and R-M/M’ indirect exchange via 4f - 5d - 3d states. Early studies based on effective Heisenberg models for large unit-cell systems concluded that M-M exchange > R-M exchange > R-R exchange^{11,12,13,14,15,16,17}. For an isostructural R-M series with R varying from Ce to Yb, the R-M exchange coupling is always ferromagnetic (FM) for light rare-earths and anti-ferromagnetic (AFM) for heavy rare-earths, which constitutes the “FM-AFM rule”. In addition, varying M or M’ can also lead to competition of bulk FM vs. AFM order^9,10. Using element-specific T-dependent XMCD to address the interplay of f and d electrons in the series Gd₆(Mn_1−xFe_x)₂₃, we resolve these issues by showing that element specific T_C’s and changes in the M-M’ exchange compared to R-M and R-R exchange plays a critical role in their unusual magnetism.

The R₆Mn₂₃ intermetallics crystallize in the Th₆Mn₂₃ (G-phase) type cubic structure and show very interesting magnetic properties^{9,15,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37}. Early work concluded that the R₆Mn₂₃ compounds did not apparently fit with the FM-AFM variation of the R-M exchange coupling for the light and heavy rare-earths, respectively¹⁸. Polarized neutron diffraction (ND) of isostructural Y₆Mn₂₃ at 4.2 K showed that the Mn sublattice consists of up-spin ‘f₁, f₂’ sites (with magnetic moment µ₁ and µ₂ respectively), and down-spin ‘b, d’ sites (with magnetic moment µ₃ and µ₄ respectively). The results show that µ₁ = µ₂~ +1.8 µ_B, µ₃~ −2.8 µ_B and µ₄~ −2.1 µ_B, respectively, for the four different sites²⁵. In contrast, Y₆Fe₂₃ showed all four Fe sites (b, d, f₁, f₂) were aligned with an average µ_Fe~ + 1.94µ_B^27,38. Since it is not easy to measure ND of Gd-based structures, it was assumed that Gd₆(Mn_1−xFe_x)₂₃ possesses the same ferrimagnetic Mn sublattice structure as Y₆Mn₂₃. Also, with Gd-moments interacting more strongly with the ‘b, d’ sites compared to the ‘f₁, f₂’ sites, it was concluded that the R₆Mn₂₃ compounds were not an exception to the FM-AFM rule^25,28,33. However, ${M}_{{Tot}}^{B}$ of Y₆Fe₂₃ is larger than Gd₆Fe₂₃, but that of Y₆Mn₂₃ is smaller than Gd₆Mn₂₃. Further, upon Fe substitution in Y₆Mn₂₃, ${M}_{{Tot}}^{B}$ of  Y₆(Mn_1−xFe_x)₂₃ increases with increasing x, but in isostructural Gd₆(Mn_1−xFe_x)₂₃, ${M}_{{Tot}}^{B}$ reduces on increasing x^{21,24,27,30,32,36}. Thus, magnetism of the composite Fe-Mn sublattice and its relation with the R-sublattice cannot be explained as an additive mixture of the parent compounds and it is necessary to determine the evolution of element-specific µ with x and T.

The non-monotonic behavior of T_C’s in Gd₆(Mn_1−xFe_x)₂₃ is also seen in Y₆(Mn_1−xFe_x)₂₃^21,30,32. This suggests that T_C’s of Gd₆(Mn_1−xFe_x)₂₃ are decoupled from the R-sublattice and originate from the M-M’ sublattices. Magnetocaloric studies of Gd₆(Mn_1−xFe_x)₂₃ revealed two maxima in the magnetic entropy changes (∆S_M), at T = T_C and at a lower T~100 K. It was inferred that the T~100 K maximum could be due to Gd sublattice ordering or due to modifications in the magnetic structure for small x = 0.0 − 0.2³². However, element-specific T_C’s of the Gd, Mn and Fe sublattices using XAS-XMCD have not been reported to date. In addition, T-dependence of the XMCD signal in terms of Ising, Heisenberg or mean-field type critical behavior would help to model these complex systems.

In this work, we carry out T -dependent XAS and XMCD studies to determine element-specific magnetic moments and T_C’s in Gd₆(Mn_1−xFe_x)₂₃, x = 0.0 − 0.75. The results identify the elemental origin of coexisting distinct sublattice T_C’s with 3-D Heisenberg-type criticality, and provide an understanding of the non-monotonic T_C’s and monotonic magnetization as a function of x in Gd₆(Mn_1−xFe_x)₂₃. Moreover, since there are no reported band structure calculations even for the parent compounds, we have carried out band structure calculations of Gd₆M₂₃ (M = Mn, Fe) based on the Density Functional Theory with on-site Coulomb energies (DFT + U) for Gd, Mn and Fe. The calculated element specific magnetic moments and total magnetization are in agreement with XMCD results and reported bulk magnetization measurements. In addition, the band structure calculations provide the partial density of states (PDOS) and total DOS which are consistent with experimental valence band spectra measured by Hard x-ray photoemission spectroscopy (HAXPES).

Results and Discussion

XAS and XMCD results

Figure 1a-c shows representative XAS measurements of Gd M-edge and Mn L-edge for x = 0.0 and the Fe L-edge for x = 0.5, respectively. The Gd M-edge, Mn L-edge and Fe L-edge XAS spectra without applied field for all x are shown in Supplementary Fig. 1 and discussed in Supplementary Note 1. The Mn and Fe L-edge XAS spectra show peak positions and shapes matching well with the Mn and Fe metal spectra^{39,40,41,42,43,44}. Figure 1d–f, shows the Gd M-edge, Mn L-edge and Fe L-edge XMCD for in-situ cleaved samples of the Gd₆(Mn_1−xFe_x)₂₃ series (x = 0, 0.2, 0.5 and 0.75) at T = 29 K, the lowest sample temperature attained on our spectrometer. The Gd M-edge XAS spectra shown in Fig. 1a give rise to a large XMCD (~ 36%) and are shown for all x in Fig. 1d. Their spectral shape is very similar to earlier XMCD results of Gd intermetallics like GdFe, GdNi, and GdCo^{42,45,46,47,48,49}. The values of spin and orbital magnetic moments (µ_spin, µ_orb) of Gd from the measured intensities of XAS and XMCD spectra was determined by a sum rule analysis as detailed in Supplementary Note 2. Based on the Gd³⁺ configuration, the number of holes for Gd 4f states is taken to be n_h(Gd) = 7. The obtained µ_spin and µ_orb are shown in Supplementary Table 1 for all x. The µ_orb of Gd is not exactly zero but very small µ_orb ≈ 0.13 ± 0.02 µ_B, which is attributed to a combination of 4f-4f multiplet interactions and the 4f SOC^42,50. The total moment of Gd, µ_Gd is very close to 7 µ_B for all x, corresponding to the localized Gd³⁺ 4f ⁷ configuration with S = 7/2.

Fig. 1: X-ray absorption and magnetic circular dichroism spectra.

Representative XAS spectra with an applied field of ±1 T for (a) Gd M-edge, (b) Mn L-edge of the parent compound, and (c) the Fe L-edge of Gd₆(Mn_0.5Fe_0.5)₂₃ measured at T = 29 K, from which we obtained the XMCD spectra, as shown for all x in (d–f). d Gd M-edge, (e) Mn L-edge and (f) Fe L-edge experimental XMCD spectra of the series Gd₆(Mn_1−xFe_x)₂₃ (x = 0, 0.2, 0.5 and 0.75) measured at T = 29 K. Arrows in (d–f) show the relative magnitude and orientation of the spins.

For x = 0, although the Mn L-edge XMCD peak signal is small (~4% at hν ~639 eV), it is clear and indicates the net Mn moment µ_Mn is oriented parallel to µ_Gd. Surprisingly, as shown in Fig. 1e for Fe substitution with x = 0.2, the Mn XMCD signal switches to an antiparallel orientation with respect to Gd, and becomes smaller (~2% at hν ~640 eV). This originates from the clear reversal of the L₃ and L₂ peak intensities of XAS spectra with ± 1 T for x = 0.2 compared to x = 0.0, as shown in Supplementary Fig. 2 and discussed in Supplementary Note 3. The shape and intensity of the Mn XMCD signals are very similar for x = 0.2, 0.5 and 0.75. Thus, our results indicate that in the parent compound Gd₆Mn₂₃, the Mn moment associated with 32f₁, 32f₂ sites are parallel to Gd, while 24b, 4d sites are antiparallel to Gd. This results in a net Mn sublattice magnetization parallel to Gd in Gd₆Mn₂₃, as XMCD is proportional to magnetization. Upon Fe substitution, for x ≥ 0.2, the XMCD shows a switching of the net Mn sublattice magnetization from parallel to antiparallel with respect to Gd. In contrast, the Fe XMCD signal indicates that the Fe sublattice magnetization exhibits antiparallel orientation with the Gd moments and increases systematically with x, as shown in Fig. 1f. The Mn and Fe µ_spin and µ_orb values were also obtained by sum rule analyses as detailed in Supplementary Note 2. We used n_h(Mn) = 4.5 based on values known for Mn alloys^{44,51,52,53,54}. Similarly, we used n_h(Fe) = 3.7 for Fe, based on values known for Fe alloys^42,43,44. The obtained values of µ_spin and µ_orb and total moments (µ_Mn, µ_Fe) are listed in Supplementary Table 2.

Supplementary Table 3 shows ${M}_{{Tot}}^{X}$, the total magnetization using magnetic moments obtained from the XMCD sum rule analysis according to the formula ${M}_{{Tot}}^{X}$ = 6µ_Gd + 23{(1-x) µ_Mn + xµ_Fe}. The obtained values of ${M}_{{Tot}}^{X}$ from XMCD are in good agreement with ${M}_{{Tot}}^{B}$ from magnetization results reported earlier at 1 T^21,30,32. Since ref. ³⁰ reported the values at T = 77 K, they are consistently lower by a factor of 1.22 compared to the present results as well as refs. ^21,32. measured at lower T. The results show the monotonic reduction in ${M}_{{Tot}}^{B}$ is caused by the systematic increase of µ_Fe aligned antiparallel to µ_Gd, while µ_Mn is very small for Fe substituted cases. It is also noted that even if we assume that all the substituted Fe for x = 0.2 occupies the ‘f₁, f₂’ sites with µ_Fe aligned antiparallel to µ_Gd, ${M}_{{Tot}}^{X}$ is consistent with ${M}_{{Tot}}^{B}$ because µ_Mn shows a switching, indicating a breakdown of the magnetization as an additive mixture of the parent compounds; this behaviour has not been recognized earlier in the absence of element-specific magnetic moments. Moreover, the results are fairly consistent with the change in magnetic moments µ_Fe and µ_Mn estimated from the 3s core-level HAXPES⁵⁵, which also showed a monotonic change in total magnetization.

Band structure calculations

In order to understand the electronic structure responsible for the magnetism, we carried out DFT based spin-polarized generalized-gradient approximation (GGA) band structure calculations with on-site Coulomb energies for Gd₆Mn₂₃ and Gd₆Fe₂₃. The spin-polarized calculations were carried out using the experimental crystal structures as the starting point (Fig. 2a), i.e. cubic Gd₆Mn₂₃⁵⁶ and Gd₆Fe₂₃⁵⁷, and the details are described in the Methods section. Structural optimizations performed within the GGA-PBE (Perdew-Burke-Ernzerhof) approximation led to cubic cell parameter a in reasonable agreement with the experimental ones: a_exp(Gd₆Mn₂₃) = 12.54 Å and a_cal(Gd₆Mn₂₃) = 11.78 Å while a_exp(Gd₆Fe₂₃) = 12.13 Å and a_cal(Gd₆Fe₂₃) = 11.84 Å. Electronic structure calculations were performed for the optimized structures using the simplified (rotationally invariant) approach to the DFT + U, introduced by Dudarev et al. ⁵⁸. In this approach, the parameters for the Coulomb (U) and Hund’s exchange (J) interactions do not enter separately, and only the difference U-J = U^DFT is considered as a parameter.

Fig. 2: Crytal structure schematic and comparison of HAXPES valence band with DOS calculations.

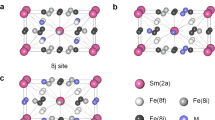
a The crystal structure of Gd₆Mn₂₃ showing the magnetic moments from band structure calculations of the Gd-site, Mn ‘b, d’ sites and Mn ‘f₁, f₂’ sites. b The valence band spin-integrated PDOS and total DOS of Gd₆Mn₂₃ obtained from the DFT + U calculations with ${U}_{{Mn}}^{{DFT}}$ = 0.75 eV and ${U}_{{Gd}}^{{DFT}}$ = 6.5 eV, together with the bulk-sensitive valence band spectrum measured by HAXPES. The calculations identify the contributions of the Gd 4f, Gd 5d, Mn 4s and Mn 3d PDOS contributions to the experimental spectrum. c The valence band spin-integrated PDOS and total DOS of Gd₆Fe₂₃ obtained from the DFT + U calculations. The calculations identify the contributions of the Gd 4f, Gd 5d, Fe 4s, and Fe 3d PDOS contributions to the experimental spectrum. d The valence band spin-integrated total DOS of Gd₆(Mn_0.25Fe_0.75)₂₃ is approximated by an additive mixture of 25% Gd₆Mn₂₃ and 75% Gd₆Fe₂₃ calculations, plotted together with the bulk-sensitive valence band spectrum measured by HAXPES⁵⁵.

It is known that even for Gd metal, the XAS-XMCD behaves like a typical atomic Gd³⁺ 4f ⁷ configuration with S = 7/2. Hence, the ground state can be described by a single Slater determinant and the one electron DFT is valid. In fact, it was shown early on that the two main parameters, the average energies of the Coulomb U_ff and exchange J_ff interactions could be calculated using the local spin-density approximation^59,60. The resulting values of U_ff = 6.7 eV and J_ff = 0.7 eV gave DOS consistent with the experimental N − 1 and N + 1 final states for one electron-removal (PES) and electron-addition (inverse-PES) spectra⁶¹, with a ${U}_{{Gd}}^{{eff}}$= U_ff + 6J_ff ≈ 11 eV. In our case, using the Dudarev approach, we varied ${U}_{{Gd}}^{{DFT}}$ (= U_ff − J_ff) from 6.0 eV to 12 eV and confirmed that ${U}_{{Gd}}^{{DFT}}$ = 6.5 eV gave a suitable match with the Gd 4f  PDOS in valence band HAXPES spectrum (Fig. 2b). Further, the average magnetic moment of Gd is calculated to be μ_Gd = +7.18 μ_B, in good agreement with the localized Gd³⁺ 4f ⁷ configuration and the sum rule analysis discussed above. Assuming J_ff = 0.7 eV, we obtain ${U}_{{Gd}}^{{eff}}$ = U_ff + 6J_ff = ${U}_{{Gd}}^{{DFT}}$ + 7J_ff = 11.4 eV. Similarly, in order to obtain calculated Mn magnetic moments close to the experimental values, ${U}_{{Mn}}^{{DFT}}$ was varied from 0.0 to 2.5 eV. It was found that$\,{U}_{{Mn}}^{{eff}}$ = ${U}_{{Mn}}^{{DFT}}$ = 0.75 eV gave magnetic moments close to the experimental values, and hence, U_dd = 1.65 eV if we consider J_dd = 0.9 eV⁶⁰.

Next, we discuss the obtained values of magnetic moments from the band structure calculations in comparison with the experimental values. The net magnetic moments per unit cell and per atom from the band structure calculations and the sum rule analysis are listed in Table 1 in comparison with the ND data and the Van Vleck analysis. The net magnetic moments were obtained using the average atomic magnetic moments from the band structure calculations as detailed in Supplementary Note 4. The average calculated magnetic moments for the ‘f₁, f₂’ sites (with μ₁~ +1.87 μ_B and μ₂~ +1.76 μ_B (Fig. 2a) shows good agreement with values known from ND studies. However, the average magnetic moment of ‘b, d’ sites (with μ₃~ −2.95 μ_B and μ₄~ −2.57 μ_B (Fig. 2a) is slightly higher compared to ND results. The magnetic moments are also consistent with values estimated from a Van Vleck analysis of 3s core-level photoemission spectra⁵⁵. The average magnetic moment of Gd is calculated to be μ_Gd = +7.18 μ_B, also in good agreement with the localized Gd³⁺ 4f ⁷ configuration as well as the result from sum rule analysis discussed above. The calculated moments with antiferromagnetic coupling between the Mn ‘b, d’ sites with Mn ‘f₁, f₂’ sites leads to a net Mn moment parallel to the Gd moment, and gives a total magnetization M_Tot = 53.8 μ_B. This value is consistent with bulk magnetization M = 54.7 μ_B measured at 5 T³². It is slightly higher compared to the ${M}_{{Tot}}^{X}$ from sum rule analysis measured at 1 T, as expected, because magnetic field dependent studies indicated a weak metamagnetic behavior with an increase around 4.5 T³².

Table 1 Comparison of magnetic moments from different methods

The valence band total DOS and spin-integrated PDOS of Gd₆Mn₂₃ obtained from the DFT + U calculations with said optimal parameters is shown in Fig. 2b, together with the bulk-sensitive valence band spectrum measured by HAXPES. The spin-resolved PDOS are discussed in Supplementary Note 4 and shown in Supplementary Fig. 3. The calculated spectra were obtained by applying the known photoionization cross-sections (PICS) at 10 keV⁶², and convoluted by a Gaussian function (1.0 eV FWHM for Mn 3d, Mn 3s and Gd 5d PDOS; and 1.5 eV FWHM for Gd 4f PDOS). As can be seen in Fig. 2b, the Gd 4f PDOS is positioned at ~7 eV binding energy (BE) below E_F, quite like Gd metal⁶⁰, while Mn 3d and Gd 5d PDOS are spread from E_F to nearly 6 eV BE. The Mn 4s states are spread from E_F to nearly 8 eV and show sizable intensity due to higher cross-sections for the incident hard x-ray energies⁶², leading to a bump feature at about 4.5 eV BE. On the other hand, at and near E_F, the total DOS is dominated by Gd 5d PDOS with a weaker contribution from Mn 3d states at E_F, and nearly similar contributions from both for the feature at ~3 eV BE. As discussed in Supplementary Note 4, the spin resolved PDOS shows that the localized Gd³⁺ configuration leads to 4f ⁷ up-spin states well-separated from the 4f ⁷ down-spin states due to the large ${U}_{{Gd}}^{{eff}}$ = 11.4 eV. The Mn 3d up-spin and down-spin states show a relatively large bandwidth, but nonetheless, the ${U}_{{Mn}}^{{eff}}$ = ${U}_{{Mn}}^{{DFT}}$ = 0.75 eV leads to weak splitting in up and down spin states, with a net Mn magnetic moment parallel to the Gd moments.

Similarly, DFT + U calculations were carried out for Gd₆Fe₂₃, and the results gave the average magnetic moment of Fe consistent with the experimental value, µ_Fe = −2.39 µ_B for ${U}_{{Fe}}^{{eff}}={U}_{{Fe}}^{{DFT}}$=$\,0.75$ eV i.e. with U_dd = 1.65 eV and J_dd = 0.9 eV. For Gd in Gd₆Fe₂₃, a value of µ_Gd = +7.55 µ_B was obtained for ${U}_{{Gd}}^{{eff}}=$ 11.4 eV. Since a full calculation for substituted compounds requires an extremely large unit cell, we have approximated the calculated valence band total and spin-integrated PDOS of Gd₆(Mn_0.25Fe_0.75)₂₃ as an additive mixture of 25% Gd₆Mn₂₃ and 75% Gd₆Fe₂₃. The same analysis for the total DOS of Gd₆(Mn_1−xFe_x)₂₃, x = 0.0 - 0.75 is shown in Supplementary Fig. 4. The calculated valence band total and spin-integrated PDOS of Gd₆(Mn_0.25Fe_0.75)₂₃ obtained from the DFT + U calculations is shown in Fig. 2d, together with the bulk-sensitive valence band spectrum measured by HAXPES. The spin-resolved PDOS are discussed in Supplementary Note 4. The calculated spectra were obtained by applying the known PICS as for Gd₆Mn₂₃. A fairly good match is obtained between the calculated and experimental spectrum. In particular, it is seen that contribution from Fe 3d and 4s PDOS (Fig. 2c) shows higher relative intensities compared to Mn 3d and 4s PDOS (Fig. 2b), leading to a small shape change between 3 and 5 eV BEs in Gd₆(Mn_0.25Fe_0.75)₂₃ compared to Gd₆Mn₂₃. More importantly, the Gd 5d and Fe 3d PDOS at E_F and within 2 eV BE are enhanced and broadened leading to a rounding of the sharp feature at E_F seen in Gd₆Mn₂₃. The results show that DFT + U calculations help to identify the Gd 4f, Gd 5d, Mn 4s and Mn 3d PDOS contributions to the experimental spectra.

Kouvel-Fisher analyses to characterize element-specific T_C’s

Early studies^15,21,30,32 used ${M}_{{Tot}}^{B}(T)$ to determine the Curie temperature T_C derived from the magnetic ordering of the M sublattice, while the Gd sublattice T_C for the series Gd₆(Mn_1−xFe_x)₂₃ has not been reported. As the magnetization of Gd is proportional to the Gd M-edge XMCD intensity I(T), it provides a direct measure of the sublattice ordering in Gd₆(Mn_1−xFe_x)₂₃. We have thus measured the Gd sublattice T_C for the series Gd₆(Mn_1−xFe_x)₂₃ using T-dependent Gd M₅-edge XMCD intensity I(T) and the results are summarized in Fig. 3a. As seen from Fig. 3a, the normalized XMCD intensity I^X(T) of Gd for the series reduces systematically on increasing T. The Gd sublattice T_C’s could be directly obtained by a power law least-squares fit to the equation I^X(T) = I₀(1 − T/T_C)^β (where I₀ is the intensity at T = 0 K, β is the critical exponent, and I^X(T) = I(T)/I(T = 29 K), indicating the critical behavior of the XMCD signal. The fit matches with I^X(T) over a limited T-range below T_C, as shown in Fig. 3a. The XMCD results show that the Gd sublattice exhibit values of T_C = 273.5 K, 172 K, 135 K and 273.5 K (with an error bar of ±5 K) for x = 0.0, 0.2, 0.5 and 0.75, respectively (Supplementary Table 3). In comparison, ${M}_{{Tot}}^{B}(T)$ shows T_C = 489 K, 176 K, 120 K and 309 K for x = 0.0, 0.2, 0.5 and 0.75 (error bars shown in Supplementary Table 3), respectively^30,32. The T_C for x = 0.0 and x = 0.75 was determined from ${M}_{{Tot}}^{B}$(T) measured by a Physical Property Measurement System (PPMS) as shown in Supplementary Fig. 5 and Supplementary Fig. 6, respectively, and discussed in Supplementary Note 5^30,32. The Gd sublattice T_C’s are lower than the bulk magnetization T_C’s only when the bulk T_C > 273.5 K i.e. for x = 0.0 and 0.75. On the other hand, when the bulk T_C < 273.5 K (i.e., for x = 0.2 and 0.5), Gd T_C also gets reduced together with the bulk T_C. This clearly shows that the Gd sublattice T_C equals the transition metal M sublattice only for intermediate x and it is lower for x = 0.0 and 0.75 compared to ${M}_{{Tot}}^{B}\hskip-1pt(T)$ results. More importantly, by plotting the normalized XMCD intensity as a function of T/T_C − 1, we can scale the critical behavior for the entire Gd₆(Mn_1−xFe_x)₂₃ series. Figure 3b shows that I^X(T) below T_C for all x falls on a single curve near T_C with β = 0.38 ± 0.01, indicating validity of the three-dimensional (3-D) Heisenberg model⁶³. For x = 0.0, a small deviation at T ~100 K was also observed in ${M}_{{Tot}}^{B}$(T) results measured with 1 T applied magnetic field¹⁵.

Fig. 3: Element-specific power law and Kouvel-Fisher analyses of XMCD.

a T-dependence of the Gd M₅-edge XMCD intensity of Gd₆(Mn_1−xFe_x)₂₃ fitted by a power law with β = 0.38 ± 0.01 (dashed black line). b Critical scaling behavior for the Gd₆(Mn_1−xFe_x)₂₃ series. The inset shows temperature dependence of Gd M-edge XMCD intensity of Gd₆(Mn_0.25Fe_0.75)₂₃ at a few selected temperatures, and a full figure showing the spectra for more temperature values is shown in Supplementary Fig. 7 and described in Supplementary Note 6. c T-dependence of the Gd M₅-edge XMCD intensity and ${M}_{{Tot}}^{B}(T)$ of Gd₆(Mn_0.8Fe_0.2)₂₃ fitted by a power law with β = 0.38 ± 0.01 (black line). d, e Show the power-law and Kouvel-Fisher analyses fits for ${M}_{{Tot}}^{B}(T)$ (black empty circles), respectively. The Gd M₅-edge XMCD intensity I^X(T) plotted together (red empty circles) also follows the Kouvel-Fisher analysis of ${M}_{{Tot}}^{B}(T)$ near T_C. f T-dependence of the Gd M₅-edge (blue squares) and Fe L₃-edge (red squares) XMCD intensity of Gd₆(Mn_0.5Fe_0.5)₂₃ fitted to a power law with β = 0.37 ± 0.01 (dashed blue-red line). g, h Show the power-law and Kouvel-Fisher analyses, respectively, for both Gd M₅-edge and Fe L₃-edge XMCD intensities plotted together. i T-dependence of the Gd M₅-edge (blue squares) and Fe L₃-edge (red squares) XMCD intensity of Gd₆(Mn_0.25Fe_0.75)₂₃ fitted by a power law with β = 0.38 ± 0.01 (blue and red lines, respectively). j, k Show the power-law and Kouvel-Fisher analyses for Gd M₅-edge XMCD intensities and (l, m) show the power-law and Kouvel-Fisher analyses for Fe L₃-edge XMCD intensities, respectively. The red and blue lines in (d, e, g, h, j–m) are the fits below and above T_C, respectively. All XMCD were obtained with an applied field of ±1 T. Error bars represent standard error (SE).

We have carried out a power-law analysis for the Gd₆(Mn_0.8Fe_0.2)₂₃ bulk magnetization ${M}_{{Tot}}^{B}(T)$ from a PPMS measurement using the same power-law with I^X(T) replaced by the intensity of ${M}_{{Tot}}^{B}(T)$ below T_C and compared it with the T-dependent Gd XMCD data to test the validity of the method. As shown in Fig. 3c, the power law analysis of the normalized ${M}_{{Tot}}^{B}(T)$ was then used to determine T_C independently and gave values of T_C = 175 K with β = 0.38. These values of T_C and β are consistent with values obtained from T-dependence of the Gd M₅-edge XMCD intensity for Gd₆(Mn_0.8Fe_0.2)₂₃ from Fig. 3b. It is noted that we could not obtain the T- dependent XMCD intensity of transition metal Mn or Fe for x = 0.2 due to very low XMCD intensities. As a further check of the ordering behavior, we also carried out a power law analysis for the ${M}_{{Tot}}^{B}(T)$ data above T_C to the equation χ^X(T)⁻¹ = ${\chi }_{0}^{-1}$(T/T_C − 1)^γ. Here, χ^X(T) is replaced by the intensity of ${M}_{{Tot}}^{B}(T)$ above T_C, χ₀ is critical amplitude and γ is the critical exponent. The above-T_C (χ^X(T)⁻¹) power law analysis gives a T_C value of 174.5 K (with γ = 1.28), and this T_C value is comparable to the value obtained from the below-T_C (I^X(T)) analysis (with β = 0.38), as shown in Fig. 3d and listed in Supplementary Table 4.

In order to accurately determine the critical behavior, we then carried out a Kouvel-Fisher analysis of the ${M}_{{Tot}}^{B}(T)$ signal as shown in Fig. 3e. Accordingly, the critical exponents could be determined from the equations I^X(T)/(dI^X(T)/dT)=(T − T_C)/β and χ^X(T)⁻¹/(dχ^X(T)⁻¹/dT)=(T − T_C)/γ⁶⁴ with I^X(T), χ^X(T) replaced by intensity of ${M}_{{Tot}}^{B}(T)$ below and above T_C, respectively. From a linear fit to the experimental bulk magnetization ${M}_{{Tot}}^{B}(T)$ data, we have obtained values of T_C = 175 K, β = 0.38 and γ = 1.30, and these values are very consistent with the power law analyses. It is noted that the values of β confirm that ${M}_{{Tot}}^{B}(T)$ of Gd₆(Mn_0.8Fe_0.2)₂₃ follows the 3-D Heisenberg-type critical behavior. We have then plotted the Gd M-edge XMCD intensity I^X(T) on the same scale in Fig. 3d, e, for Gd₆(Mn_0.8Fe_0.2)₂₃. The good match between the bulk magnetization ${M}_{{Tot}}^{B}(T)$ (black empty symbols) and the Gd XMCD intensity I^X(T) (red empty symbols) indicates that a Kouvel-Fisher analysis can be reliably used for determining the T_C and critical exponents from XMCD measurements.

Thus, we have similarly carried out a power-law and Kouvel-Fisher analysis for Gd M-edge and Fe L-edge XMCD intensity of Gd₆(Mn_0.5Fe_0.5)₂₃. Similar to the Gd M-edge XMCD intensity, the magnetization of Fe sublattice is proportional to the Fe L-edge XMCD intensity I(T). As shown in Fig. 3f–h, the T-dependence of Fe and Gd XMCD intensities I^X(T) for Gd₆(Mn_0.5Fe_0.5)₂₃ exhibits a very similar T-dependence. To confirm the Fe sublattice T_C we carried out a power law analysis for the data and obtained a T_C = 135 K for Fe with β = 0.37 ± 0.01. The T_C is consistent with ${M}_{{Tot}}^{B}$(T)^21,30 within experimental error. Further, the T_C and β values for Fe XMCD are also consistent with the T_C and β values of the Gd XMCD (Fig. 3b), as discussed earlier. Similarly, we also carried out a power law analysis for the XMCD signal above T_C. The above-T_C (χ^X(T)⁻¹) power law analysis also showed very similar T_C values compared to the values obtained from the below-T_C (I^X(T)) analysis, with γ = 1.35 ± 0.02 as listed in Supplementary Table 4. From the Kouvel-Fisher results, the analyses showed values of T_C = 134.4 K, β = 0.36 ± 0.01 and γ = 1.33 ± 0.02.

To study the inter-relation between sublattices, we compared the T-dependent XMCD of Gd and Fe moments for x = 0.75 which showed a Gd sublattice T_C ~ 273.5 K, while ${M}_{{Tot}}^{B}(T)$-studies showed a T_C = 309 K³². The normalized I^X(T) of Gd and Fe decrease systematically on increasing T but deviate from each other and become nearly zero at different T as shown in Fig. 3i–m. We confirm this point by fitting the T-dependence of Fe XMCD intensity I^X(T) to the power law used above and find T_C(Fe) = 306 K and β = 0.37 ± 0.01. The T_C(Fe) is consistent with ${M}_{{Tot}}^{B}(T)$³², while β is consistent with the Gd XMCD which showed a T_C(Gd) = 273.5 K, as discussed in Fig. 3b. We also carried out a power law analysis for the XMCD signal above T_C.

Before doing the power law and Kouvel-Fisher analysis for the XMCD data above T_C, we ensured that the x = 0.75 sample is actually in the paramagnetic phase. We have measured the XMCD for the full spectral range (not shown) for 22 different temperatures, and the extracted XMCD intensities at the Fe L₃ peak are plotted in Fig. 3i. Supplementary Fig. 8 shows the Fe L-edge XMCD measured for Gd₆(Mn_0.25Fe_0.75)₂₃ from 29 K to 323 K over the full spectral energy range for a subset of temperatures, and is discussed in Supplementary Note 7. In particular, it is clearly seen in Supplementary Fig. 8 that the XMCD signal at T = 316 K and 323 K is reversed compared to all the temperatures below T_C = 306 K. In the ferrimagnetic phase with T < T_C, the XMCD of Gd and Fe showed opposite signs. However, above T_C, the sign of the XMCD signal did not change for the Gd XMCD but the sign of the Fe XMCD switched and showed the same sign as the Gd signal. Thus, the XMCD signal corresponds to the paramagnetic phase. The XMCD signal observed above T_C is attributed to the disordered local moments aligned by the applied magnetic field⁶⁵.

The above-T_C (χ^X(T)⁻¹) power law analysis shows very similar T_C values compared to the values obtained from the below-T_C (I^X(T)) analysis, as listed in Supplementary Table 4. Further, β = 0.37 ± 0.01 and γ = 1.35 ± 0.02 for Fe and Gd are very similar to each other (Supplementary Table 4). As shown in Fig. 3k, m, we also carried out a Kouvel-Fisher analysis of the Gd and Fe XMCD signals above and below T_C. From the linear fits to the data, we have obtained values of T_C, β and γ values for the Gd and Fe sublattice ordering, very consistent with the power law analyses. The results again show that a Kouvel-Fisher analysis can be reliably used for determining the T_C and critical exponents from XMCD measurements.

For the parent compound with x = 0.0, i.e. Gd₆Mn₂₃, it is known from ${M}_{{Tot}}^{B}$(T) that the sample T_C = 489 K³². Since the Mn XMCD signal is very small at T = 29 K, we could not measure the Mn sublattice T-dependent XMCD as a function of T. However, using the ${M}_{{Tot}}^{B}$(T) data reported earlier, we have confirmed that it also follows a power law with β = 0.38 ± 0.01 and T_C = 489 K, as shown in Supplementary Fig. 5. Similarly, we have confirmed for x = 0.75 that ${M}_{{Tot}}^{B}$(T) follows a power law with β = 0.36 ± 0.01 and T_C = 309 K as shown in Supplementary Fig. 6. Considering the origin of the maxima observed in magnetic entropy measurements, it is clear that the high temperature maximum matches the bulk T_C, while the low temperature maximum for x = 0.0 at T~100 K is not due to the Gd sublattice T_C, which is measured to be 273.5 K. Instead, the entropy maxima at T~100 K is related to the XMCD step observed at T~100 K, consistent with T-dependent magnetization with 1 T magnetic field reported earlier¹⁵ (Supplementary Fig. 5). It is noted that in the fit for x = 0.0, the Gd XMCD with T_C = 273.5 K (Fig. 3b) matched with the Gd XMCD for x = 0.75 (Fig. 3j, k). Accordingly, for all x, element specific T_C’s, critical exponents β as well as γ, obtained from a power-law and Kouvel-Fisher analyses of T-dependent XMCD results, are listed in Supplementary Table 4. It is seen from Supplementary Table 4 that for all x, β = 0.37 ± 0.01, and is close to the theoretical estimate of β = 0.365⁶³, indicating a robust 3D Heisenberg criticality in Gd₆(Mn_1−xFe_x)₂₃.The exponent γ = 1.35 ± 0.02 is also close to the theoretically expected γ = 1.386 and only for x = 0.2, the value of γ (= 1.29 ± 0.02) deviates a little from for the 3D Heisenberg model⁶³.

In comparison, we would like to clarify that element specific XMCD in combination with magnetic measurements was used to study a variety of magnetic phenomena in rare-earth materials^66,67,68. For example, T-dependent study of Co K-edge and Pr L-edge XMCD on the compound La_0.75Pr_0.5Co₂P₂, the Co sublattice showed a FM T_C1 = 167 K and the Pr sublattice showed a T_C2 = 66 K⁶⁶. In a study of the origin of perpendicular magnetic anisotropy in amorphous Nd_xCo_1−x thin films, XMCD at the Co L_2,3- and Nd M_4,5-edges was used to show a decoupling of Nd and Co moments⁶⁷. Regarding single element critical behavior, using T-dependent Eu L-edge and M-edge XMCD, it was shown that ferrimagnetic Eu_0.95Fe₄Sb₁₂ exhibits a mean-field power-law exponent (β = 0.52 ± 0.05), while a reference FM clathrate material Eu₈Ga₁₆Ge₃₀ showed a 3D Heisenberg-type exponent (β = 0.356 ± 0.03)⁶⁸. However, multi-element critical behavior using T-dependent XMCD with Kouvel-Fisher analyses showing distinct T_C’s has not been reported earlier and our study shows it provides valuable insights to understand multi-element magnetic systems.

In Fig. 4a, we summarize the element specific T_Cs, ${M}_{{Tot}}^{X}$ and ${M}_{{Tot}}^{B}$, while Fig. 4b shows the Mn and Fe magnetic moments (µ_Mn, µ_Fe) as a function of x, obtained from experimental results and analyses. The T_C plot can be divided into three regions: (i) For 0.0 < x  ≤ 0.15, the bulk T_C is determined by Mn sublattice, and Gd moments exhibit a lower T_C = 273.5 K compared to Mn moments. (ii) In the intermediate composition range 0.15 < x ≤ 0.72, the Gd and Fe sublattices show the same T_C. (iii) For 0.72 < x ≤ 1.0, the Fe moments determine the bulk T_C, which is larger than the Gd sublattice T_C = 273.5 K. The results thus show coexistence of the 3-D Heisenberg-type critical behavior for the Gd and Mn/Fe sublattice spins even when the sublattices have different T_C’s.

Fig. 4: Magnetic phase diagram of Gd₆(Mn_1−xFe_x)₂₃.

a Summary of element specific T_Cs, ${M}_{{Tot}}^{X}$ and ${M}_{{Tot}}^{B}$ as a function of x. The plots of T_C(Gd) (empty red circle ) and T_C(Fe) (red cross circle ) can be divided into three regions: (i) For 0.0 < x ≤ 0.15, bulk T_C is determined by Mn sublattice, and T_C(Gd) = 273.5 K < bulk T_C. (ii) For 0.15 < x ≤ 0.72, the Gd and Fe sublattices show same T_C = bulk T_C. (iii) For 0.72 < x ≤ 1.0, the Fe moments determine the bulk T_C, and T_C(Gd) = 273.5 K < bulk T_C. b Summary of Mn and Fe magnetic moments (µ_Mn, µ_Fe) as a function of x, showing switching of Mn moments for x ≥ 0.2 plotted with magnetic moments from 3s HAXPES analysis⁵⁵. Error bars represent standard error (SE).

Figure 4b shows a relatively abrupt reduction of the Mn moment upon Fe substitution, with a switching of the net Mn moment µ_Mn from parallel (x = 0.0) to antiparallel (x = 0.2) orientation with respect to Gd moments µ_Gd. The Fe moments show a nearly linear gradual increase with x up to x = 0.75. The intermediate x region exhibits a nearly flat minimum of T_C for x = 0.3-0.5, with the Fe sublattice moment effectively overcoming the Mn sublattice and in region (iii), the Fe sublattice is dominantly responsible for determining the Curie temperature. Thus, the Mn-moment switching and gradual increase in Fe-moment cause the non-monotonic T_C’s and monotonic decrease in magnetization with increasing x. It is clear that region (i) and (iii) are dominated by M-M and M’-M’ exchange, respectively, and implies a weaker R-R exchange in these regions. In region (ii), M-M’ exchange gets reduced below the R-R exchange of regions (i) and (iii). However, T_C of the Gd, Mn and Fe sublattices get reduced together, and indicates that R-(M, M’) exchange is active and coupled to M-M’ exchange in region (ii), and results in lowest T_C. As discussed in the introduction, earlier studies did not recognize the possible role of R-(M,M’) exchange but from the present results of the Gd sublattice T_C with respect to bulk T_C, we can conclude that (R-M,M’) exchange is active in region (ii). This evolution of exchange interactions has not been recognized in earlier studies and indicates the importance of element-specific T_C’s for tuning magnetic properties. The study shows that power-law and Kouvel-Fisher analyses of T-dependent XMCD provides a reliable method to precisely investigate the role of element-sensitive magnetism in any general R_a(M_1−xM’_x)_b series of alloys.

Methods

Sample preparation and characterization

The Gd₆(Mn_1−xFe_x)₂₃ were synthesized using stoichiometric amounts of high-purity metals (Gd 99.9 wt.% from Rhodia, Mn 99.99 wt.%, and Fe 99.8 wt.% from Alfa Aesar) by melting them in a high frequency induction furnace (CELES) under pure argon atmosphere. The crystal structure was verified to be cubic by powder X-ray diffraction, using a Philips X-Pert Pro Diffractometer, Cu Kα)^32,35,36, and it confirmed the absence of impurity phases. The chemical purity and composition of each sample was checked by microprobe analysis (CamecaSX 100) on mirror polished powder samples dispersed in a cold resin. The purity was evaluated from backscattered electron (BSE) micrographs on different particles and the chemical composition was confirmed to be the nominal composition from an average of six randomly chosen pinpoints on the sample surface.

Spectroscopy experiments

XAS and XMCD measurements were performed at the Dragon Beamline (BL 11A) of the Taiwan Light Source. The samples were cleaved in-situ in an ultrahigh vacuum (UHV) chamber of 8 × 10⁻¹⁰ mbar at T = 29 K. The total electron yield (TEY) method was used to measure XAS and XMCD across the Gd M_4,5-edges (3d − 4f), Mn L_2,3-edges (2p − 3d) and Fe L_2,3-edges (2p − 3d) with circularly polarized light. An external magnetic field of ±1 T was applied along the surface with a circular polarization degree of 80% and was 30^o with respect to circularly polarized light direction. The total energy resolution at the Fe L-edge was 0.2 eV for the XAS-XMCD spectra. The incident photon energy has an accuracy of ±10 meV at Fe L-edge and ±20 meV at Gd M-edge. The photon energy was calibrated using a reference Mn metal sample, Fe metal sample, MnO sample, Fe₂O₃ sample, and Dy metal sample. The sample was cooled using a liquid-He flow-type cryostat, and the measurements were carried out from T = 29 K to T = 340 K. The net orbital and spin moments of Gd, Mn as well as Fe were derived using the well-known sum rules for x-ray magnetic circular dichroism^69,70.

Calculation methods

All calculations were performed with Density Functional Theory (DFT) using the Vienna ab initio simulation package (VASP)^71,72,73. Spin-polarized calculations were performed with plane-wave basis set and projector-augmented wave (PAW) method⁷³. The following electrons were treated explicitly: 3s² 3p⁶ 3d⁶ 4s¹ (Mn), 3s² 3p⁶ 3d⁷ 4s¹ (Fe), 5s² 6s² 5p⁶ 5d¹ 4f ⁷ (Gd). The strong on-site Coulomb interaction of localized electrons was treated through the DFT + U approach⁶¹. Moreover, the on-site Coulomb energy for Mn and Fe, ${U}_{{Mn}}^{{DFT}}$ and ${U}_{{Fe}}^{{DFT}}$ were varied from 0.0 to 2.5 eV and for Gd, ${U}_{{Gd}}^{{DFT}}$ was varied from 6.0 to 12 eV to obtain magnetic moments close to the experimental values. The optimal magnetic moments (s, p, d, f) for a unit cell containing 116 atoms corresponding to 4 formula units of Gd₆M₂₃ (M = Mn, Fe) obtained from the calculations are listed in Supplementary Table 5 for Gd₆Mn₂₃, and for Gd₆Fe₂₃ in Supplementary Table 6. The one-electron Kohn–Sham orbitals were expanded in a plane-wave basis set with a kinetic energy cutoff of 360 eV. Total energies were minimized until the energy differences were less than 10⁻⁴ eV between two electronic cycles. The reciprocal space integration was approximated with a Monkhorst–Pack k-point grid of 9 × 9 × 9.