Introduction

The two-dimensional (2D) triangular-lattice systems with antiferromagnetic interaction have been extremely attractive for exploring exotic ground states. One of the frontier research topics is the quantum spin-liquid (QSL) state initially proposed by Anderson1. In this framework, the effective spin is 1/2, so that the spin can be treated as a fermion1,2,3. Despite extensive theoretical investigation3 and great potential for applications4,5, experimental progress has been slow. To date, the most promising candidates are organic materials6,7. While a few inorganic materials have been investigated including TbInO38, Sr2Cu(Te0.5W0.5)O69, Lu2Mo2O5N210, and Cs2CuCl411, none of these cases is settled.

In the search for new QSL candidates, rare-earth (RE)-based triangular lattice materials have recently attracted wide attention. Due to the strong spin–orbit coupling (SOC) and crystal electric field (CEF) effect, the low-temperature magnetic properties of rare-earth-based magnets can be described by an effective spin-1/2 state with strong quantum fluctuations12,13. For example, YbMgGaO4 is considered a QSL candidate14,15,16,17, where Yb3+ (4f 13) with the angular momentum J = 7/2 at high temperatures forms an effective spin-1/2 state at low temperatures under the combination of SOC and CEF. However, the mixed sites for Mg and Ga in YbMgGaO4 could perturb the system leading to another disordered state other than the QSL state18. Recently, the AYbCh2 (A = Li, Na, K, Rb, Cs; Ch = O, S, Se, Te) family has been investigated for the possible QSL behavior19,20,21,22,23. Compared to YbMgGaO4, AYbCh2 provides a homogeneous environment for the Yb triangle lattice without mixed sites. The effective spin-1/2 state of AYbCh2 has been confirmed based on multiple experimental methods, such as electron spin resonance, magnetization, and neutron scattering measurements24,25,26,27,28,29,30,31. The lack of long-range ordering (LRO) down to millikelvin implies the QSL state19,22,31,32,33,34,35,36. The continuum of magnetic excitation is found in NaYbSe2 in inelastic neutron scattering (INS) measurement, suggesting the ground state of NaYbSe2 is a QSL with a spinon Fermi surface37. Recently inelastic neutron scattering results have revealed a slightly weak next nearest neighbor (NNN) coupling in AYbSe2 (A = K and Cs) and the ground state is located near the boundary between the 120° magnetically ordered state and QSL state38,39.

In fact, replacing Yb with other rare-earth elements can give rise to long-range antiferromagnetic ordering as observed in KCeS220,40,41,42 and KErCh243,44. These indicate that the realization of the QSL state requires delicate atomic arrangement in addition to spin-1/2. This includes RE-RE distance within the layer and between layers. Compared to Yb-based compounds, Nd-based ANdCh2 (A = Na, K, Rb, Cs; Ch = O, S, Se, Te) has a larger intralayer and interlayer Nd-Nd distance due to larger Nd ion size, thus changing the magnetic interactions. In this article, we report the magnetic properties of CsNdSe2 measured by DC and AC magnetic susceptibilities down to 0.04 K. Our results demonstrate that CsNdSe2 is an excellent candidate for studying QSL physics. Although Nd3+ (4f 3) has a large angular momentum J = 9/2 at high temperatures, an effective spin-1/2 state with AFM interactions is obtained at low temperatures (due to strong SOC and CEF). While the AC susceptibility shows a broad hump below 0.5 K due to quantum fluctuations, there is no sign of long-range ordering down to 0.04 K. First-principles calculations are performed with the inclusion of the spin–orbit coupling and Coulomb correlations in support of the QSL state with multiple degenerated magnetic configurations.

Results and discussion

DC susceptibility

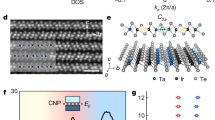
As described in the Methods, we have performed single crystal X-ray diffraction refinement, which indicates that our single crystal forms the \(R\bar{3}m\) (No. 166) symmetry with stoichiometry and the lattice parameters a = 4.3468(7) Å and c = 24.945(8) Å, illustrated in Fig. 1a. The Nd-Nd distance in the ab plane is 4.3468(8) Å (see Fig. 1b). The flat surface shown in the inset of Fig. 1c corresponds to the ab plane as reflected by the X-ray diffraction pattern in Fig. 1c. The formation of the trigonal symmetry (\(R\bar{3}m\)) in CsNdSe2 implies a perfect triangular lattice. Compared to CsYbSe2, both lattice parameters a and c for CsNdSe2 are larger due to the larger Nd ionic radius than Yb45. Figure 2a–c presents the temperature dependence of the inverse DC susceptibility for a CsNdSe2 single crystal along three directions: HDC∣∣a (Fig. 2a), HDC∥b (Fig. 2b), HDC∣∣c (Fig. 2c). For clarity, data shown in Fig. 2a–c is obtained from the field-cooling (FC) mode. Measurements obtained from the zero-field-cooling (ZFC) mode reveal undistinguishable results from that in the FC mode. At room temperature, there is little anisotropy in χ−1(T) at 0.1 T, which exhibits linear behavior above 250 K for all three directions. The Curie-Weiss expression, χ(T) = χ0 + C/(T − θCW), is used to fit the data between 250 K and 350 K, where χ0 and C are constants and θCW is the Curie-Weiss temperature. The fitting parameters are shown in Table 1. The effective moment is 3.67–4.00 μB, close to 3.87 μB for free Nd3+ ion with S = 3/2. The negative Curie-Weiss temperature (θCW < 0) indicates AFM interaction between Nd3+ ions.

Fig. 1: CsNdSe2 structural characterization.
figure 1

a Crystal structure of CsNdSe2 (\(R\bar{3}m\)); b Nd triangular layer (ab plane); c X-ray diffraction pattern of a CsNdSe2 single crystal. Inset: Picture of a CsNdSe2 single crystal.

Full size image
Fig. 2: Magnetization results of CsNdSe2.
figure 2

a–c Temperature dependence of the inverse DC susceptibility at HDC = 0.1 T for the CsNdSe2 single crystal with HDC∥ a, HDC∥b*, and HDC∥ c. Dash lines show the fit to the Curie-Weiss law (χ(T) = χ0 + C/(T − θCW)) at high temperatures (HT) (250 − 350 K) and low temperatures (LT) (2−4 K). The fitting parameters are shown in Table 1. d–f Isothermal magnetization at 1.9 K with HDC∥ a, HDC∥b*, and HDC∥ c. The dash lines guide the linear relation at the high magnetic field area. g–i Temperature dependence of 1/(χ-χ0) below 10 K. The dash lines present the linear behavior below 4 K. j Illustration of the Nd3+ moment due to the effects of SOC and CEF.

Full size image
Table 1 Curie-Weiss fitting results
Full size table

At low temperatures (T < 100 K), the temperature dependence of the inverse magnetic susceptibility deviates from the high-temperature (HT) Curie-Weiss behavior with increased anisotropy between the in-plane and out-of-plane. Similar behavior is observed in AYbCh2 compounds22,34. This was explained by Li et al.12 for Yb3+. For Nd3+, SOC leads to the total angular momentum Jtotal = 9/2 with orbital angular momentum L = 3 and total S = 3/2. The total ten states (2J + 1) are degenerate at high temperatures. The CEF further splits to ten Jtotal = 9/2 states into five pairs of Kramer’s doublets12. At low temperatures, the ground state is well separated from the excited states12. Thus, the effective spin-1/2 ground state may be formed as illustrated in Fig. 2j. At low temperatures, the Curie-Weiss expression is also used to fit the data between 2 K and 4 K. The related fitting parameters are shown in Table 1. To check χ0 for the low-temperature region, we measure the isothermal magnetization up to 14 T along the three directions, which is shown in Fig. 2d–f. Note that the magnetization along either direction increases nonlinearly with HDC. However, no hysteresis has been found with all field directions, suggesting that there is negligible ferromagnetic interaction. The low-field nonlinearity can be attributed to the Zeeman effect with Ez = gμBH resulting in the energy level change (see Fig. 2j), where g is the Landé factor, μB is Bohr magneton. The linear fitting of M(HDC) in high magnetic fields allows us to obtain the slope in three directions: \({\chi }_{{{{{{{{\rm{0}}}}}}}}}^{a}=0.024{\mu }_{{{{{{{{\rm{B}}}}}}}}}\)T\({}^{-1},{\chi }_{{{{{{{{\rm{0}}}}}}}}}^{{b}^{* }}=0.025{\mu }_{{{{{{{{\rm{B}}}}}}}}}\)T−1, and \({\chi }_{{{{{{{{\rm{0}}}}}}}}}^{c}=0.028{\mu }_{{{{{{{{\rm{B}}}}}}}}}\)T−1. These values are consistent with our LT Curie-Weiss fitting parameters.

After the subtraction of χ0, the temperature dependence of 1/(χ − χ0) presents linear behavior at low temperatures (LT), as shown in Fig. 2g–i. The LT effective moment is ~ 2μB, which is lower than the Nd3+ moment at the high-temperature region due to the effects of SOC and CEF, which is illustrated in Fig. 2j. The LT effective moment corresponds to an effective spin-1/2 state, similar to that in Nd2O346 and Nd2Zr2O747. Compared to the HT case, the θCW value is much smaller at LT in all three directions, implying much weaker AFM interaction. Interestingly, θCW(HDC∣∣a) is almost the same as θCW(HDC∣∣b*), while θCW(HDC∣∣c) is much smaller. This indicates that magnetic interaction is stronger in the ab plane than that in the c direction at low temperatures.

Magnetic interactions

Considering the XXZ model for \(R\bar{3}m\) space group33,48, we adapt the general spin Hamiltonian that includes a nearest neighbor exchange interaction and Zeeman coupling to the external field:

$$H = \mathop{\sum}\limits_{ < ij > }\left\{{J}_{\perp }\left({S}_{i}^{x}{S}_{j}^{x}+{S}_{i}^{y}{S}_{j}^{y}\right)+{J}_{z}{S}_{i}^{z}{S}_{j}^{z}+\frac{1}{2}{J}_{\Delta }\left({e}^{i{\phi }_{ij}}{S}_{i}^{-}{S}_{j}^{-}+{e}^{-i{\phi }_{ij}}{S}_{i}^{+}{S}_{j}^{+}\right)\right. \\ +\left.\frac{1}{2i}{J}_{yz}\left[{e}^{i{\phi }_{ij}}\left({S}_{i}^{z}{S}_{j}^{+}+{S}_{i}^{+}{S}_{j}^{z}\right)-{e}^{-i{\phi }_{ij}}\left({S}_{i}^{z}{S}_{j}^{-}+{S}_{i}^{-}{S}_{j}^{z}\right)\right]\right\} \\ -{\mu }_{0}{\mu }_{B}\mathop{\sum}\limits_{i}\left[{g}_{\perp }\left({H}_{x}{S}_{i}^{x}+{H}_{y}{S}_{i}^{y}\right)+{g}_{| | }{H}_{z}{S}_{i}^{z}\right],\hfill\\ {\phi }_{ij}= \left\{\begin{array}{ll}0,&{\overrightarrow{R}}_{i}-{\overrightarrow{R}}_{j}=(\pm 1,0),\hfill\\ \frac{2\pi }{3},&{\overrightarrow{R}}_{i}-{\overrightarrow{R}}_{j}=\pm \left(-\frac{1}{2},\frac{\sqrt{3}}{2}\right),\hfill\\ -\frac{2\pi }{3},&{\overrightarrow{R}}_{i}-{\overrightarrow{R}}_{j}=\pm \left(-\frac{1}{2},-\frac{\sqrt{3}}{2}\right),\end{array}\right.$$
(1)

with \({S}_{l}^{\pm }={S}_{l}^{x}\pm {S}_{l}^{y}\). Here, J⊥ = 1/2(Ja + Jb), JΔ = 1/2(Ja − Jb), Jz = Jc. From this spin Hamiltonian, we can estimate exchange interactions Ja and Jc through the following relationship:

$${\theta }_{{{{{{{{\rm{cw}}}}}}}}}^{a}=-(3/2){J}_{a}/{k}_{{{{{{{{\rm{B}}}}}}}}}$$
(2)
$${\theta }_{{{{{{{{\rm{cw}}}}}}}}}^{c}=-(3/2){J}_{c}/{k}_{{{{{{{{\rm{B}}}}}}}}}.$$
(3)

Using \({\theta }_{{{{{{{{\rm{cw}}}}}}}}}^{a}\) and \({\theta }_{{{{{{{{\rm{cw}}}}}}}}}^{c}\) in Table 1, we obtain the nearest neighbor anisotropic spin exchange parameters: in-plane component Ja/kB = 1.42 K and out-of-plane component Jc/kB = 0.44 K. The anisotropy ratio Ja/Jc is slightly higher than that in NaYbSe232 and CsYbSe234. This can be explained by large Nd and Cs ionic radii, inducing higher anisotropy.

Ground state

Since the DC magnetic susceptibility shows no sign of any magnetic transition down to 1.8 K, we further measure the AC susceptibility down to 0.04 K to investigate the magnetic properties of the ground state. Figure 3a presents the temperature dependence of the real component of the AC susceptibility \({\chi }^{{\prime} }\) at the zero DC field in three directions (HAC∥ a, HAC∥ b*, and HAC∥ c). A broad hump centered ~ 0.4 K in \({\chi }_{a}^{{\prime} }\) and \({\chi }_{{b}^{* }}^{{\prime} }\) but ~ 0.3 K in \({\chi }_{c}^{{\prime} }\) is revealed. We can use the Padé approximation to estimate the exchange J33,49

$$\begin{array}{r}{\chi }^{{\prime} }(T)\propto \frac{{N}_{{{{{{{{\rm{A}}}}}}}}}{\mu }_{0}{g}^{2}{\mu }_{{{{{{{{\rm{B}}}}}}}}}^{2}}{4{k}_{{{{{{{{\rm{B}}}}}}}}}T}\frac{1+{b}_{1}x+\cdot \cdot \cdot +{b}_{6}{x}^{7}}{1+{c}_{1}x+\cdot \cdot \cdot +{c}_{7}{x}^{7}}.\end{array}$$
(4)

where x = J/(4kBT), NA is Avogadro constant, and the coefficients bi and ci are based on a spin-1/2 triangular-lattice AFM model50. The fittings are shown in the inset of Fig. 3a with Ja/kB = 1.32 K and Jc/kB  = 0.55 K. Both Ja and Jc are close to our estimations from θCW. According to Ref. [48], the broad hump of the magnetic susceptibility is expected at T < J/kB in a quasi-2D magnet. As shown in Fig. 3b, the broad hump remains at the same temperature between 79 Hz and 991 Hz. This indicates that the increased activated energy does not affect the temperature for the broad hump, excluding scenarios like short-range AFM correlation, spin glass, or spin ice transition51.

Fig. 3: AC susceptibility of CsNdSe2 at zero DC field.
figure 3

a Temperature dependence of the real component of the AC susceptibility at zero DC field. Inset: the Padé approximation fitting for spin-1/2 triangular-lattice antiferromagnet. b Temperature dependence of the real component of the AC susceptibility under different frequencies. The offset has been set for each data for the visual guide.

Full size image

AC susceptibility and H−T phase diagram

To gain insight into magnetic interaction, we measure the AC susceptibility down to 0.04 K by applying DC magnetic field HDC∥ a, HDC∥b*, and HDC∥ c. As shown in Fig. 4a, the temperature dependence of \({\chi }^{{\prime} }\) remains a broad hump up to HDC = 0.04 T. Upon the increase of the DC field, a small peak gradually emerges above 0.11 T at HDC∥ a. This peak enhances and shifts to higher temperatures until the merge with the broad hump at T  = 0.3 K and HDC = 0.53 T. With the further increase of the applied DC field, the peak shifts to lower temperatures until vanishing. When the DC magnetic field is applied parallel to b*, the broad hump becomes sharper with the center shifts to lower temperatures. The feature also occurs when the DC magnetic field is applied to the c axis, as shown in Fig. 4c.

Fig. 4: Field-induced LROs in CsNdSe2.
figure 4

a–c Temperature dependence of the real component of the AC susceptibility under DC magnetic field from 0 T to 1.98 T at HDC∥ a, HDC∥ b*, and HDC∥ c. The offset has been set for each data for the visual guide. d–f H−T phase diagram at HDC∥ a, HDC∥ b*, and HDC∥ c.

Full size image

The characteristic temperature at each applied DC field is plotted in Fig. 4d–f. The green circles represent the broad hump at low fields and the violet squares denote temperatures at sharp peaks. The general trend is that the DC magnetic field forces AFM magnetic alignment, resulting in a long-range AFM ordering (TN) with the highest ordering temperature at 0.3 K. The dome-like H-TN diagram is typical for quantum magnetic systems, as the result of competing field-enhanced spin interaction and the quantum effects of exchange randomness32,52.

We also measure the DC field dependence of the AC susceptibility at 0.04 K to check the field-induced states. Figure 5a, b present the magnetic field dependence of the real component of the AC susceptibility at HDC∥ a and HDC∥ c, respectively. Four anomalies for HDC∥ a and three for HDC∥ c are observed as indicated by arrows in Fig. 5. The first upturn is observed at 0.05 T for HDC∥ a and 0.09 T for HDC∥ c, which may be related to the Zeeman effect that splits each state to two levels (see Fig. 2j). The in-plane shoulder-like anomalies are similar to previously reported dM/dH in AYbSe222,32,34, suggesting field-induced spin reorientation in CsNdSe2. The potential spin structures with applied magnetic fields are illustrated in Fig. 5. When the DC magnetic field is applied along the a axis, an oblique 120∘ state is induced. With the further increase of HDC > 0.5 T, \({\chi }_{a}^{{\prime} }\) reaches a plateau.

Fig. 5: Spin states under DC magnetic fields in CsNdSe2.
figure 5

a, b DC magnetic field dependence of the real component of the AC susceptibility at HDC∥ a, and HDC∥ c up to 2.5 T. The green dash lines indicate the first peak position through the field scan. c, d DC magnetic field dependence of moment.

Full size image

By calculating the magnetization through integrating \({\chi }^{{\prime} }\) with the DC magnetic field in two directions as shown in Fig. 5c–d, respectively, we note that the plateau corresponds to the magnetization of 30% Ma,sat and 34% Mc,sat, where Ma,sat and Mc,sat are saturation values for the a and c directions. This suggests the up-up-down magnetic configuration as observed in other quantum magnets22,33. Such a magnetic configuration is also predicted in the quantum phase diagram of the triangular-lattice XXZ model in the magnetic field for J⊥/Jz < ~ 1.453. However, our low-temperature magnetization suggests Ja/Jc > 3 for CsNdSe2, which is beyond the phase diagram presented in ref. 53. With further increasing \({H}_{{{{{{{{\rm{DC}}}}}}}}},{\chi }_{a}^{{\prime} }\) shows another plateau around 1 T, which corresponds to 1/2Ma,sat (see the corresponding vertical dashed line). Such a 1/2 plateau state was theoretically and experimentally studied in triangular lattice systems, which occurs when the interaction with the next nearest neighbors is not negligible31,54,55. Because of this, three aligned spins in one sublattice are anti-aligned with the spin in the next sublattice, forming the so-called up-up-up-down (uuud) configuration. Note that the 1/2 plateau is absent in \({\chi }_{c}^{{\prime} }\), as the spin interaction with the next nearest neighbors is negligible along the c direction.

First-principles calculations

To find out possible magnetic states, we construct supercells that host several long-range ordered magnetic configurations and evaluate their total energies at zero magnetic fields. The magnetic configurations are illustrated in Fig. 6, including stripe (a), up-up-up-down (b), 120∘ noncollinear (c), two in-equivalent antiferromagnetic spins in a 2 × 2 × 1 supercell (d), 2 \(\times \sqrt{3} \times\) 1 supercell (e), an up-up-down (f), and ferromagnetic (FM) spin configuration. With spin–orbit coupling, all spins favor in-plane orientations, yielding in-plane magnetic anisotropy for all considered spin configurations. The energies per formula unit (f.u.) are shown in the histogram [see Fig. 6g], referenced to the total energy of the stripe spin configuration (case (a)), are shown in Fig. 6g, denoted as b-a, c-a, d-a, e-a, f-a, and FM-a. Here, FM represents ferromagnetic spin configuration (not shown). The stripy configuration (case(a)) has the lowest total energy among the seven considered spin configurations, which is further set as a reference. The calculated spin moment on Nd is 3μB and the orbital moment is −1.5μB, yielding a net moment of 1.5μB on each Nd. This is close to the measured μeff (~2μB) at low temperatures. The two antiferromagnetic spin configurations (d–e), which give zero net magnetization, possess competing total energies (less than 5 meV f.u.−1) to the stripe configuration (see Fig. 6). The discovery of multiple energy-competing spin configurations indicates strong spin fluctuation and the disordered spin-liquid state could be formed. The total energy of the up-up-down spin configuration is modest (36 meV f.u.−1), which can be achieved under an applied magnetic field, yielding a 1/3 magnetization that is consistent with our experimental observation. Surprisingly, the up-up-up-down (case (b)) spin configuration possesses a lower total energy than the up-up-down case, which needs to be further investigated. For the ferromagnetic state and the 120∘ noncollinear spin configuration, greater total energies (>46 meV f.u.−1) are observed, indicating a strong antiferromagnetic coupling that could go beyond the next nearest neighbor56. In fact, the spin state in CsNdSe2 is reflected from in-plane shoulder-like anomalies under a DC magnetic field (see Fig. 5). The calculated total energy of 120∘ noncollinear spin configurations in CsNdSe2 may indicate that this state could be achieved.

Fig. 6: Spin configurations with relative energies.
figure 6

a–f Multiple spin configurations investigated for CsNdSe2. Red arrows indicate the spin directions, and the thick green boundaries denote the unit cell boundary to simulate the corresponding spin configurations. g Relative energies (per formula unit) for different spin configurations referenced to the total energy of the strip spin configuration, including the ferromagnetic (FM) case.

Full size image

The in-plane H−T phase diagram of CsNdSe2 (Fig. 4d–f) is close to that in CsYbSe234,38. One unique feature of CsNdSe2 is that a much weaker in-plane field (H < 0.11 T) could induce long-range ordering in CsNdSe2. On the other hand, the out-of-plane field could also induce clear anomalies in DC field dependence of \({\chi }^{{\prime} }\). Compared to Ce or Yb compounds, this feature is closer to transition metal triangular-lattice antiferromagnet Ba3CoSb2O957. Based on our AC and DC magnetization, CsNdSe2 is an effective spin-1/2 quasi-2D material with anisotropic exchange. Compared to AYbCh2, CsNdSe2 only needs a 2–3 T magnetic field to reach excited magnetic states. Our work extends the quantum magnetism investigation to quasi-2D materials with Nd triangular lattice and sheds light to further investigate the magnetism with effective spin-1/2 Nd triangular-lattice antiferromagnets.

Conclusion

In conclusion, we successfully synthesize CsNdSe2 single crystals with the triangular lattice and measure the DC and AC susceptibility along three crystal orientations, H∥ a, H∥ b*, and H∥ c. Through the DC susceptibility, an effective spin-1/2 of Nd state with AFM interactions has been found at the low-temperature region. There is no evidence for any long-range magnetic ordering down to 0.04 K. A broad hump appears in the AC susceptibility below 0.5 K. Anisotropic in-plane interaction Ja/kB = 1.42 K and out-of-plane interaction Jc/kB = 0.44 K have been found by fitting experimental data to the XXZ model. The low-temperature AC susceptibility under DC magnetic fields reveals the field-induced long-range antiferromagnetic ordering in CsNdSe2. These results suggest the anisotropic magnetism in quasi-2D CsNdSe2, which may be close to the boundary of the QSL state and ordered state.

Methods

Materials and structural characterization

Millimeter-sized (inset of Fig. 1c) CsNdSe2 single crystals are synthesized by the CsCl salt flux method20. X-ray diffraction is performed by Rigaku MiniFlex 600 diffractometer with Cu Kα1 radiation (λ = 1.5406 Å). The crystal structure of CsNdSe2 is shown in Fig. 1a, forming a \(R\bar{3}m\) symmetry. As demonstrated in Fig. 1b, the shortest Nd-Nd distance is 4.3468(8) Å within the ab plane. The interlayer distance of Nd triangular layers is 8.315(2) Å. The X-ray diffraction pattern of a flat surface is shown in Fig. 1c. The sharp (00l) peaks suggest the good quality of our single crystals (l = integer).

Magnetic susceptibility measurements

The DC magnetization is measured using a Quantum Design (QD) DynaCool with Vibrating Sample Magnetometer (VSM) option up to 14 T and magnetic property measurement system (MPMS) up to 7 T. AC susceptibility is measured using an apparatus at SCM1 of National High Magnetic Field Laboratory (NHMFL) down to 0.04 K. Data shown in this manuscript are obtained with HAC ~ 2 Oe. An empirical background of the coil is removed for the integration of the AC susceptibility.

First-principles calculation methods

Density functional theory (DFT) calculations were performed using projector augmented wave (PAW)58 potentials as implemented in the Vienna Ab-initio Simulation Package59,60. A 500-eV kinetic energy cutoff has been chosen for plane wave expansion. The PAW pseudopotentials correspond to the valence-electron configuration 6s15p65s2 for Cs, 4f 45p65s26s2 for Nd, and 4s24p4 for Se. The exchange correlation is treated within the generalized gradient approximation, parameterized by Perdew, Burke, and Ernzerhof 61. The Coulomb correlations within the 4f shells of Nd were described using the spherically averaged GGA + U method62, with Ueff = 6 eV. Spin polarization was included in all calculations and spin–orbit coupling was included, which allows for the assessment of the magnetic anisotropy. The lattice constants of the unit cell of CsNdSe2 were fixed to the experimental values, with a = 4.3468 Å and c = 24.9450 Å. The Brillouin Zone (BZ) integration for the primitive cell is performed using a Γ-centered 6 × 6 × 1 k-point mesh. The internal atomic positions were relaxed until the maximum force on each atom was less than 10 meV Å−1. The total energies were converged to 10−6 eV.